用焦利氏称测量液体表面张力系数

实验二用焦利氏秤测定液体的表面张力实验二：用焦利氏秤测定液体的表面张力一、实验目的1.掌握用焦利氏秤测量液体表面张力的原理和方法。

2.通过实验观察和理解液体表面张力的现象和规律。

二、实验原理液体表面张力是指液体表面分子之间的相互吸引力，是液体内部分子之间的凝聚力作用于液体表面的结果。

表面张力的大小反映了液体分子间的相互吸引程度。

焦利氏秤是测量液体表面张力的一种常用仪器，其原理是利用弹簧秤测量微小形变时的弹力，通过已知弹簧常数和形变量计算出表面张力。

三、实验步骤1.准备实验器材：焦利氏秤、三角支架、尺子、纸巾、待测液体（如水、乙醇等）。

2.将焦利氏秤挂在三角支架上，调整焦利氏秤的零点。

3.用纸巾擦拭焦利氏秤的金属片，将其插入待测液体中，待稳定后读取弹簧秤的示数（注意读取时要消除振动）。

4.用尺子测量金属片在液体中的深度h。

5.重复步骤3和4三次，取平均值。

6.根据公式计算表面张力。

四、实验结果与分析1.实验结果：在实验过程中，我们得到了待测液体（如水）的表面张力数值。

根据实验数据，可以发现不同液体的表面张力存在差异。

例如，水的表面张力较大，而乙醇的表面张力较小。

这表明不同液体的分子间相互吸引力存在差异。

2.结果分析：表面张力的大小与液体的性质、温度等因素有关。

例如，水分子间的氢键较强，因此水的表面张力较大。

通过实验，我们可以深入理解液体表面张力的性质和规律，为后续的理论学习和应用打下基础。

五、实验结论本实验通过使用焦利氏秤测定液体的表面张力，验证了液体表面张力的存在和测量方法。

实验结果表明，不同液体的表面张力存在差异，反映了液体分子间的相互吸引力。

通过实验，我们深入理解了液体表面张力的性质和规律，为后续的理论学习和应用提供了有益的实践经验。

同时，实验也锻炼了我们的实验技能和观察能力，提高了我们的科学素养和实践能力。

六、思考与探讨1.在实验过程中，如何保证测量结果的准确性？例如，如何消除振动对测量结果的影响？2.除了使用焦利氏秤，还有哪些方法可以测定液体的表面张力？其优缺点是什么？3.在实际应用中，液体表面张力有哪些现象和规律？例如，在自然界中存在的露珠、雨滴等现象与液体表面张力有何关系？4.能否通过实验探究温度对液体表面张力的影响？如果可以，应如何设计实验方案？5.在工业生产和日常生活中，液体表面张力有哪些应用？例如，在制作化妆品、涂料等领域中与液体表面张力相关的现象和规律有哪些？。

. .实验五 用焦利氏秤测定液体的表面张力系数【实验目的】1．学习使用焦利秤，测量纯水和其它液体的表面张力系数；2．观察拉脱法测液体表面张力的物理过程和物理现象,并用物理学基本概念和定律进行分析和研究,加深对物理规律的认识。

【实验仪器】焦利秤，金属框及钢丝，砝码，游标卡尺，温度计，蒸发皿，酒精灯，蒸馏水等。

【实验原理】液体表面层内的分子，由于受到不对称分子力的作用，力图进入液体内部，使液体自由表面犹如一张拉紧的弹性薄膜，都有收缩的趋势，因此液体表面内存在张力，称为表面张力。

假设在液面上任画一条长为l 的线段，则张力f 就表现为线段两侧液膜之间相互作用的拉力，力的方向与所画的线段垂直，其大小与线段长l 成正比，即：l f ⋅=α （11-1）式(11-1)中,α称为液体的表面张力系数，表示单位长度直线两侧液面之间的拉力，其单位在SI 制中为1N m -⋅，在CGS 制中为1dyn cm -⋅。

表面张力系数与温度有关，温度升高，α减小。

实验证明α与温度的关系近似地为线性关系，即βθααθ-=0 （11-2）式(11-2)中,0α和θα分别为0℃和θ℃时的表面张力系数，β为表面张力系数的温度系数。

如果在金属框中间拉一条细金属丝ab ，如图11-1所示，将框和细丝浸入待测液体中，然后再慢慢拉出液面，则金属细丝带出—层液膜。

设液膜将被拉断时向上的拉力为F ，膜宽(即金属丝的长度)为l ，膜高为h ，膜厚(即金属丝直径)为d 。

被拉起的液膜有两个表面，再考虑到这部分液体的重量之后，有g ldh l W F ρα++=2 （11-3）式(11-3)中,W 是金属框和金属丝所受的重力和浮力差，ρ为液体密度，g 为重力加速度。

不难看出，lα2为表面张力，g ldh ρ为液膜的重量。

由式(11-3)可得 图11-1()lg ldh W F 2ρα--= （11-4） 【仪器介绍】焦利秤如图11-2所示，是弹簧秤的一种。

焦利氏秤测量液体表面张力系数实验改进
吴魏霞;史萍;张孟佳;李福芸;张翱;孙兆永
【期刊名称】《大学物理实验》
【年(卷),期】2022(35)6
【摘要】对我校大学物理实验项目“焦利氏秤测量液体表面张力系数”进行改进,其中将容易变形的门形丝改为不易变形且形状规则的长方形卡片或空心圆柱桶;将焦利氏秤上的长度刻度改为直接可读的微小力刻度,并采用动态摄影技术,通过慢放精准定位读出力的大小。

此改进方法不仅降低了操作难度,简化了实验过程,最重要的是减小了读数和测量结果误差。

【总页数】4页(P63-66)
【作者】吴魏霞;史萍;张孟佳;李福芸;张翱;孙兆永
【作者单位】北京印刷学院基础教育学院;北京印刷学院印刷与包装工程学院【正文语种】中文
【中图分类】O441.5
【相关文献】
1.用焦利秤测量液体表面张力系数实验中弹簧的零点测量分析
2.用焦利秤测液体表面张力系数的实验探讨
3.用焦利秤测液体表面张力系数实验测量公式的研究
4.用焦利秤测量液体表面张力系数
5.焦利秤测定液体表面张力系数实验中测量公式的修定
因版权原因，仅展示原文概要，查看原文内容请购买。

实验七液体表面张力系数的测定【实验目的】1. 了解焦利氏秤测微小力的原理、结构和方法；2．用拉脱法测量室温下水的表面张力系数；3．掌握用逐差法处理数据。

【实验仪器】焦利氏秤，Π型金属丝框，法码，游标卡尺，玻璃杯，酒精，金属镊子，温度计及蒸馏水。

【实验原理】许多涉及液体的物理现象都与液体的表面性质有关，液体表面的主要性质就是表面张力。

例如液体与固体接触时的浸润与不浸润现象、毛细现象、液体泡沫的形成等，工业生产中使用的浮选技术，动植物体内液体的运动，土壤中水的运动等都是液体表面张力的表现。

液体表面层中分子的受力情况与液体的内部不同。

在液体内部，任一个分子受其他分子引力、斥力在各方向上均相等，则所受的合力为0；而在表面层，由于液体上方气体分子密度较小，液体表面层分子间的距离大于正常距离，这时引力大于斥力。

这种状态下，整个液面如同绷紧的弹性薄膜，这时产生的沿液面并使之收缩的力称为液体表面张力，用表面张力系数来描述。

液体的表面张力系数与液体的性质、杂质情况、温度等有关。

当液面与其蒸汽相接触时，表面张力仅与液体性质及温度有关。

一般来讲，密度小，易挥发液体小；温度愈高，愈小。

如果在液体表面想象一条直线段，那么,表面张力就表现为线段两边的的液面会以一定的拉力相互作用,此拉力方向垂直于线段,大小与此线段的长度成正比,即（7-1）其中，为液体表面张力系数,它表示单位长线段两侧液体的相互作用，国际制中单位为牛顿/米，记为N?M-1。

拉脱法测定液体表面张力系数是基于液体与固体接触时的表面现象提出的。

由分子运动论可知，当液体分子和与其接触的固体分子之间的吸引力大于液体分子的内聚力时，就会产生液体浸润固体的现象。

现将一洁净Π型金属丝浸入水中，由于水能浸润金属，当拉起金属丝时，在Π型金属丝框内就形成双面水膜。

设Π型金属丝的直径为，内宽为，重量，受浮力，弹簧向上的拉力，液体的表面张力为。

则Π型丝的受力平衡条件为（7-2）设接触角为，由于水膜宽度为（L+d）,则表面张力为（7-3）缓慢拉起Π型丝至水面时，接触角趋近于零，上式中。

用焦利秤测液体表面张力系数实验测量公式的研究
邵建新
【期刊名称】《物理与工程》
【年(卷),期】2005(15)6
【摘要】指出了某些文献中所给出的用焦利秤测液体表面张力系数实验测量公式存在的问题,并给出了正确的测量公式.
【总页数】4页(P34-37)
【作者】邵建新
【作者单位】石河子大学师范学院物理系,新疆,石河子,832000
【正文语种】中文
【中图分类】O4;G42
【相关文献】
1.焦利氏称测液体表面张力系数的探讨 [J], 段坤杰;衡丽君
2.用焦利秤测量液体表面张力系数实验中弹簧的零点测量分析 [J], 何仲
3.用焦利秤测液体表面张力系数的实验探讨 [J], 黄曙江
4.用焦利秤测量液体表面张力系数 [J], 王雅红;潘政;赵鹏程;张丁立;李维;乔月;林芃杉;Pascaline UMUHIRE;Tandong Christerbel BIN
5.焦利秤测定液体表面张力系数实验中测量公式的修定 [J], 岳应利;陈荐俊
因版权原因，仅展示原文概要，查看原文内容请购买。

实验二用焦利氏秤测定液体的表面张力【实验目的】1．学习使用焦利氏秤测定水的表面张力系数2．研究溶质对液体表面张力系数的影响【实验仪器】焦利氏秤（含配件）一台、物理天平一台、镊子、酒精灯、火柴、烧杯、游标卡尺【仪器描述】（见图2-1）焦利氏秤实际上就是弹簧秤。

但一般的弹簧秤，弹簧的上端固定不动，在弹簧下端挂重物时，弹簧则伸长，物体重量可由指针所指示的标尺直接标出。

而焦利氏秤上的弹簧是挂在可以上下移动的有刻度的管子（6）上的，管外面套有外管（4），外管（4）上有游标（5），旋转旋钮（3）即可使管（6）上下移动。

在外管上，有夹子，夹子中央有带标线的短玻璃管（10），弹簧下端挂一细金属杆（9），金属杆中部有一长形小镜，镜中央有一刻痕，金属杆从玻璃管中通过，在金属杆的下端可挂砝码托盘（12）与钢丝码（14）。

当上下移动管（6），使细金属杆上镜子的标线和玻璃管（10）上的标线在镜中的像三者重合（以后简称三线重合）时，相当于弹簧秤对准零点，零点的读数可由管（6）的刻度和外管（4）上的游标（5）读出。

如果我们在砝码托盘上加X克砝码，弹簧（8）伸长了某一长度，细金属杆上镜中的标线即向下移动，此时三线不再重合。

转动旋钮（3）使管（6）向上移动，因而细金属杆也随之向上移动。

当三线又重合时，在管（6）及管（4）的游标上可读出第二个读数，该读数与第一个读数这差就是弹簧在增加X克重量时所伸长的长度。

图2-1 焦利氏秤实验装置练习一测定弹簧的弹性系数【实验原理】弹簧的弹性系数就是弹性限度内弹簧所受的力F（牛顿）和弹簧伸长的长度S（米）之比，即伸长单位长度弹簧所受的力，如以K表示，则：【实验步骤】1．安装仪器如图（1），但此时不要放上烧杯及钢丝码而是在小金属杆（9）下只挂小砝码盘（12），调节三脚架上的螺旋，使管（4）竖直（即金属杆（9）恰在玻璃管（10）的正中），转动旋钮（3），使三线重合，记下此时游标的读数。

2．置1克砝码于盘中，转动旋钮（3），使仍保持三线重合，记下游标读数，此读数与步骤1所得读数之差即为弹簧下加1克重量时弹簧的伸长量。

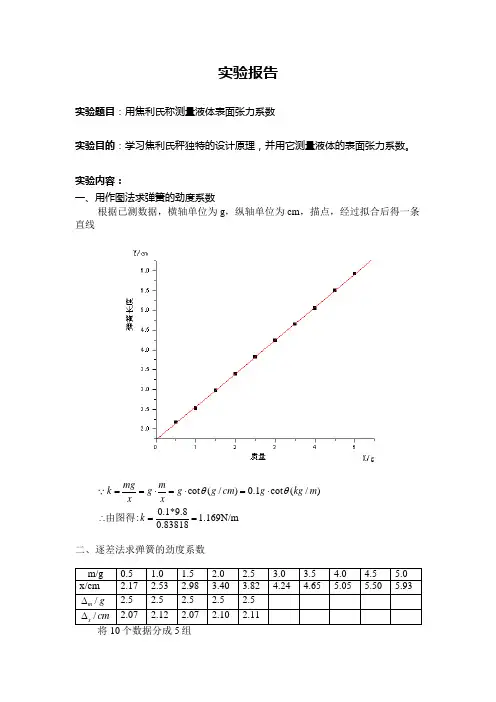
表⾯张⼒实验报告（附数据及处理）实验报告实验题⽬：⽤焦利⽒称测量液体表⾯张⼒系数实验⽬的：学习焦利⽒秤独特的设计原理，并⽤它测量液体的表⾯张⼒系数。

实验内容：⼀、⽤作图法求弹簧的劲度系数根据已测数据，横轴单位为g ，纵轴单位为cm ，描点，经过拟合后得⼀条直线cot (/)0.1cot (/)0.1*9.8 1.169N/m 0.83818mg m k g g g cm g kg m x x k θθ==?=?=?∴==Q 由图得:⼆、逐差法求弹簧的劲度系数m/g 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.04.55.0 x/cm 2.17 2.53 2.98 3.40 3.82 4.24 4.65 5.055.50 5.93 /m g ? 2.5 2.5 2.5 2.5 2.5 /x cm ? 2.07 2.12 2.07 2.10 2.11由上表数据得：550.6822222()()3.500, 2.094cm,()=0.0103cm() 1.140.005251cm ()0.005773cm ()()()0.005251+0.0057730.005()0.00163j j j j A x B A B m B m m m k x x x m g x x u x t u x C u x u x u x g u m C σ++-?==-??=?=??===?===?=?+=?===∑∑()()() ()()2222222222267g 2.5 1.1939g/cm=1.1700N/m 2.094()()()0.005251+0.0057730.0016672.094 2.50.000014330.0037860.004520g/cm=0.004430N/mk=(1.1700.004)N/mA B B m g k cmx U k u x u x u m k x m U k kU k ?===+=+ ?=+===∴± 三、⾃来⽔的表⾯张⼒系数1）⽤⾦属圈测定⾦属圈直径：41 2.900 2.900 2.950 2.850 2.9000.0290044ii d cm cm cm cm d cm m =+++====∑ 周长：3.14159*0.029000.09111l d m π===膜破时⾦属圈上升的距离：515(2.44 1.50)(2.44 1.50)(2.52 1.50)(2.54 1.50)(2.52 1.50)50.00992i i x x x cm cm cm cm cm cm cm cm cm cm m=?=-+-+-+-+-==∑（-）表⾯张⼒：'22F mg k x F l d δδπ-?===→⽔膜质量可忽略1.1690.009920.06364/20.091112k x N m dδπ??∴===? 每次测量得的表⾯张⼒系数：11223344 1.169/(2.44 1.50)0.06030/20.091112 1.169/(2.44 1.50)0.06030/20.091112 1.169/(2.52 1.50)0.06544/20.091112 1.169/(2.54 1.502k x N m cm cm N m m dk x N m cm cm N m m dk x N m cm cm N m m dk x N m cm dδπδπδπδπ??-===-===-===-==55)0.06672/20.091111.169/(2.52 1.50)0.06544/20.091112cm N m m k x N m cm cm N m m dδπ=-===? 表⾯张⼒系数的标准差：()0.00138/N mσδ===计算表⾯张⼒系数的A 类不确定度：0.68() 1.140.0007036/A t u N m δ?==(0.063640.00070)/N m δ∴=±2）⽤⾦属丝测定⾦属丝的长度：41 3.450 3.400 3.450 3.400 3.4250.0342544i i S cm cm cm cm S cm m =+++====∑ 膜破时⾦属丝上升的距离： 515(1.49 1.09)(1.52 1.09)(1.53 1.09)(1.50 1.09)(1.51 1.09)50.0042i i x x x cm cm cm cm cm cm cm cm cm cm m=?=-+-+-+-+-==∑（-）表⾯张⼒：'22F mg k x F l S δδ-?===→⽔膜质量可忽略1.1690.00420.07168/20.034252k x N m Sδ??===? 每次测量得的表⾯张⼒系数：11223344 1.169/(1.49 1.09)0.06826/20.034252 1.169/(1.52 1.09)0.07338/20.034252 1.169/(1.53 1.09)0.07509/20.034252 1.169/(1.50 1.09)22k x N m cm cm N m m Sk x N m cm cm N m m Sk x N m cm cm N m m Sk x N m cm cm Sδδδδ??-===-===-===-==550.06997/0.034251.169/(1.51 1.09)0.07168/20.034252N m m k x N m cm cm N m m S δ=-===? 表⾯张⼒系数的标准差：()0.00121/N mσδ===计算表⾯张⼒系数的A 类不确定度：0.68() 1.140.0006169/A t u N m δ?== (0.071680.00062)/N m δ∴=±三、洗洁精溶液的表⾯张⼒系数1）⽤⾦属圈测定⾦属圈直径：41 2.900 2.900 2.950 2.850 2.9000.0290044ii d cm cm cm cm d cm m =+++====∑ 周长：3.14159*0.029000.09111l d m π===膜破时⾦属圈上升的距离：15(1.89 1.50)(1.90 1.50)(1.96 1.50)(1.95 1.50)(1.92 1.50)50.00424i x cm cm cm cm cm cm cm cm cm cm m=?=-+-+-+-+-== 表⾯张⼒：'22F mg k x F l d δδπ-?===→⽔膜质量可忽略表⾯张⼒系数：1.1690.004240.02720/20.091112k x N m dδπ??∴===? 每次测量得的表⾯张⼒系数：11223344 1.169/(1.89 1.50)0.02502/20.091112 1.169/(1.90 1.50)0.02566/20.091112 1.169/(1.96 1.50)0.02951/20.091112 1.169/(1.95 1.502k x N m cm cm N m m dk x N m cm cm N m m dk x N m cm cm N m m dk x N m cm dδπδπδπδπ??-===-===-===-==55)0.02887/20.091111.169/(1.92 1.50)0.02694/20.091112cm N m m k x N m cm cm N m m dδπ=-===? 表⾯张⼒系数的标准差：()0.000875/N mσδ===计算表⾯张⼒系数的A 类不确定度：0.68() 1.140.0004461/A t u N m δ?==(0.027200.00045)/N m δ∴=±2）⽤⾦属丝测定⾦属丝的长度：41 3.450 3.400 3.450 3.400 3.4250.0342544i i S cm cm cm cm S cm m =+++====∑ 膜破时⾦属圈上升的距离：15(1.22 1.00)(1.20 1.00)(1.23 1.00)(1.21 1.00)(1.19 1.00)50.0021i x cm cm cm cm cm cm cm cm cm cm m=?=-+-+-+-+-== 表⾯张⼒：'22F mg k x F l S δδ-?===→⽔膜质量可忽略表⾯张⼒系数：1.1690.00210.03584/20.034252k x N m Sδ??===? 每次测量得的表⾯张⼒系数：11223344 1.169/(1.22 1.00)0.03754/20.034252 1.169/(1.20 1.00)0.03413/20.034252 1.169/(1.23 1.00)0.03925/20.034252 1.169/(1.21 1.00)22k x N m cm cm N m m Sk x N m cm cm N m m Sk x N m cm cm N m m Sk x N m cm cm Sδδδδ??-===-===-===-==550.03584/0.034251.169/(1.19 1.00)0.03242/20.034252N m m k x N m cm cm N m m S δ=-===? 表⾯张⼒系数的标准差：()0.00121/N mσδ===计算表⾯张⼒系数的A 类不确定度：0.68() 1.140.0006169/A t u N m δ?== (0.035840.00062)/N m δ∴=±四、思考题焦利⽒秤测定液体的表⾯张⼒有什么优点？⽤焦利⽒秤能够迅速准确测定出液膜即将破裂时的F 值，因⽽可以⽅便地算出表⾯张⼒值。

实 验五 用焦利氏秤测定液体的表面张力系数【实验目的】1．学习使用焦利秤，测量纯水和其它液体的表面张力系数；2．观察拉脱法测液体表面张力的物理过程和物理现象 , 并用物理学基本概念和定律进行分析和研究 , 加深对物理规律的认识。

【实验仪器】焦利秤，金属框及钢丝，砝码，游标卡尺，温度计，蒸发皿，酒精灯，蒸馏水等。

【实验原理】液体表面层内的分子，由于受到不对称分子力的作用，力图进入液体内部，使液体自由表面犹如一张拉紧的弹性薄膜，都有收缩的趋势，因此液体表面内存在张力，称为表面张力。

假设在液面上任画一条长为 l 的线段，则张力 f 就表现为线段两侧液膜之间相互作用的拉力，力的方向与所画的线段垂直，其大小与线段长 l 成正比，即：f l（11-1 ）式(11-1) 中,称为液体的表面张力系数，表示单位长度直线两侧液面之间的拉力，其单位在SI 制中为 N m 1 ，在CGS 制中为 dyn cm 1 。

表面张力系数与温度有关，温度升高， 减小。

实验证明 与温度的关系近似地为线性关系，即（ 11-2 ）式 (11-2) 中 , 0和分别为 0℃和℃时的表面张力系数，为表面张力系数的温度系数。

如果在金属框中间拉一条细金属丝ab ，如图 11-1所示，将框和细丝浸入待测液体中，然后再慢慢拉出液面，则金属细丝带出—层液膜。

设液膜将被拉断时向上的拉力为 F ，膜宽 ( 即金属丝的长度) 为 l ，膜高为 h ，膜厚 ( 即金属丝直径 ) 为 d 。

被拉起的液膜有两个表面，再考虑到这部分液体的重量之后，有F W 2 l ldh g （11-3）式(11-3) 中, W 是金属框和金属丝所受的重力和浮力差， 为液体密度 ， g 为重力加 速度 。

不难 看 出， 2 l为表 面张力， ldhg 为 液膜的重 量 。

由式 (11-3) 可得图 11-1FWldh g（11-4）2l【仪器介绍】焦利秤如图 11-2 所示，是弹簧秤的一种。

液体表面张力系数的测定报告液体表面张力系数的测定实验报告模板【实验目的】1．了解水的表面性质，用拉脱法测定室温下水的表面张力系数。

2．学会使用焦利氏秤测量微小力的原理和方法。

【实验仪器】焦利秤，砝码，烧杯，温度计，镊子，水，游标卡尺等。

【实验原理】液体表面张力是液体表面的重要特性，存在于液体极薄的表面层内，是液体表面层内分子力作用的结果。

将一块表面洁净的矩形金属薄片竖直地浸入液体中，然后轻轻提起，则其附近的液面在外界拉力下将形成一张水膜。

各力平衡的条件为： F =mg +f (1)式中，F 是所施外力，mg 为薄片和它所附的液体的总重力，f 为表面张力。

由于表面张力与接触面的周长成正比，故有f =2α(l +d ) (2) 式中，比例系数α称为表面张力系数，其值等于作用在液体表面单位长度的力，将(4-20)代入(4-19)式中，可得：α=F -m g(3)2(l +d )式中，l 为的长度，d 为金属丝得直径。

由于l >>d ，所以上式可简化为：α=F -mg(4) 2l当在弹簧下端的砝码盘内加入砝码时，弹簧受力而伸长。

由胡克定律知，在弹性限度内对弹簧所施外力F 与弹簧伸长量∆x ，就可算出作用于弹簧上的外力。

当把金属片挂在焦利秤的弹簧秤下端时，弹簧所受拉力为mg 。

当把金属片浸入水中再缓缓拉起时，由于表面张力的作用，一部分液体被金属片带起形成液体膜，当所施加外力大于f 时，被带起的液膜破裂，金属片脱出液面。

再液体膜破裂的瞬间弹簧所受为F =mg +f (略去水膜自重) 。

此时弹簧所受的表面张力为f ＝F －mg 。

这一很小的作用力使弹簧发生形变∆x '，则f =k ∆x '。

将这两式代入(4)式中，有k ∆x 'α=(5)2l由以上讨论知，要测量表面张力系数α，只要测出金属片的长度l ，弹簧的倔强系数k 以及以及液膜破裂的瞬间由于表面张力引起的弹簧伸长量∆x '即可。

焦利氏称法测液体的表面张力PB10011064 赵康菲一．实验题目：焦利氏称法测液体的表面张力二．实验目的：了解表面张力的意义，学习焦利氏称独特的设计原理，并用它测量液体的表面张力系数。

三．实验仪器：焦利氏称，自来水，洗洁精溶液，砝码，金属丝，金属圈，钢板尺四．实验原理：（详见预习报告）五．实验内容：1．确定焦利称上锥形弹簧的劲度系数。

（1）把锥形弹簧，带小镜子的挂钩和小砝码盘依次安装到秤框上的金属杆上，调节支架底座的底脚螺丝，使秤框竖直，小镜子正好位于玻璃管中间，挂钩上下运动时不致于管摩擦。

（2）逐次在砝码盘中放入砝码，调节升降钮，做到三线对齐，记录升降杆的位置读数。

2.测量自来水的表面张力系数。

（1）用钢板尺测量金属圈直径和金属丝两脚之间的距离。

金属圈：金属丝：（3）分别把盛有自来水和肥皂水的烧杯放在焦利氏秤平台上，调节平台的微调螺丝和升降钮，使金属圈侵入水面以下。

（4）缓慢地旋转平台微调旋转平台微调螺丝和升降钮，注意烧下降和金属杆上升时，始终保持三线对齐，当液膜刚要破裂时，记下金属杆的读数，测量5次。

（5）用金属丝代替金属圈，重新确定弹簧的起始位置，重复上述测量过程。

得到的数据见下表：1.用逐差法和作图法计算出弹簧的劲度系数。

逐差法：∆x=15∆x i5i=1=154.59−2.13+5.01−2.64+ 5.54−3.11+6.03−3.60+ 6.51−4.04=2.43cmU A∆x=(∆x i−∆x)2 5i=1=2.46−2.432+ 2.37−2.432+ 2.43−2.432+ 2.43−2.432+(2.47−2.43)220=0.017cmk=∆m∗g∆x=2.5∗10−3∗9.8−21.008N/mU∆x=(t p∗U A∆x)2+(k p ∆B)2=(3.25∗0.017)2+(3∗0.01)2=0.06cm∆x= 2.43±0.06cm (P=0.997)U m=k p ∆B=3∗0.05=0.05gU k k =U∆x∆x2+U mm2U k=k U∆x∆x2+U mm2=1.008∗(0.062.43)2+(0.052.5)2=0.03N/m k= 1.008±0.03N/m (P=0.997)作图法：k=0.971N/m 2.根据测量结果处理金属圈直径d和金属丝长度l金属丝：l=l i3i=1n=4.14+4.15+4.153=4.15cm U A l=l−l23i=13∗2=0.004cmU l=t p∗U A l 2+(k p∆B)2=9.93∗0.0042+3∗0.12=0.11cm l= 4.15±0.11cm (P=0.997)金属圈：d=d i3i=1n=2.90+2.92+2.933=2.92cm U A d=(d−d)23i=13∗2=0.009cmU d=t p∗U A l 2+(k p∆B)2=9.93∗0.0092+3∗0.12=0.13cm d= 2.92±0.13cm (P=0.997)3.计算表面张力系数和不确定度（1）金属丝测量水的表面张力：弹簧拉伸长度h：h=h i 5i=1=2.16−1.71+ 2.13−1.71+ 2.17−1.71+ 2.14−1.71+ 2.13−1.71=0.44cmσ=h i−h2 5i=1n−1=0.45−0.442+0.42−0.442+0.46−0.442+0.43−0.442+0.42−0,442 =0.019cmU A h=σn=0.01950.008cmU h=t p∗U A h 2+(k p∆BC)2= 4.60∗0.0082+3∗0.0132=0.04cm h=0.44±0.04cmF`=F−mg2=kh2=σlσ=hk2l=0.44∗1.012∗4.15=0.054N/m(Uσ)2=(U k)2+(U h)2+(U l)2Uσ=σU k2+U h2+U l2=0.054(0.03)2+(0.04)2+(0.11)2=0.005N/m σ=0.054±0.005N/m (P=0.997)（2）金属丝测洗洁精溶液的表面张力弹簧拉伸长度h：h=h i 5i=1n=1.98−1.72+ 1.97−1.72+ 1.95−1.72+ 1.97−1.72+ 1.93−1.725=0.24cmσ=h i−h2 5i=1n−1=0.26−0.242+0.25−0.242+0.23−0.242+0.25−0.242+0.21−0.242 =0.020cmU A h=n =50.009cmU h=t p∗U A h 2+(k p∆B)2= 4.60∗0.0092+3∗0.012=0.04cm h=0.24±0.04cmF`=F−mg=kh=σlσ=hk=0.24∗1.01=0.029N/m(Uσ)2=(U k)2+(U h)2+(U l)2Uσ=σU k2+U h2+U l2=0.029(0.03)2+(0.04)2+(0.11)2=0.005N/m σ=0.029±0.005N/m (P=0.997)（3）金属圈测水的表面张力：弹簧拉伸长度h：h=h i 5i=1n=2.94−2.13+ 2.92−2.13+ 2.95−2.13+ 2.92−2.13+ 2.93−2.135=0.80cmσ=h i−h2 5i=1=0.81−0.802+0.79−0.802+0.82−0.802+0.79−0.802+0.80−0.8024=0.013cmU A h=σn=0.01350.006cmU h=t p∗U A h 2+(k p∆BC)2= 4.60∗0.0062+3∗0.0132=0.03cm h=0.80±0.03cmF`=F−mg=kh=σπdσ=hk2πd=0.80∗1.012∗π∗2.92=0.044N/m(Uσ)2=(U k)2+(U h)2+(U d)2Uσ=σU kk2+U hh2+U dd2=0.044(0.031.01)2+(0.030.80)2+(0.132.92)2=0.003N/m σ=0.044±0.003N/m (P=0.997)（4）金属圈测洗洁精溶液的表面张力h=h i 5i=1n=2.44−2.15+ 2.47−2.15+ 2.43−2.15+ 2.43−2.15+ 2.46−2.155=0.30cmσ=h i−h2 5i=1n−1=0.29−0.302+0.32−0.302+0.28−0.302+0.28−0.302+0.31−0.302 =0.019cmU A h=n =50.008cmU h=t p∗U A h 2+(k p∆B)2= 4.60∗0.0082+3∗0.012=0.04cm h=0.30±0.04cmF`=F−mg2=kh2=σπdσ=hk=0.30∗1.01=0.016N/m(Uσσ)2=(U kk)2+(U hh)2+(U dd)2Uσ=σU k2+U h2+U d2=0.016(0.03)2+(0.04)2+(0.13)2=0.002N/m σ=0.016±0.002N/m (P=0.997)实验结果为：七．误差分析：1.实验仪器的系统误差，以及在实验中周围环境对实验仪器性能影响所带来的误差。

用焦利氏秤测定液体的表面张力系数焦利氏秤是一种专门用于测量液体表面张力系数的仪器。

其原理是基于拉脱法，通过测量液滴从毛细管中滴出时的力矩来计算表面张力。

下面将详细说明使用焦利氏秤测定液体的表面张力系数的步骤和可能的注意事项。

一、实验准备1.焦利氏秤：包括支架、尺子、砝码、滴定管、毛细管等部件。

在实验前需对所有部件进行检查，确保其清洁干燥，且无损坏。

2.待测液体：选择适当的液体进行测试。

要求液体的纯度高，无杂质，以减少误差。

3.其他设备：烧杯、吸水管、纸巾等。

二、实验步骤1.安装焦利氏秤：将支架放置在水平桌面上，然后依次安装尺子、砝码、滴定管和毛细管。

确保所有部件都安装牢固，无倾斜或摇晃。

2.准备待测液体：将待测液体倒入烧杯中，确保液体的纯度和清洁度。

3.毛细管插入液体：用吸水管将毛细管插入待测液体中，注意不要让液面超过毛细管的顶部，以免液体进入滴定管。

4.滴定开始：轻轻挤压滴定管，使液体从毛细管中滴出。

当液滴达到一定大小后，松开手，让液滴从毛细管中自然下落。

用纸巾擦拭滴定管下端的残留液体，以备下次使用。

5.数据记录：观察并记录液滴从毛细管中滴出时的力矩。

这可以通过测量砝码的移动距离来实现。

注意要记录多次测量得到的数据，以便后续分析。

6.计算表面张力：根据记录的数据，可以利用公式计算液体的表面张力系数。

公式为：γ = (mgh)/(2πR) 其中，γ为表面张力系数，m为液滴的质量，g为重力加速度，h为液滴的高度，R为毛细管的半径。

三、注意事项1.实验过程中要保持桌面水平，以免影响测量的准确性。

2.毛细管插入液体时要小心，避免产生气泡，否则会影响液体的表面张力测量。

3.在滴定过程中，要控制好液滴的大小，以便于观察和测量。

同时，要注意液滴下落的速度，这也可以反映液体的表面张力情况。

4.实验过程中要保证所有设备干燥清洁，避免杂质对测量结果的影响。

5.在数据记录过程中，要保证砝码的位置和测量尺的位置在同一水平线上，以减少误差。

液体表面张力系数的测定【实验目的】1．学会用拉脱法测定液体的表面张力系数。

2．了解焦利氏秤的构造和使用方法。

3．通过实验加深对液体表面现象的认识。

【仪器与器材】焦利氏秤1把，U 形金属丝1条，砝码1盒，镊子1把，玻璃皿1个，温度计1支，酒精灯1个，蒸馏水100ml ，游标尺1把。

【原理与说明】一、 实验原理由于液体分子与分子间的相互作用，使液体表面层形成一张紧的膜，其上作用着张力，叫做表面张力。

如图3-1所示，设想在液体MN 上划出一条线s s ',s s '把MN 分成A 、B 两部分。

由于A 、B 两部分之间的分子相互作用，在s s '两侧就形成表面张力f ,f 的方向与液体表面相切且垂直于s s '，f 的大小与s s '的长度l 成正比，用公式表示为 )13(-=l f α 式中，α为表面张力系数，即作用在s s '的每单位长度上的力。

表面张力系数是研究液体表面性质所要用到的物理量，不同种类的液体，α值不同；同一种液体的α值随温度上升而减小；液体不纯净，α值也会改变。

因此，在测定α值时必须注明在什么温度下进行，液体必须保持纯净。

测量表面张力系数α的方法很多，本实验用拉脱法测定。

将U 形金属丝浸入液体中，然后慢慢拉起，这时在金属丝内带起了一层薄膜，如图3-2所示。

要想使金属丝由液面拉脱，必须用一定的力 F ，这个力的大小应等于金属丝所受液面的表面张力 f F 2= (注意有两个表面)l F α2=图3-1 图3-2lF2=α （3-2） 本实验用焦利氏秤测出F ，然后代入式（3-2）计算出α值。

二、 仪器构造焦利氏秤实际上就是一个比较精确的弹簧秤，用焦利氏秤测力是根据虎克定律x k F ∆= （3-3） 式中，k 为弹簧的倔强系数，等于弹簧伸长单位长度的拉力, x ∆为弹簧伸长量，如果已知k 值，再测定弹簧在外力作用下的伸长量x ∆，就可以算出作用力F 的大小。

液体表面张力系数的测定实验报告【实验目的】1．学会用拉脱法测定液体的表面张力系数。

2．了解焦利氏秤的构造和使用方法.3．通过实验加深对液体表面现象的认识。

【实验仪器】焦利氏秤1把，U形金属环1条,砝码1盒，镊子1把,玻璃皿1个，温度计1支，酒精灯1个，蒸馏水100ml，游标尺1把。

【实验原理】由于液体分子与分子间的相互作用，使液体表面层形成一张紧的膜，其上作用着张力，叫做表面张力。

设想在液面上作长为L的线段，线段两侧便有张力f相互作用,其方向与L垂直,大小与线段长度L成正比，如图3—1所示.即有=Lfα图3—1 式中α为表面张力系数,其单位为mN/。

表面张力系数是研究液体表面性质所要用到的物理量，不同种类的液体，α值不同;同一种液体的α值随温度上升而减小；液体不纯净，α值也会改变。

因此，在测定α值时必须注明在什么温度下进行，液体必须保持纯净。

测量表面张力系数α的方法很多,本实验用拉脱法测定.将环形金属环浸入液体中,然后慢慢拉起，这时在金属环内带起了一层薄膜，如图3—2所示。

要想使金属环由液面拉脱，必须用一定的力F 。

21f f mg F ++=（注意有两个表面）)(21d d mgF +-=πα （3—2）本实验用焦利氏秤测出F ，然后代入式(3-2）计算出α值。

二、 仪器构造焦利氏秤实际上就是一个比较精确的弹簧秤，焦利氏秤的构造如图所示，用焦利氏秤测力是根据胡克定律x k F ∆=式中，k 为弹簧的劲度系数，等于弹簧伸长单位长度的拉力， x ∆为弹簧伸长量，如果已知k 值，再测定弹簧在外力作用下的伸长量x ∆，就可以算出作用力F 的大小.【实验步骤】一、k 值的测定1．按图3—3挂好弹簧，小指针和砝码盘,再调节底板三角底座上的螺丝，使图3-2小指针处于镜子中,能上下自由振动且不与镜子相碰;2．调节旋钮D ，使镜子上的标线处于“三线重合"位置(镜子刻线、小指针和小指针的像重合），读出标尺上的读数0x 。