2.2 基本不等式
- 格式:ppt
- 大小:2.28 MB
- 文档页数:42

2.2基本不等式教材分析:“基本不等式”是必修1的重点内容,它是在系统学习了不等关系和不等式性质,掌握了不等式性质的基础上对不等式的进一步研究,同时也是为了以后学习选修教材中关于不等式及其证明方法等内容作铺垫,起着承上启下的作用.利用基本不等式求最值在实际问题中应用广泛.同时本节知识又渗透了数形结合、化归等重要数学思想,有利于培养学生良好的思维品质.教学目标 【知识与技能】1.学会推导并掌握基本不等式,理解这个基本不等式的几何意义,并掌握定理中的不等号“≥”取等号的条件是:当且仅当这两个数相等;2.2a b+≤;会应用此不等式求某些函数的最值;能够解决一些简单的实际问题 【过程与方法】通过实例探究抽象基本不等式; 【情感、态度与价值观】通过本节的学习,体会数学来源于生活,提高学习数学的兴趣.教学重难点 【教学重点】应用数形结合的思想理解不等式,并从不同角度探索不等式2a bab +≤的证明过程; 【教学难点】 1.基本不等式2a bab +≤等号成立条件; 2.利用基本不等式2a bab +≤求最大值、最小值. 教学过程 1.课题导入前面我们利用完全平方公式得出了一类重要不等式:一般地,,有a 2+b 2≥2ab ,当且仅当a =b 时,等号成立特别地,如果a >0,b >0,我们用,分别代替上式中的a ,b ,可得①当且仅当a =b 时,等号成立.通常称不等式(1)为基本不等式(basicinequality ).其中,叫做正数a ,b 的算术平均数,叫做正数a ,b 的几何平均数.基本不等式表明:两个正数的算术平均数不小于它们的几何平均数.思考:上面通过考察a 2+b 2=2ab 的特殊情形获得了基本不等式,能否直接利用不等式的性质推导出基本不等式呢?下面我们来分析一下. 2.讲授新课1)2a bab +≤特别的,如果a >0,b >0,我们用分别代替a 、b ,可得2a b ab +≥,(a>0,b>0)2a bab +≤2)2a bab +≤用分析法证明: 要证2a b ab +≥(1)只要证a +b ≥(2)要证(2),只要证a +b -≥0(3) 要证(3),只要证(-)2≥0(4)显然,(4)是成立的.当且仅当a =b 时,(4)中的等号成立. 探究1:在右图中,AB 是圆的直径,点C 是AB 上的一点,AC =a ,BC =b .过点C 作垂直于AB 的弦DE ,连接AD 、BD .你能利用这个图形得2a bab +≤的几何解释吗? 易证Rt △A CD ∽Rt △D CB ,那么CD 2=CA ·CB即CD =ab .这个圆的半径为2b a +,显然,它大于或等于CD ,即ab b a ≥+2,其中当且仅当点C 与圆心重合,即a =b 时,等号成立. 因此:基本不等式2a bab +≤几何意义是“半径不小于半弦” 评述:1.如果把2b a +看作是正数a 、b 的等差中项,ab 看作是正数a 、b 的等比中项,那么该定理可以叙述为:两个正数的等差中项不小于它们的等比中项.2.在数学中,我们称2b a +为a 、b 的算术平均数,称ab 为a 、b 的几何平均数.本节定理还可叙述为:两个正数的算术平均数不小于它们的几何平均数.【设计意图】老师引导,学生自主探究得到结论并证明,锻炼了学生的自主研究能力和研究问题的逻辑分析能力. 例1已知x >0,求x +的最小值.分析:求x +的最小值,就是要求一个y 0(=x 0+),使x >0,都有x +≥y .观察x +,发现x=1.联系基本不等式,可以利用正数x 和的算术平均数与几何平均数的关系得到y 0=2. 解:因为x >0,所以x +=2当且仅当x =,即x 2=1,x =1时,等号成立,因此所求的最小值为2.在本题的解答中,我们不仅明确了x>0,有x+≥2,而且给出了“当且仅当x=,即=1,x=1时,等号成立”,这是为了说明2是x+(x>0)的一个取值,想一想,当y0<2时,x+=y0成立吗?这时能说y.是x+(x>0)的最小值吗?例2已知x,y都是正数,求证:(1)如果积xy等于定值P,那么当x=y时,和x+y有最小值;(2)如果和x+y等于定值S,那么当x=y时,积xy有最大值.证明:因为x,y都是正数,所以.(1)当积xy等于定值P时,,所以,当且仅当x=y时,上式等号成立.于是,当x=y时,和x+y有最小值.(2)当和x+y等于定值S时,,所以,当且仅当x=y时,上式等号成立.于是,当x=y时,积xy有最大值例3(1)用篱笆围一个面积为100m2的矩形菜园,当这个矩形的边长为多少时,所用篱笆最短?最短篱笆的长度是多少?(2)用一段长为36m的篱笆围成一个矩形菜园,当这个矩形的边长为多少时,菜园的面积最大?最大面积是多少?分析:(1)矩形菜园的面积是矩形的两邻边之积,于是问题转化为:矩形的邻边之积为定值,边长多大时周长最短.(2)矩形菜园的周长是矩形两邻边之和的2倍,于是问题转化为:矩形的邻边之和为定值,边长多大时面积最大.解:设矩形菜园的相邻两条边的长分别为xm,ym,篱笆的长度为2(x+y)m.(1)由已知得xy=100.由,可得x+y≥2=20,所以2(x+y)≥40,当且仅当x=y=10时,上式等号成立因此,当这个矩形菜园是边长为10m的正方形时,所用篱笆最短,最短篱笆的长度为40m.(2)由已知得2(x+y)=36,矩形菜园的面积为xym2.由,可得xy≤81,当且仅当x=y=9时,上式等号成立.因此,当这个矩形菜园是边长为9m的正方形时,菜园的面积最大,最大面积是81m2.例4某工厂要建造一个长方体形无盖贮水池,其容积为4800m2,深为3m.如果池底每平方米的造价为150元,池壁每平方米的造价为120元,那么怎样设计水池能使总造价最低?最低总造价是多少?分析:贮水池呈长方体形,它的高是3m,池底的边长没有确定.如果池底的边长确定了,那么水池的总造价也就确定了.因此,应当考察池底的边长取什么值时,水池的总造价最低.解:设贮水池池底的相邻两条边的边长分别为xm,ym,水池的总造价为2元.根据题意,有z =150×+120(2×3x +2×3y )=240000+720(x +y ).由容积为4800m 3,可得3xy =4800,因此xy =1600.所以z ≥240000+720×2,当x =y =40时,上式等号成立,此时z =297600.所以,将贮水池的池底设计成边长为40m 的正方形时总造价最低,最低总造价是297600元. 【设计意图】例题讲解,学以致用. 3.随堂练习1.已知a 、b 、c 都是正数,求证:(a +b )(b +c )(c +a )≥8abc 分析:对于此类题目,选择定理:ab b a ≥+2(a >0,b >0)灵活变形,可求得结果.解:∵a ,b ,c 都是正数 ∴a +b ≥2>0 b +c ≥2>0c+a≥2>0∴(a+b)(b+c)(c+a)≥2·2·2=8abc即(a+b)(b+c)(c+a)≥8abc.【设计意图】讲练结合,熟悉新知.4.课时小结本节课,我们学习了重要不等式a2+b2≥2ab;两正数a、b 的算术平均数(),几何平均数()及它们的关系().它们成立的条件不同,前者只要求a、b都是实数,而后者要求a、b都是正数.它们既是不等式变形的基本工具,又是求函数最值的重要工具(下一节我们将学习它们的应用).我们还可以用它们下面的等价变形来解决问题:ab≤,ab ≤()2.我们用两个正数的算术平均数与几何平均数的关系顺利解决了函数的一些最值问题.在用均值不等式求函数的最值,是值得重视的一种方法,但在具体求解时,应注意考查下列三个条件:(1)函数的解析式中,各项均为正数;(2)函数的解析式中,含变数的各项的和或积必须有一个为定值;(3)函数的解析式中,含变数的各项均相等,取得最值即用均值不等式求某些函数的最值时,应具备三个条件:一正二定三取等.。


知识点一:基本不等式1. 如果,00>>b a ,有2b a ab +≤,当且仅当a=b 时,等号成立。
其中,2b a +叫做正数a,b 的算术平均数,ab 叫做a,b 的几何平均数。
2. 两个正数的算术平均数不小于它们的几何平均数。
知识点二:应用基本不等式求最值1. 已知x,y 都是正数,则:(1)如果积xy 等于定值P ,那么当x=y 时,和x+y 有最小值P 2。
(2)如果和x+y 等于定值S ,那么当x=y 时,积xy 有最大值241S 。
一、选择题1.若1a >,则11a a +-的最小值是 ( C ) A .1 B .2 C .3 D .4【答案】C 【解析】1a >则10a ->,()1111311a a a a +=-++≥--,当2a =时取“=”,所以正确选项为C 2. 若0<a <b ,则下列不等式中成立的是( B ) A .a <b <√ab <a+b 2 B .a <√ab <a+b 2<b C .a <√ab <b <a+b 2 D .√ab <a <a+b 2<b 答案:B 解析:若取a =2,b =8,则√ab =4,a+b 2=5,所以a <√ab <a+b 2<b.3.已知25≥x ,则()24524x x f x x -+=-有( D )基本不等式同步练习A .最大值54B .最小值54C .最大值1D .最小值1【答案】D 【解析】2245(2)1111()(2)2(1242(2)222x x x f x x x x x x -+-+⎡⎤===-+⨯=⎢⎥---⎣⎦当且仅当122x x -=-即3x =时取等号,故选:D . 4.函数233(1)1x x y x x ++=>-+的最小值为 ( ) A .3 B .2 C .1D .1- 【答案】A 【解析】1x >-,则10x +>,()()()22111331113111x x x x y x x x x ++++++===+++≥+++,当0x =时取“=”,所以正确选项为A .5. 已知a ,0b >,且满足21a ab +=,则3a b +的最小值为( )A B C .D .【答案】C 【解析】∵21a ab +=,∵1b a a =-.即11332a b a a a a a +=+-=+≥=当且仅当2a =时取等号.∵3ab +的最小值为选:C 6. 已知实数,x y 满足22 455--=x xy y ,则222x y +的最小值为( )A .53B .103C .109 D .4【答案】B 【解析】设222x y m +=,则222x m y =-,22 455x xy y --=,22455xy x y ∴=--,则()222221655x y x y =--,()()222216257y m y m y -=--, 42281(3070)(5)0y m y m --+-=,设2y t =,则2281(3070)(5)0t m t m --+-=,22(3070)481(5)0m m ∴∆=--⨯-,解得103m ≥,∴222x y +的最小值为103.故选:B 7.将一根铁丝切割成三段,做一个面积为22m ,形状为直角三角形的框架,在下列4种长度的铁丝中,选用最合理共用且浪费最少的是( )A .6.5mB .6.8mC .7mD .7.2m【答案】C 【解析】设直角三角形的框架的两条直角边为x ,y (x >0,y >0)则xy =4,此时三角形框架的周长C 为:x +y =x +y∵x +y ≥24∵C =x +y 故用7米的铁丝最合适.故选C .二、填空题1. 若0<a<b,且a+b=1,则12,a,b,2ab,a 2+b 2的大小顺序为a<2ab<12<a 2+b 2<b .解析:因为0<a <b ,a +b =1,所以a <12<b , ① 2ab <a 2+b 2, ②下面寻找②中数值在①中的位置.因为a 2+b 2>2(a+b 2)2=12,a 2+b 2=a ·a +b 2<a ·b +b 2=(1-b )b +b 2=b ,所以12<a 2+b 2<b. 又因为2ab <2(a+b 2)2=12,2ab >2×12a =a ,所以a <2ab <12.所以a <2ab <12<a 2+b 2<b. 2. 已知函数()4(0,0)a f x x x a x=+>>在3x =时取得最小值,则a =________. 【答案】36【解析】因为()4(0,0)a f x x x a x=+>>,所以,当且仅当即,由题意,解得3.已知0,0a b >>,122a b+=,则a b +的最小值为_______________;1的替换,()1121213332222b a a b a b a b a b a b ⎛+⎛⎫⎛⎫+=++=++≥+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,当2b a a b =即1222a b +==时等号成立,所以答案为32+. 4.设1x <-,求()()521x x y x ++=+的最大值 . 【答案】1【解析】∵1x <-,∵10x +<∵()10x -+>所以()()()()225215147104151111x x x x x x y x x x x x ++++++++====+++++++ ()41551(1)x x ⎡⎤=--+++≤-=⎢⎥-+⎣⎦ 当且仅当2(1)4x +=,即3x =-时等号成立,所以()()521x x y x ++=+的最大值为1三、解答题1. 已知x>0,y>0,且 x+2y+xy=30,求xy 的取值范围.解:因为x >0,y >0,所以30=x +2y +xy ≥2√2xy +xy ,当且仅当x =2y ,即x =6,y =3时,等号成立.所以xy +2√2√xy -30≤0.令t =√xy ,则t >0,t 2+2√2t -30≤0,(t +5√2)(t -3√2)≤0,所以-5√2≤t ≤3√2.又因为t >0,所以0<√xy ≤3√2,所以0<xy ≤18.2. 已知c b a ,,均为正数c b a ,,不全相等.求证:c b a cab b ac a bc ++>++ 解析:证明 ∵0,0,0>>>c b a ∵a bc +bac ≥ab abc 22=c 2 b ac +cab ≥bc bc a 22=a 2a bc +cab ≥ac acb 22=2b. 当且仅当a=b=c 时上式等号均成立,又c b a ,,不全相等,故上述等号至少有一个不成立.∵c b a cab b ac a bc ++>++. 3. 已知a ,b 都是正数,求证:114a b a b ⎛⎫⎛⎫++≥ ⎪⎪⎝⎭⎝⎭.【解析】∵0,0a b >>,∵由均值不等式得12a a +≥=,12b b +≥=. 由不等式的性质,得114a b a b ⎛⎫⎛⎫++≥ ⎪⎪⎝⎭⎝⎭,当且仅当1a =且1b =时,等号成立.4. 已知a ,b ,c 均为正数,求证:a a c b -+32+b b c a 223-++cc b a 332-+≥3. 解析:证明 ∵a ,b ,c 均为正数, ∵a b 2+ba 2≥2(当且仅当a=2b 时等号成立), ac 3+ca 3≥2(当且仅当a=3c 时等号成立),bc 23+cb 32≥2(当且仅当2b=3c 时等号成立), 以上三式相加,得a b 2+b a 2+a c 3+c a 3+b c 23+cb 32≥6(当且仅当a=2b=3c 时等号成立), ∵(a b 2+b a 2-1)+(a c 3+c a 3-1)+(b c 23+cb 32-1)≥3(当且仅当a=2b=3c 时等号成立), 即a a c b -+32+b b c a 223-++cc b a 332-+≥3. (当且仅当a=2b=3c 时等号成立).5. 如图,某人计划用篱笆围成一个一边靠墙(墙的长度没有限制)的矩形菜园.设菜园的长为xm ,宽为ym . (1)若菜园面积为272m ,则,x y 为何值时,可使所用篱笆总长最小?(2)若使用的篱笆总长度为30m ,求12x y+的最小值.【解析】∵1)由已知可得72xy =,而篱笆总长为2x y +∵又因为224x y +≥=∵当且仅当2x y =,即12,6x y ==时等号成立.所以菜园的长x 为12m ,宽y 为6m 时,可使所用篱笆总长最小.∵2)由已知得230x y +=∵ 又因为()12222559y x x y x y x y ⎛⎫+++=++≥+= ⎪⎝⎭∵所以12310x y +≥∵ 当且仅当x y =,即10,10x y ==时等号成立.所以12x y +的最小值是310.。




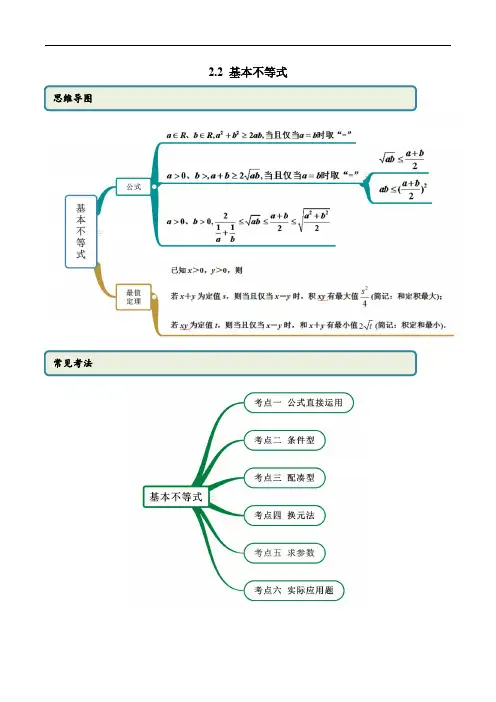

2.2 基本不等式【基本不等式(或)均值不等式】知识点一:基本不等式1.对公式222a b ab +≥及2a b+≥的理解.(1)成立的条件是不同的:前者只要求,a b 都是实数,而后者要求,a b 都是正数;(2)取等号“=” 的条件在形式上是相同的,都是“当且仅当a b =时取等号”.2a b+≤的证明方法一:几何面积法如图,在正方形ABCD 中有四个全等的直角三角形.方法二:代数法∵2222()0a b ab a b +-=-≥,当a b ≠时,2()0a b ->;当a b =时,2()0a b -=.所以22()2a b ab +≥,(当且仅当a b =时取等号“=”).2a b+≤的几何意义如图,AB 是圆的直径,点C 是AB 上的一点,AC a =,BC b =,过点C 作DC AB ⊥交圆于点D ,连接AD 、BD .易证~Rt ACD Rt DCB ∆∆,那么2CD CA CB =⋅,即CD =.这个圆的半径为2a b +,它大于或等于CD ,即2a b+≥其中当且仅当点C 与圆心重合,即a b =时,等号成立.知识点诠释:在数学中,我们称2a b+为,a b 的算术平均数,称,a b 的几何平均数. 因此基本不等式可叙述为:两个正数的算术平均数不小于它们的几何平均数.2a b+≤求最大(小)值在用基本不等式求函数的最值时,应具备三个条件:一正二定三取等.① 一正:函数的解析式中,各项均为正数;② 二定:函数的解析式中,含变数的各项的和或积必须有一个为定值;③ 三取等:函数的解析式中,含变数的各项均相等,取得最值.【基本不等式的变形与拓展】1.(1)若R b a ∈,,则ab b a 222≥+;(2)若R b a ∈,,则222b a ab +≤(当且仅当b a =时取“=”).2.(1)若00a ,b >>,则ab ba ≥+2;(2)若00a ,b >>,则ab b a 2≥+(当且仅当b a =时取“=”);(3)若00a ,b >>,则22⎪⎭⎫⎝⎛+≤b a ab (当且仅当b a =时取“=”).3.若0x >,则12x x +≥(当且仅当1x =时取“=”);若0x <,则12x x+≤-(当且仅当1x =-时取“=”);若0x ≠,则12x x+≥,即12x x +≥或12x x +≤-(当且仅当b a =时取“=”).4.若0>ab ,则2≥+ab b a (当且仅当b a =时取“=”);若0ab ≠,则2a b b a +≥,即2a b b a +≥或2a bb a +≤-(当且仅当b a =时取“=”).5.一个重要的不等式链:2112a b a b+≤≤≤+.6.函数()()0,0bf x ax a b x=+>>图象及性质(1)函数()0)(>+=b a xbax x f 、图象如右图所示:(2)函数()0)(>+=b a xbax x f 、性质:①值域:(),⎡-∞-+∞⎣;②单调递增区间:,,⎛⎫-∞+∞ ⎪ ⎪⎝⎭;单调递减区间:0,,0⎛⎡⎫- ⎪⎢ ⎪⎝⎣⎭.7.(1)当两个正数的积为定植时,可以求它们的和的最小值,当两个正数的和为定植时,可以求它们的积的最小值,正所谓“积定和最小,和定积最大”;(2)求最值的条件“一正,二定,三相等”;(3)均值定理在求最值、比较大小、求变量的取值范围、证明不等式、解决实际问题方面有广泛的应用.重难点突破(一) 基本不等式的简单应用重难点突破(二) 利用基本不等式求最值例2.(1)、(2022·陕西·榆林市第十中学高一期末)函数()4111y x x x =++>-+的最小值为______.【答案】4【解析】【分析】利用基本不等式直接求解即可【详解】因为1x >-,所以10x +>,所以4141y x x =++≥=+,当且仅当411x x +=+,即1x =时取等号,所以()4111y x x x =++>-+的最小值为4,故答案为:4【变式训练2-2】.(2023·山东烟台·统考三模)(多选题)已知0,0a b >>且42a b +=,则( )【变式训练3-1】、(2022·四川资阳·高一期末)已知正实数x ,y 满足111x y +=,则4x y +最小值为______.【答案】9【解析】【分析】利用基本不等式的性质直接求解即可.【详解】正数x ,y 满足:111x y+=,∴()11444559y x x y x y x y x y ⎛⎫+=+⋅+=++≥+= ⎪⎝⎭,当且仅当4y x x y =,即2x y =,233x y ==,时 “=”成立,故答案为:9.重难点突破(四) 不等式的证明技巧与综合处理技巧重难点突破(五) 均值不等式在实际问题中的应用【答案】()800f x ⎛=⨯ ⎝价为36000元.重难点突破(六) 挑战满分(压轴题)【点睛】本题考查了“乘1法”与基本不等式的性质的应用,同时考查转化思想和计算能力.。


高一数学2.2基本不等式笔记一、基本不等式的内容。
1. 定义。
- 对于任意实数a,b,有a^2+b^2≥slant2ab,当且仅当a = b时,等号成立。
- 证明:(a - b)^2=a^2-2ab + b^2≥slant0,移项可得a^2+b^2≥slant2ab。
2. 基本不等式√(ab)≤slant(a + b)/(2)(a>0,b>0)- 当且仅当a = b时,等号成立。
- 证明:- 因为(√(a)-√(b))^2=a - 2√(ab)+b≥slant0(a>0,b>0)。
- 移项可得a + b≥slant2√(ab),即√(ab)≤slant(a + b)/(2)。
二、基本不等式的几何解释。
1. 对于a^2+b^2≥slant2ab- 设直角三角形的两条直角边为a和b,则斜边为√(a^2)+b^{2}。
- 根据直角三角形的面积,S=(1)/(2)ab,同时S≤slant(1)/(2)×frac{a^2+b^2}{2}(当且仅当a = b时取等号),这就从几何角度解释了a^2+b^2≥slant2ab。
2. 对于√(ab)≤slant(a + b)/(2)(a>0,b>0)- 设a,b为正数,以a + b为长的线段AB,点C将AB分成AC=a,CB = b。
- 以AB为直径作半圆,过点C作CD⊥ AB交半圆于点D,则CD=√(ab),半径r=(a + b)/(2)。
- 由图形可知CD≤slant r,即√(ab)≤slant(a + b)/(2),当且仅当a = b时,C为AB中点,等号成立。
三、基本不等式的应用。
1. 求最值。
- 已知x>0,y>0,若xy = P(定值),则x + y≥slant2√(xy)=2√(P),当且仅当x = y=√(P)时,x + y取得最小值2√(P)。
- 若x + y = S(定值),则xy≤slant((x + y)/(2))^2=frac{S^2}{4},当且仅当x = y=(S)/(2)时,xy取得最大值frac{S^2}{4}。
人教A版高中数学必修第一册《基本不等式》(第一课时)单位:山东省单县第五中学姓名:陈洪飞时间:2019年9月2.2基本不等式(第一课时)教材:人民教育出版社A版必修第一册课题:2.2基本不等式(一)一、教学目标1.通过一个探究实例,引导学生从几何图形中获得基本不等式,了解基本不等式的几何背景,体会数形结合的思想;2.进一步提炼、完善基本不等式,并从代数角度给出不等式的证明,组织学生分析证明方法,加深对基本不等式的认识,提高逻辑推理论证能力;3.结合课本的探究图形,引导学生进一步探究基本不等式的几何解释,强化数形结合的思想;4.借助例1尝试用基本不等式解决简单的最值问题,通过三个探究引导学生领会运用基本不等式2ba ab +≤的三个限制条件(一正二定三相等)在解决最值中的作用,锻炼学生的交流合作探究能力,体会方法与策略.以上教学目标结合了教学实际,将知识与能力、过程与方法、情感态度价值观的三维目标融入各个教学环节.二、教学重点和难点重点:1、应用数形结合的思想理解基本不等式,并从不同角度探索不等式2ba ab +≤的证明过;2、熟练掌握基本不等式求代数式的最值;难点:在几何背景下抽象出基本不等式,并理解基本不等式.三、教学过程:1、动手操作,几何引入先将两张正方形纸片沿它们的对角线折成两个等腰直角三角形,再用这两个三角形拼接构造出一个矩形(两边分别等于两个直角三角形的直角边,多余部分折叠).假设两个正方形的面积分别为a 和b (b a ≥),考察两个直角三角形的面积与矩形的面积,你能发现一个不等式吗?抽象出不等式. 通过学生动手操作,探索发现:2ba ab +≤接着让学生探讨取等号的条件,及a 、b 的取值范围;得出结论,展示课题内容.根据上述几何背景,初步形成不等式结论:0,0>>∀b a 有2b a ab +≤(当且仅当a=b 时等号成立) 深化认识: 称ab 为a 、b 的几何平均数;称2b a +为a 、b 的算术平均数 基本不等式2b a ab +≤又可叙述为: 两个正数的几何平均数不大于它们的算术平均数。