工程力学第8章第9章作业答案

第一章静力学基本概念1.1 解F=F x+F y=F x i+F y jF1=1000N=-1000Cos30ºi-1000Sin30ºjF2=1500N=1500Cos90ºi- 1500Sin90ºjF3=3000N=3000 Cos45ºi+3000Sin45ºjF4=2000N=2000 Cos60ºi-2000Sin60ºj1.2因为前进方向与力F A，F B之间均为45º夹角，要保证二力的合力为前进方向，则必须F A=F B。

所以：F B=F A=400N1.3解：M O(F)=F l解：M O(F)=0解： M O(F)=F l sinβ解： M O(F)=F l sinθ解： M O(F)= -F a解：M O(F)= F(l＋r)解:1.4解:1.5解：1位置：M A(G)=02位置：M A(G)=-G l sinθ3位置：M A(G)=-G l1.6解：M O(F n)=-F n cosθ·D/2=-75.2N·m 1.71.8第二章平面力系2.1 力系简化解：（1）主矢大小与方位：F/R x＝∑F x＝F1cos45º+F3+F4cos60º＝100Ncos45º+200N+250cos60º＝395.7N F/R y＝∑F y＝F1sin45º-F2-F4sin60º＝100Nsin45º-150N-250sin60º＝-295.8N（2）主矩大小和转向：M O＝∑M O(F)＝M O(F1)+M O(F2)+M O(F3)+M O(F4)+m＝0-F2×0.3m+F3×0.2m+F4sin60×0.1m+F×0.1m＝0-150N×0.3m+200N×0.2m+250Nsin60×0.1m+50N×0.1m ＝21.65N·m( )向O点的简化结果如图所示。

eBook工程力学习题详细解答教师用书(第8章)2011-10-1范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan ,s Education & Teaching Studio习题8－1 习题8－2 习题8－3 习题8－4 习题8－5 习题8－6 习题8－7 习题8－8 习题8－9 习题8－10 习题8－9 习题8－10习题8－11 习题8－12 习题8－13 习题8－14 习题8－15 习题8－16 习题8－17 习题8－18 习题8－19 习题8－20习题8－21工程力学习题详细解答之八第8章 弯曲强度问题8－1 直径为d 的圆截面梁，两端在对称面内承受力偶矩为M 的力偶作用，如图所示。

若已知变形后中性层的曲率半径为ρ；材料的弹性模量为E 。

根据d 、ρ、E 可以求得梁所承受的力偶矩M 。

现在有4种答案，请判断哪一种是正确的。

(A) ρ64π4d E M ＝(B) 4π64d E M ρ＝(C) ρ32π3d E M ＝(D) 3π32dE M ρ＝正确答案是 A 。

8－2 矩形截面梁在截面B 处铅垂对称轴和水平对称轴方向上分别作用有F P1和F P2，且F P1=F P2，如图所示。

关于最大拉应力和最大压应力发生在危险截面A 的哪些点上，有4种答案，请判断哪一种是正确的。

(A) +max σ发生在a 点，−max σ发生在b 点M习题8－1图A Ba b cd P2z固定端习题8－2图(B) +max σ发生在c 点，−max σ发生在d 点 (C) +max σ发生在b 点，−max σ发生在a 点 (D) +max σ发生在d 点，−max σ发生在b 点正确答案是 D 。

8－3 关于平面弯曲正应力公式的应用条件，有以下4种答案，请判断哪一种是正确的。

(A) 细长梁、弹性范围内加载；(B) 弹性范围内加载、载荷加在对称面或主轴平面内；(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内；(D) 细长梁、载荷加在对称面或主轴平面内。

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。

（a)（b）(c）（d）2 第一章静力学基础（e）（f）（g）1-2 试画出图示各题中AC杆（带销钉)和BC杆的受力图（a）（b）（c）第一章静力学基础 3(a)1—3 画出图中指定物体的受力图.所有摩擦均不计,各物自重除图中已画出的外均不计。

(a)4 第一章静力学基础(b）（c）（d)第一章静力学基础 5 (e）6 第一章静力学基础（f）(g）第四章 材料力学基本概念 7第二章 平面力系2—1 电动机重P=5000N ，放在水平梁AC 的中央,如图所示。

梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。

如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力.题2—1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得:N P F F B A 5000===8 第一章 静力学基础2—2 物体重P=20kN ，用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上，如图所示。

转动绞车,物体便能升起.设滑轮的大小及轴承的摩擦略去不计，杆重不计,A 、B 、C 三处均为铰链连接.当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。

题2—2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得:PF P F BC AB 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间，形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。

电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。

第9章 弹性杆件横截面上的切应力分析9－1 扭转切应力公式p /)(I M x ρρτ=的应用范围有以下几种，试判断哪一种是正确的。

（A ）等截面圆轴，弹性范围内加载； （B ）等截面圆轴；（C ）等截面圆轴与椭圆轴；（D ）等截面圆轴与椭圆轴，弹性范围内加载。

正确答案是 A 。

解：p )(I M x ρρτ=在推导时利用了等截面圆轴受扭后，其横截面保持平面的假设，同时推导过程中还应用了剪切胡克定律，要求在线弹性范围加载。

9－2 两根长度相等、直径不等的圆轴承受相同的扭矩受扭后，轴表面上母线转过相同的角度。

设直径大的轴和直径小的轴的横截面上的最大切应力分别为max 1τ和max 2τ，切变模量分别为G 1和G 2。

试判断下列结论的正确性。

（A ）max 1τ＞max 2τ； （B ）max 1τ＜max 2τ；（C ）若G 1＞G 2，则有max 1τ＞max 2τ； （D ）若G 1＞G 2，则有max 1τ＜max 2τ。

正确答案是 C 。

解：因两圆轴等长，轴表面上母线转过相同角度，指切应变相同，即γγγ==21由剪切胡克定律γτG =知21G G >时，max 2max 1ττ>。

9－3 承受相同扭矩且长度相等的直径为d 1的实心圆轴与内、外径分别为d 2、)/(222D d D =α的空心圆轴，二者横截面上的最大切应力相等。

关于二者重之比（W 1/W 2）有如下结论，试判断哪一种是正确的。

（A ）234)1(α-；（B ）)1()1(234αα--；（C ）)1)(1(24αα--；（D ）)1/()1(2324αα--。

正确答案是 D 。

解：由max2max1ττ=得)1(π16π1643231α-=D M d M xx即31421)1(α-=D d（1）)1(222212121α-==D d A A W W （2）（1）代入（2），得2324211)1(αα--=W W9－4 由两种不同材料组成的圆轴，里层和外层材料的切变模量分别为G 1和G 2，且G 1 = 2G 2。

第8章 压杆稳定习题：1.【解】d 图临界力最大，b 图临界力最小。

2.【解】σBC =11.25MPa <[σst ]=16.83MPa ,BC 杆满足稳定性要求3.【解】最合理的情况为AB 、BC 两杆同时失稳，此时F 最大。

()βθ22222cr cos ππcos AC AB AB l EI l EI F F === ()βθ22222cr sin ππsin AC BC BCl EI l EI F F === 两式相除得到βθ2cot tan =即()βθ2cot arctan = 4. 【解】由于杆端的约束在各个方向相同，因此，压杆将在抗弯刚度最小的平面内失稳，即杆件横截面将绕其惯性矩为最小的形心主惯性轴转动。

32123min min b bh hb AI i === 欧拉公式适用于λ≥p λ，即min i l μ≥p2πσE 由此得到 l ≥m 76.1m 10200102105.032π103032π693p =⨯⨯⨯⨯⨯=-σμE b 故此压杆适用于欧拉公式时的最小长度为1.76m 。

5. 【解】（1）F cr =329.64kN（2）n =2.29<[n st ]=2.5，结构不安全6. 【解】（1）求挺杆的柔度挺杆的横截面为圆形，两端可简化为铰支座，μ=1，i=d/4计算柔度λ=μli=4μld=4×1×0.2570.008=128.5λ1=π√EσP =π√210×109240×106=92.9挺杆是细长压杆，使用欧拉公式计算临界压力（2）校核挺杆的稳定性I=πd464=π×0.008464=2.01×10−10m4P cr=π2EI(μl)2=π2×210×109×2.01×10−10(1×0.257)2=6.31kN工作安全系数n=P crP max=6.311.76=3.59所以挺杆满足稳定性要求7. 【解】[F]=53.31kN8. 【解】（1）F cr=355.31kN（2）bℎ=0.525。

8.3图示一销钉受拉力 F 作用,销钉头地直 径D =32 mm , h = 12 mm ，销钉杆地直径 d = 20 mm ,许用切应力 L I -120 MPa , 许用 挤 压 应 力 L 「bs 1 - 300 MPa , 丨-160 MPa .试求销 钉可承受地最大拉力 F max .8.2图示螺栓联接，第八章连接件地实用计算 习题8.1矩形截面木拉杆地接头如图所示 .已知 轴向拉力F=50 k ,截面宽度 b=2 5 0 ，休材地顺纹许用挤压应力 [%] = 10MPa ，顺纹许用切应力 a . L.-bJ -200 MPa ,试设计螺栓地直径I. .1-1 MPa .试求接头处所需地尺寸 丨和 A bsd 0.02题8.1图.200 103A s =2二 r 2 As = ab50 103AC a 250 106-10 106F/2 F/2题8.2图F s 200 103l.d 2 2=td< 200 10612丿d 2_80 106因此 d _ 0.05m故5 0 130 “ a - - 20mm250 10剪切面：A bs = lbF S5 0 130 …・S6 = 1 1 0 A S l 2 5 0 1 0 故已知外力F =200 kN , 板厚度t =20 mm，板与螺栓地材料相同，其许用切应力丨.1-80 MPa ,许用挤压应力解:1 h D - I|hrZZZ/////.-d-*\\、\\题8.3图.拉杆头部地切应力拉杆头部D2 -d2F s 二A s - "：dhAs 二dh 挤压应力3.14 20 10” 12 10120 106N =90.4KN 乞F maxF =%Abs=% 兀（D2-d2）=300 心0*3.= 587.8 KN _Fmax所以应取F =90.4 KN ；F ■d 290.4 KN_3223.14 20 10 m2题8.4图.解：先考虑受剪切力时地情况，在钢板和铆钉都达到许用剪切应力时，. F S兀 2由一,A Q = na s和a s = —d 得,n =a s 2s d4将L I - 140MPa,d = 0.020m代入上式，得n 二n a s-UF S-bs3160 10兀2TT314 2 6qd _… 4 0.020 140 10A bsA bs = n a bs〉a bs = dt得_ a bs 事bs dt 竽bs _S4^再尬代入上式,得F Fa bs -上bJ dt 士bs1160"030.020 0.01 320 106由以上两式可以确定铆钉地个数为四个，下=3.64 :::=2.5 ：：3=72.0MP 确定排列方式为（n1为一行中铆钉个数）8.4图示两块钢板用直径d = 20 mm地铆钉搭接，钢板与铆钉材料相同.已知F ^1 6 0 !两板尺寸相同，厚度t =10 mm , 宽度b =1 2 0 ,m许用拉应力kr】=1 6 0 M R许a用切应力I. ）-140 MPa ,许用挤压应力L「bs丄320 MPa ,试求所需要地铆钉数，并加以排列，然后校核板地拉伸强度.F NA -山兀得，n1-l- |,A = 0.01 0.12 = 0.0012m2,a bs = 0.0002m2代入上式得160汉103 '0.0012_------ 6. 160"06£ =10.0002—1k6所以每排只排一个，共四排,在此种排列情况下,强度符合条件8.5图示直径为 30 mm 地心轴上安装着一 个手摇柄，杆与轴之间有一个键K,键长36mm,截面为正方形，边长8 mm,材料地许用切 应力LI -5 6 0 MP 锻用挤压应力L 「bs 1 = 200 MPa ,试求手摇柄右端 F 地最 大许可值.30mm解：挤压面为 傀=4 36 = 144mm 2故最大挤压应力为F bs "bs A bs =Abs bbs li 44m m 2x 20°MP a= 28.8kN剪切面为 A = 8^36=288mm 故最大剪切应力为F s= Ab 】 = 288mm 2 汉560MPa=161.28kN由于 F bs ::: Fs ,所以取 F bs 二 28.2kN , 由力矩平衡条件，得15 F bs -750 F = 0F =576N手摇柄右端F 地最大许为576N.8.6图示冲床地冲头，在F 力地作用下，冲剪 钢板，设板厚t =10 mm ，板材料地剪切强度 极限-b =360 MPq 当需冲剪一个直径 d -20 mm 地圆孔，试计算所需地冲力 F 等 于多少？解：剪切面S 二二dt由于b因此F ss ■: dt750mm题8.5图.F - ■ dt 3.14 0.02m 0.01m 360 106p a钢板。

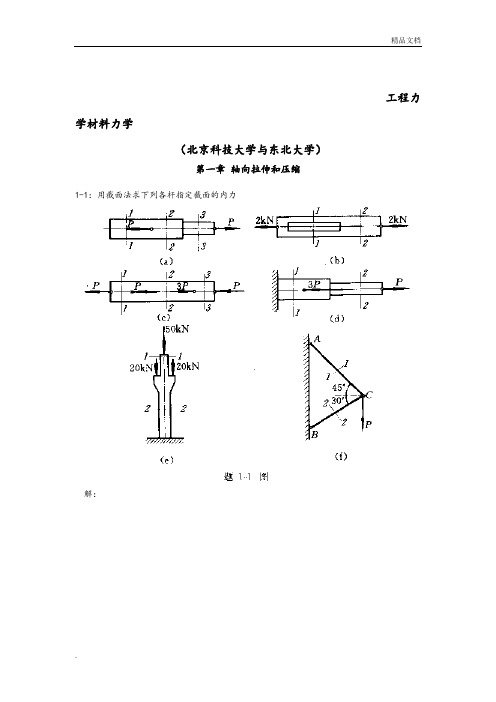
工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。

解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa 上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127ACACCBCBPMPaSPMPaSσσ====ACACACLNLEA EAσε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:QNllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。

第9章平面体系的几何组成分析习题.【解】若上部结构与地基之间的连接比较多（N4）,能够考虑先将上部结构中的某•刚片与地基连成一个大刚片。

然后，在考虑这个大刚片与上部其它杆件的连接。

本例中，上部结构与地基之间用4个约束连接。

杆件ABE与地基之间用钗A和一根不同过该絞的链杆B相连，组成几何不变体系，且没有多余约束。

所以，能够将杆件ABE与地基看成一个没有多余约束的大刚片。

杆件FCD用三根既不相互平行又不相交于一点的链杆（链杆EF、链杆C、链杆D）与这个大刚片相连，组成一个更大的几何不变体系，且没有多余约束。

杆件ABE与地基之间用平行链杆A和一根不同过该絞的链杆B相连，组成几何不变体系，且没有多余约束。

将杆件ABE与地基看成一个没有多余约束的大刚片。

杆件FCD用三根既不相互平行又不相交于一点的链杆（链杆EF、链杆C、链杆D）与这个大刚片相连，组成一个更大的几何不变体系，且没有多余约束。

-I*羡诊为习题（C）图若上部结构中有皎接三角形，能够考虑将这些三角形看成刚片，然后在进行分析。

刚片I与地基组成•个没有多余约束的大刚片。

这个大刚片与刚片II用三根既不相互平行又不相交于一点的链杆相连，组成一个更大的几何不变体系，且没有多余约束。

习题（d）图将扩大的三角形看成刚片。

先分析一部分：左边的刚片与地基组成一个大刚片ABCD。

增加二元体：在大刚片ABCD上增加二元体DE杆和链杆E,组成一个更大的刚片。

此刚片与刚片GH1F由三根延长线交于H点的链杆（杆件CG、杆件FE、链杆1）相连。

故，体系为瞬变体系。

若上部结构与地基之间用三个约束连接，且符合几何不变体系的组成规律，能够只分析上部结构。

上部结构的分析结论就是整个体系的分析结论。

若折杆只用两个较与其它物体相连，能够将折杆看成是连接两个钗的直杆。

去掉二元体。

剩下部分为两个刚片用两个钗连接，为几何不变体系,且有一个多余约束。

故，整体体系也为几何不变体系，且有一个多余约束。

习题9-1图 x15-'x x'σy'x'τ 1.25MPa15 (b-1)15a 4MP15-y'x'τx'x'σa1.6MP x (a-1) 习题9-2图302MPa 0.5MPa-60x'σ'x ''y x τ 工程力学（工程静力学与材料力学）习题与解答第9章 应力状态分析9－1 木制构件中的微元受力如图所示，其中所示的角度为木纹方向与铅垂方向的夹角。

试求： 1．面内平行于木纹方向的切应力；2．垂直于木纹方向的正应力。

知识点：平面应力状态、任意方向面上的应力分析 难度：易 解答：（a ）平行于木纹方向切应力6.0))15(2cos(0))15(2sin(2)6.1(4=︒-⨯⋅+︒-⨯---=''y x τMPa 垂直于木纹方向正应力84.30))15(2cos(2)6.1(42)6.1(4-=+︒-⨯---+-+-='x σMPa （b ）切应力08.1))15(2cos(25.1-=︒-⨯-=''y x τMPa正应力625.0))15(2sin()25.1(-=︒-⨯--='x σMPa9－2 层合板构件中微元受力如图所示，各层板之间用胶粘接，接缝方向如图中所示。

若已知胶层切应力不得超过1MPa 。

试分析是否满足这一要求。

知识点：平面应力状态、任意方向面上的应力分析 难度：易 解答：55.1))60(2cos(5.0))60(2sin(2)1(2-=︒-⨯⋅+︒-⨯---=''y x τMPa 1MPa 55.1||>=''y x τMPa ，不满足。

9－3 结构中某点处的应力状态为两种应力状态的叠加结果。

试求叠加后所得应力状态的主应力、面内最大切应力和该点处的最大切应力。

知识点：平面应力状态分析 难度：难 解答：习题9-2图yσxσxyτ=yσxσxyτx=yσxσxyτ=左微元⎪⎪⎪⎩⎪⎪⎪⎨⎧-='-='-=-='+=--+='000000022cos 122sin )2sin(222cos 10)2cos(22σθσσσσθθστσθθσσσx y xy x 叠加 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=+'=-=+=+=+'=''000022cos 1022sin 022cos 3σθσσσθττσθσσσy y y x xy x x0)cos 1()cos 1( )22sin (4)22cos 122cos 3(21222cos 122cos 330020202021=⎩⎨⎧-+=-+--+±-++=⎭⎬⎫σσθσθσθσθθσθθσσ 面内最大切应力：θσσστcos 2021max=-='该点最大切应力：031max2cos 12σθσστ+=-=左微元0023))30(2sin()(ττσ=︒-⨯-='x ，0230τσσ-='-='x y ，2))30(2cos(00τττ=︒-⨯='xy 右微元0023)302sin()(ττσ=︒⨯-=''x，0230τσσ-=''-=''x y ，2))30(2cos()(00τττ-=︒⨯-=''xy 叠加 03τσσσ='+'=y x x ，03τσσσ-=''+'=y y y ，0=''+'=xyxy xy τττ 013τσ=，02=σ，033τσ-= 面内031max32||τσστ=-='xABOσOσαα(a)习题9-4图A60CB60100-x σxσyxτxyτ92MPa(a)习题9-5图该点031max 32||τσστ=-=叠加[]⎪⎪⎪⎩⎪⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡︒-⨯--+==--+==⎥⎦⎤⎢⎣⎡︒-⨯--+-++=MPa 30))45(2sin(2)30(5070MPa 1010)3050(0MPa 90))45(2cos(2)30(502)30(5080xy y x σσσ主应力0MPa 0MPa100304)]100(90[212109022231=⎩⎨⎧=⨯+-±+=⎭⎬⎫σσσ面内及该点：5021002||||31max max=-=-=='σσττMPa9－4 已知平面应力状态的最大正应力发生在与外力作用的自由表面AB 相垂直的面上，其值为0σ。

工程力学第一章简答练习本卷共分为3大题10小题，总分100 分。

本卷得分:100一、简答题(本大题共2小题，共20分)∙1[简答题,10分]一质点在铅垂平面内作圆周运动，当质点恰好转过一周时，其重力的功为零，对吗?为什么?您的答案:高度差的乘积|零|重力的功.本题得分：10o收藏本题o展开解析∙2[简答题,10分]平面图形在什么情况下作瞬时平动?瞬时平动的特征是什么?您的答案:速度相同|角速度|加速度.本题得分：10o收藏本题o展开解析二、名词解释题(本大题共3小题，共30分)∙3[名词解释题,10分]刚体您的答案:任意两点|距离|保持不变本题得分：10o收藏本题o展开解析∙4[名词解释题,10分]加减平衡力系原理您的答案:平衡力系|刚体本题得分：10o收藏本题o展开解析∙5[名词解释题,10分]二力平衡公理您的答案:保持平衡|充分条件|大小相等本题得分：10o收藏本题o展开解析三、填空题(本大题共5小题，共50分)∙6[填空题,10分]物体的平衡是指物体相对于地面__________或作________运动的状态您的答案:保持静止|匀速直线本题得分：10o收藏本题o展开解析∙7[填空题,10分]刚体在作平动过程中，其上各点的__________相同，每一瞬时，各点具有__________的速度和加速度您的答案:轨迹形状|相同本题得分：10o收藏本题o展开解析∙8[填空题,10分] AB杆质量为m，长为L，曲柄O1A、O2B质量不计，且O1A=O2B=R，O1O2=L，当υ=60°时，O1A杆绕O1轴转动，角速度ω为常量，则该瞬时AB杆应加的惯性力大小为__________，方向为__________您的答案:Fgh=mRω2|过质心C平行O1A指向向下本题得分：10o收藏本题o展开解析∙9[填空题,10分]平面汇交力系平衡的必要与充分条件是：_____。

该力系中各力构成的力多边形____您的答案:该力系的合力为零|自行封闭本题得分：10o收藏本题o展开解析∙10[填空题,10分]一物块重600N，放在不光滑的平面上，摩擦系数f=0.3，在左侧有一推力150N，物块有向右滑动的趋势Fmax=__________,所以此物块处于静止状态，而其F=__________。

`第8章 弹性杆件横截面上的正应力分析8－1 图示的三角形中b 、h 。

试用积分法求I z 、I y 、I yz 。

解：⎰=Az Ay I d 2图（a ）：yh by y y b A d d )(d ==34244d hb h h b y h byy I h z =⋅=⋅=⎰⎰=AyAzId 2图（a ）：zz b bh z z b A d )(d )(d +-=-=1241)(3)()(3433202hb b b b b h zz bz bh z z b bh z I bby =⎪⎭⎫ ⎝⎛+-⋅-=+-=+⋅-=⎰⎰--d d图（b ）：⎰⎰⎰⎰====AAA A yz yzy h by hby yzy y yzb A yz I d d d )(d 2hby y b z 22)(-==842d 2224220hb hh by y h by h b I hyz -=⋅-=-=⎰8－2解：1．图（a ）中y 、z 即为形心主轴64310843.56464π1210080⨯=⨯-⨯=z I mm 4半圆对其形心轴y '的惯性矩：52241015.1864π)π3642(12864π⨯=⨯⨯⨯-⨯='y I mm 4故整个图形：⎪⎪⎭⎫⎝⎛⨯⨯+⨯-⨯=864π1015.1212801002253a I y式中4.26π364240=⨯-=a mm625610792.1)16084.261015.1(210267.4⨯=⨯+⨯⨯-⨯=y I mm 42．先求图（b ）形心位置： z C = 03.25440π601000)20(601002-=⨯-⨯--⨯⨯=C y mm64310674.16440π1260100⨯=⨯-⨯=y I mm 4⎪⎪⎭⎫⎝⎛⨯⨯+⨯-⎪⎪⎭⎫⎝⎛⨯⨯+⨯=440π3.256440π100603.5121006022423z I655610239.410)0436.8256.1()10685.1105(⨯=⨯+-⨯+⨯=mm 48－3 图中所示组合截面为两根No.20a 的普通热轧槽形钢所组成的截面，今欲使I x = I y ，试求b =？（提示：计算所需要数据均可由型钢表中查得。