minitab应用实例

MINITAB应用案例就近一个文章说：对2010 年全国大学生调查的分析。

该调查利用随机分层法，抽取了19 所的5000 多名大四学生进行调查。

在这19 所高校中，有10 所“211 工程”的重点大学和9 所普通大学。

调查中搜集了学生的来源省份、家庭背景、高考成绩和高中表现等多项数据。

统计结果发现，如果其父母在政府、国企和事业单位有干部身份，那么这些学生有更大几率上“211”。

而如果其父母是工人，农民，文员，技术员或企业家，那么这些学生上重点大学的几率则会降低。

统计结果说明，在控制了父母教育水平和家庭收入两个变量之后，父母职业这个变量的影响还是显著。

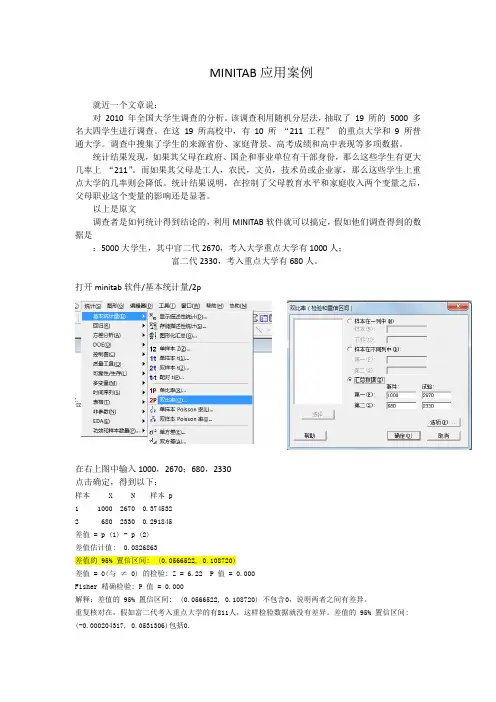
以上是原文调查者是如何统计得到结论的，利用MINITAB软件就可以搞定，假如他们调查得到的数据是：5000大学生，其中官二代2670，考入大学重点大学有1000人；富二代2330，考入重点大学有680人。

打开minitab软件/基本统计量/2p在右上图中输入1000，2670；680，2330点击确定，得到以下：样本 X N 样本 p1 1000 2670 0.3745322 680 2330 0.291845差值 = p (1) - p (2)差值估计值: 0.0826863差值的 95% 置信区间: (0.0566522, 0.108720)差值 = 0(与≠ 0) 的检验: Z = 6.22 P 值 = 0.000Fisher 精确检验: P 值 = 0.000解释：差值的 95% 置信区间: (0.0566522, 0.108720) 不包含0，说明两者之间有差异。

重复核对在，假如富二代考入重点大学的有811人，这样检验数据就没有差异。

差值的 95% 置信区间: (-0.000204317, 0.0531306)包括0.样本 X N 样本 p1 1000 2670 0.3745322 811 2330 0.348069差值 = p (1) - p (2)差值估计值: 0.0264632差值的 95% 置信区间: (-0.000204317, 0.0531306)差值 = 0(与≠ 0) 的检验: Z = 1.94 P 值 = 0.052Fisher 精确检验: P 值 = 0.055以上用实际生活案例来引发MINITAB的应用。

minitab doe案例
以下是一个使用Minitab进行DOE（实验设计）的案例：
案例：PCB板的镀铜线质量优化
1. 确定每个因子的高低水平，例如温度、时间、电流等。

2. 打开Minitab软件，创建一个新的DOE计划。

3. 选择合适的因子数、区组中心点数、角点仿行数和区组数，以满足实验需求。

4. 生成正交试验矩阵，并按照计划进行实验。

5. 将实验数据复制到Minitab中进行DOE分析。

6. 选择因子和响应，进行效应图和方差分析。

7. 根据分析结果，优化因子水平，以提高镀铜线的质量。

通过以上步骤，可以使用Minitab进行DOE，优化PCB板的镀铜线质量。

Minitab 19 Excel实例是一个用于数据分析的软件工具，它提供了多种数据导入选项，包括直接从Excel中导入数据、从数据库导入数据以及从其他数据文件格式导入数据等。

一旦数据导入完成，接下来的一步是对数据进行清洗。

Minitab 19 Excel实例提供了多种数据清洗工具，如去除空值、去除重复值、纠正数据格式等。

通过使用这些工具，可以确保数据完全准确且适合进行后续的分析。

在Minitab 19 Excel实例中，可以进行基本统计分析。

Minitab 19 Excel实例提供了广泛的统计分析工具，包括描述性统计、频率分析、方差分析等。

通过使用这些工具，可以获得数据的基本统计特征，如中位数、平均数、标准差等。

此外，Minitab 19 Excel实例还提供了图形和图表功能，可以帮助用户更好地理解和解释数据。

例如，可以使用柱状图、折线图、散点图等来展示数据的分布和趋势。

总之，Minitab 19 Excel实例是一个功能强大的数据分析工具，可以帮助用户更好地管理和分析数据，为决策提供支持。

doe(实验设计)与minitab培训doe案例实验设计（DOE，Design of Experiments）是一种系统化的方法，用于确定和优化实验参数以实现特定的目标或解决特定的问题。

在制造业、工程、科学研究和其他领域中，DOE被广泛用于提高产品质量、降低成本、改进生产过程等。

Minitab是一款流行的统计软件，用于数据分析、假设检验、回归分析等。

它提供了丰富的工具和功能，帮助用户轻松地分析和解释数据。

以下是一个关于DOE和Minitab培训的案例：假设一家制造公司想要提高其产品的抗拉强度。

通过实验设计，该公司确定了以下几个因素可能影响产品的抗拉强度：温度、压力和材料类型。

目标是找到最佳的温度、压力和材料类型组合，以最大化产品的抗拉强度。

为了解决这个问题，公司使用Minitab软件进行实验设计。

首先，Minitab 帮助确定因素和水平，并生成一个实验矩阵，其中包括每个实验的条件和结果。

然后，公司按照实验矩阵进行实验，并记录每个实验的结果。

在收集完数据后，Minitab帮助进行数据分析。

通过分析结果，公司确定了最佳的温度、压力和材料类型组合。

此外，Minitab还提供了其他有用的统计信息，如因素对结果的影响程度、因素的交互作用等。

通过这个案例，Minitab培训的目标是使参与者能够：1. 了解实验设计的基本概念和方法；2. 使用Minitab软件进行实验设计和数据分析；3. 掌握如何解释和分析实验结果；4. 应用实验设计的方法来解决实际问题。

总之，通过DOE和Minitab培训，参与者可以学习如何系统地设计和分析实验，并使用统计软件来分析和解释数据。

这将有助于提高产品质量、改进生产过程和提高企业的竞争力。

Minitab应用实例引言Minitab是一款流行的统计分析软件，可用于数据分析、质量管理和过程改进。

它提供了广泛的功能和工具，使用户能够轻松地进行数据探索、统计分析和报告生成。

本文将通过介绍几个实际应用实例，展示Minitab的一些主要功能和应用场景。

这些实例将涵盖数据探索、假设检验、回归分析和质量控制等方面。

数据探索数据探索是数据分析的第一步，它可以帮助我们了解数据的特征和结构。

Minitab提供了多种方式来进行数据探索，包括数据摘要、描述性统计、数据可视化等。

例如，我们有一组销售数据，想要了解销售额的分布和趋势。

我们可以使用Minitab的柱状图和直方图功能，绘制销售额的分布图。

这样可以直观地看到销售额在哪个区间的数据更多，是否存在异常值等。

另外，Minitab还提供了箱线图、散点图等图表类型，可以帮助我们分析数据间的相关性和趋势。

假设检验假设检验是统计学中常用的技术，用于验证关于总体参数的假设。

Minitab提供了多种假设检验的功能，可以帮助我们进行参数估计和假设检验。

举个例子，我们有一份某公司员工的薪资数据，我们想要检验该公司的平均薪资是否高于行业平均水平。

我们可以使用Minitab的t检验功能来进行假设检验，得出结论是否拒绝原假设。

除了t检验，Minitab还支持多种其他假设检验方法，如方差分析、卡方检验等。

回归分析回归分析是用于建立因果关系模型的一种统计技术。

Minitab提供了强大的回归分析功能，可以帮助我们建立和评估回归模型。

例如，我们有一份汽车销售数据，想要预测汽车销售量与价格、广告费用和促销活动等变量之间的关系。

我们可以使用Minitab的多元线性回归功能来建立回归模型，并通过分析回归系数和显著性水平来评估模型的拟合优度。

此外，Minitab还提供了其他回归分析方法，如逐步回归、逻辑回归等。

质量控制质量控制是制造业中重要的环节，用于监控和改善产品的质量。

Minitab提供了一系列用于质量控制的统计工具和方法。

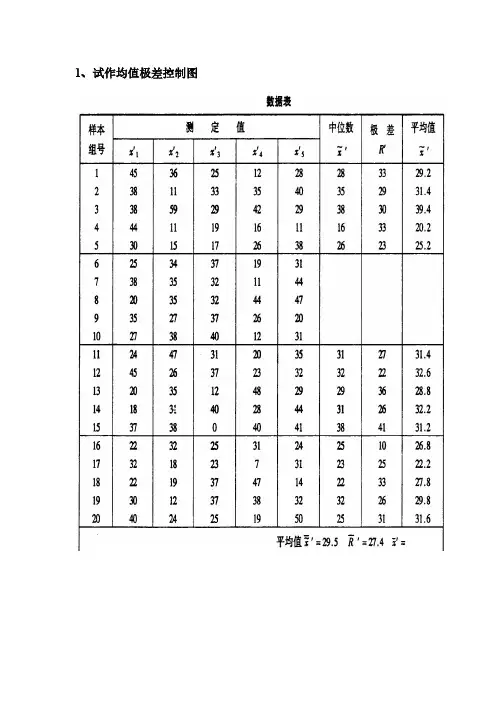
1、试作均值极差控制图
2、试作均值极差控制图、中位数极差控制图和均值标准差控制图
3、试作移动极差控制图
4、试作样本大小n 相等时的p
控制图
5、试作样本大小n 相等时的pn
控制图
6. 试作样本大小n不相等时的p控制图
〔案例〕
某电机厂生产洗衣机用小型电机，构成交验批的批量各不相等，现每隔1
小时抽取一个样本，共25批，经检验将不合格品数及不合格品率记入数据
表，试作分析用控制图。

7. 试作C控制图
某电线生产过程中，每隔一定时间对100m导线进行检查，检查的结果如表所示，试作C控制图。

8. 试作U控制图
某电子产品检查的结果如表所示，试作U控制图。

msa minitab例题详解MSA（Measurement System Analysis）是对测量系统进行全面评估的一种统计技术，主要用于确定测量系统测量的准确性、重复性和再现性。

在质量控制领域，MSA是确保测量数据准确性的重要手段。

以下是一个使用MINITAB软件进行MSA分析的示例：1. 假设我们要分析一个测量设备在测量长度方面的准确性，首先需要收集数据。

可以请3名检验员使用该设备对同一个部件进行多次测量，得到一系列的测量值。

将这些数据记录在表格中，包括检验员编号、部件编号、测量长度等。

2. 将数据输入MINITAB软件中，选择“质量工具”-“量具研究”-“量具R&R研究（交叉）”。

3. 在弹出的对话框中，输入检验员编号、部件编号和测量长度等变量，并指定部件号和检验员作为分类变量。

点击“确定”开始分析。

4. MINITAB软件会自动进行方差分析，计算测量系统的重复性和再现性。

分析结果会显示量具的R&R值、P/T值、可区分类别数等指标。

5. 根据分析结果，可以对测量系统进行评估。

如果R&R值和P/T值都大于30%，则说明测量系统的重复性和再现性较差，需要采取措施改进。

如果可区分类别数小于5，则说明测量系统的分辨力较低，也需要进行改进。

6. 如果需要进一步了解方差的构成，可以在MINITAB中选择“方差分量”，软件会分别计算重复性和再现性的方差分量，以及合计量具R&R的方差分量。

这些信息有助于了解测量系统各组成部分对总变异的贡献。

7. 除了方差分析外，还可以使用线性回归分析等方法对测量系统进行分析，以评估其准确性和可靠性。

例如，可以请更高一级别的测量设备对同一部件进行多次测量，取其平均值作为真值，然后将该值与被评估设备的测量值进行线性回归分析，以评估被评估设备的准确性。

8. 在完成MSA分析后，可以根据分析结果采取相应的措施，如对设备进行校准、培训检验员等，以提高测量系统的准确性和可靠性。

minitab 实例操作使用Minitab进行数据分析的实例操作Minitab是一款功能强大的统计分析软件，广泛应用于各个领域的数据分析中。

本文将以实例操作的方式，演示如何使用Minitab进行数据分析。

我们假设有一家电商公司希望分析其在线销售数据，以便优化运营策略。

我们将使用Minitab来对该公司的销售数据进行分析。

第一步，导入数据。

我们首先需要将公司的销售数据导入到Minitab中。

在Minitab的主界面上，点击"File"，然后选择"Open Worksheet"，导入数据文件。

在导入数据之前，我们可以先查看数据的结构和格式，以确保数据的准确性。

第二步，数据清洗。

一般来说，导入的数据可能存在一些缺失值、异常值或错误值，需要进行清洗。

在Minitab中，可以使用"Data"菜单下的"Code"功能来对数据进行清洗。

例如，我们可以将缺失值替换为平均值或中位数，排除异常值等。

第三步，描述性统计。

在数据清洗完毕后，我们可以使用Minitab 进行描述性统计分析。

在"Stat"菜单下，选择"Basic Statistics"，然后选择"Display Descriptive Statistics"。

这将显示数据的均值、中位数、标准差、最小值和最大值等统计指标。

通过这些指标，我们可以对数据的分布和变异程度有一个初步的了解。

第四步，数据可视化。

数据可视化是数据分析的重要环节之一。

在Minitab中，可以使用"Graph"菜单下的各种功能来对数据进行可视化。

例如，我们可以绘制直方图、散点图、线图等，以便更直观地观察数据的分布和趋势。

第五步，假设检验。

在数据分析中，我们常常需要进行假设检验来验证某些假设是否成立。

Minitab提供了多种假设检验的功能，例如t检验、方差分析、相关性分析等。