当前位置：文档之家 › 普通物理学上册第七章

普通物理学上册第七章

  • 格式：ppt
  • 大小：5.11 MB
  • 文档页数：209

下载文档原格式

  / 209

合集下载

普通物理学第二版第七章课后习题答案

普通物理学第二版第七章课后习题答案

第七章 刚体力学7.1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s?估算地球赤道上一点因地球自转具有的线速度和向心加速度.估算地心因公转而具有的线速度和向心加速度（自己搜集所需数据）.[解 答]7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.（1）假设转动是匀加速转动，求角加速度.(2)在此时间内，发动机转了多少转？[解 答]（1）22(30001200)1/601.57(rad /s )t12ωπβ⨯-⨯===（2）22222()(30001200)302639(rad)2215.7πωωθβ--===⨯所以 转数=2639420()2π=转7.1.3 某发动机飞轮在时间间隔t 内的角位移为球t 时刻的角速度和角加速度.[解 答]7.1.4 半径为0.1m 的圆盘在铅直平面内转动，在圆盘平面内建立O-xy 坐标系，原点在轴上.x 和y 轴沿水平和铅直向上的方向.边缘上一点A当t=0时恰好在x 轴上，该点的角坐标满足21.2t t (:rad,t :s).θθ=+求（1）t=0时，（2）自t=0开始转45时，（3）转过90时，A 点的速度和加速度在x 和y 轴上的投影.[解 答]（1） A ˆˆt 0,1.2,R j 0.12j(m/s).0,0.12(m/s)x y ωνωνν====∴==（2）45θ=时，由2A 1.2t t ,t 0.47(s)42.14(rad /s)v R πθωω=+==∴==⨯得 （3）当90θ=时，由7.1.5 钢制炉门由两个各长1.5m 的平行臂AB 和CD 支承，以角速度10rad/s ω=逆时针转动，求臂与铅直45时门中心G 的速度和加速度.[解 答]因炉门在铅直面内作平动，门中心G 的速度、加速度与B 或D 点相同。

所以：7.1.6 收割机拔禾轮上面通常装4到6个压板.拔禾轮一边旋转，一边随收割机前进.压板转到下方才发挥作用，一方面把农作物压向切割器，另一方面把切割下来的作物铺放在收割台上，因此要求压板运动到下方时相对于作物的速度与收割机前进方向相反.已知收割机前进速率为1.2m/s ，拔禾轮直径1.5m ，转速22rev/min,求压板运动到最低点挤压作物的速度.[解 答]取地面为基本参考系，收割机为运动参考系。

普通物理学第7章

普通物理学第7章
Am(x,t)具有沿x方向传播的简谐波的形式,它的角频 率和波数分别为 m 2, km k 2, 波速 ug m km k 群速度 两个频率相近、等振幅的简谐波叠加的结果是一 个振幅缓慢变化的波,它的角频率为 波数为 k , 波 u k p 它的振幅的变化也像一个传播的波 2 速为 ug k , k 2 它的角频率为 , 波数为 波速为 上述讨论的合成波称为波包。

)

)
上页 下页 返回 退出
两个同方向同频率简谐运动的合成
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )
A2
2
0

A
x
x
x x1 x2
x A cos(t )
2 1 2 2
x2
1

x1
A1
A A A 2 A1 A2 cos( 2 1 )
S1
S1P r1

yS1 A10 cos( t 10 ) yS2 A20 cos( t 20 )
P
S2
S 2 P r2
S1和 S2单独存在时,在P点引起的振动的方程为:
y1 A1 cos(t 10
y2 A2 cos(t 20
2 r1
2 r2
衍射是波动的共同特征
上页 下页 返回 退出
*三、波的反射和折射
反射与折射也是波的特征，当波传播到两种介 质的分界面时，波的一部分在界面返回，形成反射 波，另一部分进入另一种介质形成折射波。 折 射 定 律 的 推 导
i
n1 A
u 2t
C
i
r D
u1t 2
u1t

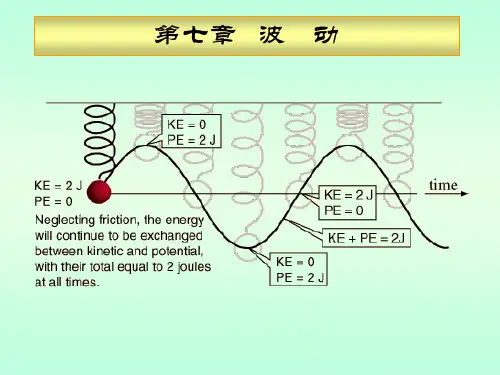
108847-大学物理-普通物理学-Chap 7-2

108847-大学物理-普通物理学-Chap 7-2
➢ E增大时，体积元从一侧吸收能量； E减小时，从 另一侧输出能量，从而实现能量的传递。
2、波的能流、能流密度：
能流：单位时间内通过某一面积的波的能量。
平均能流（一个周期内）： E w uS 1 2 A2 u S
2
能流密度（波的强度）：
类似于功率
通过垂直于波传播方向单位面积的平均能流。
I E w u 1 2 A2 u
y
0.1 sin1.75π 7.07 102 m
x1.5 m ,t 3.25s
υ
0.1π cos 1.75π 0.22 m / s
x1.5 m ,t 3.25s
§7-3 波的能量和能流密度
1、波的能量、能量密度：
设一列简谐纵波沿均匀细杆传播，波的表达式：
y Acos ω( t x ) u
(2) 波的叠加原理：几列波相遇处质元的位移为各列 波单独存在时在该点引起位移的矢量和。
波的叠加原理
2、波的干涉：
任意两列波在空间的叠加情况是很复杂的，但当两 列简谐波满足相干条件时，可在波场中得到稳定的 干涉图样。
相干条件： (1) 两列波具有相同的频率；
(2) 两列波具有相同的振动方向； (3) 两列波的相位相同或相位差保持恒定。
(1) 当x一定时，波函数为x位置处质点的振动方程：
y Acos[2 t ( 2 x )] y
式中： 2 x
o
为p位置处质点的振动初相位。
u
p
x
x
而： 2 x 为p点处振动落后于o点处振动的相位。
位移—时间图上相邻y 两个同相点的间隔即为周期T。
t o
T
(2) 当t 一定时，波函数为t 时刻各质元的位移分布情况： 波形图上相邻同相位点的间隔为波长λ。

高教版《普通物理学》chapter-7

高教版《普通物理学》chapter-7

1. 在电场的不同点上放同样的 试验电荷q0；
• 电场中各处的力学性质不同。
2. 在电场的同一点上放不同的试
验电荷。
•
F q0
与q0无关。
电场强度（intensity of electric
field）：
E
F
q0
返回 退出
E
F
q0
场强的大小： F/q0 场强的方向：正电荷在该处所受 电场力的方向。
§7-1 物质的电结构 库仑定律 一、电荷
最初对电的认识：摩擦起电和雷电 两种电荷（charge）：正电荷和负电荷 电性力：同号相斥、异号相吸 电荷量(electric quantity)：物体带电
的多少。
返回 退出
二、电荷守恒定律 在一个与外界没有电荷交换的系统内，无论进
行怎样的物理过程，系统内正、负电荷量的代数和 总是保持不变。
2. 距离平方反比关系，指数2的误差<10-16。
3. 静电力叠加原理
设有n个点电荷组成的点电荷系，点电荷 q
受到其他点电荷 qi 作用的总静电力为
F
i
Fi
1
4π 0
i
qqi ri 3
ri
q
qi
ri
返回 退出
例7-1 按量子理论，在氢原子中，核外电子快速地运 动着，并以一定的概率出现在原子核（质子〕的周 围各处，在基态下，电子在半径 r = 0.529×10-10 m的 球面附近出现的概率最大.试计算在基态下,氢原子内 电子和质子之间的静电力和万有引力,并比较两者的 大小。引力常量为G = 6.67×10-11 Nm2/kg2。
k
q1q2 r2
er12
k
q1q2 r3

普通物理学第7章第9节

普通物理学第7章第9节
E
2
S1
P dS
0
0 S 1 - S 2
P

0

P dS
由于S1在导体中， 0 P
S1

P dS
S2
+++ +++++++ - - - - - - ---
又
P

P dS
S

P dS
§7-9 有电介质时的高斯定理 电位移
一、有电介质时的高斯定理 电位移
在有电介质存在的电场中，高斯定理仍成立，但要 同时考虑自由电荷和束缚电荷产生的电场。 自由电荷 总电场

1 E dS
S
0
q
0

q
极化电荷
上式中由于极化电荷一般也是未知的，用其求解电 场问题很困难，为便于求解，引入电位移矢量，使 右端只包含自由电荷。
D dS q0
则可得有电介质 S 时的高斯定理 电位移线的描画方法同电场线相同。垂直于电位移 线单位面积上通过的电位移线数目等于该点电位移 的量值，称为电通量。
上页 下页 返回 退出
从有电介质时的高斯定理可知：通过电介质中任 一闭合曲面的电位移通量等于该面包围的自由电荷的 代数和。
P e 0 E
有电介质存在时的高斯定理的应用
（1）分析自由电荷分布的对称性，选择适当的高斯面 求出电位移矢量。 （2）根据电位移矢量与电场的关系，求出电场。
上页 下页 返回 退出
• 例题

上页 下页 返回 退出
选择进入下一节 §7-0 教学基本要求 §7-1 物质的电结构 库仑定律 §7-2 静电场 电场强度 §7-3 静电场的高斯定律 §7-4 静电场的环路定律 电势 §7-5 电场强度与电势梯度的关系 §7-6 静电场中的导体 §7-7 电容器的电容 §7-8 静电场中的电介质 §7-9 有电介质时的高斯定律 电位移 §7-10 静电场的能量

物理第七章

物理第七章

第七章、能量守恒第一节. 追寻守恒量1.小球下落实例这里举一个小球在两个对接的斜坡上来回滚动的例子，如果我们忽略摩擦力和空气阻力而只考虑重力，那么小球一定会两个斜坡之间来回滚动而且上升的高度都相同。

这是因为小球可以记住自己的高度，而这个记忆就是指能量或者能。

2.势能和动能小球被提升到高处具有了势能。

互相作用的物体凭借其位置而具有的能量，叫做势能。

小球从坡上滑落具有了动能。

物体由于运动而具有的能量，叫做动能。

小球在最高点下滑到最低点这个过程，势能转化为了动能：小球由最低点运动到最高点这个过程，动能又转化成了势能。

如果在整个过程中没有任何阻力，那么能量的总量就是势能与动能的和，总能量保持不变，能量的形式在动能和势能之间转化。

第二节、功1.功在人类认识能量的历程中建立了功的概念。

功和能量是两个密切相关的物理量，如果物体在力的作用下能量发生了变化，那么这个力一定对物体做了功。

我们用手按压桌子，桌子发生微小形变;用手按压弹簧，弹簧发生明显的形变；起重机吊起重物等等等，都是在力的作用下使物体发生了一定的状态改变，也就是发生了位移，那么引出力做功的两个要素，一个要素是力另一个要素是在力的方向上发生的位移。

力对物体所做的功，等于力的大小乘以沿着力的正方向或者反方向的位移的乘积（要么把力分解到位移上，要么把位移分解到力上），功是一个标量，单位J。

2.正功和负功我们可以将正功理解为作用方向和有效位移方向相同的力所做的功；负功反之，力的作用方向和有效位移方向相反。

第三节、功率1.功率力是一个物体对另一个物体的作用，所以我们说的做功是一个物体对另一个物体做功，比如说我骑着自行车载着一个人，那么我消耗了体力而坐车的人却没有，再比如说汽车载着我，汽车消耗了油箱里的汽油而我并没有消耗体力。

我们之前已经了解了速度，速度是衡量物体位置变化快慢的物理量，等于位移除以发生这段位移所用的时间；加速度是描述速度变化快慢的物理量，等于速度变化量除以发生这个速度变化量作用的时间。

普通物理学第二版第七章课后习题答案

普通物理学第二版第七章课后习题答案

第七章 刚体力学7.1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s 估算地球赤道上一点因地球自转具有的线速度和向心加速度.估算地心因公转而具有的线速度和向心加速度（自己搜集所需数据）.[解 答]7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.（1）假设转动是匀加速转动，求角加速度.(2)在此时间内，发动机转了多少转[解 答]（1）22(30001200)1/601.57(rad /s )t 12ωπβ⨯-⨯===V V（2）222220()(30001200)302639(rad)2215.7πωωθβ--===⨯所以 转数=2639420()2π=转7.1.3 某发动机飞轮在时间间隔t 内的角位移为球t 时刻的角速度和角加速度.[解 答]7.1.4 半径为0.1m 的圆盘在铅直平面内转动，在圆盘平面内建立O-xy 坐标系，原点在轴上.x 和y 轴沿水平和铅直向上的方向.边缘上一点A 当t=0时恰好在x 轴上，该点的角坐标满足21.2t t (:rad,t :s).θθ=+求（1）t=0时，（2）自t=0开始转45o 时，（3）转过90o时，A 点的速度和加速度在x 和y 轴上的投影.[解 答]（1） A ˆˆt 0,1.2,R j 0.12j(m/s).0,0.12(m/s)x y ωνωνν====∴==v（2）45θ=o时，由2A 1.2t t ,t 0.47(s)42.14(rad /s)v R πθωω=+==∴==⨯v v v得（3）当90θ=o时，由7.1.5 钢制炉门由两个各长1.5m 的平行臂AB 和CD 支承，以角速度10rad/s ω=逆时针转动，求臂与铅直45o 时门中心G 的速度和加速度.[解 答]因炉门在铅直面内作平动，门中心G 的速度、加速度与B 或D点相同。

所以：7.1.6 收割机拔禾轮上面通常装4到6个压板.拔禾轮一边旋转，一边随收割机前进.压板转到下方才发挥作用，一方面把农作物压向切割器，另一方面把切割下来的作物铺放在收割台上，因此要求压板运动到下方时相对于作物的速度与收割机前进方向相反. 已知收割机前进速率为1.2m/s ，拔禾轮直径1.5m ，转速22rev/min,求压板运动到最低点挤压作物的速度.[解 答]取地面为基本参考系，收割机为运动参考系。

物理大一上册第七章知识点

物理大一上册第七章知识点

物理大一上册第七章知识点第一节：力和弹簧物理学中的力是指作用在物体上使其发生形变、速度改变或者状态改变的因素。

常见的力有引力、电磁力、弹力等。

其中，弹力是一种在物体形变时产生的力。

弹簧是一种常见的储存弹性势能的装置。

当弹簧受到拉伸或压缩时，会产生弹力。

弹簧的弹力与其形变量成正比，比例常数称为弹簧的弹性系数，用符号k表示。

第二节：弹簧的胡克定律胡克定律是描述弹簧弹性力学性质的重要定律，它建立了弹簧形变和弹力之间的关系。

根据胡克定律，当弹簧形变量为x时，弹簧的弹力F和形变量之间的关系可以表示为F = -kx，其中负号表示弹力的方向与弹簧形变方向相反。

胡克定律适用于比较小的形变范围，并且在弹簧的材料性质不发生改变的情况下成立。

第三节：弹簧的势能弹簧在受到形变时具有弹性势能。

根据胡克定律，当弹簧形变量为x时，弹簧的弹性势能可以表示为Ep = 1/2kx^2，其中Ep表示弹簧的势能。

弹性势能是一种由形变引起的储存能量，当弹簧恢复原状时，势能会转化为其他形式的能量，如动能。

第四节：弹簧振子弹簧振子是由一个弹簧和一个与之相连的物体组成的物理系统。

当弹簧振子受到外力作用时，会发生振动。

弹簧振子的振动频率与弹簧的劲度系数和振子的质量有关。

振动频率可以用公式f = 1/2π√(k/m)表示，其中f表示振动频率，k表示弹簧的劲度系数，m表示振子的质量。

第五节：仰角和摩擦力物体在斜面上运动时，存在着与斜面接触的正压力、重力、法向加速度、摩擦力等因素。

斜面上物体的运动可以通过分解力的方式来分析。

其中，物体沿着斜面方向的分力可以分为重力和正压力的合力，与此方向相反的分力是摩擦力。

摩擦力可以分为静摩擦力和动摩擦力两种情况。

静摩擦力的大小与物体受到的正压力成正比，动摩擦力的大小与物体受到的正压力无关。

通过计算物体所受的合外力，可以确定物体在斜面上的加速度和运动状态。

第六节：滑车组滑车组是由多个滑轮组成的机械系统，常用于改变力的方向和大小。

普通物理学第二版第七章课后习题答案

普通物理学第二版第七章课后习题答案

普通物理学第二版第七章课后习题答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第七章 刚体力学7.1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s?估算地球赤道上一点因地球自转具有的线速度和向心加速度.估算地心因公转而具有的线速度和向心加速度（自己搜集所需数据）.[解 答]7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.（1）假设转动是匀加速转动，求角加速度.(2)在此时间内，发动机转了多少转？[解 答]（1）22(30001200)1/601.57(rad /s )t12ωπβ⨯-⨯===（2）22222()(30001200)302639(rad)2215.7πωωθβ--===⨯所以 转数=2639420()2π=转7.1.3 某发动机飞轮在时间间隔t 内的角位移为球t 时刻的角速度和角加速度.[解 答]7.1.4 半径为0.1m 的圆盘在铅直平面内转动，在圆盘平面内建立O-xy 坐标系，原点在轴上.x 和y 轴沿水平和铅直向上的方向.边缘上一点A 当t=0时恰好在x 轴上，该点的角坐标满足21.2t t (:rad,t :s).θθ=+求（1）t=0时，（2）自t=0开始转45时，（3）转过90时，A 点的速度和加速度在x 和y 轴上的投影.[解 答]（1） A ˆˆt 0,1.2,R j 0.12j(m/s).0,0.12(m/s)x y ωνωνν====∴==（2）45θ=时，由2A 1.2t t ,t 0.47(s)42.14(rad /s)v Rπθωω=+==∴==⨯得（3）当90θ=时，由7.1.5 钢制炉门由两个各长1.5m 的平行臂AB 和CD 支承，以角速度10rad/s ω=逆时针转动，求臂与铅直45时门中心G 的速度和加速度.[解 答]因炉门在铅直面内作平动，门中心G 的速度、加速度与B 或D 点相同。

普通物理学上册第七章

普通物理学上册第七章
3.电场强度 EF q0
4.点电荷的电场强度
E
1
4π0
q r2
er
5.电场强度的叠加原理
EEi
点电荷系的场强
E
1
4π0
rqi2i eri
连续带电体的场强
E
1
4π0
drq2 er
电荷线分布 dqdl 电荷面分布 dqdS
电荷体分布 dqdV
6.电通量
Ψ ESEdS
7.高斯定理
SEdS10 S内qi
三. 有导体和电介质时的电场 1.导体的静电平衡
导体内部场强处处为零 场强
表面附近场强垂直于表面
导体是等势体 电势
导体表面是等势面 2. 静电平衡时导体上电荷的分布
导体内部处处没有净电荷， 电荷只能分布在导体表面。
E 0
3.电容器的电容
C Q U
平行板电容器
C0
0S d
并联 C C 1 C 2 C n
三个点电荷间的静电力 FF 1F 2
F1
1
4π0
qr11q20er1
F2 4π10 qr22q20er2
F 1
4π0
q1q2 r2
er
e r2 q 2
q1 e r1
r1
r2 q0
F1
F2
3.静电力的叠加原理
作用在某一点电荷上的总静电力等于其他 各点电荷单独存在时对该点电荷所施静电力的 矢量和。
F F 1 F 2 F i
四. 库仑定律
1.点电荷
形状、体积与观察距离相比可以忽略的带电体。
2.库仑定律
两个静止点电荷之间相互作用力的大小与这两 个点电荷的电荷量的乘积成正比，而与这两个点电 荷之间的距离的平方成反比，作用力的方向沿着这 两个点电荷的连线，同号电荷相互排斥，异号电荷 相互吸引。

《普通物理学》课件-第七章 振动

《普通物理学》课件-第七章 振动

5g
等效劲度系数 （ke） f ke x
f: 恢复力 x: 偏离平衡位置的位移
0
ke m
弹簧的串联和并联
• 串联公式： 1/k = 1/k1 +1/k2
• 并联公式： k = k1 + k2
k1
k2
k1
k2
例：一劲度系数为 k 的弹簧均分为二，试求 均分后两弹簧并联的等效劲度系数 k'。
解：串联公式：
sinθ≈θ (θ<5o 0.3 rad)
O
l
T
当振幅很小时，单摆的振动为简谐振动。
mg
Quasi 1-D restoring force
f = -mgsinθ≈-mgθ= -mgx/l
k = mg/l, ω02 = k/m = g/l ω0 = √g/l
T 2 l
g
单摆实验 可以测g
复摆（物理摆）
A
ωt+
0
xx
旋 转 矢量 A的
x 端点在
轴上的投
影点的运
动为简谐
运动.
x Acos(t )
x Acos(t )
•复数表示：
将xy平面看作一个复平面
矢量端点对应于一个复数 （包含模和辐角）
xt Acost 0
x t Aeit0辐角
eit0 cost 0 i sin t 0
设B的质量为m， A的质量便是γm
A
v0
B
B
第一阶段是弹性碰撞
第二阶段：A做匀速直线运动；B，B '的质心做匀速直线运动，
B，B '相对质心作简谐振动。
弹性碰撞
mvA
mvB
(0)

普通物理学第7章第1节

普通物理学第7章第1节
12
q1q2 F12 k er12 2 r12
F12
q1q2 er12 F21 2 4π 0 r12 1
上页 下页 返回 退出
说明： 1.“静止”是指惯性系中相对于观察者静止。 2.适用于点电荷。 3.q1、q2取代数值。 4.遵守牛顿第三定律。 静电力的叠加原理： 实验证明，当空间中有两个 q 以上的点电荷时，作用在某一 点电荷上的总静电力等于其它 F 各点电荷单独存在时对该点电 q 荷所施静电力的矢量和，这一 结论叫做静电力的叠加原理。
1
q2
2
F
F F1 F2
i
q0 qi r0i 2 4π 0 r0i 1
F 1
上页 下页 返回 退出
选择进入下一节 §7-0 教学基本要求 §7-1 物质的电结构 库仑定律 §7-2 静电场 电场强度 §7-3 静电场的高斯定律 §7-4 静电场的环路定律 电势 §7-5 电场强度与电势梯度的关系 §7-6 静电场中的导体 §7-7 电容器的电容 §7-8 静电场中的电介质 §7-9 有电介质时的高斯定律 电位移 §7-10 静电场的能量
四、 库仑定律
点电荷 库仑定律 可以简化为点电荷的 1785年，库仑从扭秤实验 条件: 当带电体的形状和大小与 结果总结出了库仑定律 它们之间的距离相比可忽 扭 略时，这些带电体可看作 秤 是点电荷。 q1 q2
r
d
上页 下页 返回 退出
库仑定律
单位制 在真空中，两个静止点 有理化 电荷之间相互作用力与 1 k 这两个点电荷的电荷量 4 π 0 q1和q2的乘积成正比， 而与这两个点电荷之间 2 1 C 8.85 10 的距离r12（或r21）的平 0 2 Nm 4πk 方成反比，作用力的方 向沿着这两个点电荷的 ε0为真空电容率，则真空中 连线，同号相斥，异号 库仑定律数学形式: 相吸。

2020-2021人教版高一物理必修第七章功率课件ppt

2020-2021人教版高一物理必修第七章功率课件ppt

如图所示，质量为M的长木板放在光滑的水平面上，一个质量 为m 的滑块以某一速度沿木板表面从A端滑到B端，在木板上 前进了L，而木板前进了s 。若滑块与木板间的动摩擦系数为μ, 则摩擦力对滑块做的功为多少？对木板做的功多少？
解：
对滑块和木板进行受力分析，可知摩擦力对滑块 做负功，对木板做正功． 滑块相对于地面的位移为l1=l+L， 摩擦力对滑块做的功为
动2m时拉力的功率？
(g取10 m/s2，sin37°＝0.6，cos37°＝0.8)
解：
拉力 重力 支持力 摩擦力
WF＝Flcos37°＝10×2×0.8=16J． WG＝0J． WN＝0J．
f＝μFN＝μ(mg-Fsin37 °）
＝ ×3 (2×10-10×0.6)=6N 7
Wf＝-fl＝-6×2=-12J．
外力做的总功为 W总＝WF＋WG＋WN＋Wf＝16+0+0+(-12)=4J．
由牛顿第二定律可得：
a F1 f F cos 370 (mg F sin 370 )
m
m
lt 由1 a2t2l
可得
2a
解得t=2s
解得a=1m/s2
P1
W拉力 1的6 平 8均W功率： t2
（3）物体移动2m时的速度：
（3）若汽车以v1=6m/s的速度匀变速行驶求汽车实际功率 （4）若汽车从静止开始且保持以a=0.5m/s2的加速度做匀加 速运动这一过程能保持多少时间?
解（1）当牵引力和阻力相等的时候V最大，有P=Fv可得
v P 60000 m / s 12m / s F 0.1500010
（2）汽车车速为2m/s时的牵引力：F
A、W1>W2 P1<P2 C、W1=W2 P1>P2

普通物理7

普通物理7
ɶ dx ɶ v = Re( ) = Re(v ) = −ω A sin(ω t + ϕ ) dt ɶ d2x ɶ a = Re( 2 ) = Re(a ) = −ω 2 A cos(ω t + ϕ ) dt
同样，速度、加速度均取复数的实部。 同样，速度、加速度均取复数的实部。
例2：一个质点沿x轴作简谐运动，振幅A=0.06m，周期T=2s，初 ：一个质点沿 轴作简谐运动，振幅 ，周期 ， 轴作简谐运动 始时刻质点位于x 处且向x轴正方向运动 始时刻质点位于 0=0.03m处且向 轴正方向运动。求：（ ）初相 处且向 轴正方向运动。 ：（1） ；（2） 处且向x轴负方向运动时物体回到平衡位置 位；（ ）在x=-0.03m处且向 轴负方向运动时物体回到平衡位置 处且向 所需要的最短时间。 所需要的最短时间。 解：（1）用旋转矢量法，则初相位在第四象限 ：（ ）用旋转矢量法，
系统的总能量
1 1 2 2 2 2 E＝E k＋E p = mA ω sin (ωt + ϕ )＋ kA cos 2 (ωt + ϕ ) 2 2
k ω＝ m
1 1 2 2 2 E＝ mA ω ＝ kA 2 2
弹簧振子作简谐运动的能量与振幅的平方成正比
二、能量平均值 1、动能的时间平均值 、
1 Ek = T 1 1 1 2 2 2 2 2 2 ∫ 2 mA ω sin (ωt + ϕ )dt = 4 mA ω = 4 kA 0
图示
ϕ =−
π
3
处且向向x轴负方向运动到平衡位置 （2）从x=-0.03m处且向向 轴负方向运动到平衡位置，意 ） 处且向向 轴负方向运动到平衡位置， 味着旋转矢量从M 点转到M 味着旋转矢量从 1点转到 2点，因而所需要的最短时间满 足
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

前页 后页 目录 31
第7章 静止电荷的电场
例1 求电偶极子中垂线上的电场强度。P255
例解题：4
E
E E E
E
P
E
E
1
4π 0
(a2
q l2
/
4)
E E cos E cos
E
a
+
q
l
q
E
2
1
4π 0
(a2
q l2
/
4)
(a2
l/2 l2 /
4)1/ 2
前页 后页 目录 32
第7章 静止电荷的电场
r1
r2 q0
F1
F2
前页 后页 目录 21
第7章 静止电荷的电场
3.静电力的叠加原理
作用在某一点电荷上的总静电力等于其他 各点电荷单独存在时对该点电荷所施静电力的 矢量和。
F F1 F2 Fi
F1
1
4π 0
q1q0 r12
er1
Fi
1
4π 0
qiq0 ri2
eri
qn q2
q1
qi eri ri q0
量子化是微观世界的一个基本概念。
前页 后页 目录 17
第7章 静止电荷的电场
四. 库仑定律
1.点电荷
形状、体积与观察距离相比可以忽略的带电体。
2.库仑定律 两个静止点电荷之间相互作用力的大小与这两
个点电荷的电荷量的乘积成正比，而与这两个点电 荷之间的距离的平方成反比，作用力的方向沿着这 两个点电荷的连线，同号电荷相互排斥，异号电荷 相互吸引。
a r er
o x dx
x
(dE x )i (dE y ) j
Exi Ey j
dE
1
4π 0
dx
r2
er
前页 后页 目录 38
第7章 静止电荷的电场
dE
1
4π 0
dx
r2
er
dE
1
4π 0
dx
r2
dE x
1
4π 0
dx
r2
cos
dE y
1
4π 0
dx
r2
sin
y dE
P
a r er
o x dx
x
x2
)3/ 2
i
E
q
4π0 x2
i
x>>R，成为点电荷
。
本题完
前页 后页 目录 44
第7章 静止电荷的电场
例4 均匀带电圆盘轴线上一点P处的场强。
P解26：0例取半题径7 为r，宽度为dr细
环，由上例结论，细环在P
处的d场E 强
4π
0
xdq (r2
x
2
)3/
2
R
P
x 2πrdr 4π0(r 2 x2 )3/2
(R2
x x2 )1/2
E
1
4π 0
dq r2
er
dq er r
P dE
前页 后页 目录 34
第7章 静止电荷的电场
带电细线dq dl
E
L
1
4π 0
dl
r2
er
带电薄 dq dS
面
E
S
1
4π 0
dS
r2
er
带电 dq dV
体
E
V
1
4π 0
dV
r2
er
电荷线密度
dl
电荷面密度
dS
电荷体密度
dV
前页 后页 目录 35
dS
q0
S内
前页 后页 目录 12
第7章 静止电荷的电场
四. 静电场的能量
点电荷在电场中的静电能量
W q0V 电场能量密度
we
1 2
0
E
2
电场能量
W wedV
介质中
we
1ED 2
前页 后页 目录 13
第7章 静止电荷的电场
电容器的静电能
W 1 Q2 1 QU 1 CU 2
2C 2
前页 后页 目录 25
第7章 静止电荷的电场
3.电场对点电荷的作用 力
F E q
F qE
负点电荷受力 方向与该点的场强 方向相反。
E A
F
q
注意：E 是点电荷q存在时A点的场
强。
前页 后页 目录 26
第7章 静止电荷的电场
4.电场对带电体的作用 力
dF Edq
F dF
Edq
电荷元
dq dF
b
Uab Va Vb
E dl
a
4.电场力的功
b
Aab a q0E dl q0Uab
5.电场强度与电势梯度的关系
E gradV
E ( V i V j V k ) x y z
前页 后页 目录 8
第7章 静止电荷的电场
三. 有导体和电介质时的电场 1.导体的静电平衡
导体内部场强处处为零 场强
第7章 静止电荷的电场
点电荷系的场强
E
1
4π 0
qi ri2
eri
连续带电体的场强
E
1 dq
4π0 r 2 er
电荷线分布 dq dl 电荷面分布 dq dS 电荷体分布 dq dV
前页 后页 目录 3
第7章 静止电荷的电场
6.电通量
Ψ E S E dS
7.高斯定理
S
E
dS
1
Cn
前页 后页 目录 10
第7章 静止电荷的电场
4.电介质对电场的影响
电极化强度 P pi V
P e0E
电位移矢量 D 0E P
D r0E r 1 e
极化电荷面密度 P en
前页 后页 目录 11
第7章 静止电荷的电场
充满电介质的电容器
C rC0
5. 电介质中的高斯定理
S
D
E
1
4π 0
(a2
ql l2 /
4)3/ 2
电偶极矩p ql
E
1
4π 0
(a 2
p l2 /
4)3/2
a >> l
E
1
4π 0
p a3
E
E
P
E
a
+
q
l
q
本题
前页 后页 目录完 33
第7章 静止电荷的电场
3. 连续分布电荷的电场强 度 电荷元：dq
E
1
4π 0
q r2
er
dE
1
4π 0
dq r2
er
库仑力或静电力
前页 后页 目录 18
第7章 静止电荷的电场
F
k
q1q2 r2
真空中 k 8.99 109 N m2 /C2
r q1 er
F q2
两电荷同号时
F
k
q1q2 r2
er
er 是另一电荷指向受力电荷的单位矢量
前页 后页 目录 19
第7章 静止电荷的电场
单位制有理化 k 1
4π 0
F
前页 后页 目录 27
第7章 静止电荷的电场
三. 电场强度的计算
1. 点电荷的电场强 度 EF
q0
E
1
4π 0
q r2
er
大小：E
1
4π 0
q r2
方向：沿er 方向
F
1
4π 0
q0q r2
er
q0 E F rP q er
前页 后页 目录 28
第7章 静止电荷的电场
E
1
4π 0
q r2
er
E
1
4π 0
L E dl 0
2.电势
电势零点
VP P
E dl
点电荷的电势
V 1 q
4π0 r
V W q0
前页 后页 目录 6
第7章 静止电荷的电场
电势叠加原理
V Vi
i
点电荷系的电势
V
1 qi
i 4π0 ri
带电物体的电势
V 1 dq
4π0 r
前页 后页 目录 7
第7章 静止电荷的电场
3.电势差
dq r x
dE
dr
P处的场强
E
R x 2πrdr 0 4π0(r 2 x2 )3/2
2 0
1
(R2
x x2 )1/2
前页 后页 目录 45
第7章 静止电荷的电场
E
2 0
1
(R2
x x2 )1/2
讨论：
1. R>>x E
，
2 0
2. R<<x，
无限大均匀带电平面两侧是 匀强电场，场强方向垂直于该平 面。图中是带正电的电场。
第7章 静止电荷的电场
第7章 静止电荷的电场
一. 电场强度
1.库仑定律
F
1
4π 0
q1q2 r2
er
2.静电力的叠加原理
F F1 F2 Fn
前页 后页 目录 1
第7章 静止电荷的电场
3.电场强度
E F q0
4.点电荷的电场强度
E
1
4π 0
q r2
er
5.电场强度的叠加原理
E Ei
前页 后页 目录 2
Fi
前页 后页 目录 22
第7章 静止电荷的电场
4.带电物体对点电荷的作用力
dF