下载文档原格式
08年交大自主招生试题注意事项：1、本试卷共三部分，16题，满分100分。
2、考试时间为90分钟。
3、计算题的解答必须写出必要的解题过程，只有结果，没有过程的不能得分。
一、选择、填空题（共9题，每题4分）1、有一劲度系数为k 的轻弹簧，竖直放置，下端悬一质量为m 的小球。
先使弹簧为原长，而小球恰好与地接触。
再将弹簧上端缓慢地提起，直到小球离开地面h 为止。
在此过程中外力所作的功为________________。
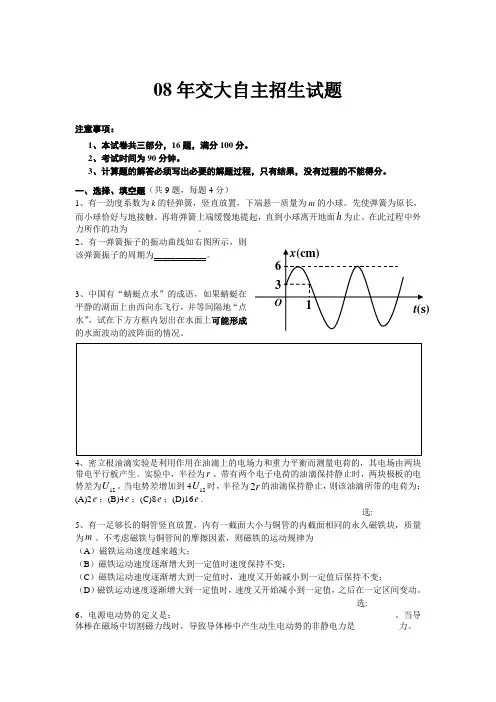
2、有一弹簧振子的振动曲线如右图所示，则该弹簧振子的周期为____________。
3、中国有“蜻蜓点水”的成语，如果蜻蜓在平静的湖面上由西向东飞行，并等间隔地“点水”，试在下方方框内划出在水面上可能形成的水面波动的波阵面的情况。
4、密立根油滴实验是利用作用在油滴上的电场力和重力平衡而测量电荷的，其电场由两块带电平行板产生。
实验中，半径为r 、带有两个电子电荷的油滴保持静止时，两块极板的电势差为12U 。
当电势差增加到412U 时，半径为r 2的油滴保持静止，则该油滴所带的电荷为： (A)2e ；(B)4e ；(C)8e ；(D)16e .选:___________5、有一足够长的铜管竖直放置，内有一截面大小与铜管的内截面相同的永久磁铁块，质量为m 。
不考虑磁铁与铜管间的摩擦因素，则磁铁的运动规律为 （A ）磁铁运动速度越来越大；（B ）磁铁运动速度逐渐增大到一定值时速度保持不变；（C ）磁铁运动速度逐渐增大到一定值时，速度又开始减小到一定值后保持不变； （D ）磁铁运动速度逐渐增大到一定值时，速度又开始减小到一定值，之后在一定区间变动。
选:____________6、电源电动势的定义是：__________________________________________________。
当导体棒在磁场中切割磁力线时，导致导体棒中产生动生电动势的非静电力是__________力。
（b ）7、如图所示，质量为m ，带电量为q 的粒子，在重力作用下由静止下落h 高度后垂直进入一高度为L 的匀强磁场区域，磁感应强度方向垂直纸面向内，大小为B 。
2008年全国普通高等学校招生统一考试上海数学试卷（文史类）__________录入者：福建泉州第七中学 林志敏老师考生注意：1．答卷前，考生务必将姓名、高考准考证号、校验码等填写清楚．2．本试卷共有21道试题，满分150分，考试时间120分钟．请考生用钢笔或圆珠笔将答案直接写在试卷上．一、填空题（本大题满分44分）本大题共有11题，只要求直接填写结果，每个空格填对得4分，否则一律得零分．1．不等式11x -＜的解集是 ． 2．若集合{}|2A x x =≤，{}|B x x a =≥满足{2}AB =，则实数a = ．3．若复数z 满足(2)z i z =- (i 是虚数单位)，则z = ． 4．若函数f (x )的反函数为12()log fx x -=，则()f x = ．5．若向量a ，b 满足12a b ==，且a 与b 的夹角为3π，则a b += ． 6．若直线10ax y -+=经过抛物线24y x =的焦点，则实数a = ． 7．若z 是实系数方程220x x p ++=的一个虚根，且2z =，则p = ．8．在平面直角坐标系中，从六个点：(00)(20)(11)(02)(22)A B C D E ，，，，，，，，，中任取三个，这三点能构成三角形的概率是 （结果用分数表示）．9．若函数()()(2)f x x a bx a =++（常数a b ∈R ，）是偶函数，且它的值域为(]4-∞，，则该函数的解析式()f x = ．10．已知总体的各个体的值由小到大依次为2，3，3，7，a ，b ，12，13.7，18.3，20，且总体的中位数为10.5．若要使该总体的方差最小，则a 、b 的取值分别是 ．11．在平面直角坐标系中，点A B C ，，的坐标分别为(01)(42)(26)，，，，，．如果()P x y ，是ABC △围成的区域（含边界）上的点，那么当w xy =取到最大值时，点P 的坐标是 ______ ．二、选择题（本大题满分16分）本大题共有4题，每题都给出代号为A 、B 、C 、D 的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分．12．设p 是椭圆2212516x y +=上的点．若12F F ，是椭圆的两个焦点，则12PF PF +等于（ ） A ．4 B ．5 C ．8 D ．1013．给定空间中的直线l 及平面α．条件“直线l 与平面α内两条相交直线都垂直”是“直线l 与平面α垂直”的（ ）Ａ．充分非必要条件 Ｂ．必要非充分条件C ．充要条件 Ｄ．既非充分又非必要条件14．若数列{}n a 是首项为l ，公比为32a -的无穷等比数列，且{}n a 各项的和为a ，则a 的值是（ ） Ａ．1 Ｂ．2 Ｃ．12 Ｄ．5415．如图，在平面直角坐标系中，Ω是一个与x 轴的正半轴、y 轴的正半轴分别相切于点C 、D 的定圆所围成的区域（含边界），A 、B 、C 、D 是该圆的四等分点．若点()P x y ，、点()P x y '''，满足x x '≤且y y '≥，则称P 优于P '．如果Ω中的点Q 满足：不存在Ω中的其它点优于Q ，那么所有这样的点Q 组成的集合是劣弧（ ） Ａ．ABB ．BCC ．CD D ．DA三、解答题（本大题满分90分）本大题共有6题，解答下列各题必须写出必要的步骤．16．(本题满分12分)如图，在棱长为2的正方体1111ABCD A B C D -中，E 是BC 1的中点．求直线DE 与平面ABCD 所成角的大小（结果用反三角函数值表示）．17．（本题满分13分）如图，某住宅小区的平面图呈扇形AOC ．小区的两个出入口设置在点A 及点C 处，小区里有两条笔直的小路AD DC ，，且拐弯处的转角为120．已知某人从C 沿CD 走到D 用了10分钟，从D 沿DA 走到A 用了6分钟．若此人步行的速度为每分钟50米，求该扇形的半径OA 的长（精确到1米）．18．（本题满分15分）本题共有2个小题，第1个题满分5分，第2小题满分10分． 已知函数f (x )=sin2x ，g (x )=cos π26x ⎛⎫+ ⎪⎝⎭，直线()x t t =∈R 与函数()()f x g x ，的图像分别交于M 、N 两点． （1）当π4t =时，求｜MN ｜的值； （2）求｜MN ｜在π02t ⎡⎤∈⎢⎥⎣⎦，时的最大值．19．（本题满分16分）本题共有2个小题，第1小题满分8分，第2小题满分8分． 已知函数||1()22x x f x =-． （1）若()2f x =，求x 的值；（2）若2(2)()0tf t mf t +≥对于[12]t ∈，恒成立，求实数m 的取值范围．20．（本题满分16分）本题共有3个小题，第1小题满分3分，第2小题满分6分，第3小题满分7分．已知双曲线2212x C y -=：．（1）求双曲线C 的渐近线方程；（2）已知点M 的坐标为(01)，．设p 是双曲线C 上的点，Q 是点P 关于原点的对称点．记MP MQ λ=．求λ的取值范围；（3）已知点D E M ，，的坐标分别为(21)(21)(01)---，，，，，，P 为双曲线C 上在第一象限内的点．记l 为经过原点与点P 的直线，s 为DEM △截直线l 所得线段的长．试将s 表示为直线l 的斜率k 的函数． 21．（本题满分18分）本题共有3个小题，第1小题满分４分，第2小题满分６分，第3小题满分8分． 已知数列{}n a ：11a =，22a =，3a r =，32n n a a +=+（n 是正整数），与数列 {}n b ：11b =，20b =，31b =-，40b =，4n n b b +=（n 是正整数）． 记112233n n n T b a b a b a b a =++++．（1）若1231264a a a a ++++=，求r 的值；（2）求证：当n 是正整数时，124n T n =-；（3）已知0r >，且存在正整数m ，使得在121m T +，122m T +，，1212m T +中有4项为100．求r 的值，并指出哪4项为100．2008年全国普通高等学校招生统一考试上海数学试卷（文史类）答案要点及评分标准__________录入者：福建泉州第七中学 林志敏老师一、（第1题至第11题） 1. （0，2）. 2. 2.3. 1+i.4. ()2xx R ∈.5..6. -1.7. 4.8.45.9. 224x -+10. 10.5,10.5a b ==11. 5,52⎛⎫ ⎪⎝⎭.二、（第12题至第15题）三、（第16题至第21题）16. 【解】过E 作EF ⊥BC ，交BC 于F ，连接DF . ∵ EF ⊥平面ABCD ，∴ ∠EDF 是直线DE 与平面ABCD 所成的角. ……………4分 由题意，得EF =111.2CC = ∵11,2CF CB DF ==∴=..8分 ∵ EF ⊥DF ， ∴ tan EF EDF DF ∠==……………..10分 故直线DE 与平面ABCD 所成角的大小是arctan5….12分 17. 【解法一】设该扇形的半径为r 米. 由题意，得CD =500（米），DA =300（米），∠CDO=060……………………………4分 在CDO ∆中，2222cos 60,CD OD CD OD OC +-⋅⋅⋅=……………6分 即()()22215003002500300,2r r r +--⨯⨯-⨯=…………………….9分 解得490044511r =≈（米）. …………………………………………….13分【解法二】连接AC ，作OH ⊥AC ，交A C 于H …………………..2分由题意，得CD =500（米），AD =300（米），0120CDA ∠=………….4分2220222,2cos12015003002500300700,2ACD AC CD AD CD AD ∆=+-⋅⋅⋅=++⨯⨯⨯=在中 ∴ AC =700（米） …………………………..6分22211cos .214AC AD CDCAD AC AD +-∠==⋅⋅………….…….9分在直角11,350,cos 0,14HAO AH HA ∆=∠=中（米） ∴ 4900445cos 11AH OA HAO ==≈∠（米）. ………………………13分18、【解】（1）sin 2cos 2446MN πππ⎛⎫⎛⎫=⨯-⨯+ ⎪ ⎪⎝⎭⎝⎭…………….2分 231cos.32π=-=………………………………5分 （2）sin 2cos 26MN t t π⎛⎫=-+⎪⎝⎭3sin 2cos 222t t =- …………...8分26t π⎛⎫=-⎪⎝⎭…………………………….11分 ∵ 0,,2,,2666t t πππππ⎡⎤⎡⎤∈-∈--⎢⎥⎢⎥⎣⎦⎣⎦ …………13分∴ ｜MN . ……………15分 19、【解】（1）()()100;0,22x xx f x x f x <=≥=-当时，当时. …………….2分由条件可知，2122,22210,2x x x x -=-⋅-=即解得 21x =…………6分∵ (220,log 1x x >∴= …………..8分（2）当2211[1,2],2220,22t t t ttt m ⎛⎫⎛⎫∈-+-≥ ⎪ ⎪⎝⎭⎝⎭时 ……………10分即 ()()242121.t t m -≥--()22210,21.t t m ->∴≥+ ………………13分 ()2[1,2],12[17,5],t t ∈∴-+∈--故m 的取值范围是[5,)-+∞ …………….16分20、【解】（1）所求渐近线方程为0,0y y =+= ……………...3分（2）设P 的坐标为()00,x y ，则Q 的坐标为()00,x y --， …………….4分()()000,1,1o MP MQ x y x y λ=⋅=-⋅---22200031 2.2x y x =--+=-+ ……………7分02x ≥λ∴的取值范围是(,1].-∞-……………9分（3）若P 为双曲线C 上第一象限内的点，则直线l 的斜率.2k ⎛∈ ⎝⎭……………11分由计算可得，当()1(0,],2k s k ∈=时当()1,22k s k ⎛∈= ⎝⎭时……………15分∴ s 表示为直线l 的斜率k 的函数是()1(0,],21.2k s k k ∈=⎛∈ ⎝⎭….16分21、【解】（1）()()()12312...12342564786a a a a r r r r ++++=++++++++++++++484.r =+………………..2分∵ 48464, 4.r r +=∴= ………………..4分【证明】（2）用数学归纳法证明：当12,4.n n Z T n +∈=-时① 当n=1时，1213579114,T a a a a a a =-+-+-=-等式成立….6分 ② 假设n=k 时等式成立，即124,k T k =- 那么当1n k =+时，()121211231251271291211121k k k k k k k k T T a a a a a a +++++++=+-+-+-………8分 ()()()()()()481884858488k k k r k k k r k =-++-+++-++++-+()4441,k k =--=-+等式也成立.根据①和②可以断定：当12,4.n n Z T n +∈=-时…………………...10分【解】（3）()1241.121,12241;123,12441;125,12645;127,1284;129,121044;m n n n n T m m n m m T m n m m T m r n n m m T m r n m m T m r n m m T m =-≥=++=+=++=-+-=++=+-=++=--=++=+当时，当时，当时，当时，当时，1211,1212,4 4.n n m m T m =++=--当时………………………..13分∵ 4m+1是奇数，41,4,44m r m r m -+-----均为负数，∴ 这些项均不可能取到100. ………………………..15分此时，293294297298,,,T T T T 为100. …………………………18分。
高校自招数学试题及答案一、选择题（每题4分，共40分）1. 下列哪个数是无理数？A. 0.33333…（循环）B. πC. √2D. 1答案：B、C2. 已知函数f(x) = 2x - 3，求f(5)的值。
A. 7B. 4C. 1D. 2答案：A3. 若a > b > 0，下列不等式中正确的是：A. a^2 > b^2B. a + b > 2√(ab)C. a/b > b/aD. a^3 > b^3答案：D4. 已知等差数列的首项为1，公差为2，求第10项的值。
A. 19C. 17D. 16答案：A5. 圆的半径为5，求圆的面积。
A. 25πB. 50πC. 75πD. 100π答案：B6. 已知三角形ABC，∠A = 90°，AB = 3，AC = 4，求BC的长度。
A. 5B. 6C. 7D. 8答案：A7. 函数y = x^2 - 4x + 4的顶点坐标是什么？A. (2, 0)B. (-2, 0)C. (2, 4)D. (-2, 4)答案：A8. 已知正弦函数sin(x)的周期为2π，求余弦函数cos(x)的周期。
B. 2πC. 4πD. 8π答案：B9. 根据勾股定理，直角三角形的斜边长度是两直角边长度的平方和的平方根。
设a和b是直角边，c是斜边，下列哪个表达式是正确的？A. c = √(a^2 + b^2)B. a = √(c^2 + b^2)C. b = √(c^2 - a^2)D. c = √(b^2 - a^2)答案：A10. 已知一个数列的前三项为1, 1, 2，且每一项都是前两项的和，求第5项的值。
A. 4B. 5C. 6D. 7答案：C二、填空题（每题4分，共20分）11. 根据二项式定理，展开式(a + b)^3的通项公式是________。
答案：T_{r+1} = C_{3}^{r}a^{3-r}b^{r}12. 如果一个函数是奇函数，那么f(-x)等于________。
自主招生真题分类解析（下午课程）函数性态例1、若()f x 为R 上函数，且(10)(10)f x f x +=-，(20)(20)f x f x -=-+，则()f x 为（ ）(A) 奇函数且周期函数； (B) 奇函数且非周期函数； (C) 偶函数且周期函数； (D) 偶函数且非周期函数．例2、设()f x 和()g x 是定义在R 上的两个函数，12,x x 是R 上任意两个不等的实数.（1）设1212|()()||()()|f x f x g x g x +≥+恒成立，且()y f x =是奇函数， 判断函数()y g x =的奇偶性并说明理由；（2）设1212|()()||()()|f x f x g x g x -≥-恒成立，且()y f x =是周期函数， 判断函数()y g x =的周期性并说明理由；（3）设1212|()()||()()|f x f x g x g x ->-恒成立，且()y f x =是R 上的增函数， 判断函数()h x =()()f x g x +与函数'()()()h x f x g x =-在R 上的单调性并说明理由.例3、（交大2000联读）函数()f x =()x R ∈的反函数是_______________.例4、（交大2002保送）设()|lg |,,f x x a b =为实数，且0,,()()2()2a ba b a b f a f b f +<<==若满足，试写出a 与b 的关系，并证明在这一关系中存在b 满足34b <<.例5、（复旦2004保送）若存在M ，使任意t D ∈（D 为函数()f x 的定义域），都有()f x M ≤，则称函数()f x 有界．问函数11()sin f x x x =在1(0,)2x ∈上是否有界？例6、（交大2008冬令营）已知函数2()f x ax bx c =++(0)a ≠，且()f x x =没有实数根．那么(())f f x x =是否有实数根？并证明你的结论．导数积分例1、已知函数32()33(2)1f x x ax a x =++++有极大值又有极小值，则a 的取值范围是 .例2、设010211()cos ,()'(),()'(),,()'()n n f x x f x f x f x f x f x f x +====,,n N *∈则2008()f x ．例3、请您设计一个帐篷。
+y 2=1有交点,则11a 2+1b2 1,即有1a 2+1b2 1.2 隐性轨迹为抛物线例3 (2008年重庆文)函数f (x )=si n x5+4co s x(0 x 2 )的值域是( ).A [-14,14]B [-13,13]C [-12,12]D [-23,23]常规解法 令5+4cos x =t(1 t 3),则sin 2x =16-(t 2-5)216,当0 x时,si n x =16-(t 2-5)216=-t 4+10t 2-94,f (x )=si n x 5+4co s x=-t 4+10t 2-94t =-(t 2+9t2)+104-2t 29t 2+104=12,当且仅当t =3时取等号.同理可得当 <x 2 时,f(x ) -12,综上可知f (x )的值域为[-12,12],故选C.图3轨迹解法 令Y =f 2(x )=sin 2x 5+4cos x ,则Y =sin 2x 5+4cos x =1-cos 2x 5+4cos x设P (-4cos x ,cos 2x )则Y 表示两点P (-4cos x,cos 2x ),A (5,1)连线的斜率,而点P 的轨迹为抛物线y =x 216(0 y 1)的一段,如图3,当直线AP 平行于x 轴时,Y 取最小值;当直线AP 与抛物线相切时,Y 取最大值14,所以0 Y 14,即-12f (x )12.所以函数f (x )的值域为[-12,12].介绍几道2008年自主招生数学试题湖北省十堰市东风高级中学 442001 甘志国高校自主招生考试数学试题材料鲜活,试题的结构常以5~7道解答题的形式出现(如2008年清华大学、北京大学、浙江大学的自主招生试题),也有与本省高考数学试卷的形式类似的(如2008年山东大学自主招生试题),试题的难度一般略高于高考题.下面介绍几道2008年自主招生数学试题,且这里给出的解答多与原参考答案不同.题1(2008年北京大学自主招生数学试题)求证:边长为1的正五边形对角线长为1+52.原参考解答是用平面几何中的三角形相似证得的,下面给出一种三角解法.解 选择正五边形的两条共顶点的对角线及其一边组成等腰三角形,再作其底边上的高,又设这个正五边形对角线长为x,得si n18 =0.5x ,x =12si n18.下面求sin18 (实际上,有很多资料把si n18 =5-14作为特殊角的三角函数值列出此值为黄金分割数5-120.618的一半,挺好记的;高一数学老师应当介绍si n18 的值及其算法,并不难):由公式sin2 =2s i n cos ,cos3 =4cos 3 -3cos 及si n36 =cos54 ,立得2si n18 cos18 =4cos 318 -3co s18 ,2sin18 =4co s 218 -3=4(1-sin 218 )-3,4sin 218 +2sin18 -1=0,si n18 =5-14所以所求正五边形对角线长为x =12s i n18 =1+52.题2(2008年复旦大学自主招生数学试题)请证明2是一个无理数.证明 假设2是有理数,则可设2=mn(m,n 是两个互质的正整数),得m 2=2n 2,所以m 2是偶数,进而得m 也是偶54ZHONGXUESHUXUEZAZHI中学数学杂志 2009年第1期数(因为当m 是奇数时,m 2是奇数),又可得m 2(=2n 2)是4的倍数,n 2是偶数,n 也是偶数,得m,n 均是偶数,这与m,n 互质矛盾!说明2是无理数.以上证明初二学生即可弄懂,反证法教科书上虽然作了介绍,但平时训练的极少,所以学生对这种证法很陌生(而2008年高考数学江苏卷第19题第(2)问就是需要用反证法证明的题目),我们在平时的教学中应当重视这方面的训练.2还是人类历史上发现的第一个无理数,是Py thagoras (约公元前500年,希腊学者)学派的成员H i ppasus 所发现的,从而产生了数学史上的第一次危机,所以学生还应当尽可能的通过课外阅读等手段扩大知识面.题3 (2008年浙江大学自主招生数学试题),A ={(x,y )|(x -1)2+(y -2)254},B ={(x,y )||x -1|+2|y -2| a },A B,求a 的取值范围.原参考解答是:通过换元后可知,题意即,若{(x,y )|x 2+y 254} {(x,y )||x |+2|y | a },求正数a 的取值范围.再通过画图(由对称性,可以只考虑第一象限的图形),得圆x 2+y 254的圆心即坐标原点到直线x +2y =a 的距离不小于该圆的半径52,得所求a 的取值范围是[52,+ ).下面给出一种所用知识更少的解法.解 题意即,若(x -1)2+(y -2)2 54|x -1|+2|y -2| a,求实数a 的取值范围.因为(x -1)2+(y -2)2 54|y -2|54-(x -1)2,所以题设等价于|x -1|+254-(x -1)2 a 恒成立.设|x -1|=t ,得t 0,题设即函数z =t+5-4t 2(t 0)的最大值z m ax a,下面用两种方法求z m ax .法1 可得(z -t)2=5-4t 2,5t 2-2z t+(z 2-5)=0, =4z 2-20(z 2-5) 0-52z52,还可得当且仅当t =12即x =32或-12时,z =52,所以z m ax =52.法2 可得5-4t 2 0,0 t52,所以可设t =52s i n (02),得z =t +5-4t 2=52s i n +5cos ,=52(15s i n +25cos )=52si n ( + )(02),其中 =arccos15.由此也可得:当且仅当 + = 2即 =arcsin 15也即t =12就是x =32或-12时,z m ax =52.所以所求a 的取值范围是[52,+ ).题4 (2008年浙江大学自主招生数学试题)已知x >0,y >0,a =x +y,b =x 2+xy +y 2,c =mx y,问是否存在正数m 使得对于任意正数x,y,可使a 、b 、c 为一个三角形的三条边,如果存在,求出m 的值;如果不存在,请说明理由.解 因为a >b ,所以存在正数m 满足题意的充要条件是对于任意的正数x,y 有下式成立:x +y +x 2+xy +y 2>mxyx 2+xy +y 2+mx y >x +y可设y =k 2x,(k >0),得1+k 2+1+k 2+k 4>mk1+k 2+k 4+m k >1+k 2(k +1k )+(k +1k )2-1m i n>mm >(k +1k)-(k +1k )2-1m ax设k +1k =t ,得t 2,所以(t +t 2-1)m in >mm >(1t +t 2-1)m ax再由函数的单调性,可立得满足题意的正数m 存在,且m 的值有无数多个,其取值范围是(2-3,2+3).题5 (2008年南京大学自主招生数学试题)若正数a 、b 、c 满足a +b +c =1,求证:(a +1a )(b +1b )(c +1c) 100027.高中生在学习 不等式的证明 时,大多都证明过这样的题:若正数a、b 满足a +b =1,求证:(a +1a )(b +1b) 254.简证如下:先得0<ab (a +b 2)2=14,又函数f (x )=55中学数学杂志 2009年第1期ZHON GXUES HUXUEZAZHIx +1x 在(0,1)上是减函数,所以ab +1ab 14+4=174,再得(a +1a )(b +1b )=(ab +1ab )+(b a +a b ) 174+2=254,对于该题的深入研究,就会得到题5的问题.下面给出题5的两个简证,并推广其结论.证法1 因为在题5的不等式中,当且仅当a =b =c =13时取等号,为了使a +1a =a +1m a +1m a + +1ma (共m 个1m a )能使用均值不等式且等号能取到,应让a =1ma且a =13,得m =9,所以有如下证法:a +1a=a +19a +19a + +19a (共9个19a ) 1010a(9a)9,同理,有b +1b10 10b (9b )9,c +1c 10 10c(9c)9所以(a +1a )(b +1b )(c +1c ) 10310abc(93abc)9,再由0<abc(a +b +c 3)3=127,可得:(a +1a)(b +1b )(c +1c ) 100027(当且仅当a =b =c =13时取等号).由此思路,还可证得.推广1 若正数a 1,a 2, ,a n 满足ni=1a i =1,则ni=1(a i+1a i ) (n +1n )n (当且仅当a 1=a 2= =a n =1n 时取等号).证法2 (a +1a )(b +1b )(c +1c )=a 2+1b 2+1c 2+1=a 2b 2c 2+(a 2b 2+b 2c 2+c 2a 2)+(a 2+b 2+c 2)+1abca 2b 2c 2+3 (3a 2b 2c 2)2+3 (3a 2b 2c 2)+1abc =(3abc +13abc )3,再由0<abc(a +b +c 3)3=127,及函数f(x )=x +1x在(0,1)上是减函数,可得要证结论成立!推广2 若a,a 1,a 2, ,a nR +,ni=1a in a ,则ni=1(a i +aa i)ni=1a in+nani=1a in(当且仅当a 1=a 2= =a n 时取等号).证明ni=1(a i +aa i )=ni=1(a 2i +a)ni=1a i=1ni=1a i(a n +a n-11 i 1 na 2i 1+a n-21 i 1<i2 na 2i 1a 2i 2++a1 i 1<i 2< <i n-1 na 2i 1a 2i 2 a 2i n-1+a 21a 22 a 2n )=a n+nk =1a n-k1 i 1<i 2< <i k n(a i 1a i 2 a i k )2ni=1a i,注意到和式1 i 1<i 2< <i k n(a i 1a i 2 a i k )2是C k n 项的和,由均值不等式,得1 i 1<i 2< <i k n(a i 1a i 2 a i k )2 C k nC k n1 i 1<i 2< <i k n(a i 1a i 2 a i k)2=C k nC k n(a 1a 2 a n )2kC k n n=C k nnni=1a i2k(当且仅当a 1=a 2= =a n 时取等号).所以ni=1a i +aa ia n+nk =1an-kCk nnni=1a i2kn i=1a i=a +nni=1a i2nnn i=1a inni=1a i +a a inni=1a i +anni=1a in(当且仅当a 1=a 2= =a n 时取等号).又由均值不等式,得0<nni=1a ini=1a in(当且仅当a 1=a 2= =a n 时第一个 中取等号)再由函数f (x )=x +ax 在(0,a ]上是减函数,可得nni=1a i +anni=1a ini=1a i n+nani=1a i>0(当且仅当a 1=a 2= =a n 时 中取等号)从而可得推广2成立.(推广1显然是推广2的特例)56ZHONGXUESHUXUEZAZHI中学数学杂志 2009年第1期。
2008年上海市普通高等学校春季招生考试数 学 试 卷考生注意：1．答卷前，考生务必将姓名、高考座位号、校验码等填写清楚．2．本试卷共有22道试题，满分150分．考试时间120分钟．一．填空题（本大题满分48分）本大题共有12题，只要求直接填写结果，每题填对得4分，否则一律得零分．1．已知集合{1A x x =<-或}23x ≤<，{}24B x x =-≤<，则AB = ． 【答案】{}4x x <【详解】略 2．计算：131lim 32n n n n +→∞+=+ ． 【答案】13【详解】 113131133lim lim 3232333n n n n n n n n n n n n ++→∞→∞++==++． 3．函数()1f x x =-的定义域是 ． 【答案】[2,1)(1,3]-【详解】 定义域满足22360110x x x x x -≤≤⎧-++≥⎧ ⇒⎨⎨≠-≠⎩⎩4．方程2cos 14x π⎛⎫-= ⎪⎝⎭在区间(0,)π内的解是 ． 【答案】712x π= 【详解】 12cos 1cos 44243x x x ππππ⎛⎫⎛⎫-=⇒-=⇒-= ⎪ ⎪⎝⎭⎝⎭．5．已知数列{}n a 是公差不为零的等差数列，11a =．若125a a a 、、成等比数列，则n a =．【答案】21n a n =-【详解】设公差为d ，则251,14a d a d =+=+，则21(14)(1)2d d d ⨯+=+⇒=．6．化简：cos sin 36ππαα⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭． 【答案】cos α【详解】（方法一）：利用＂两角和公式＂直接求解；（方法二）：cos sin sin sin 36236πππππαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+++=-+++ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ sin sin 2sin cos cos 666πππαααα⎛⎫⎛⎫=-++== ⎪ ⎪⎝⎭⎝⎭． 7．已知P 是双曲线22219x y a -=右支上的一点，双曲线的一条渐近线方程为30x y -=．设12F F 、分别为双曲线的左、右焦点．若23PF =，则1PF = ．【答案】5【详解】由双曲线的一条渐近线方程为30x y -=可得：2a =，又双曲线的定义知12112325PF PF a PF PF -=⇒-=⇒=．8．已知一个凸多面体共有9个面，所有棱长均为1，其平面展开图如右图所示，则该凸多面体的体积V = ．【答案】16+【详解】凸多面体为：下半部分为正方体3111V ==，上半部分为正四棱锥221132V =⨯⨯．9．已知无穷数列{}n a 前n 项和113n n S a =-，则数列{}n a 的各项和为 ．【答案】1-【详解】 由113n n S a =-可得：11113n n S a --=-，两式相减得并化简：112n n a a -=-， 又11113132a a a =-⇒=-．所以1lim 11n x a S q →∞==--． 10．古代“五行”学说认为：“物质分金、木、土、水、火五种属性，金克木，木克土，土克水，水克火，火克金．”将五种不同属性的物质任意排成一列，设事件A 表示“排列中属性相克的两种物质不相邻”，则事件A 出现的概率是 （结果用数值表示）． 【答案】112【详解】如下图，当左边的位置排定后（例如：金），第二位（除去金本身）只有“土、水”两种属性。
上海交通大学2007年冬令营选拔测试数学试题一、填空题(每小题5分，共50分)1 设函数f(x)满足2f(3x) f (2 3x) 6x 1，贝卩f(x) ________________________ .2.设a,b,c均为实数，且3a 6b 4，则1丄.a b3 .设a 0且a 1 ,则方程a x 1 x2 2x 2a的解的个数为____________ .4. _______________________________________________ 设扇形的周长为6,则其面积的最大值为___________________________ .5. 1 1! 2 2! 3 3! L n n! ____________________ .6•设不等式x(x 1) y(1 y)与x2 y2 k的解集分别为M和N.若M N ,贝H k的最小值为___________ .7 设函数f(x)- , 则xS 1 2 f (x) 3f2(x) L nf n1(x) _____________ .8 .设a 0 ,且函数f (x) (a cosx)(a sin x)的最大值为空,则2a ________________ .9. 6名考生坐在两侧各有通道的同一排座位上应考，考生答完试卷的先后次序不定，且每人答完后立即交卷离开座位，则其中一人交卷时为到达通道而打扰其余尚在考试的考生的概率为 _______________ .10. 已知函数f1(x)気」，对于n 1,2,L，定义f n 1(x) f1(f n(x))，若x 1f35 ( x) f s(x)，贝S f28(X) _____________ .二、计算与证明题(每小题10分，共50分)11.工件内圆弧半径测量问题.为测量一工件的内圆弧半径R，工人用三个半径均为r的圆柱形量棒O1Q2Q3放在如图与工件圆弧相切的位置上，通过深度卡尺测出卡尺水平面到中间量棒02顶侧面的垂直深度h，试写出R用h表示的函数关系式，并计算当r 10mm, h 4mm 时，R 的值.12. 设函数f(x) |sinx cosx，试讨论f(x)的性态(有界性、奇偶性、单调性和周期性)，求其极值，并作出其在0,2内的图像.13. 已知线段AB长度为3，两端均在抛物线x y2上，试求AB的中点M 到y轴的最短距离和此时M点的坐标.参考答案:1. 2x 12. 1丄3. 2 4. n 1 ! 1 6. 242410.7. 11. !n n 12n11 2n 1 42 2R r r ,h12.1^.21k 2d min14.略; 反证法x 08.x 060mm15. 2 29.；周期为2；3; 3 43 45222n2008年交大冬令营数学试题参考答案 1.若 f(x)2 1 3厂，g(x) f1(x)'则 g(5)2x 3 5 3x2008.1.1xH 的最大值为 ------------ .13 .等差数列中，5a 8 3^3，则前n 项和S n 取最大值时,2.函数y.204 .复数|z| 1 ,若存在负数a 使得z 2 2az a 25.若 cosx sin xcos 3x2.3sin x111613.n 的值为a 0，则6.数列a.的通项公式为a n1 nn 1 (n 1). n,则这个数列的前 99乙厂生产的占20%甲厂商品的合格率为95%乙厂商品的合格率为 90%若某人购买了此商品发现为次品，贝眦次品为甲厂生产的概率10.若曲线C i ：x 2 y 2 0与C 2：(x a)2 y 2 1的图像有3个交点，则a _______ . 1二.解答题1. 30个人排成矩形，身高各不相同.把每列最矮的人选出，这些人 中最高的设为a ;把每行最高的人选出，这些人中最矮的设为 b .(1) a 是否有可能比b 咼？ (2)a 和b 是否可能相等？1. 解：1不可能① 若a 、b 为同一人，有a b ;② 若a 、b 在同一行、列，则均有a b ;③ 若a 、b 不在同一行、列，同如图1以5*6的矩形为例，记a所在列与b 所在行相交的人为x 。
上海卷一、填空题（本大题满分44分）本大题共有11题，只要求直接填写结果，每个空格填对得4分，否则一律得零分. 1.不等式11x -＜的解集是.2.若集合A ={x ｜x ≤2}、B ={x ｜x ≥a}满足{2}A B = ，则实数a = .3.若复数z 满足z =i (2-z ) (i 是虚数单位)，则z = .4.若函数f (x )的反函数为f -1(x )=x 2(x ＞0),则f (4)= .5.若向量a b 、满足1,2,a b == 且a 与b 的夹角为3π，则a b+ ＝ .6.函数f (xsin 2x x π⎛⎫++ ⎪⎝⎭的最大值是.7.在平面直角坐标系中，从六个点：A (0，0)、B （2,0）、C （1,1）、D (0,2)、E (2,2)、F (3,3)中任取三个，这三点能构成三角形的概率是 （结果用分数表示）. 8.设函数f (x )是定义在R 上的奇函数.若当(0,)x ∈+∞时，f (x )=lg x ，则满足f (x )＞0的x 的取值范围是 .9.已知总体的各个体的值由小到大依次为2，3，3，7，a ,b ,12，13.7，18. 3，20，且总体的中位数为10.5.若要使该总体的方差最小，则a 、b 的取值分别是 .10.某海域内有一孤岛.岛四周的海平面（视为平面）上有一浅水区（含边界），其边界是长轴长为2a 、短轴长为2B r 椭圆.已知岛上甲、乙导航灯的海拔高度分别为h 1、h 2，且两个导航灯在海平面上的投岸恰好落在椭圆的两个焦点上.现有船只经过该海域（船只的大小忽略不计），在船上测得甲、乙导航灯的仰角分别为θ1、θ2，那么船只已进入该浅水区的判别条件是 . 11.方程x 2+2x -1＝0的解可视为函数y -x +2的图像与函数y ＝x1的图像交点的横坐标.若方程x 4+ax -4=0的各个实根x 1, x 2,…，x k （k ≤4）所对应的点⎪⎪⎭⎫ ⎝⎛14,x x i （I=1,2,…，k ）均在直线y ＝x 的同侧，则实数a 的取值范围是 .二、选择（本大题满分16分）本大题共有4题，每题都给出代号为A 、B 、C 、D 的四个结论，其中有只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分. 12.组合数C r n r n rn 、,1(≥>∈Z ）恒等于[答]（ ）（A ）.1111--++r n C n r (B)(n +1)(r +1)C 11--r n (C)nrC 11--r n (D)C rn 11--r n .13.给定空间中的直线l 及平面α.条件“直线l 与平面α内无数条直线都垂直”是“直线l 与平面α垂直”的 [答]（ ）（A ）充要条件. （B ）充分大必要条件. （C ）必要非充分条件. （D ）既非充分又非必要条件. 14.若数列｛a n ｝是首项为l ，公比为a 23-的无穷等比数列，且｛a n ｝各项的和为a ，则A r 值是[答]（ ）（A ）1. (B)2. (C).21 (D).45 15.如图，在平面直角坐标系中，Ω是一个与x 轴的正半轴、y 轴的正半轴分别相切于点C 、D 的定圆所围成的区域（含边界），A 、B 、C 、D 是被圆的四等分点.若点P （x ，y ）、点P ′(x ′，y ′)满足x ≤ x ′且y ≥y ′，则称P 优于P ′.如果Ω中的点O 满足，不存在Ω中的其它点优于Q ，那么所有这样的点Q 组成的集合是劣弧 [答]（ ） （A ） AB（B ） BC（C ） CD（D ） DA 三、解答题（本大题满分90分）本大题共有6题，解答下列各题必须写出必要的步骤.16.(本题满分12分)如图，在棱长为2的正方体ABC-A 1B 1C 1D 1中，E 是BC 1的中点.求直线DE 平平面ABCD 所成角的大小（结果用反三角函数值表示）.17.（本题满分13分）如图，某住宅小区的平面图呈圆心角为120°的扇形AOB .小区的两个出入口设置在点A 及点C 处，且小区里有一条平等于BO 的小路CD .已知某人从C 沿CD 走到D 用B 10分钟，从D 沿DA 走到A 用了6分钟.若此人步行的速度为每分钟50米，求该扇形的半径OA 的长（精确到1米）18.（本题满分15分）本题共有2个小题，第1个题满分5分，第2小题满分10分. 已知函数f (x )=sin2x ,g (x )=cos ⎪⎭⎫⎝⎛+62πx ,直线x =t (t ∈R)与函数f (x )、g (x )的图像分别交于M 、N 两点. (1) 当t=4π时，求｜MN ｜的值；(2) 求｜MN ｜在t ∈⎥⎦⎤⎢⎣⎡2,0π时的最大值.AEB 1D 1 D C 1A 1BCAODBC19.（本题满分16分）本题共有2个小题，第1小题满分8分，第2小题满分8分. 已知函数f (x )=pqx212-.(1) 若f (x )＝2，求x 的值；(2) 若2tf （2t ）+mf （t ）≥0对于t ∈［1，2］恒成立，求实数m 的取值范围.20.（本题满分16分）本题共有3个小题，第1小题满分3分，第2小题满分5分，第3小题满分8分。
