结构力学第四章习题集与答案解析

第4章　静定拱4.1　复习笔记【知识框架】【重点难点归纳】一、拱的基本概念及特点　★★表4-1-1　拱的基本概念及特点表4-1-2　有拉杆和无拉杆三铰拱的区别与联系二、三铰拱的计算　★★★★★1．支座反力的计算（见表4-1-3）表4-1-3　支座反力的计算2．内力的计算（见表4-1-4）表4-1-4　三铰拱的内力计算三、三铰拱的合理拱轴线（见表4-1-5）　★★★表4-1-5　三铰拱的合理拱轴线4.2　课后习题详解复习思考题1．拱的受力情况和内力计算与梁和刚架有何异同？答：（1）拱与梁的受力情况和内力计算的区别①约束反力方面，拱在竖向荷载作用下会产生水平反力（推力），而梁在竖向荷载作用下不会产生水平反力（推力）；②内力分布方面，由于水平推力的存在，拱的弯矩常比跨度、荷载相同的梁的弯矩小得多，使得拱截面上的应力分布较为均匀；③内力分析方法方面，若只有竖向荷载时，梁只需进行简单的整体分析即可求解，而拱由于水平力的存在，需要整体分析与局部分析相结合。

（2）拱与刚架的受力情况和内力计算的异同①内力分析方法方面，拱与刚架的受力情况和内力计算的特点和所应用方法基本一致，例如三铰刚架也属于拱式结构；②拱的轴线是曲线，刚架杆的轴线是直线，在应用平衡条件计算内力时，拱仍然取投2．在非竖向荷载作用下怎样计算三铰拱的反力和内力？能否使用式（4-1）和（4-2）？答：（1）对于三铰拱承受非竖向荷载的情况，可将非竖向荷载分解为水平荷载和竖向荷载。

（2）仍然可以应用式（4-1）和（4-2），将水平反力加上非竖向荷载水平方向上的分量一起代入公式中进行求解。

(4-1)o AV AV o BV BV o c H F F F F M F f ⎫⎪=⎪⎪=⎬⎪⎪=⎪⎭cos sin (4-2)sin cos o H o S S H o N S H M M F y F F F F F F ϕϕϕϕ⎫=-⎪⎪=-⎬⎪=+⎪⎭3．什么是合理拱轴线？试绘出图4-2-1各荷载作用下三铰拱的合理拱轴线形状。

朱慈勉_结构⼒学_第4章课后习题（全）同济⼤学朱慈勉结构⼒学第4章习题答案（1）4-5 试⽤静⼒法作图⽰结构中指定量值的影响线。

(a)01571(5),77,(02)()2,(25)ARB RB QDB DC Md F d d x xx F F dd x x d M CD d d x d =?+?=?-∴=-=≤≤?=?≤≤?∑知以右侧受拉为正ACC DA2d5/7QDBF DCM(b)RA A 0F 1()F xa ≤≤=→=-↑∑F 以为坐标原点，向右为x 轴正⽅向。

弯矩M 以右侧受拉为正当0x a 时，M 分析以右部分，GCD 为附属部分，可不考虑x/aG E NE M F xxa==-G 31a x a ≤≤=-E NE 当时，去掉AF,GCD 附属部分结构,分析中间部分M=(2a-x),F4-x/aG RD NE 4033,F 4a x a x a x xa a a≤≤=-==-=-+∑G E 当3时，由M 知M =x-4a,F1E M 的影响线NE F 的影响线(c)2mN3N3N3N2()08()0F [(10)(1)10]/220420()(1)10200F 524F 01F20x C x xxx x D xx CD C D x↑≤≤=→=---?=-≤≤-?=→=-=-≤≤=→-+∑∑∑RA I I y 上承荷载时：x以A 点为坐标原点，向右为x 轴正⽅向。

F =1-20当点以左时，取1-1截⾯左侧考虑由M 当12点以右时，由M 在之间的影响线⽤点及的值。

直线相连。

当0x 8时，取1-1截⾯左侧分析由F N2N13N22 sin 451F 20F F F cos 4545x x==-=→=-+=-∑x 知由F A B CDEFN3F N2F N1F(d)BRA RA RA RB RB N1RB N1N1RA N1RB N2N2M01(8)F 8F 18F F 1F 803110F F 0F 8110F F F 04220F 4F 20F x d x d dx dx d x d x d d d =→?-=?→=-+=→=≤≤-=→+=→=≤≤-=→=→=≤≤-=→?+?=→=-∑∑∑∑y y C上承荷载时当时，取截⾯右侧分析。

A B
l
l
C
1 ql 4
2
1 2 ql 4
5 ql 4
A
M P图
1 2 ql 8
l 2
1
1 2 1 2 1 l l ql EI 3 8 2 2
ql 4 1 1 1 ql 4 EI 48 24 48 24EI
A
M图
1 2 3
4－3 试用图乘法求图示结构中B处的转角和C处的竖向 ql 位移。EI=常数。 2 q
（b）解：作 M图、M P图，
CV 1 1 1 2 l 2 l ql EI 2 4 2 3 2
1 1 1 2 1 2 ql l l EI 2 4 2 3
l
q
B
M 1
EI
A
在B点沿水平方向设单位力矩 M 1 。 故 M 1
1 1 qx3 M P qx x x 2 3 6l
l
MM P 1 qx3 ql 3 则 B dx dx EI EI 0 6l 24EI
l
q
4－2 试求桁架结点B的竖向位移，已知桁架各 杆的 EA 21 10 4 KN。
（c）求
BH、 B。
q qx x l
B
解：在B点沿水平方向设单位力 FP 1 。

q qx l x
故 M x 则
BH
1 1 qx3 M P qx x x 2 3 6l
l
EI
A
FP 1
MM P 1 x qx3 ql 4 dx dx EI EI 0 6l 30EI
BV FN FNP l EA

4-2(b) 答：本题三次超静定，但在横向荷载下轴力为零，因此可如下求解：
FP
X1 FP
X2
A l/2
B l/2
A B
基本体系
FP A
B FPl/4 MP 图
1
1
A X1 =1
B
M 1图
FPl/8
FPl/8
A
X2 =1 B
M 2图
A M图
B FPl/4
在上述荷载及单位弯矩图下，可图乘求系数、建立力法方程并求解，最后叠加出最终
F
G
3 C
3 3D
E 3
X1 =1
A
B
48 120
M 1图
F
G
72
E
CD
72
120 48
A
B
M (kN ⋅ m)
4-4 (c)本题求解过程如下面图形所示
A
MB
D
C l
基本体系
X1 l
M
M
M
M
图
P
l
M 1图
X1 =1
0.75M 0.25M
M图
δ11 X1 + ∆1P = 0
∑ ∫ δ11 =
2
M1 dx =
A
M图
本体也可取变 B 结点为铰以一对力矩为未知力求解，工作量和上述解法相同。
4-3 (b) 本题也一次超静定，基本体系、荷载与单位弯矩图如下所示
10 kN/m
10 kN/m
B
C
20 kN
B
C
20 kN
X1
3m 3m
A 6m
A
基本体系
180 B
180

李廉锟《结构⼒学》笔记和课后习题（含考研真题）详解-第4章静定拱【圣才出品】第4章　静定拱4.1　复习笔记【知识框架】【重点难点归纳】⼀、拱的基本概念及特点　★★表4-1-1　拱的基本概念及特点表4-1-2　有拉杆和⽆拉杆三铰拱的区别与联系⼆、三铰拱的计算　★★★★★1．⽀座反⼒的计算（见表4-1-3）表4-1-3　⽀座反⼒的计算2．内⼒的计算（见表4-1-4）表4-1-4　三铰拱的内⼒计算三、三铰拱的合理拱轴线（见表4-1-5）　★★★表4-1-5　三铰拱的合理拱轴线4.2　课后习题详解复习思考题1．拱的受⼒情况和内⼒计算与梁和刚架有何异同？答：（1）拱与梁的受⼒情况和内⼒计算的区别①约束反⼒⽅⾯，拱在竖向荷载作⽤下会产⽣⽔平反⼒（推⼒），⽽梁在竖向荷载作⽤下不会产⽣⽔平反⼒（推⼒）；②内⼒分布⽅⾯，由于⽔平推⼒的存在，拱的弯矩常⽐跨度、荷载相同的梁的弯矩⼩得多，使得拱截⾯上的应⼒分布较为均匀；③内⼒分析⽅法⽅⾯，若只有竖向荷载时，梁只需进⾏简单的整体分析即可求解，⽽拱由于⽔平⼒的存在，需要整体分析与局部分析相结合。

（2）拱与刚架的受⼒情况和内⼒计算的异同①内⼒分析⽅法⽅⾯，拱与刚架的受⼒情况和内⼒计算的特点和所应⽤⽅法基本⼀致，例如三铰刚架也属于拱式结构；②拱的轴线是曲线，刚架杆的轴线是直线，在应⽤平衡条件计算内⼒时，拱仍然取投2．在⾮竖向荷载作⽤下怎样计算三铰拱的反⼒和内⼒？能否使⽤式（4-1）和（4-2）？答：（1）对于三铰拱承受⾮竖向荷载的情况，可将⾮竖向荷载分解为⽔平荷载和竖向荷载。

（2）仍然可以应⽤式（4-1）和（4-2），将⽔平反⼒加上⾮竖向荷载⽔平⽅向上的分量⼀起代⼊公式中进⾏求解。

(4-1)o AV AV o BV BV o c H F F F F M F f ??=??=?=cos sin (4-2)sin cos o H o S S H o N S H M M F y F F F F F F =-??=-?=+3．什么是合理拱轴线？试绘出图4-2-1各荷载作⽤下三铰拱的合理拱轴线形状。

结构力学 第四章习题 参考答案2005级4－1 图示抛物线拱的轴线方程24(fy x l l=−)x ，试求截面K 的内力。

解：（1） 求支座反力801155 kN 16AV AV F F ×=== 0805(5580)0.351500.93625 kN 16BV BV F F ×==−×+×== 0Mc 55880350 kN 4H F f ×−×===（2） 把及代入拱轴方程有:16m l =4m f =(16)16xy =−x （1）由此可得:(8)tan '8x y θ−==（2） 把截面K 的横坐标 ,代入（1），（2）两式可求得: 5m x ==＞, 3.44m y =tan 0.375θ= 由此可得:20.56θ= 则有sin 0.351θ=,cos 0.936θ=最后得出截面k 处的内力为: (上标L 表示截面K 在作用力左边，R 则表示截面在作用力右边)055550 3.44103 kN m K H M M F y =−=×−×=i0cos sin 550.936500.35133.93 kN L sK s H F F F θθ=−=×−×= (5580)0.936500.35140.95 kN R sK F =−×−×==40.95 KN 0sin cos 550.351500.93666.1 kN L NK s H F F F θθ=+=×+×= (5580)0.351500.93638.03 kN R NK F =−×+×=4－2 试求拉杆的半圆三铰拱截面K 的内力。

解：（1）以水平方向为X 轴,竖直方向为Y 轴取直角坐标系，可得K 点的坐标为：2m6mK K x y =⎧⎪⎨==⎪⎩ （2）三铰拱整体分别对A ，B 两点取矩，由平衡方程可解得支座反力：0 20210500 20210500 2100A By B Ay x Ax M F M F F F ⎧=×−××⎪⎪=×+××⎨⎪=−×=⎪⎩∑∑∑=== =＞ 5 kN ()20 kN () 5 kN ()Ay Ax By F F F =−⎧⎪=−⎨⎪=⎩向下向上向左（3）把拱的右半部分隔离，对中间铰取矩，列平衡方程可求得横拉杆轴力为：CN 0 105100MF =×−×∑=＞N 5 kN F =（4）去如图所示的α角，则有：=＞cos 0.6sin 0.8θθ=⎧⎨=⎩于是可得出K 截面的内力，其中：22(6)206525644 kN m 2K M ×=−+×−×−×=isK F (20265)sin 5cos 0.6 kN θθ=−×−×−×=− NK F (20265)cos 5sin 5.8 kN θθ=−−×−×−×=−13K M F r Fr ==（内侧受拉） K 截面作用有力，剪力有突变 且有01sin3032LSK 2F F F F =−=−×=− （2） 22R SK F FF F =−=（3）011sin30(326NKF F F F ==×=拉力）（4）4-4 试求图示三铰拱在均布荷载作用下的合理拱轴线方程。

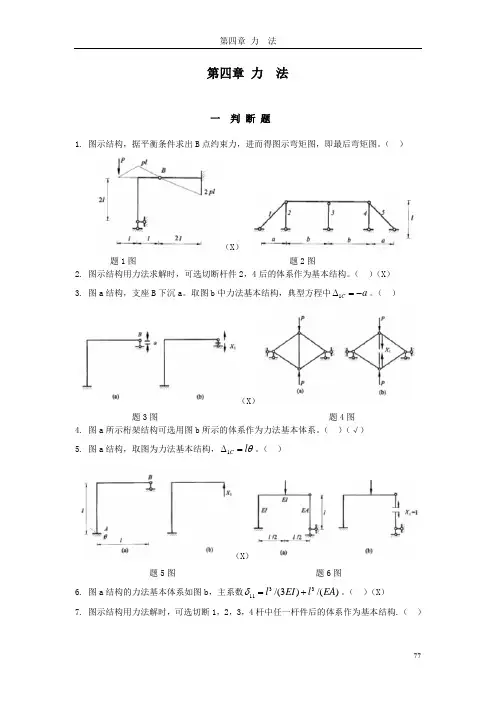
第四章 力 法一 判 断 题1. 图示结构，据平衡条件求出B 点约束力，进而得图示弯矩图，即最后弯矩图。

（ ）（X ）题1图 题2图2. 图示结构用力法求解时，可选切断杆件2，4后的体系作为基本结构。

（ ）（X ）3. 图a 结构，支座B 下沉a 。

取图b 中力法基本结构，典型方程中1C a ∆=-。

（ ） （X ）题3图 题4图4. 图a 所示桁架结构可选用图b 所示的体系作为力法基本体系。

（ ）（√）5. 图a 结构，取图为力法基本结构，1C l θ∆=。

（ ） （X ）题5图 题6图6. 图a 结构的力法基本体系如图b ，主系数3311/(3)/()l EI l EA δ=+。

（ ）（X ）7. 图示结构用力法解时，可选切断1，2，3，4杆中任一杆件后的体系作为基本结构.（ ）（X ）题7图 题9图 8. 图示结构受温度变化作用，已知α，h ，选解除支杆B 为力法基本体系(设B X 向上为正)，典型方程中自由项2121()/(4)t a t t l h ∆=--。

（ ）（X ）9. 图a 结构，力法基本体系如图b ，自由项412/(8)P ql EI ∆=-。

（ ）（X ）题10图 题11图10.图示超静定梁在支座转动1A ϕ=时的杆端弯矩26.310AB M KN m =⨯⋅，22( 6.310)EI KN m =⨯⋅。

（ ）（√） 11. 图a 结构，取图b 为力法基本结构，h 为截面高度，α为线胀系数，典型方程中2121()/(2)t a t t l h ∆=--。

（ ）（X ）题12图 题13图 12. 图a 结构，取力法基本体系如图b 所示，则1/C l ∆=∆（ ）。

（X ）13. 超静定结构在荷载作用下的反力和内力，只与各杆件刚度的相对数值有关。

（ ）（√）14. 图示结构的超静定次数为4。

（ ）（X ）题15图 题16图15. 图示结构，选切断水平杆为力法基本体系时，其3112/(3)h EI δ=。

《结构力学习题集》4-静定位移(总7页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--- 20 -第四章 静定结构位移计算一、是非题1、虚位移原理等价于变形谐调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、用图乘法可求得各种结构在荷载作用下的位移。

5、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M k M p21y 1y 2**ωω7、图示桁架各杆EA 相同，结点A 和结点B 的竖向位移均为零。

A8、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。

aa9、图示简支梁，当P 11=，P 20=时，1点的挠度为0.01653l EI /，2点挠度为0.0773l EI /。

当P 10=，P 21=时，则1点的挠度为0.0213l EI /。

（ ）l10、图示为刚架的虚设力系，按此力系及位移计算公式即可求出杆AC 的转角。

C1P11、图示梁AB 在所示荷载作用下的M 图面积为ql 33。

lAl /212、图示桁架结点C 水平位移不等于零。

2113、图示桁架中，结点C 与结点D 的竖向位移相等。

二、选择题1、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;;B.D.C.=1=12、图示结构A 截面转角（设顺时针为正）为：A.22Pa EI / ;B.-Pa EI 2/ ;C.542Pa EI /() ; 542Pa EI /() 。

aa3、图示刚架l a >>0 , B 点的水平位移是：A .不定，方向取决于a 的大小；B .向左；C .等于零；D .向右。

By

0l
MPM EI
ds


0 2
MPM EI
Rd
PR3
4EI
()
同理有：
Bx


PR3 2EI
()
三铰拱的分析同此类似，但一般要考
虑轴力对位移的贡献，也即
P


MM Pds EI

FN FNP ds EA
例 3：求对称桁架D点的竖向位移 Dy。图中
右半部各括号内数值为杆件的截面积A
2x6 2
3
AC段
0 x 2
80x qx 2
1 x 3

D

2720 9EI
()
例题：计算D处竖向位移，B处角位移？（EI为常数）
解：1.构造虚设状态
x
2.分别列出实际状态和虚拟状态中各杆的内力方程
x'
40kN 20kN/m
M
实际状态
虚拟状态
A
C
B
D
DB段
0 x2
P 轴向

FN FNP EA

kFQ FQP GA

MM P EI
ds
式中：
剪切 弯曲
E 弹性模量； G 剪切模量；
A 横截面积； I
截面惯性矩；
k 截面形状系数。如：对矩形截 面k=6/5;圆形截面k=10/9。
例 1：求刚架A点的竖向位移。
解：1.构造虚设状态
2.分别列出实际状态和虚拟状态中各杆的内力方程
x'
40kN 20kN/m
M
实际状态
虚拟状态
A
C
B
D

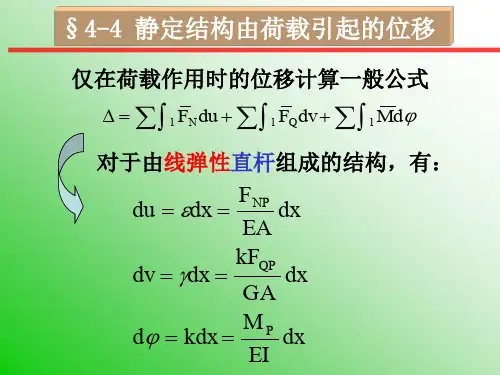
结构力学 第四章习题 参考答案2005级4－1 图示抛物线拱的轴线方程24(fy x l l=−)x ，试求截面K 的内力。

解：（1） 求支座反力801155 kN 16AV AV F F ×=== 0805(5580)0.351500.93625 kN 16BV BV F F ×==−×+×== 0Mc 55880350 kN 4H F f ×−×===（2） 把及代入拱轴方程有:16m l =4m f =(16)16xy =−x （1）由此可得:(8)tan '8x y θ−==（2） 把截面K 的横坐标 ,代入（1），（2）两式可求得: 5m x ==＞, 3.44m y =tan 0.375θ= 由此可得:20.56θ= 则有sin 0.351θ=,cos 0.936θ=最后得出截面k 处的内力为: (上标L 表示截面K 在作用力左边，R 则表示截面在作用力右边)055550 3.44103 kN m K H M M F y =−=×−×=i0cos sin 550.936500.35133.93 kN L sK s H F F F θθ=−=×−×= (5580)0.936500.35140.95 kN R sK F =−×−×==40.95 KN 0sin cos 550.351500.93666.1 kN L NK s H F F F θθ=+=×+×= (5580)0.351500.93638.03 kN R NK F =−×+×=4－2 试求拉杆的半圆三铰拱截面K 的内力。

解：（1）以水平方向为X 轴,竖直方向为Y 轴取直角坐标系，可得K 点的坐标为：2m6mK K x y =⎧⎪⎨==⎪⎩ （2）三铰拱整体分别对A ，B 两点取矩，由平衡方程可解得支座反力：0 20210500 20210500 2100A By B Ay x Ax M F M F F F ⎧=×−××⎪⎪=×+××⎨⎪=−×=⎪⎩∑∑∑=== =＞ 5 kN ()20 kN () 5 kN ()Ay Ax By F F F =−⎧⎪=−⎨⎪=⎩向下向上向左（3）把拱的右半部分隔离，对中间铰取矩，列平衡方程可求得横拉杆轴力为：CN 0 105100MF =×−×∑=＞N 5 kN F =（4）去如图所示的α角，则有：=＞cos 0.6sin 0.8θθ=⎧⎨=⎩于是可得出K 截面的内力，其中：22(6)206525644 kN m 2K M ×=−+×−×−×=isK F (20265)sin 5cos 0.6 kN θθ=−×−×−×=− NK F (20265)cos 5sin 5.8 kN θθ=−−×−×−×=−13K M F r Fr ==（内侧受拉） K 截面作用有力，剪力有突变 且有01sin3032LSK 2F F F F =−=−×=− （2） 22R SK F FF F =−=（3）011sin30(326NKF F F F ==×=拉力）（4）4-4 试求图示三铰拱在均布荷载作用下的合理拱轴线方程。

（4）习题5.1(3)图(a)和(b)所示两结构的变形相同。（ ）
习题7.2填空题
（1）习题5.2(1)图(a)所示超静定梁的支座A发生转角，若选图(b)所示力法基本结构，则力法方程为_____________，代表的位移条件是______________，其中1c=_________；若选图(c)所示力法基本结构时，力法方程为____________，代表的位移条件是______________，其中1c=_________。
(a)
习题3.7改正习题3.7图所示刚架的弯矩图中的错误部分。
(a)(b)(c)
(d)(e)(f)
习题3.7图
习题3.8作习题3.8图所示刚架的内力图。
(a)
(b)
习题3.8图
第4章 静定拱习题解答
习题4.1是非判断题
(1) 三铰拱的水平推力不仅与三个铰的位置有关，还与拱轴线的形状有关。（ ）
(2) 所谓合理拱轴线，是指在任意荷载作用下都能使拱处于无弯矩状态的轴线。 （ ）
习题3.2(2)图
习题3.3作习题3.3图所示单跨静定梁的M图和 图。
(a) (b)
(c) (d)
(e) (f)
习题3.3图
习题3.4作习题3.4图所示单跨静定梁的内力图。
(c)
习题3.4图
习题3.5作习题3.5图所示斜梁的内力图。
习题3.5图
习题3.6作习题3.6图所示多跨梁的内力图。
(a)
习题3.6图
(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。( )
(5) 习题2.1(5) 图所示体系去掉二元体CEF后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。( )
习题 2.1(5)图

P
P
P
1
P
(b)
(b)解：对称结构，在反对称载荷作用下，在对称轴上对称的内力为零。受力分析如图所示
有 2 根对称轴，结合平衡方程，剩下三个未知数，为 3 次静不定。 本题中通过对称性条件的使用，将 6 次静不定问题转化为 3 次静不定。
(c) (c)解：对称结构，在对称载荷作用下，在对称轴上反对称内力为零。
(
)
N13 = P + X 1 ⋅ 1 =
(182 2⎞ 1− 9 2 ⎟=− P + X1 ⋅ ⎜ − P ⎜ 2 ⎟ 2 18 ⎝ ⎠
N 24 = 0 + X 1 ⋅ 1 = −
5+ 2 P 23
N34 = −
4、校核。 结点 2： 结点 3：
⎛ 2 2 ⎞ 1− 9 2 ⎟ P + X1 ⋅ ⎜ − ⎜ 2 ⎟ = 18 P 2 ⎝ ⎠
3
4 -2 √3 1 2 <1>
a
3
2 <P>
计算影响系数
∆1 P =
a ⎡ 2 ⎤ Pa 3P × (− 2 ) + (− 2 P )× 3 × =− 4+ 2 3 ⎢ ⎥ EA ⎣ EA 3⎦
(
)
δ11 =
列正则方程：
a ⎛ 2 ⎞ a + 1× 1× 2 ⎟ = 6+2 3 ⎜2× 2 + 3× 3 × EA ⎝ 3 ⎠ EA
(
)
N13 = 2 P + X 1 ⋅1 =
(2 + 2 ) P
4
⎛ 2 ⎞ 3− 2 ⎟ N14 = 0 + X 1 ⋅ ⎜ P ⎜− 2 ⎟ = 4 ⎝ ⎠ ⎛ 2 ⎞ 3− 2 ⎟ N 23 = 0 + X 1 ⋅ ⎜ − P ⎜ 2 ⎟= 4 ⎝ ⎠

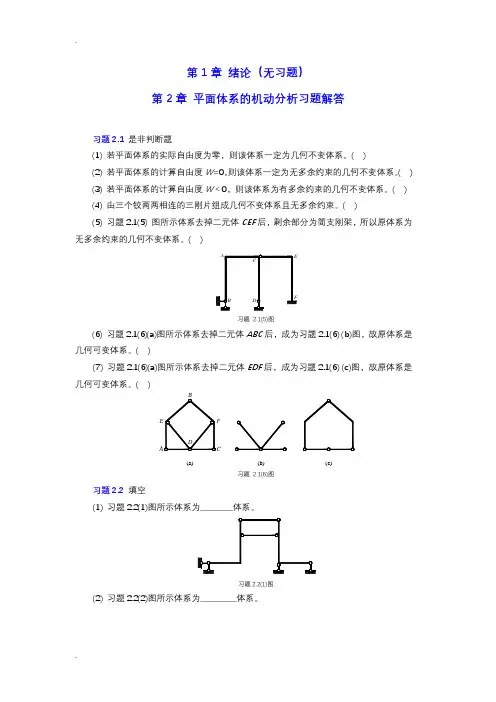
第四章静不定结构的内力计算一、结构静不定度数的判断4-1、分析图4-2中所示的平面桁架结构的静不定度数，并指出哪些是多余约束。

解：结构1234567可以看成是以三角形桁架为基础，分别用两根不咋同一直线上的双铰杆逐次连接6、3、7、4而组成的简单桁架。

结构本身是静定结构，此结构相对基础有三个自由度，N=3。

现在用三个平面铰1、6、4将结构与基础相连，约束数C=23=6，所以K=C-N=3。

此结构静不定度数为3，可将平面铰6的水平垂直约束和平面铰4的水平约束看成多余约束。

4-2、（例题）：试分析图4-3中所示平面刚架的组成，计算多余约束数，吧并指出哪些约束是多余约束。

解：结构可看成是由杆件用刚节连接形成的平面刚架。

这时一个闭合刚架，因此多余约束数K=3，多余约束是闭合刚架123任意截面上的轴力、剪力和弯矩。

将此结构固定在基础上，需要3个约束即可，现在用两个平面铰1、4与基础相连，，可将铰4处y方向约束看成多余约束。

所以结构多余约束数。

封闭刚架任意切面上的轴力，剪力和弯矩及铰支点4处y方向约束为多余约束。

4-3、判断图4-4中所示平面桁架的静不定度数，并指出多余约束力。

（1）；杆5-6及1铰支点处xy方向约束视为多余约束；（2）；杆2-9、3-10、10-13的约束视为多余约束；（3）4-4、（例题）图4-5中所示为MD-82机身隔框简化计算模型。

此框为一倒8字封闭刚框，框凹进处之间支撑一地板梁。

地板梁与框式刚接。

在地板梁和货仓壁之间有两根撑杆，撑杆两端用铰链与结构相连。

试分析此结构的静不定度数。

解：地板梁在框凹进处与框刚接，因此行程两个封闭刚框，静不定度数，两根撑杆是双铰杆，各为一个约束。

所以结构静不定度数。

4-5、试分析图4-6中所示各刚架及混合杆系的静不定度数，并指出多余约束力。

（1）；有一个封闭刚框，并且1铰支点处多余一个x方向的约束。

（2）（3）；有5个封闭刚框；（4）；有5个封闭刚框，并且有4根多余的双铰杆。

静定结构的位移计算习题4—1 (a)用单位荷载法求图示结构B 点的水平位移解：1. 设置虚拟状态选取坐标如图。

2. M P 图和 如图示3. 虚拟状态中各杆弯矩方程为实际状态中各杆弯矩方程为M P =F P x4. 代入公式（4—6）得 △BH =l 实际状态 1虚拟状态5F P l 15l 1 M P 图图M 图M xM =141012118111EI F EI x F x EI x F x EI dx M M P l l P l P P =⨯⨯+⨯⨯=∑⎰⎰⎰(←)4—1 (b)单位荷载法求图示刚架B 点的水平位移 解：1. 设置虚拟状态选取坐标如图。

2. M P 图和 如图示3. 虚拟状态中各杆弯矩方程为 BD: DC: CA: 实际状态中各杆弯矩方程为 BD: M P =0 DC: M P =40x CA: M P =160+5x 24. 代入公式（4—6）得图M x M =3=M xM-=3△BH =4—2试求图示桁架结点B 的竖向位移，已知桁架各杆的EA =21×104KN 。

1M P 图图M 3KN •m340KN •m3KN •m3KN •m5160)3(40306012401301+⨯-+⨯+*=∑⎰⎰⎰⎰EI x x x EI x EI x EI dxM M P解：虚拟状态如图示。

实际状态和虚拟状态所产生的杆件内力均列在表中，4—1根据式4—7可得结点B 的竖向位移为表4—1中)(768.010215.16124↓=⨯•=∆cm KNm KNBV实际状态虚拟状态4—3 （a）、（b）试用图乘法求图示结构B处的转角和C处的竖向位移。

EI=常数。

（a ）解：M P 图、单位力偶下作用于BM=ql 2M P图ql 2/81M=1点的1M 图、单位力下作用于C 点的2M 图EIql ql l ql l EI B 3)21223232221(1222=⨯⨯⨯-⨯⨯⨯=ϕ（ ）（b ）解：M P图、单位力偶下作用于B 点的1M 图、单位力作用于C 点的2M 图)2183232421(122⨯⨯⨯-⨯⨯⨯=ql l l ql EI B ϕ=ql 3/24EI( ))23242212832232421(1222ql ql l ql ql l ql l ql EI cv ⨯⨯⨯⨯+⨯⨯⨯-⨯⨯⨯⨯=∆= ql 4/24EI(↓))(24)2852232322213221(14222↑-=⨯⨯⨯⨯⨯+⨯⨯⨯-⨯⨯⨯-=∆EI qll ql l ql l l ql l l EI CV（（b ）ql/2ll单位力偶作用于B点的1M图、单位力作用于C点时的2M图EIlFlFllFlEIPPPB1223121122322121(12=⨯⨯⨯⨯+⨯⨯⨯⨯⨯-=ϕ( ))(12231212232221(12↓=⨯⨯⨯⨯+⨯⨯⨯⨯⨯-=∆EIlFlFlllFllEIPPPcv4—4（a）试求图示结构C点的竖向位移。

第四章思考题4.1 何谓单向板？何谓双向板？如何判别？P85.86答：在板面均布荷载作用下，从板中沿支座正交方向取出的矩形板单元，只有一个方向受弯，成为单向板；而在板面均布荷载作用下，荷载沿两个方向传递到周边的支座，故称为双向板。

对四变支撑213l l ≥的板按单向板计算，对212l l ≤的板按双向板计算；当213l l <时，宜按双向板计算。

4.2 结构平面布置的原则是什么？板、次梁、主梁的常用跨度是多少？P86答：单向板肋梁楼盖由板、次梁和主梁组成。

其中，次梁的间距决定了板的跨度；主梁的间距决定了次梁的跨度；柱或墙的间距决定了主梁的跨度。

单向板、次梁、主梁的常用跨度如下：单向板：4m ≤，荷载较大时取小值。

次梁：4~6m 。

主梁：5~8m 。

4.3 单向板中有哪些受力钢筋何构造钢筋？各起什么作用？如何设置？P94.95答：板中受力钢筋分为承受负弯矩板面负筋和承受正弯矩板底正筋，对于绑扎钢筋，当板厚150mm ≤时，间距不宜大于200mm ；板厚150h mm >，不宜大于1.5h ，且不宜大于250mm 。

钢筋间距也不宜小于70mm 。

在支梁支座处或连续板端支座及中间支座处，下部正钢筋伸入支座的长度不应小于5d 。

板中构造钢筋及其作用和设置：1.分布钢筋：分布钢筋布置在受力钢筋的内侧，其作用时与受力钢筋组成钢筋网，便于施工中固定受力钢筋的位置；承受由于温度变化和混凝土收缩所产生的内力；承受并分布板上局部荷载产生的内力；对四边支撑板，可承受在计算中未计及但实际存在的长跨方向的弯矩。

2.沿墙边和墙角处设置板面附加钢筋，承受板上部拉应力，钢筋直径不小于8mm ，间距不大于200mm ，伸出墙边长度大于等于07l 。

3.垂直于主梁的板面附加钢筋：承受主梁边缘处板面产生的支座负弯矩，在主梁上部的板面配置，数量不小于，且主梁单位长度内的总截面面积不小于板中单位宽度内受力钢筋截面积的13；4.板角附加短钢筋：两边嵌入砌体墙内的板内的板角部分，应在板面双面配置附加的短负钢筋。

第4章影响线4.1复习笔记一、移动荷载和影响线的概念1．移动荷载移动荷载作用点在结构上是移动的，研究移动荷载要确定荷载的最不利位置——即使结构某个内力或支座反力达到最大值的荷载位置。

2．影响线（1）表示单位移动荷载作用下内力变化规律的图形称为内力影响线；（2）影响线是研究移动荷载作用的基本工具。

二、静力法作简支梁内力影响线静定结构的内力或支座反力影响线有两种基本作法，静力法和机动法。

1．静力法概念静力法是以荷载的作用位置x为变量，通过平衡方程，从而确定所求内力（或支座反力）的影响函数，并作出影响线。

2．支座反力影响线图4-1-1（1）支座反力R A F 的影响线：对B 点取矩，R P ()A F l F l x ⋅=⋅-，影响线如图4-1-2（a）所示；（2）支座反力R B F 的影响线：对A 点取矩，R P B F l F x ⋅=⋅，影响线如图4-1-2（b）所示。

图4-1-23．剪力与弯矩影响线截面C 处的影响线：由于A 、B 的支座反力已经计入了移动荷载，可以作为已知条件，因此，为了避免再次计算移动荷载，可分两段进行计算：（1）当移动荷载在C 左边移动时，取BC 段计算，列平衡方程：Q R C B F F =-，R C B M F b =⋅；（2）当移动荷载在C 右边移动时，取AC 段计算，列平衡方程：Q R C A F F =，R C A M F a =⋅。

由图4-1-2叠加可得剪力和弯矩的影响线分别如图4-1-3与图4-1-4所示。

图4-1-3剪力影响线图4-1-4弯矩的影响线三、结点承载方式下梁的内力影响线对于某些结构，荷载不是直接作用在主梁上，而是通过纵梁的结点传递到主梁上，不管纵梁承受何种荷载，此时主梁只在横梁处承受集中力，因此主梁承受结点荷载。

1．结点荷载作用下的主梁影响线的作法（1）将单位荷载直接作用在主梁上，作出影响线；（2）从纵梁的各个结点引竖线与上一步作出的影响线相交；（3）从上一步得到各个交点，相邻交点间用直线连接，得到结点荷载下的静定梁的影响线。

实例演示
通过实例演示内力图的 绘制过程，帮助读者掌
握绘制技巧。
04 静定拱的位移计算
位移计算基本概念
位移的定义
位移是指在外力作用下，结构物 某一点或某一截面位置的变化。
静定拱的位移
静定拱在荷载作用下的位移包括 拱顶竖向位移、拱脚水平位移和
转角位移等。
位移计算的意义
位移计算是结构力学中的重要内 容，对于评估结构的安全性、稳 定性和使用功能具有重要意义。
虚功原理在位移计算中的应用
虚功原理的基本概念
01
虚功原理是结构力学中的一个基本原理，它建立了外
力功与结构内部应变能之间的关系。
虚功原理在静定拱位移计算中的应用
02 通过构建静力可能位移和虚力状态，利用虚功原理可
以求解静定拱在各种荷载作用下的位移。
虚功原理的适用条件
03
虚功原理适用于线弹性结构，即结构在受力过程中满
解题思路
同样需要构建静力可能位移和虚力 状态，利用虚功原理求解位移。
解题步骤
详细列出解题步骤，并解释每一步 的意义和计算方法。
05 静定拱的稳定性分析
稳定性分析基本概念
稳定性
结构在受到外部扰动后，能够恢复原有平衡状态的能力。
临界荷载
使结构失去稳定或发生破坏的最小荷载。
稳定性分析
研究结构在荷载作用下是否会发生失稳或破坏，以及如何提高结 构的稳定性。
通过截取拱的任意截面，利用静 力平衡条件求解截面上的内力。
叠加法
将复杂的拱结构分解为若干简单结 构，分别计算内力后再进行叠加。
力法
通过引入多余未知力，建立力法方 程求解拱的内力。
典型例题解析
圆弧拱内力计算
01