下载文档原格式
第4版《液压与气压传动》课后习题答案第一章 习题1-1某液压油在大气压下的体积是50L ，当压力升高后其体积减少到49.9L ，设液压油的体积弹性模量Pa K 5107000⨯=，求压力升高值。
解：V V p K ⋅∆∆-= Pa Pa V V K p 551014)(50)509.49(107000⨯=-⨯⨯-=∆⋅-=∆∴1-2用恩氏粘度计测得3/850m kg =ρ的某种液压油200mL 流过的时间s t 1531=。
20℃时200mL 蒸馏水流过的时间s t 512=。
问该液压油的E 0为多少？动力粘度)(s Pa ⋅μ为多少？运动粘度)/(2s m ν为多少？解：351153210===t t E s m s m E E v /1083.19)/(10)331.6331.7(10)31.631.7(2626600---⨯=⨯-⨯=⨯-= s Pa s Pa v ⋅⨯=⋅⨯⨯==-5610169.0)(1083.19850ρμ1-3如题1-3图所示，容器A 内充满着3/900m kg =ρ的液体，汞U 形测压计的m s m h A 5.0,1==，求容器A 中心压力。
解：设B 、C 为等压面，容器A 中心压力为p A ，则：aC A A B cB p gh P p gZ p p p +=+==汞ρρ得：a A A p gh p gZ +=+汞ρρ容器A 中心的绝对压力为：PaPa p Z h g p aA A 55331031.2)(1001.1)5.0109.01106.13(81.9)(⨯=⨯+⨯⨯-⨯⨯⨯=+-=ρρ汞容器A 中心的相对压力为： Pa Pa Z h g p p A a A 533103.1))(5.0109.01106.13(81.9)(⨯=⨯⨯-⨯⨯⨯=-=-ρρ汞1-4 如题1-4图所示，具有一定真空度的容器用一根管子倒置于一液面与大气相同的槽中，液体在管中上升的高度m h 5.0=，设液体的密度3/1000m kg =ρ，试求容器内的真空度。
液压与气压传动（第4版）刘银水简介《液压与气压传动（第4版）刘银水》是一本介绍液压传动和气压传动的教材。
本书详细讲解了液压传动和气压传动的原理、组成、工作原理、应用以及维护保养等方面的内容。
是液压与气压传动领域的重要参考书之一。
内容概述本书共分为八个章节，内容涵盖了液压传动和气压传动的基础知识、元件介绍、系统设计、系统性能、系统应用、系统维护以及案例分析等方面的内容。
下面将对每个章节的内容进行简要介绍。
第一章：液压与气压传动概述本章介绍了液压传动和气压传动的基本概念和发展历程，阐述了液压传动和气压传动的优点和缺点，以及与其他传动方式的比较。
第二章：液压传动元件本章详细介绍了液压传动中常用的元件，包括液压泵、液压阀、液压缸、液压马达等。
对每个元件的工作原理、结构和特点进行了详细说明。
第三章：气压传动元件本章介绍了气压传动中常用的元件，包括气压泵、气缸、气动阀等。
对每个元件的工作原理、结构和特点进行了详细说明。
第四章：液压传动系统设计本章介绍了液压传动系统的设计原则和步骤。
包括系统的布置原则、元件的选择原则、系统的供油方式等内容。
同时，还介绍了常见的液压传动系统，并对其进行了分析和比较。
第五章：气压传动系统设计本章介绍了气压传动系统的设计原则和步骤。
包括系统的布置原则、元件的选择原则、系统的供气方式等内容。
同时，还介绍了常见的气压传动系统，并对其进行了分析和比较。
第六章：液压传动系统性能本章介绍了液压传动系统的性能参数和测试方法。
包括流量、压力、速度、功率等参数的测试方法和分析。
同时，还介绍了常见的液压传动系统故障分析和解决方法。
第七章：气压传动系统性能本章介绍了气压传动系统的性能参数和测试方法。
包括流量、压力、速度、功率等参数的测试方法和分析。
同时，还介绍了常见的气压传动系统故障分析和解决方法。
第八章：液压与气压传动应用与维护本章介绍了液压与气压传动在工程实践中的应用和维护。
包括工程机械、冶金装备、船舶等领域的典型应用案例，以及系统的日常维护和故障排除方法。
第4版《液压与气压传动》课后习题答案第一章 习题 1-1某液压油在大气压下的体积是50L ，当压力升高后其体积减少到49.9L ，设液压油的体积弹性模量Pa K 5107000⨯=，求压力升高值。
解：V Vp K ⋅∆∆-= Pa Pa V V K p 551014)(50)509.49(107000⨯=-⨯⨯-=∆⋅-=∆∴1-2用恩氏粘度计测得3/850m kg =ρ的某种液压油200mL 流过的时间s t 1531=。
20℃时200mL 蒸馏水流过的时间s t 512=。
问该液压油的E 0为多少动力粘度)(s Pa ⋅μ为多少运动粘度)/(2s m ν为多少 解：351153210===t t E s m s m E E v /1083.19)/(10)331.6331.7(10)31.631.7(2626600---⨯=⨯-⨯=⨯-= s Pa s Pa v ⋅⨯=⋅⨯⨯==-5610169.0)(1083.19850ρμ|1-3如题1-3图所示，容器A 内充满着3/900m kg =ρ的液体，汞U 形测压计的m s m h A 5.0,1==，求容器A 中心压力。
解：设B 、C 为等压面，容器A 中心压力为p A ，则：aC A A B cB p gh P p gZ p p p +=+==汞ρρ得：a A A p gh p gZ +=+汞ρρ容器A 中心的绝对压力为：PaPa p Z h g p aA A 55331031.2)(1001.1)5.0109.01106.13(81.9)(⨯=⨯+⨯⨯-⨯⨯⨯=+-=ρρ汞容器A 中心的相对压力为： Pa Pa Z h g p p A a A 533103.1))(5.0109.01106.13(81.9)(⨯=⨯⨯-⨯⨯⨯=-=-ρρ汞）1-4 如题1-4图所示，具有一定真空度的容器用一根管子倒置于一液面与大气相同的槽中，液体在管中上升的高度m h 5.0=，设液体的密度3/1000m kg =ρ，试求容器内的真空度。
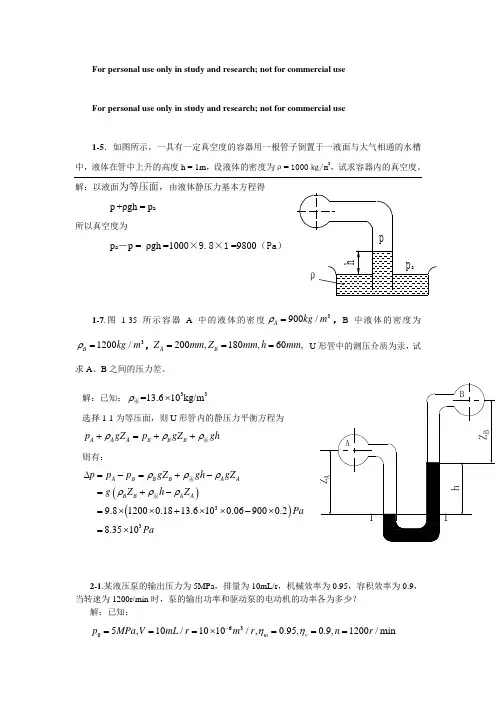
For personal use only in study and research; not for commercial useFor personal use only in study and research; not for commercial use1-5．如图所示，一具有一定真空度的容器用一根管子倒置于一液面与大气相通的水槽中，液体在管中上升的高度h = 1m ，设液体的密度为ρ= 1000㎏/m 3，试求容器内的真空度。
解：以液面为等压面，p +ρgh = p a 所以真空度为p a －p = ρgh1-7.图1-3531200/B kg m ρ=，A Z 求A 、B 之间的压力差。
2-1.某液压泵的输出压力为5MPa ，排量为10mL/r ，机械效率为0.95，容积效率为0.9，当转速为1200r/min 时，泵的输出功率和驱动泵的电动机的功率各为多少？解：已知：6305,10/1010/,0.95,0.9,1200/min m v p MPa V mL r m r n r ηη-===⨯===则泵的输出功率：663000510101012000.9100.960t v P p q p q kw η--⨯⨯⨯⨯===⨯⨯=驱动泵的电动机功率：0.9 1.0530.950.9i P kwP kw η===⨯2-2.某液压泵在转速n=950r/min 时，排量为v=168ml/r 。
在同样的转速和压力29.5MP a 时，测得泵的实际流量为150L/min ，总效率η=087，求： (1) 泵的理论流量；(2) 泵在上述工况下的泵的容积效率机械效率； (3) 泵在上述工况下所需的电动功率； (4) 驱动泵的转矩多大？解：(1) 泵的理论流量 q t =v ·n=168×950=159600ml/min=159.6L/min=2.66×10-3m 3/s（2）94.060/106.15960/1015033=⨯⨯==--t v q q η93.094.087.0.===∴=v m m V ηηηηηη (3) 电机的驱动功率6329.51015010/6084770()84.770.87Oi P pqP W kW ηη-⨯⨯⨯===== (4) 驱动泵的转矩284770852.53()22 3.14950/60i i iii p T nT P T N m n ωππ==∴===⋅⨯⨯ 另解:)(77.8453.85260/95014.322)(53.85287.060/95014.3260/10150105.292236KW nT p m N n pq T nT pq i i i i=⨯⨯⨯==⋅=⨯⨯⨯⨯⨯⨯==∴=-πηππη3-1.液压马达的排量V=250 ml/r ，入口压力p 1=10.5MPa ，出口压力p 2=1.0MPa ，容积效率ηv =0.92，机械效率ηm =0.9，若输入流量q=22 L/min ，求马达的实际转速n 、输出转矩T 、输入功率和输出功率各为多少？ 解：()()()()()1362666333022100.9280.96min 2501010.519.59.510250100.9340.422 3.149.5102210 3.4810600.90.92 3.48102881.4t v m i m v i q q r n V V p p p MPa p V T N m P p q W P P W ηηπηη----⨯===⨯=⨯∆=-=-=∆⋅⨯⨯⨯==⨯=⋅⨯⨯⨯⨯=∆⋅==⨯==⨯⨯⨯=3-3.为两个结构相同相互串联的液压缸，无杆腔的面积A 1=100×10-4m 2，有杆腔的面积A 2=80×10-4m 2，缸1的输入压力p 1=0.9MPa ，输入流量q=12 L/min ，不计摩擦损失和泄漏，求：（1） 两缸承受相同负载（F 1=F 2）时，该负载的数值及两缸的运动速度； （2） 缸2的输入压力是缸1的一半（P 2=P 1/2）时，两缸各能承受多少负载？ （3） 缸1不承受负载（F 1=0）时，缸2能承受多少负载？解： （1）3P 为大气压 30P ∴≈()M P aA A A P P 5.010801010010100109.0444621112=⨯+⨯⨯⨯⨯=+=--- ()N A P A P F F 500010100105.046231221=⨯⨯⨯=-==∴-()s m A q V /02.01010060/10124311=⨯⨯==-- ()s m A q V /016.01010002.010804422=⨯⨯⨯==--（2）P 3()N A P A P A P A P F 540010802/109.010100109.0 24646211122111=⨯⨯⨯-⨯⨯⨯=-=-=-- ()N A P A P A P F 4500101002/109.02461123122=⨯⨯⨯==-=-(3) 因为 022111=-=A P A P F所以 ()MPa A A P P 125.1108010100109.04462112=⨯⨯⨯⨯==-- ()KN A P A P A P F 25.111010010125.1461223122=⨯⨯⨯==-=-4-5.如图所示的液压系统，两液压缸的有效面积A 1=100×10-4m 2，缸I 负载F=35000N ，缸Ⅱ运动时负载为零。
答案不尽相同谨请谅解1-1 某液压油在大气压下的体积是335010m -⨯，当压力升高后，其体积减少到3349.910m -⨯，取油压的体积模量为700.0K Mpa =，求压力升高值。
解： ''33343049.9105010110V V V m m ---∆=-=⨯-⨯=-⨯由0P K V V ∆=-∆知： 643070010110 1.45010k V p pa Mpa V --∆⨯⨯⨯∆=-==⨯ 1-2 用恩式粘度计测的某液压油（3850/kg m ρ=）200Ml 流过的时间为1t =153s ，20C ︒时200Ml 的蒸馏水流过的时间为2t =51s ，求该液压油的恩式粘度E ︒，运动粘度ν和动力粘度μ各为多少？ 解：12153351t E t ︒=== 62526.31(7.31)10/ 1.9810/E m s m s E ν--=︒-⨯=⨯︒ 21.6810Pa s μνρ-==⨯⋅1- 3图示为一粘度计，若D=100mm ，d=98mm,l=200mm,外筒转速n=8r/s 时，测得转矩T=40N ⋅cm,试求其油液的动力粘度。
解：设外筒内壁液体速度为0u08 3.140.1/ 2.512/2fu n D m s m s F TA r rlπτπ==⨯⨯===由 dudy du dyτμτμ=⇒= 两边积分得0220.422()()22 3.140.20.0980.10.0510.512a a T l d D p s p s u πμ-⨯-⨯⨯∴===1-4图示一液压缸，其缸筒内径D ＝12厘米，活塞直径d ＝11.96厘米，活塞长度L ＝14厘米，若油的粘度μ＝0.065Pa.s ，活塞回程要求的稳定速度为v=0.5m/s ，试求不计油液压力时拉回活塞所需的力F 等于多少？解：对活塞列平衡方程：2f du duF F Arl dr drμμπ==-=- 12F dr ldu rμπ⇒=-对上式两边积分得：02d 21F 2D v dr l du rμπ=⎰⎰ 23.140.06514108.5812ln ln 11.96lF N N D d πμ-⨯⨯⨯∴=== 1-5 如图所示，一具有一定真空度的容器用一根管子倒置一液面与大气相通的水槽中，液体与大气相通的水槽中，液体在管中上升的高度h=1m,设液体的密度为31000/kg m ρ=，试求容器内真空度。
《液压与气压传动》(第4版)教材习题答案第1章习题小节习题： P4（1）机械能、液压能。
（2）动力元件、执行元件、控制调节元件、辅助元件和工作介质。
（3）动力元件。
（4）机械能、机械能。
（5）压力、流量和流动方向。
（6）a.液压传动的优点１）能方便地实现无级调速，且调速范围大。
２）容易实现较大的力和转矩的传递。
液压传动装置的体积小、重量轻、运动惯性小。
３）液压传动装置工作平稳，反应速度快，换向冲击小，便于实现频繁换向。
４）易于实现过载保护，而且工作油液能实现自行润滑，从而提高元件的使用寿命。
５）操作简单，易于实现自动化。
６）液压元件易于实现标准化、系列化和通用化。
b.液压传动的缺点1）液体的泄漏和可压缩性使液压传动难以保证严格的传动比。
2）在工作过程中能量损失较大，传动效率较低。
3）对油温变化比较敏感，不宜在很高或很低的温度下工作。
4）液压传动出现故障时，不易诊断。
小节习题：P7（1）由于液体内磨擦力的作用，而产生阻止液层间的相对滑动。
（2）动力黏度、运动黏度、相对黏度。
（3）运动黏度，υ，m2/s，mm2/s。
（4）黏度较低。
（5） 40℃运动黏度，mm2/s。
（6）石油型、乳化型和合成型。
（7）水分、空气、微小固体颗粒、胶质状生成物。
（8）a.堵塞过滤器，使液压泵吸油困难，产生噪声，堵塞阀类元件小孔或缝隙，使阀动作失灵。
微小固体颗粒还会加剧零件磨损，擦伤密封件，使泄漏增加。
b.水分和空气混入会降低液压油的润滑能力，加速氧化变质，产生气蚀；还会使液压液压系统出现振动、爬行等现象。
（9）a.严格清洗元件和系统。
b.尽量减少外来污染。
c.控制液压油的温度。
d.定期检查、清洗和更换滤芯。
e.定期检查和更换液压油。
本章习题1.填空题（1）法向力， 2N m 即 pa 。
（2）压力 和 流量 。
（3）绝对压力 和 相对压力，相对压力 。
（4）输入流量。
（5）沿程压力损失 和局部压力损失 。
（6）功率损失 、油液发热 、泄漏增加 。
第4版《液压与气压传动》课后习题答案第一章 习题1-1某液压油在大气压下的体积是50L ，当压力升高后其体积减少到49.9L ，设液压油的体积弹性模量Pa K 5107000⨯=，求压力升高值。
解：V Vp K ⋅∆∆-= Pa Pa V V K p 551014)(50)509.49(107000⨯=-⨯⨯-=∆⋅-=∆∴1-2用恩氏粘度计测得3/850m kg =ρ的某种液压油200mL 流过的时间s t 1531=。
20℃时200mL 蒸馏水流过的时间s t 512=。
问该液压油的E 0为多少？动力粘度)(s Pa ⋅μ为多少？运动粘度)/(2s m ν为多少？解：351153210===t t E s m s m E E v /1083.19)/(10)331.6331.7(10)31.631.7(2626600---⨯=⨯-⨯=⨯-= s Pa s Pa v ⋅⨯=⋅⨯⨯==-5610169.0)(1083.19850ρμ1-3如题1-3图所示，容器A 内充满着3/900m kg =ρ的液体，汞U 形测压计的m s m h A 5.0,1==，求容器A 中心压力。
解：设B 、C 为等压面，容器A 中心压力为p A ，则：aC A A B cB p gh P p gZ p p p +=+==汞ρρ得：a A A p gh p gZ +=+汞ρρ容器A 中心的绝对压力为：PaPa p Z h g p aA A 55331031.2)(1001.1)5.0109.01106.13(81.9)(⨯=⨯+⨯⨯-⨯⨯⨯=+-=ρρ汞容器A 中心的相对压力为： Pa Pa Z h g p p A a A 533103.1))(5.0109.01106.13(81.9)(⨯=⨯⨯-⨯⨯⨯=-=-ρρ汞1-4 如题1-4图所示，具有一定真空度的容器用一根管子倒置于一液面与大气相同的槽中，液体在管中上升的高度m h 5.0=，设液体的密度3/1000m kg =ρ，试求容器内的真空度。
第4版《液压与气压传动》课后习题答案第一章 习题1-1某液压油在大气压下的体积是50L ，当压力升高后其体积减少到49.9L ，设液压油的体积弹性模量Pa K 5107000⨯=，求压力升高值。
解：V V p K ⋅∆∆-= Pa Pa V V K p 551014)(50)509.49(107000⨯=-⨯⨯-=∆⋅-=∆∴1-2用恩氏粘度计测得3/850m kg =ρ的某种液压油200mL 流过的时间s t 1531=。
20℃时200mL 蒸馏水流过的时间s t 512=。
问该液压油的E 0为多少？动力粘度)(s Pa ⋅μ为多少？运动粘度)/(2s m ν为多少？解：351153210===t t E s m s m E E v /1083.19)/(10)331.6331.7(10)31.631.7(2626600---⨯=⨯-⨯=⨯-= s Pa s Pa v ⋅⨯=⋅⨯⨯==-5610169.0)(1083.19850ρμ1-3如题1-3图所示，容器A 内充满着3/900m kg =ρ的液体，汞U 形测压计的m s m h A 5.0,1==，求容器A 中心压力。
解：设B 、C 为等压面，容器A 中心压力为p A ，则：aC A A B cB p gh P p gZ p p p +=+==汞ρρ得：a A A p gh p gZ +=+汞ρρ容器A 中心的绝对压力为：PaPa p Z h g p aA A 55331031.2)(1001.1)5.0109.01106.13(81.9)(⨯=⨯+⨯⨯-⨯⨯⨯=+-=ρρ汞容器A 中心的相对压力为： Pa Pa Z h g p p A a A 533103.1))(5.0109.01106.13(81.9)(⨯=⨯⨯-⨯⨯⨯=-=-ρρ汞1-4 如题1-4图所示，具有一定真空度的容器用一根管子倒置于一液面与大气相同的槽中，液体在管中上升的高度m h 5.0=，设液体的密度3/1000m kg =ρ，试求容器内的真空度。
第4版《液压与气压传动》课后习题答案第一章 习题1-1某液压油在大气压下的体积是50L ，当压力升高后其体积减少到49.9L ，设液压油的体积弹性模量Pa K 5107000⨯=，求压力升高值。
解：V Vp K ⋅∆∆-= Pa Pa V V K p 551014)(50)509.49(107000⨯=-⨯⨯-=∆⋅-=∆∴1-2用恩氏粘度计测得3/850m kg =ρ的某种液压油200mL 流过的时间s t 1531=。
20℃时200mL 蒸馏水流过的时间s t 512=。
问该液压油的E 0为多少？动力粘度)(s Pa ⋅μ为多少？运动粘度)/(2s m ν为多少？ 解：351153210===t t E s m s m E E v /1083.19)/(10)331.6331.7(10)31.631.7(2626600---⨯=⨯-⨯=⨯-= s Pa s Pa v ⋅⨯=⋅⨯⨯==-5610169.0)(1083.19850ρμ1-3如题1-3图所示，容器A 内充满着3/900m kg =ρ的液体，汞U 形测压计的m s m h A 5.0,1==，求容器A 中心压力。
解：设B 、C 为等压面，容器A 中心压力为p A ，则：aC A A B cB p gh P p gZ p p p +=+==汞ρρ得：a A A p gh p gZ +=+汞ρρ容器A 中心的绝对压力为：PaPa p Z h g p aA A 55331031.2)(1001.1)5.0109.01106.13(81.9)(⨯=⨯+⨯⨯-⨯⨯⨯=+-=ρρ汞容器A 中心的相对压力为： Pa Pa Z h g p p A a A 533103.1))(5.0109.01106.13(81.9)(⨯=⨯⨯-⨯⨯⨯=-=-ρρ汞1-4 如题1-4图所示，具有一定真空度的容器用一根管子倒置于一液面与大气相同的槽中，液体在管中上升的高度m h 5.0=，设液体的密度3/1000m kg =ρ，试求容器内的真空度。
第4版《液压与气压传动》课后习题答案第一章 习题1-1某液压油在大气压下的体积是50L ，当压力升高后其体积减少到49.9L ，设液压油的体积弹性模量Pa K 5107000⨯=，求压力升高值。
解：V V p K ⋅∆∆-= Pa Pa V V K p 551014)(50)509.49(107000⨯=-⨯⨯-=∆⋅-=∆∴1-2用恩氏粘度计测得3/850m kg =ρ的某种液压油200mL 流过的时间s t 1531=。
20℃时200mL 蒸馏水流过的时间s t 512=。
问该液压油的E 0为多少？动力粘度)(s Pa ⋅μ为多少？运动粘度)/(2s m ν为多少？解：351153210===t t E s m s m E E v /1083.19)/(10)331.6331.7(10)31.631.7(2626600---⨯=⨯-⨯=⨯-= s Pa s Pa v ⋅⨯=⋅⨯⨯==-5610169.0)(1083.19850ρμ1-3如题1-3图所示，容器A 内充满着3/900m kg =ρ的液体，汞U 形测压计的m s m h A 5.0,1==，求容器A 中心压力。
解：设B 、C 为等压面，容器A 中心压力为p A ，则：aC A A B cB p gh P p gZ p p p +=+==汞ρρ得：a A A p gh p gZ +=+汞ρρ容器A 中心的绝对压力为：PaPa p Z h g p aA A 55331031.2)(1001.1)5.0109.01106.13(81.9)(⨯=⨯+⨯⨯-⨯⨯⨯=+-=ρρ汞容器A 中心的相对压力为： Pa Pa Z h g p p A a A 533103.1))(5.0109.01106.13(81.9)(⨯=⨯⨯-⨯⨯⨯=-=-ρρ汞1-4 如题1-4图所示，具有一定真空度的容器用一根管子倒置于一液面与大气相同的槽中，液体在管中上升的高度m h 5.0=，设液体的密度3/1000m kg =ρ，试求容器内的真空度。
解：根据液体静力学基本方程gh p p A B ρ+= （1）液面的压力即为大气压，即：a B p p = （2）将（2）代入（1）得：gh p p A a ρ+=容器内的真空度：Pa Pa gh p p A a 4900)(5.081.91000=⨯⨯==-ρ1-5如题1-5图所示，直径为d ，质量为m 的柱塞浸入充满液体的密闭容器中，在力F 的作用下处于平衡状态。
若浸入深度为h ，液体密度为ρ，试求液体在测压管内上升的高度x 。
解：设柱塞底部的压力为p以柱塞为研究对象，列受力平衡方程式：mg F d p +=⋅⋅24π （1）)(h x g p +=ρ （2）将（2）代入（1）2244)(d g mg F h x mg F d h x g ⋅⋅+=++=⋅⋅+πρπρh gd mg F x -+=ρπ2)(41-6 如题1-6图所示，将流量min /16L q =的液压泵安装在油面以下，已知油的运动粘度s cm /11.02=ν，油的密度3/880m kg =ρ，弯头处的局部阻力系数2.0=ξ，其他尺寸如图所示。
求液压泵入口处的绝对压力。
解：①求吸油管中的流速s m s m d q v /85.0)/()1020(14.3604101642332=⨯⨯⨯⨯⨯==--π ②求雷诺数管中流体为层流，232015451011.0102085.0Re 43<=⨯⨯⨯==--νvd③求沿程压力损失Pa Pa v d l R p e 87.1361)(285.088002.0315********2=⨯⨯⨯=⋅⋅=∆ρλ ④求局部压力损失Pa Pa v p 58.63)(285.08802.0222=⨯⨯=⋅=∆ρξξ ⑤求总压力损失Pa Pa p p p 45.1425)(58.6387.1361=+=∆+∆=∑∆ξλ⑥求液压泵的进口压力以液压泵轴线为基准，对1-1、2-2截面列伯努利方程Pa Pa p sm v z v m z Pa p p p v v z z g p p pv gz p v gz p a 5252221151222121122222211110053.1)(45.1425285.08807.081.98801001.1/85.0,0,0,7.0,1001.1)(2)(22⨯=-⨯-⨯⨯+⨯=====⨯==∑∆--+-+=∑∆+++=++已知：ρρρρρρ1-7 如题1-7图所示为一种抽吸设备。
水平管出口通大气，当水平管内液体流量达到某一数值时，处于面积为A 1处的垂直管子将从液箱内抽吸液体，液箱表面为大气压力。
水平管内液体（抽吸用）和被抽吸介质相同。
有关尺寸如下：面积m h A A cm A 1,4,2.31221===，不计液体流动时的能量损失，问水平管内流量达到多少时才能开始抽吸。
解：对水平管1-1、2-2列伯努利方程 2222222111v g z p v g z p ++=++ρρ 因为：a p p z z ==221,，在刚从垂直管内抽水时，垂直管内液体可视为静止液体，由液体静压力基本方程式可得：a p gh p =+ρ1，所以：gh p p a ρ-=1，将这些代入伯努利方程：222221v p v ghp a a +=+-ρρρ 化简得： 222221v p v gh p a a+=+-ρρ gh v v 22221=- （1）根据流量连续性方程2211A v A v =，已知124A A =，得：214v v = （2）将（2）代入（1）得：gh v 21522=s m gh v /14.115181.921522=⨯⨯== 管内的流量m in /6.87/1046.1102.314.1443341222L s m A v A v q =⨯=⨯⨯⨯===--1-8 如题1-8图所示，管道输送2/900m kg =ρ的液体，已知,15,20,10m h m L mm d ===液体的运动粘度s m /104526-⨯=ν，点1处的压力为Pa 5105.4⨯，点2处的压力为Pa 5104⨯，试判断管中液流的方向并计算流量。
解：假设管中液体从点1流向点2，即1→2以点1所在的平面为基准水平面，选取点1和点2的截面1-1、2-2列伯努利方程：g h v g z p v g z p w +++=++2222222111ρρ 因为：,,021h z z ==根据流量连续性方程A v A v q 21==,得21v v =代入伯努利方程并化简得:gh gh p p g h hg p p w w ρρρρ++=++=2121令：p g h w ∆=ρ为压力损失，则：010822.0)(1581.9900104105.455521<⨯-=⨯⨯-⨯-⨯=--=∆Pa Pa gh p p p ρ故液体流向假设不成立，应由点2流向点1，即2→1假设管道内的液流为层流，则：根据层流时沿程压力损失计算公式232d Lu p μ=∆ 得管道中液流的流速为：s m s m p L d u /32.0)/(10822.020104590032)1010(3256232=⨯⨯⨯⨯⨯⨯⨯=∆⋅=--μ νudR e ==2320711045)1010(32.0623<=⨯⨯⨯-- 流态假设成立。
管道流量为：m in /5.1/10025.0)/(32.04)1010(4333232L s m s m u d q =⨯=⨯⨯⨯=⋅=--ππ1-9 如题1-9图所示，活塞上作用有外力N F 3000=，活塞直径mm D 50=，若使油从缸底部的锐缘孔口流出，设孔口的直径mm d 10=，流量系数61.0=d C ，油的密度3/900m kg =ρ，不计摩擦，试求作用在液压缸缸底壁面上的力。
解：作用在活塞上的外力F 在缸体内产生的压力为：Pa Pa D F p 52321029.15)()1050(14.3430004⨯=⨯⨯⨯==-π孔口的流量为：s m p A C q d /1078.21029.1590024)1010(14.361.02335230--⨯=⨯⨯⨯⨯⨯=∆⋅=ρ 活塞的运动速度为：s m D qv /42.1)1050(14.341078.242332=⨯⨯⨯⨯==--π 孔口的液流速度为：s m d qv /41.35)1010(14.341078.2423320=⨯⨯⨯⨯==--π 取缸内的液体为控制液体，缸底壁面对控制液体的作用力为R 。
根据动量定理：NN v v q F R v v q R F 96.2914))(42.141.35(1078.29003000)()(300=-⨯⨯-=--=-=--ρρ液流对缸底壁面的作用力为： N R R 96.2914==' 方向向右1-10 如题1-10图所示，已知液体密度为3/1000m kg =ρ。
当阀门关闭时压力表的读数为Pa 5103⨯，阀门打开时压力表的读数为Pa 5108.0⨯，如果mm d 12=，不计损失，求阀门打开时管中的流量。
解： 在阀前、阀后各取一个截面1-1、2-2列伯努利方程：2222222111v g h p v g h p ++=++ρρ 阀门开启前，阀前液体为静止液体。
阀门开启瞬间， 也可将阀前液体视为静止液体。
即：211,0h h v ==，代入伯努利方程并化简得：22221v p p +=ρρ s m s m p p v /98.20)/(10)8.03(10002)(25212=⨯-=-=ρ阀门开启时管中液流的流量为：m in /2.142/1037.2)/(98.204)1012(14.343332322L s m s m v d q =⨯=⨯⨯⨯=⋅=--π1-11 如题1-11所示，一个水深2m ，水平截面积为m 33⨯的水箱，底部接一直径、长2m 的竖直管，在水箱进水量等于出水量下作恒定流动，求点3处的压力及出流速度（略去各种损失）。
解：由于水箱的进水量等于出水量，液面高度保持不变，可将水箱中的液体视为静止液体。
点3处的压力可由静压力基本方程式求得： a a a p p gh p p 53533103.1))(12(81.9101001.1⨯=+⨯⨯+⨯=+=ρ对点1、点2所在的截面1-1和2-2列伯努利方程2222222111v g h p v g h p ++=++ρρ 因为：0,,02211====h p p p v a ，代入伯努利方程并化简得：s m s m v d v A q sm s m gh v v g h /156.0)/(86.8415.014.34/86.8)/()112(81.922213322222212221=⨯⨯====++⨯⨯===π1-12 如题1-12所示的弯管，试利用动量方程求流动液体对弯管的作用力。
