Li6 的对称 操作为绕轴旋转 60 。再反伸 , 其效果等于一个 L3和一个对称面(P)的组合 , 即 Li6 = L3 + P (见图 3.12 (d))。
(c) Li4
(d) Li6 = L3 + P
图 3.12 各种旋转反伸轴作用示意图
只有 Li4 是一个独立的对称元素 , 其相 应的对称操作为绕轴旋转 90 。再反伸(见图 3.12 (c))。
3.2 晶体的宏观对称性
物体相同部分有规律的重复称为对称。 只 要稍加留意 , 你就会发现 , 自然界中到处都存在 着对称现象 , 例如:雪花、鲜花、花布、汽车、 飞机、大楼等等都表现出一定形式的对称。例 如 , 雪花有六个瓣 , 即绕其中心每转动 60。雪花 复原 , 许多草木的花朵有 5 个瓣 , 即每转动 360 。 /5 , 花朵复原 , 好象没转动一样 , 人的左 右手、汽车的左右两半也是对称的。
前面已经提到 , 同一种晶体 , 晶面的大小 和数目可能有相当程度的变化。通过测量晶面 夹角可以达到去伪存真的目的 , 即反映出晶体 外形的真正规律性。但是一种晶体往往有若干 晶面 , 要逐一画出每种晶体的外形图 , 第一是 十分困难的 ; 第二是往往被一些假象掩盖 , 而 不易看出其对称性方面的规律性。
图36位于球心的晶体其晶面法线与球面相交给出的极点以投影球的两个极点即过基圆中心的法线与球面相交的两个点中之一作为视点如以基圆下面的极点作为视点将此视点与基圆上面的晶面极点作连线与基圆相交交点就是晶面极点在投影平面上的极射赤平投影点图37
第三章 几何结晶学基础
2
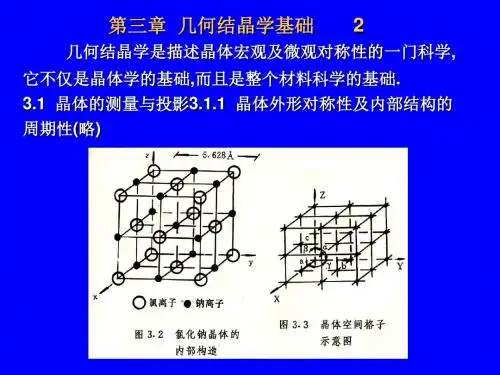
几何结晶学是描述晶体宏观及微观对称性的一门科学, 它不仅是晶体学的基础,而且是整个材料科学的基础.
3.1.3 晶体的测量与投影