焦耳定律

焦耳定律的表达式
焦耳定律是定量说明传导电流将电能转换为热能的定律。

内容是：电流通过导体产生的热量跟电流的二次方成正比，跟导体的电阻成正比，跟通电的时间成正比。

焦耳定律数学表达式：Q=I²Rt；对于纯电阻电路可推导出：Q=W=Pt;Q=UIt;Q=(U²/R)t。

其中Q指热量，单位是焦耳（J），I指电流，单位是安培（A），R指电阻，单位是欧姆（Ω），t指时间，单位是秒（s），以上单位全部用的是国际单位制中的单位。

电流通过导体时会产生热量，这叫做电流的热效应，而电热器是利用电流的热效应来加热的设备，电炉、电烙铁、电熨斗、电饭锅、电烤炉等都是常见电热器。

电热器的主要组成部分是发热体，发热体是由电阻率大，熔点高的电阻丝绕在绝缘材料上制成。

焦耳定律规定：电流通过导体所产生的热量和导体的电阻成正比，和通过导体的电流的平方成正比，和通电时间成正比。

该定律是英国科学家焦耳于1841年发现的。

焦耳定律是一个实验定律，它可以对任何导体来适用，范围很广，所有的电路都能使用。

遇到电流热效应的问题时，例如要计算电流通过某一电路时放出热量；比较某段电路或导体放出热量的多少，即从电流热效应角度考虑对电路的要求时，都可以使用焦耳定律。

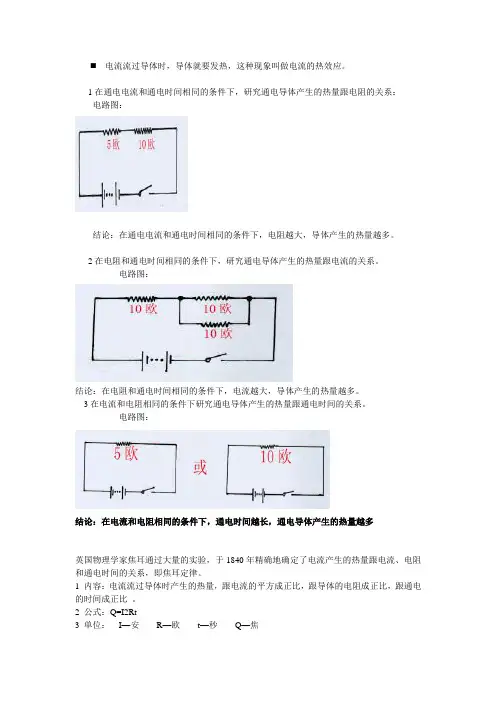
电流流过导体时，导体就要发热，这种现象叫做电流的热效应。

1在通电电流和通电时间相同的条件下，研究通电导体产生的热量跟电阻的关系：电路图：结论：在通电电流和通电时间相同的条件下，电阻越大，导体产生的热量越多。

2在电阻和通电时间相同的条件下，研究通电导体产生的热量跟电流的关系。

电路图：结论：在电阻和通电时间相同的条件下，电流越大，导体产生的热量越多。

3在电流和电阻相同的条件下研究通电导体产生的热量跟通电时间的关系。

电路图：结论：在电流和电阻相同的条件下，通电时间越长，通电导体产生的热量越多英国物理学家焦耳通过大量的实验，于1840年精确地确定了电流产生的热量跟电流、电阻和通电时间的关系，即焦耳定律。

1 内容：电流流过导体时产生的热量，跟电流的平方成正比，跟导体的电阻成正比，跟通电的时间成正比。

2 公式：Q=I2Rt3 单位：I—安R—欧t—秒Q—焦例题（1）某导体的电阻是2欧，当1安的电流通过时，1分钟产生的热量是多少焦？ 解：Q= I2Rt=(1安)2 × 2欧× 60秒=120焦答：1分钟产生的热量是120焦。

（2） 一只“220V 45W ”的电烙铁，在额定电压下使用，每分钟产生的热量是多少？你能用几种方法解此题？⎪⎩⎪⎨⎧===UItW Q U P I 额额（ 3）Q=W= t R U 2 （4）Q=W=Pt3 、一台电动机正常工作时线圈两端的电压为380伏，线圈的电阻为2欧,线圈中的电流为10安,若这台电动机正常工作1秒钟，求：1 ）消耗的电能W 。

2 ）产生的热量Q 。

解：1 ） W ＝UIt＝380×10×1＝3800焦2 ） Q ＝I2Rt＝10 ×10 ×2 ×1＝200焦答： 消耗的电能是3800焦；产生的热量是200焦。

为什么电炉接入照明电路后，能放出大量的热来，而与电炉连接的导线却不怎么热？ 因为电线和电炉串联，通过它们的电流是一样的，而电炉的电阻比电线的电阻大的多，所以根据焦耳定律Q=I2Rt 可知，在相同时间内电流通过电炉产生的热量比通过电线产生的热量大，因此电炉热而电线却不热。

焦耳定律和电功率的计算方法电力是我们日常生活中不可或缺的能源，而了解电力的基本原理和计算方法对于我们正确使用电力和解决电力问题至关重要。

本文将介绍焦耳定律和电功率的计算方法，帮助读者更好地理解和应用电力知识。

焦耳定律是描述电能转化为热能的物理定律。

它表明，通过电阻器流过的电流在电阻器内部会产生热量，且该热量与电流强度、电阻值和时间的乘积成正比。

具体而言，焦耳定律可以用如下公式表示：Q = I^2 * R * t其中，Q代表电阻器产生的热量（单位为焦耳），I代表电流强度（单位为安培），R代表电阻值（单位为欧姆），t代表时间（单位为秒）。

根据焦耳定律，我们可以计算出在特定条件下电阻器产生的热量。

例如，如果一个电阻器的电流强度为2安培，电阻值为10欧姆，持续通过电流的时间为5秒，那么根据焦耳定律的公式，可以计算出该电阻器产生的热量为：Q = 2^2 * 10 * 5 = 200焦耳通过焦耳定律，我们可以更好地理解电能转化为热能的过程，并在实际应用中合理利用电能。

除了焦耳定律，电功率也是电力领域中一个重要的概念。

电功率是指电流通过电器元件时所做的功率，是描述电能转化速率的物理量。

电功率可以用如下公式表示：P = I * V其中，P代表电功率（单位为瓦特），I代表电流强度（单位为安培），V代表电压（单位为伏特）。

根据电功率的计算方法，我们可以计算出电器元件消耗的功率。

例如，一个电器元件的电流强度为3安培，电压为220伏特，那么根据电功率的公式，可以计算出该电器元件消耗的功率为：P = 3 * 220 = 660瓦特通过电功率的计算，我们可以了解电器元件的能耗情况，合理安排用电，从而节约能源和降低电费。

除了单一的电阻器和电器元件，实际的电路往往包含多个元件，这时我们可以通过串联和并联的方式来计算整个电路的电阻值和电功率。

串联是指将多个电阻器或电器元件连接在一起，电流在其中依次流过；并联是指将多个电阻器或电器元件的两个端口分别连接在一起，电流在其中分流。

第7讲焦耳定律姓名____________★知识要点★1、焦耳定律焦耳通过大量实验精确地确定了电流产生热量跟电流强度、电阻和时间的关系：电流通过导体产生的热量，跟电流强度的平方成正比，跟导体的电阻成正比，跟通电的时间成正比。

即：Q=I2Rt。

它适用于任何用电器热量的计算。

在仅有电流热效应存在的电路中（纯电阻电路），电能全部转化成了内能，而没有转化为其他形式的能，这时电流产生的热量等于电流所做的功。

即：Q=W。

再根据W=UIt和U=IR可推导得出Q=I2Rt。

焦耳定律的公式也可以表述为Q=U2t/R，用它解决某些问题比较方便，但必须注意它适用于只存在电流热效应的电路中。

问：观察上图，请判断这样使用插线板是否安全，可能导致怎样的后果？请简述理由。

2、电功和电热的关系:纯电阻电路：电阻R,电路两端电压U,通过的电流强度I。

电功:W= , 电热:Q= ，电热和电功的关系；表明:在纯电阻电路中,电功电热。

也就是说电流做功将电能全部转化为电路的非纯电阻电路：电流通过电动机M时：电功:W= ，电热:Q= ，电热和电功的关系： =机械能+ 。

表明: 在包含有电动机,电解槽等非纯电阻电路中,电功仍 UIt,电热仍I2Rt，但电功不再等于电热而是电热了。

3、探究课题：研究电流产生的热量与哪些因素有关装置及原理：组装了如图所示的实验装置，在两个相同的烧瓶中装满煤油，瓶中各放一根电阻丝，甲瓶中电阻丝的电阻比乙瓶中的大。

通电后电流通过电阻丝产生热量使煤矿油的温度升高，体积膨胀，煤油上升的高度越。

实验过程：①接通电路一段时间，比较两瓶中的煤油哪个上升得高，实验结果是：瓶中的煤油上升得高。

这表明，电阻越大，产生的热量越多。

②在两玻璃管中的液柱降回原来的高度后，调节滑动变阻器，加大电流，重做上述实验，通电时间与前次相同。

在两次实验中，比较甲瓶（或乙瓶）中的煤油哪次上升得高。

实验结果：在第二次实验中，瓶中煤油上升得较。

这表明，电流越大，电流产生的热量越多。

什么是欧姆定律和焦耳定律？
欧姆定律和焦耳定律是电学中两个重要的定律，用于描述电路中电压、电流和电阻之间的关系。

欧姆定律是指在恒温条件下，电阻的电流与通过该电阻的电压成正比。

即电压和电流之间的比例关系。

欧姆定律的数学表达式为：
V = I * R
其中，V表示电压，I表示电流，R表示电阻。

欧姆定律表明，当电压施加在电阻上时，电流的大小与电阻的比例成正比。

这个比例常数就是电阻的阻值。

欧姆定律的实质是电压施加在电阻上产生的电场力与电荷的流动速度之间的平衡关系。

焦耳定律是指电阻上消耗的功率与电压和电流的乘积成正比。

即功率和电压、电流之间的关系。

焦耳定律的数学表达式为：
P = I^2 * R = V^2 / R
其中，P表示功率，I表示电流，R表示电阻。

焦耳定律表明，当电流通过电阻时，电阻会消耗一定的电能，这个电能转化为热能，即功率。

功率的大小与电流的平方成正比，与电压的平方成反比。

焦耳定律的实质是电能转化为热能的过程。

欧姆定律和焦耳定律在电路中具有广泛的应用。

欧姆定律可以用于计算电路中的电流和电压关系，帮助我们理解和设计电路。

焦耳定律可以用于计算电路中的功率消耗，帮助我们理解和优化电路的效能。

在物理学教育中的学习材料中，欧姆定律和焦耳定律的概念应该以生动有趣的方式呈现，结合实际应用和实验，让学生能够深入理解和应用这些定律。

同时，可以通过电路图的分析和计算实例来加深学生对欧姆定律和焦耳定律的理解和掌握。

九年级物理——焦耳定律一、焦耳定律内容1.电流通过导体时,导体发热,电能转化成,这种现象叫做电流的热效应。

2.电流通过导体产生的热量跟电流的二次方成,跟导体的电阻成,跟通电时间成,这个规律叫做焦耳定律。

3.如果热量用Q表示,电流用I表示,电阻用R表示,时间用t表示,则焦耳定律的表达式为。

例：生活举例:生活中像取暖器这样的用电器,通电以后会产生热量的用电器还有很多,你能列举一下吗?例1：一根60 Ω的电阻丝接在36 V的电源上,在5 min内共产生多少热量?二、实验探究过程1.两个透明容器中密封着等量的空气,密闭容器中各有一段电阻丝,右边的电阻丝的电阻比较大。

两电阻丝串联起来接到电源两端,通电一段时间后,比较U形管中液面高度的变化。

2.两个透明容器中密封着等量的空气,密闭容器中各有一段电阻丝,两电阻丝的电阻相同。

右边的电阻丝与一个相同的电阻丝并联后再与左边的电阻丝串联起来接到电源两端,通电一段时间后,比较U形管中液面高度的变化。

方法指导:在实验中,将不易观察到的现象通过其他方式直观、形象地显示出来的方法,我们称之为转换法。

归纳总结:在电流相同、通电时间相同的情况下,电阻越大,产生的热量。

在电阻相同、通电时间相同的情况下,电流越大,产生的热量。

例2：如图是研究电流通过导体产生的热量与哪些因素有关的实验，下列分析正确的是A．甲、乙两次实验都应用了控制变量法B．甲实验通电一段时间后，左侧容器内空气吸收的热量更多C．乙实验时为了研究电流产生的热量与电阻的关系D．乙实验通电一段时间后，右侧U形管中液面的高度差比左侧的小三、电热的利用与危害生活中我们是如何利用电热的？生活中和许多产业中都要用到电热。

家里的电熨斗、电饭锅、电热水器等都是利用电热的电器。

有时电热会给我们造成什么危害？我们又是如何防止的呢？电热过多会烧坏用电器,产生很多安全隐患;电视机的后盖有很多孔,就是为了通风散热,使用时一定要把防尘布罩拿开。

电脑里安装了微型风扇及时散热。

焦耳定律微观解释
焦耳定律是热力学中的一个重要定律，它描述了能量转换的机制。

它的原始表述是：当热量Q传递给物体时，物体的内能增加ΔU，这
个增量与Q成正比，即ΔU=Q。

从微观角度来看，焦耳定律可以解释为：当物体吸收热量时，分子的热运动加强，分子速度增加，能量增加，因此内能也随之增加。

这个过程中，物体的温度上升，说明分子的热运动变得更加剧烈。

当物体释放热量时，分子的热运动减弱，分子速度减小，能量减少，因此内能也随之减少。

这个过程中，物体的温度下降，说明分子的热运动变得更加缓慢。

总之，焦耳定律描述了热量传递和内能变化的关系，是能量守恒定律在热力学中的具体应用。

- 1 -。

初三物理焦耳定律知识点笔记焦耳定律是研究电能转化问题的重要定律之一，对于初中物理学习的电学基础知识来说，是非常重要的知识点之一、下面是对焦耳定律的一些基本概念和要点进行了笔记总结，希望对你的学习有所帮助。

一、焦耳定律的基本概念1.电功：电流通过导线时，电流对导线所做的功称为电功，用符号W 表示，单位是焦耳（J）。

2.电功率：单位时间内做的电功称为电功率，用符号P表示，单位是瓦特（W）。

3.焦耳定律：电功率等于电流强度与电压的乘积，即P=I*U，其中P 表示电功率，I表示电流强度，U表示电压。

二、焦耳定律的推导及物理意义1.推导过程：设导线的电阻为R，电流强度为I，电压为U，在导线中通过电流的功为W=U*I*t，将电流强度I代入可得W=U*(U/R)*t，化简即可得焦耳定律P=U*I。

2.物理意义：焦耳定律实际上描述了电能的转化关系，即电能转化成热能的速率等于电流强度与电压的乘积。

三、使用焦耳定律解题的基本方法1.已知电功率和电流强度，求电压：根据焦耳定律P=U*I，可以通过将已知量代入公式求解未知量。

2.已知电功率和电压，求电流强度：同样可以利用焦耳定律P=U*I求解未知量。

3.已知电流强度和电压，求电功率：同样可以利用焦耳定律P=U*I求解未知量。

4.在计算题中，根据题目给出的已知条件，运用焦耳定律进行代入计算，得出结果。

四、焦耳热的计算和应用1.焦耳热的计算：焦耳热是指电流通过导线时产生的热量，用符号H 表示，单位是焦耳（J）。

计算公式为H=I^2*R*t，其中I为电流强度，R 为电阻，t为时间。

2.焦耳热的应用：焦耳热广泛应用于电器设备中，比如电炉、电热水器等，通过电流通过导线时的热量来进行加热。

五、注意事项和习题解析1.在计算题中，需要注意单位的换算，比如将秒换算成小时等。

2.在应用题中，需要根据实际情况进行问题的分析，并运用所学知识解决问题。

3.习题解析：根据所给条件，运用焦耳定律进行代入计算即可得到所要求的结果。

初中焦耳定律知识点焦耳定律是物理学中的一个重要定律，描述了电流通过导线时产生的热量与电流强度、电阻和时间的关系。

下面将详细介绍焦耳定律的知识点。

1.定义：焦耳定律是指电流通过导体时，导体单位时间内所产生的热量与电流强度、电阻和时间的乘积成正比。

2.公式表示：根据焦耳定律可以得到以下公式：Q=I²Rt其中Q表示导体产生的热量（单位为焦耳），I表示电流强度（单位为安培），R表示电阻（单位为欧姆），t表示时间（单位为秒）。

3.应用实例：焦耳定律在日常生活中有很多应用，例如电炉、电灯、电吹风等电器的工作原理都与焦耳定律密切相关。

4.等效电阻：当电流通过多个电阻串联时，可以将它们的电阻值求和得到一个等效电阻。

根据焦耳定律，等效电阻所产生的热量与单个电阻串联时所产生的热量相同。

5.电功率：根据焦耳定律可以得到以下公式：P=IV其中P表示电功率（单位为瓦特），I表示电流强度（单位为安培），V表示电压（单位为伏特）。

电功率表示单位时间内电能的消耗或转化速率。

6.选择性吸收：根据焦耳定律，不同物质对电流的阻抗不同，因此导体的电阻与其材料的选择有关。

有些物质对电流的阻抗较小，可以作为导体使用，而有些物质对电流的阻抗较大，可以作为绝缘体使用。

7.温度变化：根据焦耳定律，当电流通过导体时，导体会产生热量，从而使导体的温度升高。

导体的温度升高会导致电阻的变化，从而影响电流的强度和电阻的功率消耗。

8.合理利用电能：根据焦耳定律，电能可以通过电流转化为热能，因此在使用电器时应合理利用电能，避免浪费电能，减少能源消耗。

总结：焦耳定律描述了电流通过导线时产生的热量与电流强度、电阻和时间的关系。

通过应用焦耳定律，可以计算电阻消耗的功率、选用适合的材料作为导体和绝缘体，并合理利用电能。

同时，焦耳定律的理解也有助于我们理解电路中的能量转化和热效应。

《焦耳定律》知识清单一、焦耳定律的发现在电学的发展历程中，焦耳定律的发现具有重要的意义。

詹姆斯·普雷斯科特·焦耳（James Prescott Joule）通过大量的实验和观察，揭示了电流通过导体时产生热量的规律。

焦耳在实验中，使用了不同的电阻、电流和通电时间，精确地测量了产生的热量。

他的坚持不懈和严谨的科学态度，为我们带来了这一重要的电学定律。

二、焦耳定律的内容焦耳定律指出：电流通过导体产生的热量跟电流的二次方成正比，跟导体的电阻成正比，跟通电的时间成正比。

数学表达式为：Q ＝ I²Rt 。

其中，Q 表示热量，单位是焦耳（J）；I 表示电流，单位是安培（A）；R 表示电阻，单位是欧姆（Ω）；t 表示通电时间，单位是秒（s）。

这个定律告诉我们，当电流通过导体时，电流越大、电阻越大、通电时间越长，产生的热量就越多。

三、焦耳定律的推导我们可以从电能转化为热能的角度来推导焦耳定律。

当电流通过导体时，电能转化为热能。

假设在时间 t 内，电流 I 通过电阻 R 的导体，根据电功的公式 W ＝ UIt ，而对于纯电阻电路，欧姆定律 U ＝ IR 成立。

将 U ＝ IR 代入 W ＝ UIt 中，得到 W ＝ I²Rt 。

因为电能全部转化为热能，所以产生的热量 Q 等于电功 W ，即 Q ＝ I²Rt 。

四、焦耳定律的应用1、电热器生活中常见的电热器，如电热水器、电暖器、电饭锅等，都是利用焦耳定律工作的。

这些电器通过电阻丝将电能转化为热能，从而为我们提供所需的热量。

在设计和选择电热器时，需要根据焦耳定律来考虑电阻的大小、电流的强度和工作时间，以达到所需的加热效果。

2、电路中的发热问题在电路中，电阻的存在会导致电流通过时产生热量。

如果电流过大或电阻过高，产生的热量可能会损坏电路元件，甚至引发火灾。

因此，在电路设计和使用中，需要合理控制电流和电阻，以避免过热带来的问题。

《焦耳定律》讲义一、引入同学们，在我们的日常生活中，电的应用无处不在。

从照明的灯泡到驱动各种电器的电源，电在为我们的生活带来便利的同时，也隐藏着一些有趣的科学规律。

今天，我们就来一起探讨一个与电和能量转化密切相关的重要定律——焦耳定律。

二、什么是焦耳定律焦耳定律是定量说明传导电流将电能转换为热能的定律。

具体表述为：电流通过导体产生的热量跟电流的二次方成正比，跟导体的电阻成正比，跟通电的时间成正比。

用公式来表示就是：Q ＝ I²Rt 。

其中，Q 表示热量，单位是焦耳（J）；I 表示电流，单位是安培（A）；R 表示电阻，单位是欧姆（Ω）；t 表示时间，单位是秒（s）。

这个定律告诉我们，当电流通过导体时，会有一部分电能转化为热能，而转化的热量多少取决于电流、电阻和通电时间这三个因素。

三、焦耳定律的实验探究为了验证焦耳定律，我们可以进行一个简单的实验。

实验器材：电源、导线、开关、不同阻值的电阻丝、温度计、量热器等。

实验步骤：1、我们将阻值不同的电阻丝串联在电路中，保证通过它们的电流相同。

2、同时测量电阻丝在通电一段时间后的温度变化。

实验结果：我们会发现，在相同电流和通电时间下，电阻越大，产生的热量越多。

接下来，我们再将阻值相同的电阻丝分别接入不同电流的电路中，同样测量它们在通电一段时间后的温度变化。

结果表明，电流越大，产生的热量越多。

最后，保持电流和电阻不变，改变通电时间，会发现通电时间越长，产生的热量越多。

通过这个实验，我们直观地验证了焦耳定律的正确性。

四、焦耳定律的应用焦耳定律在我们的生活和工业生产中有着广泛的应用。

1、电暖器电暖器就是利用焦耳定律的原理工作的。

通过让电流通过电阻较大的发热元件，将电能转化为热能，从而为我们提供温暖。

2、电饭煲电饭煲在煮饭时，内部的电阻丝发热，将电能转化为热能，使米饭煮熟。

3、工业中的电阻加热在许多工业生产过程中，如金属熔炼、热处理等，都需要利用电阻加热来达到所需的温度。

焦耳定律一.网上课堂(一)主要内容1.焦耳定律:(1)电流通过导体产生的热量跟电流的二次方成正比,跟导体的电阻成正比,跟通电时间成正比,这个规律叫做焦耳定律.电流通过导体要产生一些效应,其中包括热效应. 电流通过导体产生热量, 即电流的热效应. 电流通过不同导体以及电流大小不同产生的热量不同.通过实验, 科学家焦耳找到了电流产生热量多少的影响因素, 及它们之间的关系, 总结成焦耳定律.电流的热效应是电流做功的结果,做功越多, 电流通过导体产生热量就越多. 在纯电阻电路中(例电炉丝、电暖器)电流所做的功全部转化为热能, 释放出热量. 即W=Q(2)焦耳定律基本公式: t R I Q ⋅⋅=2(3)单位:焦1焦=1安2·欧·秒 (4)导出式:在纯电阻电路中(例电阻元件、电热器等)电流通过导体所做的功全部转化为热能, 释放出热量, 故t P t RU t I U W Q ⋅=⋅=⋅⋅==2注: 以上导出式只适用于纯电阻电路中电热计算. 2.电热利用:(1)电热器: 利用电来加热的设备电热器主要组成部分是发热体.而发热体又是由电阻率大、熔点高的电阻绕在绝缘材料上做成的.(2)电热的利用:电流通过电阻丝放出热量, 供人们利用. 电热器清洁卫生, 没有环境污染, 热效率高, 可方便控制和调节温度, 还可制成电热保温装置.(3)防止电热的危害:电热会对某些不需要发热设备和电路造成不利影响, 对这些设备要采取散热措施, 防止电热的危害.(二)学习指导:1.某电动机, 直流电阻为5欧, 接在220伏电路中正常工作,电流为4安, 试求:(1)该电动机在一分钟内有多少电能转化为其它形式的能量.(2)电动机在一分钟内放出了多少热量?(3)电动机将电能转变为机械能的功率是多少?分析与解: 电动机主要是通过电流做功将电能转化为机械能的装置, 但电流通过机器就会产生热量, 故电能不能全部转化为机械能, 还要有一部分热能的损耗.(1)该电动机一分钟内消耗的电能即电流所做的总功.t I U W ⋅⋅=总=220伏秒安604⋅⋅=5.28⨯104(J) (2)电动机一分钟内放出的热量, 根据焦耳定律有: =⋅⋅=t R I Q 2(4安)2⋅⋅欧560秒 =4.8310⨯(J )(3)电动机将在1分钟内将电能转化为机械能的有用功为 W 有=W 总-Q)(108.4)108.41028.5(434J J ⨯=⨯-⨯=则转化成机械能的功率为P 有sJ t W 60)(108.44⨯==有=800(W ) 说明:电流通过用电器所做的总功即消耗的电能有一部分转化为热能, 另一部分转化为其它形式的能量, W 总>Q, 只有在纯电阻电流中,电流所做的功全部转化为热能,W 总=Q.那么, 当用电器是非纯电阻时,计算消耗电能产生热量只能用焦耳定律t R I Q ⋅⋅=2, 其它导出式UIt t RU Q =⋅=2都不适用.2.如图15-1中R 1=10Ω, R 2=200Ω, 电源电压保持6V 不变, 当S 1, S 2同时断开时，R 1消耗功率为0.1W, 求当S 1, S 2同时闭合时, 电路在一分钟内放出的热量?分析与解: 当S 1, S 2同时断开时, R 1, R 3串联∵P 1=0.1W, R 1=10Ω∴1111=⋅=RPU(V)又∵1131UUURR-=∴501)16(10)(1113=-=-=UUURR(Ω)当S1, S2均闭合时, R2R3并联.1分钟电路放出热量, 根据焦耳定律的导出式, 在纯电阻电路中Q=W=tRU⋅并2其中40250100003232==+⋅=RRRRR并(Ω)则546040622=⋅=⋅==tRUWQ并(J)说明:本题属于电路变换题目, 在电路第一个状态下可利用已知求出电阻R3的阻值, 当电路状态变化后,此阻值不变.仍要注意此电路为纯电阻电路, 电流所做的功全部转化为热能,故tRUQW⋅==2,成立.3.若使一个可调电阻器在相同时间里产生的热量减少为原来的1/4, 那么下面采取的方法中正确的是:A. 电压、电阻同时减半B. 电压、电阻都减小到原来的41C. 电压不变, 电阻减半D. 电压增大一倍, 电阻减半分析与解:因可调电阻器属纯电阻原件, 故电流通过电阻器所做的功全部转化为热能, 释放出热量, 故tRUWQ⋅==2.在相同时间内, 当电压、电阻同时减半时,221)(22222QtRUttRUQRU=⋅⋅=⋅=⋅''=', 故A错;当电压不变, 电阻减半时Q t R U t R U t R U Q 222/222=⋅=⋅=⋅'=';当电压增大一倍, 电阻减半时,Q t R U t R U t R U Q 882/)2(2222=⋅=⋅=⋅''=',故C 、D 都不符合题意;只有当电压, 电阻减小到原来的1/4时, 4414/)4/(2222Qt R U t R U t R U Q =⋅⋅=⋅=⋅''=',故B 正确. 说明:此题还是要先判断是否为纯电阻电路, 选择好应用的公式, 最后利用数学手段,判断当电压和电阻发生变化后,电热如何变化.4.两个电炉额定电压是220伏, 各自正常工作,甲炉的电阻为48Ω, 乙炉电阻为80欧,通电时间相同,下面结论中正确的是:A. 甲炉电阻小, 产生的热量多B. 乙炉的电阻大, 产生热量多C. 甲, 乙两炉的电压相等, 产生的热量相等D. 由于甲电阻小于乙电阻, 甲电流大于乙的电流,所以产生的热量多少,无法比较确定.分析与解: 由于此电路为纯电阻电路故Q=W=t RU t R I ⋅=⋅⋅22.,由于两电阻丝正常工作时,电压相同,根据Q=W=t RU ⋅2, R 甲<R 乙, 则Q 甲>Q 乙, 故A 正确. 说明:此题解决关键在于选择电热公式是Q=t R I ⋅⋅2还是Q=t RU ⋅2.这取决于电路中电压相同, 还是电流相同.本题中两电炉丝的额定电压是相同的,故选择Q=t RU ⋅2公式, 由于R 甲>R 乙, 相同时间内电热甲大于乙.二.网上能力训练题(一)能力训练部分[A]基础性训练题:1.电流通过导体产生的热量跟_______________成正比, 跟_______成正比跟______________成正比.2.电热器是利用电流的____________效应制成的加热设备, 它的主要组成部分是_______________________________, 两个电热器的电阻之比为3:4, 如果把它们串联在某电路里,在相同时间内,它们产生的热量之比为__________; 若它们并联在电路中, 在相同时间内, 它们产生的热量之比为______________.3.电阻R=2Ω, 若加在R两端的电压U=8伏, 通电时间t=20秒,则电流产生的热量为__________.4.某导体两端的电压是6伏, 当导体通过8 库仑的电量时,电流通过导体所产生的热量为______________.5.一度电可供一盏“220V40W”灯泡正常工作_______小时, 若它正常工作5小时,所消耗的电能___________焦耳.6.两根导线的电阻分别是10欧和5欧, 若将它们串联后接在一个电源上,在相等时间里,电流通过两根导线产生的热量之比是___________.7.一根电阻丝通过1分钟产生的热量为3104.2⨯焦, 测得电流为2安, 这根电阻丝的阻值为___________.8.电阻R1R2并联在电源上, 两电阻电功率之比为P1:P2=3:1, 若使R1R2串联在同一电源上,两电阻电功率之比''21:PP=____________此时,两电阻在相同时间内放出的热量这之比Q1:Q2_____________.9.一电阻丝接在电压为U的电源上, 每分钟产生热量为Q, 若使该电阻丝每分钟产生热量为Q/2, 则应接电源电压为_____________.10. 若将通过某一电阻上的电流增大到原来的3倍, 则在单位时时间内( )A. 电流产生的热量是原来的3倍B. 电流产生的热量增大到原来的6倍C. 电流产生的热量增大到原来的3倍D. 电流产生的热量是原来的9倍11.R1R2阻值的比是1:2, 先后把它们串联, 并联在同一电源上, 在相等时间里电流两次在R1上产生的热量之比是( )A. 1:3B. 1:9C. 1:2D. 1:412.一段导体中的电流强度为2安时, 产生的热量为Q, 若通电时间不变,使通电导体的电流强度变为4安时, 则通电导体产生的热量则为:A. Q/4B. Q/2C. 2QD. 4Q13.将标有“220V40W”和“220V60W”两灯串联起来接在220伏电路中,则两盏灯在相同时间内消耗的电能之比( )A. 2:1B. 2:3C. 3:2D. 1:214.R1R2并联,R1阻值为R2的1/3, 电路的总电阻为24欧, 干路上的电流强度为2安, 求:通过R1的电流强度和10分钟内R2放出的热量.15.如图15-2所示电路中, 已知R1=30欧, R2=20欧, 当开关闭合时, 电流表的示数为0.4安, 若开关S断开后电源电压不变, 求:5分钟内电流通过R2所放出的热量.[B]提高性训练题:16.标有“220V1000W”的电炉接在220伏的电路中, 每分钟产生_______焦耳的热量, 半小时耗电__________度.17.一条电阻丝先后接在两个电路中,通过它的电流是I1=3I2, 当两种情况放出热量相同时, 两次通电时间之比t1:t2______________18.将两电阻之比为2:3的电热器串联后,接在电路中, 相同时间里放出的热量之比为_________, 如改接成并联后接在电路中, 相同时间里放出的热量之比_______________.19.电热器A标有“220V500W”, 电热器B标有“2201.25KW”各自在实际电压下工作,若通过两电热器电流强度之比I A:I B=5:1, 要使它们产生相同的热量所需时间之比为( )A. 1:10B. 10:1C. 1:20D. 20:120.把两根由同种材料制成的粗细相同而长度不同的电阻丝接入电路中, 下列说法中正确的是( )A. 把两根电阻丝串联, 长的电阻丝两端电压大,放出热量多B. 把两根电阻丝并联时,通过长的电阻丝电流强度大,放出热量多C. 把两根电阻丝并联时,短电阻丝两端电压小,放出热量相同.D. 把两根电阻丝串联时,通过它们的电流强度大小相同, 放出热量相同21.甲灯标有“110V60W”乙灯“110V40W”, 若将它们串联接在220V的电源上,则甲灯,乙灯各自在10分内实际消耗的电能?22.如图15-3中电压表示数为6伏,电阻R的阻值为5 ,电流每分钟在R上产生的热量是12焦, 灯泡L的额定功率为4W, 若灯丝电阻不变,求灯的额定电压.[C]研究性习题:23．一只标有“220V,110V·40W”电烙铁，其尾部的接线端及和电对应的电热丝连接如图15-4所示,其中B为电热丝AC中点抽头, 下列说法正确的是:( )A. 将AC端与220V的电源相连,电烙铁单位时间内放出40J热量.B. 将AB端与110V电源相连电烙铁单位时间内放出40J热量.C. 将AC连在一起作为一个接线端, 再将AB端与110V电源相等,电烙铁单位时间内放出40J热量.(二)能力训练题答案1.电流的平方,电阻, 通电时间.2.热, 电阻率大, 熔点高的电阻丝绕在绝缘材料上制成的发热体. 3:4, 4:3. 点拨:R 1R 2串联时, I 1=I 2, 根据t R I Q ⋅⋅=2,则Q 1:Q 2=R 1:R 2=3:4; R 1R 2并联时,U 1=U 2, 根据t RU W Q ⋅==2, 则Q 1:Q 2=R 2:R 1=4:3. 3. 640J点拨: t R U W Q ⋅==2=64020282=⋅(J) 4. 48J点拨: 电流通过导体放出热量4886=⋅=⋅=⋅==c V q U t UI W Q (J) 5. 25, 7.2510⨯ 点拨: 根据t P W ⋅=, 千瓦时千瓦04.01⋅==P W t =25小时 )(102.72.0504.05J KWh h KW t P W ⨯==⋅=⋅='.6. 2:17. 10点拨: 10602104.2232=⋅⨯=⋅=t I Q R 欧 8. 1:3, 1:3点拨: R 1R 2并联时,1312212212===R R P P R U R U , 若R 1R 2串联时,3121221221==⋅⋅=''R R R I R I P P ; t R I t R I Q Q ⋅⋅⋅⋅=221221=3121=R R 说明: 由此题我们可以看到:在串联电路中21212121R R Q Q W W P P ===,即电功, 电功率, 电热与电阻均成正比, 而在并联电路中212121Q Q W W P P ===12R R , 即电功率, 电功, 电热与电阻均成反比.9.U 22. 点拨: 根据t RU W Q ⋅==2得t R Q U ⋅=,当2Q Q ='时, 22/U t R Q U =⋅='10. D点拨: 根据t R I Q ⋅⋅=2, 当I I 3='时, Q t R I Q 992=⋅⋅=', 电流产生热量是原来的9倍.11. B点拨: R 1R 2串联时, Q 1=I 12t R ⋅⋅1t R R R U⋅⋅+=1221)(;当R 1R 2并联时, t R U W Q ⋅=='121,则91)211()11()(2222111)(1112122212=+=+=+=⋅⋅⋅='+R R R U R R U R R R tt R Q Q12. D 点拨:当I=2A 时, Q=t R I ⋅⋅2; 当A I I 42=='时, Q t R I t R I Q 4422=⋅⋅=⋅⋅'=' 13. C点拨: 由铭牌知)(12104022021211Ω===P U R , )(324206022022222Ω===P U R ,串联接在220伏电路中, 相等时间的电能之比23121032420221221==⋅⋅⋅⋅=t R I t R I W W .14．点拨:R 1R 2并联 , 因R并24422323212122==+⋅=+⋅=R R R R R R R R R (Ω), R 2=96(Ω), 则32321==RR (Ω), 又因I=2安,则5.1232969621212121=⋅+=⋅+=⇒+=I R R R I R R R I I 安 10分钟内R 2放出热量t R I I t R I Q ⋅⋅-=⋅⋅=2212222)(1440060096)5.12(2=⋅⋅-=(J)15.当开关S 闭合时, R 2被短接, 电源电压 304.01⨯=⋅=R I U =12伏; 当开关S 断开时, R 1R 2串联, 24.020301221=+=+=R R U I 安, 5分钟内电流通过R 2所放出的热量3002024.02222⋅⋅=⋅⋅=t R I Q =345.6(J)16. 4106⨯, 0.5点拨: “220V1000W ”电炉接在220伏电路中正常工作, 故4106601000⨯=⋅=⋅==s W t P W Q (J), 5.05.01=⋅='⋅'='='h KW t P W Q 度.17. 9:1点拨: 因t R I Q ⋅⋅=2, 则RI Qt ⋅=2,故19)(2122122221211===⋅⋅I I t t R I Q R I Q 18. 2:3, 3:2点拨: 3221=R R , R 1R 2串联3221221221==⋅⋅⋅⋅=R R t R I t R I Q Q , R 1R 2并联时, 2312212212===⋅⋅R R Q QtR U t R U . 19. A点拨: ∵t R I Q ⋅⋅=2 ∴RI Qt ⋅=2∴12221212222121212122122121)()()()(额额额额额额额额P P U U I IP U P U I I R R I I Q Q t t ⋅⋅=⋅=⋅⋅= 101)5001250()51(2=⋅=20.A点拨: 同种材料制成的粗细相同的电阻丝, 长的电阻大, 串联时两端电压大, 又根据t R I Q ⋅⋅=2, 串联时电流与通电时间相同, 则放出的热量也多, 故A 正确,D 错. 把两根电阻丝并联, 长的电阻通过电流小, 又根据t RU W Q ⋅==2,并联时两电阻两端电压相等, 通电时间也相等, 长的电阻丝电阻大, 放出热量小, 故B 错. 两根电阻丝并联时, 短电阻丝电阻小, 通过电流大, 两端电压相等. 又因t RU Q ⋅=2, 故短电阻丝放出热量多, 故C 错.21. 由甲, 乙两灯铭牌知)(36056011022Ω===甲甲甲P U R ==乙乙乙R U R 2)(5.302401102Ω=甲, 乙串联, )(5524)5.3023605(220安欧伏乙甲=+=+=R R U I 甲灯10分钟内实际消耗电能t R I W ⋅⋅=甲甲2=230406003605)5524(2=⋅⋅(J) 乙灯10分钟内实际消耗电能==t R I W 乙乙2345606002605)5524(2=⋅⋅(J)22. R 与灯L 串联, 电源电压为6伏, R=5Ω 又∵R 上热量J t R I Q 122=⋅⋅= ∴)(2.060512A tR QI =⋅=⋅=, )(2552.06Ω=-=-=R I U R L ∵W P L 4=额∴伏额额10=⋅=L L R P U23. A, C点拨: 由电烙铁的铭牌 “220V 110V 40W ”知, 当电烙铁分别接在220V 与110V 电源电压下时, 均正常工作,额定功率为40W. 要使其正常工作,∵W P P U U 40,22121===额额额额 ∴222121R U R U 额额=,则R 1=4R 2又∵R AB 与R AC 并联后总电阻是R AC 的41 故将AC 端与220伏电源相连时, 正常工作, 单位时间内放出40J 热量. 将AC 连在一起作为一个接线端, 再将AB 端与110V 电源相连,电烙铁仍正常工作, 单位时间内放出40J 热量.。

焦耳计算公式
焦耳计算公式是一种简便的方式来计算两个变量之间的关系的计算公式，它可以帮助科学家或工程师们快速，准确地计算出特定的结果。

焦耳计算公式也被称为焦耳定律，它是在充电电容器中被发现的，并由19世纪的德国物理学家戈特拉德赫尔穆特焦耳来发现。

焦耳定律解释了充电电容器中的电流和电压之间的关系，它简洁地表达了以下方程式：
I = C dV/dt
在这里，I是电流，C是电容器容量，dV/dt是电压变化时间微分。

焦耳计算公式由此而来，它在其他情况下也得到了广泛的应用。

它可以用来估计电流，或者解决特定问题，比如求解电动机中的电压和加速度变化。

一般来说，焦耳计算公式可以用来计算两个变量之间的关系，尤其是当一个变量的变化导致另一个变量的变化时。

焦耳计算公式也可以用来计算磁场强度和如何影响它的力是怎样的。

焦耳计算公式也被广泛应用于电气工程中，在涉及到电阻，电感，电压降等电路相关的问题中，都可以使用此公式来计算。

它可以用来测量抗感应能力，电压电流的平衡，电子设备的承受能力，以及调节电流的增量。

此外，还有一些更复杂的应用，比如使用焦耳计算公式来计算
经济学问题中各种变量的变化。

在货币的发行中，它可以帮助经济学家估算出货币的通货膨胀和利率水平。

最后，尽管焦耳计算公式可以解决许多物理学和工程学问题，但在某些情况下，它仍然无法解决一些更复杂的问题。

因此，使用这个计算公式时，最好是进行仔细的评估，以确保能够得到有效的结果。

焦耳定律名词解释1. 焦耳定律呀，简单来说就是电流通过导体产生的热量跟电流的平方成正比，跟导体的电阻成正比，跟通电时间成正比！就好比你冬天用的电暖器，电流越大、电阻越大、通电时间越长，那散发出来的热量就越多，哇，是不是很神奇？2. 焦耳定律哦，它就像是一个热量的魔法法则！你想想看，当电流在导体里流动时，热量就悄悄地产生啦。

就像你给手机充电时，手机会发热，这其中就有焦耳定律在起作用呢！3. 嘿，焦耳定律呢，其实就是在告诉你电流和热量之间的秘密关系呀！比如说电热水壶，它工作的时候，就是根据焦耳定律产生大量的热来把水烧开的呀，你说有趣不有趣？4. 焦耳定律呀，这可是个很重要的东西呢！就好像你跑步会累一样，电流通过导体也会产生热量这种“累”的效果。

像家里的电炉，不就是靠这个来发热做饭的嘛！5. 哇哦，焦耳定律呀，它可是解释热量怎么来的关键呢！好比夏天你吹的电风扇，电流通过电机产生热量，但同时风扇又把热量吹散了，这背后就是焦耳定律在主宰呢！6. 焦耳定律哟，它可是决定热量多少的法则呀！你看那些电灯泡，亮起来的时候会发热，这就是因为电流和电阻在按照焦耳定律产生热量呀，神奇吧！7. 哈哈，焦耳定律呢，不就是告诉你电和热之间的联系嘛！像吹风机，靠电流产生热量来吹干头发，这都是焦耳定律在默默工作呀！8. 焦耳定律呀，这简直就是热量生成的指南！好比你玩的电动玩具，里面的电池通过电线产生热量，这都是因为焦耳定律呀，你懂了吧？9. 哎呀呀，焦耳定律呀，它就是解释热量从何而来的定律呀！像电烤箱烤面包，就是利用了它，让面包变得香香脆脆的，是不是很厉害？10. 焦耳定律嘛，就是那个能让你明白电流怎么产生热量的定律呀！就像电饭煲煮饭，电流通过电阻产生大量的热把饭煮熟，你说这焦耳定律是不是很重要呢？我的观点结论：焦耳定律在我们的日常生活中无处不在，它让我们更好地理解和利用电与热的关系，真的是非常神奇又实用的定律呀！。

《焦耳定律》知识清单一、焦耳定律的发现在电学的发展历程中，焦耳定律的发现具有重要的意义。

詹姆斯·普雷斯科特·焦耳（James Prescott Joule）通过大量的实验和研究，揭示了电流通过导体时产生热量的规律。

焦耳自幼对科学有着浓厚的兴趣，并展现出了非凡的实验能力。

他通过坚持不懈的努力，在不同的条件下进行实验，最终得出了这一重要的定律。

二、焦耳定律的内容焦耳定律指出：电流通过导体产生的热量跟电流的二次方成正比，跟导体的电阻成正比，跟通电的时间成正比。

用公式表示为：Q ＝ I²Rt 。

其中，Q 表示热量，单位是焦耳（J）；I 表示电流，单位是安培（A）；R 表示电阻，单位是欧姆（Ω）；t 表示通电时间，单位是秒（s）。

这个公式清晰地表明了电流、电阻和时间与产生热量之间的定量关系。

三、焦耳定律的推导我们可以通过一些基本的电学知识来推导焦耳定律。

假设在一段导体两端加上电压 U，通过的电流为 I，根据欧姆定律U ＝ IR 。

在时间 t 内，电场力对这段导体做的功 W ＝ UIt 。

而电流通过这段导体产生的热量 Q ，在纯电阻电路中，电能全部转化为热能，所以 W ＝ Q 。

将 U ＝ IR 代入 W ＝ UIt 中，得到 Q ＝ I²Rt ，这就是焦耳定律的表达式。

四、焦耳定律的应用1、计算电流通过导体产生的热量在实际问题中，只要知道电流、电阻和通电时间，就可以利用焦耳定律计算出产生的热量。

例如，一个电阻为10Ω 的导体，通过的电流为 2A，通电时间为 5s ，则产生的热量 Q ＝ I²Rt ＝ 2²×10×5 ＝ 200J 。

2、选择合适的导体材料在设计电路和电器时，需要考虑导体产生的热量。

对于一些需要长时间通电且对热量敏感的设备，要选择电阻较小的导体材料，以减少热量的产生。

3、解释生活中的现象（1）电暖器：电暖器通过电阻丝通电发热，电阻丝的电阻较大，根据焦耳定律，在电流和通电时间一定时，电阻越大产生的热量越多，从而达到取暖的目的。