2016年春人教版七年级数学下册名校课堂练习8.2.1用代入消元法解方程组.doc
- 格式:doc
- 大小:68.36 KB
- 文档页数:6



8.2 消元一一解二元一次方程组第1课时用代入消元法解方程组基础题知识点1用一个未知数表示另一个未知数1 •在方程2x —3y = 6中,用含有x的代数式表示y,得()A. y= 23x —6B. y ——23x —6C. y—23x —2 D . y——23x + 22 .用含有x或y的式子表示y或x:(1)已知x + y —5,则y—⑵已知x —2y —1,则y—(3)已知x + 2(y —3)—5,贝U x —⑷已知2(3y —7)—5x —4,贝U x—知识点2用代入法解二元一次方程3 .用代入法解方程组x —2y, y —x —3,①②下列说法正确的是()A .直接把①代入②,消去yB .直接把①代入②,消去xC. 直接把②代入①,消去yD. 直接把②代入①,消去x4. 用代入法解方程组y —1 —x, x —2y —4时,代入正确的是()A. x—2—x—4 B . x —2 —2x —4C. x—2+ 2x —4 D . x —2 + x —45. (丹东中考)二元一次方程组x + y —5, 2x —y—4的解为()A.x —1y —4B.x —2y —3C.x —3y —2D.x —4y —16. (贵阳中考)方程组x+ y—12, y —2的解为x —7. 用代入法解下列方程组:(1)(重庆中考)①y—2x — 4 ,②3x+ y— 1 ;(2) y —3 —x,① 2x + 3y —7;②(3) 3m —5n ,①2m —3n —1;②⑷3x + 2y = 19 ,①2x —y= 1.②知识点3代入法解二元一次方程组的简单应用8. (柳州中考)小张把两个大小不同的苹果放到天平上称,当天平保持平衡时的砝码重量如图所示. 问: 这两个苹果的重量分别为多少克?中档题9. 用代入法解方程组2x —5y = 0,①3x + 5y —1 = 0②时,最简单的方法是()A .先将①变形为x= 52y,再代入②B .先将①变形为y= 25x,再代入②C. 先将②变形为x= 1 —5y3,再代入①D. 先将①变形为5y = 2x,再代入②10 .方程组x = y + 5,2x —y = 5的解满足x+ y+ a= 0,则a的值是()A. 5 B . —5 C . 3 D . —311.在二元一次方程4x —3y = 14中,若x,y互为相反数,则x= 2,y= —2.12 .(哈尔滨中考)美术馆举办的一次画展中,展出的油画作品和国画作品共有100幅,其中油画作品数量是国画作品数量的2倍多7幅,则展出的油画作品有幅.13 .用代入法解下列方程组:(1)5x + 2y = 15,①8x + 3y = — 1 ;②⑵3 (y —2)= x—17,2 (x — 1 )= 5y —8;(3) x + y3 + x—y2 = 6,3 (x+ y) —2 (x—y)= 28.14 .已知x = 2, y = —1是方程组ax + y= b, 4x —by = a + 5的解,求a, b的值.15 .(日照中考)已知关于x, y的二元一次方程组x+ 2y = 3, 3x + 5y = m + 2的解满足x+ y= 0,求实数m的值.综合题16 .先阅读材料,然后解方程组.材料:解方程组x —y — 1 = 0①,4 (x —y)—y= 5.①答案:8.2 消元一一解二元一次方程组第1课时用代入消元法解方程组基础题知识点1用一个未知数表示另一个未知数1 .在方程2x —3y = 6中,用含有x的代数式表示y,得(C)A. y= 23x —6B. y ——23x —6C. y—23x —2 D . y——23x + 22 .用含有x或y的式子表示y或x:(1)已知x + y —5,贝U y—5 —x;⑵已知x —2y —1,则y—12(x —1);⑶已知x + 2(y —3) —5,贝U x—11 —2y;⑷已知2(3y —7) —5x —4,则x—6y5 — 2 .知识点2用代入法解二元一次方程3 .用代入法解方程组x —2y , y —x —3,①②下列说法正确的是(B) A .直接把①代入②,消去yB .直接把①代入②,消去x消去y 消去xy = 1 — x , x — 2y = 4时,代入正确的是(C)A . x — 2— x = 4C . x — 2+ 2x = 4D . x — 2 + x = 4 5. (丹东中考)二元一次方程组x + y = 5, 2x — y = 4的解为(C) A.x = 1y = 4B.x = 2y = 3C.x = 3y = 2D.x = 4y = 16. (贵阳中考)方程组x + y = 12, y = 2的解为x = 10y = 2 .7. 用代入法解下列方程组:(1) (重庆中考)y = 2x — 4 ,①3x + y = 1 ;②解:把方程①代入方程②,得3x + 2x — 4 = 1.解得x = 1.把x = 1代入①,得y = — 2.•••原方程组的解为x = 1 , y =一 2.(2) y = 3 — x ,①2x + 3y = 7;②解:把①代入②,得2x + 3(3 — x) = 7.解得x = 2.把x = 2代入①,得y = 1.•••原方程组的解是x = 2, y = 1.(3) 3m = 5n ,①2m — 3n = 1;②解:将①变形为m = 5n3.③把③代入②,得2X5n3 — 3n = 1.解得n = 3.把n = 3代入③,得m = 5X 33 = 5.•••原方程组的解为m = 5, n = 3.⑷3x + 2y = 19 ,①2x — y = 1.②解:由②,得y = 2x — 1.③将③代入①,得3x + 4x — 2 = 19.解得x = 3.将x = 3代入③,得y = 5.•••原方程组的解为x = 3, y = 5.知识点3代入法解二元一次方程组的简单应用8.(柳州中考)小张把两个大小不同的苹果放到天平上称, 当天平保持平衡时的砝码重量如图所示. 问: 这两个苹果的重量分别为多少克? 解:根据题意,得 x = y + 50, x + y = 300 + 50,解得 x = 200 , y = C •直接把②代入①,D •直接把②代入①, 4•用代入法解方程组 C .150.答:大苹果的重量为200 g,小苹果的重量为150 g. 中档题9•用代入法解方程组2x —5y = 0,①3x + 5y- 1 = 0②时,最简单的方法是(D)A •先将①变形为x= 52y,再代入②B •先将①变形为y= 25x,再代入②C. 先将②变形为x= 1 —5y3,再代入①D. 先将①变形为5y = 2x,再代入②10 .方程组x = y + 5,2x —y = 5的解满足x+ y+ a= 0,则a的值是(A)A. 5 B . —5 C . 3 D . —311.在二元一次方程4x —3y = 14中,若x,y互为相反数,则x= 2,y= —2.12 .(哈尔滨中考)美术馆举办的一次画展中,展出的油画作品和国画作品共有100幅,其中油画作品数量是国画作品数量的2倍多7幅,则展出的油画作品有69幅.13 .用代入法解下列方程组:(1)5x + 2y = 15,①8x + 3y = —1 ;②解:由①,得x= 3—25y.③把③代入②,得8(3 —25y) + 3y + 1 = 0.解得y = 125.把y = 125代入③,得x = —47.•••原方程组的解是x = —47,y = 125.⑵3 (y —2)= x—17,2 (x — 1 )= 5y —8;解:原方程组变形为x= 3y + 11,①2x —5y = — 6.②将①代入②,得2(3y + 11) —5y = —6,6y + 22 —5y= —6.解得y = —28.把y = —28 代入①,得x = 3冬—28) + 11 = —73.•••原方程组的解是x = —73,y = —28.(3)x + y3 + x—y2 = 6,3 (x+ y) —2 (x—y)= 28.解:原方程组可化为5x —y = 36,①x + 5y = 28,②由①,得y = 5x —36,③把③代入②,得x + 5(5x —36) = 28,解得x= 8.把x = 8代入③,得y = 4.•这个方程组的解是x= 8y = 4.14 .已知x = 2,y = —1是方程组ax + y= b,4x —by = a + 5的解,求a,b的值. 解:把x= 2,y=—1 代入ax + y= b,4x —by = a + 5 得2a —1 = b,①8 + b = a + 5.② 把①代入②,得8 + (2a —1) = a+ 5,解得a= — 2.把a = —2代入①,得2^—2) —1 = b,解得b = —5.• a= —2, b = — 5.15 .(日照中考)已知关于x, y的二元一次方程组x+ 2y = 3, 3x + 5y = m + 2的解满足x+ y= 0,求实数m的值.解:解关于x, y 的二元一次方程组x + 2y = 3, 3x + 5y = m + 2.得x = 2m —11 , y = 7 —m.I x+ y= 0, ••• 2m —11 + 7 —m = 0,解得m = 4. 综合题16 .先阅读材料,然后解方程组.材料:解方程组x —y — 1 = 0, 4 (x —y) —y = 5.①②由①,得x —y = 1.③把③代入②,得4X1 —y= 5,解得y二—1.把y二—1代入③,得x = 0.•••原方程组的解为x = 0,y =一1.这种方法称为整体代入法”你若留心观察,有很多方程组可采用此方法解答,请用这种方法解方程组:2x—3y — 2 = 0,① 2x —3y + 57 + 2y = 9.②解:由①,得2x —3y = 2.③把③代入②,得2 + 57 + 2y = 9,解得y = 4.把y = 4代入③,得2x —3X4 = 2,解得x = 7.•••原方程组的解为x = 7,y = 4.。

8.2.1 用代入法解二元一次方程组一、选择题1.将方程3x +y =5转化为用含x 的式子表示y 的形式,正确的是( ) A .y =-3x +5 B .y =5+3x C .-y =3x +5 D .y -5=3x 2.用代入法解方程组⎩⎨⎧=-=+②,①52,243y x y x 使得代入后化简比较容易的变形是( )A .由①得x =2-4y 3B .由①得y =2-3x4 C .由②得x =y +52 D .由②得y =2x -5 3.对于二元一次方程组⎩⎨⎧=+-=②,①72,1y x x y 将①式代入②式,消去y 可以得到( )A .x +2x -1=7B .x +2x -2=7C .x +x -1=7D .x +2x +2=7 4.已知关于x ,y 的方程组⎩⎨⎧+=-=,21,3m y m x 则将y 用只含x 的式子表示为( ) A .y =2x +7 B .y =7-2x C .y =-2x -5 D .y =2x -55.若关于x ,y 的二元一次方程y =kx +b 的两个解是⎩⎨⎧x =1,y =-1,⎩⎨⎧x =-2,y =8.则这个二元一次方程是( )A .y =3x +2B .y =-3x +2C .y =-3x -2D .y =3x -26.已知⎩⎨⎧x =2,y =1是二元一次方程组⎩⎨⎧mx +ny =8,nx -my =1的解,则2m -n 的算术平方根为( )A .1B .2C .4D .67.已知|2x +y -3|+(x -3y -5)2=0,则y x 的值为( ) A .1 B .-1 C .2 D .-2二、填空题8.用代入法解方程组⎩⎨⎧=-=+②,①253,103y x y x 较简单的解法是先把方程 变形为 ,再代入方程 ,求得 的值,然后再求 的值. 9.二元一次方程组⎩⎨⎧==+yx y x 2,102的解是 . 10.一个长方形的边长如图所示,则该长方形的面积为 .11.已知方程组⎩⎨⎧-==+1,72y x y x 的解也是关于x ,y 的方程ax +y =4的一个解,则a 的值为 .12.若关于x ,y 的二元一次方程组{2x -3y =12,ax +by =1和{cx -ay =5,x +y =1的解相同,则xy = .三、解答题13.用代入法解下列方程组:(1)⎩⎨⎧y =2x -4,①3x +y =1;② (2)⎩⎪⎨⎪⎧m -n 2=2,①2m +3n =12.②14.某学校建立了劳动基地,计划在基地上种植A ,B 两种苗木共6000株,其中A 种苗木的数量比B 种苗木的数量的一半多600株.请问A ,B 两种苗木各有多少株?15.某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表所示:(1)求购进甲、乙两种矿泉水各多少箱; (2)该商场售完这500箱矿泉水,可获利多少元?16.甲、乙两人共同解方程组⎩⎪⎨⎪⎧Ax +By =2,Cx -3y =-2, 甲正确解得⎩⎪⎨⎪⎧x =1,y =-1, 乙抄错C ,解得⎩⎪⎨⎪⎧x =2,y =-6, 求A ,B ,C 的值.17.阅读材料:善于思考的小军在解方程组⎩⎨⎧=+=+②①5114,352y x y x 时,采用了一种“整体代换”的解法:解:将方程②变形为4x +10y +y =5,即2(2x +5y )+y =5③.把方程①代入③得2×3+y =5,∴y =-1.把y =-1代入①得x =4.∴方程组的解为⎩⎨⎧-==.1,4y x 请你模仿小军的“整体代换”法解方程组⎩⎨⎧=-=-.1949,523②①y x y x参考答案一、选择题1.将方程3x +y =5转化为用含x 的式子表示y 的形式,正确的是( A ) A .y =-3x +5 B .y =5+3x C .-y =3x +5 D .y -5=3x 2.用代入法解方程组⎩⎨⎧=-=+②,①52,243y x y x 使得代入后化简比较容易的变形是( D )A .由①得x =2-4y 3B .由①得y =2-3x4 C .由②得x =y +52 D .由②得y =2x -5 3.对于二元一次方程组⎩⎨⎧=+-=②,①72,1y x x y 将①式代入②式,消去y 可以得到( B )A .x +2x -1=7B .x +2x -2=7C .x +x -1=7D .x +2x +2=7 4.已知关于x ,y 的方程组⎩⎨⎧+=-=,21,3m y m x 则将y 用只含x 的式子表示为( B ) A .y =2x +7 B .y =7-2x C .y =-2x -5 D .y =2x -55.若关于x ,y 的二元一次方程y =kx +b 的两个解是⎩⎨⎧x =1,y =-1,⎩⎨⎧x =-2,y =8.则这个二元一次方程是( B )A .y =3x +2B .y =-3x +2C .y =-3x -2D .y =3x -26.已知⎩⎨⎧x =2,y =1是二元一次方程组⎩⎨⎧mx +ny =8,nx -my =1的解,则2m -n 的算术平方根为( B )A .1B .2C .4D .67.已知|2x +y -3|+(x -3y -5)2=0,则y x 的值为( A ) A .1 B .-1 C .2 D .-2二、填空题8.用代入法解方程组⎩⎨⎧=-=+②,①253,103y x y x 较简单的解法是先把方程 变形为 ,再代入方程 ,求得 的值,然后再求 的值. 【答案】① x =10-3y ② y x 9.二元一次方程组⎩⎨⎧==+yx y x 2,102的解是 . 【答案】42x ,y =⎧⎨=⎩ 10.一个长方形的边长如图所示,则该长方形的面积为 .【答案】320 11.已知方程组⎩⎨⎧-==+1,72y x y x 的解也是关于x ,y 的方程ax +y =4的一个解,则a 的值为 .【答案】1212.若关于x ,y 的二元一次方程组{2x -3y =12,ax +by =1和{cx -ay =5,x +y =1的解相同,则xy = .【答案】-6三、解答题13.用代入法解下列方程组:(1)⎩⎨⎧y =2x -4,①3x +y =1;②解:把①代入②,得3x +2x -4=1,解得x =1, 把x =1代入①,得y =-2,∴原方程组的解为⎩⎨⎧x =1,y =-2.(2)⎩⎪⎨⎪⎧m -n 2=2,①2m +3n =12.② 解:由①,得m =2+n2,③将③代入②,得2⎝⎛⎭⎫2+n2+3n =12,解得n =2,把n =2代入③,得m =2+22=3,14.某学校建立了劳动基地,计划在基地上种植A ,B 两种苗木共6000株,其中A 种苗木的数量比B 种苗木的数量的一半多600株.请问A ,B 两种苗木各有多少株? 解:设A 种苗木有x 株,B 种苗木有y 株,根据题意,得600016002x y ,x y .+=⎧⎪⎨=+⎪⎩解得24003600x ,y .=⎧⎨=⎩ 答:A 种苗木有2400株,B 种苗木有3600株.15.某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表所示:(1)求购进甲、乙两种矿泉水各多少箱; (2)该商场售完这500箱矿泉水,可获利多少元? 解:(1)设购进甲矿泉水x 箱,乙矿泉水y 箱.依题意得500253514500x y ,x y ,+=⎧⎨+=⎩解得300200x ,y .=⎧⎨=⎩ 答:购进甲矿泉水300箱,乙矿泉水200箱. (2)(35-25)×300+(48-35)×200=5600(元). 答:该商场售完这500箱矿泉水,可获利5600元.16.甲、乙两人共同解方程组⎩⎪⎨⎪⎧Ax +By =2,Cx -3y =-2, 甲正确解得⎩⎪⎨⎪⎧x =1,y =-1, 乙抄错C ,解得⎩⎪⎨⎪⎧x =2,y =-6, 求A ,B ,C 的值.解:将⎩⎪⎨⎪⎧x =1,y =-1 代入方程组⎩⎪⎨⎪⎧Ax +By =2,Cx -3y =-2, 得⎩⎪⎨⎪⎧A -B =2,C +3=-2, 解得C =-5,把⎩⎪⎨⎪⎧x =2,y =-6 代入Ax +By =2,得2A -6B =2,解方程组⎩⎪⎨⎪⎧A -B =2,2A -6B =2,得⎩⎨⎧A =52B =1217.阅读材料:善于思考的小军在解方程组⎩⎨⎧=+=+②①5114,352y x y x 时,采用了一种“整体代换”的解法:解:将方程②变形为4x +10y +y =5,即2(2x +5y )+y =5③.把方程①代入③得2×3+y =5,∴y =-1.把y =-1代入①得x =4.∴方程组的解为⎩⎨⎧-==.1,4y x 请你模仿小军的“整体代换”法解方程组⎩⎨⎧=-=-.1949,523②①y x y x解:把方程②变形为3(3x -2y )+2y =19③, 把①代入③得15+2y =19,∴y =2. 把y =2代入①得x =3.∴方程组的解为32x ,y .=⎧⎨=⎩。
初一数学8.2消元法解二元一次方程组课后练习满分:60 (2016年3月23日)一. 填空题1. 二元一次方程组⎩⎨⎧-=-=+1210y x y x 的解是 。
2. 若方程组⎩⎨⎧=+=+122y x m y x 的解满足x -y=5,则m 的值为 。
3. 若关于x 、y 的二元一次方程组⎩⎨⎧=-=+12354y x y x 和⎩⎨⎧=-=+13by ax by ax 有相同的解,则a= 、b= 。
4. 把方程2x =3y+7变形,用含y 的代数式表示x ,x = ;用含x 的代数式表示y ,则y = 。
5. 若212543y x b a ++-与12365--b a y x 是同类项,则a= ,b= ; 二. 选择题6. 若⎩⎨⎧==21y x 是方程组⎩⎨⎧=-=-30ay bx by ax 的解,则a 、b 的值为( ) A. ⎩⎨⎧==21b a B. ⎩⎨⎧-=-=21b a C. ⎩⎨⎧==11b a D. ⎩⎨⎧-=-=12b a7. 在(1)⎩⎨⎧=+--=-8512115y x y x (2)⎩⎨⎧=-=-432253t x y x (3)⎩⎨⎧=--=1232y x x y (4)⎩⎨⎧-=-=-243234y x y x 中,解是⎩⎨⎧==22y x 的有( )A. (1)和(3)B. (2)和(3)C. (1)和(4)D. (2)和(4)8. 对于方程组⎩⎨⎧=--=+ 17y 5x 4 19y 7x 4,用加减法消去x ,得到的方程是( ) A. 2y=-2 B. 2y=-36 C. 12y=-2 D. 12y=-369. 将方程-21x+y=1中x 的系数变为5,则以下正确的是( ) A. 5x+y=7 B. 5x+10y=10 C. 5x -10y=10 D. 5x -10y=-10三. 解答题10. 用代入法解下列方程组(1)⎩⎨⎧-=+=+6232y x y x (2)⎩⎨⎧=-=+56345y x y x (3)⎩⎨⎧=-=+4383y x y x (4)⎩⎨⎧-=-=+73852y x y x11. 用加减消元法解方程组(1)⎩⎨⎧-=+=+653334y x y x (2)⎩⎨⎧=-=+2463247y x y x (3)⎩⎨⎧=-=+1053552y x y x (4)⎩⎨⎧=+=+752523y x y x12. 若方程组⎩⎨⎧=++-=+ 4y )1k (x )1k ( 1y 3x 2的解中x 与y 的取值相等,求k 的值。
第八章二元一次方程组8.2解二元一次方程组(第一课时代入消元法)精选练习答案基础篇一、单选题(共10小题)1.用代入消元法解方程组3+4=225x yx y⎧⎨-=⎩①②使得代入后化简比较容易的变形是()A.由①得243yx-=B.由①得234xy-=C.由②得52yx+=D.由②得y=2x-5【答案】D【详解】解:观察方程①②可知,②中的系数为-1,比其它未知数的系数更为简单,所只要将②变形为y=2x-5③,再把③代入①即可求出方程组的解.故应选D.2.解二元一次方程组34225x yx y+=⎧⎨-=⎩①②,最恰当的变形是()A.由①得243yx-=B.由②得y=2x﹣5C.由①得234yx-=D.由②得52yx+=【答案】B【详解】根据二元一次方程的解法—代入消元法,可把某一个系数为1或为-1的项,移项变形即可,因此可由②得y=2x-5.故选B.3.方程1325y xx y=-⎧⎨+=⎩的公共解是()A.32xy=⎧⎨=⎩B.34xy=-⎧⎨=⎩C.32xy=⎧⎨=-⎩D.32xy=-⎧⎨=-⎩【答案】C【详解】把方程y=1﹣x代入3x+2y=5,得3x+2(1﹣x)=5,解得:x=3.把x=3代入方程y=1﹣x ,得y=﹣2.故选C .4.同时满足二元一次方程9x y -=和431x y +=的x ,y 的值为()A .45x y =⎧⎨=-⎩B .45x y =-⎧⎨=⎩C .23x y =-⎧⎨=⎩D .36x y =⎧⎨=-⎩【答案】A【详解】解:有题意得:9431x y x y -=⎧⎨+=⎩①②由①得x=9+y ③将③代入②得:36+4y+3y=1,解得y=-5则x=9+(-5)=4所以x=4,y=-5.故选:A .5.用代入法解方程组238355x y x y +=⎧⎨-=⎩①②有以下过程,其中错误的一步是()(1)由①得x=83y 2-③;(2)把③代入②得3×83y 2--5y=5;(3)去分母得24-9y-10y=5;(4)解之得y=1,再由③得x=2.5.A .()1B .()2C .()3D .()4【答案】C【详解】其中错误的一步为(3),正确解法为:去分母得:24−9y −10y =10,移项合并得:−19y =−14,解得:14.19y =故选C.6.已知4x 4myn ﹣3m 与5xny 是同类项,则m 与n 的值分别是()A .4、1B .1、4C .0、8D .8、0【答案】B解:∵4x 4m y n-3m 与5x n y 是同类项,∴431m n n m =⎧⎨-=⎩①②,①代入②得:4m-3m=1,即m=1,将m=1代入①得:n=4,故选B .7.二元一次方程组224x y x y +=⎧⎨-=⎩的解是()A .02x y =⎧⎨=⎩B .20x y =⎧⎨=⎩C .31x y =⎧⎨=-⎩D .11x y =⎧⎨=⎩【答案】B【详解】224x y x y ①②+=⎧⎨-=⎩,①+②得:3x=6,即x=2,把x=2代入①得:y=0,则方程组的解为20x y =⎧⎨=⎩,故答案选B.8.解二元一次方程组47194517x y x y +=-⎧⎨-=⎩,用代入消元法整体消去4x ,得到的方程是()A .22y =-B .236y =-C .122y =-D .1236y =-【答案】D【详解】47194517x y x y +=-⎧⎨-=⎩①②,由②得:4517x y =+③把③代入①得:12y=-36,故选D .9.小明在解关于x ,y 的二元一次方程组331x y x y +⊗=⎧⎨-⊗=⎩时得到了正确结果1x y =⊕⎧⎨=⎩后来发现“⊗”“⊕”处被污损了,则“⊗”“⊕”处的值分别是()A .3,1B .2,1C .3,2D .2,2【答案】B解:将1x y =⊕⎧⎨=⎩代入方程组,两方程相加,得x=⊕=1;将x=⊕=1,y=1代入方程x+⊗y=3中,得⊗=2,所以B 选项是正确的.10.已知方程组242x y x y m-=⎧⎨-=⎩中的x ,y 互为相反数,则m 的值为()A .2B .2-C .0D .4【答案】D【详解】由题意得:x+y=0,即y=-x ,代入方程组得:343x x m =⎧⎨=⎩,解得:m=3x=4,故选D .提升篇二、填空题(共5小题)11.二元一次方程组2222x y x y +=-⎧⎨+=⎩的解为___.【答案】22x y =⎧⎨=-⎩【详解】解:2222x y x y +=-⎧⎨+=⎩①②,由①式得:22x y =--,代入②式,得:2(22)2y y --+=,解得2y =-,再将2y =-代入①式,222x -´=-,解得2x =,∴22x y =⎧⎨=-⎩,故填:22x y =⎧⎨=-⎩.12.若(x ﹣y +3)2+=0,则x +y 的值为______.【答案】1【详解】根据非负数的性质,可得二元一次方程组30{20x y x y -+=+=,解方程组可得12x y =-⎧⎨=⎩,故x+y=-1+2=1.故答案为1.13.若(a+b+5)2+|2a ﹣b+1|=0,则(b ﹣a )2017=_____.【答案】﹣1.【详解】∵(a+b+5)2+|2a-b+1|=0,∴521a b a b +-⎧⎨--⎩==,解得:23a b -⎧⎨-⎩==,则原式=-1,故答案为-114.用代入消元法解二元一次方程组32143x y x y +=⎧⎨=+⎩①②,将②代入①后得到的方程为___________.【答案】()33214y y ++=【详解】解:32143x y x y +=⎧⎨=+⎩①②将②代入①得:()33214y y ++=故答案为:()33214y y ++=.15.若方程mx +ny =6的两个解是11x y =⎧⎨=⎩,21x y =⎧⎨=-⎩,则m =_____,n =_____.【答案】42【详解】将两个解代入方程可得:626m n m n +=⎧⎨-=⎩,解得:42m n =⎧⎨=⎩.三、解答题(共2小题)16.解方程组3{3814x y x y -=-=【答案】21 xy=⎧⎨=-⎩【详解】解:由①得③把③代入②得把代人③得∴原方程组的解为17.若(am+1bn+2)(a2n﹣1b2n)=a5b3,则求m+n的值.【答案】14 3.【详解】解:(am+1bn+2)(a2n﹣1b2n)=am+1×a2n﹣1×bn+2×b2n =am+1+2n﹣1×bn+2+2n=am+2nb3n+2=a5b3.∴25 323 m nn+=⎧⎨+=⎩,解得:n13=,m133=,m+n14 3 =.。
《8.2.1代入消元法解二元一次方程组》课后作业重庆市南川区合溪镇中心小学校 袁朝洪一. 填空题1.已知x =2,y =2是方程ax -2y =4的解,则a =________.2.已知方程x -2y =8,用含x 的式子表示y ,则y =_________________,用含y 的式子表示x ,则x =________________3.方程x +y =4有_______个解,有________个正整数解,它们是___________________________________________.4.方程2x -y =7与x +2y =-4的公共解是________________________.5.若x 、y 互为相反数,且x +3y =4,,3x -2y =_____________.二.用代入法解方程组:6. y =3x -1 7. 4x -y =52x +4y =24 3(x -1)=2y -38. 8116052=+=+y x y x 9. 53215.05.1=+=-y x y x三.解答题10.已知 12-==y x 是方程组 54+=-=+a by x by ax 的解.求a 、b 的值.11.已知方程组 12338=-=+y x y x 的解为 b y a x ==,求ab 2的值.12.若 24==y x 与 12=-=y x 都满足方程b kx y +=(1)求k 和b 的值; (2)当8=x 时,求y 的值; (3)当3=y 时,求x 的值.13.超市里某种罐头比解渴饮料贵1元,小彬和同学买了3听罐头和2听解渴饮料一共用了16元,你能求出罐头和解渴饮料的单价各是多少元吗?。
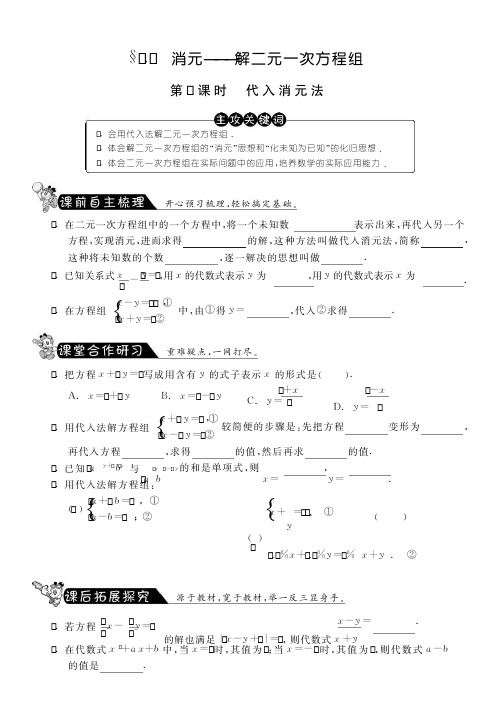
8.2 消元——解二元一次方程组
第1课时 用代入消元法解方程组
课前预习
要点感知1 把二元一次方程组中一个方程的一个未知数用含________的式子表示出来,再代入________方程,实现________,进而求得这个二元一次方程组的解,这种方法叫做代入消元法,简称________.这种将未知数的个数________,逐一解决的思想叫做________. 预习练习1-1 对于方程3x -2y -5=0,用含y 的代数式表示x ,应是( )
A .y =6x -10
B .y =32x -25
C .x =13
(2y +5) D .x =6y +15 要点感知2 用代入消元法解二元一次方程组的步骤:
(1)从方程组中选取一个系数比较简单的方程,把其中的一个未知数用含另一个未知数的式子表示出来;
(2)把(1)中所得的式子代入________,消去一个________;
(3)解所得到的________,求得一个________的值;
(4)把所求得的一个未知数的值代入(1)中求得的式子,求出另一个未知数的值,从而确定方程组的解.
预习练习2-1 用代入法解方程组⎩⎪⎨⎪⎧x =2y ,y -x =3,
①②下列说法正确的是( ) A .直接把①代入②,消去y
B .直接把①代入②,消去x
C .直接把②代入①,消去y
D .直接把②代入①,消去x
当堂训练
知识点1 用一个未知数表示另一个未知数
1.在方程2x -3y =6中,用含有x 的代数式表示y ,得( )
A .y =23x -6
B .y =-23
x -6 C .y =23x -2 D .y =-23
x +2 知识点2 用代入法解二元一次方程组
2.用代入法解方程组⎩
⎪⎨⎪⎧y =1-x ,x -2y =4时,代入正确的是( ) A .x -2-x =4 B .x -2-2x =4
C .x -2+2x =4
D .x -2+x =4
3.(黔南中考)二元一次方程组⎩
⎪⎨⎪⎧x +y =3,x -y =-1的解是( ) A.⎩⎪⎨⎪⎧x =2y =1 B.⎩⎪⎨⎪⎧x =1y =2
C.⎩⎪⎨⎪⎧x =1y =-2
D.⎩
⎪⎨⎪⎧x =2y =-1 4.用代入法解下列方程组:
(1)⎩⎪⎨⎪⎧3m =5n ,①2m -3n =1;②
(2)⎩
⎪⎨⎪⎧3x +2y =19,①2x -y =1.② 知识点3 代入法解二元一次方程组的简单应用
5.(柳州中考)小张把两个大小不同的苹果放到天平上称,当天平保持平衡时的砝码重量如图所示.问:这两个苹果的重量分别为多少g?
课后作业
6.用代入法解方程组⎩
⎪⎨⎪⎧2x -5y =0,①3x +5y -1=0②时,最简单的方法是( ) A .先将①变形为x =52
y ,再代入② B .先将①变形为y =25
x ,再代入② C .先将②变形为x =1-5y 3
,再代入①
D .先将①变形为5y =2x ,再代入②
7.(崇左中考)方程组⎩
⎪⎨⎪⎧x +y =60,x -2y =30的解是( ) A.⎩⎪⎨⎪⎧x =70y =-10 B.⎩
⎪⎨⎪⎧x =90y =-30 C.⎩⎪⎨⎪⎧x =50y =10 D.⎩⎪⎨⎪⎧x =30y =30
8.方程组⎩
⎪⎨⎪⎧x =y +5,2x -y =5的解满足x +y +a =0,则a 的值是( ) A .5 B .-5 C .3 D .-3
9.已知方程4x -y =1,用含x 的代数式表示y 为:________;用含y 的代数式表示x 为:________.
10.用代入法解下列方程组:
(1)⎩
⎪⎨⎪⎧y =3-x ,①2x +3y =7;② (2)⎩
⎪⎨⎪⎧x -4y =-1,①2x +y =16;② (3)⎩
⎪⎨⎪⎧5x +2y =15,①8x +3y =-1.② 11.已知⎩⎪⎨⎪⎧x =2,y =-1是方程组⎩
⎪⎨⎪⎧ax +y =b ,4x -by =a +5的解,求a ,b 的值.
12.已知:方程组⎩⎪⎨⎪⎧4x +3y =12,①x -32
y =12②与方程y =kx -1有公共解.求k 的值.
挑战自我
13.先阅读材料,然后解方程组.
材料:解方程组⎩⎪⎨⎪⎧x -y -1=0,4(x -y )-y =5.
①② 由①得x -y =1,③
把③代入②,得4×1-y =5,解得y =-1.
把y =-1代入③,得x =0.
∴⎩
⎪⎨⎪⎧x =0,y =-1. 这种方法称为“整体代入法”.你若留心观察,有很多方程组可采用此方法解答,请用这
种方法解方程组:⎩
⎪⎨⎪⎧2x -3y -2=0,①2x -3y +57+2y =9.②
参考答案
课前预习
要点感知1 另一个未知数 另一个 消元 代入法 由多化少 消元思想
预习练习1-1 C
要点感知2 (2)另一个方程 未知数 (3)一元一次方程 未知数
预习练习2-1 B
当堂训练
1.C 2.C 3.B
4.(1)将①变形为m =5n 3.③把③代入②,得2×5n 3
-3n =1.解得n =3.
把n =3代入③,得m =5×33=5.所以原方程组的解为⎩
⎪⎨⎪⎧m =5,n =3. (2)由②得y =2x -1.③将③代入①,得3x +4x -2=19.解得x =3.
将x =3代入③,得y =5.所以原方程组的解为⎩
⎪⎨⎪⎧x =3,y =5. 5.根据题意,得⎩⎪⎨⎪⎧x =y +50,x +y =300+50,解得⎩
⎪⎨⎪⎧x =200,y =150. 答:大苹果的重量为200 g ,小苹果的重量为150 g.
课后作业
6.D 7.C 8.A 9.y =4x -1 x =14y +14
10.(1)把①代入②,得2x +3(3-x)=7.解得x =2.
把x =2代入①,得y =1.∴原方程组的解是⎩
⎪⎨⎪⎧x =2,y =1. (2)由①得x =4y -1.③把③代入②,得2(4y -1)+y =16.解得y =2.
把y =2代入③,得x =7.∴原方程组的解是⎩
⎪⎨⎪⎧x =7,y =2. (3)由①得x =3-25y.③把③代入②,得8(3-25
y)+3y +1=0.解得y =125. 把y =125代入③,得x =-47.∴原方程组的解是⎩
⎪⎨⎪⎧x =-47,y =125. 11.把⎩⎪⎨⎪⎧x =2,y =-1代入⎩
⎪⎨⎪⎧ax +y =b ,4x -by =a +5得⎩⎪⎨⎪⎧2a -1=b ,①8+b =a +5.② 把①代入②,得8+(2a -1)=a +5,解得a =-2.
把a =-2代入①,得2×(-2)-1=b ,解得b =-5.所以⎩
⎪⎨⎪⎧a =-2,b =-5. 12.由②,得x =12+32y.③把③代入①,得4(12+32
y)+3y =12.解得y =-4. 把y =-4代入③,得x =12+32×(-4)=6.∴原方程组的解是⎩
⎪⎨⎪⎧x =6,y =-4. 把⎩
⎪⎨⎪⎧x =6,y =-4代入y =kx -1,得-4=6k -1,∴k =-12.
13.由①得2x -3y =2.③把③代入②,得2+57
+2y =9,解得y =4. 把y =4代入③,得2x -3×4=2,解得x =7.∴原方程组的解为⎩
⎪⎨⎪⎧x =7,y =4.。