迭代求信道容量

中文摘要信道是信息传递的通道，承担信息的传输和储存的任务，是构成通信系统的重要组成部分。

信道容量是指信道能够传输信息量的大小。

信道容量的研究在现实中有着非常重要的理论意义。

而信道容量的计算是一个比较复杂的问题，所以我们要借助于数学软件Matlab来解决这个难题。

本文的第一部分从信道容量的基本概念、基本原理、信道模型及分类等方面系统的介绍了信道容量。

并在此基础上，介绍了一般信道容量的计算步骤。

本文的第二部分开始介绍信道容量的迭代算法及迭代算法在Matlab中的实现，举例检验迭代算法在Matlab中实现的程序的可行性关键词信道容量 Matlab 迭代算法AbstractChannel is a channel of information transmission. And it take on the task of information transmission and storage. Channel is an important part of communication system. Channel capacity is the size of the amount of information can be transmitted. It has important significances in reality. However, calculating the channel capacity is a complex issue. So we must use the mathematical software Matlab to solve this problem.The first part of the article, it introduces channel capacity by the basic concepts, principles and the classification of channel models. On this basis, introduce and discuss the calculation steps of the general channel capacity.The second part of the article, it introduces the Iterative algorithm of the channel capacity and implementes the iterative algorithm in Matlab. After that, by realizing the feasibility of the procedure, we make some examples. And also analyze the procedure.Key word ：channel capacity、matlab目录引言 (6)1、离散信道的数学模型 (6)2、信道容量和最佳输入概率分布 (6)2.1信道容量 (6)2.2最佳输入概率分布 (7)3、信道容量和平均互信息的计算步骤 (7)3.1平均互信息的计算 (7)3.2信道容量的计算 (7)4、信道容量的迭代算法 (8)5、实例分析 (9)结论 (10)参考文献 (11)附 (12)引言本文主要结合实例对离散信道及其信道容量进行相关阐述，及用迭代算法实现离散信道容量1、离散信道的数学模型设离散信道的输入为一个随机变量X ，相应的输出的随机变量为Y ，如图所示： 规定一个离散信道应有三个参数： 输入信号：X={X1, X2, …, XN} 输出信号：Y={Y1, Y2, …, YN}信道转移概率：P(y|x) 描述了输入信号和输出信号之间的依赖关系 。

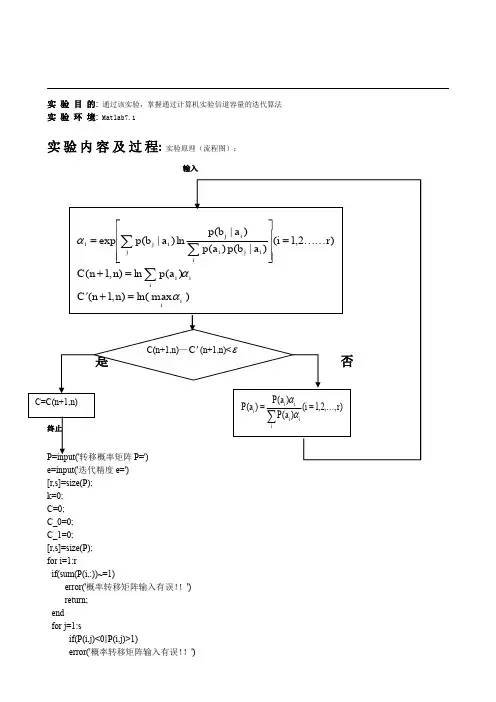
信道容量的计算实验一：信道容量的计算一、实验目的（1）进一步熟悉信道容量的迭代算法。

（2）学习如何将复杂的公式转化为程序。

（3）掌握高级语言数值计算程序的设计和调试技术。

二、实验原理：迭代算法计算信道容量的原理如图所示：三、实验步骤11. 初始化信源分布：pi=，循环变量k=1，门限△，C（0）=-∞； r(k)2. φ(k)pjiij=pi∑rp(k)ipjii=1sexp[k)jilogφ(ij]3. p(k+1)∑pi=j=1∑rsexp[∑pk)jilogφ(ij]i=1j=1)rs4. C(k+1=log[∑exp(∑p(k)jilogφij)]i=1j=1+1)5. 若C(k-C(k)C(k+1)>∆，则k=k+1，转第2步6. 输出P*=(P(k+1)i)k+1)r和C(，终止。

7. 。

分别对两个矩阵⎡⎢0.690.260.05⎤⎡⎣0.05 0.25 0.7⎥⎦⎢0.690.26⎤⎣0.05 0.7⎥⎦四、实验程序clc;clear all;N = input('输入信源符号X的个数N=');M = input('输出信源符号Y的个数M=');p_yx=zeros(N,M); %程序设计需要信道矩阵初始化为零 fprintf('输入信道矩阵概率\n')for i=1:Nfor j=1:Mp_yx(i,j)=input('p_yx=');%输入信道矩阵概率 if p_yx(i)error('不符合概率分布')endendendfor i=1:N %各行概率累加求和s(i)=0;for j=1:Ms(i)=s(i)+p_yx(i,j);endendfor i=1:N %判断是否符合概率分布if (s(i)=1.000001) 进行计算比较结果error('不符合概率分布')endendb=input('输入迭代精度：');%输入迭代精度for i=1:Np(i)=1.0/N; %取初始概率为均匀分布endfor j=1:M %计算q(j)q(j)=0;for i=1:Nq(j)=q(j)+p(i)*p_yx(i,j);endendfor i=1:N %计算a(i)d(i)=0;for j=1:Mif(p_yx(i,j)==0)d(i)=d(i)+0;elsed(i)=d(i)+p_yx(i,j)*log(p_yx(i,j)/q(j)); endenda(i)=exp(d(i));endu=0;for i=1:N %计算uu=u+p(i)*a(i);endIL=log2(u); %计算ILIU=log2(max(a));%计算IUn=1;while((IU-IL)>=b) %迭代计算for i=1:Np(i)=p(i)*a(i)/u; %重新赋值p(i)endfor j=1:M %计算q(j)q(j)=0;for i=1:Nq(j)=q(j)+p(i)*p_yx(i,j);endendfor i=1:N %计算a(i)d(i)=0;for j=1:Mif(p_yx(i,j)==0)d(i)=d(i)+0;elsed(i)=d(i)+p_yx(i,j)*log(p_yx(i,j)/q(j)); endenda(i)=exp(d(i));endu=0;for i=1:N %计算uu=u+p(i)*a(i);endIL=log2(u); %计算ILIU=log2(max(a));%计算IUn=n+1;endfprintf('信道矩阵为：\n');disp(p_yx);fprintf('迭代次数n=%d\n',n);fprintf('信道容量C=%f比特/符号',IL);例一的运行结果：输入信源符号X的个数N=2输出信源符号Y的个数M=2五、实验结果对矩阵⎢⎡0.690.260.05⎤⎥进行运算后结果为： 0.050.70.25⎣⎦⎡0.690.26⎤而对矩阵⎢⎥运算发生错误0.050.7⎣⎦六、分析讨论利用迭代算法求信道容量试验中，我们可以看出，当信道矩阵符合概率分布，且其小数表示精度较高时，在判定门限合适的情况下，其计算的信道容量比较符合实际值；当其信道矩阵不符合概率分布，程序报错。

§4.2信道容量的计算这里，我们介绍一般离散信道的信道容量计算方法，根据信道容量的定义，就是在固定信道的条件下，对所有可能的输入概率分布)(x P 求平均互信息的极大值。

前面已知()Y X I ;是输入概率分布的上凸函数，所以极大值一定存在。

而);(Y X I 是r 个变量)}(),(),({21r x p x p x p 的多元函数。

并且满足1)(1=∑=ri i x p 。

所以可用拉格朗日乘子法来计算这个条件极值。

引入一个函数：∑-=iix p Y X I )();(λφ解方程组0)(])();([)(=∑∂-∂∂∂i ii i x p x p Y X I x p λφ1)(=∑iix p （4.2.1）可以先解出达到极值的概率分布和拉格朗日乘子λ的值，然后在解出信道容量C 。

因为)()(log)()();(11i i i i i ri sj i y p x y Q x y Q x p Y X I ∑∑===而)()()(1i iri ii x yQ x p y p ∑==，所以e e y p y p i i i i i x y Q i x p i x p log log ))(ln ()(log )()()(==∂∂∂∂。

解（4.2.1）式有0log )()()()()()(log )(111=--∑∑∑===λe y p x y Q x y Q x p y p x y Q x y Q ii i i i r i s j i i i i sj i i （对r i ,,2,1 =都成立） 又因为)()()(1j k krk ky p x yQ x p =∑=ri x y Q sj i j,,2,1,1)(1==∑=所以(4.2.1)式方程组可以转化为),,2,1(log )()(log)(1r i e y p x y Q x y Q j i j sj i j =+=∑=λ1)(1=∑=ri ix p假设使得平均互信息);(Y X I 达到极值的输入概率分布},,{21r p p p 这样有e y p x y Q x y Q x p j i j i j r i sj i log )()(log)()(11+=∑∑==λ从而上式左边即为信道容量，得 e C log +=λ 现在令)()(log)();(1j i j sj i j i y p x y Q x y Q Y x I ∑==式中，);(Y x I i 是输出端接收到Y 后获得关于i x X =的信息量，即是信源符号i x X =对输出端Y 平均提供的互信息。

C语言方法实现，源程序如下：#include <stdio.h>#include <math.h>#include<stdlib.h>#define N 4#define M 4 /*转移矩阵行数为N，列数为M，自行调整*/ void Init(double *Pa); /* 输入概率分布初始化函数*/void Input(double *Pa,double *a); /*迭代输入概率分布重新调整函数*/void Output(double *Pa,double P[N][M],double *Pb); /*输出概率分布函数*/void Infor(double *Pb,double P[N][M],double *a); /*计算a(i)的函数*/double capacity1(double *Pa,double *a); /*计算C(n+1,n)*/double capacity2(double *a); /*计算C'(n+1,n)的函数*/void main(){ double c1,c2,s,temp;double Pa[N],a[N],Pb[M];double P[N][M];int i,j,count=0; /*count记录迭代次数*/for(i=0;i<N;i++)for(j=0;j<M;j++){ printf("please input P[%d][%d]:",i+1,j+1);scanf("%lf",&P[i][j]);} /*输入转移概率矩阵P*/for(i=0;i<N;i++){ temp=0.0;for(j=0;j<M;j++)temp+=P[i][j];if(temp!=1) { printf("Error!\n");exit(0);}} /*检查输入的转移概率矩阵是否正确：各行之和为1，则继续进行；否则退出程序*/printf("请输入精度：\n");scanf("%lf",&s);Init(Pa);while(1){ count++;Output(Pa,P,Pb);Infor(Pb,P,a);c1=capacity1(Pa,a);c2=capacity2(a);if(fabs(c1-c2)<s) break;else Input(Pa,a);}printf("迭代次数=%d次\n",count);printf("信道容量C=%fbit/符号\n",(1.0/log(2))*c1);printf("输入概率分布为:\n");for(i=0;i<M;i++){ printf("%10f",Pa[i]);if(i==N-1) printf("\n");}}void Init(double *Pa){ double s=N;int i;for(i=0;i<N;i++)Pa[i]=1.0/s;}void Input(double *Pa,double *a){ int i; double temp=0.0;for(i=0;i<N;i++)temp+=Pa[i]*a[i];for(i=0;i<N;i++)Pa[i]=(Pa[i]*a[i])/temp;}void Output(double *Pa,double P[N][M],double *Pb) { int i,j;double temp=0.0;for(j=0;j<M;j++){ for(i=0;i<N;i++)temp+=Pa[i]*P[i][j];Pb[j]=temp;temp=0.0;}}void Infor(double *Pb,double P[N][M],double *a) { int i,j;double temp=0.0;for(i=0;i<N;i++){ for(j=0;j<M;j++)if(P[i][j]==0)temp+=0;else temp+=P[i][j]*log(P[i][j]/Pb[j]);a[i]=exp(temp);temp=0.0;}}double capacity1(double *Pa,double *a){ int i; double temp=0.0;for(i=0;i<N;i++)temp+=Pa[i]*a[i];temp=log(temp);return temp;}double capacity2(double *a){ int i;double max;max=a[0];for(i=1;i<N;i++)if(max<a[i])max=a[i];max=log(max);return max;}实际运行结果如下：1、如果输入的转移概率矩阵不正确：2、正确输入转移概率矩阵：MATLAB语言方法实现，源程序如下：1、M-程序如下（命名为capacity.m）:clear;P=input('请输入信道矩阵P='); %输入信道矩阵[r,s]=size(P);e=input('请输入迭代精度：'); %输入迭代精度for i=1:rPa(i)=1.0/r;end %初始概率为均匀分布count=0; %迭代次数while 1Pb=Pa*P; %计算输出概率分布for i=1:ra(i)=0;for j=1:sif P(i,j)==0a(i)=a(i)+0;elsea(i)=a(i)+P(i,j)*log(P(i,j)/Pb(j));endenda(i)=exp(a(i));end %计算a(i)temp=Pa*a'; %计算ΣPa(i)*a(i)C1=log(temp); %计算C(n+1,n)C2=log(max(a)); %计算C'(n+1,n)count=count+1;if abs(C1-C2)<eC=log2(exp(1))*C1;break;elsePa=(Pa.*a)/temp; %重新调整输入概率分布endenddisp('输入分布：');Padisp('信道矩阵为：');Pdisp('迭代次数');countdisp('信道容量');C2、命令窗口指令如下：>> capacity请输入信道矩阵P=[0.5,0.25,0,0.25;0,1,0,0;0,0,1,0;0.25,0,0.25,0.5]请输入迭代精度：0.00000001输入分布：Pa =0.1333 0.3667 0.3667 0.1333 信道矩阵为：P =0.5000 0.2500 0 0.25000 1.0000 0 00 0 1.0000 00.2500 0 0.2500 0.5000 迭代次数count =16信道容量C =1.3219>>。

信道容量迭代计算实验报告王升10271051信科1002信道容量迭代计算实验报告一、实验目的：了解信道容量的定义和计算方法，能编写出正确的程序进行迭代计算得出信道容量。

二、实验要求：1）输入：输入信源个数、信宿个数和信道容量的精度，程序能任意生成随机的信道转移概率矩阵。

2）输出：输出最佳信源分布和信道容量。

三、实验环境：Matlab四、实验原理：五、源程序代码：clear;r=input('输入信源个数：');s=input('输入信宿个数：');deta=input('输入信道容量的精度：');Q=rand(r,s); %创建m*n随机分布矩阵A=sum(Q,2);B=repmat(A,1,s);disp('信源转移概率矩阵:'),p=Q./B %信源转移概率矩阵i=1:1:r;q(i)=1/r;disp('原始信源分布：'),qc=-10e-8;C=repmat(q',1,s);for k=1:1:100000m=p.*C; %后验概率的分子部分a=sum(m); %后验概率的分母部分su1=repmat(a,r,1);t=m./su1; %后验概率矩阵D=exp(sum(p.*log(t),2)); %信源分布的分子部分su2=sum(D); %信源分布的分母部分q=D/su2; %信源分布C=repmat(q,1,s);c(k+1)=log(sum(exp(sum(p.*log(t),2))))/log(2);kk=abs(c(k+1)-c(k))/c(k+1);if(kk<=0.000001)break;endenddisp('最大信道容量时的信源分布：q='),disp(q') disp('最大信道容量：c='),disp(c(k+1))六、实验结果：。

C语言程序:#include<stdio.h>#include<math.h>#include<stdlib.h>int main(){int r,s,i,j,k=0;double p[20]; %存放输入信源概率矩阵double z[20];double q[20][20]; %存放信道转移概率矩阵p x y的概率分布矩阵的转置double F[20][20]; %存放(|)i idouble x,y,a;double epsilon=1e-5; %门限double C=-1000.0; %取初始迭代时的信道容量为一个较大的负数printf("\n请输入信源符号个数: ");scanf("%d",&r);printf("\n请输入信宿符号个数: ");scanf("%d",&s);printf("\n请输入信道转移概率矩阵: \n\n");for(i=0;i<r;i++){for(j=0;j<s;j++)scanf("%lf",&q[i][j]);printf("\n");}for(i=0;i<r;i++)p[i]=(double)(1.0/(double)r); %设初始信源分布为等概分布do{k++;a=C;for(j=0;j<s;j++){x=0.0;for(i=0;i<r;i++)p x y的分母部分x=x+(p[i])*(q[i][j]); % x 为(|)i iif(x>0)for(i=0;i<r;i++)p x y的概率分布矩阵的转置F[i][j]=(p[i])*(q[i][j])/x; % F为(|)i ielsefor(i=0;i<r;i++)F[i][j]=0.0; %的分母部分为0时, 令F=0}y=0.0;for(i=0;i<r;i++){z[i]=0.0;for(j=0;j<s;j++){if(F[i][j]>0)p的分子部分z[i]=z[i]+(q[i][j]*(log(F[i][j])/log(2.0))); %z[i]为i}z[i]=(pow(2.0,z[i]));p的分母部分y=y+z[i]; %z[i]为i}for(i=0;i<r;i++){p[i]=z[i]/y; %更新输入信源概率矩阵}C=(log(y)/log(2.0)); %求信道容量单位为“bit”}while(fabs((C-a)/C)>epsilon);printf("\n迭代次数为;k=%d\n",k); %输出迭代次数printf("\n最佳信源分布为: \n\n");for(i=0;i<r;i++){printf("%.3lf ",p[i]); %输出信源的最佳分布, 保留3位小数}printf("\n");printf("\n信道容量为:C=%.3lf bit\n\n",C); %输出信道容量, 保留3位小数}问题1的执行结果:问题2 的执行结果:。

实验三信道容量计算一、实验目的：了解对称信道与非对称信道容量的计算方法。

二、实验原理：信道容量是信息传输率的极限，当信息传输率小于信道容量时，通过信道编码，能够实现几乎无失真的数据传输；当数据分布满足最佳分布时，实现信源与信道的匹配，使得信息传输率能够达到信道容量。

本实验利用信道容量的算法，使用计算机完成信道容量的计算。

实验采用迭代算法计算信道容量，即：设DMC的转移概率pyx(i,j)，p(i)是任意给定的一组初始给定输入分布，开始为等概率分布，以后逐次迭代更新p(i)的取值。

其所有分量P (i)均不为0。

按照如下方法进行操作：具体方法：1、计算q(j)=∑ijipyxip),(*)(，pyx(i,j)为信道转移概率2、计算a(i)先算中间变量d(i)=∑jjqjipyxjipyx)(/),(log(*),(然后，a(i)=exp(d(i))3、计算中间变量U=∑iip ia)(*)(4、计算IL=log2(u)5、计算IU=log2(max(a(i))6、当IU-IL>ε（ε为设定的迭代精度）时，进入以下循环，否则输出迭代次数n，信道容量C=IU计算结果，最佳分布p(i)。

①重新计算p(i)=p(i)*a(i)/U②计算q(j),方法同1③计算a(i)，方法同2④计算中间变量U=∑iip ia)(*)(⑤计算IL=log2(u)⑥计算IU=log2(max(a(i))⑦计次变量n=n+1返回6判断循环条件是否满足。

四、实验内容：假设离散无记忆二元信道如图所示，编程，完成下列信道容量的计算2e1． 令120.1e e p p ==和120.01e e p p ==，先计算出信道转移矩阵，分别计算该对称信道的信道容量和最佳分布，将用程序计算的结果与用对称信道容量计算公式的结果进行比较，并贴到实验报告上。

2． 令10.15e p =，20.1e p =和10.075e p =20.01e p =，分别计算该信道的信道容量和最佳分布；四、实验要求：在实验报告中给出源代码，写出信道对应的条件转移矩阵，计算出相应结果。