管理线性规划入门—形考答案优选稿

企业运营管理线性规划题1. 引言企业运营管理是指企业在生产经营过程中，通过科学的方法和有效的策略，合理分配资源、优化生产过程、提高效率和效益的管理活动。

线性规划作为运筹学中的一个重要分支，在企业运营管理中有着广泛的应用。

本文将通过一个具体的线性规划题，来帮助读者了解企业运营管理中线性规划问题的求解过程。

该问题涉及到了物资采购和库存管理方面的决策，通过合理的规划和优化，帮助企业降低采购成本和库存风险，提高运营效率。

2. 问题描述一家食品公司需要在未来三个月内采购原材料，该原材料每月的需求量、单价以及库存限制如下表所示：月份需求量（吨）单价（元/吨）库存限制（吨）1 500 1500 10002 600 1600 12003 400 1700 900供应商提供的采购方案如下表所示：月份最小供应量（吨）单价（元/吨）1 600 14002 500 15003 800 1600该公司需要制定一个采购计划，以满足每个月的需求量，并且要求在三个月内总采购成本最低。

同时，出于库存管理的考虑，需要保持每个月结束时的库存量不低于库存限制。

3. 模型建立根据问题描述，我们可以将每个月的采购量设为变量，记为x1、x2、x3，则目标是将总采购成本最小化，即Minimize: 1400x1 + 1500x2 + 1600x3其中，x1、x2、x3表示第1个月、第2个月、第3个月的采购量。

根据供应商提供的采购方案，我们可以得到如下约束条件：•第1个月的采购量不能低于最小供应量600吨：x1 ≥ 600•第2个月的采购量不能低于最小供应量500吨：x2 ≥ 500•第3个月的采购量不能低于最小供应量800吨：x3 ≥ 800同时，由于每个月结束时的库存量不能低于库存限制，我们可以得到如下约束条件：•第1个月的库存量为初始库存量加上采购量减去需求量，不能低于库存限制1000吨：1000 + x1 - 500 ≥ 1000，即x1 ≥ 500•第2个月的库存量为第1个月的库存量加上采购量减去需求量，不能低于库存限制1200吨：1000 + x1 - 500 + x2 - 600 ≥ 1200，即x1 + x2 ≥800•第3个月的库存量为第2个月的库存量加上采购量减去需求量，不能低于库存限制900吨：1000 + x1 - 500 + x2 - 600 + x3 - 400 ≥ 900，即x1 + x2 + x3 ≥ 1000综上所述，建立好线性规划模型后，我们即可通过求解器求解得到最优的采购方案。

线性规划例题和知识点总结线性规划是运筹学中研究较早、发展较快、应用广泛且方法较成熟的一个重要分支，它是辅助人们进行科学管理的一种数学方法。

下面通过一些例题来帮助大家更好地理解线性规划，并对相关知识点进行总结。

一、线性规划的基本概念线性规划问题是在一组线性约束条件下，求一个线性目标函数的最大值或最小值问题。

线性约束条件通常是由一组线性等式或不等式组成。

例如：＄2x ＋3y ≤ 12$，＄x y ≥ 1$等。

目标函数一般表示为$Z ＝ ax ＋ by$的形式，其中$a$、＄b$为常数，＄x$、＄y$为决策变量。

可行解是满足所有约束条件的解，可行域是所有可行解构成的集合。

最优解则是使目标函数达到最大值或最小值的可行解。

二、线性规划的例题例 1：某工厂生产甲、乙两种产品，已知生产甲产品 1 件需消耗 A原料 3 千克、B 原料 2 千克；生产乙产品 1 件需消耗 A 原料 2 千克、B 原料 4 千克。

A 原料有 12 千克，B 原料有 16 千克。

甲产品每件利润为 5 元，乙产品每件利润为 8 元，问该工厂应如何安排生产，才能使利润最大？设生产甲产品$x$件，生产乙产品$y$件。

则约束条件为：＄＼begin{cases}3x ＋2y ≤ 12 ＼＼ 2x ＋4y ≤ 16 ＼＼x ≥ 0, y ≥0\end{cases}＄目标函数为$Z ＝ 5x ＋ 8y$画出可行域，通过解方程组找到可行域的顶点坐标，分别代入目标函数计算，可得当$x ＝ 2$，＄y ＝ 3$时，利润最大为$34$元。

例 2：某运输公司有两种货车，每辆大型货车可载货 8 吨，每辆小型货车可载货 5 吨。

现要运输 60 吨货物，且大型货车的使用成本为每次 100 元，小型货车的使用成本为每次 60 元，问如何安排车辆才能使运输成本最低？设使用大型货车$x$辆，小型货车$y$辆。

约束条件为：＄＼begin{cases}8x ＋5y ≥ 60 ＼＼x ≥ 0, y ≥ 0\end{cases}＄目标函数为$Z ＝ 100x ＋ 60y$画出可行域，计算顶点坐标代入目标函数，可知当$x ＝ 5$，＄y ＝4$时，成本最低为$740$元。

管理运筹学课后习题答案管理运筹学课后习题答案一、线性规划线性规划是管理运筹学中的一种重要方法，它通过建立数学模型，寻找最优解来解决实际问题。

下面我们来讨论一些常见的线性规划习题。

1. 一家工厂生产两种产品A和B，每单位产品A需要3小时的加工时间和2小时的装配时间，每单位产品B需要2小时的加工时间和4小时的装配时间。

工厂每天有8小时的加工时间和10小时的装配时间。

已知产品A的利润为300元，产品B的利润为400元。

如何安排生产，使得利润最大化？解答：设生产产品A的数量为x，生产产品B的数量为y。

根据题目中的条件，可以得到以下线性规划模型：目标函数：max 300x + 400y约束条件：3x + 2y ≤ 82x + 4y ≤ 10x, y ≥ 0通过求解上述线性规划模型，可以得到最优解，即生产4个产品A和1个产品B时，利润最大化，为2000元。

2. 一家超市有两种品牌的洗衣液，品牌A和品牌B。

品牌A每瓶售价20元，每瓶利润为5元；品牌B每瓶售价25元，每瓶利润为7元。

超市每天销售洗衣液的总利润不能超过100元，并且每天至少要销售10瓶洗衣液。

如何安排销售，使得利润最大化？解答：设销售品牌A的瓶数为x，销售品牌B的瓶数为y。

根据题目中的条件，可以得到以下线性规划模型：目标函数：max 5x + 7y约束条件：20x + 25y ≤ 100x + y ≥ 10x, y ≥ 0通过求解上述线性规划模型，可以得到最优解，即销售5瓶品牌A和5瓶品牌B时，利润最大化，为60元。

二、排队论排队论是管理运筹学中研究排队系统的一种方法，它通过数学模型和概率统计来分析和优化排队系统。

下面我们来讨论一些常见的排队论习题。

1. 一家银行有两个窗口，每个窗口的服务时间服从指数分布，平均服务时间分别为3分钟和4分钟。

顾客到达的间隔时间也服从指数分布，平均间隔时间为2分钟。

如果顾客到达时，两个窗口都有空闲，顾客会随机选择一个窗口进行服务。

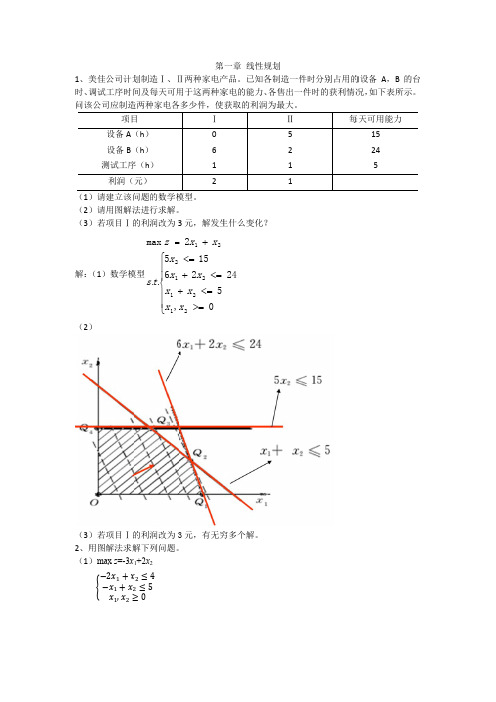
任务1客观题共6题（满分30分）一、单项选择题（共6题，每题5分）第1题(已答).在MATLAB软件中，求解线性规划的命令函数为（）。

A.rrefB.inprogC.invD.eye【参考答案】A【答案解析】Linprog第2题(已答). 在MATLAB软件中，矩阵A=的正确输入方式是（）。

A.B.C.D.【参考答案】A【答案解析】A第3题(已答).A.B.C.D.【参考答案】D【答案解析】第4题(已答). 下列（）为单位矩阵。

A.B.C.D.【参考答案】A【答案解析】第5题(已答).线性规划问题中，通常要求决策变量（）。

A.非负B.小于0C.大于0D.没有限制【参考答案】A【答案解析】非负第6题(已答).线性规划模型的标准形式要求目标函数（）。

A.求最大值B.求最小值C.没有限制D.不求最优值【参考答案】B【答案解析】求最小值主观题共8题（满分70分）二、填空题（共6题，每题5分）第7题(已答).【参考答案】10【答案解析】10【本题分数】5分【本题得分】0.0分第8题(已答).【参考答案】9【答案解析】9【本题分数】5分【本题得分】5.0分第9题(已答). 在MATLAB软件的算术运算符中，“^”表示（）运算。

【参考答案】乘方【答案解析】乘方【本题分数】5分【本题得分】5.0分第10题(已答).【参考答案】1.5【答案解析】1.5【本题分数】5分【本题得分】5.0分第11题(已答). 在MARLAB软件中，计算矩阵A的逆矩阵的命令函数为：( )。

【参考答案】inv(A)【答案解析】inv(A)【本题分数】5分【本题得分】5.0分第12题(已答).【参考答案】3【答案解析】3【本题分数】5分【本题得分】5.0分三、实践题（共2题，每题20分）第13题(已答).则a=( ),b=( ),c=( ),d=( ),e=( ),f=( ),g=( ),h=( ).【参考答案】7,5,7,1,0,2,4,-2【本题分数】20分【本题得分】20.0分第14题(已答).某企业有两种化学原料A1和A2都含有三种化学成分B1，B2，B3。

《管理线性规划入门》 一、单项选择题 1．已知矩阵1212377x x ⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦A B ，，并且A B =，则x ＝（C ）。

A 。

0 B 。

2C。

32D.32．建立线性规划模型时.首先应（B ）. A ．确定目标函数 B ．设置决策变量 C ．列出约束条件 D ．写出变量的非负约束3．在MATLAB 软件中,乘法运算的运算符是（A)。

A ．^ B ．／ C ．* D ．+4．在MATLAB 软件的命令窗口(command window ）中矩阵114321002B -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦的正确输入方式为（A)。

A ．>>B=[—1 1 4;3 —2 1；0 0 2］B ．〉>B=[—1 3 0;1 —2 1;4 1 2]C ．>〉B=[-1 1 4 3 -2 1 0 0 2]D ．>>B=［-1 1 ；4 3 ； -2 1 ；0 0 2］ 5．在MATLAB 软件中,命令函数clear 的作用为(D)。

A ．关闭MATLAB B ．查询变量的空间使用情况 C ．清除命令窗口的显示内容 D ．清除内存中变量(D)2．线性规划模型的标准形式要求约束条件(D)。

A ．只取大于等于不等式 B ．只取小于等于不等式 C ．没有限制D ．取等式或小于等于不等式3．在MATLAB 软件中，乘法运算的运算符是(C)。

A ．A B ．／ C ．* D ．+4．用MATLAB 软件计算矩阵2A+B T输入的命令语句为(A)。

A ．>>2＊A+B ’B ．〉〉2*A+B TC ．〉〉2A+BTD ．〉〉2A+B'5．在MATLAB 软件的命令窗口（command window)中输入的命令语句为:〉〉rref(A ），则进行的运算为（B ）. A ．求矩阵A 的逆B ．将矩阵A 化为行简化阶梯型矩阵C ．将矩阵A 化为单位矩阵D ．求矩阵A 的乘方（ B ）2．线性规划模型的标准形式中，要求（ A ） A ．目标函数取最小值 B ．目标函数取最大值C ．约束条件取大于等于不等式D ．约束条件只取等式3．在MATLAB 软件中,运算符”/"表示（ B ）运算. A ．乘方 B ．除法 C ．矩阵转置 D ．乘法 4．在MATLAB 软件的命令窗口（command window ）中矩阵101221A ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦的输入方式为（D ）。

《管理运筹学》（第二版）课后习题参考答案第1章 线性规划（复习思考题）1．什么是线性规划？线性规划的三要素是什么？答：线性规划（Linear Programming ，LP ）是运筹学中最成熟的一个分支，并且是应用最广泛的一个运筹学分支。

线性规划属于规划论中的静态规划，是一种重要的优化工具，能够解决有限资源的最佳分配问题。

建立线性规划问题要具备三要素：决策变量、约束条件、目标函数。

决策变量是决策问题待定的量值，取值一般为非负；约束条件是指决策变量取值时受到的各种资源条件的限制，保障决策方案的可行性；目标函数是决策者希望实现的目标，为决策变量的线性函数表达式，有的目标要实现极大值，有的则要求极小值。

2．求解线性规划问题时可能出现几种结果，哪种结果说明建模时有错误？ 答：（1）唯一最优解：只有一个最优点； （2）多重最优解：无穷多个最优解；（3）无界解：可行域无界，目标值无限增大； （4）没有可行解：线性规划问题的可行域是空集。

当无界解和没有可行解时，可能是建模时有错。

3．什么是线性规划的标准型？松弛变量和剩余变量的管理含义是什么？答：线性规划的标准型是：目标函数极大化，约束条件为等式，右端常数项0≥i b ，决策变量满足非负性。

如果加入的这个非负变量取值为非零的话，则说明该约束限定没有约束力，对企业来说不是紧缺资源，所以称为松弛变量；剩余变量取值为非零的话，则说明“≥”型约束的左边取值大于右边规划值，出现剩余量。

4．试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。

答：可行解：满足约束条件0≥=X b AX ，的解，称为可行解。

基可行解：满足非负性约束的基解，称为基可行解。

可行基：对应于基可行解的基，称为可行基。

最优解：使目标函数最优的可行解，称为最优解。

最优基：最优解对应的基矩阵，称为最优基。

它们的相互关系如右图所示：5．用表格单纯形法求解如下线性规划。

32124max x x x Z ++=s .t . ⎪⎩⎪⎨⎧≥≤++≤++0,,86238321321321x x x x x x x x x解：标准化 32124m a xx x x Z ++= s .t . ⎪⎩⎪⎨⎧≥=+++=+++0,,,,862385432153214321x x x x x x x x x x x x x 列出单纯形表故最优解为T X )6,0,2,0,0(*=，即2,0,0321===x x x ，此时最优值为4*)(=X Z ． 6．表1—15中给出了求极大化问题的单纯形表，问表中d c c a a ,,,,2121为何值及变量属于哪一类型时有：（1）表中解为唯一最优解；（2）表中解为无穷多最优解之一；（3）下一步迭代将以1x 代替基变量5x ；（4）该线性规划问题具有无界解；（5）该线性规划问题无可行解。

《运筹学》线性规划部分练习题一、思考题1.什么是线性规划模型，在模型中各系数的经济意义是什么？2 .线性规划问题的一般形式有何特征？3.建立一个实际问题的数学模型一般要几步？4.两个变量的线性规划问题的图解法的一般步骤是什么？5.求解线性规划问题时可能出现几种结果，那种结果反映建模时有错误？6.什么是线性规划的标准型，如何把一个非标准形式的线性规划问题转化成标准形式。

7•试述线性规划问题的可行解、基础解、基础可行解、最优解、最优基础解的概念及它们之间的相互关系。

8•试述单纯形法的计算步骤，如何在单纯形表上判别问题具有唯一最优解、有无穷多个最优解、无界解或无可行解。

9.在什么样的情况下采用人工变量法，人工变量法包括哪两种解法？10.大M法中，M的作用是什么？对最小化问题，在目标函数中人工变量的系数取什么？最大化问题呢？11 •什么是单纯形法的两阶段法？两阶段法的第一段是为了解决什么问题？在怎样的情况下，继续第二阶段？二、判断下列说法是否正确。

1.线性规划问题的最优解一定在可行域的顶点达到。

2.线性规划的可行解集是凸集。

3.如果一个线性规划问题有两个不同的最优解，则它有无穷多个最优解。

4.线性规划模型中增加一个约束条件，可行域的范围一般将缩小，减少一个约束条件，可行域的范围一般将扩大。

5 .线性规划问题的每一个基本解对应可行域的一个顶点。

6.如果一个线性规划问题有可行解，那么它必有最优解。

7.用单纯形法求解标准形式（求最小值）的线性规划问题时，与j' 0对应的变量都可以被选作换入变量。

8 .单纯形法计算中，如不按最小非负比值原则选出换出变量，则在下一个解中至少有一个基变量的值是负的。

9.单纯形法计算中，选取最大正检验数二k对应的变量xk作为换入变量，可使目标函数值得到最快的减少。

10 . 一旦一个人工变量在迭代中变为非基变量后，该变量及相应列的数字可以从单纯形表中删除，而不影响计算结果。

三、建立下面问题的数学模型1.某公司计划在三年的计划期内，有四个建设项目可以投资：项目I从第一年到第三年年初都可以投资。

习题一P.361.一个毛纺厂用羊毛和兔毛生产A,B,C 三种混纺毛料,生产1单位产品需要的原料如下表所示.三种产品的单位利润分别是4,1,5.每月可购进的原料限额为羊毛8000单位,兔毛3000单位,问此毛纺厂应如何安排生产能获得最大利润?A B C 羊毛314兔毛214解：设生产A,B,C 三种产品的量分别是，则模型为123,,x x x 123123123123max 4538000..243000,,0z x x x x x x s t x x x x x x =++++≤⎧⎪++≤⎨⎪≥⎩2.某饲料厂生产的一种饲料由6种配料混合配成.每种配料中所含营养成分A,B 以及单位配料购入价由下表所示.每单位饲料中至少含9单位的A,19单位的B.问饲料厂如何配方,使得饲料成本最低且满足要求?123456A12212B 013132配料原价353060502712解：设每单位饲料中每种配料所需的量为，则有()1,2,3,4,5,6i x i =1234561345623456123456min 3530605027122229..33219,,,,,0z x x x x x x x x x x x s t x x x x x x x x x x x =+++++++++≥⎧⎪++++≥⎨⎪≥⎩4.某产品的一个完整单位包括四个A 零件和三个B 零件.这两种零件(A 和B)由两种不同的原料制成,而这两种原料可利用的数量分别是100单位和200单位.三个车间进行生产,而每个车间制造零件的方法各不相同.下表中给出每个生产班组的原料耗用量和每一种零件的产量.目标是要确定每一个车间的生产班组数使得产品的配套数达到最大.车间每班进料每班产量/个数原料1原料2零件A 零件B 186752596933884解：设每个车间的生产组数分别为，则可生产123,,x x x 个单位产品，则线性规划如()()123123768594min ,43x x x x x x y ++++⎧⎫=⎨⎬⎩⎭下：123123123123123max 853100698200..76845943,,0yx x x x x x s t x x x y x x x yx x x ++≤⎧⎪++≤⎪⎪++≥⎨⎪++≥⎪⎪≥⎩6．设三地各有某种纺织原料90,30,70吨,需要调运给123,,,A A A 五地,后者各需要80,10,30,50,20吨.从到12345,,,,B B B B B ()1,2,3i A i =的路程(千米)如下表所示.现要求设计一个调拨方案,(1,2,3,4,5)j B j =使得总运输吨公里数最少.B1B2B3B4B5A1130286240523153A26422074457309A3718518146443解: 设从运往的运量为，则线性规划()1,2,3i A i =()1,2,3,4,5j B j =ij x 模型为如下形式，其中表示从到的运价。

《管理运筹学》（第二版）课后习题参考答案第1章 线性规划（复习思考题）1．什么是线性规划？线性规划的三要素是什么？答：线性规划（Linear Programming ，LP ）是运筹学中最成熟的一个分支，并且是应用最广泛的一个运筹学分支。

线性规划属于规划论中的静态规划，是一种重要的优化工具，能够解决有限资源的最佳分配问题。

建立线性规划问题要具备三要素：决策变量、约束条件、目标函数。

决策变量是决策问题待定的量值，取值一般为非负；约束条件是指决策变量取值时受到的各种资源条件的限制，保障决策方案的可行性；目标函数是决策者希望实现的目标，为决策变量的线性函数表达式，有的目标要实现极大值，有的则要求极小值。

2．求解线性规划问题时可能出现几种结果，哪种结果说明建模时有错误？ 答：（1）唯一最优解：只有一个最优点； （2）多重最优解：无穷多个最优解；（3）无界解：可行域无界，目标值无限增大； （4）没有可行解：线性规划问题的可行域是空集。

当无界解和没有可行解时，可能是建模时有错。

3．什么是线性规划的标准型？松弛变量和剩余变量的管理含义是什么？答：线性规划的标准型是：目标函数极大化，约束条件为等式，右端常数项0≥i b ，决策变量满足非负性。

如果加入的这个非负变量取值为非零的话，则说明该约束限定没有约束力，对企业来说不是紧缺资源，所以称为松弛变量；剩余变量取值为非零的话，则说明“≥”型约束的左边取值大于右边规划值，出现剩余量。

4．试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。

答：可行解：满足约束条件0≥=X b AX ，的解，称为可行解。

基可行解：满足非负性约束的基解，称为基可行解。

可行基：对应于基可行解的基，称为可行基。

最优解：使目标函数最优的可行解，称为最优解。

最优基：最优解对应的基矩阵，称为最优基。

它们的相互关系如右图所示：5．用表格单纯形法求解如下线性规划。

32124max x x x Z ++=s .t . ⎪⎩⎪⎨⎧≥≤++≤++0,,86238321321321x x x x x x x x x解：标准化 32124m a xx x x Z ++= s .t . ⎪⎩⎪⎨⎧≥=+++=+++0,,,,862385432153214321x x x x x x x x x x x x x 列出单纯形表故最优解为T X )6,0,2,0,0(*=，即2,0,0321===x x x ，此时最优值为4*)(=X Z ． 6．表1—15中给出了求极大化问题的单纯形表，问表中d c c a a ,,,,2121为何值及变量属于哪一类型时有：（1）表中解为唯一最优解；（2）表中解为无穷多最优解之一；（3）下一步迭代将以1x 代替基变量5x ；（4）该线性规划问题具有无界解；（5）该线性规划问题无可行解。