北师大九年级数学上册1.1 菱形的性质与判定(1)

2018-2019学年数学北师大版九年级上册1.1菱形的性质与判定（1）同步训练一、选择题1.平行四边形的一条边长是10cm ，那么它的两条对角线的长可能是（）A 、6cm 和8cmB 、10cm 和20cmC 、8cm 和12cmD 、12cm 和32cm +2.如图,菱形ABCD 的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD 的周长 是( )A 、24B 、16C 、4D 、2 +3.菱形 的两条对角线长分别为和，则它的周长和面积分别为（）A 、B 、C 、D 、 + 4.如图，在菱形中点，则 中， ， ，、分别是边 、周长 等于（）A、B、C、D、+5.如图，在菱形ABCD中，AB=5，∠B：∠BCD=1：2，则对角线AC等于（??）A、5B、10C、15D、20+6.如图，已知菱形ABCD的周长为16，面积为，E为AB的中点，若P为对角线BD上一动点，则EP+AP的最小值为( )A、2B、2C、4D、4+7.在如图直角坐标系内，四边形AOBC是边长为2的菱形，E为边OB的中点，连结AE与对角线OC交于点D，且∠BCO=∠EAO，则点D坐标为（），）D、（1，）A、（，）B、（1，）C、（+8.如图，已知菱形ABCD的边长等于2，若∠DAB=60°，则对角线BD的长为( )A、1B、C、2D、+9.如图，在平面直角坐标系中，已知点，若平移点到点为顶点的四边形是菱形，则正确的平移方法是( )，使以点A、向左平移（）个单位，再向上平移1个单位B、向左平移个单位，再向下平移1个单位C、向右平移个单位，再向上平移1个单位D、向右平移2个单位，再向上平移1个单位+二、填空题10.如图，四边形ABCD是菱形，∠BAD=60°，AB=6，对角线AC与BD相较于点O，点E在AC上，若OE=2 ，则CE的长为+11.菱形的两条对角线长分别为2和2 ，则该菱形的高为．+12.如图，点E、F分别是菱形ABCD的边BC、CD上的点，且∠EAF=∠D=60°，∠FA D=45°，则∠CFE= 度．+13.如图，在菱形ABCD中，AC=8，BD=6，则△ABC的周长是．+14.菱形ABCD中，∠A=60°，其周长为32，则菱形面积为.+15.如图，菱形ABC的对角线相交于点O，过点D作DE∥AC，且DE=AC，连接CE、OE、AE，AE交OD于点F，若AB=2，∠ABC=60°，则AE的长．+三、解答题16.如图，已知四边形ABCD是菱形，DE⊥AB，DF⊥BC，求证：△ADE≌△CDF．+17.如图，四边形ABCD是边长为2的菱形，E，F分别是AB，AD的中点，连接EF，EC，将△FAE绕点F旋转180°得到△FDM．(1)、补全图形并证明：EF⊥AC；(2)、若∠B=60°，求△EMC的面积．+18.如图，已知E、F分别是?ABCD的边BC、AD上的点，且．(1)、求证：四边形AECF是平行四边形；(2)、若四边形AECF是菱形，且BC=10，∠BAC=90°，求BE的长．+19.如图，在菱形ABCD中，AC和BD相交于点O，过点O的线段EF与一组对边AB，CD分别相交于点E，F．(1)、求证：AE=CF；(2)、若AB=2，点E是AB中点，求EF的长．+20.已知，在菱形ABCD中，∠ADC=60°，点H为CD上任意一点（不与C、D重合），过点H作CD的垂线，交BD于点E，连接AE．(1)、如图1，线段EH、CH、AE之间的数量关系是；(2)、如图2，将△DHE绕点D顺时针旋转，当点E、H、C在一条直线上时，求证：AE+EH=CH．+21.如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（﹣3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H，连接BM.(1)、菱形ABCO的边长(2)、求直线AC的解析式；(3)、动点P从点A出发，沿折线ABC方向以2个单位/秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，①当0＜t＜时，求S与t之间的函数关系式；②在点P运动过程中，当S=3，请直接写出t的值．+。

第一章特殊平行四边形1.1 菱形的性质与判定（一）学习目标：①通过折、剪纸张的方法，探索菱形独特的性质。

②通过学生间的交流、计论、分析、类比、归纳、运用已学过的知识总结菱形的特征教学重点：菱形的概念和菱形的性质，菱形的面积公式的推导。

教学难点：菱形的性质的理解及菱形性质的灵活运用。

学习过程：活动一：自学课本例题以上的内容，完成下列问题：______________________ 的四边形叫做菱形，生活中的菱形有______________________________2.按探究步骤剪下一个四边形。

①所得四边形为什么一定是菱形?②菱形为什么是轴对称图形？有_________ 对称轴。

图中相等的线段有：__________________________________图中相等的角有：___________________________________③你能从菱形的轴对称性中得到菱形所具有的特有的性质吗？自己完成证明性质:证明:活动二：对比菱形与平行四边形的对角线菱形的对角线：平行四边的对角线:活动三：菱形性质的应用1.菱形的两条对角线的长分别是6cm和8cm，求菱形的周长和面积2.如图，菱形花坛ABCD勺边长为20cm, / ABC=60沿菱形的两条对角线修建了两条小路AC和BD, 求两条小路的长和花坛的面积。

课效检测：一、填空（1）菱形的两条对角线长分别是12cm, 16cm，它的周长等于____________ ，面积等于_______ 。

（2）菱形的一条边与它的两条对角线所夹的角比是3：2,菱形的四个内角是___________________________________________________________________________________________ 。

（3）已知：菱形的周长是20cm，两个相邻的角的度数比为1：2,则较短的对角线长是。

（4已知：菱形的周长是52 cm, —条对角线长是24 cm,则它的面积是________________ 。

第一章特殊平行四边形1.1 菱形的性质与判定1.1.1 菱形的判定1.探索并掌握菱形的判定方法,积累经验,并能综合运用,形成解决问题的能力;2.经历菱形的判定方法的探索过程,在活动中发展合情推理的意识和主动探究的习惯,初步掌握说理的基本方法,发展有条理表达的能力.3.通过设置问题情境,丰富学生的生活经验,激发学生学习数学和应用数学的兴趣和意识.菱形的判定方法.菱形的判定方法的综合运用.复习引入:1.菱形的定义:有一组邻边相等的平行四边形叫作菱形.2.菱形的特殊性质:(1)菱形是轴对称图形;(2)菱形的四条边相等;(3)菱形的对角线互相垂直.今天我们就来研究一下如何判定一个四边形是菱形.思考(1):除了运用菱形的定义,你还能找出判断一个平行四边形是菱形的其他方法吗?猜想1:如果一个平行四边形的两条对角线互相垂直,那么这个平行四边形是菱形.已知:如图1-1-5,在平行四边形ABCD中,对角线AC,BD互相垂直且交于点O. 求证:四边形ABCD是菱形.证明:∵四边形ABCD是平行四边形,∴OA=OC(平行四边形的对角线相互平分).又∵AC⊥BD,∴BD所在直线是线段AC的垂直平分线,∴AB=BC,∴四边形ABCD是菱形(有一组邻边相等的平行四边形是菱形).得出结论:判定定理1对角线互相垂直的平行四边形是菱形.·议一议已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?小刚做法:如图1-1-7,分别以A,C为圆心,以大于12AC的长为半径作弧,两条弧分别相交于点B,D,依次连接A,B,C,D,四边形ABCD看上去是菱形.你认为小刚的做法正确吗?你是怎样做的?图1-1-8学生:小刚的做法正确.还可以作AC的垂直平分线MN,交AC于点O,在MN上取OB=OD,依次连接A,B,C,D,四边形ABCD是菱形,思考(2):除了运用对角线,你还有其他判定菱形的方法吗?猜想2:四边相等的四边形是菱形.已知:如图1-1-9,在四边形ABCD中,AB=BC=CD=DA.求证:四边形ABCD是菱形.证明:∵AB=CD,BC=AD,∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).又∵AB=BC,∴四边形ABCD是菱形(有一组邻边相等的平行四边形是菱形).得出结论:判定定理2四边相等的四边形是菱形.思考:这里的条件能否再减少一些呢?能否有三条边相等的四边形就是菱形了呢?猜一猜,并试着画一画.学生:动手操作,得到有三条边相等的四边形不一定是菱形.·做一做你能用折纸等办法得到一个菱形吗?动手试一试.你能说说小颖这样做的道理吗?学生:小颖这样做的道理,四边相等的四边形是菱形.例题讲解图1-1-6例2如图1-1-6,已知平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F,求证:四边形AFCE是菱形.证明:∵四边形ABCD是平行四边形,∴AE∥FC(平行四边形的对边平行),∴∠1=∠2.∵EF垂直平分AC,∴AO=OC,∠AOE=∠COF=90°.∴△AOE≌△COF(ASA),∴EO=FO,∴四边形AFCE是平行四边形(对角线互相平分的四边形是平行四边形).又∵EF⊥AC,∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).·例题讲解图1-1-10例3已知:如图1-1-10,在ABCD中,对角线AC与BD相交于点O,AB=5,OA=2,OB=1.求证:ABCD是菱形.证明:在△AOB中,∵AB=5,OA=2,OB=1,∴AB2=AO2+OB2.∴△AOB是直角三角形,∠AOB是直角.∴AC⊥BD.∴ABCD是菱形(对角线互相垂直的平行四边形是菱形).图1-1-11例4如图1-1-11,四边形ABCD是边长为13 cm的菱形,其中对角线BD 为10 cm.求:(1)对角线AC的长度;(2)菱形ABCD的面积.解:(1)∵四边形ABCD是菱形,AC与BD相交于点E,∴∠AED=90°(菱形的对角线互相垂直),DE=12BD=12×10=5(cm)(菱形的对角线互相平分).∴AE=AD2-DE2=132-52=12(cm).∴AC=2AE=2×12=24(cm)(菱形的对角线互相平分).(2)S菱形ABCD=S△ABD+S△CBD=2S△ABD=2×12×BD×AE=2×12×10×12=120(cm2).·做一做图1-1-12如图1-1-12,两张等宽的纸条交叉重叠在一起,重叠部分ABCD是菱形吗?为什么?解:重叠部分ABCD是菱形.理由如下:过点A作AH⊥BC交BC于点H,过点C作CQ⊥AB交AB于点Q.∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形.又∵S ABCD=BC·AH=AB·CQ,且两张纸条等宽,∴AH=CQ,∴AB=BC.∴四边形ABCD是菱形.【巩固练习】1.用两个边长为a的等边三角形纸片拼成的四边形是 ( ).A.等腰梯形B.正方形C.矩形D.菱形2.下列说法中正确的是( ).A.有两边相等的平行四边形是菱形B.两条对角线互相垂直平分的四边形是菱形C.两条对角线相等且互相平分的四边形是菱形D.四个角相等的四边形是菱形本节课应掌握：菱形的判定方法:(1)对角线互相垂直的平行四边形是菱形;(2)四边相等的四边形是菱形.课本习题1.2,1.3。

菱形的判定说课稿一、说教材1、教材的地位和作用本节课选自北师大九年级上册第一章第一节《菱形的性质与判定》的第二课时，主要内容是菱形的判定，尝试从不同角度寻求菱形的判定方法，并能有效地解决问题。

它是在探究平行四边形之后，一个特殊四边形判定方法的探索，它不仅是三角形、四边形知识的延伸，更为探索矩形的性质与判定指明了方向。

学习本课时，通过观察猜想，归纳证明，培养学生的推理能力和演绎能力，为以后圆等知识的学习奠定基础。

2、教学目标根据本节课的教学内容，结合新课标理念, 我制定了以下教学三维目标：知识目标：理解菱形的判别条件及其证明，并能利用这两个定理解决一些简单的问题。

能力目标：（1）经历运用几何符号和图形描述命题的条件和结论的过程，建立初步的符号感，发展抽象思维．（2）经历实际操作，探索菱形判定定理的证明过程，发展合情推理能力和初步的演绎推理的能力；（3）在具体问题的证明过程中，有意识地渗透实验论证、逆向思维的思想，提高学生的能力。

情感态度价值观（1）积极参与数学学习活动，对数学有好奇心和求知欲．（2）通过“实验—猜想—证明—应用“的数学活动提升科学素养.3、教学重点、难点基于本节课的主要内容是围绕着菱形的判定方法而展开的，菱形的判定方法在本节课中处于核心地位，所以我确定本节课的教学重点为菱形判定方法的探究。

由于学生还没有具备辨证分析问题的能力，所以我确定本节课的教学难点是菱形判定方法的探究及灵活运用。

4、教材处理根据教学目标，为突出重点，突破难点，在探索菱形的有关对角线的判定定理时，用教具演示，四边形的两条对角线在保持互相平分的前提下进行转动，当它们的位置关系是垂直时，平行四边形变为菱形，给学生以直观感受，印象深刻；在探索菱形的另一个判定定理时，让学生根据它的特殊点去猜想边之间满足的关系，从而得出定理，拓展学生的思维空间。

二、说教法1、创设问题情境，恰当设疑，引发学生兴趣。

2、采用直观操作和几何论证相结合的探究式的教学方法。

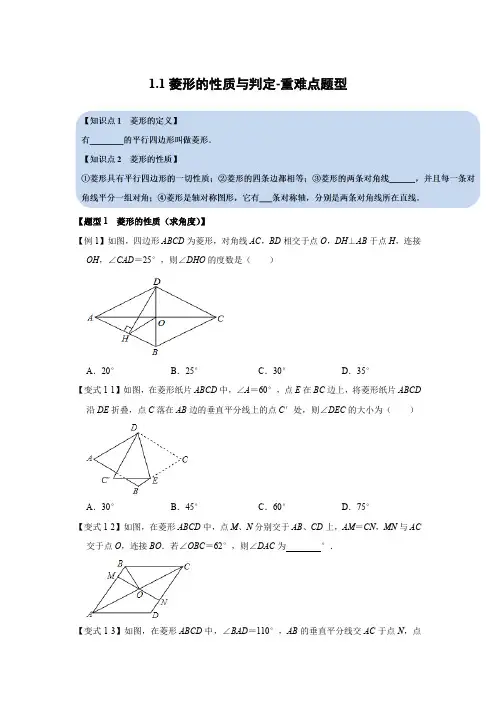
1.1菱形的性质与判定-重难点题型【题型1 菱形的性质（求角度）】【例1】如图，四边形ABCD为菱形，对角线AC，BD相交于点O，DH⊥AB于点H，连接OH，∠CAD＝25°，则∠DHO的度数是（）A．20°B．25°C．30°D．35°【变式1-1】如图，在菱形纸片ABCD中，∠A＝60°，点E在BC边上，将菱形纸片ABCD 沿DE折叠，点C落在AB边的垂直平分线上的点C′处，则∠DEC的大小为（）A．30°B．45°C．60°D．75°【变式1-2】如图，在菱形ABCD中，点M、N分别交于AB、CD上，AM＝CN，MN与AC 交于点O，连接BO．若∠OBC＝62°，则∠DAC为°．【变式1-3】如图，在菱形ABCD中，∠BAD＝110°，AB的垂直平分线交AC于点N，点M 为垂足，连接DN ，则∠CDN 的大小是 ．【题型2 菱形的性质（求长度）】【例2】如图，在菱形ABCD 中，BC ＝10，点E 在BD 上，F 为AD 的中点，FE ⊥BD ，垂足为E ，EF ＝4，则BD 长为（ ）A ．8B ．10C ．12D ．16【变式2-1】如图四边形ABCD 为菱形，点E 为BC 的中点，点F 在CD 上，若∠DAB ＝60°，∠DF A ＝2∠EAB ，AD ＝4，则CF 的长为（ ）A ．45B ．45√3C ．65D ．85 【变式2-2】如图，在菱形ABCD 中，AB ＝13cm ，AC ＝24cm ，E ，F 分别是CD 和BC 的中点，连接EF 并延长与AB 的延长线相交于点G ，则EG 的长度为 cm ．【变式2-3】如图，在菱形ABCD 中，AB ＝BD ，点E ，F 分别在BC ，CD 边上，且CE ＝DF ，BF 与DE 交于点G ，若BG ＝3，DG ＝5，则CD ＝ ．【题型3 菱形的性质（等积法）】【例3】如图，菱形ABCD 的对角线AC ，BD 交于点O ．过O 作OE ⊥AB 于点E ．延长EO 交CD 于点F ，若AC ＝8，BD ＝6，则EF 的值为（ ）A ．5B ．125C ．245D ．485【变式3-1】如图，在菱形ABCD 中，对角线AC 、BD 交于点O ，且AC ＝6，BD ＝8，过A 点作AE 垂直BC ，交BC 于点E ，则BE CE 的值为（ ）A ．512B ．725C ．718D ．524【变式3-2】如图，在菱形ABCD 中，AB ＝10，AC ＝16，过点D 作DE ⊥BA ，交BA 的延长线于点E ，则线段DE 的长为 ．【变式3-3】如图，在菱形ABCD中，∠ADC＝120°，AB＝3，点E在BC上，且BE＝2EC，BF⊥AE，垂足为F，则BF的值为．【题型4 菱形的判定（选择条件）】【例4】在四边形ABCD中，对角线AC，BD相交于点O，且OA＝OC，OB＝OD．若要使四边形ABCD为菱形，则可以添加的条件是（）A．∠AOB＝60°B．AC⊥BD C．AC＝BD D．AB⊥BC【变式4-1】已知平行四边形ABCD，下列条件：①AC⊥BD；②∠BAD＝90°；③AB＝BC；④AC＝BD．其中能使平行四边形ABCD是菱形的有（）A．①③B．②③C．③④D．①②③【变式4-2】如图，在▱ABCD中，M，N是BD上两点，BM＝DN，连接AM，MC，CN，NA，添加一个条件，使四边形AMCN是菱形，这个条件是（）A．OM=12AC B．MB＝MO C．BD⊥AC D．∠AMB＝∠CND【变式4-3】如图，在△ABC中，点D、E、F分别在边AB、BC、CA上，且DE∥CA，DF ∥BA，下列四种说法：①四边形AEDF是平行四边形；②如果∠BAC＝90°，那么四边形AEDF是菱形；③如果AD平分∠BAC，那么四边形AEDF是菱形；④如果AB＝AC，那么四边形AEDF是菱形．其中，正确的有．（只填写序号）【题型5 菱形的判定（证明题）】【例5】如图，在▱ABCD中，点E、F在对角线BD上，BE＝DF．（1）求证：四边形AECF是平行四边形；（2）若BD平分∠ABC，求证：四边形AECF是菱形．【变式5-2】已知：如图，在四边形ABCD中，AB∥DC，对角线AC、BD交于点O，过点C作CE⊥CD交AB的延长线于点E，联结OE，OC＝OE．（1）求证：OE=12AC；（2）如果DB平分∠ADC，求证：四边形ABCD是菱形．【变式5-3】如图，在平行四边形ABCD中，E，F是对角线BD上的点，且BE＝DF，连接AE，CF．（1）求证△ADE≌△CBF；（2）连接AF，CE，若AB＝AD，求证：四边形AFCE是菱形．【变式5-3】如图，在平行四边形ABCD中，点O是BC的中点，连接DO并延长，交AB 延长线于点E，连接BD，EC．（1）求证：四边形BECD是平行四边形；（2）若∠A＝50°，则当∠ADE＝°时，四边形BECD是菱形．【题型6 菱形的判定与性质综合（最值问题）】【例6】如图，已知菱形ABCD的边长为6，点M是对角线AC上的一动点，且∠ABC＝120°，则MA+MB+MD的最小值是（）A．3√3B．3+3√3C．6+√3D．6√3【变式6-1】如图，菱形ABCD的边长为2√3，∠ABC＝60°，点E、F在对角线BD上运动，且EF＝2，连接AE、AF，则△AEF周长的最小值是（）A．4B．4+√3C．2+2√3D．6【变式6-2】如图所示，四边形ABCD中，AC⊥BD于点O，AO＝CO＝4，BO＝DO＝3，点P为线段AC上的一个动点．过点P分别作PM⊥AD于点M，作PN⊥DC于点N．连接PB，在点P运动过程中，PM+PN+PB的最小值等于．【变式6-3】如图所示，在菱形ABCD中，AB＝4，∠BAD＝120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．（1）证明不论E、F在BC、CD上如何滑动，总有BE＝CF；（2）当点E、F在BC、CD上滑动时，分别探讨四边形AECF的面积和△CEF的周长是否发生变化？如果不变，求出这个定值；如果变化，求出最小值．【题型7 菱形的判定与性质综合（多结论问题）】【例7】如图，▱ABCD中，对角线AC、BD相交于点O，AD=12AC，M、N、P分别是OA、OB、CD的中点，下列结论：①CN⊥BD；②MN＝NP；③四边形MNCP是菱形；④ND平分∠PNM．其中正确的有（）A．1 个B．2 个C．3 个D．4 个【变式7-1】如图，平行四边形ABCD中，对角线AC，BD交于点O，BD＝2AD，E，F，G 分别是OC，OD，AB的中点．下列结论正确的是（）①EG＝EF；②△EFG≌△GBE；③FB平分∠EFG；④EA平分∠GEF；⑤四边形BEFG是菱形．A．③⑤B．①②④C．①②③④D．①②③④⑤【变式7-2】如图，在菱形ABCD中，∠A＝60°，E、F分别是AB，AD的中点，DE、BF 相交于点G，连接BD，CG．有下列结论：①∠BGD＝120°；②BG+DG＝CG；③△BDF ≌△CGB；④S菱形ABCD＝AB2；⑤2DE=√3DC；⑥BF＝BC，正确结论的有（）个．A．1B．2C．3D．4【变式7-3】如图，在菱形ABCD中，AB＝BD，点E、F分别是AB、AD上任意的点（不与端点重合），且AE＝DF，连接BF与DE相交于点G，连接CG与BD相交于点H．给出如下几个结论：①∠DBC＝60°：②△AED≌△DFB；③GC与BD一定不垂直；④∠BGE 的大小为定值．其中结论正确的是（）A．①②③B．①②④C．①③④D．②③④【题型8 菱形的判定与性质综合（动点问题）】【例8】如图，在菱形ABCD 中，AB ＝5cm ，∠ADC ＝120°，点E 、F 同时由A 、C 两点出发，分别沿AB 、CB 方向向点B 匀速移动（到点B 为止），点E 的速度为1cm /s ，点F 的速度为2cm /s ，经过t 秒△DEF 为等边三角形，则t 的值为（ ）A ．34B ．43C ．32D ．53 【变式8-1】如图，菱形ABCD 中，∠BAD ＝60°，AB ＝8，对角线AC ，BD 交于点O ，E 是线段OC 上一动点，F 是射线AD 上一动点，若∠BEF ＝120°，则在点E 运动的过程中，EF 长度为整数的个数有（ ）A ．6个B ．5个C ．4个D ．3个【变式8-2】如图，▱ABCD 的对角线AC 、BD 相交于点O ．AB ＝10，AC ＝12，BD ＝16．（1）求证：▱ABCD 是菱形；（2）若点P 是对角线BD 上一动点（不与点B 、D 重合），PE ⊥AB 于点E ，PF ⊥AD 于点F ，PE +PF 是否为定值？若是，求出这个定值；若不是，请说明理由．【变式8-3】如图1，四边形ABCD 为菱形，对角线AC ，BD 相交于点O ，点E 为OC 上的动点．（1）当AD ＝AE 时，OE ＝1，OD ＝5，求菱形ABCD 的面积；（2）如图2，当OE ＝OD 时，过点A 作CD 的垂线，垂足为F ，交ED 延长线于点G ，求证：GE=√2AO．。

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！课时练第1单元菱形的性质与判定一、选择题（本大题共12小题，共36分）1.菱形不具备的性质（）A.是轴对称图形B.是中心对称图形C.对角线互相垂直D.对角线一定相等2.菱形的两条对角线长分别是6和8,则此菱形的周长是（）A.5B.20C.24D.323.如图,在菱形ABCD中,对角线AC,BD相交于点O,则图中全等的直角三角形共有()A.3对B.4对C.5对D.6对4.如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为（）A.20B.30C.40D.505.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8,BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是（）6.C.3D.4A.2B.527.已知菱形的周长为8,两邻角的度数比为1:2,则菱形的面积为（）A.83B.8C.43D.238.如图,菱形ABCD的对角线AC,BD交于点O,AC=4,BD=16,将△ABO沿点A到点C的方向平移,得到△'''.当点'与点C重合时,点A与点'之间的距离为()A.6B.8C.10D.129.下列条件中,不能判定一个四边形是菱形的是()A.一组邻边相等的平行四边形B.一条对角线平分一组对角的四边形C.四条边都相等的四边形D.对角线互相垂直平分的四边形10.下列条件中,能判定▱ABCD是菱形的是（）A..=B.⊥.C.=D..⊥11.如图,下列四个条件中,能判定平行四边形ABCD为菱形的是（）A.∠=90∘B.=C.=.D.=.12.如图,在△ABC中,AB=AC,将△ABC沿边BC翻转,得到的△DBC与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是（）A.一组邻边相等的平行四边形是菱形B.四条边相等的四边形是菱形C.对角线互相垂直的平行四边形是菱形D.对角线互相垂直平分的四边形是菱形13.用直尺和圆规作一个以线段AB为边的菱形，作图痕迹如图所示，能得到四边形ABCD是菱形的依据是()A.一组邻边相等的四边形是菱形B.四边相等的四边形是菱形C.对角线互相垂直的平行四边形是菱形D.每条对角线平分一组对角的平行四边形是菱形二、填空题（本大题共7小题，共21分）14.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥AD于点E,交BC于点F,则EF的长为.15.16.如图,在菱形ABCD中,对角线AC、BD相交于点O,点E在线段BO上,连接AE,若CD=2BE,∠DAE=∠DEA,EO=1,则线段AE的长为.17.18.如图,在菱形ABCD中,AB=6,∠ABC=60∘,M为AD的中点,P为对角线BD上一动点,连接PA和PM,则PA+PM的最小值是。