20xx小学六年级创新杯数学竞赛试题.doc

数学竞赛创新杯试题及答案试题一：代数问题题目：若x, y, z是正整数，且满足以下条件：1. \( x + y + z = 30 \)2. \( xy + xz + yz = 50 \)3. \( xyz = 24 \)求x, y, z的值。

答案：首先，我们可以将第三个条件写为 \( x = \frac{24}{yz} \)。

将这个表达式代入第二个条件中，我们得到：\[ yz + z\left(\frac{24}{yz}\right) +y\left(\frac{24}{yz}\right) = 50 \]化简后，我们得到：\[ yz + 24/z + 24/y = 50 \]\[ yz - 50 + 24(1/y + 1/z) = 0 \]由于 \( x, y, z \) 是正整数，我们可以通过尝试不同的组合来找到满足条件的 \( y \) 和 \( z \)。

经过尝试，我们发现当 \( y = 3 \) 和 \( z = 4 \) 时，满足条件：\[ 3 \times 4 - 50 + 24\left(\frac{1}{3} + \frac{1}{4}\right) = 12 - 50 + 28 = 0 \]因此，\( x = \frac{24}{3 \times 4} = 2 \)。

所以，\( x = 2, y= 3, z = 4 \)。

试题二：几何问题题目：在一个直角三角形ABC中，∠C是直角，AB是斜边，AC = 5，BC = 12。

求斜边AB的长度。

答案：根据勾股定理，直角三角形的斜边的平方等于两直角边的平方和。

因此，我们有：\[ AB^2 = AC^2 + BC^2 \]\[ AB^2 = 5^2 + 12^2 \]\[ AB^2 = 25 + 144 \]\[ AB^2 = 169 \]\[ AB = 13 \]所以，斜边AB的长度是13。

试题三：组合问题题目：有5个不同的球和3个不同的盒子，将这些球放入盒子中，每个盒子至少有一个球。

第十届“创新杯”全国数学邀请赛小学六年级试卷一、选择题 （4 分× 10=40 分）（以下每题的四个选项中，仅有一个是正确的） 。

1．2012+2011-2010-2009+2008+2007-2006-2005+ +4+3-2-1=( )A ．2012B ．2010C ．4020D ．40482．有 n 个自然数（数可以重复）其中包括 2012，不包括 0，这 n 个自然数的平均数是 572。

如果去掉 2012 后，剩下 n-1 个数的平均数为 412，那么这 n 个 数中最大的数可以是（ ） A ．2012 B ． 4024 C ．3700 D ．38001 33331 1 7 ）3．计算 999966662012 的结果为（629 9A ．3333B ．1331C ．1332D ．13214．某次知识竞赛共 5 道题，全班 52 人，答对一题得 1 分。

已知全班共得 181分。

已知每人至少得 1 分，且得 1 分的有 7 人，得 2 分和得 3 分的人一样多， 得 5 分的人有 6 人，则得 4 分的有（ ）人。

A ．25B ．30C ． 31D ．35 5．李军有一个闹钟，但它走时不准，这天下午 6∶ 00 把它对准北京时间，可到晚上 9∶00 时，它才走到 8∶ 45。

第二天早上李军看闹钟走到 6∶17 的时候赶去上学，这时候北京时间为（ ） A ．7∶15B ．7∶24C ． 7∶ 30D ．7∶356．A 、B 、C 为正整数，且 A1 24，则 A+2B+3C= （）B15C 1A ．10B ．12C ．14D ．157．下列图形，第 10 个图中△比○多（）个A ．44B ．60C ．56D ．45（ ）（ 2（ 3 18．某校学生到郊外植树，已知老师是学生人数的 ） 1。

若每位男生种 13 棵树，女3生每人种 10 棵树，每个老师种 15 棵树，他们共种了 204 棵树，那么老师有 （ ）人。

一、选择题（每题3分，共30分）1. 下列哪个数是质数？A. 18B. 19C. 20D. 212. 下列哪个图形是轴对称图形？A. 长方形B. 正方形C. 三角形D. 圆形3. 一个长方形的长是8厘米，宽是5厘米，它的周长是多少厘米？A. 23厘米B. 27厘米C. 30厘米D. 35厘米4. 小明有12个苹果，他每天吃3个，几天后他吃完了所有的苹果？A. 2天B. 3天C. 4天D. 5天5. 一个分数的分子是4，分母是6，它的分数值是多少？A. 2/3B. 3/4C. 4/6D. 6/46. 小华有5个球，小刚有3个球，他们一共有多少个球？A. 8个B. 9个C. 10个D. 11个7. 一个数加上它的3倍等于18，这个数是多少？A. 3B. 4C. 5D. 68. 下列哪个数是偶数？A. 25B. 26C. 27D. 289. 一个三角形的三边长分别是3厘米、4厘米、5厘米，这个三角形是？A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等边三角形10. 下列哪个单位是面积的单位？A. 平方米B. 千克C. 米D. 秒二、填空题（每题5分，共25分）11. 2乘以3等于__________，3乘以2等于__________。

12. 下列分数中，最小的是__________。

13. 一个长方形的长是8分米，宽是5分米，它的面积是__________平方分米。

14. 下列图形中，是轴对称图形的是__________。

15. 下列数中，是质数的是__________。

三、解答题（每题10分，共30分）16. 小华有苹果和橘子一共20个，苹果比橘子多4个，请问小华有多少个苹果？17. 小明从家到学校步行需要10分钟，如果他每小时走60米，请问他家离学校有多远？18. 一个正方形的边长是6厘米，求这个正方形的周长和面积。

四、应用题（每题10分，共20分）19. 小红有铅笔和圆珠笔一共30支，铅笔比圆珠笔多10支，请问小红有多少支铅笔？20. 小明买了3千克苹果，每千克苹果的价格是10元，小明一共花了多少钱？答案：一、选择题1. B2. D3. C4. B5. A6. A7. A8. B9. A10. A二、填空题11. 6；612. 1/413. 4014. 正方形15. 2，3，5，7，11，13，17，19，23，29三、解答题16. 小华有16支铅笔。

创新杯数学试题及答案一、选择题（每题4分，共20分）1. 下列哪个选项不是偶数？A. 2B. 4C. 6D. 7答案：D2. 一个数的平方等于36，这个数可能是？A. 6B. -6C. 6或-6D. 以上都不是答案：C3. 一个等差数列的首项是2，公差是3，那么第5项的值是多少？A. 17B. 14C. 11D. 8答案：A4. 以下哪个图形的面积是π？A. 半径为1的圆B. 半径为2的圆C. 半径为1的半圆D. 半径为2的半圆答案：A5. 一个直角三角形的两条直角边长分别为3和4，那么斜边的长度是多少？A. 5B. 6C. 7D. 8答案：A二、填空题（每题3分，共15分）6. 如果一个数的立方等于-64，那么这个数是________。

答案：-47. 一个等比数列的首项是1，公比是2，那么第4项的值是________。

答案：88. 一个圆的半径是5厘米，那么它的周长是________厘米。

答案：31.49. 一个长方体的长、宽、高分别是2、3、4，那么它的体积是________立方单位。

答案：2410. 一个三角形的内角和是________度。

答案：180三、解答题（每题10分，共30分）11. 已知一个二次方程ax^2 + bx + c = 0，其中a=1，b=-3，c=2，求解这个方程的根。

答案：x1 = 2, x2 = 112. 一个工厂生产的产品数量在第一季度是100个，第二季度是150个，第三季度是200个，求这个工厂在这三个季度的平均生产数量。

答案：15013. 一个班级有30个学生，其中20个学生喜欢数学，15个学生喜欢英语，10个学生两门都喜欢。

问这个班级有多少学生既不喜欢数学也不喜欢英语？答案：5结束语：以上是本次创新杯数学试题及答案，希望同学们通过这次练习能够更好地掌握数学知识，提高解题能力。

一、选择题（每题5分，共25分）1. 下列哪个数是质数？A. 28B. 29C. 30D. 312. 下列哪个图形的周长是6.28厘米？A. 正方形B. 长方形C. 等腰三角形D. 梯形3. 一个长方形的长是10厘米，宽是6厘米，它的面积是多少平方厘米？A. 60B. 64C. 66D. 1004. 一个圆的半径是3厘米，它的直径是多少厘米？A. 6B. 9C. 12D. 185. 下列哪个分数是最简分数？A. 3/6B. 4/8C. 5/10D. 7/14二、填空题（每题5分，共25分）6. 5个苹果的重量是3千克，那么一个苹果的重量是______千克。

7. 一个数加上它的3倍等于24，这个数是______。

8. 下列数中，最小的偶数是______。

9. 1千米等于______米。

10. 一个正方形的边长是4厘米，它的周长是______厘米。

三、解答题（每题10分，共40分）11. 小明有12个乒乓球，他打算平均分给他的5个好朋友。

请问小明至少需要准备多少个乒乓球盒子？（请列出解题步骤）12. 一辆汽车从A地出发，以每小时60千米的速度行驶，经过2小时到达B地。

然后以每小时80千米的速度返回A地。

请问汽车返回A地需要多少小时？（请列出解题步骤）13. 一个长方体的长、宽、高分别是4厘米、3厘米、2厘米，求这个长方体的体积。

（请列出解题步骤）14. 小华有3个苹果，小丽有5个苹果，他们一共有多少个苹果？（请列出解题步骤）四、应用题（每题15分，共30分）15. 小明去图书馆借了5本书，其中2本数学书，3本语文书。

他一共看了15个小时，数学书看了6个小时，语文书看了9个小时。

请问小明平均每本书看了多少个小时？16. 一家农场有鸡和兔共36只，鸡的脚有94只。

请问农场里有多少只鸡和多少只兔？（请列出解题步骤）答案：一、选择题：1. B2. A3. A4. A5. D二、填空题：6. 0.67. 88. 29. 100010. 16三、解答题：11. 解答：12÷5=2...2，所以至少需要3个乒乓球盒子。

2022年第2届创新杯数学邀请赛小学6年级第2试试题第二届“创新杯”数学邀请赛试题第二试一、选择题(每小题6分，共60分.以下每题的四个选项中，仅有一个是正确的．请将表示正确答案的英文字母填在每题后面的圆括号内．)1.三个连续偶数的和是162,则它们的乘积是().(A)157248(B)125748(C)157284(D)1725842.某市2002年底统计10年平均降雨量为631毫米.一年后再统计10年平均降雨量为601毫米,2003年常年的降雨量是450毫米.那么,1993年降雨量(以毫米为单位)是().(A)1232(B)616(C)750(D)4803.一个两位数,它的十位数字加上个位的7倍,还是等于这个两位数,这样的两位数有().(A)一个(B)两个(C)三个(D)四个4.传统拼花被单是由一些正方形和直角等腰三角形的布片拼接而成的,如图所示.其中有阴影部分的面积是整个拼花被单面积的().(A)36%(B)40%(C)45%(D)48%5.在下面四个算式中,得数最大的是().1111)20(B)()60171915211111)100(D)()140(C)(13231125(A)(6.如图,在高速公路上,从3千米处开始,每隔4千米设计一个速度限制标志,而且从10千米处开始,每隔9千米设一个测速照相标志,则刚好在19千米处同时设置这两种标志.那么,下一个同时设置这两种标志的地点的千米数是().(A)32千米处(B)37千米处(C)55千米处(D)90千米处7.某商场的营业额2000年和2001年连续两年平均每年比上一年上升10％,而2002年和2003年连续两年平均每年比上一年下降10％,那么2003年的营业额比1999年的营业额().(A)下降了2％(B)下降了1.99％(C)上升了2％(D)没有变化8.古埃及时代，人们喜欢的是分子为1的分数，如1111,,,,,等，我们不妨称这234n些分数为分数单位，其他的分数数据，只有它能写成若干个不同的分数单位之和时，人们才承认它是分数。

小学六年级数学竞赛试卷（参考答案）小学六年级数学竞赛试卷（参考答案）一、填空题，(每题4分，共80分)1、42、363、884、575、1306、367、51，7 8、四 9、2 10、28 11、6812、630 13、15，5 14、10，60 15、52，25616、100，150 17、18 18、45 19、2 20、4.5二、应用题，(每题4分，共20分)21、车速：12000÷（75-15）=20（米/秒）车长：20×15＝300（米）22、23、3.5×9÷（14－5）=6.3（吨）24、解：在△ABC与△ADE中，∠BAC=∠DAE。

因为AB=6AD，AC=3AE，所以S△ABC=6×3×S△ADE=18×1=18（平方厘米）。

25、解答：由于运费是以每吨货物运输1千米为单位（即吨·千米）计量的，因此要使运费最省，就要把所有货物运往离货物最多的仓库适当近的地方集中。

我们依次计算以一、二、…、五号仓库为集中点所需的运费：0.8×（20×100+40×400）=14400（元），0.8×（10×100+40×300）=10400（元），0.8×（100×200+20×100+40×200）=9600（元），0.8×（10×300+20×200+40×100）=8800（元），0.8×（10×400＋20×300）=8000（元）。

因此，把所有货物集中到五号仓库所需的运费最少，运费为8000元。

一、选择题（每题5分，共50分）1. 下列各数中，最小的数是（）A. 0.5B. 0.05C. 0.005D. 0.00502. 如果一个长方形的长是12cm，宽是6cm，那么它的周长是（）A. 18cmB. 24cmC. 36cmD. 48cm3. 一个数加上它的平方，等于36，这个数是（）A. 6B. 7C. 8D. 94. 下列哪个图形是轴对称图形？（）A. 正方形B. 长方形C. 平行四边形D. 梯形5. 小明有5个苹果，小红有3个苹果，小明比小红多（）A. 2个苹果B. 3个苹果C. 4个苹果D. 5个苹果6. 下列哪个数是质数？（）A. 15B. 16C. 17D. 187. 一个圆的半径是5cm，它的周长是（）A. 15πcmB. 25πcmC. 30πcmD. 35πcm8. 小华的年龄是小丽的3倍，小丽的年龄加上小华的年龄等于48岁，小丽的年龄是（）A. 12岁B. 15岁C. 18岁D. 21岁9. 下列哪个数既是偶数又是质数？（）A. 2B. 4C. 6D. 810. 一个三角形的三个内角分别是30°、60°、90°，这个三角形是（）A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形二、填空题（每题5分，共50分）11. 0.5乘以4等于______。

12. 12除以3等于______。

13. 100米跑，小明用了12秒，小红用了14秒，小明的速度比小红______。

14. 一个数的平方根是3，这个数是______。

15. 一个长方形的长是8cm，宽是5cm，它的面积是______cm²。

16. 下列数中，质数有______个。

17. 一个正方形的周长是24cm，它的边长是______cm。

18. 下列哪个数是正数？（）A. -1B. 0C. 119. 一个三角形的两个内角分别是45°、45°，这个三角形是______。

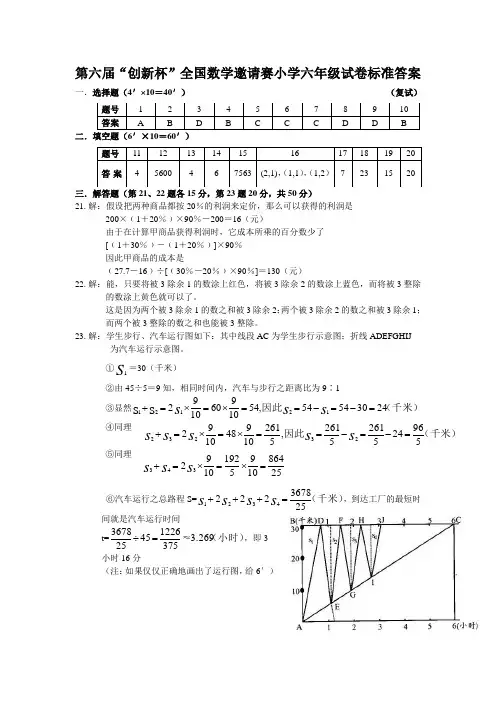
第六届“创新杯”全国数学邀请赛小学六年级试卷标准答案一．选择题（4′×10＝40′） （复试）二．填空题（6′×10＝60′）三．解答题（第21、22题各15分，第23题20分，共50分）21. 解：假设把两种商品都按20％的利润来定价，那么可以获得的利润是 200×﹙1＋20％﹚×90％－200＝16（元）由于在计算甲商品获得利润时，它成本所乘的百分数少了 [﹙1＋30％﹚－﹙1＋20％﹚]×90％ 因此甲商品的成本是﹙27.7－16﹚÷[﹙30％－20％﹚×90％]＝130（元）22. 解：能，只要将被3除余1的数涂上红色，将被3除余2的数涂上蓝色，而将被3整除 的数涂上黄色就可以了。

这是因为两个被3除余1的数之和被3除余2；两个被3除余2的数之和被3除余1； 而两个被3整除的数之和也能被3整除。

23. 解：学生步行、汽车运行图如下：其中线段AC 为学生步行示意图；折线ADEFGHIJ 为汽车运行示意图。

①S1＝30（千米）②由45÷5＝9知，相同时间内，汽车与步行之距离比为9∶1③显然（千米）因此24305454,5410960109212121s s =-=-==⨯=⨯=+s s s ④同理 ⑤同理⑥汽车运行之总路程S=（千米）2536782224321=+++s s s s ，到达工厂的最短时 间就是汽车运行时间t=（小时）3.269≈375122645253678=÷，即3小时16分 （注：如果仅仅正确地画出了运行图，给6′）题号 1 2 3 4 5 6 7 8 9 10 答案ABDBCCCDDB题号 11 12 13 14 15161718 19 20 答案45600467563 (2,1)，（1,1），（1,2） 7231520（千米）因此5962452615261,526110948109223232=-=-==⨯=⨯=+s s s s s 2586410951921092343=⨯=⨯=+s s s。

创新杯六年级试题及答案一、选择题（每题2分，共20分）1. 以下哪项是创新杯比赛的宗旨？A. 促进学生全面发展B. 选拔优秀学生C. 培养学生创新能力D. 提高学生考试成绩答案：C2. 创新杯比赛通常包括哪些学科？A. 语文、数学、英语B. 物理、化学、生物C. 信息技术、艺术、体育D. 所有学科答案：A3. 创新杯比赛的参赛对象是？A. 所有学生B. 六年级学生C. 初中生D. 高中生答案：B4. 创新杯比赛的举办周期是多久？A. 每年一次B. 每两年一次C. 每学期一次D. 每季度一次答案：A5. 创新杯比赛的奖项设置通常包括哪些？A. 一等奖、二等奖、三等奖B. 金奖、银奖、铜奖C. 特等奖、一等奖、二等奖D. 所有选项答案：D6. 创新杯比赛的评分标准主要依据是什么？A. 答题速度B. 答题正确率C. 创新思维D. 团队协作答案：B7. 以下哪项不是创新杯比赛的参赛要求？A. 遵守比赛规则B. 独立完成试题C. 使用指定教材D. 携带个人学习资料答案：D8. 创新杯比赛的试题难度通常如何？A. 非常难B. 适中C. 非常简单D. 随机答案：B9. 创新杯比赛的成绩公布时间是？A. 比赛结束后立即公布B. 比赛结束后一周内公布C. 比赛结束后一个月内公布D. 比赛结束后三个月内公布答案：B10. 创新杯比赛的获奖证书由谁颁发？A. 学校B. 教育局C. 创新杯组委会D. 参赛学生家长答案：C二、填空题（每题2分，共20分）1. 创新杯比赛的目的是_________。

答案：选拔具有创新精神和实践能力的学生。

2. 创新杯比赛的参赛者需要_________。

答案：在规定时间内完成所有试题。

3. 创新杯比赛的试题设计注重_________。

答案：考察学生的综合运用能力和创新思维。

4. 创新杯比赛的评分标准包括_________。

答案：答题的正确性、创新性和解题思路。

5. 创新杯比赛的奖项设置旨在_________。

“创新杯”赛前模拟试题小学六年级卷(考试时间：120分钟)一、选择题（4’×10=40’）以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的字母填在下面的表格中。

1. 如果规定a ※b=13×a-b ÷8，那么17※24的最后结果是（ ）。

A 、218B 、208C 、198D 、2002. 甲乙二人同时开始加工一批零件，每人加工零件总数的一半，甲完成任务的1/3时乙加工了50个零件，甲完成3/5时乙完成了一半。

这批零件共（ ）个。

A 、360 B、420 C 、600 D 、153. 用1、2、3、4、5这五个数字可组成（ ）个比20000大且百位数字不是3的无重复数字的五位数。

A 、78B 、62C 、84D 、124 4. 如果a =20052006，b =20062007，那么a ，b 的大小关系为（ ）。

A 、a ＞b B 、b ＞a C 、a=b D 、无法比较5. 春风小学原计划栽种杨树、柳树和槐树共1500棵。

植树开始后，当栽种了杨树总数的3/5和30棵柳树以后，又临时运来了15棵槐树，这时剩下的3种树的棵数恰好相等。

则原计划要栽植杨树（ ）棵。

A 、360B 、315C 、825D 、2006. 已知半圆所在的圆的面积为62.8平方厘米，求阴影部分的面积为( )平方厘米。

BA 、3.6B 、5.7C 、4.8D 、5.27. 一件工程，甲队独做12天可以完成任务．如果甲队做3天后乙队做2天，则恰好完成工程的一半．现在甲、乙两队合做若干天后，由乙队单独完成，已知两队合做的时间与乙队独做的时间相等．完成任务共有（ ）天。

A 、8B 、4C 、6D 、108. 一班和二班的人数之比是8:7，如果将一班的8名同学调到二班去，则一班和二班的人数比变为4:5．原来两班的人数为（ ）人．A 、30B 、40C 、42D 、609.10名同学参加数学竞赛，前4名同学平均得分150分，后6名同学平均得分比10人的平均分少20分，这10名同学的平均分是（）分。

六年级数学竞赛试题及答案[1](word版可编辑修改)六年级数学竞赛试题及答案[1](word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（六年级数学竞赛试题及答案[1](word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为六年级数学竞赛试题及答案[1](word版可编辑修改)的全部内容。

六年级数学竞赛试题及答案[1](word 版可编辑修改)六年级综合知识竞赛数学卷（考试时间：8：00～10:30 总分:80分）一、填一填.（每空1分，共10分)1、1时24分=（ )时（填分数） 5.4吨=( )千克2、被除数是除数的31,被除数是商的32，除数与商的最简整数比是( ）. 3、把71化成小数后，小数点后第一百位上的数字是（ ）。

4、一个三角形的内角和是180°，对折后去掉一半，内角和是( )。

5、一根绳子的长度等于它的53加上53米，这根绳子长（ )米。

6、用一只2倍的放大镜看一个30°的角,放大镜下这个角现在是（ ）.7、用6、7。

5、30和1.5四个数写出一个比例式( ）.8、一个三角形三个内角度数的比是1：4：5，最小的内角是（ ）度，这个三角形是( ）三角形。

二、选择正确答案的序号填在括号里。

(每小题1分、共6分) 1、种杨树50棵，死了2棵，成活率是（ ）①98％ ②94％ ③96％2、甲正方体的棱长是3厘米,乙正方体的棱长是2厘米，甲乙两个正体体积的比是（ )。

①3：2 ②9:4 ③27:83、原来用6个同样大小的纸箱装每袋重10千克的洗衣粉，共装若干袋。

如果每袋的重量增加6千克，要使每箱的重量和原来的相同,每箱装的袋数应减少（ ）。

参考答案（六六老师详解版本）一、选择题1、D【解析】显然，10个连续自然数的和是5的奇数倍，所以D 不满足2、C【解析】设涨价x 元，则利润为(10)(50010)10(10)(50)x x x x +⨯-=⨯+⨯-当1050x x +=-即20x =时，利润最大此时售价为50＋20=70（元）3、D【解析】取出80、240、400、……、2000，总共13个数4、C 【解析】1111111111111[()()()()]35577920112013235577920112013++++=⨯-+-+-++-⨯⨯⨯⨯ 3352013=5、B【解析】设另两条边为11a b ≤≤，则6b ≥则当11b =时，a =11、10、9、……、1，共11种；当b =10时，a =10、9、8、……、2，共9种；当b =9时，a =9、8、7、……、3，共7种；当b =8时，a =8、7、6、5、4，共5种；当b =7时，a =7、6、5，共3种；当b =6时，a =6，共1种。

所以，总共有11＋9＋7＋5＋3＋1=36个不同的三角形。

6、B【解析】总数10×10=100符合条件的排列（1,2）、（2,3）、……、（9,10），由于对称性，共有9×2=18种所以可能性为9507、A【解析】要有两组两张连号的，列举可以得到10种情况：（1,2,3,4）、（1,2,4,5）、（1,2,5,6）、（1,2,6,7）、（2,3,4,5）、（2,3,5,6）、（2,3,6,7）、（3,4,5,6）、（3,4,6,7）、（4,5,6,7）所以总共有10×（5×4×3×2×1）=1200（种）8、C【解析】连AC 、FD ，由于AC//FD ，所以AFO OCD S S ∆∆=，可以得到一个14圆，所以面积为11212364ππ⨯⨯⨯=9、A【解析】乙、丙步行路程一样，乘车路程也一样时，三人同时到达。

For pers onal use only in study and research; not for commercial use膄第五届“创新杯”全国数学邀请赛虿小学六年级试题荿一、选择题(5'10= 50')以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的字母填在下面的表格中。

膆题号袄1螁2蒇3薆4薅5螂6衿7肅8莅9蕿10羈答案蒄袁蚁肆袄薂螂葿薇莂葿1•与30以内的奇质数的平均数最接近的数是薇A • 12 B • 13 C • 14 D • 15羇2 .把10个相同的小正方体按如图所示的位置堆放，它的外表含有肃若干个小正方形，如图将图中标有字母A的一个小正方体搬去，薁这时外表含有的小正方形个数与搬动前相比衿A .不增不减 B .减少1个蒆C .减少2个n .减少3个螃3•一部电视剧共8集，要在3天里播完，每天至少播一集，则安排蚂播出的方法共有_______________ 种。

肇A . 21 B . 22 C . 23 D . 24袅4 .甲、乙、丙三人出同样多的钱买同样的笔记本，最后甲、乙都比丙多得3本，甲、乙都给了丙2.4元，那么每本笔记本的价格是________________ 元.薃A . 0.8 B . 1.2 C . 2.4 D . 4.8蒀5.用0, 1, 2,…，9这十个数字组成一个四位数，一个三位数，一个两位数与一个一位数，每个数字只许用一次，使这四个数的和等于2007，则其中三位数的最小值是莀A . 201 B . 203 C . 204 D . 205芅6 ．有2007 盏亮着的灯，各有一个拉线开关控制着，拉一下拉线开关灯会由亮变灭，再拉一下又由灭变亮，现按其顺序将灯编号为 1 , 2，…，2007,然后将编号为2的倍数的灯线都拉一下, 再将编号为 3 的倍数的灯线都拉一下, 最后将编号为5 的倍数的灯线都拉一下,三次拉完后亮着的灯有 _________ 盏．芄A ．1004 B ．1002 C ．1000 D．998蒁7．已知一个三位数的百位、十位和个位分别是a,b, c,而且a x b x c=a+b+c，那么满足上述条件的三位数的和为蒈A ．1032 B , 1132 C ．1232 D ．133 2螄8．某次数学考试共5道题，全班52人参加，共做对181题．已知每人至少做对1 题；做对1 道题的有7人,做对2道题的人和做对3道题的人一样多,做对5道题的有6人,那么做对4 道题的人数是肄A ．29 B ．31 C ．33 D ．35薂9 .一个三角形将平面分成2个部分，2个三角形最多将平面分成8个部分，…，那么5 个三角形最多能将平面分成的部分数是蚇A . 62 B . 92 C . 512 D . 1024蒈10. 一条单线铁路上有5个车站A, B, C, D, E,它们之间的路程如图所示.两辆火车同时从A, E两站相对开出，从A站开出的每小时行60千米，从E站开出的每小时行50千米.由于单线铁路上只有车站才铺有停车的轨道,要使对面开来的列车通过,必须在车站停车, 才能让开行车轨道. 那么应安排在某个站相遇, 才能使停车等候的时间最短. 先到这一站的那一列火车至少需要停车的时间是螄二、填空题(5 ' X 12 二60')莀11.观察58*2 = 5 十55 二60, 7*4 = 7+77+777+7777= 8638，推知9* 5 的值是____________ •罿12.如图,将宽2米的一些汽车停在长度为30米的未划停袇车格的路边,最好的情况下可停________________ 部车,最差的情况下可停_______________ 部车.薅13.如图，一个圆被四条半径分成四个扇形，每个扇形的周长为7.14cm ,那么该圆的面积2为_____________ c m (圆周率n取3.14).14.按以下模式确定,在第n 个正方形内应填人的数是_____________________________ ,其中, n 是非零的自然数．15．篮子里装有不多于500 个苹果,如果每次二个,每次三个,每次四个,每次五个,每次六个地取出来,篮子中都剩下一个苹果,而如果每次七个地取出,那么没有苹果剩下,篮子中共有苹果 _____________ 个.16. 一个国家的居民不是骑士就是无赖， 骑士不说谎，无赖永远说谎.我们遇到该国居民 A,B , C, A 说：“如果C 是骑士，那么B 是无赖C 说：“ A 和我不同，一个是骑士，一个 是无赖.”那么这三个人中 ___________________________是骑士， ___________ 是无赖.17•甲、乙两人对同一个数做带余数除法，甲将它除以 8，乙将它除以9，现知甲所得的商数与乙所得的余数之和为 13，那么甲所得的余数是 _________________ •行，第一周内，他们在 C 点相遇.在D 点第二次相遇.已知 C 点离A 点80米，D 点离B 点 60米.则这个圆的周长是 ______________________________ 米.21. 九个连续的自然数，它们都大于 _____ 80,那么其中质数至多有 个.22. 把从1开始的奇数1, 3，5,…，排成一行并分组，使得第 n 组有n 个数，即(1)，(3 , 5) , (7 , 9, 11) , (13 , 15, 17, 19)，…那么2007位于第 _________ 组，是这一组的第 ________ 个数. 三、解答题(共40分)23. (20分)如图，A, B 两地相距1500米，实线表示甲上午8时由A 地出发往B 地行走，到达B 地后稍作休息，又从 B 地出发返回A 地的步行情况；又虚线表示乙上午 8时从B 地出发向A 地行走，到了 A 地，立即返回B 地的步行情况.(1) 观察此图，解下列问题：① 甲在B 地休息了多长时间？算一算，休息前、后步行的 速度各是多少？② 乙从B 地到A 地，又从A 地到B 地的步行速度各是多 少？(2) 甲、乙二人在途中相遇两次，结合图形、 算一算，第一次，第二次相遇的时刻各是几点几分23 4 5620072008如上图，将2008个方格排成一行，在最左边的方格中放有一枚棋子，甲、乙二人交替 地移动这枚棋子，甲先乙后，每人每次可将棋子向右移动若干格， 但移动的格数不能是合数将棋子移到最右边格子的人获胜.(1) 按每人每次移动的格子数分类，有哪4类走法？(2) 如果甲第1次走了 3格，对于乙的四类走法，甲应分别采取怎样的对策才能保证自 己(甲)一定获胜？并简单说明，为什么采取这样的对策，甲一定获胜仅供个人用于学习、研究；不得用于商业用途For personal use only in study and research; not for commercial use.18.如图，以△ ABC 的两条边为边长作两个正方形BDEC 和ACFG 已知 &ABC ：S 四边形BDEC =2:7，正方形BDEC 和正方形ACFG 的边长之比为 3: 5，那么△ CEF 与整个图形面积的最 简整数比是 _____________________ •19. 一个口袋中装有 3个一样的球，3个球上分别写有数字 2, 3和4.出一个球，记下球上的数字a ，并将球放回袋中.第二次又从袋子中取球上的数字b .然后算出它们的积.'则所有不同取球情况所得到的积的和是 ______________若第一次从袋子中取 出一个球，记下：.>D:同时出发逆时针而Nur f u r den pers?nlichen f u r Studien, Forschung, zu kommerziellen Zwecken verwendet werden.Pour l ' e tude et la recherche uniquement a des fins personnelles; pas a des fins commerciales. TO员BKO g^A.nrogeHKO TOpMeno^b3ymm0ai6yHeH u ac^ egoB u HHue肉go 员冶HBIucno 员B30BaTbCE B KOMMepqeckux qe 员EX.____________ 以下无正文__________ For personal use only in study and research; not for commercial use仅供个人用于学习、研究；不得用于商业用途For personal use only in study and research; not for commercial use.Nur f u r den pers?nlichen f u r Studien, Forschung, zu kommerziellen Zwecken verwendet werden.Pour l ' e tude et la recherche uniquement a des fins personnelles; pas a des fins commerciales. TO员BKO g^A.nrogeHKO TOpMeno^b3ymoiflCH6yHeH u ac^ egoB u HHuefigo^^HMucno 员B30BaTbCE B KOMMepqeckux qe 员EX.____________ 以下无正文___________。

六年级数学竞赛试题姓名_________ 成绩_______一、填空。

（27分）1、一个数由32个百、56个百分之一组成，这个数是（），它含有（）个0.01，这个数保留到十分位是（）。

2、填上合适的单位名称：一间教室面积是54（）汽车每小时行90（）一瓶矿泉水容积是255（）3、5.02吨=（）吨（）千克 1.75小时=（）小时（）分4、2÷（）=0.4=（）：15=8（）=（）%5、215：0.6化成最简整数比是（），比值是（）。

6、桌子每张a元，椅子每把b元，买20套桌椅共需（）元。

（一张桌子配两把椅子）7、小丽和小红同时从学校出发，小丽向东走80米，记作+80米，小红向西走60米，记作（）米，此时两人相距（）米。

8、一个圆柱形木块削去18.84立方分米加工成最大的圆锥体，这个圆柱形木块体积是（）立方分米。

9、三角形三个内角度数比是1：3：5，这个三角形是（）三角形。

10、29的分子增加6，要使分数大小保持不变，分母应为（）。

11、王奶奶5月1日去银行存了一年定期储蓄2万元，年利率1.98%，利息税20%，她到期可得本金和税后利息共（）元。

12、一个圆的周长是12.56厘米，以它的一条直径为底边，在圆内画一个最大的三角形，这个三角形面积是（）平方厘米。

13、一张精密零件图纸的比例是5：1，在图上量得某个零件长度是48毫米，这个零件实际长度是（）。

14、自来水管的内直径是2厘米，水管内水的流速是每秒8厘米，一位同学去水池洗手，走时忘记关掉水龙头，5分钟会浪费（）升水。

15、九张卡片上分别写着1-9九个数字。

甲、乙、丙、丁四人每人拿两张。

甲的数字之和是9，乙的两张数字之差是6，丙的两张数字之积是12，丁的两张数字之商是3，剩下一张的数字是（）。

二、判断题。

（8分）1、10克盐放入100克水中，含盐率是10%。

（ ）2、分子一定，分母和分数值成正比例。

（ ）3、已知圆的半径是r ，半圆的周长是（2+π）r 。