08第八讲

数学分析第十二章数项级数积分判别法第八讲数学分析第十二章数项级数定理12.9（积分判别法）积分判别法由于比式和根式判别法的比较对象是几何级数,局限性较大,所以还需要建立一些更有效的判别法.设[1,)f +∞为上非负减函数,+1()d f x x 与反常积分∞⎰同时收敛或同时发散.证由假设[1,)f 为+∞上非负减函数, f 在[1, A ]上可积,于是对任何正数A ,那么正项级数()f n ∑数学分析第十二章数项级数-≤≤-=⎰1()()d (1),2,3,.nn f n f x x f n n 依次相加可得11221()()d (1)().(12)m m m m n n n f n f x x f n f n -===≤≤-=∑∑∑⎰若反常积分收敛,有111()(1)()d (1)()d .m m m n S f n f f x x f f x x +∞==≤+≤+∑⎰⎰根据定理12.5, 级数()f n ∑收敛.则由(12)式左边, 对任何正整数m ,数学分析第十二章数项级数反之, 若()f n ∑为收敛级数, 一正整数m (>1)有-≤≤=∑⎰11()d ().(13)mm f x x S f n S 10()d , 1.A n f x x S S n A n ≤≤<≤≤+⎰因为f (x )为非负减函数, 法, 可以证明+1()()d f n f x x 与∞∑⎰是同时发散的.11221()()d (1)().(12)m mm m n n n f n f x x f n f n -===≤≤-=∑∑∑⎰则由(12)式右边，对任故对任何正数A ,都有111.2,()d .f x x +∞⎰根据定理反常积分收敛用同样方数学分析第十二章数项级数例12 讨论1.p p n级数的敛散性∑1(),0[1,)p f x p x当时在=>+∞解函数上是非负减函时发散.是发散的.数，1d 1p x p x+∞>⎰反常积分在时收敛，.1时发散≤p 故1()p f n n=∑∑由积分判别法得01p <≤当≤0p 的情形, 则可由收敛的必要条件知它也至于1p >当时收敛，数学分析第十二章数项级数例13 讨论下列级数的敛散性.∞∞==∑∑2311(i);(ii).(ln )(ln )(lnln )p p n n n n n n n 解2d ,(ln )p x x x 研究反常积分由于+∞⎰(i)1,1.p p 数在时收敛时发散>≤3d (ii),,(ln )(lnln )p x x x x 对于考察反常积分同样可+∞⎰1p ≤推得级数(ii) 在p > 1时收敛, 在时发散. ()()()22d ln d ln ln p p x x x x x +∞+∞=⎰⎰ln 2d pu u +∞=⎰时发散，时收敛，当11≤>p p 根据积分判别法得级复习思考题数学分析第十二章数项级数1.设n u ∑为收敛的正项级数，则一定存在收敛的正n v ∑lim 0n n nu v →∞=项级数,使得. 也就是说没有收敛得最慢的级数.1,1n n u u +<有n u ∑n N >2.如果正项级数满足对一切(1),?n n n u u <∑或能否得出收敛4.总结判别法使用规律.3.如果对每个正整数p ，正项级数都有?n u ∑能否得出收敛12lim()0n n n p n u u u +++→∞+++= ，是否存在发散得最慢的级数？。

第八章 记忆与学习关键词节省法 再现法 经典性条件反射 中性刺激 条件刺激 条件反应 操作性条件反射 强化 退化 系列回忆 对偶联合回忆 自由回忆 感觉记忆 短时记忆 长时记忆 前瞻记忆 回溯记忆 错误记忆 真实记忆 DRM 范式 内隐激活反应假设 模糊痕迹理论 元记忆 客体记忆 启动效应 多重记忆系统说 迁移适当加工理论 任务分离 加工分离 人工语法范式 序列反应时任务 矩阵扫描任务 序列推测任务 复杂系统控制范式课程讲义第一节 记忆与学习的传统研究一、记忆的早期研究（一）艾宾浩斯和节省法研究艾宾浩斯使用无意义音节作为记忆研究的材料，并发明了节省法来测量记忆效果。

他用节省量作为记忆效果的量化指标，即重新学习时所节省的时间或遍数与初次学习时间或遍数比值。

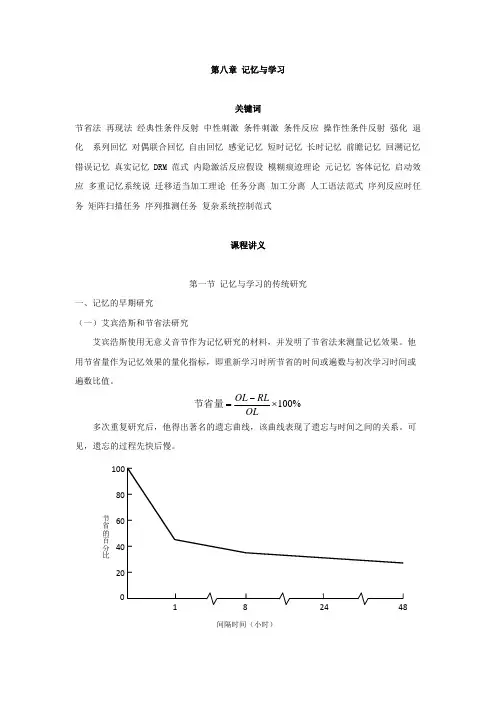
%100×−=OLRL OL 节省量 多次重复研究后，他得出著名的遗忘曲线，该曲线表现了遗忘与时间之间的关系。

可见，遗忘的过程先快后慢。

节省的百分比2040 60 801001 82448 间隔时间（小时）图8-1 遗忘曲线（采自Ebbinghaus，1885）（二）巴特莱特和再生实验巴特莱特使用故事和图画等有意义的材料进行研究。

研究主要包括两种方法：重复再生和系列再生。

由此发现当信息从一个人传到另一个人时是怎样被扭曲的，而这些扭曲信息的出现是记忆功能不完善的表现。

巴特莱特认为在系列再生过程中人们记忆的变化存在以下几种趋势：①习惯性表征的变形②精心组织③简单化④命名⑤细节的保存。

因此他指出，任何学习和记忆都是在已有图式的基础上进行的，当这些图式与正在记忆的内容相冲突时，人们便会歪曲记忆内容，使之更适合于头脑中已有的图式。

（三）我国心理学家的研究除了国外的一些经典研究，我国心理学家也进行过关于记忆内容变化和遗忘曲线的研究。

（1）对图形记忆变化的研究：曹日昌对这种变化进行了分类，他指出和识记图形相比较，记忆所表现出来的变化大致可以分为：①简略、概括②完整、合理③详细、具体④夸张、突出。

第八讲分段函数分段函数是高考取的热门，但在高中教材中并无特地的章节去学习，这直接致使了学生进入高三后，对分段函数的认识仍是很陌生，这直接影响了学生函数的复习。

为了让新高一学生更好的学习函数，在连接教材中，特地选用了分段函数的一些要点题型进行解说。

1、有些函数在它的定义域中,对于自变量x 的不一样取值范围,对应法例不一样 ,这样的函数往常称为分段函数 .2、分段函数是一个函数,不要把它误以为是几个函数.3、写分段函数的分析式,在注明定义域时,必定注意“上一段”与“下一段”的定义域不可以有重叠部分 .如第一段是x∈ (0,20], 第二段是x∈ [20,40], 这样写是错误的.(一 ).求分段函数的定义域,值域求分段函数的定义域是各段定义域的并集,值域也是分别求出各段上的值域后取并集.【例 1】、求函数y 2x 4 2x 6 的值域(二 ).求分段函数的函数值【例 2】、已知f (x)x21,( x0),求f [ f (1)] 的值x1,(x0)（三）解分段函数不等式1 x1,( x0)【例 3】、设函数 f ( x)2,若 f (a)a, 则实数a的取值范围是_______.1 ,(x0)x（四）分段函数图像问题【例 4 】（2011a, a b1天津）对实数 a, b ，定义新运算+：a bb，设函数b, a1f ( x)( x22)( x x2 ), x R .若函数 y f (x) c 的图像与x轴恰有两个公共点，则实数 c 的取值范围是.练 习A 组x 1,( x 0)1、已知函数 f (x), ( x 0) , 求 f { f [ f ( 1)]} __________.0,( x 0)x 2 2 ( x 1),则 f [ f (1 )]2. 设 f ( x)1( x 1). （）1 x 221 B.4C.9 D.25A.135 4123. 已知 f ( x)sin x( x 0),11) f (11) 的值为.f (x则 f (1) 1( x 0).664、已知 f ( x)1 x 1,x 0 ， 则使 f ( x) 1建立的 x 的取值范围是.2 1)2 , x( x 05.（ 1）作函数（ 2）作函数yx 1 x 2 的图象。

第八讲归一问题
导语：在解答某些应用题时，常常需要先求出“单一量”，然后以这个“单一量”为标准，根据其它条件求出结果。

用这种解题思路解答的应用题，称为归一问题。

所谓“单一量”是指单位时间的工作量（工作效率）、物品的单价、单位面积的产量、单位时间所走的路程（速度）等。

例1、一种钢轨，4根共重1900千克，现在有95000千克钢，可以制造这种钢轨多少根？（损耗忽略不计）
分析：以一根钢轨的重量为单一量。

例2 、王家养了5头奶牛，7天产牛奶630千克，照这样计算，8头奶牛15天可产牛奶多少千克？
分析：以1头奶牛1天产的牛奶为单一量。

例3、三台同样的磨面机2.5时可以磨面粉2400千克，8台这样的磨面机磨25600千克面粉需要多少时间？
分析：以1台磨面机1时磨的面粉为单一量。

例4 、4辆大卡车运沙土，7趟共运走沙土336吨。

现在有沙土420吨，要求5趟运完。

问：需要增加同样的卡车多少辆？
分析：以1辆卡车1趟运的沙土为单一量。

练习测试：
1、2台拖拉机4时耕地20公顷，照这样速度，5台拖拉机6时可耕地多少公顷？
2、4台织布机5时可以织布2600米，24台织布机几小时才能织布24960米？
3、一种幻灯机，5秒钟可以放映80张片子。

问：48秒钟可以放映多少张片子？
4、3台抽水机8时灌溉水田48公顷，照这样的速度，5台同样的抽水机6时可以灌溉水田多小公顷？
对比练习：
甲5小时做12个零件，乙6小时做14个相同的零件。

甲乙两人谁的速度快些？。

第八讲微粒间的相互作用一、路易斯结构理论二十世纪初，在玻尔原子结构模型的基础上，路易斯（1916年，G．C．Lewis，美国化学家）提出了化学键的电子对理论。

他认为，原子相互化合形成化学键的过程可以简单地归结为未成对电子的配对活动。

当A原子的一个未成对电子和B原子的一个未成对电子配成一对被双方共用的电子对，就形成一个化学健，这种化学键称为―共价键‖。

这样，就可以把表示化学健的―—‖改成―：‖，以表示一对电子。

这种化学符号就是所谓共价键的―电子结构式‖。

几乎在提出共价键的同时，人们还建立了配价键和电价键（即离子键）的概念。

当A原子和B 原子化合，A原子供出一对电子对而B原子接受这对电子对，形成一对共用电子对，所形成的化学键就称为―配价键‖。

当A原子和B原子形成化学键时，A原子的未成对电子和B原子的未成对电子配成对，但这对电子并不是共用电子对而是为一方所独有，这样，一方失去电子，变成正离子，另一方得到电子，变成负离子，正负离子以静电引力相互吸引，形成的化学键称为―电价键‖或称为―离子键‖。

所谓―路易斯结构式‖，通常是指如下所示的化学符号：在路易斯结构式中，线段的意义，如前所述，代表共用电子对，仍称―单键‖、―双键‖和―叁键‖（代表1，2，3对共用电子对）。

成对的小黑点则代表未用来形成化学键的―价层电子对‖，非共用电子叫做―孤对电子对‖。

[例题1] [2005年江苏省高中学生化学竞赛试题]已知S2Cl2分子结构与H2O2相似，请写出S2Cl2的电子式。

二、价层电子对互斥理论（VSEPR）现代化学的重要基础之一是分子的立体结构。

单写出路易斯结构式是不能得知分子的立体结构的。

分子的立体结构通常是指其σ—键骨架在空间的排布。

现代实验手段可以测定一个具体的分子或离子的立体结构。

例如，我们可以根据分子或离子的振动光谱（红外光谱或拉曼光谱）来确定分子或离子的振动模式，进而确定分子的立体结构：也可以通过X—衍射、电子衍射、中子衍射等技术测定结构。