最全最详的画法几何及工程制图之直线的投影2

又因 BC∥bc 故 bc ⊥ABba平面
因此 bc⊥ab 即 ∠abc为直角
.b
a
c
直线在H面上的
投影互相垂直
30
例：过C点作直线与AB垂直相交。
Ⅰ、Ⅱ是Ｖ面的重影点， 用其可帮助判断两直线 Ⅲ、Ⅳ是H面的重影点。 的空间位置。
26
例题 判断两直线的相对位置
c
b
1
a
d
X a
d
1
cb
1d 1c 27
判断两直线重影点的可见性
a
X
c 1 (3)4
2
d
b
B
C 13
2 4D O
A
c
3
b
a
4
1(2)
d
判断重影点的可见 性时，需要看重影点 在另一投影面上的投 影，坐标值大的点投 影可见，反之不可见， 不可见点的投影加括 号表示。
例：过C点作水平线CD与AB相交。
b
c●
k
d
a
a
d
k c●
b
先作正面投影
25
⒊ 两直线交叉
a c’
1(2)
3 ●
●
●4
c 2
●
d
两直投为线什影相么特交？性吗：？
b ★ 同名投影可能相交， 但 “交点”不符合空间
b 一个点的投影规律。
●
a
●
1
Байду номын сангаас3(4 )
d
★ “交点”是两直线上 的一 对重影点的投影，
1 从属性 若点在直线上，则点的各个投影必在直线的各同面投 影上。利用这一特性可以在直线上找点，或判断已知点是否在直 线上。
2 定比性 属于线段上的点分割线段之比等于其投影之比。即

垂直于V 面 （正垂线）
垂直于W 面 （侧垂线）
Z
V a'
(b') B
b"
X Hb
A O
a"
W
a
Y
Z
Va' b' B a"
X
A O (b")
aH
W bY
a' (b')
Z b" a"
a' b' Z a"
(b")
X
b a
O YW X
O YW
ab
YH
YH
1. a'b'积聚为一点. 1. a"b"积聚为一点.
ad
YH
AB与CD不相交
两直线交叉
两直线交叉 既不平行、也不相交的两直线称为交叉两直线。
交叉二直线的同面投影可能平行，但不可能所有同面投 影都平行；其同面投影可能相交，但交点连线不垂直于 投影轴。
V
b'
g'(j') c'
B E
a'
d'
X
AJ
DO
C
a
GF d
c e(f)
b
H
两直线交叉
重影点 重影点：分属两直线的两个点在某投影面上的重合投影叫重影点。
c
b
k'
a' c' X
c
O b
反之，若两直线的同面投 a A k d H a
kd
影均相交，且交点的连线 垂直于投影轴，则两直线 相交。
Z
a'
c' ｌ'

d c 分析： D a b C 因为ABBC,且 ABH 根据直角投影定理 有ab bc A b d c
水平线
Z
a’ A
a
b’ B b” b
β
a’ X
b’ Z
b”
a’ YW
X
a”
γ Y a
β
b
γ
水平线的投影特性：
反映真长TL YH
1.水平线的H投影反映真长，真长投影与OX夹角为β；与 OY轴的夹角为γ；α= 0°。
2.水平线的V投影 a’b’∥OX；W投影 a”b”∥OY；
正平线
b′ Z B α γ A
【例题1】判定下题中，点K是否在直线AB上？
b′ k′
Z
b″
a′
a″
X O
k″
YW
a
k b YH
K 点 在 直 线 AB 上
【例题2】判断点K是否在直线AB上。 a′
Z a″
k′ b′ X O
k″ b″ YW
a
k b
K 点 不 在 直 线 AB 上
YH
【例题3】已知点C在线段AB上，求点C 的正面投影。 V b c a X A a B C O X b c cb
2.2 直线的投影
• 直线的投影
• 直线上的点
a′ V b′ β A b aH Y γ
Z B b″
W a″
• 直线的真长及其倾角
• 两直线间的相对位置 X • 一边平行于投影面的直 角投影规律
α
1、直线的投影
直线的投影特性： 一般来说，直线的投影 仍然为直线。当直线垂直于 投影面时，直线的投影则积 聚为一点。
a
如何判断？
求出侧面投影后可知：

[例2]已知侧平线CD上一点E的正面投影e′,求e。
第五节 两直线的相对位置
一、平行两直线 二、相交两直线 三、交叉两直线
[例4-5] [例4-6] [例4-7]
一、平行两直线
如果空间两直线互相平行，则此两直线的各同面投影 必互相平行。 若两直线的各同面投影互相平行，则此两直线在空间 一定互相平行。
第四章 直线的投影
第一节 直线的投影
第二节 直线与投影面的相对位置
第三节 线段的实长及其对投影面的倾角 第四节 直线上的点 第五节 两直线的相对位置直线的投影
第六节 垂直两直线的投影
第一节 直线的投影
一、直线的投影一般仍为直线 二、直线的投影可由直线上两点的同面 投 投影确定
一.直线的投影一般仍为直线

W
H
三、投影面垂直线
铅垂线 正垂线
侧垂线

垂直于W 面的线

小结：
⑴.

投影面垂直线的投影面上的投影集聚成一点；
W
⑵ .投影面垂直线在其它两个投影面上的投影分别垂直于
相应的投影轴，且反映该直线段的实长。
H
第三节
线段的实长及对投影面的倾角
一、线段的实长及其对H面的倾角α
二、线段的实长及其V面的倾角
C
D
c( d )
直线的投影一般仍为直线
特殊情况下积聚为一点
二.直线的投影可由直线上两点的同面投影确定


第二节 直线与投影面的相对位置
一、一般位置直线 二、投影面平行线 三、投影面垂直线
平行于某一投影面而 与其余两投影面倾斜
正平线（平行于Ｖ面）
投影面平行线 侧平线（平行于Ｗ面）
水平线（平行于Ｈ面） 正垂线（垂直于Ｖ面） 投影面垂直线 侧垂线（垂直于Ｗ面） 铅垂线（垂直于Ｈ面）

a
定比作图方法
c
b
§2－2 直线的投影
例2 已知点C在线段AB上，求点C的正面投影。
b Z
b
V
b
c a C B
X
A
O
a
X
a
a
O
a
c YW
a
c Hb
c b
YH
§2－2 直线的投影
例3. 在直线AB上取一点C, 使AC = L，求点C的两投影。
b c
a
L
b c
a
a
X
a
b
L
c
ZAB
O
b
c
ZAB
b0
L
c0
平面对 投影面的倾 角、、
二、各种位置平面的投影特性
§2－3 平面的投影
投影面垂直面： 垂直于一个、倾斜 于另两个投影面的 平面
V面—正垂面 H面—铅垂面 W面—侧垂面
特殊位 置平面
投影面平行面： 平行于一个、同时 垂直于另两个投影 面的平面
V面—正平面 H面—水平面 W面—侧平面
投影面倾斜面： 对三个投影面都倾 斜的平面
c b
X
b O c
YW
当两直线均为
b
一般位置直线时， c
若有两个同面投影 满足上述条件，则 空间两直线相交。
d
a
YH
§2－2 直线的投影
3. 交叉两直线
既不平行又不相交的两直线
b
1(2 )
d
c
a
Ⅱ
2 Ⅰd
c
b
a1
b d
1(2 )
c
X a
O
d
c
a

b
c
B
C A
ac
b H
定比定理
直线上的点具有两个特性：
从属性 若点在直线上，则点的各个投影必在直线的各同面投影 上。利用这一特性可以在直线上找点，或判断已知点是 否在直线上。
定比性 属于线段上的点分割线段之比等于其投影之比。即
A C: C B = a c : c b= ac : cb = ac : c b
投影特性：
b a
A
a
V d
B c
C
D
c
b
dH
空间两直线平 行，则其各同名投 影必相互平行，反 之亦然。
例1：判断图中两条直线是否平行。
① b
d a
c
a
c
bd
AB//CD
对于一般位置直 线，只要有两个同名 投影互相平行，空间 两直线就平行。
例2：判断图中两条直线是否平行。
② c
a
d b
c b
c a
⒉ 两直线中有一条平行于某一投影面时， 在该投影面上的投影反映直角。
⒊ 两直线均为一般位置直线时， 在三个投影面上的投影都不 直角定理 反映直角。
●b a●
直线倾斜于投影面 投影比空间线段短
ab=ABcosα
二、 直线在三个投影面中的投影特性
投影面 平行线
正平线（平行于Ｖ面） 侧平线（平行于Ｗ面） 水平线（平行于Ｈ面）
平行于某一投影面而 与其余两投影面倾斜
统称特殊位置直线
投影面 垂直线
正垂线（垂直于Ｖ面） 侧垂线（垂直于Ｗ面） 垂直于某一投影面
d b
对于特殊位置直 线，只有两个同名投 影互相平行，空间直 线不一定平行。
da 如何判断？

本节回顾
• 直线的投影
– 直线投影的定义，直线实长及其与各投影面夹 角的求法
– 直线投影和点投影的关系 – 各种位置直线的投影 – 两直线的相对位置
• 作业
– 习题集17-20页
3-2 直线的投影
一、直线的投影图 二、各种位置直线的投影 三、直线上点的投影 四、两直线的相对位置
一、直线的投影图 z
b’ b”
a’
a”
X
o
YW
b
a
YH
两点决定一条直线。因此，直线直线的的投投影影图可以由直 线上任意两个点的投影来决定。
1. 直线对一个投影面的投影特性
A
B
B
M
A
B
α
A
b
b
a(b)(m) H
b’
c’
Z坐标差
a’
a c
C0

b
三、直线上点的投影
1. 从属性。若点在直线上，则点的各个投影必定在该直线的 同面投影上，并且符合空间一点的投影特性。
2. 定比性。若点在直线上，则点分线段之比等于其投影之比。
AC:CB= ac:cb = a’c’:c’b’ = a”c”:c”b”
b’
z
b”
c’
c”
例6 已知AB∥V面，试过点C作一直线CD与AB垂 直相交。
b’
d’
a’
X
a
d
直线CD与正平线AB所成的 直角正面投影上反映直角。
c’ b
c
例7 求两直线AB、CD的公垂线。
公垂线MN是水平
D N
线 c’
A
n’ d’
a’ m’
M
C
BX

有三种情况：平行、相交、交错（交叉）。
相交 平行
交错
第二章 直线
21
§2-5 两直线的相对位置
一、两直线平行
空间平行的两直线，其所有的同面投影都各自保持平行关 系。 反之，若三面体系中两直线的所有同面投影都各自保持平行 关系，则空间两直线平行。
第二章 直线
22
§2-5 两直线的相对位置
只要有一组同面投影不平行，空间两直线就不平行。 注意：一般情况下，只要检查两组同面投影就能判断出两直线 是否平行。对于平行于同一投影面的两直线，则需要求出它们在该 投影面上的投影，或根据两直线共面、定比等关系作图进行判断。
第二章 直线
29
§2-6 一边平行于投影面的直角的投影
直角投影法则:
当构成直角的两条直线中，有一直线是投影面平行 线，则此两直线在该投影面上的投影仍相交成直角。 逆定理也成立 。
第二章 直线
30
§2-6 一边平行于投影面的直角的投影
证明：AB⊥BC、AB⊥Bb , ∴ AB⊥BbcC 又 ab∥AB ∴ ab⊥BbcC , ∴ ab⊥bc 即 ∠abc=90°
迹点是直线穿越相邻两分角或卦角间的投影面上的点；
直线在其两相邻迹点之间的部分，必处在同一分角或卦角 中，这部分直线段上所有点的同名坐标值的正、负号相同。
第二章 直线
8
§2-3 直线的倾角和直线段的实长
一、倾角和实长
空间直线与某投影面的夹角，称为 直线对该投影面的倾角。 对H 面的倾角记为α
对V 面的倾角记为β 对W 面的倾角记为γ
第二章 直线
31
§2-6 一边平行于投影面的直角的投影
直角投影法则不仅适用于相交垂直的两直线， 也适用于交错垂直的两直线。下面都是符合直角 投影法则的投影图。

案例三
电气原理图。在电气原理图中，需要利用直线投影绘制出电路的连接关系和电气元件的符 号。例如，一个简单的电路图需要标注电源、开关、灯泡等元件的符号和连接关系，这些 信息可以通过直线投影在图纸上准确地表示出来。
05
直线投影误差分析与控制
误差来源及影响因素分析
仪器误差
由于测量仪器本身的精度限制，如刻度不准确、 光学系统畸变等，导致测量结果偏离真实值。
加强数据处理和分析
03
对测量数据进行有效处理和分析，如数据平滑、滤波、异常值
剔除等，以减小数据波动对直线投影精度的影响。
06
总结与展望
本次课程重点内容回顾
直线投影的基本概念
介绍了直线在投影面上的投影，包括投影的形成、分类和性质等 。
直线投影的作图方法
详细讲解了如何利用投影原理，通过已知条件绘制直线的投影图， 包括正投影、斜投影等。
工程制图基础-直线的 投影
汇报人：XX
• 直线投影基本概念 • 正投影下直线投影规律 • 斜投影下直线投影规律 • 直线投影在工程图中的应用 • 直线投影误差分析与控制 • 总结与展望
目录
01
直线投影基本概念
投影法分类与特点
01
02
03
中心投影法
投影线汇交于一点的投影 方法，如透视投影。
平行投影法
实线
表示可见轮廓线，用于 绘制物体的外轮廓或内
轮廓。
虚线
表示不可见轮廓线，用 于绘制被遮挡部分的轮
廓。
点划线
表示轴线或对称中心线 ，用于标注物体的对称
性或旋转中心。
双点划线
表示假想轮廓线，用于 绘制物体的假想形状或
位置。
利用直线投影绘制工程图技巧和方法

投影面倾斜线—一般位置直线，与 三个投影面都倾斜
《机械制图》 第2讲 点、直线和平面的投影
4
（2）投影面平行线
思考：已知AB为水平线,求AB的投 影。
a’
a b
《机械制图》 第2讲 点、直线和平面的投影
5
Z
a’
b’ a” b”
X
Yw
a
b YH
与V面夹角
与W面夹角
投影特性： 一个投影反映实长及与投
16
2.2.4 直线的迹点（简介）
概念--直线与投影面的交点，称为该直线的迹点。 迹点既在直线上（或延长线上），又在投影面上。
规定-直线与 H 面的交点—水平迹点（M） 直线与 V 面的交点—正面迹点（N） 直线与 W 面的交点—侧面迹点（S）
a’
注意--因迹点是投影面上的点， X m’ 所以，迹点的一个投影必在轴上！
c’ k’
b’
d’
a’
a
d
ck
b
《机械制图》 第2讲 点、直线和平面的投影
14
• 两直线交叉
c’ a’
4’(3’) 1’ 2’
b’ d’
a
3
d
c
4 1(2)
b
投影特征： 同名投影可能相交， 但“交点”不符合点 的投影规律。 “交点”代表两直线 上的一对重影点。 利用重影点可以帮助 想象两直线在空间的 相对位置。
直线平行于投影面----投影反映实长
直线倾斜于投影面----投影仍为直线，但小于实长。
《机械制图》 第2讲 点、直线和平面的投影
3
• 直线在三投影体系中的投影特性
（1）直线的种类
投影面平行线 投影面垂直线

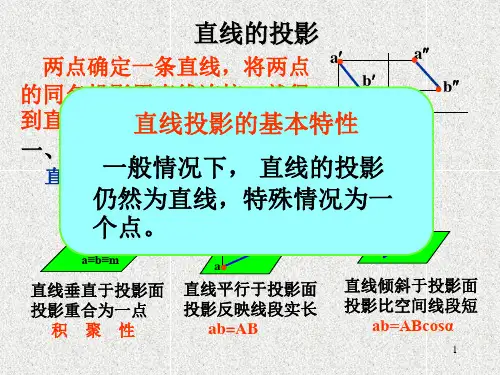
1、平行两直线投影特性
两直线的同面投影相互平行，且其长度之比等 于投影长度之比。
如何利用投影特性根据投影判断两直线是否平 行？
如果两直线都不平行于投影轴，则有两个投影面投 影平行则可以认为直线平行。
如果两直线都平行于某投影面，则必须根据第三投 影或比例关系判断。
2．已知直线 AB 平行直线 CD，试完成直线
2、水平投影cd ⊥ox轴,侧 面投影c"d" ⊥oz,且均反映
实长。
1、侧面投影积聚成一点
e"(f")。 2、水平投影ef oxH 正面 投影e f oz,且均反映
实长。
总结：投影面垂直线的投影特性
在所垂直的投影面上积聚为一点； 其它两投影垂直于相应的投影轴。 “一点两平行”
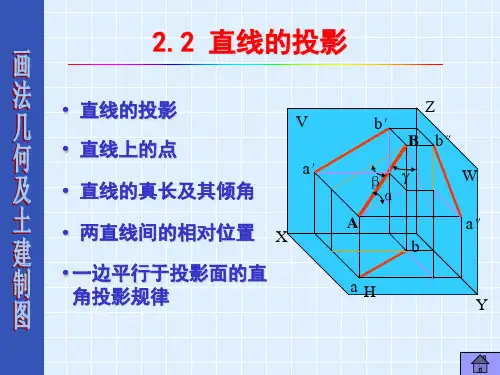
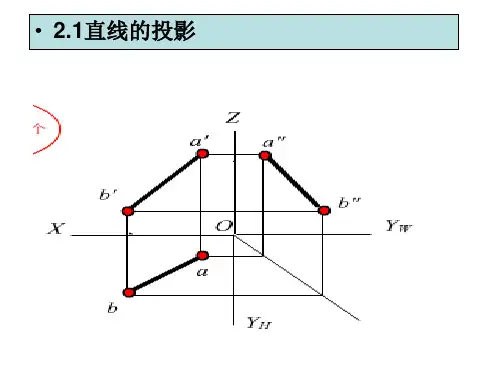
三、一般位置直线的投影特性
直线
水 平 线
正 平 线
侧 平 线
直观图
Y
H
Y
投影图
YW
YH
YW
YH
YW
YH
投影特征
1、水平投影ab反映实长 及直线的倾角β和γ。 2、正面投影a b //ox轴, 侧面投影a"b"//oy w 轴，且
均短于实长。
1、正面投影e f 反映实长 及直线的倾角α和γ。 2、水平投影ef //ox轴,侧 面投影e"f "//oz轴，且均
短于实长。
1、侧面投影e"f" 反映实 长及直线的倾角α和β。 2、水平投影ef//oy H 轴,正 面投影e f //oz轴，且均
短于实长。
总结:投影面平行线的投影特性
在所平行的投影面上的投影反映实长；且 反映直线对另外两个投影面的倾角； 其它两投影平行于相应的投影轴，且小于 实长。 “一斜两平行“ ”

d˝
b˝
O
Yw
YH
两条平行的投影面垂直线
A C
B
D
a (b)
c (d)
ac=AB和CD的距离
例3－7：已知直线AB平行直线CD，试完成直线AB和CD的三面投影
c′ a′ d′
c″
a″ d″
b′ b″
d
b
c
a
二、两直线相交
a’
A c’
d’
k’
D
b’
K
C
B
a
ck
d b
1、两直线相交，则它们的同名投影必相交，并且交点的投影符合点的投影规律
2、其他两个投影平行于相应的投影轴，并且 小于实长。
三、 投影面垂直线
(一)含义：垂直于投影面的直线称为投 影面垂直线
垂直于H面的直线称为铅垂线 垂直于V面的直线称为正垂线 垂直于W面的直线称为侧垂线
(二) 铅垂线的投影特性 （1）铅垂线
铅垂线的投影特 性
1、水平投影积聚为 一点a(b)
2、正面投影a’b’垂直 于ox轴，侧面投影 a”b”垂直于OYw轴， 且都反映实长。
b˝
a´
d´
c a
a˝ d˝
d b
AB和CD相交
c´
c˝
b´
b˝
a´
d´
d a
d˝ a˝
c b
AB和CD不相交
例3－8：已知三条直线A、B、C，作直线DE平行直线C，并与 直线A、B交于D、E点
e´ b´ d´
c´
a´
ad
c
e
b
三、两直线交叉
空间既不平行又不相交的两直线为交叉直线(异面直线)

点到垂足的距离为点到直线的距离。 已知CD为正垂线，则与之垂直的直线 [作图]过a’作b’c’的垂线，交点为d’； 为正平线，正平线又与AB垂直，则该 正平线在正面的投影应与a’b’垂直。 相应作ad；作AD直线的真长
b’ d’ a’ X O b d △y a c a f b e c d f’ b’
投影面平行线
●特征：在平行的投影面上的投影反映真长，与投影轴的夹角为
直线与另外两个投影面的倾角；另两个面的投影平行投影轴
●水平线
a’ b’ b” a”
●正平线
b’ b” a”
●侧平线
a’ b’ b β b” α a”
γ
a’ γ a β b α
a
b
a
Lab = LAB ab∧OX =β ab∧OYH =γ a’b’∥OX a”b”Байду номын сангаасOYW
b’ A0 a’ X a c C0 d’ c’ O X s’0 Δy b f’0 s f p’0 e p f’ O f” p’ s’
p”
s”
d
图解直线上的点（2） [例]已知直线AB通过原点，且 对V面的倾角β=30°，补全 直线AB的三面投影。
a’ Z
图解直线上的 点（2）
[例]已知直线CD的两面投影， 求作直线上两点E、F，使得 CE:ED=1:3；F为V、W的等 距点。 c”
两直线相交
e’ c’ b’ b’
e’ c’
X b’
g’ e’
d’ f’
d’ O
[例]过E点作水平线，与AB、CD 都相交，交点分别为G、F。
●两交叉直线
两交叉直线
交叉直线：既不平行又不相交的两条直线 投影特征：直线在某一面上投影的交点不是直线的交点，而是 两直线对该投影面上的重影点的投影。