波函数与原子轨道

波函数与原子轨道在量子力学中，波函数是描述微观粒子的数学函数，它包含了粒子的位置、动量和能量等信息。

而原子轨道则是描述电子在原子周围运动的概念。

波函数和原子轨道是量子力学中的重要概念，它们的理解对于我们理解原子结构和化学反应机制具有重要意义。

一、波函数的性质波函数通常用希腊字母Ψ表示，它是一个复数函数。

波函数的平方模的积分表示了粒子存在于空间中的概率密度。

波函数的性质包括：1. 归一化：波函数的平方模的积分等于1，表示粒子存在的概率为100%。

这是由于量子力学的粒子是离散的，不存在连续的状态。

2. 可观测量：波函数可以用来计算粒子的可观测量，如位置、动量和能量等。

这些可观测量的平均值可以通过对波函数进行操作得到。

3. 波粒二象性：波函数既可以表示粒子的波动性，也可以表示粒子的粒子性。

这是量子力学的基本原理之一，也是对经典物理学的革命性突破。

二、原子轨道的类型原子轨道是描述电子在原子周围运动的概念。

根据量子力学的理论，原子轨道可以分为不同的类型，包括s轨道、p轨道、d轨道和f轨道等。

1. s轨道：s轨道是最简单的一种原子轨道，它是球对称的。

s轨道只有一个能级，可以容纳最多两个电子。

2. p轨道：p轨道是具有两个节点的原子轨道，它有三个不同的方向：x、y和z轴。

p轨道一共有三个能级，每个能级可以容纳最多六个电子。

3. d轨道：d轨道是具有四个节点的原子轨道，它有五个不同的方向：x、y、z、xy和xz。

d轨道一共有五个能级，每个能级可以容纳最多十个电子。

4. f轨道：f轨道是具有六个节点的原子轨道，它有七个不同的方向：x、y、z、xy、xz、yz和xyz。

f轨道一共有七个能级，每个能级可以容纳最多十四个电子。

三、波函数与原子轨道的关系波函数和原子轨道之间存在着密切的关系。

波函数描述了粒子在空间中的行为，而原子轨道描述了电子在原子周围的运动。

波函数可以用来计算原子轨道的性质，如能级、形状和能量等。

波函数的形式取决于原子轨道的类型。

原子轨道原子轨道（Atomic orbital）是单电子薛定谔方程的合理解ψ（x，y，z)。

若用球坐标来描述这组解，即ψ（r，θ，φ)=R(r)·Y(θ，φ)，这里R(r)是与径向分布有关的函数，称为径向分布函数，用图形描述就是原子轨道的径向分布函数；Y(θ，φ)是与角度分布有关的函数，用图形描述就是角度分布函数。

1简介原子轨道（英语：atomic orbital），又称轨态，是以数学函数描述原子中电子似波行为[1][2]。

此波函数可用来计算在原子核外的特定空间中，找到原子中电子的机率，并指出电子在三维空间中的可能位置[1][3]。

“轨道”便是指在波函数界定下，电子在原子核外空间出现机率较大的区域。

具体而言，原子轨道是在环绕着一个原子的许多电子（电子云）中，个别电子可能的量子态，并以轨道波函数描述。

电子的原子与分子轨道，依照能阶排序现今普遍公认的原子结构是波耳氢原子模型：电子像行星，绕着原子核（太阳）运行。

然而，电子不能被视为形状固定的固体粒子，原子轨道也不像行星的椭圆形轨道。

更精确的比喻应是，大范围且形状特殊的“大气”（电子），分布于极小的星球（原子核）四周。

只有原子中存在唯一电子时，原子轨道才能精准符合“大气”的形状。

当原子中有越来越多电子时，电子越倾向均匀分布在原子核四周的空间体积中，因此“电子云”[4]越倾向分布在特定球形区域内（区域内电子出现机率较高）。

早在1904年，日本物理学家长冈半太郎首度发表电子以类似环绕轨道的方式在原子内运转的想法[5]。

1913年，丹麦物理学家尼尔斯·波耳提出理论，主张电子以固定的角动量环绕着体积极小的原子核运行[6]。

然而，一直到1926年、量子力学发展后，薛定谔方程式才解释了原子中的电子波动，定下关于新概念“轨道”的函数[1][7]。

由于这个新概念不同于古典物理学中的轨道想法，1932年美国化学家罗伯特·马利肯提出以“轨道”（orbital）取代“轨道”（orbit）一词[8]。

原子轨道的含义
原子轨道是描述电子在原子周围运动的概念，也是量子力学中的重要概念。

它可以用来描述电子在原子核周围的运动轨迹，每个原子轨道对应着不同的能量和几何结构。

原子轨道的概念最早由量子理论的奠基人之一，德国物理学家波尔提出。

他认为电子绕原子核运动时，只能在特定的轨道上运动，并且这些轨道对应着不同的能量。

这就是所谓的能级概念，也是原子轨道理论的基础。

原子轨道可以分为不同的类型，包括s轨道、p轨道、d轨道和f轨道等。

每个轨道都有不同的形状和空间分布，s轨道是球对称的，p 轨道是双球对称的，d轨道是复杂的四叶花状，f轨道则更为复杂。

这些轨道的形状和分布决定了电子在空间中的可能位置。

原子轨道的含义不仅仅是描述电子运动的几何结构，还可以通过波函数来描述电子的性质。

每个原子轨道都有一个波函数，用来描述
电子的概率密度。

概率密度表示了电子在轨道上的分布情况，即电子在轨道的某个位置被探测到的可能性。

由于原子轨道的存在，电子在原子中的运动不再像经典物理学中那样可以精确描述。

根据不确定性原理，我们无法同时确定电子的位置和动量。

因此，原子轨道的引入使得我们能够更好地理解电子的运动行为，并解释许多原子和分子的性质。

总的来说，原子轨道是描述电子在原子周围运动的概念，每个轨道对应着不同的能量和几何结构。

原子轨道的存在使得我们能够更好地理解电子的性质和行为。

通过研究原子轨道，我们可以深入探索原子和分子的结构，为化学、物理等领域的研究提供基础。

⑵.波函数和量子数因为原子轨道的能量是量子化的，因此可以通过一系列相关的量子数描述原子轨道（即波函数ψ）．ψ（ｘ，ｙ，ｚ）可变换为ψ（r, θ，φ），r与能级相关，而θ，φ与电子运动的角速度相关，因此，ψ可用量子数ｎ，Ｌ，ｍ来描述．ｎ：主量子数（能级），ｎ＝１，２，３，４，……∞，规定轨道能量；ｌ：角量子数（亚层），Ｌ＝０，１，２，３，……（ｎ－１），规定轨道图像；亚层符号：ｓ，ｐ，ｄ，ｆ，ｍ：磁量子数（轨道），ｍ＝０，±１，±２，±３，…±Ｌ，规定轨道方向；ｎ，Ｌ，ｍ之间的关系：ｎ决定Ｌ的数目，从而决定该能级亚层的数目ｎ＝１，Ｌ取一个值，即Ｌ＝０，（１ｓ亚层）ｎ＝２，Ｌ可取二个值，Ｌ＝０，（２ｓ亚层）Ｌ＝１,（２ｐ亚层）ｎ和Ｌ共同决定轨道的能量：ｎ的能量顺序：ｎ＝１<ｎ＝２<ｎ＝３<ｎ＝４<……Ｌ的能量顺序：Ｌ＝０<Ｌ＝１<Ｌ＝２<Ｌ＝３< Ｌ＝４<……即：ｎｓ<ｎｐｎｄ<ｎｆ<……Ｌ决定ｍ的数目，从而决定轨道的数目Ｌ＝０，ｍ取一个值，ｍ＝０（一个ｓ轨道）Ｌ＝１，ｍ取０,＋１,－１三个值（三个ｐ轨道）Ｌ＝２，ｍ取０，＋１，－１，＋２，－２五个值（五个ｄ轨道）若ｎ和Ｌ已确定，即能量已确定，不同的ｍ值只区分轨道在空间不同的伸展方向，不影响轨道的能量．例如上述三个ｐ轨道ｐx，ｐy，ｐz能量相同，五个ｄ轨道能量相同．ｎ，Ｌ，ｍ的组合可描述各种原子轨道．ｎ和Ｌ的组合可以确定能级和亚层，ｎ，Ｌ，ｍ的组合才能确定原子轨道例如：ｎ＝１，Ｌ＝０：１ｓ亚层ｎ＝１，Ｌ＝０，ｍ＝０：１ｓ轨道符号３ｐ用量子数表示为：ｎ＝３，Ｌ＝１符号３P X 用量子数表示为ｎ＝３，Ｌ＝１，ｍ＝０符号3P Y 用量子数表示为ｎ＝３，Ｌ＝１，ｍ＝＋1符号３P Z 用量子数表示为ｎ＝３, Ｌ＝１，ｍ＝－１处于原子轨道中的电子，其自旋有顺时针，反时针二个方向，可用自旋量子数ｍs 描述，ｍs 取值为：＋１／２或－１／２．故每一个轨道中最多能容纳二个电子，且自旋相反．处可容纳的电子总数为２ｎ２．一．二．基态原子核外电子的分布和元素的金属性和非金属性１．１．核外电子的分布式和价层电子构型⑴．⑴．核外电子分布原理：Ⅰ．能量最低原理：能级顺序（能级组）１ｓ < ２ｓ<２ｐ<３ｓ<３ｐ<４ｓ<３ｄ<４ｐ━━━━━━━━━━━━━━━━━━━<５ｓ<４ｄ<５ｐ< ６ｓ<４ｆ<５ｄ<６ｐ< ……━━━━━━━━━━━━━━━━━４ｓ<３ｄ，５ｓ<４ｄ，６ｓ<４ｆ……属于能级交错现象．Ⅱ．泡利不相容原理每个轨道最多容纳２个自旋相反的电子，每个原子中不可能存在四个量子数完全相同（运动状态完全相同）的二个电子．Ⅲ．洪特规则在同一亚层中，电子将尽可能单独占不同的等价轨道，且自旋平行．ｎｐ3(2).核外电子分布式，价电子构型及元素在周期表中的位置按能级组顺序排列电子按主量子数的顺序书写核外电子分布式例如：Ｎａ１ｓ２２ｓ２２ｐ６３ｓ１１１电子分布式为：１ｓ２２ｓ２２ｐ６３ｓ１Ｆｅ１ｓ２２ｓ２２ｐ６３ｓ２３ｐ６4ｓ２３ｄ６２６电子分布式为:１ｓ２２ｓ２２ｐ６３ｓ２３ｐ６３ｄ６４ｓ２Ｃｒ１ｓ２２ｓ２２ｐ６３ｓ２３ｐ６４ｓ１３ｄ５２４电子分布式为:１ｓ２２ｓ２２ｐ６３ｓ２３ｐ６３ｄ５４ｓ１(半充满稳定态)29Ｃｕ１ｓ２２ｓ２２ｐ６３ｓ２３ｐ６４ｓ１３ｄ１０电子分布式为：１ｓ２２ｓ２２ｐ６３ｓ２３ｐ６３ｄ１０４ｓ１(全充满稳定态)主族元素（Ａ），价电子构型：ｎｓ１→２，ｎｓ２ｎｐ１→６副族元素（Ｂ），价电子构型：（ｎ－１）ｄ１→１０ｎｓ１→２２．元素的金属性和非金属性及其递变规律从元素周期表中看出，元素分为金属元素和非金属元素，金属约占４／５，非金属１／５．金属原子容易失去电子变为阳离子，越容易失去电子，金属性越强；非金属原子容易得到电子变成阴离子，越容易得到电子，非金属性越强．金属元素分布于ｓ区（ⅠA，ⅡA）和ｐ区ⅢA，ⅣA的部分元素以及全部ｄ区（ⅢB──Ⅷ），ｄs区（ⅠB，ⅡB），ｆ区的元素．元素金属性非金属性的强弱和原子半径，核电荷数，价层电子数有关，可用电负性加以比较.电负性（Ｘ）是指元素原子与其他原子结合时吸引电子的能力．非金属元素电负性越大，非金属性越强，指定非金属性最强的氟（Ｆ）电负性Ｘ＝４．０，金属元素电负性越小，金属性越强，最活泼的金属铯（Ｃｓ）电负性才等于０．７．有效核电荷数增大，原子半径减小，电负性增大同一周期自左向右──────────────→金属性逐渐减弱，非金属性逐渐增强电子层数增加，原子半径增大，电负性减小同一族自上而下━━━━━━━━━━━━━━→金属性逐渐增强，非金属性逐渐减弱主族元素有效核电荷数，原子半径，电负性递变幅度较大，因此金属向非金属过渡明显；副族元素上述变化幅度较小，因此，金属性递变缓慢，镧系元素（希土金属）变化幅度更小，因此这些元素性质极其相似，以致于很难分离．§１．２共价键，分子的结构，分子间作用力基本要求：1．共价键的本质、特征、类型；2．杂化轨道的类型和分子空间几何构型的关系；3．共价键的极性和分子的极性的区别；4．分子间力（范德华力）和氢键对物质性质的影响：重点: 共价键的本质、特征、类型，分子的空间几何构型和极性；难点: 杂化轨道的类型和分子空间几何构型的关系；一．一．共价键，杂化轨道和分子的空间几何构型1.1.共价键：两个原子电负性相差不大（ΔＸ<１．７）时，通过共用电子对结合，形成共价键．共价键成键的条件是：成键原子双方必须具有未成对电子，且自旋相反．共价键的本质是：原子轨道的重迭；共价键的类型是：σ键和π键；例如Ｈ2中Ｈ－Ｈ共价单键形成时，二个１ｓ轨道重迭，二个自旋相反的未成对电子相互成对，形成σ键：↑↓↑↓１ｓ１１ｓ１（ｓ－ｓ）σ键共价单键即σ键，如ＨＣｌ中的Ｈ－Ｃｌ键，Ｈ２Ｏ中的Ｈ－Ｏ键，ＣＨ４中的Ｃ──Ｈ键，ＣＯ２中的Ｃ＝Ｏ键，Ｃ２Ｈ４中的Ｃ＝Ｃ键等共价双键中有一条σ键和一条π键，而共价三键中有一条σ键和二条π键．如: Ｎ2中的Ｎ≡Ｎ共价三键中包括有σ键和π键Ｎ的价电子层构型为２ｓ２２ｐ３Ｎ原子相互结合时，２ｐｘ─２ｐｘ形成σ键，２ｐｙ─２ｐｙ和２ｐｚ─２ｐｚ形成π键(正面重迭形成σ键)２ｐy１（或ｐz）２ｐy１（或ｐz）（ｐy－ｐy）π键（ｐz－ｐz）π键2.2.杂化轨道和分子的空间几何构型共价键形成共价分子．对于ＡＢx型共价分子有双原子分子，三原子分子，四原子分子，五原子分子……之分，其中，Ａ为中心原子，Ｂ为配位原子．它们分别有各自的空间几何构型，与中心原子价层轨道杂化以及所形成杂化轨道的空间几何构型有关．几种杂化轨道及其对应的空间几何构型：（１）．等性ｓｐ杂化和直线形对称Ｂｅ２ｐ（未杂化）2s 2p sp杂化轨道（二条sp杂化轨道互为１８０°夹角,直线形对称）( 2 ).等性s p2杂化和平面正三角形对称（三条sp2杂化轨道互为１２０°夹角，平面正三角形对称）（３）．等性ｓｐ３杂化和正四面体对称例如：ＣＨ4中，Ｃ为中心原子２ｓ２ｐ（四条sp3杂化轨道互为１０９°２８’夹角为正四面体对称,若CH3Cl,CH2Cl2,CHCl3为一般四面体）（４）．不等性ｓｐ３杂化和三角锥形，Ｖ字形等不对称空间构型例如：ＮＨ3中，Ｎ为中心原子，２ｓ２ｐ（三条互为１０７夹角，为三角锥形不对称结构）在Ｈ2Ｏ中，Ｏ为中心原子，２ｓ２ｐ不等性ｓｐ３杂化（二条互为１０４°夹角,为Ｖ字形不对称结构）在ＨＣｌ中,Cl为中心原子,3s 3p 不等性sp3杂化（为一字形）3.3.分子的极性：共价键的极性：共用电子对偏向电负性较大的原子，使共价键具有极性，如：Ｈ──────Ｃｌ分子的极性：分子中正，负电中心不重合，分子具有极性，是极性分子；正，负电中心重合，分子无极性，是非极性分子．如：ＨＣｌ为极性分子Ｈ2为非极性分子．对于多原子分子，凡形成空间对称（直线形，平面正三角形，正四面体等）的，由于分子中健的极性被抵消，成为非极性分子；如：ＣＯ2，ＢｅＣｌ2，Ｃ2Ｈ2，ＢＦ3，Ｃ2Ｈ4，ＣＨ4，ＣＣｌ4为非极性分子；空间不对称（ｖ字形，三角锥形等）的，分子中键的极性不能抵消，为极性分子．如：Ｈ2Ｏ，Ｈ2Ｓ，ＮＨ3，ＮＣｌ3,ＰＨ3为极性分子．一、排布原理1、泡利原理每一个原子轨道中，最多只能容纳2个自旋相反的电子。

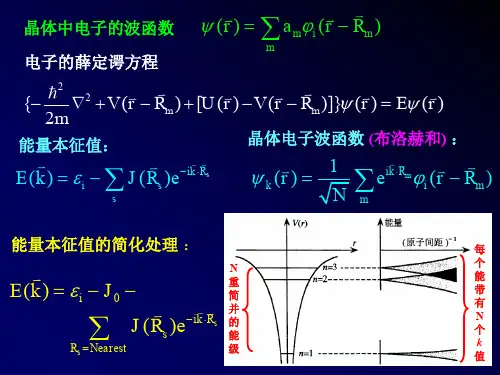
有机化合物的结构理论：1、原子轨道：用薛定谔方程描述电子的能量和运动状态，薛定谔方程的解即是描述电子状态的波函数，称为原子轨道，即能量为E的电子在相应能级轨道中出现的几率.一个原子有许多原子轨道。

有机化学中涉及的主要是1S,2S,2P,轨道。

S轨道的形状是以原子核为中心的圆球，轨道是两瓣互不接触的椭球体（纺锤形）.电子在整个空间出现的几率为1，在单位微体积内出现的几率为电子密度。

电子密度在空间不是均匀分布的，如果用一个小点表示电子密度的分布，则可以看到有的地方比较密集。

有的地方比较稀疏，象一团云雾，称为电子云。

原子轨道就是电子云相对比较密集的空间范围.A B CD E按照能量最低原则，互不相容原理和最多轨道规则，基态时电子尽量占据最低轨道，每个轨道只能容纳两个自旋相反的电子，电子尽可能多地占据原子轨道。

最外层为价层轨道，如2S,2P。

已有一对电子的称孤对电子，一个电子称单电子，没有电子称为空轨道。

各种轨道能量不同，在成键时，电子可以得到能量从低能级跃迁到高能量轨道。

1S22S22P2 ——→1S22S12P32、价键理论:价键理论认为，两个原子各有成单电子且自旋方向相反，则这两个单电子可以通过原子轨道重叠而配成一对形成共价键。

轨道重叠后，电子密度更多地集中在量重叠范围内，即两个原子核间，同时吸引着两个原子核，并且屏蔽两原子核间的斥力，于是两个原子结合在一起形成共价键。

轨道重叠或电子配对后，体系能量降低，所以是一种稳定的结合。

一个原子的单电子与另一个原子的单电子配对后，就不能与第三个电子配对，所以原子的成单电子个数就等于它所能形成的共价键数，即共价键的饱和性.形成共价键时轨道要实现最大重叠，原子轨道在看空间伸展的方向不同，电子云密度不同，要实现最大重叠，只有在原子轨道的一定方向上即电子云密度最大的地方重叠，所以共价键具有方向性.若一个原子的价层轨道有孤对电子，而另一个原子或离子有空的轨道，两个原子也可以成键而共用电子对，称为配位键。

分子轨道和原子轨道一、引言分子轨道和原子轨道是量子力学中的重要概念，它们是描述分子和原子中电子运动状态的数学函数。

本文将从以下几个方面介绍分子轨道和原子轨道的基本概念、性质以及应用。

二、原子轨道1. 原子轨道的定义原子轨道是描述单个原子中电子运动状态的数学函数。

根据量子力学理论，电子在原子内运动时，其位置和速度不能同时确定，因此需要用波函数来描述其运动状态。

2. 原子轨道的分类根据量子力学理论，每个电子都具有一个唯一的四量数(n,l,m,s)，其中n表示主量子数，l表示角量子数，m表示磁量子数，s表示自旋量子数。

主量子数决定了能级大小，角量子数决定了轨道形状，磁量子数决定了空间取向，自旋量子数则决定了自旋方向。

根据角量子数l的不同取值，可以将原子轨道分为s、p、d、f等不同类型。

s轨道具有球对称性，p轨道具有两个不同方向上的叶片形状，d和f则更加复杂。

3. 原子轨道的性质原子轨道具有一些重要的性质，例如：(1) 正交性：不同角量子数l的原子轨道在空间上是正交的，即它们之间不存在重叠。

(2) 归一化：原子轨道是归一化的，即其积分值等于1。

(3) 能级分裂：在外磁场作用下，原子轨道能级会发生分裂。

三、分子轨道1. 分子轨道的定义分子轨道是描述分子中电子运动状态的数学函数。

与原子轨道类似，分子轨道也需要用波函数来描述其运动状态。

2. 分子轨道的组成根据量子力学理论，当两个或多个原子之间发生化学键形成分子时，它们中的电子将会重新排布，并形成新的电荷分布。

因此，在分子中存在着新的能级和新的波函数——分子轨道。

根据不同类型化学键形成方式和电荷排布情况，可以将分子轨道分类为σ、π、δ等不同类型。

3. 分子轨道与原子轨道之间的关系在某些情况下，可以将一个由多个原子组成的复杂系统看作一个整体，从而得到分子轨道。

而分子轨道又可以看作是原子轨道的线性组合。

具体来说，分子轨道可以由不同原子的原子轨道线性组合而成，其中每个原子轨道的系数称为分子轨道系数。

原子轨道正负号和自旋方向
原子轨道本身没有正负极之分，但轨道波函数的正负是指波函数的符号，这本身没有物理意义。

当两个原子轨道重合时，如果一正一负，那么加起来绝对值必然会减小，因此电子出现的概率减小。

若均为正或者均为负则叠加，电子出现的概率增大。

至于自旋方向，电子在原子轨道上不仅做自转，而且公转。

公转由离心力产生，为了保证原子核的电势为0，则要抵消离心力，使两电子平衡，所以自转方向相反。

可以将两个电子看做平行两根导线，电流方向相反，所以相互吸引，抵消离心力。

此外，电子的自旋方向可能会因为特定的物理过程而发生改变。

例如，当电子从原子的一个部分跃迁到另一个部分时，其自旋方向可能会发生变化。

这种变化通常与电子与原子核或其他电子的相互作用有关。

总的来说，原子轨道的正负号和电子的自旋方向是两个独立的概念，它们之间没有直接的联系。

原子分子中的求解波函数波函数是量子力学中最为基础的概念之一。

通过求解波函数，可以得出粒子在空间中的分布情况和运动状态，进而探究物质的性质和相互作用。

本文将讨论原子分子中的求解波函数的相关问题。

一、波函数的定义波函数描述了一个物理系统中任意一个粒子的状态。

在一维情况下，波函数是一个关于坐标的复函数。

在三维情况下，波函数是一个关于空间坐标的复函数。

波函数的物理意义是通过对它的平方模长来得到概率密度，即某个粒子在空间中出现的几率。

波函数通常用Ψ来表示。

二、原子分子中的波函数求解原子和分子是量子力学中两个重要的研究对象。

在量子力学中，原子和分子的波函数要遵守薛定谔方程（Schrodinger Equation）。

薛定谔方程是量子力学中最为基础的方程之一，它描述了体系的时间演化和状态变化。

通过求解薛定谔方程，我们可以得到原子分子的所有波函数。

原子分子的薛定谔方程可以写成：HΨ = EΨ其中H表示哈密顿算子，Ψ是波函数，E是能量。

这个方程解决的是一个由一组分子核和若干个电子组成的量子系统。

在求解时需要使用量子化学中的很多方法，如基组扩展、变分法、Hartree-Fock方法等。

三、分子轨道分子轨道是描述分子中电子运动的波函数。

分子轨道可以看作是原子轨道的线性组合。

分子轨道具有一定的分子对称性，从而影响分子的性质和反应。

分子轨道被分为成键轨道和反键轨道两种，其中成键轨道代表电子在分子中准确地配对，反键轨道代表电子没有匹配。

成键轨道对于分子稳定非常重要，反键轨道对于分子的反应性质有很大的影响。

四、电子密度电子密度是波函数的平方模长，也就是描述电子在空间中出现概率的大小。

在分子中，电子密度可以通过计算分子轨道的平方模长来得到。

电子密度的大小决定了分子化学反应性质。

通过在不同的原子核之间测量电子密度，可以得到分子的形状和结构。

五、总结在量子力学的框架下，波函数是粒子在空间中的表现。

原子分子中的波函数求解是理解分子结构、性质和反应的关键。

6.2.4波函数的图形描述波函数的图形描述波函数ψ数学表达式复杂Ψ(r,θ,φ) =R(r) ·Y(θ,φ)径向部分角度部分Y(θ,φ)对θ,φ做图波函数(原子轨道)的角度分布图影响化学键的形成3π1),,(a r e a φθr ψ-=H 原子的1s 轨道 a 0:玻尔半径角度部分：4π1),(=φθY 球形对称分布xzy+p 轨道： )0(2=m p z θe a r πa ψa -r/p zcos 2141020302)(=l =1 , m = +1, 0, -1H 原子的 θπφ)Y(θcos 43=,θcos A =角度部分θθφθcos A cos π43),(==Y θ 0o 30o 60o 90o 120o 180o cos θ1 0.866 0.5 0 -0.5 -1 A0.866A 0.5A 0 -0.5A -AzY p 2x ,yz+ －30°60°θ◆从原点出发，引出一条与z 轴成θ角的线段◆令线段的长度等于Y◆连接所有线段的端点xyz-+yY2pxyz+-xyzzY2p+-正负号代表原子轨道角度部分取值的正负在z轴上出现极大值，称为p z轨道xY2p22d 3y x xyz- -++ xzd 3xy z-- + + yzd 3xyz-- + + xyd 3x yz- -+ + 2d 3z xyz ++（分别在xy,yz,xz 平面夹角为45度处伸展）原子轨道的角度分布图正负号极大值方向。