山东省胶州市2018届高考数学一轮复习专题函数及其性质课前学案(无答案)文
- 格式:doc
- 大小:299.00 KB
- 文档页数:3

绝对值不等式学习目标(1)含绝对值的不等式|x|〈a与|x|>a的解集(2)(2)|ax+b|≤c,|ax+b|≥c(c〉0)型不等式的解法:①|ax+b|≤c⇔-c≤ax+b≤c;②|ax+b|≥c⇔ax+b≥c或ax+b≤-c.(3)|x-a|+|x-b|≥c,|x-a|+|x-b|≤c(c>0)型不等式的解法:①利用绝对值不等式的几何意义求解.②利用零点分段法求解.③构造函数,利用函数的图象求解.重点①利用绝对值不等式的几何意义求解,体现了数形结合的思想;②利用“零点分段法”求解,体现了分类讨论的思想;1.绝对值不等式的解法(1)|ax+b|≤c(c〉0)和|ax+b|≥c(c〉0)型不等式的解法①|ax+b|≤c⇔②|ax+b|≥c⇔(2)|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c〉0)型不等式的解法法一:利用绝对值不等式的几何意义求解,体现了数形结合思想;法二:利用“零点分段法”求解,体现了分类讨论思想;法三:通过构造函数,利用函数的图象求解,体现了函数与方程的思想.2.绝对值三角不等式(1)定理1:如果a,b是实数,则|a+b|≤|a|+|b|,当且仅当时,等号成立.(2)定理2:如果a,b,c是实数,那么|a-c|≤|a-b|+|b-c|,当且仅当时,等号成立.课堂设计学生随堂手记错误!1.判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)若|x|>c的解集为R,则c≤0.()(2)不等式|x-1|+|x+2|<2的解集为∅。
()(3)对|a+b|≥|a|-|b|当且仅当a>b>0时等号成立.( )(4)对|a|-|b|≤|a-b|当且仅当|a|≥|b|时等号成立.( )(5)对|a-b|≤|a|+|b|当且仅当ab≤0时等号成立.( )答案:(1)×(2)√(3)×(4)×(5)√2.若关于x的不等式|x-a|<1的解集为(1,3),则实数a的值为________.解析:由|x-a|<1,则-1<x-a<1,∴a-1〈x<a+1,∴a=2。


绝对值不等式
学习目标(1)含绝对值的不等式|x|<a与|x|>a的解集
(2)(2)|ax+b|≤c,|ax+b|≥c(c>0)型不等式的解法:①|ax+b|≤c⇔-c≤ax +b≤c;
②|ax+b|≥c⇔ax+b≥c或ax+b≤-c.
(3)|x-a|+|x-b|≥c,|x-a|+|x-b|≤c(c〉0)型不等式的解法:
①利用绝对值不等式的几何意义求解.
②利用零点分段法求解.
③构造函数,利用函数的图象求解.
重点①利用绝对值不等式的几何意义求解,体现了数形结合的思想;
②利用“零点分段法"求解,体现了分类讨论的思想;
合作探究
考向一含绝对值不等式的解法
例1解下列不等式:
(1)|2x+1|-2|x-1|〉0。
(2)|x+3|-|2x-1|〈错误!+1。
课堂设计
学生随堂手记
解](1)法一:原不等式可化为|2x+1|〉2|x-1|,两边平方得4x2+4x+1>4(x2-2x+1),
|≤16
,证明绝对值不等式的三种主要方法
(1)利用绝对值的定义去掉绝对值符号,转化为普通不等式再证明.
(2)利用三角不等式||a |-|b ||≤|a ±b |≤|a |+|b |进行证明.
(3)转化为函数问题,利用数形结合进行证明.
★★【我要挑战】例3 设函数f (x )=x +|x -a |.
3 4,解得
+
1172
-+≤.117}2
-+≤。


第2讲 等差数列及其前n 项和1.等差数列的有关概念(1)定义 如果一个数列从第 项起,每一项与它的前一项的差都等于 ,那么这个数列就叫做等差数列.符号表示为 (n ∈N *,d 为常数).(2)等差中项数列a ,A ,b 成等差数列的充要条件是 ,其中A 叫做a ,b 的 .(3)等差数列的通项公式:an= ,可推广为an= 。
(4)等差数列的前n 项和公式:2.等差数列的性质 (1)(2)若k +l =m +n (k ,l ,m ,n ∈N *),则 (m,n ,p ,q ∈N*);m+n=2p,则 (m ,n,p ∈N*)。
(2)数列S m ,S 2m -S m ,S 3m -S 2m ,…构成等差数列(3)若{a n }的公差为d ,则{a 2n }也是等差数列,公差为2d .(4)若{b n }是等差数列,则{pa n +qb n }也是等差数列.(5)若等差数列{a n }的前n 项和为Sn ,则S2n-1=3.等差数列的四种判断方法(1)定义法:a n +1-a n =d (d 是常数)⇔{a n }是等差数列.(2)等差中项法:2a n +1=a n +a n +2(n ∈N *)⇔{a n }是等差数列.(3)通项公式法:a n =pn +q (p ,q 为常数)⇔{a n }是等差数列.(4)前n 项和公式法:S n =An 2+Bn (A 、B 为常数)⇔{a n }是等差数列.3.等差数列的通项公式及前n 项和公式与函数的关系(1)a n =a 1+(n —1)d 可化为a n =dn+a 1—d 的形式.当d ≠0时,a n 是关于n 的一次函数;当d>0时,数列为递增数列;当d 〈0时,数列为递减数列.(2) 当d ≠0时,它是关于n 的二次函数.数列{a n }是等差数列⇔Sn=An2+Bn(A,B 为常数)。
1.下列结论正确的打“√”,错误的打“×”.(1)若一个数列从第2项起,每一项与它的前一项的差都是常数,则这个数列是等差数列。
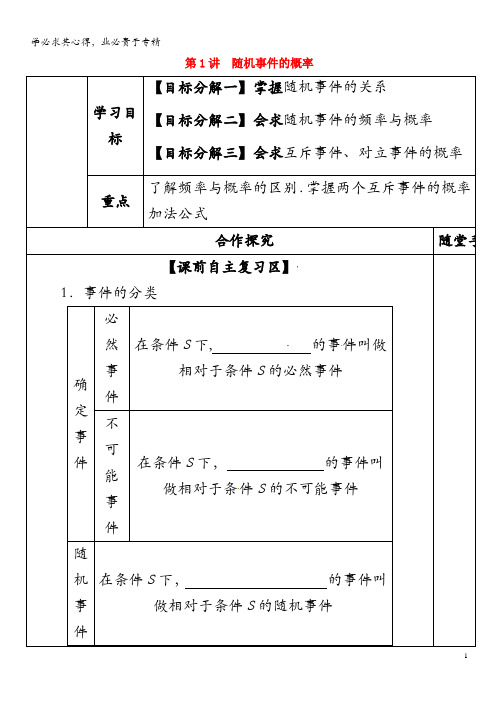
第1讲随机事件的概率学习目标【目标分解一】掌握随机事件的关系【目标分解二】会求随机事件的频率与概率【目标分解三】会求互斥事件、对立事件的概率重点了解频率与概率的区别.掌握两个互斥事件的概率加法公式合作探究随堂手记【课前自主复习区】1.事件的分类确定事件必然事件在条件S下, 的事件叫做相对于条件S的必然事件不可能事件在条件S下,的事件叫做相对于条件S的不可能事件随机事件在条件S下,的事件叫做相对于条件S的随机事件2.概率与频率(1)在相同的条件S下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数n A为事件A出现的频数,称事件A出现的比例f n(A)=为事件A出现的频率.(2)对于给定的随机事件A,由于事件A发生的频率f n(A)随着试验次数的增加稳定于概率,因此可以用来估计概率P(A).3.事件的关系与运算定义符号表示包含关系如果,这时称事件B包含事件A(或称事件A包含于事件B)B⊇A(或A⊆B)相等关系若,那么称事件A与事件B相等A=B并事件(和事件)若某事件发生,则称此事件为事件A与事件B的并事件(或和事件)A∪B(或A+B)交事件若某事件发A∩B(积事件)生,则称此事件为事件A与事件B的交事件(或积事件)(或AB)互斥事件若A∩B为事件,那么称事件A与事件B互斥A∩B=∅对立事件若A∩B为事件,A∪B为,那么称事件A与事件B互为对立事件A∩B=∅且A∪B=Ω4.概率的几个基本性质(1)概率的取值范围: .(2)必然事件的概率:P(A)=.(3)不可能事件的概率:P(A)=.(4)概率的加法公式如果事件A与事件B互斥,则P(A∪B)=.(5)对立事件的概率若事件A与事件B互为对立事件,则A∪B为必然事件.P (A∪B)=,P(A)=.【双基自测】1。
错误!总数为10万张的彩票,中奖率是错误!,下列说法中正确的是( )A.买1张一定不中奖B.买1 000张一定有一张中奖C.买2 000张一定中奖D.买2 000张不一定中奖2.甲:A1,A2是互斥事件;乙:A1,A2是对立事件,那么()A.甲是乙的充分但不必要条件B.甲是乙的必要但不充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件,也不是乙的必要条件3。
函数及其性质
1。
(2013·福州模拟)函数f(x)=错误!-x 1的定义域为________________.
2.已知函数f(x2-1)的定义域为[0,3],则函数y=f(x)的定义域为________.
3.函数y=错误!的定义域是( )
A.(-∞,2)B.(2,+∞)
C.(2,3)∪(3,+∞)D.(2,4)∪(4,+∞)
4.函数f(x)的定义域是[-2,4],则函数f(x2-3x)的定义域为________________.
5.已知函数f(x)是定义域为R的偶函数,且f(x+1)=-f(x),若f(x)在[-1,0]上是减函数,那么f(x)在[1,3]上是( )
A.增函数B.减函数C.先增后减的函数D.先减后增的函数
6.函数f (x)= 3-2x +错误!的奇偶性为( )
A .是奇函数
B .是偶函数
C .既不是奇函数,也不是偶函数.
D .既是奇函数,也是偶函数.
7.已知f (x )是定义在R 上的奇函数,且满足f (x +4)=f (x),则f(8)=( )
A .0
B .1
C .2
D .3
8。
下列函数中,即是偶数又在()0,+∞单调递增的函数是( )
A 。
3y x =
B.
1y x =+ C 。
21y x =-+ D.
2x
y -=
9。
函数()(1cos )sin f x x x =-在[,]ππ-的图像大致为( )
10。
函数()(2)()f x x ax b =-+为偶函数,且在(0,)+∞单调递增,则。
函数及其性质义域与值域【课前自主复习区】 【双基自测】1.(2013·福州模拟)函数f (x )=x +2x +1-x -1的定义域为________________.2.已知函数f(x 2-1)的定义域为[0,3],则函数y =f(x)的定义域为________.3.函数y =1log 2x -的定义域是( )A .(-∞,2)B .(2,+∞)C .(2,3) ∪(3,+∞)D .(2,4)∪(4,+∞)4.函数f(x)的定义域是[-2,4],则函数f(x 2-3x)的定义域为________________.5.已知函数f (x )是定义域为R 的偶函数,且f (x +1)=-f (x ),若f (x )在[-1,0]上是减函数,那么f (x )在[1,3]上是( )A .增函数B .减函数C .先增后减的函数D .先减后增的函数 6.函数f(x)= 3-2x +2x -3的奇偶性为( )A .是奇函数B .是偶函数C .既不是奇函数,也不是偶函数.D .既是奇函数,也是偶函数. 7.已知f(x)是定义在R 上的奇函数,且满足f(x +4)=f(x),则f(8)=( )A .0B .1C .2D .3 8.下列函数中,即是偶数又在()0,+∞单调递增的函数是( )A. 3y x =B. 1y x =+C. 21y x =-+D. 2xy -=9.函数()(2)()f x x ax b =-+为偶函数,且在(0,)+∞单调递增,则(2)0f x ->的解集为(A ){|22}x x x ><-或 (B ){|22}x x -<< (C ){|04}x x x <>或 (D ){|04}x x <<【课堂互动探究区】目标分解一:会求简单函数的定义域与值域【例1】1.函数y =-x12+x -x 2+(x -1)0的定义域是( )A .[-3,1)∪(1,2]B .(-3,2)C .(-3,1)∪(1,2)D .[-3,1)∪(1,2)2.已知函数f (x )的定义域为(-1,0),则函数f (2x +1)的定义域为( ) A .(-1,1) B .1(1,)2-- C .(-1,0) D .1(,1)2【例2】(1).求函数y =13+-x x 的值域: (2).求函数y =x -x 21-的值域:【我会做】1.函数y =log 0.5x -的定义域为( )A .3{|}4x x >B .3{|1}4x x <<C .3{|1}4x x <≤D .3{|1}4x x ≤≤2..函数y =12++x x x(x >0)的值域是________. 3..函数f (x )=)13(log 2+x 的值域为 ★【我能做对】1.已知函数f (x 2)的定义域是[-1,1],则f (x )的定义域为____ ____.=2 3 C.设定义在的奇函数f(m则是偶函数,则下列结论中正确的是。
第3讲等比数列及其前n项和学习目标:1.掌握等比数列的概念.2记住并会应用等比数列的通项公式与前n项和公式及其性质.3.能在具体的问题情境中识别数列的等比关系,并能用等比数列的有关知识解决相应的问题.1。
定义:2。
等比中项如果a、G、b成等比数列,那么G叫做a与b的等比中项.即:G是a与b的等比中项⇒3.等比数列的有关公式(1)通项公式:(2)前n项和公式:4.等比数列的性质已知数列{a n}是等比数列,S n是其前n项和.(m,n,p,q,r,k ∈N*)(1)若m+n=p+q=2r,则a m·a n=a p·a q=a错误!;(2)数列a m,a m+k,a m+2k,a m+3k,;(3)数列S m,S2m-S m,S3m-S2m,…仍是等比数列(此时{a n}的公比q≠-1).5.等比数列的三种判定方法(1)定义法:错误!=q(q是不为零的常数,n∈N*)⇔{a n}是等比数列.(2)通项公式法:a n=cq n-1(c、q均是不为零的常数,n∈N*)⇔{a n }是等比数列.(3)等比中项法:a 错误!=a n ·a n +2(a n ·a n +1·a n +2≠0,n ∈N *)⇔{a n }是等比数列.1。
下列结论正确的打“√",错误的打“×"。
(1)满足a n +1=q a n (n ∈N *,q 为常数)的数列{a n }为等比数列。
( )(2)G 为a ,b 的等比中项⇔2G =ab 。
( ) (3)等比数列中不存在数值为0的项。
( )(4)若{a n }为等比数列,bn=n n a a212+-,则数列{bn }也是等比数列。
( )(5)若数列{a n }为等比数列,则数列{ln a n }是等差数列.( ) 。
2。
由正数组成的等比数列{a n }满足a 3a 8=32,则log 2a 1+log 2a 2+…+log 2a 10=________.5。