VB递归算法
- 格式:ppt
- 大小:545.50 KB
- 文档页数:25



VB排列递归算法是一种用于处理组合问题的经典算法。
它可以帮助我们在给定一组数的情况下,找出其中任意个数的排列组合。
在使用中,我们可以输入随机n个数,然后利用VB排列递归算法输出m个数的组合。
今天,我们就来详细介绍一下VB排列递归算法的原理和操作步骤。
一、VB排列递归算法的原理1.1 递归算法递归算法是一种常见的解决问题的方法,它是指在函数的定义中使用函数本身的方法。
在VB排列递归算法中,递归的核心思想是将大问题分解为小问题,然后通过递归调用来解决小问题。
1.2 排列组合在数学中,排列和组合是常见的概念。
排列是指从给定的元素中按照一定顺序选取一定数量的元素,而组合是指从给定的元素中选取一定数量的元素,顺序无关紧要。
VB排列递归算法可以帮助我们高效地求解排列和组合的问题。
二、VB排列递归算法的操作步骤现在,我们来介绍一下使用VB排列递归算法求解组合问题的具体操作步骤。
2.1 输入随机n个数我们需要输入一组随机的n个数,这些数可以是整数、小数或者是字符串,根据实际需求而定。
2.2 设置输出m个数的组合接下来,我们需要设置输出m个数的组合,即从输入的n个数中选取m个数进行组合。
2.3 编写VB排列递归算法在VB编程环境中,我们需要编写排列递归算法的具体代码。
这部分代码主要涉及递归函数的定义和递归调用的实现,通过递归的方式来实现排列组合的求解。
2.4 执行VB排列递归算法一切准备就绪后,我们可以执行VB排列递归算法,得到输出m 个数的组合结果。
这些组合结果可以是打印输出、保存到文件或者在界面中展示,根据实际需求进行选择。
三、VB排列递归算法的应用实例现在,我们通过一个具体的示例来演示VB排列递归算法的应用过程。
3.1 示例说明假设我们有一组数字{1, 2, 3, 4, 5},我们需要从中选取3个数字进行组合,那么该怎么做呢?接下来,我们就通过VB排列递归算法来解决这个问题。
3.2 操作步骤我们需要输入数字{1, 2, 3, 4, 5},然后设置输出3个数字的组合。

VB常用算法总结大全VB(Visual Basic)是一种对初学者友好的编程语言,因其简单易学的特点而受到很多人的喜爱。
在VB中,算法是编程过程中非常重要的一部分,它们用来解决各种问题,从简单的数学计算到复杂的数据处理。
本文将总结一些常用的算法,帮助VB程序员更好地应用于实际项目中。
一、排序算法1.冒泡排序冒泡排序是一种简单的排序算法,它通过不断地交换相邻的元素来对数据进行排序。
它的基本思想是从列表的第一个元素开始,依次比较相邻的两个元素,如果顺序不正确,则交换它们的位置。
重复这个过程,直到整个列表都已经排序。
2.快速排序快速排序是一种高效的排序算法,它通过选择一个基准元素,将列表分为两部分,一部分小于基准元素,一部分大于基准元素。
然后对这两部分分别进行快速排序,最后将它们合并在一起。
3.插入排序插入排序是一种简单直观的排序算法,它将列表分为已排序和未排序两部分,每次选择未排序部分的第一个元素,并插入到已排序部分的适当位置。
重复这个过程,直到整个列表都已经排序。
二、查找算法1.顺序查找顺序查找是一种简单的查找算法,它从列表的第一个元素开始,依次比较每个元素,直到找到目标元素或者遍历完整个列表。
2.二分查找二分查找是一种高效的查找算法,它要求列表已经排序。
它通过比较目标元素与列表中间元素的大小关系来确定要的部分,并缩小范围。
重复这个过程,直到找到目标元素或者确定列表中没有目标元素。
三、图算法1.深度优先(DFS)深度优先是一种用于图遍历的算法,它从一个起始点开始,沿着一个路径尽可能深地访问节点,直到遇到一个没有未访问过的相邻节点为止。
然后回溯到前一个节点,寻找其他路径。
2.广度优先(BFS)广度优先也是一种用于图遍历的算法,它从一个起始点开始,依次访问所有与起始点相邻的节点,然后再依次访问这些节点的相邻节点,直到遍历完图中的所有节点。
四、动态规划动态规划是一种解决多阶段决策问题的方法,它将问题分解为若干个阶段,并定义状态和决策。
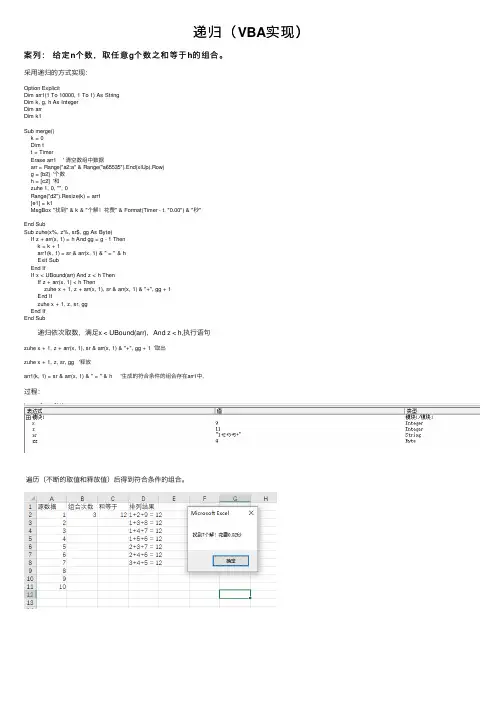
递归(VBA实现)案列:给定n个数,取任意g个数之和等于h的组合。
采⽤递归的⽅式实现:Option ExplicitDim arr1(1 To 10000, 1 To 1) As StringDim k, g, h As IntegerDim arrDim k1Sub merge()k = 0Dim tt = TimerErase arr1 ' 清空数组中数据arr = Range("a2:a" & Range("a65535").End(xlUp).Row)g = [b2] '个数h = [c2] '和zuhe 1, 0, "", 0Range("d2").Resize(k) = arr1[e1] = k1MsgBox "找到" & k & "个解!花费" & Format(Timer - t, "0.00") & "秒"End SubSub zuhe(x%, z%, sr$, gg As Byte)If z + arr(x, 1) = h And gg = g - 1 Thenk = k + 1arr1(k, 1) = sr & arr(x, 1) & " = " & hExit SubEnd IfIf x < UBound(arr) And z < h ThenIf z + arr(x, 1) < h Thenzuhe x + 1, z + arr(x, 1), sr & arr(x, 1) & "+", gg + 1End Ifzuhe x + 1, z, sr, ggEnd IfEnd Sub 递归依次取数,满⾜x < UBound(arr),And z < h,执⾏语句zuhe x + 1, z + arr(x, 1), sr & arr(x, 1) & "+", gg + 1 '取出zuhe x + 1, z, sr, gg '释放arr1(k, 1) = sr & arr(x, 1) & " = " & h '⽣成的符合条件的组合存在arr1中, 过程:遍历(不断的取值和释放值)后得到符合条件的组合。



2020年计算机等级VB语言核心知识点:递归过程
【导语】2020年计算机等级考试已经延期,目前这个阶段教材应该看完一遍,大家该强化一下自己对于教材考点的记忆,及时查漏补缺。
下面为您精心整理了2020年计算机等级VB语言核心知识点:递归过程,更多计算机等级考试的备考资讯,请关注为您实时更新的内容。
2020年计算机等级VB语言核心知识点:递归过程
1.递归的概念
通俗的讲,用自身的结构来描述自身就称为“递归”。
如对阶乘运算的定义就是递归的:
n!=n(n-1)!(n-1)!=(n-1)(n-2)!
2.递归子过程和递归函数
VB允许一个自定义子过程或函数过程在过程体的内部调用自己,这样的子过程或函数就叫递归子过程和递归函数。
递归过程包含了递推和回归两个过程。
构成递归的条件是:
(1)递归结束条件和结束时的值
(2)能用递归形式表示,并且递归向结束条件发展。
例:编制程序求fac(n)=n!的函数
3.注意事项
(1)递归算法设计简单,但消耗的上机时间和占据的内存空间比非递归大
(2)设计一个正确的递归过程或函数过程必须具备两点:
1)具备递归条件;
2)具备递归结束条件
(3)一般而言,递归函数过程对于计算阶乘、级数、指数运算有特殊效果。

vba 递归函数VBA 递归函数在VBA编程中,递归函数是一种非常有用的技巧。
递归函数是指在函数的定义中调用自身的过程。
它可以用于解决一些需要重复执行相同或类似操作的问题。
递归函数的使用可以使代码更加简洁、可读性更高,同时也能提高程序的效率。
递归函数的基本原理是将一个复杂的问题分解成一个或多个相同或相似的子问题,然后通过调用自身来解决这些子问题,最终得到问题的解。
在使用递归函数时,需要注意以下几点:1. 定义好递归函数的终止条件。
递归函数必须有一个终止条件,否则会导致无限循环,最终导致程序崩溃。
例如,计算一个数的阶乘,终止条件可以是当输入的数为0或1时,直接返回1。
2. 将原问题转化为一个或多个相同或相似的子问题。
递归函数的关键在于将原问题分解成更小的子问题,然后通过调用自身来解决这些子问题。
例如,计算一个数的阶乘,可以将问题转化为计算该数减一的阶乘,然后再乘以该数。
3. 保证递归函数的正确性。
在编写递归函数时,需要确保每次递归调用都能向着终止条件靠近,否则会导致递归深度过大,最终导致栈溢出。
同时,还需要确保递归函数能正确处理边界条件和异常情况。
下面以一个经典的例子来说明递归函数的使用:计算斐波那契数列。
斐波那契数列的定义如下:第一个数为0,第二个数为1,从第三个数开始,每个数都是前两个数之和。
根据这个定义,可以使用递归函数来计算斐波那契数列。
首先定义一个名为fib的递归函数,函数的输入参数为一个正整数n,表示要计算的斐波那契数列的第n个数。
终止条件为当n为1或2时,直接返回1。
对于其他情况,调用自身计算第n-1和n-2个数的和,然后返回结果。
以下是使用VBA编写的计算斐波那契数列的递归函数的示例代码:```vbaFunction fib(n As Integer) As IntegerIf n = 1 Or n = 2 Thenfib = 1Elsefib = fib(n - 1) + fib(n - 2)End IfEnd Function```使用该递归函数,可以方便地计算任意位置的斐波那契数。

《VB程序设计》第五章第五节递归过程第五节递归过程Sub过程可以是递归的,递归调用是指在过程中直接或间接地调用过程本身。
例如:Private Funion FNC(x As Integer)……Dim y As Integer,z As SingleZ=FNC(y As Integer)……End Function在函数FNC的过程中,要调用FNC函数本身。
递归是一种十分有用的程序设计技术,很多数学模型和算法设计本身就是递归的。
因此用递归过程描述它们比用非递归方法要简洁,可读性好,可理解性好。
从上例中看到,在函数FNC中调用函数FNC本身,似乎是无终止的自身调用,显然程序不应该有无终止的调用,而只应该出现有限次数的递归调用。
因此应该用If语句(条件语句)来控制终止的条件(称为边界条件或结束条件),只有在某一条件成立时才继续执行递归调用,否则不再继续。
若一个递归过程无边界条件,则是一个无穷的递归过程。
在编写递归程序时应考虑两个方面:这就是递归的形式和递归的结束条件。
如果没有递归的形式就不可能通过不断的递归来接近目标;如果没有递归的结束条件,递归就不会结束。
[例Ex_MuiNl]用递归的方法计算n!,即5!=4!*5,4!=3!*4,…。
根据阶乘得出表达式:n!=1*2*3*…*(n-1)*n,但这不是递归的形式,因此需要对它进行改造如下:n!=n*(n-1)!(n-1)!=(n-1)*(n-2)!……n=1时,n!=1于是得出下面的递归公式:递归的结束条件为:n=1时,n!=1。
程序代码如下,Muln函数过程就是递归求解函数:Private Function Muln(n As Integer) As IntegerIf n=0 or n=1 Then′结束条件n=0或n=lMuln=1ElseMuln=Muln(n-1)*nEnd ifEnd FunctionPrivate Sub Form_Click()Dim M As Integer, I As IntegerI=InputBox(″请输入一个正整数″)M=Muln((i)Print I; "!="; MEnd Sub递归求解的过程分成两个阶段:第一阶段是“回推”,第二阶段是“递推”。

[转载]快速排序法(VB和VBA版、递归法版)先从数据序列中选一个元素,并将序列中所有比该元素小的元素都放到它的右边或左边,再对左右两边分别用同样的方法处之直到每一个待处理的序列的长度为1, 处理结束。
在当前无序区R[1..H]中任取一个数据元素作为比较的"基准"(不妨记为X),用此基准将当前无序区划分为左右两个较小的无序区:R[1..I-1]和R[I+1..H],且左边的无序子区中数据元素均小于等于基准元素,右边的无序子区中数据元素均大于等于基准元素,而基准X则位于最终排序的位置上,即R[1..I-1]≤X.Key≤R[I+1..H](1≤I≤H),当R[1..I-1]和R[I+1..H]均非空时,分别对它们进行上述的划分过程,直至所有无序子区中的数据元素均已排序为止快速排序的基本思想是基于分治策略的。
对于输入的子序列L[p..r],如果规模足够小则直接进行排序(比如用前述的冒泡、选择、插入排序均可),否则分三步处理:分解(Divide):将待排序列L[p..r]划分为两个非空子序列L[p..q]和L[q+1..r],使L[p..q]中任一元素的值不大于L[q+1..r]中任一元素的值。
具体可通过这样的途径实现:在序列L[p..r]中选择数据元素L[q],经比较和移动后,L[q]将处于L[p..r]中间的适当位置,使得数据元素L[q]的值小于L[q+1..r]中任一元素的值。
递归求解(Conquer):通过递归调用快速排序算法,分别对L[p..q]和L[q+1..r]进行排序。
合并(Merge):由于对分解出的两个子序列的排序是就地进行的,所以在L[p..q]和L[q+1..r]都排好序后不需要执行任何计算L[p..r]就已排好序,即自然合并。
对于基数基本是取最左边一位、最中间一位或最后一位,后面的代码小Y按最中间那位做为基数,进行递归排序。
另外:小Y是非计算机专业的,有些坏毛病总是改不过来,习惯于把数组的最小的下标设置为“1”。
VB算法
一、解析法
解析法就是在分析具体问题的基础上,抽取出一个数学模型,这个数学模型能够用若干解析表达式表示出来,解决了这些表达式,问题也就得以解决。
例如:如果程火车以100千米/小时的速度从北京去上海(全程约1400千米),那么所需时间是1400/100=14小时。
数学、物理等学科中的许多问题都是用解析法解决的。
二、穷举法
穷举法也叫枚举法、列举法。
它将求解对象一一列举出来,然后逐一加以分析、处理,并验证结果是否满足给定的条件,穷举完所有对象,问题将最终得以解决。
常见问题:水仙花数问题鸡兔同笼问题百钱白鸡问题
三、递归算法
“从前有座山······”的故事反映了一个特征------自己调用自己。
如果一个函数在定义时,直接或间接地调用了自己,这种算法称为递归法
常见问题:兔子繁殖问题汉诺塔游戏四、冒泡算法
冒泡算法也叫“起泡法排序”,它通过与相邻元素进行比较和交换,逐步将一个无序序列排列成为一个有序序列。
例:将序列“4,1,2,5,3“的序列进行升序排序。
vb课程设计递归法应用一、教学目标本章节的教学目标是使学生掌握递归法的基本概念和应用,能够运用递归法解决实际问题。
具体目标如下:1.知识目标:学生能够理解递归法的定义、特点和应用场景;掌握递归法的两种形式:直接递归和间接递归;了解递归法在算法设计中的应用。
2.技能目标:学生能够运用递归法编写程序,解决实际问题,如计算阶乘、 Fibonacci数列等;能够分析递归算法的 time complexity。
3.情感态度价值观目标:学生通过学习递归法,培养逻辑思维能力、创新能力和问题解决能力,提高对计算机科学和编程的兴趣。
二、教学内容本章节的教学内容主要包括递归法的概念、特点和应用,以及递归法的两种形式。
具体安排如下:1.第一课时:介绍递归法的概念、特点和应用场景,让学生了解递归法的基本知识。
2.第二课时:讲解递归法的两种形式:直接递归和间接递归,并通过实例让学生掌握两种形式的用法。
3.第三课时:介绍递归法在算法设计中的应用,如计算阶乘、Fibonacci数列等,让学生学会运用递归法解决实际问题。
4.第四课时:分析递归算法的 time complexity,让学生了解递归法的时间复杂度。
三、教学方法为了激发学生的学习兴趣和主动性,本章节将采用以下教学方法:1.讲授法:教师通过讲解递归法的概念、特点和应用,引导学生掌握递归法的基本知识。
2.案例分析法:教师通过分析实际问题,引导学生学会运用递归法解决问题。
3.实验法:学生通过编写程序,动手实践,加深对递归法的理解和运用。
4.讨论法:学生分组讨论,分享学习心得和解决问题的经验,互相学习和提高。
四、教学资源为了支持教学内容和教学方法的实施,丰富学生的学习体验,我们将准备以下教学资源:1.教材:选取适合学生水平的编程教材,为学生提供理论知识的学习。
2.多媒体资料:制作PPT、视频等多媒体资料,帮助学生更好地理解和记忆递归法。
3.实验设备:提供计算机等实验设备,让学生能够动手实践,加深对递归法的理解和运用。