偏微分方程答案 整理第三、四、五章
- 格式:doc
- 大小:1002.50 KB
- 文档页数:34


偏微分方程教程答案【篇一:偏微分方程数值解习题解答案】class=txt>3页13页【篇二:3.1 常微分方程课后答案】方程dy=x+y2通过点(0,0)的第三次近似解; dx解:取?0(x)?0 12x 002xx11152x ?2(x)?y0??[x??1(x)]dx??[x?(x2)2]dx?x2?002220x1152x)]dx ?3(x)?y0??[x?(x2?0220115181x?x?x11= x2?2201604400dy 2 求方程=x-y2通过点(1,0)的第三次近似解;dx ?1(x)?y0??(x?y0)dx??xdx?x2x解:令?0(x)?012x 002xx12212152?(x)?y?[x??(x)]dx?[x?(x)]dx?x?x201?0?02220x1152x)]dx?3(x)?y0??[x?(x2?0220115181x?x?x11 =x2?2201604400则?1(x)?y0??(x?y0)dx??xdx?x2x3 题求初值问题:?dy??x2r:x??1,y?1 ?dx??y(?1)?0的解的存在区间,并求解第二次近似解,给出在解的存在空间的误差估计;b1解:因为 m=max{x2?y2}=4 则h=min(a,)= m41则解的存在区间为x?x0=x?(?1)=x?1? 4令 ?0(x)=0 ;11?1(x)=y0+?(x2?0)dx=x3+; 33x0x?2(x) 13xx4x7111312=y0+?[x?(x?)]dx=x---+ 3942186333?12x又 ?f(x,y)?2=l ?ym*l2311则:误差估计为:?2(x)??(x)?h= 24(2?1)2dy334 题讨论方程:?y在怎样的区域中满足解的存在唯一性定理的条件, dx21并求通过点(0,0)的一切解;?f(x,y)13解:因为=y在y?0上存在且连续; ?y2?23 而y3在y???0上连续 2dy33由 ?y有:y=(x+c)2 dx2131又因为y(0)=0 所以:y=x另外 y=0也是方程的解;?3?2故方程的解为:y=?x??0x?0 x?032或 y=0;6题证明格朗瓦耳不等式:设k为非负整数,f(t)和g(t)为区间??t??上的连续非负函数,且满足不等式:tf(t)?k+?f(s)g(s)ds,??t???t则有:f(t)?kexp(?g(s)ds),??t???t证明:令r(t)=?f(s)g(s)ds,则r(t)=f(?r(t)-r(t)g(t)= f(t)g(t)- r(t)g(t)?kg(t)r(t)- r(t)g(t)?kg(t);t两边同乘以exp(-?g(s)ds)则有:?tt r(t) exp(-?g(s)ds)-r(t)g(t) exp(-?g(s)ds)??t? kg(t) exp(-?g(s)ds)?两边从?到t积分:tttr(t) exp(-?g(s)ds)?-?kg(s)dsexp(-?g(r)dr)ds???tt即 r(t) ??kg(s)ds exp(-?g(r)dr)ds?stt又 f(t) ?1?k+r(t) ?k+k?g(s)exp(-?g(r)dr)ds?sts?k(1-1+ exp(-?g(r)dr)=k exp(?g(r)dr)stt即 f(t) ?k?g(r)dr;?7题假设函数f(x,y)于(x0,y0)的领域内是y的不增函数,试证方程dy= f(x,y)满足条件y(x0)= y0的解于x? x0一侧最多只有一个解;dx证明:假设满足条件y(x0)= y0的解于x? x0一侧有两个?(x),?(x)则满足:x?(x)= y0+?f(x,?(x))dxx0x?(x)= y0+?f(x,?(x))dxx0不妨假设?(x)??(x),则?(x)- ?(x)?0xx而?(x)- ?(x)= ?f(x,?(x))dx-?f(x,?(x))dxx0x0x=?[f(x,?(x))?f(x,?(x))dxx0又因为 f(x,y)在(x0,y0)的领域内是y的增函数,则:f(x, ?(x))-f(x, ?(x))?0x则?(x)- ?(x)= ?[f(x,?(x))?f(x,?(x))dx?0x0则?(x)- ?(x)?0所以 ?(x)- ?(x)=0,即 ?(x)= ?(x) 则原命题方程满足条件y(x0)= y0的解于x? x0一侧最多只有一个解;【篇三:同济第五版高数习题答案】试说出下列各微分方程的阶数:(1)x(y′)?2yy′+x=0;解一阶.(2)xy′?xy′+y=0;解一阶.(3)xy′′′+2y′+xy=0;解三阶.(4)(7x?6y)dx+(x+y)dy=0;解一阶.(5)解二阶.;222(6) .解一阶.2. 指出下列各题中的函数是否为所给微分方程的解:(1)xy′=2y, y=5x;解y′=10x.22 因为xy′=10x=2(5x)=2y, 所以y=5x是所给微分方程的解.(2)y′+y=0, y=3sin x?4cos x;解y′=3cos x+4sin x.因为y′+y=3cos x+4sin x+3sin x?4cos x=7sin x?cos x≠0,所以y=3sin x?4cos x不是所给微分方程的解.(3)y′′?2y′+y=0, y=xe;x2xxxx2x22 解y′=2xe+xe, y′′=2e+2xe+2xe+xe=2e+4xe+xe . 因为y′′?2y′+y=2e+4xe+xe?2(2xe+xe)+xe=2e≠0,所以y=xe不是所给微分方程的解.12122x2xx2x2xxxx2xxx2x解 , .因为=0,所以是所给微分方程的解.3. 在下列各题中, 验证所给二元方程所确定的函数为所给微分方程的解:(1)(x?2y)y′=2x?y, x?xy+y=c;解将x?xy+y=c的两边对x求导得2x?y?xy′+2y y′=0,即(x?2y)y′=2x?y,所以由x?xy+y=c所确定的函数是所给微分方程的解.(2)(xy?x)y′′+xy′+yy′?2y′=0, y=ln(xy).解将y=ln(xy)的两边对x求导得再次求导得, 即 .2222222.注意到由可得 , 所以从而(xy?x)y′′+xy′+yy′?2y′=0,即由y=ln(xy)所确定的函数是所给微分方程的解.4. 在下列各题中, 确定函数关系式中所含的参数, 使函数满足所给的初始条件:(1)x?y=c, y|=5;x=0222 ,解由y|=0得0?5=c, c=?25, 故x?y=?25.x=012222 (2)y=(c+cx)e, y|=0, y′|=1;解y′=ce+2(c+cx)e. 21222xx=02x x=02x由y|=0, y′|=1得 x=0x=0,解y′=ccos(x?c).12, 即,解之得c=1, 1, 故 , 即y=?cos x .5. 写出由下列条件确定的曲线所满足的微分方程:(1)曲线在点(x, y)处的切线的斜率等于该点横坐标的平方; 解设曲线为y=y(x), 则曲线上点(x, y)处的切线斜率为y′, 由条件y′=x, 这便是所求微分方程.(2)曲线上点p(x, y)处的法线与x轴的交点为q, 且线段pq被y轴平分.解设曲线为y=y(x), 则曲线上点p(x, y)处的法线斜率为 , 由条件第pq中点的横坐标为0, 所以q点的坐标为(?x, 0), 从而有, 即yy′+2x=0.6. 用微分方程表示一物理命题: 某种气体的气压p对于温度t的变化率与气压成正比, 所温度的平方成反比.解, 其中k为比例系数.习题12?111. 试用幂级数求下列各微分方程的解:(1)y′?xy?x=1;解设方程的解为, 代入方程得,即 .可见a?1=0, 2a?a?1=0, (n+2)a1202n+2?a=0(n=1, 2, ? ? ?),n 于是,,, , , ? ? ?. , ? ? ? ,所以,即原方程的通解为 .(2)y′′+xy′+y=0;解设方程的解为, 代入方程得,即 ,于是, , ??, , , ? ? ?.所以,即原方程的通解为.(3)xy′′?(x+m)y′+my=0(m为自然数);解设方程的解为, 代入方程得,?即 .可见(a?a)m=0, (n?m)[(n+1)a01 n+1?a]=0 (n≠m),n于是a=a, , .01所以,即原方程的通解为(其中c1, c2为任意常数).(4)(1?x)y′=x2?y;解设方程的解为, 代入方程得,即可见a1+a0=0, 2a2=0, 3a3?a2?1=0, (n+1)an+1?(n?1)a n=0(n≥3),于是a1=?a0, a2=0, , (n≥4).因此原方程的通解为(c=a(5)(x+1)y′=x20为任意常数). . ?2x+y..。

偏微分方程(周蜀林)
习题参考解答补充Writer:Dreaming Rainbow 本人仅上传至百度文库,其它人或其它地方发布的均为盗版!
关于剩下十个题的一些说明
3.16按提示,先将ϕ作周期为2的偶延拓得ϕ~
,之后作为热方程初值求解得u ,然后证明在0+→t 时,()t x u ,一致收敛于()x ϕ~(证明需用到ϕ~
的一致连续性)。
这些都很顺利,但
是到用多项式逼近K 的时候就不知道怎么办了......
3.22首先说边界条件正确的是书后的提示(正文缺负号)。
当你把所有式子都代入3.19式就会发现你根本不知道怎么解()t g ......3.23、3.24数学分析好的人进[byebye]。
4.12、4.13Fourier 变换法最难的就是逆变换,你可以去查从来没有逆变换()t a λcos 的!网上确实有文章用Fourier 变换求二维三维波动方程,不过我赌你看不懂。
4.36自古多元不好做,教科书都是避嫌不写。
4.48目测需要参考定理4.8过程,不容易。
4.49、4.50看到广义解基本就可以跳过了,想做的自己看吧。

2024年考研数学偏微分方程题目详解与答案在2024年的考研数学试卷中,偏微分方程题目一直是考生们关注和备考的重点。
本文将详细解析2024年考研数学偏微分方程题目,并提供详细的解答和答案。
一、第一题题目描述:给定二阶常系数线性偏微分方程 $\frac{{\delta^2u}}{{\delta x^2}} + c\frac{{\delta u}}{{\delta t}} + ku = f(x, t)$,其中 $u = u(x, t)$ 为未知函数,$c, k$ 为常数,$f(x, t)$ 为已知连续函数。
要求求解此偏微分方程。
解析:根据题目所给的偏微分方程可知,我们需要求解二阶常系数线性偏微分方程。
此类方程的典型特点是对时间 $t$ 的导数项和对空间$x$ 的二阶导数项。
我们可以采用特征线法来求解此类方程。
首先,我们设方程的通解形式为 $u(x, t) = X(x)T(t)$,其中$X(x)$ 和 $T(t)$ 分别是 $x$ 和 $t$ 的函数。
将通解带入方程中得到:$\frac{{X''}}{{X}} + c\frac{{T'}}{{T}} + k = \frac{{f(x, t)}}{{XT}}$由于方程的左侧只与 $x$ 有关,右侧只与 $t$ 有关,故两侧等于某个常数 $-\lambda$。
得到两个常微分方程:$X'' + \lambda X = 0$ 和 $T' + \left(c -\lambda\right) T = 0$对于方程 $X'' + \lambda X = 0$,根据 $\lambda$ 的值分为三种情况讨论:1. 当 $\lambda > 0$ 时,方程的通解为 $X(x) = A\cos(\sqrt{\lambda}x) + B\sin(\sqrt{\lambda}x)$。
2. 当 $\lambda = 0$ 时,方程的通解为 $X(x) = Ax + B$。

L试讨论逼近对蘇程詈+若。
的差分沁1)2)q1 二:行口匚1)解:设点为(X ? ,/曲)屮则町=讥心厶)=班勺厶+J + °(工心)(Y )+0(F ).ot所以截断误差为:3E=丄 ------ + ---- 「 T h 啰_喟+竺护一 o (F )T= 0(T + 力”2)解:设点为:(X y ,/林1 ) 3则町=讥勺,_)=以E ,_+1)+ (Y ) +o (巧卩 ot “;:;=班心+1 厶+i )=叽厶+i )+滋( h )+ * 臥工心)(为 2)+o ox (X)d心;=班心亠心)=班心,/+1)+敕:;D (一力)+ 3 役;D(血 2)+0(亥2)«截断误差为:2舟A 1 ” E= ------------ + ------------ — (―+ _) T h dt dx叭:=班%厶+i )+敗?心)(_勿+0 @2)〜dx-(史+空八dt dx 呼1_吋】+竺丛Q —O (X )-(叱 3 +dtdx 22・试用积分插值法推导知铁。
逼近的差分裕式班勺厶叙)一班勺,乩i)+ ——-——£)dtTq2 “-” *\ | (— 4- —)dxdt = | (un t 4- un x)ds = 0* dt & \得-U] /J+U2 r+x^ A-u4 r = 0+JE (j-l? n)F (j,n)G (j^n+l)H (j-l,n+l)^% ~ 的=旳=竹“4 = W/-lMf MTh=h T-T-ll"h + LL r H + ll:4h —LL:N =Op第二章第三章第四章第五章第六章P781.如果①'(0)二0,则称工。
是』(0)的驻点(或稳定:点)-设矩阵A对称(不必正定),求证忑是』(工)的驻点.的充要条件是1心是方程加二&的解B 42・ 试用积分插值法推导知铁。
逼近的差分裕式证: 充分性:①⑻二J 缶)+ 乂(加° -b t ^+—(Ax r x)①'(Ji) = (Ax c - A, x) + A{Ax r x) aEff))S 宀沪若①0)二Q,即(山° 一氛对=0 心怎宀A X Q -h = ()目卩 Ax-b^则帀是方程Ax^b 的解卩 必要性*若心是芳程A^ = b^\解则 Ax a —h - 0 (J 4X 0 — Z?,x) = 0+^◎ (0)=(吐命-b t x) - 0+J所以町是』0)的驻点dpg%3:证明非齐次两点边值间题心現(&)二 e it (E)二 Qu与T 7面的变分间题等价:求血EH 】,认@) = G 使 J(w t ) = min J(y)其中心SiuHU (2)-d』(#) =壬仗站)-(7» —芒⑹戲(D) +而久込叭如(2.13)(提示;先把边值条件齐衩化)+d dxO 字)+梓二/ ax13页证明:令 = w(x) + v(x)其中 w(x) = Q + (x-a)0 w(a) = a yv @) = “v(a) = 0 v(^>) = 0®所以2S = 瞥+qu = j DX DX Pd r /w 血、《, 乂 、 f"丁〔P(T + :F)]+Q(W + V )" ax dx ax* 丫 d z dv. 产 / d dw 、 豪 令 = - — O —) +(?v = /-(- —^> — +^w) = y;^ ax ax dx ax 所以(1)的等价的形式2厶” =一?0 字)= 卩ax axu(a) = a u\b) = 0a其中久=/-(-£■去字+0W )"ax ax 则由定理22知,讥是辺值间题(2)的解的充要条件是 且满定变分方程"ogf)-C/i 小 0 Vve^Pr (Zv> 一 /j )tdx + p @»: (b)f @) ① W = J(u) = J(u.+^)^— a (u^ + 兔,以.+ 无)一(/,功・ +加)[以・(E )+加@)] 2 □2=J(认)+ N[a@・,f)-(/,£)-+乙agd-Qfm 沁卜• Q dx dx 「(加•一/)加x +卩@加:(砂@)-卩@)戊@) Ja(3) => (4)所以可证得• 3必要性:若如 是边值间题(1)的解。

第一章. 波动方程§1 方程的导出。
定解条件2.在杆纵向振动时,假设(1)端点固定,(2)端点自由,(3)端点固定在弹性支承上,试分别导出这三种情况下所对应的边界条件。
解:(1)杆的两端被固定在l x x ==,0两点则相应的边界条件为 .0),(,0),0(==t l u t u(2)若l x =为自由端,则杆在l x =的张力x ux E t l T ∂∂=)(),(|lx =等于零,因此相应的边界条件为x u∂∂|lx ==0 同理,若0=x 为自由端,则相应的边界条件为xu∂∂∣00==x (3)若l x =端固定在弹性支承上,而弹性支承固定于某点,且该点离开原来位置的偏移由函数)(t v 给出,则在l x =端支承的伸长为)(),(t v t l u -。
由虎克定律有x uE∂∂∣)](),([t v t l u k lx --== 其中k 为支承的刚度系数。
由此得边界条件)(u xuσ+∂∂∣)(t f l x == 其中E k =σ特别地,若支承固定于一定点上,则,0)(=t v 得边界条件)(u xuσ+∂∂∣0==l x 。
同理,若0=x 端固定在弹性支承上,则得边界条件x uE∂∂∣)](),0([0t v t u k x -== 即 )(u xuσ-∂∂∣).(0t f x -= 3. 试证:圆锥形枢轴的纵振动方程为 2222)1(])1[(t u h x x u h x x E ∂∂-=∂∂-∂∂ρ 其中h 为圆锥的高(如图1)证:如图,不妨设枢轴底面的半径为1,则x 点处截面的半径l 为:hx l -=1 所以截面积2)1()(hx x s -=π。
利用第1题,得])1([)1()(2222xuh x E x t u h x x ∂∂-∂∂=∂∂-ππρ 若E x E =)(为常量,则得2222)1(])1[(tuh x x u h x x E ∂∂-=∂∂-∂∂ρ §2 达朗贝尔公式、 波的传抪1. 证明方程()常数011122222 h t uh x a x u h x x ∂∂⎪⎭⎫ ⎝⎛-=⎥⎥⎦⎤⎢⎢⎣⎡∂∂⎪⎭⎫ ⎝⎛-∂∂ 的通解可以写成()()xh at x G at x F u -++-=其中F,G 为任意的单变量可微函数,并由此求解它的初值问题:()().,:0x tux u t ψ=∂∂==ϕ 解:令()v u x h =-则()()()⎪⎭⎫⎝⎛∂∂+-=∂∂-∂∂+=∂∂-x v u x h xu x h xv u xu x h 2,))(()()()()[(2222xv u x h x u x h x u x h x v u x u x h x ∂∂+-=∂∂-+∂∂-+∂∂+-=∂∂-∂∂又 ()2222tv t u x h ∂∂=∂∂-代入原方程,得()()222221tv x h a x v x h ∂∂-=∂∂-即 222221t v a x v ∂∂=∂∂ 由波动方程通解表达式得()()()at x G at x F t x v ++-=,所以 ()()()x h at x G at x F u -++-=为原方程的通解。


微积分上册 一元函数微积分与无穷级数第2章 极限与连续2.1 数列的极限1.对于数列n x ,若a x k →2(∞→k ),a x k →+12(∞→k ),证明:a x n → (∞→n ). 证. 0>∀ε, a x k →2 (∞→k ), Z K ∈∃∴1, 只要122K k >, 就有ε<-a x k 2; 又因a x k →+12(∞→k ), Z K ∈∃∴2, 只要12122+>+K k , 就有ε<-+a x k 12. 取{}12,2m ax 21+=K K N , 只要N n >, 就有ε<-a x n , 因此有a x n → (∞→n ). 2.若a x n n =∞→lim ,证明||||lim a x n n =∞→,并举反例说明反之不一定成立.证明: a x n n =∞→lim ,由定义有:N ∃>∀,0ε,当N n >时恒有ε<-||a x n又 ε<-≤-||||||a x a x n n对上述同样的ε和N ,当N n >时,都有ε<-||||a x n 成立 ∴ ||||lim a x n n =∞→反之,不一定成立.如取 ,2,1,)1(=-=n x nn显然 1||lim =∞→n n x ,但n n x ∞→lim 不存在.2.2 函数的极限1. 用极限定义证明:函数()x f 当0x x →时极限存在的充要条件是左、右极限各自存在且相等.证: 必要性. 若()A x f x x =→0lim , 0>∀ε, 0>∃δ, 当δ<-<00x x 时, 就有()ε<-A x f . 因而, 当δ<-<00x x 时, 有()ε<-A x f , 所以()A x f x x =+→0lim ; 同时当δ<-<x x 00时, 有()ε<-A x f , 所以()A x f x x =-→0lim .充分性. 若()A x f x x =+→0lim ,()A x f x x =-→0lim . 0>∀ε, 01>∃δ, 当100δ<-<x x 时, 就有()ε<-A x f , 也02>∃δ, 当200δ<-<x x 时, 有()ε<-A x f . 取{}21,m in δδδ=,则当δ<-<00x x 时, 就有()ε<-A x f . 所以()A x f x x =→0lim .2.写出下列极限的精确定义:(1)A x f x x =+→)(lim 0,(2)A x f x =-∞→)(lim ,(3)+∞=+→)(lim 0x f x x ,(4)-∞=+∞→)(lim x f x ,(5)A x f x =+∞→)(lim .解:(1)设R x U f →)(:0是一个函数,如果存在一个常数R A ∈,满足关系:0,0>∃>∀δε,使得当δ<-<00x x 时,恒有ε<-|)(|A x f ,则称A 是)(x f 当+→0x x 时的极限,记作A x f x x =+→)(lim 0或 )()(0+→=x x A x f . (2)设R f D f →)(:是一函数,其中0,),,()(>>--∞⊃αααR f D .若存在常数R A ∈,满足关系:0)(,0>∈∃>∀R X ε,使得当X x -<时,恒有ε<-|)(|A x f 成立,则称A 是)(x f 当-∞→x 时的极限,记作:A x f x =-∞→)(lim 或 A x f =)()(-∞→x .(3)设R x U f →)(:0是任一函数,若0>∀M ,0>∃δ,使得当δ<-<00x x 时,恒有M x f >)(,则称当+→0x x 时)(x f 的极限为正无穷大,记作+∞=+→)(lim 0x f x x 或 +∞=)(x f )(0+→x x . (4)设R f D f →)(:是一函数,其中R f D ∈>+∞⊃ααα,0),,()(,若存在常数R A ∈,满足关系:0>∀M ,0)(>∈∃R X ,使得当X x >时,恒有M x f -<)(则称当+∞→x 时)(x f 的极限为负无穷大,记作:-∞=+∞→)(lim x f x 或 -∞=)(x f )(+∞→x .(5)设R f D f →)(:是一函数,其中R f D ∈>+∞⊃ααα,0),,()(,若存在常数R A ∈,满足关系:0,0>∃>∀X ε,使得当X x >时,恒有ε<-|)(|A x f 成立,则称A是)(x f 当+∞→x 时的极限,记作:A x f x =+∞→)(lim 或 A x f =)()(+∞→x .2.3 极限的运算法则1.求∑=∞→+⋯++Nn N n 1211lim. 解. ()()⎪⎭⎫ ⎝⎛+-=+=+=+⋯++111212211211n n n n n n n⎪⎭⎫ ⎝⎛+-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+⋯++∑=1112111312121122111N N N n Nn 21112lim 211lim1=⎪⎭⎫ ⎝⎛+-=+⋯++∴∞→=∞→∑N nN Nn N 2.求xe e xxx 1arctan11lim110-+→. 解. +∞=+→x x e 10lim , 0lim 10=-→xx e,,21arctan lim 11lim 1arctan11lim 0110110π=-+=-++++→--→→x ee x e e x xxx xxx ,21arctan lim 11lim 1arctan11lim 0110110π=-+=-+---→→→x e e x e e x x xx x x x 21arctan 11lim 110π=-+∴→x e e x xx3.设)(lim 1x f x →存在,)(lim 2)(12x f x x x f x →+=,求)(x f . 解:设 )(lim 1x f x →=A ,则A x x x f ⋅+=2)(2再求极限:A A A x x x f x x =+=⋅+=→→21)2(lim )(lim 211⇒ 1-=A∴ x x xA x x f 22)(22-=+=.4.确定a ,b ,c ,使 0)1(3)1()1(lim 2221=-+-+-+-→x x c x b x a x 成立.解:依题意,所给函数极限存在且 0)1(lim 21=-→x x∴ 0]3)1()1([lim 221=+-+-+-→x c x b x a x ⇒ 2=c∴ 上式左边=])32)(1(11[lim ))1(321(lim 21221++-+--+=-+-+-+→→x x x x b a x x x b a x x])32)(1(1)32([lim 221++---+++=→x x x x b a x同理有 0]1)32([lim 21=--++→x x b x ⇒ 21=b ∴ 163)23)(1(8)1(3lim )32)(1(1)32(21lim221221=++---=++---++-=→→x x x x x x xx a x x 故 2,21,163===c b a 为所求.2.4 极限存在准则1. 设1x =10,n n x x +=+61,( ,2,1=n ).试证数列{n x }的极限存在,并求此极限. 证: 由101=x , 4612=+=x x , 知21x x >. 假设1+>k k x x , 则有21166+++=+>+=k k k k x x x x . 由数学归纳法知, 对一切正整数n , 有1+>n n x x ,即数列{n x }单调减少. 又显然, () ,2,10=>n x n , 即{n x }有界. 故n n x ∞→lim 存在.令a x n n =∞→lim , 对n n x x +=+61两边取极限得a a +=6, 从而有062=--a a ,,3=∴a 或2-=a , 但0,0≥∴>a x n , 故3lim =∞→n n x2.证明数列 nn n x x x x ++=<<+3)1(3,3011收敛,并求其极限.证明:利用准则II ,单调有界必有极限来证明.∴301<<x ,由递推公式33312131213213)1(30111112=++<++=++=++=<x x x x x x∴ 302<<x 同理可证:30<<n x 有界又 03)3)(3(333)1(311112111112>++-=+-=-++=-x x x x x x x x x x∴ 12x x > 同理 23x x > ,… ,1->n n x x ∴数列 }{n x 单调递增,由准则II n n x ∞→lim 存在,设为A ,由递推公式有:AA A ++=3)1(3 ⇒ 3±=A (舍去负数)∴ 3lim =∞→n n x .3.设}{n x 为一单调增加的数列,若它有一个子列收敛于a ,证明a x n n =∞→lim .证明:设}{k n x 为}{n x 的一子列,则}{k n x 也为一单调增加的数列,且a x k k n n =∞→lim对于1=ε,N ∃,当N n >时有1||<-a x k n 从而||1||||||||a a a x a a x x k k k n n n +<+-≤+-=取|}|1|,|,|,max {|1a x x M N n n += ,对一切k n 都有 M x k n ≤|| 有界.由子列有界,且原数列}{n x 又为一单调增加的数列,所以,对一切n 有M x n ≤||有界,由准则II ,数列}{n x 极限存在且a x n n =∞→lim .2.5 两个重要极限1. 求]cos 1[cos lim n n n -++∞→.解: 原式 =21sin 21sin2lim nn n n n -+++-+∞→⎪⎪⎭⎫⎝⎛++=-+=-+-+-+++-=+∞→n n n n n n nn nn nn n 1110212121sin21sin2lim 2. 求)1sin(lim 2++∞→n n π.解. 原式=()()n nn n n nn n -+-=-+++∞→+∞→1sin 1lim )1sin(lim 22ππππ()()()()0111sin 1lim 222=-+⋅-+-+-=+∞→n nn n nnnn πππ3. 求x x xx )1cos 1(sinlim +∞→. 解. 原式=()[]()e t t t tttt tt xt =⎥⎦⎤⎢⎣⎡+=+=→→=22sin 2sin 10212012sin 1lim cos sin lim 令4. 设 ⎩⎨⎧+-=32)cos 1(2)(x x x x f 00≥<x x 求 20)(lim x x f x →. 解: 1lim )(lim 232020=+=++→→x x x x x f x x ,1)cos 1(2lim )(lim 2020=-=--→→x x x x f x x ∴ 1)(lim2=→xx f x .2.6 函数的连续性1. 研究函数()[]x x x g -=的连续性,并指出间断点类型. 解. n x =,Z n ∈ (整数集)为第一类 (跳跃) 间断点.2. 证明方程)0(03>=++p q px x 有且只有一个实根.证. 令()()()0,0,3>∞+<∞-++=f f q px x x f , 由零点定理, 至少存在一点ξ使得()0=ξf , 其唯一性, 易由()x f 的严格单调性可得.3.设⎪⎩⎪⎨⎧≤<-+>=-01),1ln(0 ,)(11x x x e x f x ,求)(x f 的间断点,并说明间断点的所属类型. 解. )(x f 在()()()+∞-,1,1,0,0,1内连续, ∞=-→+111lim x x e,0lim 111=-→-x x e, ()00=f , 因此,1=x 是)(x f 的第二类无穷间断点; (),lim lim 1110--→→==++e ex f x x x()()01ln lim lim 00=+=--→→x x f x x , 因此0=x 是)(x f 的第一类跳跃间断点.4.讨论nx nxn e e x x x f ++=∞→1lim )(2的连续性.解. ⎪⎩⎪⎨⎧<=>=++=∞→0,0,00,1lim)(22x x x x x e e x x x f nxnxn , 因此)(x f 在()()+∞∞-,0,0,内连续, 又()()00lim 0==→f x f x , ()x f ∴在()+∞∞-,上连续.5.设函数),()(+∞-∞在x f 内连续,且0)(lim=∞→xx f x ,证明至少存在一点ξ,使得0)(=+ξξf .证:令x x f x F +=)()(,则01]1)([lim )(lim>=+=∞→∞→x x f x x F x x ,从而0)(>xx F .由极限保号性定理可得,存在01>x 使0)(1>x F ;存在02<x 使0)(2<x F .)(x F 在],[12x x 上满足零点定理的条件,所以至少存在一点ξ使得0)(=ξF ,即0)(=+ξξf .6.讨论函数nnx x x x f 2211lim )(+-=∞→的连续性,若有间断点,判别其类型.解: ⎪⎩⎪⎨⎧-=101)(x f 1||1||1||>=<x x x ,显然 1±=x 是第一类跳跃间断点,除此之外均为连续区间.7.证明:方程)0,0(sin >>+=b a b x a x 至少有一个正根,且不超过b a +. 证明:设b x a x x f --=sin )(,考虑区间],0[b a +0)0(<-=b f ,0))sin(1()(≥+-=+b a a b a f ,当0))sin(1()(=+-=+b a a b a f 时,b a x +=是方程的根;当0))sin(1()(>+-=+b a a b a f 时,由零点定理,至少),0(b a +∈∃ξ使0)(=ξf ,即 0sin =--b a ξξ成立,故原方程至少有一个正根且不超过b a +.2.7 无穷小与无穷大、无穷小的比较1. 当0→x 时,下面等式成立吗?(1))()(32x o x o x =⋅;(2))()(2x o xx o =;(3) )()(2x o x o =. 解. (1)()()()002232→→=⋅x xx o x x o x , ()()()032→=⋅∴x x o x o x (2) ()()()0)(,00)()(2222→=∴→→=x x o x x o x x x o xxx o(3) ()2xx o不一定趋于零, )()(2x o x o =∴不一定成立(当0→x 时) 2. 当∞→x 时,若)11(12+=++x o c bx ax ,则求常数c b a ,,.解. 因为当∞→x 时,若)11(12+=++x o c bx ax , 所以01lim 111lim 22=+++=++++∞→+∞→c bx ax x x c bx ax x x , 故c b a ,,0≠任意.3.写出0→x 时,无穷小量3x x +的等价无穷小量.解: 11lim 1lim lim303630=+=+=+→→→x xx xxx x x x∴ 当0→x ,3x x +~6x第3章 导数与微分3.1 导数概念1. 设函数)(x f 在0x 处可导,求下列极限值. (1)hh x f h x f h )3()2(lim000--+→;(2)000)()(lim 0x x x xf x f x x x --→.解.(1) 原式()()()000000533)3(22)2(lim x f h x f h x f h x f h x f h '=⎥⎦⎤⎢⎣⎡⋅---+⋅-+=→(2) 原式()[]()()()()00000000)(limx f x f x x x x x x f x f x f x x x -'=----=→2.设函数R f →+∞),0(:在1=x 处可导,且),0(,+∞∈∀y x 有)()()(y xf x yf xy f += 试证:函数f 在),0(+∞内可导,且)1()()(f xx f x f '+='. 解:令1==y x ,由()()()y xf x yf xy f +=有()()121f f =得()01=f .()+∞∈∀,0x ,()()()()()()()()()()xx f f x x f xx f x x f x x f x f x x x x xf x x f x x x f x x f x x f x f x x x x +'=+∆-⎪⎭⎫⎝⎛∆+=∆-⎪⎭⎫ ⎝⎛∆++⎪⎭⎫ ⎝⎛∆+=∆-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∆+=∆-∆+='→∆→∆→∆→∆111lim 11lim 1lim lim 0000 故()x f 在()+∞,0内处处可导,且()()()xx f f x f +'='1. 3.设()f x 在(,)-∞+∞内有意义,且(0)0f =,(0)1f '=, 又121221()()()()()f x x f x x f x x ϕϕ+=+,其中22()cos xx x x e ϕ-=+, 求()f x '.解: ()()()()()()()()x x f x x f x x f x x f x x f x f x x ∆-∆+∆=∆-∆+='→∆→∆ϕϕ00lim lim()()()()()()()()()001lim 0lim 00ϕϕϕϕ'+'=∆-∆+∆-∆=→∆→∆x f x f xx x f x x f x f x x ()x e x x x 22cos -+==ϕ4.设函数0)(=x x f 在处可导,且21arctan lim )(0=-→x f x e x,求)0(f '.解:由已知,必有0]1[lim )(0=-→x f x e,从而0)(lim 0=→x f x ,而0)(=x x f 在连续,故0)0(=f .于是)0(1)0()(1lim )(lim 1arctan lim200)(0f xf x f x f x e x x x x f x '=-==-=→→→. 故21)0(='f .5.设)(x f 具有二阶导数,)(,sin )()2(lim )(2x dF t xx f t x f t x F t 求⎥⎦⎤⎢⎣⎡-+=∞→.解: 令t h 1=,则)(2 sin )()2(lim)(0x f x hhxh x f h x f x F t '=⋅-+=→.从而)(2)(2)(x f x x f x F ''+'=',dx x f x x f dx x F x dF )]()([2)()(''+'='=.6.设f 是对任意实数y x ,满足方程 22)()()(xy y x y f x f x f +++= 的函数,又假设1)(lim=→xx f x ,求:(1))0(f ;(2))0(f '; (3))(x f '. 解:(1)依题意 R y x ∈∀,,等式 22)()()(xy y x y f x f y x f +++=+ 成立令0==y x 有 )0(2)0(f f = ⇒ 0)0(=f(2)又 1)(lim=→x x f x ,即 )0(10)0()(lim 0f x f x f x '==--→,∴ 1)0(='f(3)xx f x x f x f x ∆-∆+='→∆)()(lim )(0x x f x x x x x f x f x ∆-∆⋅+∆⋅+∆+=→∆)()()()(lim 220 x x x x x x f x ∆∆⋅+∆⋅+∆=→∆220)()(lim ])([lim 20x x x xx f x ∆⋅++∆∆=→∆ ]1)0(22x x f +=+'=∴ 21)(x x f +='.7.设曲线)(x f y =在原点与x y sin =相切,试求极限 )2(lim 21nf nn ∞→. 解:依题意有 1)0()0(='='f y 且0)0(=f∴ 222)0()2(lim )2(lim 2121=⋅-⋅=⋅∞→∞→n nf n f n nf n n n .8.设函数)(x f 在0=x 处可导且0)0(,0)0(='≠f f ,证明1])0()1([lim =∞→nn f n f .证:n n n n f f n f f n f ])0()0()1(1[lim ])0()1([lim -+=∞→∞→.=10)0(11)0()01(lim )0()0()1(lim ===⋅-+-∞→∞→e ee f nf n f f f n f n n n .1.计算函数baxax xb ab y )()()(= (0,0>>b a )的导数.解. a xb bx a b a x xb a b a a x b a x a b x b x b a a x x b a b a b y )(1)()()()(ln )(121⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛+='-- ⎥⎦⎤⎢⎣⎡+-=x b x a a b a x x b a b b a x ln )()()( 2.引入中间变量,1)(2x x u +=计算1111ln 411arctan 21222-+++++=x x x y 的导数dx dy .解. 引入,1)(2x x u += 得11ln 41arctan 21-++=u u u y ,于是dxdudu dy dx dy ⋅=, 又 ()()4242422111111111141121x x x u u u u du dy +-=+-=-=⎪⎭⎫ ⎝⎛--+++=,21xx dx du +=, 则()22242121121xx x x x x x dx dy ++-=+⋅⎪⎭⎫⎝⎛+-= 3.设y y x +=2,232)(x x u +=,求dudy. 解. dudxdx dy du dy ⋅= , 又()()1223,12212++=+=x x x dx du y dy dx ,得121+=y dx dy , ()x x x du dx ++=21232, 则得()()xx x y du dy +++=2121232 4.已知 2arctan )(),2323(x x f x x f y ='+-=,求=x dx dy .解:22)23(12)2323arctan()2323()2323(+⋅+-='+-⋅+-'='x x x x x x x f y π43)23(12)2323arctan(02200=+⋅+-='=∴===x x x x x x y dxdy .1. 计算下列各函数的n 阶导数. (1) 6512-+=x x y ; (2) x e y xcos =. 解 (1)⎪⎭⎫⎝⎛+--=611171x x y ,()()()()()()⎥⎦⎤⎢⎣⎡+---=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-⎪⎭⎫⎝⎛-=∴++1161117!1611171n n nn n n x x n x x y (2) ()⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡-=-='4cos 2sin 21cos 212sin cos πx e x x e x x e y x x x()⎪⎭⎫ ⎝⎛⋅+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+=''42cos 24sin 4cos 22πππx ex x e y xx由此推得 ()()⎪⎭⎫ ⎝⎛⋅+=4cos 2πn x eyxnn2. 设x x y 2sin 2=, 求()50y .解 ()()()()()()()()()()"+'+=248250249150250502sin 2sin 2sin x x C x x C x x y⎪⎭⎫ ⎝⎛⋅+⋅⨯+⎪⎭⎫ ⎝⎛⋅+⋅+⎪⎭⎫ ⎝⎛⋅+=2482sin 2249502492sin 2502502sin 24950250πππx x x x xx x x x x 2sin 212252cos 2502sin 24950250⋅+⋅+-= ()[]x x x x 2cos 1002sin 212252249+-=3. 试从y dy dx '=1, 0≠'y , 其中y 三阶可导, 导出()322y y dy x d '''-=, ()()52333y y y y dy x d '''''-''= 解 y dy dx '=1 ,()()322211y y y y y dy dx y dx d dyx d '''-='⋅'-''=⋅⎪⎪⎭⎫ ⎝⎛'=∴ ()()()()()()52623333313y y y y y y y y y y y dy dx y y dx d dy x d '''''-''='⋅'''⋅'⋅''+''''-=⋅⎪⎪⎭⎫ ⎝⎛'''-=∴ 4. 设()x f 满足()()0 312≠=⎪⎭⎫⎝⎛+x xx f x f , 求()()()()x f x f x f n ,,'.解 以x 1代x ,原方程为()x x f x f 321==⎪⎭⎫ ⎝⎛,由()()⎪⎪⎩⎪⎪⎨⎧=+⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+x x f x f x x f x f 321 312,消去⎪⎭⎫⎝⎛x f 1,求得()x x x f 12-=,且得()212xx f +=',()()()()2!111≥-=++n x n x f n n n . 5.设()arcsin f x x =,试证明()f x 满足 (1)2(1)()()0x f x xf x '''--= (2) ,1,0,0)()()12()()1()(2)1()2(2==-+--++n x f n x xf n x f x n n n(3)求()(0)n f解 (1)()211x x f -=',()()()22221112211xx xx x x x f --=-⋅--='', ()()()012='-''-∴x f x x f x ,(2)上式两边对x 求n 阶导数得()()[]()()[]()()()()()()()()()()()()()()()[]x f n x xf x f n n x f x n x f x x f x x f x n n n n n nn⋅⋅+-⋅-⋅---+-='-''-=+++1221211021222即 ()()()()()()()()01212122=-+--++x f nx xf n x f xn n n 。

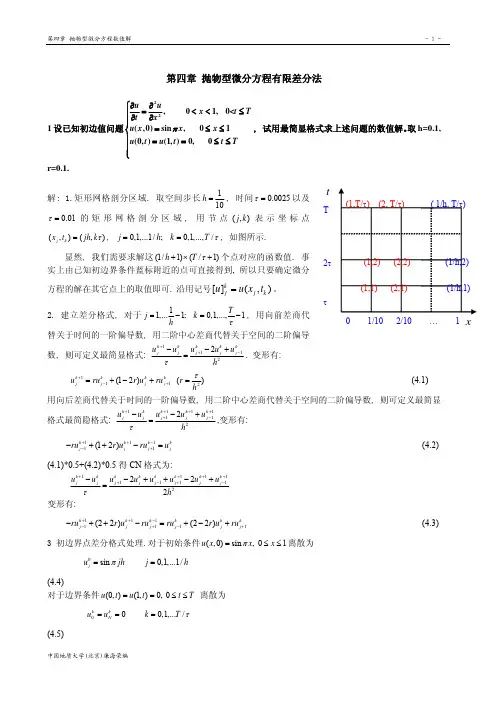
第四章 抛物型微分方程有限差分法1设已知初边值问题22, 01, 0<(,0)sin , 01(0,)(1,)0, 0 u ux t t x u x x x u t u t t T π⎧∂∂=<<⎪∂∂⎪⎪=≤≤⎨⎪==≤≤⎪⎪⎩T ≤, 试用最简显格式求上述问题的数值解。
取h=0.1,r=0.1.0 1/10 2/10 … 1 T 2τ τt解: 1.矩形网格剖分区域. 取空间步长1, 时间2510h =0.00τ=以及0.01τ=的矩形网格剖分区域, 用节点)表示坐标点(,j k (,)(,)j k x t jh k τ=, 0,1,...1/; 0,1,...,/j h k T τ==, 如图所示.显然, 我们需要求解这(1/1)(/1)h T τ+×+个点对应的函数值. 事实上由已知初边界条件蓝标附近的点可直接得到, 所以只要确定微分方程的解在其它点上的取值即可. 沿用记号[]k(,)j j k u x t =。
u 2. 建立差分格式, 对于11,...1; 0,1,...,1Tj k hτ=−=−, 用向前差商代替关于时间的一阶偏导数, 用二阶中心差商代替关于空间的二阶偏导数, 则可定义最简显格式:1122k k k k k1jj j j u u u u u h ++−+=. 变形j τ−−有:1112(12) (k k k kj j j j u ru r u ru r h τ+−+=+−+=(4.1)用向后差商代替关于时间的一阶偏导数, 用二阶中心差商代替关于空间的二阶偏导数, 则可定义最简显格式最简隐格式:111122k k k k k j jj j j u u u u u h τ++++−−+=11+−1kj +,变形有:1111(12) k k k j j j ru r u ru u ++−−−++−= (4.2)(4.1)*0.5+(4.2)*0.5得CN 格式为:111112222k k k k k k k k j jj j j j j j u u u u u u u u h τ+++−+−−++−+=111++−1kj +x x变形有:111111(22)(22) k k k k k j j j j j ru r u ru ru r u ru ++−−+−−++−=+−+ (4.3)3 初边界点差分格式处理.对于初始条件u x (,0)sin , 01=π≤≤h 离散为(4.4)0sin 0,1,...1/j u jh j π==对于边界条件离散为(0,)(1,)0, 0 u t u t t T ==≤≤00 0,1,.../k k N u u k T τ===(4.5)总结: 联立方程(4.1)(4.4)(4.5)得到已知问题的最简显格式差分方程组:11100(12)1 1,...1; 0,1,...,1sin 0,1,...1/0 0,1,.../k k k k j j j j jk k N u ru r u ru T j k h u jh j h u u k T τπτ+−+⎧=+−+⎪⎪=−=−⎪⎨⎪==⎪⎪===⎩ 联立方程(4.2)( 4.4)( 4.5)得到已知问题的最简隐格式差分方程组:1111100(12) 1 1,...1; 0,1,...,1sin 0,1,...1/0 0,1,.../k k k k j j j j jk k N ru r u ru u T j k h u jh j h u u k T τπτ++−−+⎧−++−=⎪⎪=−=−⎪⎨⎪==⎪⎪===⎩ 联立方程(4.3)( 4.4)( 4.5)得到已知问题的CN 格式差分方程组:11111100(22)(22) 1 1,...1; 0,1,...,1sin 0,1,...1/0 0,1,.../k k k k k j j j j j jk k N ru r u ru ru r u ru T j k h u jh j h u u k T τπτ++−−+−⎧−++−=+−+⎪⎪=−=−⎪⎨⎪==⎪⎪===⎩1k j + 4 求解并显示结果利用软件计算(Matlab)如上最简显格式差分方程组.h=1/10;tau=0.0025;T=0.5; r=tau/h^2;M=1/h+1;N=T/tau+1; u=zeros(M,N);for m=1:Mu(m,1)=sin((m-1)*h*pi); endu(1,1:N)=0;u(M,1:N)=0;for n=1:N-1for m=2:M-1u(m,n+1)=r*(u(m+1,n)+u(m-1,n))+(1-2*r)*u(m,n); end end u=u’ 这样我们就计算出不同时刻不同位置k t j x 对应的函数值(,)j k u x t 取tau=0.0025, 即r=0.25绘图, 取tau=0.01, r=1再绘图,如图()图4.2 习题1数值解图示(左r=0.25, 右r=1)2.试构造初边值问题 ()()()()(), 0.51, 0,,0, 0.51,0.5,0, 1,0.51,, 0u u x x x T t x x u x x x u ⎪∂u t t u t t T x ϕ⎧∂∂∂⎛⎞=<<<≤⎜⎟⎪∂∂∂⎝⎠⎪⎪=≤≤⎨⎪==−≤≤⎪∂⎩的显格式,并给出其按最大范数稳定的充分条件。

第三章椭圆形方程的有限差分法3.2两点边值问题的差分格式321L用积分插值法导出!1近徴分方程(21)的差分方程.92页Z —汕計煌2 a♦J川/八C ⑴,可遁接积分在3和內任一小区间[X F ⑺]上积分挣 彳一兰5字)女+J;u dx dx"“好理3dx pG )dx (中矩形公式)Vw (X $ W,吗丽必)】勺坷+1严如普其中s乙_ 2一 J 0(x )dxP % +^+l rqu dx= J 小⑴)i (宀+ 乂空 dx+ J dx 汕qudx= J / dx • d" <4^ r 其中W (X )=P£在3 取[X ⑴,X 門为对偶单元[XIF -1w (X 1) -_ w ( X rf r 色 dx+ f qT = J dx X I(X )=Pdxm=dx\ dxui ps4 i p (x )3.2.3p20D 4*J4.构造il近"{pu)+i^u+ru =/ 于((3 , b )的中-!>差分恪式.A解:取M+1金节点,a = Xo <可< <Xj < <心=趴卩為"厂和"12••••••,K 心豳恥X 1==(X H +兀)j=l,2,……,N2 访2也 _「咚 吗+1-如旳-%-】 紅1 闵切+1 +鸟%+1%.d dL 、 . d d^u.[群苕L 厂乔L 扌JW ------------- -------------- V饥1+闵2AA-d u. - d u Jp 乔kF 乔d^u dx * *4 dx q2ft#{P+】[年如A +如1饥2出+i_旳]"XT-Pi [如旳(^1+2 +力")如紅1%-%丿%一1——___ p.[如H 如]-沟)如 纭】%-务-1"V"2 ["宀・】如i+M 沟 Z 沟如-1 -%-2TT"3.3二阶椭圆型方程的差分格式P210*'1.用积分插值法构造逼近君程初(3. 31)一N m =— [2(疋—)+2(上更)]=了时第一辺值问题的五点差空卽 卽分格式,这里k = k (X' y ) 血刈43.3.1100页i ・l于Q 上积分(3.21)式,4-JJ V y\ dxdy = JJ f dxdy^ J G 科■p 请(碟)+鲁a 詈皿®=n 'T*r由G M M 第—公式得5 ♦■・.综上有S a=叭小其中y dxQy □九广力1力2 ff*T1)非正则内点3解. zTJ 1 •1)正则内点心j+1\/ L4L3J-1duflGfj^+k ds =— — k dn dy^kds = ^k dn BxJ1 -2 +^kds = ^k dn dy ..I 纸= d.\M 尹—22*52+^方2^kds = ^k dfi dx,斗严=%J 纸叫厂吗J 叶讥诂丁 —V —丸Mj *1 — "i 12" 2 2 +上—JJ.・补充题£用积分插值法构造11近方程(久21)冊第二边值间题的五点差分格式.341CL I■"+ ) — k ds Jj f dxdy aA 9冲Axic上一 AB^h 加f 咛L 詈上£ Q (2)上心0拠jt 尹。
偏微分方程习题及答案【篇一:偏微分方程数值解法期末考试题答案】题答案及评分标准学年学期:专业:班级:课程:教学大纲:使用教材:教材作者:出版社:数学与应用数学数学偏微分方程数值解法《偏微分方程数值解法》教学大纲(自编,2006)《偏微分方程数值解法》陆金甫、关治清华大学出版社一、判断题(每小题1分,共10分)1、(o)2、(o)3、(x)4、(x)5、(o)6、(o)7、(o)8、(x)9、(x) 10、(o)二、选择题(每小题2分,共10分) 11、(d) 12、(a) 13、(c) 14、(b)15、(c)三、填空题(每小题2分,共20分)?2?216、2?2??x1?x2?2?2 17、a=[4 5 9;23 5 17;11 23 1] 18、y=exp(-t/3)*sin(3*t) ?xn19、help 20、zeros(m,n)21、inva(a)*b或者a/b22、a=sym([cos(x-y),sin(x+y);exp(x-y),(x-1)^3])?(s)?1?(s)?c[??(s)]2?023、a[?2(s)]2?2b?224????v(?)ed? 25、i?xu(xj,tn?1)?u(xj,tn)?四、计算题:(每小题12分,共36分)?u?u?0(x?r,t?0)的有限差分方程(两层显示26、写成对流方程?a?t?x格式,用第n层计算第n+1层),并把有限差分方程改写为便于计算的迭代格式???/h为网格比。
解:在点(xj,tn)处,差分方程为?1un?unjj??anunj?1?ujh?0(j?0,?1,?2,,n?0,1,2,)(8分)便于计算的形式为?1nnn???/h (4分) un?u?a?(u?ujjj?1j),?u?2u?a2的有限差分方程(中心差分格式,用第n层27、写出扩散方程?t?x计算第n+1层),并把有限差分方程改写为便于计算的迭代格式,???/h2为网格比。
第十四章 偏微分方程物理、力学、工程技术和其他自然科学经常提出大量的偏微分方程问题.由于实践的需要和一些数学学科(如泛函分析,计算技术)的发展,促进了偏微分方程理论的发展,使它形成一门内容十分丰富的数学学科.本章主要介绍一阶偏微分方程、线性方程组及二阶线性偏微分方程的理论.在二阶方程中,叙述了极值原理、能量积分及惟一性定理.阐明了一些解的性质和物理意义,介绍典型椭圆型、双曲型、抛物型方程的常用解法:分离变量法,基本解,格林方法,黎曼方法,势位方法及积分变换法.最后,扼要地介绍了有实用意义的数值解法:差分方法和变分方法.§1 偏微分方程的一般概念与定解问题[偏微分方程及其阶数] 一个包含未知函数的偏导数的等式称为偏微分方程.如果等式不止一个,就称为偏微分方程组.出现在方程或方程组中的最高阶偏导数的阶数称为方程或方程组的阶数.[方程的解与积分曲面] 设函数u 在区域D 内具有方程中所出现的各阶的连续偏导数,如果将u 代入方程后,能使它在区域D 内成为恒等式,就称u 为方程在区域D 中的解,或称正规解. ),,,(21n x x x u u = 在n +1维空间),,,,(21n x x x u 中是一曲面,称它为方程的积分曲面. [齐次线性偏微分方程与非齐次线性偏微分方程] 对于未知函数和它的各阶偏导数都是线性的方程称为线性偏微分方程.如()()()()y x f u y x c yuy x b x u y x a ,,,,=+∂∂+∂∂就是线性方程.在线性方程中,不含未知函数及其偏导数的项称为自由项,如上式的f (x,y ).若自由项不为零,称方程为非齐次的.若自由项为零,则称方程为齐次的.[拟线性方程与半线性方程] 如果一个方程,对于未知函数的最高阶偏导数是线性的,称它为拟线性方程.如()()()()()()0,,,,,,,,,,,,22222122211=+∂∂+∂∂+∂∂+∂∂∂+∂∂u y x c y uu y x b x u u y x a yu u y x a y x u u y x a x u u y x a就是拟线性方程,在拟线性方程中,由最高阶偏导数所组成的部分称为方程的主部.上面方程的主部为()()()22222122211,,,,,,yuu y x a y x u u y x a x u u y x a ∂∂+∂∂∂+∂∂如果方程的主部的各项系数不含未知函数,就称它为半线性方程.如()()()()0,,,,,,2222=∂∂+∂∂+∂∂+∂∂y yu y x d x y u y x c yu y x b x u y x a就是半线性方程.[非线性方程] 不是线性也不是拟线性的方程称为非线性方程.如1)()1(222=∂∂+∂∂+yux u u就是一阶非线性偏微分方程.[定解条件] 给定一个方程,一般只能描写某种运动的一般规律,还不能确定具体的运动状态,所以把这个方程称为泛定方程.如果附加一些条件(如已知开始运动的情况或在边界上受到外界的约束)后,就能完全确定具体运动状态,称这样的条件为定解条件.表示开始情况的附加条件称为初始条件,表示在边界上受到约束的条件称为边界条件.[定解问题] 给定了泛定方程(在区域D 内)和相应的定解条件的数学物理问题称为定解问题.根据不同定解条件,定解问题分为三类.1︒ 初值问题 只有初始条件而没有边界条件的定解问题称为初值问题或柯西问题. 2︒ 边值问题 只有边值条件而没有初始条件的定解问题称为边值问题.3︒ 混合问题 既有边界条件也有初始条件的定解问题称为混合问题(有时也称为边值问题).[定解问题的解] 设函数u 在区域D 内满足泛定方程,当点从区域D 内趋于给出初值的超平面或趋于给出边界条件的边界曲面时,定解条件中所要求的u 及它的导数的极限处处存在而且满足相应的定解条件,就称u 为定解问题的解.[解的稳定性] 如果定解条件的微小变化只引起定解问题的解在整个定义域中的微小变化,也就是解对定解条件存在着连续依赖关系,那末称定解问题的解是稳定的.[定解问题的适定性] 如果定解问题的解存在与惟一并且关于定解条件是稳定的,就说定解问题的提法是适定的.§2 一阶偏微分方程一、 柯西-柯娃列夫斯卡娅定理[一阶偏微分方程的通解] 一阶偏微分方程的一般形式 是0),,,,,,,,(2121=∂∂∂∂∂∂nn x ux u x u u x x x F或()0,,,,,,,211=n n p p p u x x F ,其中()n i x up ii ,,2,1 =∂∂=如解出p 1,可得:p 1 = f (x 1 , x 2 ,…, x n , u , p 2 ,…, p n )当方程的解包含某些“任意元素”(指函数),如果适当选取“任意元素”时,可得方程的任意解(某些“奇异解”除外),则称这样的解为通解.在偏微分方程的研究中,重点在于确定方程在一些附加条件(即定解条件)下的解,而不在于求通解.[一阶方程的柯西问题]()()⎪⎩⎪⎨⎧==∂∂=n x x n n x x u p p u x x x f x u,,|,,,,,,,22211011 ϕ 称为柯西问题,式中),,(2n x x ϕ为已知函数,对柯西问题有如下的存在惟一性定理.[柯西-柯娃列夫斯卡娅定理] 设 f ( x 1 , x 2 ,, x n , u , p 2 ,, p n ) 在点 ( x 10 , x 20 ,, x n 0 , u 0 , p 20 ,, p n 0 ) 的某一邻域内解析,而),,(2n x x ϕ在点( x 20 ,, x n 0 ) 的某邻域内解析,则柯西问题在点 ( x 10 ,, x n 0 ) 的某一邻域内存在着惟一的解析解.这个定理应用的局限性较大,因它要求f 及初始条件都是解析函数,一般的定解问题未必能满足这种条件.对高阶方程也有类似定理.二、 一阶线性方程1. 一阶齐次线性方程[特征方程∙特征曲线∙初积分(首次积分)] 给定一阶齐次线性方程在有些书中写作0),,,,,,,,,(121=∂∂∂∂∂∂nn x u x u t u u x x x t F()()0,,,,,,211211=∂∂++∂∂nn n n x u x x x a x u x x x a (1) 式中a i 为连续可微函数,在所考虑的区域内的每一点不同时为零(下同).方程组()n i ix x x a tx ,,,d d 21 = ( i = 1,2,, n ) 或()()()n n n n n x x x a x x x x a x x x x a x ,,,d ,,,d ,,,d 2121222111 === (2)称为一阶齐次线性偏微分方程的特征方程.如果曲线l : x i = x i (t ) ( i =1,2,, n )满足特征方程(2),就称曲线l 为一阶齐次线性方程的特征曲线.如果函数ψ ( x 1 , x 2 ,, x n )在特征曲线),,2,1()(n i t x x i i ==上等于常数,即ψ ( x 1(t ) , x 2(t ) ,, x n (t ) ) = c就称函数ψ ( x 1, x 2,, x n )为特征方程(2)的初积分(首次积分). [齐次方程的通解]1o 连续可微函数u = ψ ( x 1, x 2,, x n ) 是齐次线性方程(1)的解的充分必要条件是: ψ ( x 1, x 2,, x n )是这个方程的特征方程的初积分.2o 设ψi ( x 1 , x 2 ,, x n ) ( i = 1,2,, n 1-) 是特征方程(2)在区域D 上连续可微而且相互独立的初积分(因此在D 内的每一点,矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂---n n n n n n x x x x x x x x x 121112221212111ψψψψψψψψψ 的秩为n 1-) ,则u = ω ( ψ1 ( x 1 , x 2 ,, x n ) ,, ψn -1 ( x 1 , x 2 ,, x n ) )是一阶齐次线性方程(1)的通解,其中ω为n 1-个变量的任意连续可微函数. [柯西问题] 考虑方程的柯西问题()()⎪⎩⎪⎨⎧==∂∂==∑n x x ni i n i x x u x u x x x a ,,|0,,,2121011 ϕ 式中ϕ ( x2 ,, x n )为已知的连续可微函数.设ψi ( x 1 , x 2 ,, x n ) ( i = 1,2,, n 1-) 为特征方程的任意n 1-个相互独立的初积分,引入参变量 i ψ (1,,2,1-=n i ),从方程组()()()⎪⎪⎩⎪⎪⎨⎧===--120112201212011,,,,,,,,,n n n n n x x x x x x x x x ψψψψψψ 解出x 2 ,, x n 得()()⎪⎩⎪⎨⎧==--12112122,,,,,,n n nn x x ψψψωψψψω 则柯西问题的解为u = ϕ ( ω2 ( ψ1 , ψ2 ,, ψn -1 ) ,, ωn ( ψ1 , ψ2 ,, ψn -1 ) )2. 非齐次线性方程它的求解方法与拟线性方程相同.三、 一阶拟线性方程一阶拟线性方程为()()∑==∂∂ni n i n i u x x x R x uu x x x a 12121,,,,,,,, 其中a i 及R 为x 1 , x 2 ,, x n , u 的连续可微函数且不同时为零. [一阶拟线性方程的求解和它的特征方程]()()⎪⎩⎪⎨⎧===u x x x R t un i u x x x a t x n n i i,,,,d d ),,2,1(,,,,d d 2121 或()()()u x x R uu x x a x u x x a x n n n n n ,,,d ,,,d ,,,d 11111 ===为原拟线性方程的特征方程.如果曲线l : x i = x i (t ) ( i =1,2,, n ) , u = u (t ) 满足特征方程,则称它为拟线性方程的特征曲线.设 ψi ( x 1 ,, x n ,u ) ( i = 1,2,, n ) 为特征方程的n 个相互独立的初积分,那末对于任何连续可微函数ω,ω ( ψ1 ( x 1,, x n , u ) , ψ2 ( x 1,, x n , u ) ,, ψn ( x 1,, x n , u ) ) = 0都是拟线性方程的隐式解.[柯西问题] 考虑方程的柯西问题()()()⎪⎩⎪⎨⎧==∂∂==∑n x x ni n i ni x x u u x x x R x u u x x x a ,,|,,,,,,,,212121011 ϕ ϕ为已知的连续可微函数.设 ψ1 ( x 1 , x 2 ,, x n , u ) ,, ψn ( x 1 , x 2 ,, x n , u ) 为特征方程的n 个相互独立的初积分,引入参变量 n ψψψ,,,21 , 从()()()⎪⎪⎩⎪⎪⎨⎧===nn n n n u x x x u x x x u x x x ψψψψψψ,,,,,,,,,,,,2012201212011解出 x 2 ,, x n , u()()()⎪⎪⎩⎪⎪⎨⎧===n n n n n u x x ψψψωψψψωψψψω,,,,,,,,,21212122 则由()()()()()()()0,,,,,,,,,,,,,,,,,,,,,,2121221221121=-≡n n n n n n u x x x u x x x u x x x V ψψψωψψψωϕψψω给出柯西问题的隐式解.四、 一阶非线性方程[完全解·通解·奇异解] 一阶非线性方程的一般形式为()()n i x up p p p u x x x F ii n n ,,2,10,,,,,,,,2121 =∂∂== 若一阶偏微分方程的解包含任意n 个独立的常数,则称这样的解为完全解(全积分). 若V ( x 1, x 2 ,, x n , u , c 1 , c 2,, c n ) = 0为方程的完全解,从()n i c VV i,,2,10,0 ==∂∂= 消去c i ,若得一个解,则称它为方程的奇异解(奇积分).以两个独立变量为例说明完全解与通解、奇异解的关系,设方程()yzq x z p q p z y x F ∂∂=∂∂==,,0,,,,有完全解V (x ,y ,z ,a ,b )=0 ( a ,b 为任意常数),则方程等价于从方程组()⎪⎪⎩⎪⎪⎨⎧=∂∂+∂∂=∂∂+∂∂=0,00,,,,q z Vy V p z V x V b a z y x V 消去a ,b 所得的方程.利用常数变易法把a ,b 看作x , y 的函数,将V (x ,y ,z ,a ,b )=0求关于x , y 的偏导数,得00=∂∂⋅∂∂+∂∂⋅∂∂+∂∂+∂∂=∂∂⋅∂∂+∂∂⋅∂∂+∂∂+∂∂ybb V y a a V q z V y V xbb V x a a V p z V x V那末0,0=∂∂⋅∂∂+∂∂⋅∂∂=∂∂⋅∂∂+∂∂⋅∂∂yb b V y a a V x b b V x a a V 与V=0联立可确定a ,b .有三种情况:1︒ 0≡∂∂≡∂∂bVa V ,将其与V (x ,y ,z ,a ,b )=0联立可确定不含任意常数的奇异解. 2︒ 如0=∂∂=∂∂=∂∂=∂∂yb x b y a x a ,即回到完全解. 3︒ 当0/,0/≡∂∂≡∂∂b Va V 时,必有()()0,,=∂∂y x b a ,这时,如果不属于情形2︒ ,则a 与b 存在函数关系:b=ω(a ),这里ω为任意可微函数,并从方程V (x ,y ,z ,a ,b )=0和()∂∂∂∂ωV a Vba +'=0消去a ,b ,可确定方程的通解.定理 偏微分方程的任何解包含在完全解内或通解内或奇异解内. [特征方程·特征带·特征曲线·初积分] 在一阶非线性方程:()F x x x u p p p n n 12120,,,,,,,, =中,设F 对所有变量的二阶偏导数存在且连续,称()n i uFp x F t p p F p t u p Ft x i i i ni iii i ,,2,1)(d d d d ,1 =∂∂+∂∂-=∂∂=∂∂=∂∂∑=或u F p x F p u F p x F p p Fp up F x p F xp F x n nnni i i nn ∂∂+∂∂-==∂∂+∂∂-=∂∂=∂∂==∂∂=∂∂∑=d d d d d d 11112211为非线性方程的特征方程.设特征方程的解为x i =x i (t ), u=u (t ), p i =p i (t ) (i =1,2,…,n )称它为非线性方程的特征带.在x 1,x 2,, x n ,u 空间的曲线x i =x i (t ), u=u (t ) (i=1,2,…,n )称为非线性方程的特征曲线.如果函数()n n p p p u x x x G ,,,,,,,,2121 在特征方程的任一解x i =x i (t ) (i =1,2,, n ), u=u (t ), p i =p i (t ) (i =1,2,, n )上等于常数,即()()()()()()()()G x t x t x t u t p t p t p t C n n 1212,,,,,,,, =那末函数()n n p p p u x x x G ,,,,,,,,2121 称为特征方程的初积分.[求完全解的拉格朗日-恰比方法] 考虑两个变量的情况.对于方程F (x ,y ,z ,p ,q )=0,选择使雅可比式()()0,,≠∂∂q p G F 的一个初积分G (x ,y ,z ,p ,q ).解方程组()()F x y z p q G x y z p q a,,,,,,,,==⎧⎨⎪⎩⎪0(a 为任意常数) 得p (x ,y ,z ,a )及q (x ,y ,z ,a ).则方程d z=p d x+q d y的通解V (x ,y ,z ,a ,b )=0(b 是积分d z=p d x+q d y 出现的任意常数)就是方程F (x ,y ,z ,p ,q )=0的完全解.例 求方程()z p q x y 22222+=+的完全解.解 方程的特征方程为()()()qy x z y qp q p z x p q p z z q z y p z x 22222222222d 22d 2d 2d 2d +-=+-=+== 这里成立zpxx p z z p d d d =+ 所以特征方程的一个初积分为z 2p 2 -x 2 .解方程组 ()()z p q x y z p x a22222222+-+=-=⎧⎨⎪⎩⎪ (a 为任意常数) 得 p a x zq y az=+=-22, 积分微分方程dz a x zdx y azdy =++-22 得完全解z x x a y y a a x x a y y ab 22222=++-++++-+ln(b 为任意常数)[某些容易求完全解的方程] 1︒ 仅含p ,q 的方程F (p ,q )=0G =p 是特征方程的一个初积分.从F (p ,q )=0与p=a (a 为任意常数)得q=ψ(a ),积分d z=a d x+ψ(a )d y得完全解z=ax+ψ(a )y+b (b 为任意常数)2︒ 不显含x ,y 的方程F (z ,p ,q )=0 特征方程为zFqqz F p p q F q p F p z q F y p F x ∂∂-=∂∂-=∂∂+∂∂=∂∂=∂∂d d d d d 因此q d p-p d q =0,显然G qp=为一个初积分,由F (z ,p ,q )=0,q=pa (a 为任意常数)解得p=ψ(z ,a ).于是由d z=ψ(z ,a )d x+a ψ(z ,a )d y得()⎰++=b ay x a z z,d ψ (b 为任意常数)可确定完全解.3︒ 变量分离形式的方程()f x p i i i i n,=∑=10特征方程为n n n n i i iin n n x f p x f p p f p z p f x p f x ∂∂-==∂∂-=∂∂=∂∂==∂∂∑=d d d d d 1111111 可取初积分G i =f i (x i ,p i ) , (i =1,2,, n ).从f i (x i ,p i )=a i (i =1,2,, n )解出p i =ϕi (x i ,a i )得完全解()∑⎰=+=ni i i i i b x a x z 1d ,ϕ式中a i ,b 为任意常数,且a i i n=∑=10.[克莱罗方程] 方程()z p x f p p p i i n i n=+=∑121,,,称为克莱罗方程,其完全解为()z c x f c c c i i n i n=+=∑121,,,对c i 微分得x fc i i=-∂∂ (i =1,2,…,n ) 与完全解的表达式联立消去c i 即得奇异解.例 求方程z -xp -yq -pq =0的完全解和奇异解. 解 这是克莱罗方程,它的完全解是z=ax+by+ab对a,b 微分,得x=-b,y=-a ,消去a ,b 得奇异解z=-xy[发甫方程] 方程P (x,y,z )d x+Q (x,y,z )d y+R (x,y,z )d z=0 (1)称为发甫方程,如果P,Q,R 二次连续可微并满足适当条件,那末方程可积分.如果可积分成一关系式时,则称它为完全可积.1︒ 方程完全可积的充分必要条件 当且仅当P,Q,R 满足条件0)()()(=∂∂-∂∂+∂∂-∂∂+∂∂-∂∂yP x Q R x R z P Q z Q y R P (2) 时,存在一个积分因子μ(x,y,z ),使d U 1=μ(P d x+Q d y+R d z )从而方程的通解为U 1(x,y,z )=c特别,当0,0,0=∂∂-∂∂=∂∂-∂∂=∂∂-∂∂yP x Q x R z P z Q y R 时,存在一个函数U (x,y,z )满足 zU R y U Q x U P ∂∂=∂∂=∂∂=,,从而 d U=P d x+Q d y+R d z 所以方程的通解为U (x,y,z )=c所以完全可积的发甫方程的通解是一单参数的曲面族.定理 设对于发甫方程(1)在某区域D 上的完全可积条件(2)成立,则对D 内任一点M (x,y,z )一定有方程的积分曲面通过,而且只有一个这样的积分曲面通过. 2︒ 方程积分曲面的求法设完全可积条件(2)成立.为了构造积分曲面,把z 看成x,y 的函数(设R (x,y,z )≠0),于是原方程化为y RQ x R P z d d d --=由此得方程组()()()()⎪⎪⎩⎪⎪⎨⎧≡-=∂∂≡-=∂∂4,,3,,11z y x Q R Q y z z y x P R P xz发甫方程(1)与此方程组等价.把方程(3)中的y 看成参变量,积分后得一个含有常数 c 的通解 ()cy x z ~;,ϕ= 然后用未知函数()~cy 代替常数 c ,将()()z x y c y =ϕ,;~代入方程(4),在完全可积的条件下,可得()~cy 的一个常微分方程,其通解为 ()()~,cy y c =ψ c 为任意常数,代回()()z x y cy =ϕ,;~中即得发甫方程的积分曲面 z=ϕ(x,y,ψ(y,c ))由于发甫方程关于x,y,z 的对称性,在上面的讨论中,也可把x 或y 看成未知函数,得到同样的结果.例 求方程yz d x+2xz d y+xy d z=0的积分曲面族.解 容易验证完全可积条件成立,显然存在一个积分因子μ=1xyz,用它乘原方程得 0d d 2d =++zz y y x x 积分后得积分曲面族xy 2z=c也可把方程化为等价的方程组⎪⎪⎩⎪⎪⎨⎧-=∂∂-=∂∂y z yz x z xz 2 把y 看成参变量,积分xzx z -=∂∂得通解 zx c= 用未知函数()~cy 代替 c ,将()y c zx ~=代入方程y z y z 2-=∂∂得 ()()yy cy y c ~2d ~d -= 积分后有()~cy c y =2所以原方程的积分曲面族是xy 2z=c五、 一阶线性微分方程组[一阶线性偏微分方程组的一般形式] 两个自变量的一阶线性方程组的形式是()n i F u C x u B t u A i n j j ij n j n j jij j ij ,,2,10111 ==++∂∂+∂∂∑∑∑=== 或()n i f u b x u a t u i n j j ij n j j ij i,,2,1011 ==++∂∂+∂∂∑∑== (1) 其中A ij ,B ij ,C ij ,F i ,a ij ,b ij ,f i 是(x,t )的充分光滑函数. [特征方程·特征方向·特征曲线]⎩⎨⎧=≠==-j i j i t xa ij ij ij ,1,0,0)d d det(δδ称为方程组(1)的特征方程.在点(x,t )满足特征方程的方向txd d 称为该点的特征方向.如果一条曲线l ,它上面的每一点的切线方向都和这点的特征方向一致,那末称曲线l 为特征曲线. [狭义双曲型方程与椭圆型方程] 如果区域D 内的每一点都存在n 个不同的实的特征方向,那末称方程组在D 内为狭义双曲型的.如果区域D 内的每一点没有一个实的特征方向,那末称方程组在D 内为椭圆型的. [狭义双曲型方程组的柯西问题] 1︒ 化方程组为标准形式——对角型因为det(a ij -δij λ)=0有n 个不同的实根λ1(x,t ) ,, λn (x,t ),不妨设),(),(),(21t x t x t x n λλλ<<<那末常微分方程()()n i t x txi ,,2,1,d d ==λ 的积分曲线l i (i =1,2,…,n )就是方程组(1)的特征曲线. 方程()()aijk ij k i i n-==∑λδλ1的非零解(λk (1) ,, λk (n ))称为对应于特征方向λk 的特征矢量. 作变换()()n i u v nj jj i i ,,2,11==∑=λ可将方程组化为标准形式——对角型()()()()n i t x v t x a x v t x t v i nj j ij ii i ,,2,1,,,1=+=∂∂+∂∂∑=βλ 所以狭义双曲型方程组可化为对角型,而一般的线性微分方程组(1)如在区域D 内通过未知函数的实系数可逆线性变换可化为对角型的话,(此时不一定要求 λi 都不相同),就称这样的微分方程组在D 内为双曲型的. 2︒ 对角型方程组的柯西问题 考虑对角型方程组的柯西问题()()()()()()n i x x v t x v t x a x v t x tv i inj i j ij i i i,,2,10,,,,1 =⎪⎩⎪⎨⎧=+=∂∂+∂∂∑=ϕβλ ϕi (x )是[a,b ]上的连续可微函数.设αij ,βi ,λi 在区域D 内连续可微,在D 内可得相应的积分方程组()()()n i tv x t x v il i n j j ij i i i ,,2,1d ,~1 =⎥⎦⎤⎢⎣⎡++=⎰∑=βαϕ 式中 l i 为第i 条特征曲线l i 上点(x,t )与点(x i ,0)之间的一段,(x i ,0)为l i与x 轴上[a,b ]的交点.上式可以更确切地写为()()[]()[]()[]()[]⎰∑⎭⎬⎫⎩⎨⎧+⋅+==t n j i i i j i ij i i i t x x t x x v t x x a t x x t x v 01d ,,,,,,,,,0,,,τττβττττϕ(i =1,2,, n )式中x i =x i (x ︒,t ︒,t )为过点(x ︒,t ︒)的第i 条特征曲线,利用逐次逼近法可解此积分方程.为此令()()()[]()()()()[]()[]()()[]()[]()()()()[]()[]()()[]()[]()n i t x x t x x v t x x a t x x t x v n i t x x t x x v t x x a t x x t x v n i t x x t x v i i tnj i k j i ij i i k ii i tnj i j i ij i i ii i i ,,2,1d ,,,,,,,,,0,,,,,2,1d ,,,,,,,,,0,,,,,2,10,,,}{}{01101010=+⋅+==+⋅+===⎰∑⎰∑=-=τττβττττϕτττβττττϕϕ序列{v i (k )} (k =0,1,2 ,)一致收敛于积分方程的连续可微解v i (x,t ) (i =1,2,, n ),这个v i (x,t )也就是对角型方程组的柯西问题的解.设在区域D 内对角型方程组的柯西问题的解存在,那末解与初值有下面的关系:(i) 依赖区间:过D 中任意点M (x,t )作特征曲线l 1,l n ,交x 轴于B,A ,称区间[A,B ]为M 点的依赖区间(图14.1(a )),解在M 点的值由区间[A,B ]的初值确定而与[A,B ]外的初值无关. (ii) 决定区域:过点A,B 分别作特征曲线l n ,l 1,称l n ,l 1 与区间[A,B ]围成的区域D 1为区间[A,B ]的决定区域(图14.1(b )),在区域D 1中解的值完全由[A,B ]上的初值决定.(iii) 影响区域:过点A,B 分别作特征曲线l 1,l n ,称l 1,l n 与[A,B ]围成的区域D 2为区间[A,B ]的影响区域(图14.1(c )).特别当区间[A,B ]缩为一点A 时,A 点的影响区域为D 3(图14.1(d )).在区域D 2中解的值受[A,B ]上的初值影响,而在区域D 2外的解的值则不受[A,B ]上的初值影响.图14.1[线性双曲型方程组的边值问题] 以下列线性方程组来说明:()⎪⎪⎩⎪⎪⎨⎧<++=∂∂+∂∂++=∂∂+∂∂2122221111λλλλc v b u a x v t v c v b u a xu t u (1) 1︒ 第一边值问题(广义柯西问题) 设在平面(x,t )上给定曲线段⋂AB ,它处处不与特征方向相切.过A,B 分别引最左和最右的特征曲线l 1及l 2.要求函数u (x,t ),v (x,t )在⋂AB ,l 1及l 2围成的闭区域D 上满足方程组,且在⋂AB 上取给定的函数值(图14.2(a )).2︒ 第二边值问题(古沙问题) 设l 1是过P 点的第一族特征线,l 2是第二族特征线,在l 1的一段PA 上给定v (x,t )的数值,在l 2的一段PB 上给定u (x,t )的数值,过A 点作第二族特征线,过B 点作第一族特征线相交于Q .求在闭区域PAQB 上方程组的解(图14.2(b )).3︒ 第三边值问题 设AB 为非特征曲线的曲线弧,AC 为一特征线弧,且在AB 与AC 之间不存在过A 点的另外特征曲线,过C 点作第二族特征线与过B 点的第一族特征线交于E 点,在AC 上给定v (x,t )的数值,在AB 上给定u (x,t )的数值,求ACEBA 所围成的闭区域D 上的方程组的解(图14.2(c)).图14.2[边值问题的近似解——特征线法] 以上定解问题,可用逐步逼近法求解,也可用特征线法求解的近似值.以第一边值问题为例说明.在曲线AB 上取n 个分点A 1,A 2,, A n ,并记A 为A 0,B 为A n +1,过A 0按A 0的第二特征方向作直线与过A 1按A 1的第一特征方向作直线相交于B 0;过A 1按A 1第二特征方向作直线与过A 2按A 2的第一特征方向作直线相交于B 1 ,最后得到B n (图14.3).用如下的近似公式来确定方程组(1)的解u (x,t ),v (x,t )在B i (i =0,1,2,…,n )的数值:()()()()()()(){}()[]()()()()()()(){}()[]u B u A B A a A u A b A v A c A A v B v A B A a A u A b A v A c A A i i i i i i i i i i i i i i i i i i i i -=++⨯+-=++⨯+⎧⎨⎪⎩⎪+++++++--11111111112122212121211λλ图14.3于是在一个三角形网格的节点上得到u,v 的数值.再经过适当的插值,当n 相当大,A i 、A i +1的距离相当小时,就得到所提问题的足够近似的解.[特殊形式的拟线性方程组——可化约系统] 一般的拟线性方程组的问题比较复杂,目前研究的结果不多,下面介绍一类特殊形式的拟线性方程组——可化约系统.如果方程组⎪⎪⎩⎪⎪⎨⎧=∂∂+∂∂+∂∂+∂∂=∂∂+∂∂+∂∂+∂∂0022221111x v D t v C x u B tu A xv D t v C x u B t uA 中所有的系数只是u,v 的函数,称它为可化约系统. 考虑满足条件()()0,,≠∂∂t x v u 的方程组的解u=u (x,t ),v=v (x,t ).x,t 可以表示成u,v 的函数,且()()()()()()()()v u t x u t x v v u t x u x t v v u t x v tx u v u t x v x t u ,,,,,,,,,,∂∂∂∂=∂∂∂∂∂∂-=∂∂∂∂∂∂-=∂∂∂∂∂∂=∂∂ 原方程化为⎪⎪⎩⎪⎪⎨⎧=∂∂+∂∂-∂∂-∂∂=∂∂+∂∂-∂∂-∂∂0022221111u t D u x C v t B vx A ut D u x C v t B v xA 这是关于自变量u,v 的线性方程组.这样就把求拟线性方程组满足()()0,,≠∂∂t x v u 的解,化为解线性方程组的问题.而此线性方程组满足条件()()0,,≠∂∂v u t x 的解,在(x,t )平面上的象即为原来拟线性方程组的解.§3 二阶偏微分方程一、 二阶偏微分方程的分类、标准形式与特征方程考虑二阶偏微分方程()0),,,,,,(111,2=∂∂∂∂+∂∂∂∑=nnnj i j i ij x u x u u x x F y x u x a (1) 式中a ij (x )=a ij (x 1,x 2,…,x n )为x 1,x 2,…,x n 的已知函数.[特征方程·特征方向·特征曲面·特征平面·特征锥面]代数方程()01,=∑=nj i jiijaa x a称为二阶方程(1)的特征方程;这里a 1,a 2,…,a n 是某些参数,且有012≠∑=ni i a .如果点x ︒=(x 1︒,x 2︒,…,x n ︒)满足特征方程,即()01,o =∑=nj i jiijaa x a则过x ︒的平面()01o=-∑=nk kk k x x a 的法线方向l :(a 1,a 2,…,a n )称为二阶方程的特征方向;如果一个(n 1-)维曲面,其每点的法线方向都是特征方向,则称此曲面为特征曲面;过一点的(n 1-)维平面,如其法线方向为特征方向,则称这个平面为特征平面,在一点由特征平面的包络组成的锥面称为特征锥面.[n 个自变量方程的分类与标准形式] 在点P (x 1︒,x 2︒,…,x n ︒),根据二次型()∑=nj i jinijaa x x x a 1,o o 2o 1,,, (a i 为参量)的特征根的符号,可将方程分为四类:(i) 特征根同号,都不为零,称方程在点P 为椭圆型.(ii) 特征根都不为零,有n 1-个具有同一种符号 ,余下一个符号相反,称方程在点P 为双曲型.(iii) 特征根都不为零,有m n -个具有同一种符号(n >m >1),其余m 个具有另一种符号,称方程在点P 为超双曲型.(iv) 特征根至少有一个是零,称方程在点P 为抛物型.若在区域D 内每一点方程为椭圆型,双曲型或抛物型,则分别称方程在区域D 内是椭圆型、双曲型或抛物型.在点P 作自变量的线性变换可将方程化为标准形式:椭圆型:∑==+∂∂ni ix u1220Φ双曲型:∑==+∂∂-∂∂n i ix ux u 22120Φ超双曲型:()10112222>>=+∂∂-∂∂∑∑=+=m n x ux u m i nm i ii Φ抛物型:()00122>=+∂∂∑-=m x umn i iΦ 式中Φ为不包含二阶导数的项.[两个自变量方程的分类与标准形式] 方程的一般形式为0,,,,222222122211=⎪⎪⎭⎫⎝⎛∂∂∂∂+∂∂+∂∂∂+∂∂y u x u u y x F y u a y x u a x u a (2) a 11,a 12,a 22为x ,y 的二次连续可微函数,不同时为零. 方程a 11d y 22-a 12d x d y +a 22d x 2=0称为方程(2)的特征方程.特征方程的积分曲线称为二阶方程(2)的特征曲线. 在某点P (x 0,y 0)的邻域D 内,根据Δ=a 122-a 11a 12的符号将方程分类: 当Δ>0时,方程为双曲型; 当Δ=0时,方程为抛物型; 当Δ<0时,方程为椭圆型.在点P 的邻域D 内作变量替换,可将方程化为标准形式:(i ) 双曲型:因Δ>0,存在两族实特征曲线11),(c y x =ϕ,22),(c y x =ϕ,作变换),(1y x ϕξ=,),(2y x ϕη=和,,ηηξ-=+=s t s 方程化为标准形式),,,,(2222tus u u t s t u s u ∂∂∂∂=∂∂-∂∂Φ或),,,,(12ηξηξΦηξ∂∂∂∂=∂∂∂uu u u (ii ) 抛物型: 因Δ=0,只存在一族实的特征曲线c y x =),(ϕ,取二次连续可微函数),(y x ψ,使0),(),(≠∂∂y x ψϕ,作变换),(y x ϕξ=,),(y x ψη=,方程化为标准形式),,,,(222ηξηξΦη∂∂∂∂=∂∂uu u u (iii ) 椭圆型:因Δ<0,不存在实特征曲线,设c y x i y x y x =+=),(),(),(21ϕϕϕ为11221121212d d a a a a a x y -+=的积分,y x ϕϕ,不同时为零,作变量替换),(1y x ϕξ=,),(2y x ϕη=,方程化为标准形式),,,,(32222ηξηξΦηξ∂∂∂∂=∂∂+∂∂uu u u u二、 极值原理·能量积分·定解问题的惟一性定理椭圆型方程、抛物型方程的极值原理及双曲型方程的能量守恒原理是相应方程的解所具有的最基本性质之一,在定解问题的研究中起着重要的作用. [椭圆型方程的极值原理与解的惟一性定理]1︒ 极值原理 设D 为n 维欧氏空间E n 的有界区域,S 是D 的边界,在D 内考虑椭圆型方程()()()()x x x x f u c x ub x x u a Lu ni i i n j i j i ij =+∂∂+∂∂∂≡∑∑==11,2式中a ij (x ),b i (x ),c (x ),f (x )在D 上连续,c (x )≤0且二次型()∑=nj i j i ij a a a 1,x 正定,即存在常数μ>0,对任意x D ∈和任意的a i 有()∑∑==≥ni i nj i jiija aa a 121,μx定理1 设u (x )为D 内椭圆型方程的解,它在D 内二次连续可微,在D 上连续,且不是常数,如f (x )≤0(或f (x )≥0),则u (x )不能在D 的内点取非正最小值(或非负最大值). 如果过边界S 上的任一点P 都可作一球,使它在P 点与S 相切且完全包含在区域D 内,则有 定理2 设u (x )为椭圆型方程在D 内二次连续可微,在D 上连续可微的解,且不是常数,并设f (x )≤0(或f (x )≥0).若u (x )在边界S 上某点M 处取非正最小值(或非负最大值),只要外法向导数错误!未定义书签。
偏微分方程数值解一(10分)、设矩阵A 对称正定,定义)(),(),(21)(n R x x b x Ax x J ∈-=,证明下列两个问题等价:(1)求n R x ∈0使)(min )(0x J x J n Rx ∈=;(2)求下列方程组的解:b Ax = 解: 设n R x ∈0是)(x J 的最小值点,对于任意的n R x ∈,令),(2),()()()(2000x Ax x b Ax x J x x J λλλλϕ+-+=+=, (3分)因此0=λ是)(λϕ的极小值点,0)0('=ϕ,即对于任意的n R x ∈,0),(0=-x b Ax ,特别取b Ax x -=0,则有0||||),(2000=-=--b Ax b Ax b Ax ,得到b Ax =0. (3分) 反之,若nR x ∈0满足bAx =0,则对于任意的x ,)(),(21)0()1()(00x J x Ax x x J >+==+ϕϕ,因此0x 是)(x J 的最小值点. (4分)评分标准:)(λϕ的表示式3分, 每问3分,推理逻辑性1分二(10分)、对于两点边值问题:⎪⎩⎪⎨⎧==∈=+-=0)(,0)(),()(b u a u b a x f qu dxdu p dx d Lu 其中]),([,0]),,([,0)(min )(]),,([0min ],[1b a H f q b a C q p x p x p b a C p b a x ∈≥∈>=≥∈∈建立与上述两点边值问题等价的变分问题的两种形式:求泛函极小的Ritz 形式和Galerkin 形式的变分方程。
解: 设}0)()(),,(|{11==∈=b u a u b a H u u H 为求解函数空间,检验函数空间.取),(10b a H v ∈,乘方程两端,积分应用分部积分得到 (3分))().(),(v f fvdx dx quv dxdv dx du p v u a b a ba ==+=⎰⎰,),(1b a H v ∈∀ 即变分问题的Galerkin 形式. (3分)令⎰-+=-=b a dx fu qu dxdup u f u u a u J ])([21),(),(21)(22,则变分问题的Ritz 形式为求),(1*b a H u ∈,使)(m in )(10*u J u J H u ∈= (4分) 评分标准:空间描述与积分步骤3分,变分方程3分,极小函数及其变分问题4分,三(20分)、对于边值问题⎪⎩⎪⎨⎧=⨯=∈-=∂∂+∂∂∂0|)1,0()1,0(),(,12222G u G y x yux u (1)建立该边值问题的五点差分格式(五点棱形格式又称正五点格式),推导截断误差的阶。
高等数学教材第三版答案为了方便广大高等数学学习者更好地学习,我特意整理了高等数学教材第三版的答案,希望能对大家的学习有所帮助。
下面是对教材中各章节习题的答案解析。
第一章微分学1.1 函数与极限1.2 导数与微分1.3 微分中值定理与导数的应用第二章积分学2.1 定积分2.2 反常积分2.3 定积分的应用第三章无穷级数3.1 数项级数3.2 幂级数3.3 函数项级数第四章高次方程及其解法4.1 代数方程与代数方程的根4.2 高次代数方程的整数根与有理根4.3高次代数方程的正根与实根4.4高次代数方程的复根第五章傅立叶级数5.1 傅立叶级数的定义与性质5.2 奇延拓与偶延拓5.3 傅立叶级数的收敛性第六章偏微分方程6.1 偏导数与偏微分方程6.2 一阶线性偏微分方程6.3 高阶线性偏微分方程第七章多元函数微分学7.1 多元函数的极限与连续7.2 一阶偏导数与全微分7.3 高阶偏导数与多元函数微分学应用第八章向量代数与空间解析几何8.1 向量代数8.2 空间解析几何8.3 平面与直线的夹角与距离第九章多元函数积分学9.1 二重积分9.2 三重积分9.3 三重积分的应用第十章曲线积分与曲面积分10.1 第一类曲线积分10.2 第二类曲线积分10.3 曲面积分第十一章广义重积分与格林公式11.1 广义重积分11.2 格林公式及其应用11.3 闭曲线上格林公式的应用第十二章级数的一致收敛性12.1 函数项级数的一致收敛性12.2 幂级数的一致收敛性12.3 一致收敛性的应用第十三章线性代数初步13.1 行列式13.2 向量空间与线性方程组13.3 特征值与特征向量第十四章线性代数进阶14.1 线性空间与线性映射14.2 矩阵与线性映射14.3 特征多项式与相似矩阵注意:以上只是教材中各章节的题目答案简要解析,建议在学习过程中,除了参考答案之外,还需要仔细研读教材中的知识点,并通过大量的练习来巩固和加深理解。
第四章 二阶线性偏微分方程的分类与总结§1 二阶方程的分类1. 证明两个自变量的二阶线性方程经过可逆变换后它的类型不会改变,也就是说,经可逆变换后2211212a a a -=∆的符号不变。
证:因两个自变量的二阶线性方程一般形式为fcu u b u b u a u a u a y x yy xy xx =+++++212212112经可逆变换 ⎩⎨⎧==),(),(y x y x ηηξξ 0),(),(≠y x D D ηξ化为 f u c u b u a u a u a =++++ηηηξηξξ22212112其中 ⎪⎪⎩⎪⎪⎨⎧++=+++=++=22212211222212111222212211112)(2y y x x y y x y y x x x y y x x a a a a a a a a a a a a ηηηηηξηξηξηξξξξξ所以 y x y x y x y x x y yx a a a aa a aηηξξηηξξηξηξ2211112222122221112222)(+-+=-=∆22221112222222211),(),())(()(⎥⎦⎤⎢⎣⎡∆=--=+-y x D D a a aa a x y y x y x y x ηξηξηξηξξη因0),(),(2>⎥⎦⎤⎢⎣⎡y x D D ηξ,故∆与∆同号,即类型不变。
2. 判定下述方程的类型(1)022=-yy xx u y u x (2)0)(2=++yy xx u y x u (3)0=+yyxx xyuu(4))010001(sgn 0sgn 2sgn ⎪⎩⎪⎨⎧<-=>==++x x x x xuu yu yyxy xx(5) 0424=+++-zz yy xz xy xx u u u u u 解:(1)022=-yy xx u y u x因 022>=∆y x 当0,0≠≠y x 时0,0=>∆x 或0=y 时0=∆。