下载文档原格式
第四单元《多边形的面积》知识点1：长方形的面积=长×宽字母公式：S=ab长方形的周长=（长+宽）×2 字母公式：C=（a+b）×2（长=周长÷2—宽；宽=周长÷2—长）长方形的面积、周长与长和宽之间的变化关系：（1）长方形的长加宽等于长方形周长的一半，即a+b=C÷2（2）长方形框架拉成平行四边形，周长不变，面积变小。
知识点2：正方形面积=边长×边长字母公式：S=a×a正方形周长=边长×4 字母公式：C=4a（边长=面积÷4）知识点3：平行四边形面积=底×高字母公式：s=ah（平行四边形的底=面积÷高，即a=S÷h；平行四边形的高=面积÷底, 即h=S÷a）平行四边形面积公式的推导过程：剪拼、平移平行四边形的任意一条高剪开，将其一部分平移与另一部分正好拼成一个长方形，这个长方形的长就是平行四边形的底，这个长方形的宽就是平行四边形的高。
因为长方形面积=长×宽，所以平行四边形面积=底×高，用字母表示：S=a×h。
等底等高的平行四边形面积相等。
知识点4：三角形面积=底×高÷2 字母公式：S=ah÷2（三角形的底=面积×2÷高，即a=S×÷h；三角形的高=面积×2÷底，即h=S×2÷a）三角形面积公式的推导过程：旋转、平移（将两个完全一样的三角形拼成一个平行四边形，拼成的平行四边形的底就是三角形的底，拼成的平行四边形的面积是三角形面积的2倍。
一个三角形面积是这个平行四边形面积的一半。
因为平行四边形的面积=底×高，所以三角形面积=底×高÷2，即S=ah÷2）等底等高的三角形面积相等。
北师大五年级数学上册第四单元单元知识点第四单元多边形面积（一）比较图形的面积知识点：确定一个图形面积的大小，不仅是根据图形的形状，更重要的是根据图形所占格子的多少来确定。
（二）底和高：1、认识平行四边形、三角形与梯形的底和高。
【高和底的关系是对应的】①从平行四边形一边的某一点到对边画垂直线段，这条垂直线段就是平行四边形的高，对应的这条对边是平行四边形的底。
【平行四边形有无数条高】②三角形的一个顶点到对边的垂直线段是三角形的高，这条对边是三角形的底。
【三角形有三个顶点，所以三角形有3条高】③从梯形的两条平行线中的一条上的某一点到对边画垂直线段，这条垂直线段就是梯形的高，这条对边就是梯形的底。
【梯形有无数条高】（三）用三角板画出平行四边形的高的方法：把三角板的一条直角边与平行四边形的一条边重合，让三角板的另一条直角边过对边的某一点。
从这一点沿着三角板的另一条直角边向它的对边画垂线，这条垂线（从点到垂足）就是平行四边形一条边上的高。
注意：从一条边上的任意一点可以向它的对边画高，也可以从另一条边上的任意一点向它的对边画高。
（四）用三角板画出图形的高的方法：把三角板的一条直角边对准三角形的一个顶点，另一条直角边与这个顶点的对边重合。
从这个顶点沿着三角板的另一条直角边向它的对边画垂线，这条垂线（从顶点到垂足）就是三角形形一条边上的高。
（五）探索活动知识点：两组对边平行且相等的四边形叫作平行四边形。
只有一组对边平行的四边形叫作梯形。
平行四边形的面积——【S平行四边形=拼成的长方形的面积】长方形的长就是平行四边形的底；长方形的宽就是平行四边形的高。
因此：平行四边形面积=底×高如果用S表示平行四边形的面积，用a和h分别表示平行四边形的底和高，那么，平行四边形的面积公式可以写成：S=ah补充知识点：当平行四边形的底和高相同时，其面积也是相同的。
三角形的面积——【S三角形=两个相同三角形拼成的平行四边形的面积÷2】三角形的底和高，也就是平行四边形的底和高。
北师大版数学五年级上册第4单元《多边形的面积》说课稿一. 教材分析《多边形的面积》是北师大版数学五年级上册第4单元的内容。
本节课是在学生已经掌握了平面图形的认识、线的特征、角的特征等知识的基础上进行学习的。
通过本节课的学习，学生需要掌握多边形的面积的计算方法，培养学生的空间观念和逻辑思维能力。
二. 学情分析五年级的学生已经具备了一定的数学基础，对于图形的认识和角的特征有一定的了解。
但是，学生对于多边形的面积的计算方法可能还比较陌生，需要通过实例和操作来理解和掌握。
三. 说教学目标1.知识与技能目标：学生能够掌握多边形的面积的计算方法，并能够灵活运用。
2.过程与方法目标：学生通过观察、操作、思考等过程，培养空间观念和逻辑思维能力。
3.情感态度与价值观目标：学生能够积极参与数学学习，对数学产生兴趣。
四. 说教学重难点1.教学重点：学生能够掌握多边形的面积的计算方法。
2.教学难点：学生能够理解和掌握多边形的面积的计算原理。
五. 说教学方法与手段1.教学方法：采用问题驱动法、合作学习法、实践操作法等。
2.教学手段：利用多媒体课件、实物模型、学习卡片等辅助教学。
六. 说教学过程1.导入：通过展示一些生活中的多边形图形，如足球、自行车轮胎等，引发学生对多边形的兴趣，进而导入本节课的内容。
2.探究：学生通过观察和操作，探索多边形的面积的计算方法。
教师引导学生思考多边形的面积与哪些因素有关，如何计算多边形的面积。
3.讲解：教师通过讲解和示范，引导学生理解和掌握多边形的面积的计算方法。
4.练习：学生通过练习题目的解答，巩固对多边形的面积的计算方法的理解和掌握。
5.总结：教师引导学生总结本节课的学习内容，强化对多边形的面积的计算方法的记忆。
七. 说板书设计板书设计要简洁明了，能够突出本节课的主要内容和知识点。
可以设计成流程图或者图示的形式，展示多边形的面积的计算过程和步骤。
八. 说教学评价教学评价可以从学生的知识掌握、能力培养、情感态度等方面进行。
易错点:移补后图形的面积没有改变,周长可能有变化。
易错题:判断:割补后图形的面积不变,则周长也不变。
(√) 错因分析:图形割补后形状发生了变化,所以周长也可能发生变化。
如割补后的图形周长变小了。
答案:✕重点提示:1. 梯形有无数条高。
2. 在平行四边5. 只确定了底和高,并不能却定一个图形的具体形状,等底等高可以画出无数个不同形状的图形。
6. 对应的底和高互相垂直。
．．．．．．．．．．．三、平行四边形的面积1. 通过割补法把平行四边形转化为长方形,长方形的长等于原平行四边形的底,长方形的宽等于原平行四边形的高。
平行四边形的面积=底×高;用字母表示为S=ah。
2. 长方形的长=平行四边形的底长方形的宽=平行四边形的高长方形的面积=长×宽平行四边形的面积=底×高3. 等底等高的平行四边形的面积相等。
4. 平行四边形的面积公式的应用:已知平行四边形的面积和高,求平行四边形的底,可以用“底=平行四边形的面积÷高”来解答。
四、三角形的面积求平行四边形的面积。
错解:6×7=42(cm2)错因分析:计算平行四边形的面积要用一组对应的底和高相乘。
答案:7×4=28(cm2)易错题:判断:两个面积相等的三角形一定能拼成一个平行四边形。
(√)错因分析:两个面积相等的三角形的形状不一定相同,两个完全相同的三角形才能拼成一个1. 两个完全相同的三角形能拼成一个平行四边形。
平行四边形的底和高分别是三角形的底和高。
2. 三角形的面积是与它等底等高的平行四边形面积的一半。
3. 三角形的面积=底×高÷2,用字母表示为S=ah÷2。
4. 三角形的面积公式的应用:已知三角形的面积和底,要求三角形的高,可以应用“高=三角形的面积×2÷底”来解答。
5. 等底等高的三角形的面积相等。
五、梯形的面积1. 两个完全相同的梯形,可以拼成一个平行四边形。
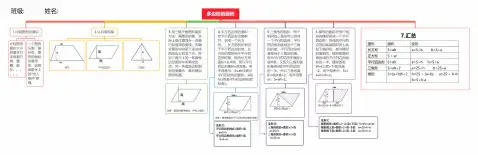
多边形的面积1.比较图形的面积①比较图形面积大小的基本方法有数方格、重叠、割补。
②一个图形分割、移补后，图形的面积没有改变，这就是数学上的“出入相补”原理。
2.认识底和高3.用三角尺画图形高的方法：画图形的高，实际上是过直线外一点画已知直线的垂线。
先确定图形中的某个顶点或图形边上的某个点，然后三角尺上的一条直角边过图形中所确定的点，另一条直角边和图形的底重合，最后画出图形的高。
注意：画高时要用虚线，并标上垂足。
4.平行四边形的面积：把平行四边形沿高剪开，拼成一个长方形，，长方形的长相当于平行四边形的底，长方形的宽相当于平行四边形的高，因为长方形面积=长X宽，所以平行四边形面积=底X高。
用字母表示：S=ah(S表示平行四边形的面积，a和h分别是平行四边形的底和高)。
注意：等底等高的平行四边形的面积相等变形式：平行四边形的底=面积÷高a=S÷h平行四边形的高=面积÷底h=S÷a5.三角形的面积：两个相同的三角形可以拼成一个平行四边形，平行四边形的底相当于三角形的底，平行四边形的高相当于三角形的高，因为平行四边形的面积=底X高，又因为三角形面积是拼成的平行四边形的一半，所以三角形面积=底X高÷2，用字母表示：S=ah÷2。
变形式：三角形的底=面积×2÷高a=2S÷h三角形的高=面积×2÷底h=2S÷a6.梯形的面积:把两个相同的梯形拼成一个平行四边形，拼成的平行四边形的底是梯形的上底和下底的和，高与梯形的高相同，梯形的面积是拼成的平行四边形面积的一半。
梯形的面积=(上底+下底)X高÷2，用字母表示：S=(a+b)×h÷2。
变形式梯形的高=面积×2÷(上底+下底) h=2S÷(a+b) 梯形的上底=面积×2÷高-下底 a=2S÷h-b 梯形的下底=面积×2÷高-上底 a=2S÷h-a7.汇总。
多边形的面积1.比较图形的面积①比较图形面积大小的基本方法有数方格、重叠、割补。
②一个图形分割、移补后，图形的面积没有改变，这就是数学上的“出入相补”原理。
2.认识底和高3.用三角尺画图形高的方法：画图形的高，实际上是过直线外一点画已知直线的垂线。
先确定图形中的某个顶点或图形边上的某个点，然后三角尺上的一条直角边过图形中所确定的点，另一条直角边和图形的底重合，最后画出图形的高。
注意：画高时要用虚线，并标上垂足。
4.平行四边形的面积：把平行四边形沿高剪开，拼成一个长方形，，长方形的长相当于平行四边形的底，长方形的宽相当于平行四边形的高，因为长方形面积=长X宽，所以平行四边形面积=底X高。
用字母表示：S=ah(S表示平行四边形的面积，a和h分别是平行四边形的底和高)。
注意：等底等高的平行四边形的面积相等变形式：平行四边形的底=面积÷高a=S÷h平行四边形的高=面积÷底h=S÷a5.三角形的面积：两个相同的三角形可以拼成一个平行四边形，平行四边形的底相当于三角形的底，平行四边形的高相当于三角形的高，因为平行四边形的面积=底X高，又因为三角形面积是拼成的平行四边形的一半，所以三角形面积=底X高÷2，用字母表示：S=ah÷2。
变形式：三角形的底=面积×2÷高a=2S÷h三角形的高=面积×2÷底h=2S÷a6.梯形的面积:把两个相同的梯形拼成一个平行四边形，拼成的平行四边形的底是梯形的上底和下底的和，高与梯形的高相同，梯形的面积是拼成的平行四边形面积的一半。
梯形的面积=(上底+下底)X高÷2，用字母表示：S=(a+b)×h÷2。
变形式梯形的高=面积×2÷(上底+下底) h=2S÷(a+b) 梯形的上底=面积×2÷高-下底 a=2S÷h-b 梯形的下底=面积×2÷高-上底 a=2S÷h-a7.汇总。
第四单元多边形的面积
㈠比较图形的面积
知识点：
借助方格纸,能直接判断图形面积的大小。
平面图形面积大小的比较有多种方法：根据图形面积的大小,可以直接进行比较；可以借助参照物进行比较；可以运用重叠的方法进行比较；借助方格,利用数方格的的方法进行比较；直接计算面积后再进行比较等。
图形面积相同,其形状可以是不同的。
补充知识点：
确定一个图形面积的大小,不仅是根据图形的形状,更重要的是根据图形所占格子的多少来确定。
㈡地毯上的图形面积
知识点：
根据地毯上所给图案探求不规则图案面积的计算方法。
直接通过数方格的方法,得出答案的面积。
将图案进行“化整为零”式的计算,即根据图案的特点,将整体的图案分割为若干个相同面积的小图案,通过求小图案的面积,得出整个图案的面积。
采用“大面积减小面积”的方法,即通过计算相关图形的面积,得到所求的面积。
补充知识点：
在解决问题时,策略和方法是多种多样的。
㈢动手做
知识点：
认识平行四边形、三角形与梯形的底和高。
从平行四边形一边的某一点到对边画垂直线段,这条垂直线段就是平行四边形的高,这条对边是平行四边形的底。
三角形的一个顶点到对边的垂直线段是三角形的高,这条对边是三角形的底。
从梯形的两条平行线中的一条上的某一点到对边画垂直线段,这条垂直线段就是梯形的高,这条对边就是梯形的底。
高和底的关系是对应的。
用三角板画出平行四边形的高的方法：
把三角板的一条直角边与平行四边形的一条边重合,让三角板的另一条直角边过对边的某一点。
从这一点沿着三角板的另一条直角边向它的对边画垂线,这条垂线（从点到垂足）就是平行四边形一条边上的高。
注意：从一条边上的任意一点可以向它的对边画高,也可以从另一条边上的任意一点向它的对边画高。
用三角板画出三角形的高的方法：
把三角板的一条直角边对准三角形的一个顶点,另一条直角边与这个顶点的对边重合。
从这个顶点沿着三角板的另一条直角边向它的对边画垂线,这条垂线（从顶点到垂足）就是三角形形一条边上的高。
用三角板画梯形的高的方法：
用同样的方法,画出梯形两条平行线之间的垂直线段,就是梯形的高。
㈣探索活动（一）平行四边形的面积
知识点：
平行四边形的面积=拼成的长方形的面积
长方形的长就是平行四边形的底；长方形的宽就是平行四边．．．．．．．．．．．．．．．．．．．．．．．．．．形的高。
．．．
因此：平行四边形面积=底×高
如果用S表示平行四边形的面积,用a和h分别表示平行四边形的底和高,那么,平行四边形的面积公式可以写成：
S=ah
运用平行四边形的面积计算公式计算相关图形的面积并解决一些实际问题。
补充知识点：
㈤探索活动（二）三角形的面积
知识点：
三角形面积=两个相同三角形拼成的平行四边形的面积÷2
三角形的底和高,也就是平行四边形的底和高。
因此：三角形面积=平行四边形的面积÷2=底×高÷2
如果用S表示三角形的面积,用a和h分别表示三角形的底和高,那么,三角形的面积公式可以写成：
S=ah÷2
运用三角形的面积公式,计算相关图形的面积,解决实际问题。
补充知识点：
决定三角形面积的大小的因素不是图形的形状,而是三角形的底与高的长度,只．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．要底和高相同,不同形状的三角形的面积也是相同的。
．．．．．．．．．．．．．．．．．．．．．．．㈥探索活动（三）梯形的面积
知识点：
梯形面积=两个相同梯形拼成的平行四边形的面积÷2
梯形的上底与下底的和就是平行四边形的底,梯形的高就是平行四边形的高。
因此：梯形面积=平行四边形面积÷2=底×高÷2=（上底+下底）×高÷2
如果用S表示梯形的面积,用a和b分别表示梯形的上底和下底,用h表示梯形的高,那么,梯形的面积公式可以写成：
S= (a+b)h÷2
运用梯形面积的计算公式,解决相应的实际问题。
补充知识点：
决定梯形面积的大小的因素不是图形的形状,而是梯形的上、下底之和与高的长．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．度,只要上下底的和与高相同,不同形状的梯形的面积也是相同的。
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．。
