大气污染指数与气象参数数学模型
- 格式:wps
- 大小:952.12 KB
- 文档页数:22



A.污染气体的传播扩散摘要钢铁生产排放的污染气体是造成雾霾的重要原因之一,研究污染气体的扩散特征,正确模拟污染气体的扩散过程,能够为钢铁生产集团提出更好的治理管理措施,具有实际意义。
针对问题一:污染气体的排放速度为300m/s,在不考虑风向风速及高度影响的情况下,此问题即为二维平面的连续点源扩散问题,由此在二维xoy 平面上建立连续点源扩散方程模型()(,,)t xx yy u u u f x y t α=++,其中α 为气体扩散系数,本文中取为常数10,f(x,y,t ) 为污染气体的排放速度,在本文中恒为300m/s ;对上述偏微分方程模型,本文采用ADI 法(Alternating direction implicit ,交替方向隐式法)求解出迭代格式,利用MATLAB 编程,求出模型一的数值解,并得到任意时刻污染气体的浓度分布情况。
通过SPSS 软件,对附件一所给的原始实际数据与模型一求解得到的模拟值进行显著性检验,检验结果显示该模型与实际情况吻合。
针对问题二:考虑风向风速对污染气体扩散过程的影响时,在基于对问题一求解的基础上,在模型一的扩散方程模型中加入风向风速的平流项,由此得到有风情况下的模型),,()(21t y x f u u u u u yy xx y x t ++=--αββ,其中12ββ, 分别为风速在x, y 方向的分量;对此模型同样采用ADI 法求出迭代格式,利用MATLAB 编程,求出模型二的数值解,并得到任意时刻污染气体的浓度分布情况。
通过SPSS 软件,对附件二所给的原始实际数据与模型二求解得到的模拟值进行显著性检验,检验结果显示该模型与实际情况吻合。
针对问题三:考虑有风时增加高度的影响,此问题即为三维空间的污染气体扩散问题,考虑到三维模型的编程复杂度,而且污染气体的扩散在xoy 平面上各向同性,可以将污染气体在y 方向的扩散等价为在x 方向上的扩散,此时便只需要建立xoz 平面上的扩散模型。

大气污染评价与预报模型作者:管正雄李懿来源:《科技风》2018年第30期摘要:本文对空气质量的评价及污染预报问题进行了分析,运用层次分析法依据处理后的数据对四个城市的空气质量进行了排序;对一周内各项污染物浓度、各气象参数运用回归模型进行了预测;就气象参数所属城市问题及污染物浓度与其的关系建立了相关性分析模型和多元线性回归模型;根据建模过程和结果,提出了具体的建议。
关键词:API评价模型;层次分析;一元多項式回归模型一、问题提出近几年来,大气污染日趋严重,为加快改善环境空气质量,党的十九大作出重大决策部署要打赢蓝天保卫战。
打赢蓝天保卫战是事关满足人民日益增长的美好生活需要,事关经济高质量发展和美丽中国建设。
因此,加强大气质量的监测和预报显得非常必要。
目前对大气质量的监测主要是监测大气中SO2、NO2、悬浮颗粒物(主要为PM10)等的浓度,研究表明,城市空气质量好坏与季节及气象条件的关系十分密切。
现有城市A、B、C、D多年测量的污染物含量及气象参数的数据。
(1)找出各个城市SO2、NO2、PM10之间的特点,并将几个城市的空气质量进行排序。
(2)对未来一周各个城市的SO2、NO2、PM10以及各气象参数作出预测。
(3)分析空气质量与季节、气象参数之间的关系。
(4)就空气质量的控制对相关部门提出建议。
二、问题分析问题一寻找各城市SO2、NO2、PM10的特点,最直观的方法就是作图,把各城市的三种污染物浓度做到一张图中进行比较分析可较容易的得到其特点,而排序题目中给出的是三种污染物浓度,必须先用一个指标将它们统一起来综合的对城市的空气质量进行评价,用同一个指标进行排序。
问题二是依据所给的2017年1月1日至9月14日的数据,预测2017年9月15日至9月21日各个城市的SO2、NO2、PM10以及各气象参数,预测的时期较短,数目多,选择时间序列进行预测。
根据给定的数据,利用一元多项式回归,求得回归模型,从而预测出需要的数据,并进行预测误差估计。

大气污染监测与预测模型研究随着城市化进程的不断加快,空气污染问题越来越受到人们的关注。
大气污染已成为制约城市可持续发展的重要问题。
据统计,全球每年因空气污染导致的过早死亡人数多达700万人。
为了有效地治理大气污染问题,大气污染监测与预测模型的研发成为当今的热点问题。
一、大气污染监测的意义大气污染监测是指对大气环境中空气污染物的种类、浓度、分布、变化等进行定量、定性分析的过程。
监测结果是大气污染治理和预测模型研究的基础数据。
目前,各地都建立了大气污染物的监测网,包括城市大气环境自动监测网、国家环境保护部级监测站网络和省级机构监测站网络等。
这些监测数据可以用于制定大气污染治理计划、评估大气污染状况以及开展科学研究等。
二、大气污染预测模型的研究大气污染预测模型是指根据大气污染监测数据、气象数据、地理信息数据等,利用计算机技术建立的大气污染物浓度预测模型。
预测模型可以用于为政府决策部门提供决策支持、指导大气污染治理以及提高环境监管部门的执行效率等。
二、1 污染物扩散模型污染物扩散模型是目前应用最广泛的污染物预测模型之一。
它根据大气扩散规律和污染物释放源的数据,预测污染物在大气中的扩散距离和浓度。
常见的污染物扩散模型包括Gaussian模型、Lagrangian模型、Eulerian模型等。
这些模型可以针对不同的气象条件和地形环境,对污染物扩散进行精确预测。
二、2 人工神经网络模型人工神经网络是借鉴生物神经元之间相互通信的过程建立的数学模型。
人工神经网络模型是目前发展最快的大气污染预测模型之一。
它通过对监测数据的处理和分析,建立神经元间的关系模型,对污染物浓度进行预测。
相对于扩散模型,人工神经网络模型更能适用于不同的环境条件,对污染物浓度预测的准确性更高。
三、未来研究方向大气污染监测与预测模型的研究是一个长期的过程。
未来,我们需要在现有的基础上,进一步完善大气污染监测网络,提高监测数据的准确性。
同时,还需要加强对大气污染预测模型的研究,开发更加准确、可靠的预测模型,为政府制定大气污染治理计划提供更为可靠的数据支持。

数学模型在环境污染中的应用环境污染是当今社会面临的一个重要挑战,对人类健康和生态系统造成了极大的威胁。
为了有效解决环境污染问题,科学家们不断探索各种方法和工具,其中数学模型在环境污染研究中发挥着重要作用。
本文将探讨数学模型在环境污染中的应用,并介绍其中几个经典案例。
一、数学模型在大气污染中的应用大气污染是当前环境问题中最为突出的一部分。
数学模型可以帮助科学家们定量描述大气污染的传播和演化规律,从而为制定有效的减排措施提供依据。
例如,研究人员可以利用数学模型模拟大气中污染物的浓度分布。
通过收集实际观测数据,建立数学方程,考虑气象因素、污染源排放量以及地形等影响,科学家们可以推算出某一特定时间和地点的污染物浓度分布情况。
数学模型还可以预测不同减排措施的效果。
通过对模型参数的调整,可以模拟不同减排方案下大气污染的减少程度,进而帮助政府和相关部门选择最佳的减排方案。
这不仅可以在一定程度上缓解环境污染问题,还可以为决策者提供科学的依据和参考。
二、数学模型在水污染中的应用水污染是另一个严峻的环境问题,而数学模型同样可以在水污染研究中发挥重要作用。
在水污染研究中,科学家们可以利用数学模型对水体中污染物的扩散和蓄积过程进行模拟。
通过考虑流体动力学、水体自净能力以及污染源等因素,科学家们可以预测水体中污染物的浓度分布和变化趋势。
基于数学模型的水污染研究还可以预测水体中污染物的去除效果。
通过模拟不同的水处理方法和减排措施,科学家们可以评估这些方法对水污染的减少效果,从而为相关部门制定水污染治理方案提供科学依据。
三、数学模型在土壤污染中的应用土壤污染是另一个重要的环境问题,其对农作物生长和地下水质量产生影响。
数学模型在土壤污染研究中可以提供有效的预测和评估手段。
科学家们可以利用数学模型模拟土壤中污染物的迁移和转化过程。
通过考虑土壤物理性质、化学反应和微生物活动等因素,科学家们可以预测污染物在土壤中的扩散效应和降解过程。

大气污染评价与预报模型摘要本文对空气质量的评价及污染预报问题进行了分析,运用层次分析法依据处理后的数据对六个城市的空气质量进行了具体细致的排序;对2010年9月15日至9月21日的各项污染物浓度、各气象参数运用一元多项式回归模型进行了预测;就气象参数所属城市问题及污染物浓度与其的关系建立了相关性分析模型和多元线性回归模型;最后,根据建模过程和结果,我们对相关部门提出了几个具体的建议。
通过将数据附件所给有效数据,即日污染物浓度,转化为对应的月污染物浓度的均值,根据各城市月均污染浓度做出其随时间的走势折线图,分析了各个城市2SO 、2NO 、PM10之间的特点。
我们拟根据API 指数值,以二级达标次数为准,对各城市之间的空气质量进行排名,但由于依据API 的区分空气质量等级时灵敏度较低,故采用了层次分析法对空气质量进行排名。
由于我们采用了全部数据进行排名,而E 、F 数据较少,故只对ABCD 进行了排名。
依据层次分析法得出的排名为:A 、B 、D 、C 。
为了精确预测各城市短期内的数据,本文选用一元多项式回归模型。
对2010年的数据进行分析整理,依据回归模型得出其与时间的关系,得出预测值,并得出其置信度为95%的置信区间,结果显示模型的预测效果尚能接受,能够对所要预测数据进行预测。
但由于F 城市数据缺失,根据假设做了合理的定性分析,并未对其进行定量预测。
分析空气质量与气象参数之间的关系时,首先根据数据完整性,气象参数应只属于其中一个城市,排除了D 、E 、F 的可能性,再根据相关性分析的方法,确定了气象参数属于A 城市。
根据污染物与气象参数之间的因果关系,建立了多元线性回归模型,由于季节对污染物的浓度存在影响,分季节得出各污染物与各气象参数之间的相关系数,定性分析该相关系数,得出污染物与气象参数之间的关系。
最后对该系数的理论与实际意义做了检验。
根据以上分析及结果,确定部分与空气质量控制相关的部门,针对其职能提出了诚恳建议。
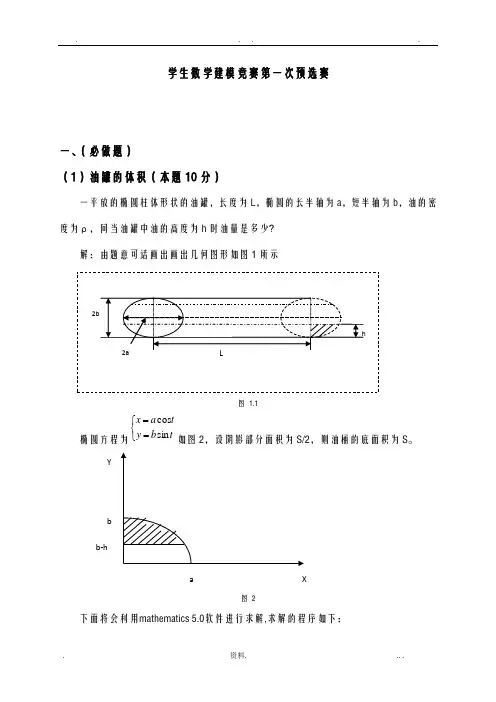
. . . .学生数学建模竞赛第一次预选赛一、(必做题)(1)油罐的体积(本题10分)一平放的椭圆柱体形状的油罐,长度为L ,椭圆的长半轴为a ,短半轴为b ,油的密度为ρ,问当油罐中油的高度为h 时油量是多少?解:由题意可话画出画出几何图形如图1所示图 1.1椭圆方程为⎩⎨⎧==t b y ta x sin cos 如图2,设阴影部分面积为S/2,则油桶的底面积为S 。
图 2下面将会利用mathematics 5.0软件进行求解,求解的程序如下:b XYab-hIntegrate[2*a*b*Cos[t]^2,{t,ArcSin[1-h/b],Pi/2}] 解得结果为:))1arccos()()2((2b hb h b bh h b a S -++--= 当b h >时,由椭圆对称性,A 中的h 用h b -2代替得到:))1arccos()()2((2-+---=b hb h b bh h b a ab S π 所以油液质量M 为:⎪⎪⎩⎪⎪⎨⎧-+---=>-++--=<==))1arccos()()2(())1arccos()()2((22b h b h b b h h b aL abL M b h b hb h b b h h b aL M b h SL M ρρπρρ,则若,则若(2)光的反射定律(本题10分)费马原理:光总是沿用时最短的光程传播。
试根据这一原理利用极值的有关知识证明光的反射定律:入射角等于反射角。
解:由于光在同一介质中的速度为常数,所以在同一介质中光总是沿直线传播。
如图3,现假设有两种介质1、2相接,光线在介质1中的传播速度为v,取两介质的分界线上的一条直线为X 轴,设有一束光线从介质1中的),0(a A 点经X 轴上的)0,(x P 点反射,并沿直线方向行进到),(b d B 点。
设直线AP 与X 轴法线的夹角为1θ,PB 直线与X 轴法线的夹角为2θ,下面,根据最短时间效应来推导出光学中的反射定理。
五邑大学数学建模课程论文考核成绩2011-2012学年度第一学期基于江门市大气污染主要成分历年数据的预测数学模型摘要有侨乡美誉之称的江门市,是国家环保模城市,但现实中的江门市,其环保工作是十分令人失望的,比如在市中心,市区工厂的各种偷排令市中心空气污染十分严重,尤其是晚上,简直令人窒息。
市中心的甘化厂、电化厂、玻璃厂、溶剂化工厂等,还有不少转制留下的各种厂场被租给私人从事各种污染生产,对江门的环境产生了极大地破坏。
随着经济的发展与人类社会的进步,环境污染问题日益受到社会的关注与重视。
作为环境污染的一个重要部分——大气污染,主要由于工厂(排出的有害烟尘,以及越来越多的汽车排出的有害烟尘所造成,这些有害烟尘因大气的扰动而扩散,随气流而漂移,造成大气污染,危害环境,同时烟尘可以通过人类的直接呼吸、饮食以及皮肤接触而影响人类的身体。
因此,对江门市的大气污染建立模型,对将近二到三年江门市的各空气污染变化趋势进行预测,通过API评价模型,对主要污染成分进行分析,以便更好地做好针对性防治措施,防于未然,在江门市成为文明城市的今天,是迫在眉睫的事情。
本题要求我们查阅江门市大气污染近年来相关数据,建立江门市大气污染模型,根据建立的模型,提出解决大气问题的措施或策略,写成一篇短小的报道性文章。
对于第一个问题,我们在江门市环保局查阅了江门市大气污染2003-2009年的相关数据(见附件1),制作成表格,由主要污染成分二氧化硫,二氧化氮,可吸入颗粒物的日均值,根据灰色系统理论,建立GM(1,1)预测模型,预测到了2010- 2012年各类污染物的对应的日均值,通过Matlab软件绘制出三种污染物的相应趋势变化散点折线图,得出三种染污的整体变化趋势为逐年减少,。
加上通过GM(1,1)预测模型得出的结果。
通过API空气质量评价模型,计算出江门市从2003-2012年每年对应的API(空气污染指数)值,进行空气质量状况评价,从而得出了江门市各年空气状况为:良,主要空气污染物应为可吸入颗粒物,最后对整个模型结果进行了总结以及原因简要说明。

环境科学中的大气污染模型的建立方法大气污染是当前全球范围内面临的重要环境问题之一,对人类健康和环境造成了严重影响。
为了解决和应对大气污染问题,科学家们开展了大量研究工作,其中之一就是建立大气污染模型。
本文将介绍环境科学中大气污染模型的建立方法。
大气污染模型是通过数学和物理方程描述大气中污染物的传输、扩散和化学反应过程,从而揭示大气污染物的来源、分布和转化规律。
它是环境科学研究中常用的工具,具有重要的理论指导和应用价值。
建立大气污染模型的第一步是收集和整理大气污染数据。
这些数据包括大气颗粒物、二氧化硫、氮氧化物等主要污染物的浓度、源排放数据、气象数据等。
通过在城市、工业区、农田等重点监测点上部署监测设备,可以获得实时的大气污染数据。
同时,还需收集相关的地理、人口、经济等社会经济数据,这些数据有助于建立全面的大气污染模型。
第二步是选择合适的大气污染模型。
根据研究目的和需要,可以选择不同的大气污染模型:物理模型、统计模型和数学模型等。
物理模型主要基于空气流动和扩散的物理原理,适用于大气污染物的传输和扩散模拟。
统计模型则通过建立统计关系来估算大气污染物的浓度和源排放量。
数学模型则通过数学表达式和方程来描述大气污染的物理现象和化学反应过程。
第三步是确定模型的输入参数。
模型的输入参数包括气象参数、排放源参数和化学反应参数等。
气象参数如风速、风向、湿度等直接影响大气污染物的传输和扩散,它们通过监测和气象预报等手段获得。
排放源参数包括排放类型、强度和位置等,可以通过监测和统计数据获得。
化学反应参数则涉及大气污染物之间的化学转化、光化学反应等过程。
第四步是模型的调试和验证。
在模型建立初期,需要对模型进行调试和验证,以确保模型的合理性和可靠性。
调试意味着根据已知的数据和知识对模型进行修改和调整,使其能够准确地模拟实际情况。
验证则是将模型应用到新的数据和场景中,进行比对和评估。
通过与实际观测数据进行对比,可以确定模型的适用性和精度。

大气环境中的模拟模型及其应用大气环境模拟模型是通过对各种气体和化学物质在大气中的传输和化学反应进行数值计算模拟,得出对大气环境的影响。
具体而言,大气模型主要分为数值天气预报模型和空气污染模型两大类,它们从不同的角度研究了大气的各种现象,为我们提供了一系列有用的信息。
数值天气预报模型是大气模型中最常使用的模型之一。
该模型利用数值计算模拟大气中的动力、热力、湍流及辐射等过程,来预报天气变化趋势和未来几天的气象情况。
基于数学方程组的求解,数值天气预报模型可预报出气温、气压、风速、降水等气象要素的变化趋势,以及天气的预警等信息。
不过数值天气预报模型也存在一些问题,如过于复杂的数学方程,无法完全准确预报未来天气等局限。
空气污染模型是大气模型中应用居多的一种模型。
该模型通过对空气中的颗粒物、气体成分进行数值计算,来预测和分析空气污染的扩散和浓度分布等数据,并为城市治理提供参考意见。
空气污染模型能够模拟气体和颗粒物在空气中的传输和涉及的化学反应,实现对气体和颗粒物的预测,为环境保护和空气污染治理提供科学依据。
但是空气污染模型也存在着诸多限制,如材料和化学反应模型的不准确性等局限。
除了数值天气预报模型和空气污染模型以外,大气环境模拟模型还包括了气候变化模型和植被行为模型等。
气候变化模型是预测未来几十年甚至更久远时段气候变化的模型。
例如,众所周知的IPCC(联合国政府间气候变化专门委员会)就是依据一系列的气候变化模型得出气温和海平面的升高情况。
植被行为模型则是关注植被和土壤应对气候变化的反应情况。
植被和土壤是大气污染吸收物质的主要来源之一,借助植被行为模型可以更好的预测未来环境与植被的互动方式。
那么大气环境模拟模型有什么应用呢?实际上,大气模型的应用非常广泛,从天气预报到空气污染治理到气候变化预测都有其身影。
其中,在环境保护、能源和气候变化方面,大气模型的应用非常重要。
例如,政府机构可以利用大气模型制定环境政策和相应的控制规范,以达到保护环境、减少空气污染和气候变化的效果。
1.问题重述大气是指包围在地球外围的空气层,是地球自然环境的重要组成部分之一。
人类生活在大气里,洁净大气是人类赖于生存的必要条件。
一个人在五个星期内不吃饭或5天内不喝水,尚能维持生命,但超过5分钟不呼吸空气,便会死亡。
随着地球上人口的急剧增加,人类经济增长的急速增大,地球上的大气污染日趋严重,其影响也日趋深刻,如由于一些有害气体的大量排放,不仅造成局部地区大气的污染,而且影响到全球性的气候变化。
因此,加强大气质量的监测和预报是非常必要。
目前对大气质量的监测主要是监测大气中2SO 、2NO 、悬浮颗粒物(主要为PM10)等的浓度,研究表明,城市空气质量好坏与季节及气象条件的关系十分密切。
附件给出城市A 、B 、C 、D 、E 、F 从2003年3月1日至2010年9月14日测量的污染物含量及气象参数的数据。
请运用数学建模的方法对下列问题作出回答:1.找出各个城市2SO 、2NO 、PM10之间的特点,并将几个城市的空气质量进行排序。
2.对未来一周即2010年9月15日至9月21日各个城市的2SO 、2NO 、PM10以及各气象参数作出预测。
3.分析空气质量与气象参数之间的关系。
4.就空气质量的控制对相关部门提出你的建议。
2.问题分析本题为生活中的实际问题,层层递进式提出四个问题,分别需要对空气污染因素以及气象参数进行分析求解。
第一问为评价性问题,先从城市内部个污染物特点出发,再到城市之间空气质量进行比较。
第二问是预测性问题,通过对给出的数据进行分析,预测各项参数之后的趋势。
第三问是寻找关联性问题,要求找出空气质量与气象参数之间的关系。
第四问为开放型问题,可通过之前得出的结论或者相关文章及模型提出建议。
2.1 问题1通过查阅资料,运用已有的API 对各个城市的各项污染指标进行计算,得出各个污染指数API 月平均的折线图,观察,得出各城市各项指标的特点。
鉴于求解城市API 时有一定的误差,故选择综合评价模型,对数据进行标准化处理之后,确定动态加权函数,对模型进行求解,排名。
大气污染的数学模型探析及预测摘 要本文针对大气污染问题,利用模糊综合评价、数理统计、回归、时间序列分析等方面的知识,, 建立了模糊综合评价模型、灰色预测模型和多元线性回归模型。
对大气污染进行定量的分析和定性的模拟,并加以分析,较好的解决这一问题。
模型Ⅰ 建立模糊综合评价模型。
我们引入空气污染指数来评价各个城市的大气污染状况。
利用EXCEL 对数据进行处理,得出六个城市的评价值,依次是0.10245、0.10125、0.0964、0.104167、0.0484、0.0679,因此六个城市的空气质量排名依次是E 、F 、C 、B 、A 、D 。
模型Ⅱ 建立灰色预测模型,通过对已有的数据进行选取,采用MATLAB 软件编程,预测出一周内空气污染指标和气象参数的变化。
由结果可知,其中城市B 的2SO 含量为-0.0052、0.0062、0.0072、0.0082、0.0092、-0.0102、-0.0113,属于异常现象。
经分析,是由于政府采取了管制措施。
而其他各地参数值波动较小,呈现稳态。
模型Ⅲ 建立多元线性回归模型,利用EVIEWS 软件进行处理,把每个季度的2SO ,2N O 和10P M 的浓度与气象参数mmhg (大气压),tem (温度),rh (湿度),ws (风速)做多元线性回归,求得12个多元线性回归方程。
每个方程的可决系数分别为0.945,0.946,0.885,0.957,0.956,0.895,0.991,0.956,0.809,0.999,0.939,0.881,表明拟合虽有误差,但相对较小。
在模型改进中,我们建立时间序列模型对模型Ⅱ进行改进,用SPSS 软件建立了(1,3,6)ARIMA 模型。
以2010年7月1日至2010年9月14日的数据来预测2010年9月15日至9月21日的数据。
以预测气象参数中mmhg 为例。
测出的结果较好,未来7天的数据分别为679.37,680.25,681.62,682.43,683.48,684.36,685.46。
大气污染预测的数学模型和方法随着工业化和城市化的快速发展,大气污染问题越来越严峻。
如何预测和控制大气污染已经成为一项重要的研究课题。
大气污染预测可以帮助我们更好地了解大气污染形成和传播的规律,为环境保护和健康保障提供科学依据。
本文将从数学建模、模型选择和算法优化等方面介绍大气污染预测的数学模型和方法。
一、数学建模数学建模是大气污染预测的基础。
大气污染的成因及其发展规律涉及多个因素,如气象条件、人类活动和自然环境等。
因此,建立数学模型需要考虑多个参数,如温度、湿度、气压、风速、风向、大气稳定度、排放源等。
语言学会通过数学公式和统计方法将这些参数进行量化,得出污染物的浓度和传播程度等结果。
目前,常见的大气污染数学模型包括:Gaussian模型、Lagrange 模型、Euler模型、CALPUFF模型、CAMx模型等。
其中,Gaussian模型是应用最为广泛的模型之一。
Gaussian模型着重考虑气象条件对污染物扩散和沉降的影响,具有简单、易于操作、要求数据量少等特点。
Lagrange模型和Euler模型分别侧重于描述污染物的运动过程和形成过程。
CALPUFF模型和CAMx模型则是最近发展起来的高级数学模型,能够更好地模拟多维空间中复杂的气象条件和污染物传播过程。
二、模型选择针对实际使用中,不同的数学模型适用于不同的污染源和环境条件。
因此,在选择大气污染数学模型时,需要结合具体情况进行综合分析和比较。
首先,要考虑污染源的位置,气象条件等。
例如,对于位于城市中心的大工厂或压力容器,要选用Gaussian模型来模拟;对于位于山区的散发源或挂靠在城市外的火电厂,可以选用CALPUFF 模型或CAMx模型等高级数学模型进行预测。
其次,还需要考虑数据的可用性和模型的复杂性。
一些高级数学模型需要大量的数据来进行预测,但是数据采集及其困难。
因此,如果数据有限,就要选择较为简单的数学模型进行预测。
三、算法优化大气污染预测虽是一项困难的任务,但是通过现代算法优化技术的应用,可以大大提高预测精度和计算效率。