2018届中考数学全程演练 第二部分 图形与几何 第七单元 三角形 第22课时 三角形全等

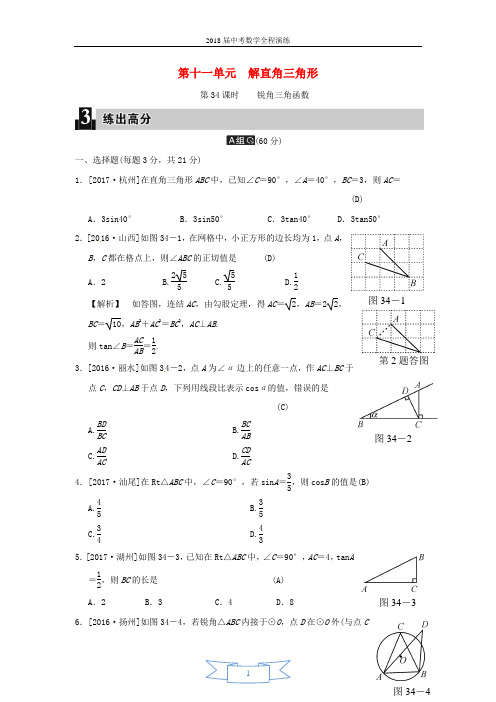
第十一单元 解直角三角形第34课时 锐角三角函数(60分)一、选择题(每题3分，共21分)1．[2017·杭州]在直角三角形ABC 中，已知∠C ＝90°，∠A ＝40°，BC ＝3，则AC ＝(D)A ．3sin40°B ．3sin50°C ．3tan40°D ．3tan50°2．[2016·山西]如图34－1，在网格中，小正方形的边长均为1，点A ，B ，C 都在格点上，则∠ABC 的正切值是 (D)A ．2B.255C.55D.12【解析】 如答图，连结AC ，由勾股定理，得AC ＝2，AB ＝22，BC ＝10，AB 2＋AC 2＝BC 2，AC ⊥AB . 则tan ∠B ＝AC AB ＝12.3．[2016·丽水]如图34－2，点A 为∠α边上的任意一点，作AC ⊥BC 于点C ，CD ⊥AB 于点D ，下列用线段比表示cos α的值，错误的是(C)A.BD BCB.BC ABC.AD ACD.CD AC4．[2017·汕尾]在Rt △ABC 中，∠C ＝90°，若sin A ＝35，则cos B 的值是(B)A.45B.35C.34D.435．[2017·湖州]如图34－3，已知在Rt △ABC 中，∠C ＝90°，AC ＝4，tan A ＝12，则BC 的长是(A) A ．2B ．3C ．4D ．86．[2016·扬州]如图34－4，若锐角△ABC 内接于⊙O ，点D 在⊙O 外(与点C第2题答图图34－1图34－2图34－3在AB 同侧)，则下列三个结论：①sin ∠C >sin ∠D ；②cos ∠C >cos ∠D ；③tan ∠C >tan ∠D 中，正确的结论为 (D)A ．①②B ．②③C ．①②③D ．①③7．[2016·日照]如图34－5，在直角△BAD 中，延长斜边BD 到点C ，使DC ＝12BD ，连结AC ，若tan B ＝53，则tan ∠CAD 的值为(D)A.33B.35C.13D.15图34－5【解析】 过点D 作DE ∥AB 交AC 于点E . ∵∠BAD ＝90°，DE ∥AB ， ∴∠ADE ＝90°，∵tan B ＝53，设AD ＝5k ，AB ＝3k ，∵DE ∥AB ，∴DE AB ＝CD BC ，DE ＝13AB ＝k ， ∴tan ∠CAD ＝DE AD ＝k 5k ＝15.第7题答图二、填空题(每题4分，共20分)8．[2016·成都模拟]如图34－6，在Rt △ABC 中，∠C ＝90°，AB ＝2BC ，则sin B 的值为2． 【解析】 ∵AB ＝2BC ， ∴AC ＝（2BC ）2－BC 2＝3BC ， ∴sin B ＝AC AB ＝3BC 2BC ＝32. 9．[2016·杭州模拟]已知∠A ，∠B ，∠C 是△ABC 的三个内角，若⎪⎪⎪⎪⎪⎪sin A －32＋⎝ ⎛⎭⎪⎫cos B －322＝0，则∠C 的度数是__90°__．【解析】 ∵⎪⎪⎪⎪⎪⎪sin A －32＋⎝ ⎛⎭⎪⎫cos B －322＝0，∴sin A ＝32，cos B ＝32， ∴∠A ＝60°，∠B ＝30°，∴∠C 的度数是90°.10．如图34－7，在⊙O 中，过直径AB 延长线上的点C 作⊙O 的一条切线，切点为D ，若AC ＝7，AB ＝4，则sinC 的值为__25__．图34－711．[2017·黄石]如图34－8，圆O 的直径CD ＝10 cm ，且AB ⊥CD ，垂足为P ，AB ＝8 cm ，则sin ∠OAP ＝__35__.12．[2016·广州]如图34－9，△ABC 中，DE 是BC 的垂直平分线，DE 交AC 于点E ，连结BE ，若BE ＝9，BC ＝12，则cos C ＝__23__．【解析】 在Rt △EDC 中，只要求出EC 和DC 即可求出cos C 的值．DE 是BC 的垂直平分线，所以BE ＝EC ＝9，BD＝DC ＝6.三、解答题(共19分)图34－6图34－8图34－913．(9分)如图34－10，在Rt △ABC 中，∠C ＝90°，AB ＝10，sin A ＝25，求BC 的长和tan B的值．图34－10解：∵sin A ＝BC AB ＝25，又∵AB ＝10，∴BC ＝4. 又∵AC ＝AB 2－BC 2＝221， ∴tan B ＝AC BC ＝212. 14．(10分)计算：(1)[2016·永州]cos30°－124＋⎝ ⎛⎭⎪⎫12－2；(2)[2016·绵阳]||1－2＋⎝ ⎛⎭⎪⎫－12－2－1cos45°＋3－8. 解：(1)原式＝32－234＋22＝32－32＋4 ＝4；(2)原式＝－(1－2)＋1⎝ ⎛⎭⎪⎫－122－122＋3（－2）3 ＝2－1＋114－22＋(－2)＝2－1＋4－2－2＝1.(28分)15．(8分)[2017·重庆]如图34－11，△ABC 中，AD ⊥BC ，垂足是D ，若BC ＝14，AD ＝12，tan ∠BAD ＝34，求sin C 的值．图34－11解：∵AD ⊥BC ， ∴tan ∠BAD ＝BD AD， ∵tan ∠BAD ＝34，AD ＝12，∴BD ＝9，∴CD ＝BC －BD ＝14－9＝5，∴在Rt △ADC 中，AC ＝AD 2＋CD 2＝122＋52＝13，∴sin C ＝AD AC ＝1213.16．(10分)[2016·酒泉]如图34－12①，将直尺摆放在三角板上，使直尺与三角板的边分别交于点D ，E ，F ，G ，已知∠CGD ＝42°.图34－12(1)求∠CEF 的度数；(2)将直尺向下平移，使直尺的边缘通过三角板的顶点B ，交AC 边于点H ，如图②所示，点H ，B 在直尺上的度数分别为4，13.4，求BC 的长(结果保留两位小数)． (参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90) 解：(1)∵∠CGD ＝42°，∠C ＝90°， ∴∠CDG ＝90°－42°＝48°， ∵DG ∥EF ，∴∠CEF ＝∠CDG ＝48°； (2)∵点H ，B 的读数分别为4，13.4， ∴HB ＝13.4－4＝9.4，∴BC ＝HB ·cos42°≈9.4×0.74≈6.96.∴BC 的长为6.96.17．(10分)[2017·长沙]如图34－13，四边形ABCD 是矩形，把矩形沿对角线AC 折叠，点B 落在点E 处，CE 与AD 相交于点O . (1)求证：△AOE ≌COD ；(2)若∠OCD ＝30°，AB ＝3，求△AOC 的面积．解：(1)证明：由折叠的性质可得：AE ＝AB ，∠E ＝∠B ＝90°， ∵四边形ABCD 是矩形， ∴CD ＝AB ，∠D ＝90°， ∴AE ＝CD ，∠E ＝∠D ＝90°， 又∵∠AOE ＝∠COD ， ∴△AOE ≌△COD (AAS )；(2)∵∠OCD ＝30°，AB ＝3＝CD ， ∴OD ＝CD ·tan ∠OCD ＝3·tan30°＝3×33＝1，OC ＝2， 由折叠知∠BCA ＝∠ACO ， ∵AD ∥BC ，∴∠OAC ＝∠BCA ， ∴∠OAC ＝∠ACO ，∴OA ＝OC ＝2， ∴S △AOC ＝12·OA ·CD ＝12×2×3＝ 3.(12分)18．(12分)[2017·遂宁]如图34－14，根据图中数据完成填空，再按要求答题：图34－14(1)sin 2A 1＋sin 2B 1＝__1__；sin 2A 2＋sin 2B 2＝__1__；sin 2A 3＋sin 2B 3＝__1__； (2)观察上述等式，猜想：在Rt △ABC 中，∠C ＝90°.都有：sin 2A ＋sin 2B ＝__1__； (3)如图④，在Rt △ABC 中，∠C ＝90°，∠A ，∠B ，∠C 的对边分别是a ，b ，c ；利用三角函数的定义和勾股定理，证明你的猜想；图34－13(4)已知：∠A ＋∠B ＝90°，且sin A ＝513，求sin B .解：(3)证明：∵sin A ＝a c ，sin B ＝b c，a 2＋b 2＝c 2，sin 2A ＋sin 2B ＝a 2c 2＋b 2c 2＝a 2＋b 2c2＝1；(4)∵sin A ＝513，sin 2A ＋sin 2B ＝1，∴sin B ＝1－⎝ ⎛⎭⎪⎫5132＝1213.。

腰三角形第23课时 等腰三角形(60分)一、选择题(每题6分，共30分)1．[xx·中考预测]等腰三角形的一个内角是80°，则它的顶角的度数是 (B) A ．80°B ．80°或20°C ．80°或50°D ．20°2．[xx·内江]如图23－1，在△ABC 中，AB ＝AC ，BD 平分∠ABC 交AC 于点D ，AE ∥BD 交CB 的延长线于点E .若∠E ＝35°，则∠BAC 的度数为 (A) A ．40° B ．45° C ．60° D ．70° 【解析】 ∵AE ∥BD ， ∴∠CBD ＝∠E ＝35°， ∴∠CBA ＝70°，∵AB ＝AC ，∴∠C ＝∠CBA ＝70°， ∴∠BAC ＝180°－70°×2＝40°.3．[xx·黄石]如图23－2，在等腰△ABC 中，AB ＝AC ，BD ⊥AC ，∠ABC ＝72°，则∠ABD ＝(B)A ．36°B ．54°C ．18°D ．64°【解析】 ∵AB ＝AC ，∠ABC ＝72°， ∴∠ABC ＝∠ACB ＝72°， ∴∠A ＝36°， ∵BD ⊥AC ，∴∠ABD ＝90°－36°＝54°.图23－1图23－2腰三角形4．如图23－3，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM＋CN＝9，则线段MN的长为(D)A．6 B．7C．8 D．9【解析】∵∠ABC，∠ACB的平分线相交于点E，∴∠MBE＝∠EBC，∠ECN＝∠ECB.∵MN∥BC，∴∠EBC＝∠MEB，∠NEC＝∠ECB，∴∠MBE＝∠MEB，∠NEC＝∠ECN，∴BM＝ME，EN＝CN.∵MN＝ME＋EN，∴MN＝BM＋CN.∵BM＋CN＝9，∴MN＝9，故选D.5．[xx·遂宁]如图23－4，在△ABC中，AC＝4 cm，线段AB的垂直平分线交AC于点N，△BCN的周长是7 cm，则BC的长为(C)A．1 cm B．2 cmC．3 cm D．4 cm【解析】∵MN是线段AB的垂直平分线，∴AN＝BN，∵△BCN的周长是7 cm，∴BN＋NC＋BC＝7(cm)，∴AN＋NC＋BC＝7(cm)，∵AN＋NC＝AC，∴AC＋BC＝7(cm)，又∵AC＝4 cm，∴BC＝7－4＝3(cm)．图23－3图23－4腰三角形二、填空题(每题6分，共30分)6．[xx·丽水]如图23－5，在△A BC 中，AB ＝AC ，AD ⊥BC 于点D .若AB ＝6，CD ＝4，则△ABC 的周长是__20__.7．[xx·绍兴]由于木质衣架没有柔性，在挂置衣服的时候不太方便操作．小敏设计了一种衣架，在使用时能轻易收拢，然后套进衣服后松开即可．如图23－6①，衣架杆OA ＝OB ＝18cm ，若衣架收拢时，∠AOB ＝60°，如图23－6②，则此时A ，B 两点之间的距离是__18__cm.图23－6【解析】 ∵OA ＝OB ，∠AOB ＝60°， ∴△AOB 是等边三角形， ∴AB ＝OA ＝OB ＝18 cm.8．[xx·乐山]如图23－7，在等腰三角形ABC 中，AB ＝AC ，DE 垂直平分AB ，已知∠ADE ＝40°，则∠DBC ＝__15__°. 【解析】 ∵DE 垂直平分AB ， ∴AD ＝BD ，∠AED ＝90°， ∴∠A ＝∠ABD ， ∵∠ADE ＝40°，∴∠A ＝90°－40°＝50°， ∴∠ABD ＝∠A ＝50°，∵AB ＝AC ，∴∠ABC ＝∠C ＝12(180°－∠A )＝65°，图23－5图23－7腰三角形∴∠DBC＝∠ABC－∠ABD＝65°－50°＝15°.9．[xx·益阳]如图23－8，将等边△ABC绕顶点A沿顺时针方向旋转，使边AB与AC重合得△ACD，BC的中点E的对应点为F，则∠EAF的度数是__60°__.图23－8 图23－910．如图23－9，在等边△ABC中，AB＝6，点D是BC的中点．将△ABD绕点A旋转后得到△ACE，那么线段DE的长度为__33__.三、解答题(共8分)11．(8分)[xx·衡阳]如图23－10在△ABC中，AB＝AC，BD＝CD，DE⊥AB于点E，DF⊥AC于点F.求证：△BED≌△CFD.证明：∵AB＝AC，∴∠B＝∠C.∵DE⊥AB，DF⊥AC，∴∠DEB＝∠DFC.又∵BD＝CD，∴△BED≌△CFD(AAS)．(20分)12．(8分)如图23－11，点D，E在△ABC的边BC上，连结AD，AE.①AB＝AC；②AD＝AE；③BD＝CE.以此三个等式中的两个作为命题的题设，另一个作为命题的结论，构成三个命题：①②⇒③；①③⇒②；②③⇒①.(1)以上三个命题是真命题的为(直接作答)图23－10图23－11腰三角形__①②⇒③；①③⇒②；②③⇒①__；(2)请选择一个真命题进行证明．(先写出所选命题，然后证明) 解：(2)选择①③⇒②， ∵AB ＝AC ，∴∠B ＝∠C ， 又∵BD ＝CE ， ∴△ABD ≌△ACE ， ∴AD ＝AE .13．(12分)[xx·南充]如图23－12，△ABC 中，AB ＝AC ，AD ⊥BC ，CE ⊥AB ，垂足分别为D ，E ，AE ＝CE .求证：(1)△AEF ≌△CEB ； (2)AF ＝2CD .证明：(1)∵AD ⊥BC ，CE ⊥AB ，∴∠BCE ＋∠CFD ＝90°，∠BCE ＋∠B ＝90°， ∴∠CFD ＝∠B ， ∵∠CFD ＝∠AFE ， ∴∠AFE ＝∠B ， 在△AEF 与△CEB 中，⎩⎨⎧∠AFE ＝∠B ，∠AEF ＝∠CEB ，AE ＝CE ，∴△AEF ≌△CEB (AAS )； (2)∵AB ＝AC ，AD ⊥BC ， ∴BC ＝2CD ， ∵△AEF ≌△CEB ， ∴AF ＝BC ，图23－12腰三角形∴A F ＝2CD .(12分)14．(12分)[xx·铜仁]已知，如图23－13，点D 在等边三角形ABC 的边AB 上，点F 在边AC 上，连结DF 并延长交BC 的延长线于点E ，EF ＝FD .求证：AD ＝CE .图23－13证明：如答图所示，作DG ∥BC 交AC 于G ，则∠DGF ＝∠ECF ，在△DFG 和△EFC 中，⎩⎨⎧∠DGF ＝∠ECF ，∠DFG ＝∠EFC ，FD ＝EF ，∴△DFG ≌△EFC (AAS )， ∴GD ＝CE ，∵△ABC 是等边三角形， ∴∠A ＝∠B ＝∠ACB ＝60°， ∵DG ∥BC ，∴∠ADG ＝∠B ，∠AGD ＝∠ACB ， ∴∠A ＝∠ADG ＝∠AG D ， ∴△ADG 是等边三角形，第14题答图腰三角形∴AD＝GD，∴AD＝CE.【感谢您的阅览，下载后可自由复制或修改编辑，敬请您的关注】。

第 24 课时直角三角形和勾股定理(60 分)一、选择题 ( 每题 5 分，共 25 分)1．[2016 ·毕节 ] 以下各组数据中的三个数作为三角形的边长，此中能组成直角三角形的是(B)A. 3，4，5B．1，2，3C．6，7，8D．2，3，42．如图 24－1，在 Rt△ABC中，∠C＝90°，AC＝9，BC＝12，则点C 到AB的距离是(A)3612A. 5B. 25933C.4D.4【分析】在 Rt△ABC中，AC＝9，BC＝12，依据勾股定理得AB＝22ABC1AC＋BC＝15，过 C作 CD⊥AB，交 AB于点 D，又S△＝2AC·BC 1＝2AB·CD，∴CD＝AC·BCAB ＝9×12＝1536，则点5C到AB的距离是365 .应选A.图 24－1第2题答图3．[2017 ·甘孜 ] 如图 24－2，点D在△ABC的边AC上，将△ ABC沿 BD翻折后，点 A恰巧与点 C重合．若BC＝5，CD＝3，则 BD的长为图 24－2(D)A．1B．2C．3D．44．将一个有45°角的三角板的直角极点放在一张宽为 3 cm 的矩形纸带边缘上，另一个极点在纸带的另一边缘上，测得三角板的一边与纸带的一边所在的直线成30°角，如图 24－ 3，则三角板最长边的长为(D)A．3 cm B．6 cmC．3 2 cm D．6 2 cm图 24－3第 4 题答图【分析】如答图，过点C作CD⊥AD于点D，∴C D＝3.在直角三角形ADC中，∵∠ CAD＝30°，∴A C＝2CD＝2×3＝6.又∵三角板是有45°角的三角板，∴A B＝AC＝6，22222∴BC＝ AB＋AC＝6＋6＝72，∴BC＝62，应选 D.5．直角三角形纸片的两直角边长分别为6，8，现将△ABC如图 24－4 那样折叠，使点A与点B重合，折痕为DE，则 tan ∠CBE的值是(C)247A. 7B. 371C.24D.3图 24－4【分析】在 Rt△BCE中，设CE＝x，则BE＝EA＝8－x，依据勾2227股定理有 (8 －x) ＝x＋6 ，解得x＝4，7CE 47∴tan ∠CBE＝＝＝ .BC 6 24二、填空题 ( 每题 5 分，共 25 分)6．[2016 ·内江 ] 在△ABC中，∠B＝30°，AB＝12，AC＝6，则BC＝__6 3__.7．[2017 ·凉山 ] 已知直角三角形两边的长分别是3 和 4，则第三边的长为 __5 或7__.8．将一副三角尺按图24－5所示叠放在一同，49若 AB＝14 cm，则暗影部分的面积是__22__cm.【分析】∵∠ B＝30°，图 24－51∴AC＝2AB＝7 cm，易证 AC＝CF，11212∴S△ACF＝2AC·CF＝2AC＝2×7＝4922 (cm ) ．9．[2017 ·无锡 ] 如图 24－6，△ABC中，CD⊥AB于D，E 是 AC的中点，若 AD＝6，DE＝5，则 CD的长等于__8__.【分析】∵△ ABC中，CD⊥AB于 D，E 是 AC的图 24－ 6中点， DE＝5，1∴DE＝2AC＝5，∴A C＝10.在直角△ ACD中，∠ADC＝90°，AD＝6，AC＝10，则依据勾股定理，得2222CD＝ AC－AD＝10－6 ＝8.10．[2016 ·遵义 ] 我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后代称其为“赵爽弦图”( 如图 24－7①) ．图 24－7②由弦图变化获得，它是由八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3.若正方形 EFGH的边长为2，则 S1＋ S2＋S3＝__12__.图24－7【分析】∵八个直角三角形全等，四边形ABCD，EFGH，MNKT是正方形，∴C G＝NF，CF＝DG＝KF，∴S1＝( CG＋DG)22 2＝C G＋ DG＋2CG·DG2＝GF＋2CG·DG，2S2＝GF，2222S3＝( KF－NF)＝KF＋NF－2NF·KF＝GF－2CG·DG，222∴S1＋S2＋S3＝ GF＋2CG·DG＋GF＋GF－22CG·DG＝3GF＝12.三、解答题 ( 共 20 分)11．(10 分) 如图 24－8，在 Rt△ABC中，∠C＝90°，∠A＝ 30°，BD是∠ABC的均分线，CD＝5 cm，求AB的长．【分析】要求的 AB在Rt△ABC中，∠ A＝图 24－81 30°，故只要求BC的长，在 Rt△BCD中，DC＝5 cm，∠DBC＝2∠ABC＝30°，故可求出 BD，BC的长，进而依据 AB＝2BC计算出结果．解：∵在 Rt△ABC中，∠C＝90°，∠A＝30°，∴A B＝2BC，∠ ABC＝60°.∵BD是∠ ABC的均分线，∴∠ ABD＝∠ CBD＝30°.∵在 Rt △CBD中，CD＝5 cm，∴B D＝10 cm，∴B C＝5 3 cm，∴A B＝2BC＝10 3 cm.12．(10 分) 如图 24－9，Rt △ABC中，∠C＝90°，AD均分∠ CAB，DE⊥AB于 E，若 AC＝6，BC＝8，CD＝3.图 24－9(1)求 DE的长;(2)求△ ADB的面积．解： (1) 在 Rt△ABC中，∠C＝90°，∴A C⊥CD.又∵ AD均分∠ CAB，DE⊥AB，∴D E＝CD，又∵ CD＝3，∴D E＝3;(2)在 Rt△ABC中，∠C＝90°，AC＝6，BC＝8，2222∴AB＝ AC＋BC＝ 6 ＋8＝10，11∴S△ADB＝2AB·DE＝2×10×3＝15.(20 分)13．(6 分)[2017 ·荆门 ] 如图 24－10，已知圆柱底面的周长为 4 dm，圆柱高为2 dm，在圆柱的侧面上，过点A和点C嵌有一圈金属丝，则这圈金属丝的周长最小为(A)A．4 2 dm B．2 2 dmC．2 5 dm D．4 5 dm图 24－10第13题答图【分析】如答图，把圆柱的侧面睁开，获得矩形，则这圈金属丝的周长最小为2AC的长度．∵圆柱底面的周长为 4 dm，圆柱高为 2 dm，∴A B＝2 dm，BC＝BC′＝2 dm，222＝4＋4＝8，∴AC＝2＋2∴AC＝22，∴这圈金属丝的周长最小为2AC＝4 2 dm.14．(6 分)[2016 ·台州 ] 假如将长为 6 cm，宽为 5 cm 的长方形纸片折叠一次，那么这条折痕的长不行能是(A)A．8 cm B ．5 2 cmC．5.5 cm D ．1 cm【分析】易知最长折痕为矩形对角线的长，依据勾股定理对角线长为62＋52＝61≈7.8 ，故折痕长不行能为 8 cm.15．(8分)[2016 ·铜仁 ] 如图 24－11，在矩形ABCD中，BC＝6，CD＝3，将△BCD沿对角线BD翻折，点C落在点C′处，BC′交AD于点 E，则线段 DE的长为(B)15A．3 B. 415C．5 D. 2【分析】设 ED＝x，则AE＝6－x;∵四边形 ABCD为矩形，∴A D∥BC，∴∠ EDB＝∠ DBC，由意得∠ EBD＝∠ DBC，∴∠ EDB＝∠ EBD，∴E B＝ED＝x，由勾股定理得222BE＝AB＋AE，22215即 x ＝3＋(6 －x) ，解得x＝4，15∴ED＝4.(10 分) 16．(10 分)[2016 · 坊 ] 如 24－12，正△ABC的 2，以BC上的高AB1作正△AB1C1，△ABC与△AB1C1公共部分的面 S1;再以正△ AB1C1 B1C1上的高 AB2作正△AB2C2，△ AB1C1与△ AB2C2公共部分的面3 3n S2，⋯，以此推，__S n＝2·4__.( 用图24－ 11图24－12含 n 的式子表示)【分析】∵等三角形 ABC的2，AB1⊥BC，∴B B1＝1，AB＝2，依据勾股定理得 AB1＝3，132∴S1＝2×4×(3)3 3 1＝2·4 ;∵等三角形 AB1C1的3，AB2⊥B1C1，3∴B1B2＝2，AB1＝3，3依据勾股定理得 AB2＝2，1 3 323 3 2∴S2＝2×4×2＝2·4;⋯3 3 n以此推， S n＝2·4.。

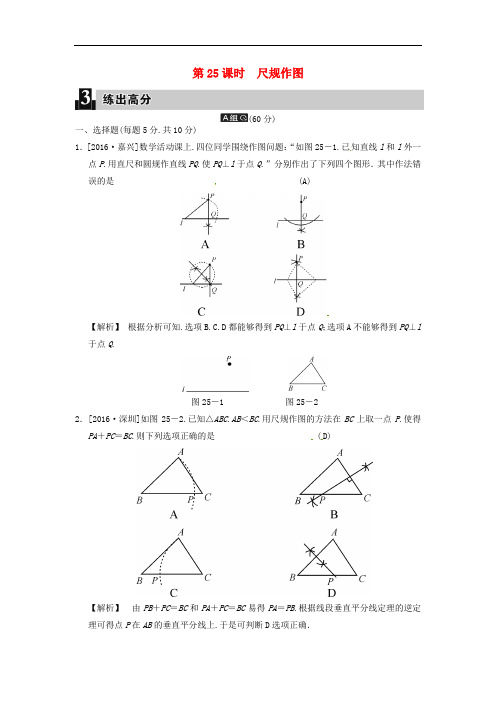
第25课时尺规作图(60分)一、选择题(每题5分.共10分)1．[2016·嘉兴]数学活动课上.四位同学围绕作图问题：“如图25－1.已知直线l和l外一点P.用直尺和圆规作直线PQ.使PQ⊥l于点Q.”分别作出了下列四个图形．其中作法错误的是 (A)【解析】根据分析可知.选项B.C.D都能够得到PQ⊥l于点Q；选项A不能够得到PQ⊥l 于点Q.图25－1 图25－22．[2016·深圳]如图25－2.已知△ABC.AB＜BC.用尺规作图的方法在BC上取一点P.使得PA＋PC＝BC.则下列选项正确的是 (D)【解析】由PB＋PC＝BC和PA＋PC＝BC易得PA＝PB.根据线段垂直平分线定理的逆定理可得点P在AB的垂直平分线上.于是可判断D选项正确．二、填空题(每题5分.共5分)3．[2017·绍兴]用直尺和圆规作△ABC .使BC ＝a .AC ＝b .∠B ＝35°.若这样的三角形只能作一个.则a .b 间满足的关系式是__sin35°＝b a或b ≥a __.【解析】 如答图所示：第3题答图若这样的三角形只能作一个.则a .b 间满足的关系式是：①当AC ⊥AB 时.即sin35°＝b a；②当b ≥a 时． 三、解答题(共40分)4．(10分)[2016·自贡]如图25－3.将线段AB 放在边长为1的小正方形网格中.点A .点B 均落在格点上.请用无刻度直尺在线段AB 上画出点P .使AP ＝2173.并保留作图痕迹．(备注：本题只是找点不是证明.只需连结一对角线就行)图25－3 第4题答图解：由勾股定理得.AB ＝42＋12＝17. 所以AP ＝2173时.AP ∶BP ＝2∶1.点P 如答图所示．5．(15分)[2016·宜昌]如图25－4.一块余料ABCD .AD ∥BC .现进行如下操作：以点B 为圆心.适当长为半径画弧.分别交BA .BC 于点G .H ；再分别以点G .H 为圆心.大于12GH 的长为半径画弧.两弧在∠ABC 内部相交于点O .画射线BO .交AD 于点E .图25－4(1)求证：AB ＝AE ；(2)若∠A ＝100°.求∠EBC 的度数． 解：(1)证明：∵AD ∥BC . ∴∠AEB ＝∠EBC .由BE 是∠ABC 的角平分线.得∠EBC ＝∠ABE . ∴∠AEB ＝∠ABE . ∴AB ＝AE ；(2)由∠A ＝100°.∠ABE ＝∠AEB . 得∠ABE ＝∠AEB ＝40°. 由(1)得∠EBC ＝∠AEB ＝40°.6．(15分)[2016·东莞]如图25－5.已知锐角△ABC .(1)过点A 作BC 边的垂线MN .交BC 于点D (用尺规作图法.保留作图痕迹.不要求写作法)； (2)在(1)的条件下.若BC ＝5.AD ＝4.tan ∠BAD ＝34.求DC 的长．图25－5 第6题答图解：(1)如答图.直线MN 即为所求； (2)∵AD ⊥BC .∴∠ADB ＝∠ADC ＝90°. 在Rt △ABD 中.∵tan ∠BAD ＝BD AD ＝34.∴BD ＝34×4＝3.∴DC ＝BC －BD ＝5－3＝2.(30分)7．(15分)[2016·珠海]如图25－6.在平行四边形ABCD 中.AB ＜BC .(1)利用尺规作图.在BC 边上确定点E .使点E 到边AB .AD 的距离相等(不写作法.保留作图痕迹)；(2)若BC ＝8.CD ＝5.求CE .图25－6 第7题答图解：(1)如答图所示.E 点即为所求； (2)∵四边形ABCD 是平行四边形. ∴AB ＝CD ＝5.AD ∥BC . ∴∠DAE ＝∠AEB . ∵AE 是∠BAD 的平分线. ∴∠DAE ＝∠BAE . ∴∠BAE ＝∠BEA . ∴BE ＝BA ＝5. ∴CE ＝BC －BE ＝3.8．(15分)[2016·武威]如图25－7.已知在△ABC 中.∠A ＝90°(1)请用圆规和直尺作出⊙P .使圆心P 在AC 边上.且与AB .BC 两边都相切(保留作图痕迹.不写作法和证明)；(2)若∠B ＝60°.AB ＝3.求⊙P 的面积．图25－7 第8题答图解：(1)如答图所示.则⊙P 为所求作的圆； (2)∵∠B ＝60°.BP 平分∠ABC . ∴∠ABP ＝30°. ∵tan ∠ABP ＝AP AB. ∴AP ＝ 3. ∴S ⊙P ＝3π.(15分)9．(15分)[2016·山西]如图25－8.△ABC 是直角三角形.∠ACB ＝90°.(1)尺规作图：作⊙C .使它与AB 相切于点D .与AC 相交于点E .保留作图痕迹.不写作法.请标明字母；(2)在你按(1)中要求所作的图中.若BC ＝3.∠A ＝30°.求劣弧DE 的长．图25－8 第9题答图解：(1)如答图.⊙C 即为所求； (2)∵⊙C 切AB 于D . ∴CD ⊥AB . ∴∠ADC ＝90°.∴∠DCE ＝90°－∠A ＝90°－30°＝60°. ∴∠BCD ＝90°－∠ACD ＝30°. 在Rt △BCD 中. ∵cos ∠BCD ＝CDBC. ∴CD ＝3cos30°＝332.∴劣弧DE 的长为60·π·332180＝32π.。

第35课时 解直角三角形(60分)一、选择题(每题6分，共24分)1．[2016·长沙]如图35－1，为测量一棵与地面垂直的树OA 的高度，在距离树的底端30 m 的B 处，测得树顶A 的仰角∠ABO 为α，则树OA 的高度为(C)A.30tan αmB ．30sin α mC ．30tan α mD ．30cos α m2．[2016·南充]如图35－2，一艘海轮位于灯塔P 的北偏东55°方向，距离灯塔为2海里的点A 处．如果海轮沿正南方向航行到灯塔的正东方向，海轮航行的距离AB 长是(C) A ．2海里B ．2sin55°海里C ．2cos55°海里D ．2tan55°海里【解析】 根据余弦函数定义“cos A ＝AB PA”得AB ＝PA ×cos A ＝2cos55°.故选C. 3．[2016·济宁]如图35－3，斜面AC 的坡度(CD 与AD 的比)为1∶2，AC ＝3 5 m ，坡顶有一旗杆BC ，旗杆顶端B 点与A 点有一条彩带相连，若AB ＝10 m ，则旗杆BC 的高度为 (A)A ．5 mB ．6 mC ．8 mD ．(3＋5)m 【解析】 设CD ＝x ，则AD ＝2x ，由勾股定理可得，AC ＝5x ，∵AC ＝3 5 m ，∴5x ＝35， ∴x ＝3 m ，∴CD ＝3 m ，∴AD ＝2×3＝6 m ， 在Rt △ABD 中，BD ＝8 m ，∴BC ＝8－3＝5 m.4．[2016·衡阳]如图35－4，为了测得电视塔的高度AB ，在D 处用高为1 m 的测角仪CD ，测得电视塔顶端A 的仰角为30°，再向电视图35－1图35－2图35－3塔方向前进100 m 到达F 处，又测得电视塔顶端A 的仰角为60°，则这个电视塔的高度AB (单位：m)为(C)A ．50 3B ．51C ．503＋1D ．101【解析】 由矩形CDFE ，得DF ＝CE ＝100 m ，由矩形EFBG ，得CD ＝GB ＝1 m ，因为∠ACE ＝30°，∠AEG ＝60°，所以∠CAE ＝30°，所以CE ＝AE ＝100 m ．在Rt △AEG 中，AG ＝sin60°·AE ＝32×100＝50 3 m ，所以AB ＝503＋1.故选C. 二、填空题(每题6分，共18分)5．[2016·邵阳]如图35－5，某登山运动员从营地A 沿坡角为30°的斜坡AB 到达山顶B ，如果AB ＝2 000 m ，则他实际上升了__1__000__m.【解析】 图35－5过点B 作BC ⊥水平面于点C ， 在Rt △ABC 中，∵AB ＝2 000 m ，∠A ＝30°，∴BC ＝AB ·sin30°＝2 000×12＝1 000(m)．6．[2016·宁波]如图35－6，在数学活动课中，小敏为了测量校园内旗杆AB 的高度，站在教学楼的C 处测得旗杆底端B 的俯角为45°，测得旗杆顶端A 的仰角为30°，若旗杆与教学楼的距离为9 m ，则旗杆AB 的高度是3__m ．(结果保留根号)【解析】 在Rt △ACD 中， ∵tan ∠ACD ＝AD CD， ∴tan30°＝AD9，∴AD ＝3 3 m ，在Rt △BCD 中，∵∠BCD ＝45°，∴BD ＝CD ＝9 m ， ∴AB ＝AD ＋BD ＝33＋9(m)．7．[2016·潍坊]观光塔是潍坊市区的标志性建筑，为测量其高度，如图35－51第5题答图图35－6图35－7，一人先在附近一楼房的底端A 点处观测观光塔顶端C 处的仰角是60°，然后爬到该楼房顶端B 点处观测观光塔底部D 处的俯角是30°.已知楼房高AB 约是45 m ，根据以上观测数据可求观光塔的高CD 是__135__m.【解析】 ∵爬到该楼房顶端B 点处观测观光塔底部D 处的俯角是30°， ∴∠ADB ＝30°，在Rt △ABD 中，tan30°＝AB AD， ∴45AD ＝33，∴AD ＝453， ∵在楼房的底端A 点处观测观光塔顶端C 处的仰角是60°， ∴在Rt △ACD 中，CD ＝AD ·tan60°＝453×3＝135(m)．三、解答题(共20分)8．(10分)[2016·台州]如图35－8，这是一把可调节座椅的侧面示意图，已知枕头上的点A 到调节器点O 处的距离为80 cm ，AO 与地面垂直．现调节靠背，把OA 绕点O 旋转35°到OA ′处．求调整后点A ′比调整前点A 的高度降低了多少厘米？(结果取整数) (参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70)图35－8解：如答图，过点A ′作A ′B ⊥AO ，交AO 于B 点，在Rt △A ′BO 中cos35°＝OBOA ′，OB ＝OA ′·cos35°＝80×0.82＝65.6≈66， ∴AB ＝80－66＝14 cm ， 答：降低了14 cm.9．(10分)[2016·遂宁]如图35－9，一数学兴趣小组为测量河对岸树AB 的高，在河岸边选择一点C ，从C 处测得树梢A 的仰角为45°，沿BC 方向后退第8题答图10 m 到点D ，再次测得点A 的仰角为30°，求树高．(结果精确到0.1 m ．参考数据：2≈1.414，3≈1.732)图35－9解：由题意，∠B ＝90°，∠D ＝30°，∠ACB ＝45°，DC ＝10 m ， 设CB ＝x ，则AB ＝x ，DB ＝3x ， ∵DC ＝10 m ， ∴3x ＝x ＋10， ∴(3－1)x ＝10， 解得x ＝103－1＝53＋5≈5×1.732＋5≈13.7.答：树高为13.7 m.(24分)10．(12分)[2016·成都]如图35－10，登山缆车从点A 出发，途经点B 后到达终点C ，其中AB 段与BC 段的运行路程均为200 m ，且AB 段的运行路线与水平面的夹角为30°，BC 段的运行路线与水平面的夹角为42°，求缆车从点A 运行到点C 的垂直上升的距离．(参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90)图35－10解：在直角△ADB 中，∵∠ADB ＝90°，∠BAD ＝30°，AB ＝200 m ， ∴BD ＝12AB ＝100 m ，在直角△CEB 中，∵∠CEB ＝90°，∠CBE ＝42°，CB ＝200 m ， ∴CE ＝BC ·sin42°≈200×0.67＝134 m ，∴BD ＋CE ≈100＋134＝234 m.答：缆车从点A 运行到点C 的垂直上升的距离约为234 m.11．(12分)[2016·泰州]如图35－11，某仓储中心有一斜坡AB ，其坡度为i ＝1∶2，顶部A 处的高AC 为4 m ，B ，C 在同一水平地面上．(1)求斜坡AB 的水平宽度BC ；(2)矩形DEFG 为长方体货柜的侧面图，其中DE ＝2.5 m ，EF ＝2 m ，将该货柜沿斜坡向上运送，当BF ＝3.5 m 时，求点D 离地面的高．(参考数据：5≈2.236，结果精确到0.1 m)图35－11解：(1)∵坡度为i ＝1∶2，AC ＝4 m ， ∴BC ＝4×2＝8 m ；(2)作DS ⊥BC ，垂足为S ，且与AB 相交于H . ∵∠DGH ＝∠BSH ，∠DHG ＝∠BHS ， ∴∠GDH ＝∠SBH ，∴GH GD ＝12， ∵DG ＝EF ＝2 m ，∴GH ＝1 m ，∴DH ＝ 5 m ，BH ＝BF ＋FH ＝3.5＋(2.5－1)＝5 m ， 设HS ＝x m ，则BS ＝2x m ， ∴x 2＋(2x )2＝52，∴x ＝ 5 m ， ∴DS ＝5＋5＝25≈4.5 m. ∴点D 离地面的高为4.5 m.(14分)12．(14分)[2017·泸州]如图35－12，海中有两个灯塔A ，B ，其中B 位于A 的正东方向上，渔船跟踪鱼群由西向东航行，在点C 处测得第11题答图灯塔A 在西北方向上，灯塔B 在北偏东30°方向上，渔船不改变航向继续向东航行30海里到达点D ，这时测得灯塔A 在北偏西60°方向上，求灯塔A ，B 间的距离．(计算结果用根号表示，不取近似值) 解：如答图，作CE ⊥AB 于点E ，AF ⊥CD 于点F ， ∴∠AFC ＝∠AEC ＝90°. ∵∠FCE ＝90°，∠ACE ＝45°， ∴四边形AFCE 是正方形．设AF ＝FC ＝CE ＝AE ＝x ，则FD ＝x ＋30， ∵tan D ＝AF FD，∠AFD ＝90°，∠D ＝30°， ∴33＝x x ＋30，解得x ＝153＋15， ∴AE ＝CE ＝153＋15.∵tan ∠BCE ＝BE CE，∠CEB ＝90°，∠BCE ＝30°， ∴33＝BE 153＋15，解得BE ＝15＋5 3. ∴AB ＝AE ＋BE ＝153＋15＋15＋53＝203＋30. ∴A ，B 间的距离为(203＋30)海里．第12题答图。

第35课时 解直角三角形(60分)一、选择题(每题6分，共24分)1．[2016·长沙]如图35－1，为测量一棵与地面垂直的树OA 的高度，在距离树的底端30 m 的B 处，测得树顶A 的仰角∠ABO 为α，则树OA 的高度为(C)A.30tan αmB ．30sin α mC ．30tan α mD ．30cos α m2．[2016·南充]如图35－2，一艘海轮位于灯塔P 的北偏东55°方向，距离灯塔为2海里的点A 处．如果海轮沿正南方向航行到灯塔的正东方向，海轮航行的距离AB 长是(C) A ．2海里B ．2sin55°海里C ．2cos55°海里D ．2tan55°海里【解析】 根据余弦函数定义“cos A ＝AB PA”得AB ＝PA ×cos A ＝2cos55°.故选C. 3．[2016·济宁]如图35－3，斜面AC 的坡度(CD 与AD 的比)为1∶2，AC ＝3 5 m ，坡顶有一旗杆BC ，旗杆顶端B 点与A 点有一条彩带相连，若AB ＝10 m ，则旗杆BC 的高度为 (A)A ．5 mB ．6 mC ．8 mD ．(3＋5)m 【解析】 设CD ＝x ，则AD ＝2x ，由勾股定理可得，AC ＝5x ，∵AC ＝3 5 m ，∴5x ＝35， ∴x ＝3 m ，∴CD ＝3 m ，∴AD ＝2×3＝6 m ， 在Rt △ABD 中，BD ＝8 m ，∴BC ＝8－3＝5 m.4．[2016·衡阳]如图35－4，为了测得电视塔的高度AB ，在D 处用高为1 m 的测角仪CD ，测得电视塔顶端A 的仰角为30°，再向电视图35－1图35－2图35－3塔方向前进100 m 到达F 处，又测得电视塔顶端A 的仰角为60°，则这个电视塔的高度AB (单位：m)为(C)A ．50 3B ．51C ．503＋1D ．101【解析】 由矩形CDFE ，得DF ＝CE ＝100 m ，由矩形EFBG ，得CD ＝GB ＝1 m ，因为∠ACE ＝30°，∠AEG ＝60°，所以∠CAE ＝30°，所以CE ＝AE ＝100 m ．在Rt △AEG 中，AG ＝sin60°·AE ＝32×100＝50 3 m ，所以AB ＝503＋1.故选C. 二、填空题(每题6分，共18分)5．[2016·邵阳]如图35－5，某登山运动员从营地A 沿坡角为30°的斜坡AB 到达山顶B ，如果AB ＝2 000 m ，则他实际上升了__1__000__m.【解析】 图35－5过点B 作BC ⊥水平面于点C ， 在Rt △ABC 中，∵AB ＝2 000 m ，∠A ＝30°，∴BC ＝AB ·sin30°＝2 000×12＝1 000(m)．6．[2016·宁波]如图35－6，在数学活动课中，小敏为了测量校园内旗杆AB 的高度，站在教学楼的C 处测得旗杆底端B 的俯角为45°，测得旗杆顶端A 的仰角为30°，若旗杆与教学楼的距离为9 m ，则旗杆AB 的高度是3__m ．(结果保留根号)【解析】 在Rt △ACD 中， ∵tan ∠ACD ＝AD CD， ∴tan30°＝AD9，∴AD ＝3 3 m ，在Rt △BCD 中，∵∠BCD ＝45°，∴BD ＝CD ＝9 m ， ∴AB ＝AD ＋BD ＝33＋9(m)．7．[2016·潍坊]观光塔是潍坊市区的标志性建筑，为测量其高度，如图35－51第5题答图图35－6图35－7，一人先在附近一楼房的底端A 点处观测观光塔顶端C 处的仰角是60°，然后爬到该楼房顶端B 点处观测观光塔底部D 处的俯角是30°.已知楼房高AB 约是45 m ，根据以上观测数据可求观光塔的高CD 是__135__m.【解析】 ∵爬到该楼房顶端B 点处观测观光塔底部D 处的俯角是30°， ∴∠ADB ＝30°，在Rt △ABD 中，tan30°＝AB AD， ∴45AD ＝33，∴AD ＝453， ∵在楼房的底端A 点处观测观光塔顶端C 处的仰角是60°， ∴在Rt △ACD 中，CD ＝AD ·tan60°＝453×3＝135(m)．三、解答题(共20分)8．(10分)[2016·台州]如图35－8，这是一把可调节座椅的侧面示意图，已知枕头上的点A 到调节器点O 处的距离为80 cm ，AO 与地面垂直．现调节靠背，把OA 绕点O 旋转35°到OA ′处．求调整后点A ′比调整前点A 的高度降低了多少厘米？(结果取整数) (参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70)图35－8解：如答图，过点A ′作A ′B ⊥AO ，交AO 于B 点，在Rt △A ′BO 中cos35°＝OBOA ′，OB ＝OA ′·cos35°＝80×0.82＝65.6≈66， ∴AB ＝80－66＝14 cm ， 答：降低了14 cm.9．(10分)[2016·遂宁]如图35－9，一数学兴趣小组为测量河对岸树AB 的高，在河岸边选择一点C ，从C 处测得树梢A 的仰角为45°，沿BC 方向后退第8题答图10 m 到点D ，再次测得点A 的仰角为30°，求树高．(结果精确到0.1 m ．参考数据：2≈1.414，3≈1.732)图35－9解：由题意，∠B ＝90°，∠D ＝30°，∠ACB ＝45°，DC ＝10 m ， 设CB ＝x ，则AB ＝x ，DB ＝3x ， ∵DC ＝10 m ， ∴3x ＝x ＋10， ∴(3－1)x ＝10， 解得x ＝103－1＝53＋5≈5×1.732＋5≈13.7.答：树高为13.7 m.(24分)10．(12分)[2016·成都]如图35－10，登山缆车从点A 出发，途经点B 后到达终点C ，其中AB 段与BC 段的运行路程均为200 m ，且AB 段的运行路线与水平面的夹角为30°，BC 段的运行路线与水平面的夹角为42°，求缆车从点A 运行到点C 的垂直上升的距离．(参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90)图35－10解：在直角△ADB 中，∵∠ADB ＝90°，∠BAD ＝30°，AB ＝200 m ， ∴BD ＝12AB ＝100 m ，在直角△CEB 中，∵∠CEB ＝90°，∠CBE ＝42°，CB ＝200 m ， ∴CE ＝BC ·sin42°≈200×0.67＝134 m ，∴BD ＋CE ≈100＋134＝234 m.答：缆车从点A 运行到点C 的垂直上升的距离约为234 m.11．(12分)[2016·泰州]如图35－11，某仓储中心有一斜坡AB ，其坡度为i ＝1∶2，顶部A 处的高AC 为4 m ，B ，C 在同一水平地面上．(1)求斜坡AB 的水平宽度BC ；(2)矩形DEFG 为长方体货柜的侧面图，其中DE ＝2.5 m ，EF ＝2 m ，将该货柜沿斜坡向上运送，当BF ＝3.5 m 时，求点D 离地面的高．(参考数据：5≈2.236，结果精确到0.1 m)图35－11解：(1)∵坡度为i ＝1∶2，AC ＝4 m ， ∴BC ＝4×2＝8 m ；(2)作DS ⊥BC ，垂足为S ，且与AB 相交于H . ∵∠DGH ＝∠BSH ，∠DHG ＝∠BHS ， ∴∠GDH ＝∠SBH ，∴GH GD ＝12， ∵DG ＝EF ＝2 m ，∴GH ＝1 m ，∴DH ＝ 5 m ，BH ＝BF ＋FH ＝3.5＋(2.5－1)＝5 m ， 设HS ＝x m ，则BS ＝2x m ， ∴x 2＋(2x )2＝52，∴x ＝ 5 m ， ∴DS ＝5＋5＝25≈4.5 m. ∴点D 离地面的高为4.5 m.(14分)12．(14分)[2017·泸州]如图35－12，海中有两个灯塔A ，B ，其中B 位于A 的正东方向上，渔船跟踪鱼群由西向东航行，在点C 处测得第11题答图灯塔A 在西北方向上，灯塔B 在北偏东30°方向上，渔船不改变航向继续向东航行30海里到达点D ，这时测得灯塔A 在北偏西60°方向上，求灯塔A ，B 间的距离．(计算结果用根号表示，不取近似值) 解：如答图，作CE ⊥AB 于点E ，AF ⊥CD 于点F ， ∴∠AFC ＝∠AEC ＝90°. ∵∠FCE ＝90°，∠ACE ＝45°， ∴四边形AFCE 是正方形．设AF ＝FC ＝CE ＝AE ＝x ，则FD ＝x ＋30， ∵tan D ＝AF FD，∠AFD ＝90°，∠D ＝30°， ∴33＝x x ＋30，解得x ＝153＋15， ∴AE ＝CE ＝153＋15.∵tan ∠BCE ＝BE CE，∠CEB ＝90°，∠BCE ＝30°， ∴33＝BE 153＋15，解得BE ＝15＋5 3. ∴AB ＝AE ＋BE ＝153＋15＋15＋53＝203＋30. ∴A ，B 间的距离为(203＋30)海里．第12题答图。

第22课时 三角形全等(60分)一、选择题(每题5分.共20分)1．[2016·宜昌]如图22－1.在方格纸中.以AB 为一边作△ABP .使之与△ABC 全等.从P 1.P 2.P 3.P 4四个点中找出符合条件的点P .则点P 有 (C)A ．1个B ．2个C ．3个D ．4个【解析】 要使△ABP 与△ABC 全等.点P 到AB 的距离应该等于点C 到AB 的距离.即3个单位长度.故点P 的位置可以是P 1.P 3.P 4三个．图22－1 图22－22．如图22－2.下列条件中.不能证明△ABD ≌△ACD 的是(D)A ．BD ＝DC .AB ＝AC B ．∠ADB ＝∠ADC .BD ＝CD C ．∠B ＝∠C .∠BAD ＝∠CAD D ．∠B ＝∠C .BD ＝DC【解析】 当BD ＝DC .AB ＝AC 时.因为AD ＝AD .由SSS 可得△ABD ≌△ACD .故A 正确；当∠ADB ＝∠ADC .BD ＝CD 时.因为AD ＝AD .由SAS 可得△ABD ≌△ACD .故B 正确；当∠B ＝∠C .∠BAD ＝∠CAD 时.因为AD ＝AD .由AAS 可得△ABD ≌△ACD .故C 正确；D 不能判定△ABD ≌△ACD .因为不能利用SSA 判定两三角形全等．3．[2016·湖州]如图22－3.已知在△ABC 中.CD 是AB 边上的高线.BE 平分∠ABC .交CD 于点E .BC ＝5.DE ＝2.则△BCE 的面积等于(C) A ．10 B ．7 C ．5D ．4图22－3第3题答图【解析】 作EF ⊥BC 于F . ∵BE 平分∠ABC .ED ⊥AB .EF ⊥BC . ∴EF ＝DE ＝2.∴S △BCE ＝12BC ·EF ＝12×5×2＝5.4.[2016·宁波]如图22－4.▱ABCD 中.E .F 是对角线BD 上的两点.如果添加一个条件.使△ABE ≌△CDF .则添加的条件不能为(C)A ．BE ＝DFB ．BF ＝DEC ．AE ＝CFD ．∠1＝∠2图22－4【解析】 A ．当BE ＝DF .△ABE ≌△CDF (SAS ).故此选项可添加； B ．当BF ＝ED .可得BE ＝DF .△ABE ≌△CDF (SAS ).故此选项可添加； C ．当AE ＝CF 无法得出△ABE ≌△CDF .故此选项符合题意； D ．当∠1＝∠2.△ABE ≌△CDF (ASA ).故此选项可添加． 二、填空题(每题5分.共20分)5．[2017·长沙]如图22－5.点B .E .C .F 在一条直线上.AB ∥DE .AB ＝DE .BE ＝CF .AC ＝6.则DF ＝__6__.图22－5 图22－66．[2016·江西]如图22－6.OP 平分∠MON .PE ⊥OM 于E .PF ⊥ON 于F .OA ＝OB .则图中有__3__对全等三角形．【解析】 ∵OP 平分∠MON .∴∠1＝∠2.由OA ＝OB .∠1＝∠2.OP ＝OP .可证得△AOP ≌△BOP (SAS ). ∴AP ＝BP .又∵OP 平分∠MON .PE ⊥OM 于E .PF ⊥ON 于F . ∴PE ＝PF .∴△PEA ≌△PFB (HL ).又∵PE ＝PF .OP ＝OP .∴△POE ≌△POF (HL ). ∴图中共有3对全等三角形．7．[2016·娄底]如图22－7.已知AB ＝BC .要使△ABD ≌△CBD .还需添加一个条件.你添加的条件是__∠ABD ＝∠CBD 或AD ＝CD __(只需写一个.不添加辅助线)．【解析】 由已知AB ＝BC .及公共边BD ＝BD .可知要使△ABD ≌△CBD .已经具备了两个边了.然后根据全等三角形的判定定理.应该有两种判定方法①SAS .②SSS .所以可添∠ABD ＝∠CBD 或AD ＝CD.图22－78．[2016·黔东南]如图22－8.在四边形ABCD 中.AB ∥CD .连结BD .请添加一个适当的条件__AB ＝CD __.使△ABD ≌△CDB .(只需写一个)图22－8【解析】 ∵AB ∥CD .∴∠ABD ＝∠CDB .而BD ＝DB . ∴当添加AB ＝CD 时.可根据“SAS ”判定△ABD ≌△CDB . 三、解答题(共20分)9．(10分)[2016·福州]如图22－9.∠1＝∠2.∠3＝∠4.求证：AC ＝AD . 证明：∵∠3＝∠4.∴∠ABC ＝∠ABD . 在△ABC 和△ABD 中. ⎩⎪⎨⎪⎧∠1＝∠2，AB ＝AB ，∠ABC ＝∠ABD ， ∴△ABC ≌△ABD (ASA ) ∴AC ＝AD .10．(10分)[2016·武汉]如图22－10.点B .C .E .F 在同一直线上.BC ＝EF .AC ⊥BC 于点C .DF ⊥EF 于点F .AC ＝DF .求证：图22－9图22－10(1)△ABC ≌△DEF ； (2)AB ∥DE .证明：(1)∵AC ⊥BC 于点C .DF ⊥EF 于点F . ∴∠ACB ＝∠DFE ＝90°. 在△ABC 和△DEF 中.⎩⎪⎨⎪⎧BC ＝EF ，∠ACB ＝∠DFE ，AC ＝DF ，∴△ABC ≌△DEF (SAS )； (2)∵△ABC ≌△DEF . ∴∠B ＝∠DEF . ∴AB ∥DE.(24分)11．(12分)[2017·杭州]如图22－11.在△ABC 中.AB ＝AC .点E .F 分别在AB .AC 上.AE ＝AF .BF 与CE 相交于点P .求证：PB ＝PC .并请直接写出图中其他相等的线段．图22－11证明：∵AB ＝AC . ∴∠ABC ＝∠ACB . 在△ABF 与△ACE 中.⎩⎪⎨⎪⎧AB ＝AC ，∠CAE ＝∠BAF ，AE ＝AF ，∴△ABF ≌△ACE (SAS ). ∴∠ABF ＝∠ACE .∴∠ABC －∠ABF ＝∠ACB －∠ACE . ∴∠FBC ＝∠ECB . ∴PB ＝PC .相等的线段还有：PE ＝PF .BE ＝CF .EC ＝FB .AE ＝AF . 12．(12分)[2016·温州]如图22－12.点C .E .F .B 在同一直线上.图22－12点A .D 在BC 异侧.AB ∥CD .AE ＝DF .∠A ＝∠D . (1)求证：AB ＝CD ；(2)若AB ＝CF .∠B ＝30°.求∠D 的度数． 解：(1)证明：∵AB ∥CD . ∴∠B ＝∠C . 在△ABE 和△DCF 中. ⎩⎪⎨⎪⎧∠A ＝∠D ，∠C ＝∠B ，AE ＝DF ，∴△ABE ≌△DCF (AAS ). ∴AB ＝CD ； (2)∵△ABE ≌△DCF . ∴AB ＝CD .BE ＝CF . ∵AB ＝CF .∠B ＝30°. ∴CD ＝CF . ∠C ＝∠B ＝30°. ∴△CDF 是等腰三角形.∴∠D ＝12×(180°－30°)＝75°.(16分)13．(16分)[2016·株洲]如图22－13.在Rt △ABC 中.∠C ＝90°.BD 是△ABC 的一条角平分线．点O .E .F分别在BD .BC .AC 上.且四边形OECF 是正方形． (1)求证：点O 在∠BAC 的平分线上； (2)若AC ＝5.BC ＝12.求OE 的长．图22－13解：(1)证明：过点O 作OM ⊥AB 于点M . ∵BD 是∠ABC 的平分线. ∴OE ＝OM.第13题答图∵四边形OECF 是正方形. ∴OE ＝OF . ∴OF ＝OM . ∵OM ⊥AB .OF ⊥AD . ∴AO 是∠BAC 的角平分线. 即点O 在∠BAC 的平分线上； (2)∵在Rt △ABC 中.AC ＝5.BC ＝12. ∴AB ＝AC 2＋BC 2＝52＋122＝13. 设CE ＝CF ＝x .BE ＝BM ＝y .AM ＝AF ＝z .∴⎩⎪⎨⎪⎧x ＋y ＝12，y ＋z ＝13，x ＋z ＝5， 解得⎩⎪⎨⎪⎧x ＝2，y ＝10，z ＝3，∴OE ＝CE ＝CF ＝2.。

第24课时 直角三角形和勾股定理(60分)一、选择题(每题5分，共25分)1．[2016·毕节]下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是(B)A.3，4， 5 B ．1，2， 3 C ．6，7，8D ．2，3，42．如图24－1，在Rt △ABC 中，∠C ＝90°，AC ＝9，BC ＝12，则点C 到AB 的距离是(A)A.365 B.1225 C.94D.334【解析】 在Rt △ABC 中，AC ＝9，BC ＝12，根据勾股定理得AB ＝AC 2＋BC 2＝15，过C 作CD ⊥AB ，交AB 于点D ，又S △ABC ＝12AC ·BC ＝12AB ·CD ，∴CD ＝AC ·BC AB ＝9×1215＝365，则点C 到AB的距离是365.故选A.图24－1 第2题答图3．[2017·甘孜]如图24－2，点D 在△ABC 的边AC 上，将△ABC 沿BD 翻折后，点A 恰好与点C 重合．若BC ＝5，CD ＝3，则BD 的长为(D) A ．1B ．2C ．3D ．44．将一个有45°角的三角板的直角顶点放在一张宽为3 cm 的矩形纸带边沿上，另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，如图24－3，则三角板最长边的长为(D)图24－2A ．3 cmB ．6 cmC ．3 2 cmD ．62 cm图24－3 第4题答图【解析】 如答图，过点C 作CD ⊥AD 于点D ， ∴CD ＝3.在直角三角形ADC 中， ∵∠CAD ＝30°， ∴AC ＝2CD ＝2×3＝6.又∵三角板是有45°角的三角板， ∴AB ＝AC ＝6，∴BC 2＝AB 2＋AC 2＝62＋62＝72， ∴BC ＝62，故选D.5．直角三角形纸片的两直角边长分别为6，8，现将△ABC 如图24－4那样折叠，使点A 与点B 重合，折痕为DE ，则tan ∠CBE 的值是(C)A.247 B.73C.724D.13图24－4【解析】 在Rt △BCE 中，设CE ＝x ，则BE ＝EA ＝8－x ，根据勾股定理有(8－x )2＝x 2＋62，解得x ＝74，∴tan ∠CBE ＝CE BC ＝746＝724.二、填空题(每题5分，共25分)6．[2016·内江]在△ABC 中，∠B ＝30°，AB ＝12，AC ＝6，则BC ＝7．[2017·凉山]已知直角三角形两边的长分别是3和4，则第三边的长为8．将一副三角尺按图24－5所示叠放在一起，若AB ＝14 cm ，则阴影部分的面积是__492__cm 2.【解析】 ∵∠B ＝30°， ∴AC ＝12AB ＝7 cm ，易证AC ＝CF ，∴S △ACF ＝12AC ·CF ＝12AC 2＝12×72＝492(cm 2)．9．[2017·无锡]如图24－6，△ABC 中，CD ⊥AB 于D ，E 是AC 的中点，若AD ＝6，DE ＝5，则CD 的长等于__8__.【解析】 ∵△ABC 中，CD ⊥AB 于D ，E 是AC 的中点，DE ＝5， ∴DE ＝12AC ＝5，∴AC ＝10.在直角△ACD 中，∠ADC ＝90°，AD ＝6，AC ＝10，则根据勾股定理，得CD ＝AC 2－AD 2＝102－62＝8.10．[2016·遵义]我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”(如图24－7①)．图24－7②由弦图变化得到，它是由八个全等的直角三角形拼接而成，记图中正方形ABCD ，正方形EFGH ，正方形MNKT 的面积分别为S 1，S 2，S 3.若正方形EFGH 的边长为2，则S 1＋S 2＋S 3＝__12__.图24－7【解析】 ∵八个直角三角形全等，四边形ABCD ，EFGH ，MNKT 是正方形， ∴CG ＝NF ，CF ＝DG ＝KF ， ∴S 1＝(CG ＋DG )2＝CG 2＋DG 2＋2CG ·DG ＝GF 2＋2CG ·DG ，S 2＝GF 2，图24－5图24－6S 3＝(KF －NF )2＝KF 2＋NF 2－2NF ·KF ＝GF 2－2CG ·DG ，∴S 1＋S 2＋S 3＝GF 2＋2CG ·DG ＋GF 2＋GF 2－ 2CG ·DG ＝3GF 2＝12. 三、解答题(共20分)11．(10分)如图24－8，在Rt △ABC 中，∠C ＝90°，∠A ＝30°，BD 是∠ABC 的平分线，CD ＝5 cm ，求AB 的长．【解析】 要求的AB 在Rt △ABC 中，∠A ＝30°，故只需求BC 的长，在Rt △BCD 中，DC ＝5 cm ，∠DBC ＝12∠ABC ＝30°，故可求出BD ，BC 的长，从而根据AB ＝2BC 计算出结果． 解：∵在Rt △ABC 中，∠C ＝90°，∠A ＝30°， ∴AB ＝2BC ，∠ABC ＝60°. ∵BD 是∠ABC 的平分线， ∴∠ABD ＝∠CBD ＝30°. ∵在Rt △CBD 中，CD ＝5 cm ， ∴BD ＝10 cm ， ∴BC ＝5 3 cm ， ∴AB ＝2BC ＝10 3 cm.12．(10分)如图24－9，Rt △ABC 中，∠C ＝90°，AD 平分∠CAB ，DE ⊥AB 于E ，若AC ＝6，BC ＝8，CD ＝3.(1)求DE 的长； (2)求△ADB 的面积．解：(1)在Rt △ABC 中，∠C ＝90°， ∴AC ⊥CD .又∵AD 平分∠CAB ，DE ⊥AB ， ∴DE ＝CD ，又∵CD ＝3， ∴DE ＝3；(2)在Rt △ABC 中，∠C ＝90°，AC ＝6，BC ＝8， ∴AB ＝AC 2＋BC 2＝62＋82＝10， ∴S △ADB ＝12AB ·DE ＝12×10×3＝15.(20分)13．(6分)[2017·荆门]如图24－10，已知圆柱底面的周长为4 dm ，圆柱高为2 dm，在圆图24－8图24－9柱的侧面上，过点A 和点C 嵌有一圈金属丝，则这圈金属丝的周长最小为(A)A ．4 2 dmB ．2 2 dmC ．2 5 dmD ．4 5 dm图24－10 第13题答图【解析】 如答图，把圆柱的侧面展开，得到矩形，则这圈金属丝的周长最小为2AC 的长度．∵圆柱底面的周长为4 dm ，圆柱高为2 dm ， ∴AB ＝2 dm ，BC ＝BC ′＝2 dm ， ∴AC 2＝22＋22＝4＋4＝8， ∴AC ＝22，∴这圈金属丝的周长最小为2AC ＝4 2 dm.14．(6分)[2016·台州]如果将长为6 cm ，宽为5 cm 的长方形纸片折叠一次，那么这条折痕的长不可能是(A) A ．8 cm B ．5 2 cm C ．5.5 cm D ．1 cm【解析】 易知最长折痕为矩形对角线的长，根据勾股定理对角线长为62＋52＝61≈7.8，故折痕长不可能为8 cm.15．(8分)[2016·铜仁]如图24－11，在矩形ABCD 中，BC ＝6，CD ＝3，将△BCD 沿对角线BD 翻折，点C 落在点C ′处，BC ′交AD 于点E ，则线段DE 的长为(B) A ．3 B.154 C ．5D.152【解析】 设ED ＝x ， 则AE ＝6－x ；∵四边形ABCD 为矩形， ∴AD ∥BC ，∴∠EDB ＝∠DBC ， 由题意得∠EBD ＝∠DBC ， ∴∠EDB ＝∠EBD ， ∴EB ＝ED ＝x ， 由勾股定理得BE 2＝AB 2＋AE 2，即x 2＝32＋(6－x )2，解得x ＝154，∴ED ＝154.(10分)16．(10分)[2016·潍坊]如图24－12，正△ABC 的边长为2，以BC 边上的高AB 1为边作正△AB 1C 1，△ABC 与△AB 1C 1公共部分的面积记为S 1；再以正△AB 1C 1边B 1C 1上的高AB 2为边作正△AB 2C 2，△AB 1C 1与△AB 2C 2公共部分的面积记为S 2，…，以此类推，则__S n ＝2·⎝ ⎛⎭⎪⎫34n__.(用含n 的式子表示)【解析】 ∵等边三角形ABC 的边长为2，AB 1⊥BC ， ∴BB 1＝1，AB ＝2， 根据勾股定理得AB 1＝3， ∴S 1＝12×34×(3)2＝32·⎝ ⎛⎭⎪⎫341； ∵等边三角形AB 1C 1的边长为3，AB 2⊥B 1C 1， ∴B 1B 2＝32，AB 1＝3， 根据勾股定理得AB 2＝32，∴S 2＝12×34×⎝ ⎛⎭⎪⎫322＝32·⎝ ⎛⎭⎪⎫342；…以此类推，S n ＝32·⎝ ⎛⎭⎪⎫34n .图24－12。

第七单元三角形第21课时三角形的基础知识(60分)一、选择题(每题6分，共36分)1．下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是(D)A．1，2，6 B．2，2，4C．1，2，3 D．2，3，42．[2016·滨州]在△ABC中，∠A∶∠B∶∠C＝3∶4∶5，则∠C等于(C) A．45°B．60°C．75°D．90°3．[2016·山西]如图21－1，在△ABC中，点D，E分别是边AB，BC的中点．若△DBE的周长是6，则△ABC的周长是(C)A．8 B．10C．12 D．14图21－14．[2017·邵阳]如图21－2，在△ABC中，∠B＝46°，∠C＝54°，AD平分∠BAC，交BC 于D，DE∥AB，交AC于E，则∠ADE的大小是 (C)A．45° B．54° C．40° D．50°图21－2 图21－35．[2016·绵阳]如图21－3，在△ABC中，∠B，∠C的平分线BE，CD相交于点F，∠ABC ＝42°，∠A＝60°，则∠BFC＝(C)A．118°B．119°C．120°D．121°【解析】∵∠A＝60°，∴∠ABC ＋∠ACB ＝120°， ∵BE ，CD 是∠B ，∠C 的平分线， ∴∠CBE ＝12∠ABC ，∠BCD ＝12∠BCA ，∴∠CBE ＋∠BCD ＝12(∠ABC ＋∠BCA )＝60°，∴∠BFC ＝180°－60°＝120°.6. 如图21－4，在折纸活动中，小明制作了一张三角形纸片ABC ，点D ，E 分别在边AB ，AC 上，将△ABC 沿着DE 折叠压平，点A 与点A ′重合，若∠A ＝75°，则∠1＋∠2＝(A)A ．150°B ．210°C ．105°D ．75°图21－4【解析】 ∵△A ′DE 是由△ADE 翻折而成， ∴∠AED ＝∠A ′ED ，∠ADE ＝∠A ′DE ， ∠A ＝∠A ′＝75°，∴∠AED ＋∠ADE ＝∠A ′ED ＋∠A ′DE ＝180°－75°＝105°， ∴∠1＋∠2＝360°－2×105°＝150°.故选A. 二、填空题(每题6分，共24分)7．[2016·衡阳]如图21－5，小明为了测量学校里一池塘的宽度AB ，选取可以直达A ，B 两点的点O 处，再分别取OA ，OB 的中点M ，N ，量得MN ＝20 m ，则池塘的宽度AB 为__40__m.图21－5图21－68．如图21－6，点B ，C ，E ，F 在一直线上，AB ∥DC ，DE ∥GF ，∠B ＝∠F ＝72°，则∠D ＝__36__度．9．在△ABC 中，三个内角∠A ，∠B ，∠C 满足∠B －∠A ＝∠C －∠B ，则∠B ＝__60__度． 10．将一副直角三角板如图21－7摆放，点C 在EF 上，AC 经过点D .已知∠A ＝∠EDF ＝90°，AB ＝AC ，∠E ＝30°，∠BCE ＝40°，则∠CDF ＝__25°__.图21－7【解析】 ∵AB ＝AC ，∠A ＝90°， ∴∠ACB ＝∠B ＝45°. ∵∠EDF ＝90°，∠E ＝30°， ∴∠F ＝90°－∠E ＝60°.∵∠ACE ＝∠CDF ＋∠F ，∠BCE ＝40°，∴∠CDF ＝∠ACE －∠F ＝∠BCE ＋∠ACB －∠F ＝40°＋45°－60°＝25°.(25分)11．(7分)[2016·广州]如图21－8，四边形ABCD 中，∠A ＝90°，AB ＝33，AD ＝3，点M ，N 分别为线段BC ，AB 上的动点(含端点，但点M 不与点B 重合)，点E ，F 分别为DM ，MN 的中点，则EF 长度的最大值为__3__. 【解析】 ∵ED ＝EM ，MF ＝FN ， ∴EF ＝12DN ，∴DN 最大时，EF 最大， ∵N 与B 重合时DN 最大， 此时DN ＝DB ＝AD 2＋AB 2＝6，∴EF 的最大值为3.12．(8分)[2017·扬州]如图21－9，△ABC 的中位线DE ＝5 cm ，把△ABC 沿DE 折叠，使点A 落在边BC 上的点F 处，若A ，F 两点间的距离是8 cm ，则△ABC 的面积为__40__cm 2.图21－9图21－1013．(10分)[2016·苏州]如图21－10，在△ABC 中，CD 是高，CE 是中线，CE ＝CB ，点A ，D 关于点F 对称，过点F 作FG ∥CD ，交AC 边于点G ，连结GE .若AC ＝18，BC ＝12，则△CEG 的周长为__27__.图21－8【解析】 ∵点A ，D 关于点F 对称， ∴点F 是AD 的中点． ∵CD ⊥AB ，FG ∥CD ， ∴FG 是△ACD 的中位线， ∵AC ＝18，BC ＝12， ∴CG ＝12AC ＝9.∵点E 是AB 的中点， ∴GE 是△ABC 的中位线， ∵CE ＝CB ＝12， ∴GE ＝12BC ＝6，∴△CEG 的周长＝CG ＋GE ＋CE ＝9＋6＋12＝27.(15分)14．(15分)[2016·邵阳]如图21－11，等边△ABC 的边长是2，D ，E 分别为AB ，AC 的中点，延长BC 至点F ，使CF ＝12BC ，连结CD 和EF .(1)求证：DE ＝CF ；图21－11(2)求EF 的长．解：(1)证明：∵D ，E 分别为AB ，AC 的中点， ∴DE 綊12BC ，∵延长BC 至点F ，使CF ＝12BC ，∴DE 綊FC ， 即DE ＝CF ； (2)∵DE 綊FC ，∴四边形DEFC 是平行四边形，∴DC＝EF，∵D为AB的中点，等边△ABC的边长是2，∴AD＝BD＝1，CD⊥AB，BC＝2，∴EF＝DC＝ 3.。