(参考资料)固体物理6-1 能带理论

第六章 能带理论 (习题参考答案)1. 一矩形晶格，原胞长10a 210m-=⨯，10b410m-=⨯（1）画出倒格子图（2）以广延图和简约图两种形式，画出第一布里渊区和第二布里渊区（3）画出自由电子的费米面（设每个原胞有2个电子）解：（1）因为a =a i=20A i b =b j=40A j倒格子基矢为12a iA*=, 014bj A*=以a *b *为基矢构成的倒格子如图。

由图可见，矩形晶格的倒格子也是矩形格子。

(2)取任一倒格子点O作为原点，由原点以及最近邻点A i,次近邻点B i的连线的中垂线可以围成第一，第二布里渊区，上图这就是布里渊区的广延图。

如采用简约形式，将第二区移入第一区，我们得到下图。

(3) 设晶体中共有N个原胞，计及自旋后，在简约布里渊区中便有2N个状态。

简约布里渊区的面积21()8A a bA ***-=⨯=而状态密度22()16()N g K N A A*==当每个原胞中有2个电子时，晶体电子总数为 22()216Fk FN g k kdk N k ππ=⨯=⎰所以1/211111()0.2()210()8F k A m π---=≈=⨯这就是费米圆的半径。

费米圆如下图所示2. 已知一维晶体的电子能带可写成()2271cos cos 2,88E k ka ka m a ⎛⎫=-+⎪⎝⎭式中a 是晶格常数。

试求： （i ）能带的宽度；（ii ）电子在波矢k 状态时的速度； （iii ）能带底部和顶部电子的有效质量。

()()()()()()()()22222m in 2m ax 22m ax m in 22222m in 71cos cos 2,8811cos 24400,2;221sin 24sin 404k i E k ka ka m a ka m a k E k E am a E E E m am aii v E kv ka ka m aiii E k kk E E mπ⎛⎫=-+⎪⎝⎭⎡⎤=--⎢⎥⎣⎦====∆=-=∴=∇∴=--==+解：当时，当时，能带的宽度为：在能带底部，将在附近用泰勒级数展开，可得：()()()22m in 22m ax 22m ax 220342203k E mm m E k k E E k mk E mm m ππδδδ****=+∴===-=+∴=-在能带顶部，将在附近用泰勒级数展开，令k=+k 可得：aa3. 试证明：如果只计及最近邻的相互作用，用紧束缚方法导出的简单立方晶体中S 态电子的能带为()2cos 2cos 2cos 2s x y z E k E A J ak ak ak πππ⎡⎤=--++⎣⎦并求能带的宽度。

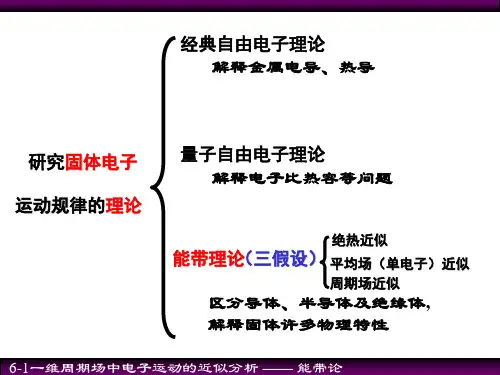
固体物理中关于能带理论的认识摘要:本文运用能带理论就晶体中的电子行为作一些讨论,以期对能带理论的概念更细致的把握。

关键词:能带理论电子共有化绝热近似平均场近似周期场假定引言能带理论(Energy band theory)是研究晶体(包括金属、绝缘体和半导体的晶体)中电子的状态及其运动的一种重要的近似理论。

它把晶体中每个电子的运动看成是独立的在一个等效势场中的运动,即是单电子近似的理论，对于晶体中的价电子而言,等效势场包括原子核的势场、其他价电子的平均势场和考虑电子波函数反对称而带来的交换作用,是一种晶体周期性的势场。

能带理论认为晶体中的电子是在整个晶体内运动的共有化电子,并且共有化电子是在晶体周期性的势场中运动。

1 能带理论的假定能带理论是目前的固体电子理论中最重要的理论。

量子自由电子理论可作为一种零级近似而归入能带理论。

能带理论是一个近似理论,下面对该理论所作的假定作为一探讨。

实际晶体是由大量电子和原子核组成的多粒子体系。

如果不采用一些简化近似,从理论上研究固体的能级和波函数是极为困难的。

1.1 绝热近似考虑到电子与核的质量相差悬殊。

可以把核与电子的运动分开考虑,相当于忽略了电子——声子相互作用。

电子运动时,可以认为核是不动的。

电子是在固体不动的原子核产生的势场中运动。

1.2 平均场近似因为所有电子的运动是关联的。

可用一种平均场来代替价电子之间的相互作用，即假定每个电子所处的势场都相同。

使每个电子的电子间相互作用能仅与该电子的位置有关，而与其它电子的位置无关，在上述近似下，每个电子都处在同样的势场中运动，既所有电子都满足同样的薛定谔方程，只要解得方程，就可得晶体电子体系的电子状态和能量。

使多电子问题简化为一个单电子问题，所以上述近似也称单电子近似。

1.3 周期场假定薛定谔方程中势能项是原子实对电子的势能，具有与晶格相同的周期性。

代表一种平均势能，应是恒量。

因此，在单电子近似和晶格周期场假定下，就把多电子体系问题简化为在晶格周期势场的单电子定态问题，上述在单电子近似基础上的固体电子理论称能带论。

固体物理学基础晶体的电子结构与能带理论在固体物理学中，研究晶体的电子结构是一项重要的课题。

晶体是由周期性排列的原子或分子组成的固体，而其电子行为对于晶体的性质以及各种物理现象的理解至关重要。

能带理论是描述晶体中电子行为的一种重要模型，通过能带理论，我们可以更好地理解晶体材料的导电、绝缘和半导体特性等基本特性。

首先，让我们来了解晶体的电子结构。

晶体中的原子或分子排列成一定的周期性结构，这种结构会对电子的行为产生重要影响。

在晶体中，电子的行为可以近似地看作是存在于一系列能级中，称为能带。

能带可以被分为价带和导带，其中价带中的电子被束缚在原子核附近，而导带则存在着自由电子。

晶体的周期性结构使得电子在其中受到布里渊区的限制。

布里渊区是倒格子中一个基本单元，它是晶体中全部电子状态所覆盖的空间。

当电子在布里渊区内运动时，具有周期性的波动特性，其波矢量（k）和波函数（Ψ）可以描述电子在晶体中的运动。

能带理论则进一步解释了电子如何填充在能级中。

根据泡利不相容原理，每个能级只能容纳一个电子，因此能带在填充时会出现能级填充顺序的规律。

根据能带的填充情况，我们将晶体分为导体、绝缘体和半导体三类。

对于金属晶体，由于其导带和价带之间存在较小的能隙，几乎所有能级都可以被电子填充，因此金属具有良好的导电性能。

对于绝缘体晶体，导带和价带之间存在较大的能隙，这意味着电子必须获取足够的能量才能从价带跃迁到导带。

由于常温下绝缘体的电子很难获得足够的能量，因此导带中很少有电子，绝缘体表现出非常低的导电性能。

而在半导体晶体中，导带和价带之间的能隙处于介于绝缘体和金属之间的状态。

半导体的电导率可以通过控制掺杂或加热等方式进行调节。

除了以上三类基本晶体材料，还有一类特殊的材料，称为拓扑绝缘体。

拓扑绝缘体是一种新兴的研究领域，它们具有特殊的能带结构和边界态，可以展现出一些非常有趣的现象和性质。

总结起来，固体物理学中研究晶体的电子结构和能带理论是了解晶体导电、绝缘和半导体等基本特性的重要途径。

本文是关于能带结构概念部分学习的小结，不保证理解准确，欢迎高中低手们批评指教，共同提高。

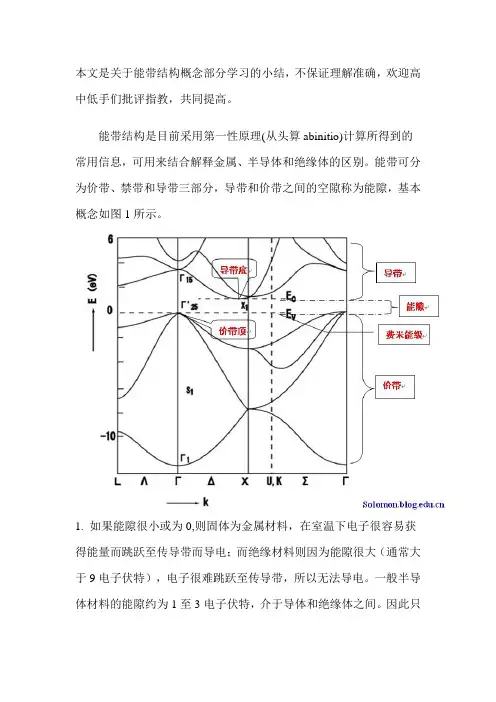
能带结构是目前采用第一性原理(从头算abinitio)计算所得到的常用信息，可用来结合解释金属、半导体和绝缘体的区别。

能带可分为价带、禁带和导带三部分，导带和价带之间的空隙称为能隙，基本概念如图1所示。

1. 如果能隙很小或为0,则固体为金属材料，在室温下电子很容易获得能量而跳跃至传导带而导电；而绝缘材料则因为能隙很大（通常大于9电子伏特），电子很难跳跃至传导带，所以无法导电。

一般半导体材料的能隙约为1至3电子伏特，介于导体和绝缘体之间。

因此只要给予适当条件的能量激发，或是改变其能隙之间距，此材料就能导电。

2. 能带用来定性地阐明了晶体中电子运动的普遍特点。

价带（valence band），或称价电带，通常指绝对零度时，固体材料里电子的最高能量。

在导带（conduction band）中，电子的能量的范围高于价带（v alence band），而所有在传导带中的电子均可经由外在的电场加速而形成电流。

对于半导体以及绝缘体而言，价带的上方有一个能隙（b andgap），能隙上方的能带则是传导带，电子进入传导带后才能再固体材料内自由移动，形成电流。

对金属而言，则没有能隙介于价带与传导带之间，因此价带是特指半导体与绝缘体的状况。

3. 费米能级(Fermi level)是绝对零度下电子的最高能级。

根据泡利不相容原理，一个量子态不能容纳两个或两个以上的费米子(电子)，所以在绝对零度下，电子将从低到高依次填充各能级，除最高能级外均被填满，形成电子能态的“费米海”。

“费米海”中每个电子的平均能量为（绝对零度下）为费米能级的3/5。

海平面即是费米能级。

一般来说，费米能级对应态密度为0的地方，但对于绝缘体而言，费米能级就位于价带顶。

成为优良电子导体的先决条件是费米能级与一个或更多的能带相交。

4. 能量色散（dispersion of energy）。

固体物理中的能带理论摘要本文综述了固体能带理论中的布洛赫定理、一维周期场中电子运动的近自由电子近似、包络函数模型(平面波展开方法)等基本理论。

还介绍了采用了包络函数法和近自由电子近似法来计算其能带结构。

可以看出，采用包络函数方法外推势能分布为体材料的势能分布时得到能带结构与利用准自由电子近似的方法得到的结果一致；另外，外推势能分布近似成为有限深势阱时与用超越方程得到的结果相吻合。

而采用近自由电子近似方法在外推势能分布为量子阱的势能分布时与直接采用近自由电子近似来处理小带阶的量子阱的结果一致。

关键词：能带理论包络函数近自由电子近似1 引言能带理论[1]是研究固体中电子运动的一个主要理论基础。

在二十世纪二十年代末和三十年代初期，在量子力学运动规律确定以后，它是在用量子力学研究金属电导理论的过程中开展起来的。

最初的成就在于定性地阐明了晶体中电子运动的普遍性的特点。

例如，在这个理论基础上，说明了固体为什么会有导体、非导体的区别；晶体中电子的平均自由程为什么会远大于原子的间距等。

在这个时候半导体开始在技术上应用，能带理论正好提供了分析半导体理论问题的基础，有利地推动了半导体技术的发展。

后来由于电子计算机的发展使能带论的研究从定性的普遍规律到对具体材料复杂能带的结构计算。

到目前，计算材料能带结构的方法有:近自由电子近似法、包络函数法(平面波展开法)[2，9，10，13]、赝势法[3，6]、紧束缚近似——原子轨道线性组合法[4，5， 7， 8， 11]、K.P方法[12]。

人们用这些方法对量子阱[2， 8， 9，10]。

量子线[11，12，13]、量子点结构[16， 17]的材料进行了计算和分析，并取得了较好计算结果。

使得对这些结构的器件的设计有所依据。

并对一些器件的特性进行了合理的解释。

固体能带论指出，由于周期排列的库仑势场的祸合，半导体中的价电子状态分为导带与价带，二者又以中间的禁带(带隙)分隔开。

从半导体的能带理论出发引出了非常重要的空穴的概念，半导体中电子或光电子效应最直接地由导带底和价带顶的电子、空穴行为所决定，由此提出的P-N结及其理论己成为当今微电子发展的物理依据。

固体物理学中的能带理论固体物理学是研究固体物质特性和行为的学科。

其中，能带理论是固体物理学中的重要内容之一。

这个理论的提出和发展，深刻地影响着我们对物质的认识和应用。

在本文中，将介绍能带理论的基本概念、理论构建的主要过程以及对实际应用的影响。

1. 能带理论的基本概念能带理论是描述固体材料中电子结构的理论框架。

它基于量子力学的原理，认为在固体中，电子的运动状态和能量分别由多个能带和能带间的禁带带宽所决定。

能带是指具有类似能量水平的电子能级。

禁带带宽则表示在能带之间禁止电子的能量范围。

2. 理论构建的主要过程能带理论的构建经历了一系列的发展过程。

最早的一些能带理论如卢瑟福模型和Drude模型，是基于经典力学和经典电动力学的假设，对于一些简单情况具有一定的解释能力。

然而，这些模型无法解释复杂固体中的行为，因为它们没有考虑到量子力学效应。

在量子力学的框架下，人们使用薛定谔方程和波函数的理论来描述电子在固体中的行为。

经典的能带理论建立在Bloch定理的基础上，该定理认为固体中的电子具有周期性的晶格势场作用下的波函数形式。

通过求解薛定谔方程，我们可以得到电子的能量本征值和本征态。

3. 对实际应用的影响能带理论的提出和发展对固体物理学的研究产生了深远的影响。

首先，能带理论提供了解释固体材料电子运动行为的一个理论模型。

它可以解释金属、绝缘体和半导体等不同类型材料的电导特性，以及它们在外界条件下的响应。

其次，能带理论对材料的设计和合成起着重要作用。

通过对能带结构的调控，我们可以设计出具有特定能带特性的新材料。

例如，针对光电子器件应用的材料，我们可以通过调节能带结构来实现不同波长的能带过渡和光电转换。

而且，能带理论也对半导体器件的工作原理给出了关键的解释。

例如，能带理论对于理解和优化半导体二极管、晶体管和太阳能电池等器件的性能至关重要。

它可以揭示不同物理机制对器件行为的影响，为器件的设计和优化提供了指导。

总结起来，能带理论是固体物理学中一项重要的理论构建。