作业讲解1解析

计算机应用基础第一次作业(含答案)讲解计算机应用基础第一次作业(含答案)讲解本文将为大家详细解析计算机应用基础第一次作业题目，并给出相应的答案解析。

通过本文的讲解，相信大家对于这次作业的内容和题目要求会有更深入的理解和掌握。

一、题目一：编程题要求：编写一个程序，输出1到100之间的所有偶数。

解析：这道题要求我们编写一个程序，在给定范围内输出所有的偶数。

首先，我们需要使用循环来遍历1到100之间的所有数字。

然后，对每一个数字进行判断，若该数字能够被2整除，则输出该数字。

下面是一个示例代码：```for i in range(1, 101):if i % 2 == 0:print(i)```上述代码使用了for循环来遍历1到100之间的所有数字，然后使用if语句判断每个数字是否能够被2整除。

如果能够整除，则输出该数字。

通过运行上述代码，我们就可以得到1到100之间的所有偶数。

二、题目二：选择题要求：在下列四个选项中，选择正确的答案。

解析：这道题目属于选择题，我们需要在给出的四个选项中选择正确的答案。

在计算机应用基础课程中，这种形式的题目经常出现，我们需要具备良好的逻辑思维能力和对基础知识的掌握。

下面是一个示例选择题：```下列哪个操作系统是开源的？A. WindowsB. macOSC. LinuxD. iOS```正确答案是C. Linux。

Linux操作系统是一个开源操作系统，而Windows、macOS和iOS等操作系统是闭源的。

三、题目三：简答题要求：请简要回答下列问题。

解析：这道题目是一个简答题，我们需要简要回答下面的问题。

一般来说，简答题会要求我们用简明扼要的语言回答问题，不需要过多的拓展或者举例。

以下是一个示例问题及其回答：问题：什么是二进制？回答：二进制是一种数制系统，使用0和1两个数字来表示数值。

在计算机领域中，二进制常用于表示和存储数据。

计算机中的所有数据最终都会被转化为二进制形式进行处理和存储。

1．1 概述数字计算机的发展经过了哪几个代？各代的基本特征是什么？略。

1．2 你学习计算机知识后，准备做哪方面的应用？略。

1．3 试举一个你所熟悉的计算机应用例子。

略。

1．4 计算机通常有哪些分类方法？你比较了解的有哪些类型的计算机？略。

1．5 计算机硬件系统的主要指标有哪些？答：机器字长、存储容量、运算速度、可配置外设等。

答：计算机硬件系统的主要指标有：机器字长、存储容量、运算速度等。

1．6 什么是机器字长？它对计算机性能有哪些影响？答：指CPU一次能处理的数据位数。

它影响着计算机的运算速度，硬件成本、指令系统功能，数据处理精度等。

1．7 什么是存储容量？什么是主存？什么是辅存？答：存储容量指的是存储器可以存放数据的数量（如字节数）。

它包括主存容量和辅存容量。

主存指的是CPU能够通过地址线直接访问的存储器。

如内存等。

辅存指的是CPU不能直接访问，必须通过I/O接口和地址变换等方法才能访问的存储器，如硬盘，u盘等。

1．8 根据下列题目的描述，找出最匹配的词或短语，每个词或短语只能使用一次。

（1）为个人使用而设计的计算机，通常有图形显示器、键盘和鼠标。

（2）计算机中的核心部件，它执行程序中的指令。

它具有加法、测试和控制其他部件的功能。

（3）计算机的一个组成部分，运行态的程序和相关数据置于其中。

（4）处理器中根据程序的指令指示运算器、存储器和I/O设备做什么的部件。

（5）嵌入在其他设备中的计算机，运行设计好的应用程序实现相应功能。

（6）在一个芯片中集成几十万到上百万个晶体管的工艺。

（7）管理计算机中的资源以便程序在其中运行的程序。

（8）将高级语言翻译成机器语言的程序。

（9）将指令从助记符号的形式翻译成二进制码的程序。

（10）计算机硬件与其底层软件的特定连接纽带。

供选择的词或短语：1、汇编器2、嵌入式系统3、中央处理器（CPU）4、编译器5、操作系统6、控制器7、机器指令8、台式机或个人计算机9、主存储器 10、VLSI答：（1）8，（2）3，（3）9，（4）6，（5）2，（6）10，（7）5，（8）4，（9）1，（10）7计算机系统有哪些部分组成？硬件由哪些构成？答：计算机系统硬件系统和软件系统组成。

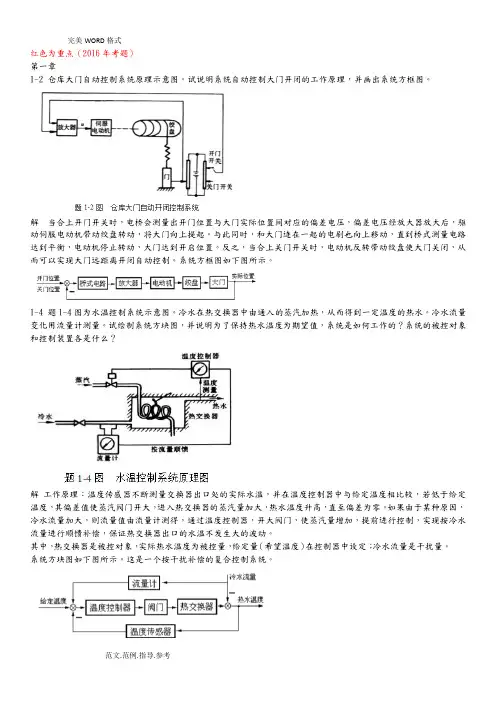
红色为重点（2016年考题）第一章1-2 仓库大门自动控制系统原理示意图。

试说明系统自动控制大门开闭的工作原理，并画出系统方框图。

解当合上开门开关时，电桥会测量出开门位置与大门实际位置间对应的偏差电压，偏差电压经放大器放大后，驱动伺服电动机带动绞盘转动，将大门向上提起。

与此同时，和大门连在一起的电刷也向上移动，直到桥式测量电路达到平衡，电动机停止转动，大门达到开启位置。

反之，当合上关门开关时，电动机反转带动绞盘使大门关闭，从而可以实现大门远距离开闭自动控制。

系统方框图如下图所示。

1-4 题1-4图为水温控制系统示意图。

冷水在热交换器中由通入的蒸汽加热，从而得到一定温度的热水。

冷水流量变化用流量计测量。

试绘制系统方块图，并说明为了保持热水温度为期望值，系统是如何工作的？系统的被控对象和控制装置各是什么？解工作原理：温度传感器不断测量交换器出口处的实际水温，并在温度控制器中与给定温度相比较，若低于给定温度，其偏差值使蒸汽阀门开大，进入热交换器的蒸汽量加大，热水温度升高，直至偏差为零。

如果由于某种原因，冷水流量加大，则流量值由流量计测得，通过温度控制器，开大阀门，使蒸汽量增加，提前进行控制，实现按冷水流量进行顺馈补偿，保证热交换器出口的水温不发生大的波动。

其中，热交换器是被控对象，实际热水温度为被控量，给定量（希望温度）在控制器中设定；冷水流量是干扰量。

系统方块图如下图所示。

这是一个按干扰补偿的复合控制系统。

1-5图为工业炉温自动控制系统的工作原理图。

分析系统的工作原理，指出被控对象、被控量及各部件的作用，画出系统方框图。

解加热炉采用电加热方式运行，加热器所产生的热量与调压器电压Uc的平方成正比，Uc增高，炉温就上升，Uc 的高低由调压器滑动触点的位置所控制，该触点由可逆转的直流电动机驱动。

炉子的实际温度用热电偶测量，输出电压Uf。

Uf作为系统的反馈电压与给定电压Ur进行比较，得出偏差电压Ue，经电压放大器、功率放大器放大成au后，作为控制电动机的电枢电压。

红色为重点（2016年考题）第一章1-2 仓库大门自动控制系统原理示意图。

试说明系统自动控制大门开闭的工作原理，并画出系统方框图。

解当合上开门开关时，电桥会测量出开门位置与大门实际位置间对应的偏差电压，偏差电压经放大器放大后，驱动伺服电动机带动绞盘转动，将大门向上提起。

与此同时，和大门连在一起的电刷也向上移动，直到桥式测量电路达到平衡，电动机停止转动，大门达到开启位置。

反之，当合上关门开关时，电动机反转带动绞盘使大门关闭，从而可以实现大门远距离开闭自动控制。

系统方框图如下图所示。

1-4 题1-4图为水温控制系统示意图。

冷水在热交换器中由通入的蒸汽加热，从而得到一定温度的热水。

冷水流量变化用流量计测量。

试绘制系统方块图，并说明为了保持热水温度为期望值，系统是如何工作的？系统的被控对象和控制装置各是什么？解工作原理：温度传感器不断测量交换器出口处的实际水温，并在温度控制器中与给定温度相比较，若低于给定温度，其偏差值使蒸汽阀门开大，进入热交换器的蒸汽量加大，热水温度升高，直至偏差为零。

如果由于某种原因，冷水流量加大，则流量值由流量计测得，通过温度控制器，开大阀门，使蒸汽量增加，提前进行控制，实现按冷水流量进行顺馈补偿，保证热交换器出口的水温不发生大的波动。

其中，热交换器是被控对象，实际热水温度为被控量，给定量（希望温度）在控制器中设定；冷水流量是干扰量。

系统方块图如下图所示。

这是一个按干扰补偿的复合控制系统。

1-5图为工业炉温自动控制系统的工作原理图。

分析系统的工作原理，指出被控对象、被控量及各部件的作用，画出系统方框图。

解加热炉采用电加热方式运行，加热器所产生的热量与调压器电压Uc的平方成正比，Uc增高，炉温就上升，Uc 的高低由调压器滑动触点的位置所控制，该触点由可逆转的直流电动机驱动。

炉子的实际温度用热电偶测量，输出电压Uf。

Uf作为系统的反馈电压与给定电压Ur进行比较，得出偏差电压Ue，经电压放大器、功率放大器放大成au后，作为控制电动机的电枢电压。

食品标准与法规_在线作业_1交卷时间：2016-04-21 23:20:19一、单选题1.(5分)国家未制定卫生标准的食品，省、自治区、直辖市人民政府可以制定（），报国务院卫生行政部门和国务院标准化行政主管部门备案。

A. 其他卫生标准B. 地方卫生标准C. 行业卫生标准D. 企业卫生标准知识点：3 食品添加剂的卫生2.(5分)（）级以上地方人民政府卫生行政部门在管辖范围内行使食品卫生监督职责。

A. 市B. 乡C. 镇D. 县知识点：3 食品添加剂的卫生二、多选题1.(5分)以下属于绿色食品标准的有（）。

A. 绿色食品生产技术标准B. 绿色食品检验标准C. 绿色食品产品标准D. 绿色食品产地环境质量标准知识点：2.11 其他食品相关标准2.(5分)以下（）不是《食品卫生法中》规定的食品卫生监督职责。

A. 对违反本法的行为进行巡回监督检查；B. 对食品生产经营企业的新建、扩建、改建工程进行设计；C. 协助培训食品生产经营人员，监督食品生产经营人员的健康检查；D. 对企业生产的每批食品进行进行检验，并出具检验合格证明；知识点：1 绪论3.(5分)以下属于管理标准的有（）。

A. 技术管理标准B. 管理设备标准C. 生产经营管理标准D. 管理基础标准知识点：2.1 食品包装与标签标准4.(5分)下列（）是《中华人民共和国食品卫生法》第八条食品生产经营过程必须符合的卫生要求。

A. 设备布局和工艺流程应当合理，防止待加工食品与直接入口食品、原料与成品交叉污染，食品不得接触有毒物、不洁物B. 用水必须符合国家规定的城乡生活饮用水卫生标准C. 保持内外环境整洁，采取消除苍蝇、老鼠、蟑螂和其它有害昆虫及其孳生条件的措施，与有毒、有害场所保持规定的距离D. 食品生产经营人员应当经常保持个人卫生，生产、销售食品时，必须将手洗净，穿戴清洁的工作衣、帽；销售直接入口食品时，必须使用售货工具知识点：1 绪论5.(5分)标准的特点包括：非强制性、技术法规和标准的制定目的不同还包括：（）。

受力分析1。

如图所示，质量分别为2m和m的A B、两物块，用一轻弹簧相连，将A用轻绳悬挂于某处，调整细绳的长度，当系统处于静止状态时，物块B恰好对地面没有压力,此时轻弹簧的形变量为x。

已知重力加速度为g,若突然剪断细绳，则下列说法正确的是（）A.剪断细绳后,A物块向下运动x时速度最大B。

剪断细绳后,A物块向下运动时速度最大C.剪断细绳瞬间,A物块的加速度大小为3gD.剪断细绳瞬间,A物块的加速度大小为g2.如图所示，A B，设地面对A的支持力为N F,绳子对A的拉力m m为F，地面对A的摩擦力为2F,若水平方向用力F拉A，使B匀速1上升，不计滑轮摩擦，则在此过程中( ）A.N F增大,2F增大，1F不变B。

N F减小，2F减小，1F不变C。

N F减小,2F减小,1F增大 D.N F增大,2F减小,1F增大3。

如图所示，带有光滑竖直杆的三角形斜劈固定在水平地面上，放置于斜劈上的光滑小球与套在竖直杆上的小滑块用轻绳连接,开始时轻绳与斜劈平行。

现给小滑块施加一个竖直向上的拉力,使小滑块沿杆缓慢上升，整个过程中小球始终未脱离斜劈，则有（）A。

小球对斜劈的压力保持不变B。

轻绳对小球的拉力先减小后增大C.竖直杆对小滑块的弹力先增大再减小D。

对小滑块施加的竖直向上的拉力逐渐增大4.如图,在挪威的两座山峰间夹着一块岩石，吸引了大量游客前往观赏.该景观可简化成如图所示的模型，右壁竖直，左壁稍微倾斜.设左壁与竖直方向的夹角为θ，由于长期的风化，θ将会减小。

石头与山崖间的摩擦很小，可以忽略不计。

若石头质量一定,θ减小，石头始终保持静止,下列说法正确的是（）A．山崖左壁对石头的作用力将增大B．山崖右壁对石头的作用力不变C．山崖对石头的作用力减小D ．石头受到的合力将增大5。

如图所示，小球放在光滑的墙与装有铰链的光滑薄板之间，薄板在 F 作用下逆时针缓慢转动，在墙与薄板之间的夹角 θ缓慢地从90°逐渐减小的过程中（ )A.小球对薄板的压力可能小于小球的重力B 。

细胞膜的结构和功能时间：45分钟满分:100分一、选择题每小题5分，共60分1．细胞膜功能的复杂程度，主要取决于膜上的(B)A．磷脂含量B．蛋白质的种类和数量C．糖的种类D．水含量解析:细胞膜主要由脂质和蛋白质组成，蛋白质是生命活动的主要承担者，因此蛋白质的种类和数量决定细胞膜功能的复杂程度.2．对细胞膜成分的描述最全面的是（C）A．磷脂、蛋白质B．脂质、蛋白质C．脂质、蛋白质和糖类D．磷脂、蛋白质和糖类解析:细胞膜的成分主要是脂质和蛋白质，还有2％～10％的糖类。

细胞中的脂质主要是磷脂，此外还有少量胆固醇。

蛋白质的含量与种类决定细胞膜功能的复杂程度。

3．下列关于细胞膜功能的叙述中，错误的是（D）A．控制物质进出细胞B．将产生的抗体分泌到细胞外C．维持细胞内部环境的相对稳定D．进行细胞间信息交流，且细胞间各种信息交流方式都离不开细胞膜上的受体解析：细胞膜具有以下功能：保护性屏障作用，将细胞与外界环境分隔开;控制物质进出细胞；进行细胞间信息交流。

植物细胞的胞间连丝贯穿细胞壁，将相邻两细胞细胞质连通在一起，为细胞间物质运输与信息传递的重要通道，这种交流信息的方式和细胞膜上的受体无关。

4．下列关于细胞膜功能的叙述中，不正确的是(C）A．细胞间的信息交流大多与细胞膜的结构和功能有关B．细胞间的信息交流使生物体作为一个整体完成生命活动C．相邻两个细胞间的信息交流全靠细胞间接触D．细胞膜能控制物质进出细胞，这种功能是相对的解析：细胞膜上含有蛋白质和糖类,这是细胞膜进行细胞间信息交流的基础；多细胞生物体是一个繁忙而有序的细胞社会，细胞间的信息交流使生物体作为一个整体完成生命活动;细胞间的信息交流有多种方式，除细胞直接接触传递信息外，还可通过细胞通道进行信息交流；细胞膜可根据生命活动的需要控制物质的进出,但这种控制作用是相对的,细胞不需要的物质，甚至病菌、病毒有时也能进入细胞。

5．取细胞膜上糖蛋白成分相同的两种海绵动物，将其细胞都分散成单个后混合培养，发现两种细胞能够结合在一起；但将细胞膜上糖蛋白成分不相同的两种海绵动物的细胞分散后混合培养,发现两种细胞不能结合在一起。

地球的宇宙环境(建议用时：40分钟)[合格过关练]读图，回答1～2题。

1．图中所示天体系统层次中的最低一级的是( )A．地月系B．总星系C．银河系D．太阳系2．图中的M天体可能是( )A．月球或水星B．水星或金星C．金星或木星D．火星或土星1．A 2．B[第1题，结合图示与所学知识可知，图示天体系统中的最低一级的是地月系。

第2题，M居于地球公转轨道内侧，为地内行星，有可能是水星或金星。

] 凌日是指地内行星(运行轨道在地球轨道和太阳之间的行星)在绕日运行时恰好处在太阳和地球之间，这时地球上的观测者可看到日面上有一个小黑点缓慢移动。

当金星与太阳、地球排成一条直线时，就会发生金星凌日现象。

据此完成3～4题。

3．假若发生金星凌日现象，则下列四图能正确表示此现象的是( )4．下列关于金星的叙述，正确的是( )A．金星绕日公转的方向是自东向西B．金星的“左邻右舍”分别是水星和火星C．金星属于地内行星D．金星属于巨行星3．C 4．C[第3题，由题目中“凌日”的含义可知，若出现金星凌日现象，必然是太阳、地球、金星在一条直线上，且地球、金星在太阳的同一侧，金星在内。

第4题，金星绕日公转的方向是自西向东，其“左邻右舍”是水星和地球，金星属于地内行星。

] 天文学家研究发现一颗绕昏暗恒星运转的类地行星，距地球仅40光年。

它是一个热气腾腾的“水世界”，体积是地球的6倍。

据推测，这个“水世界”同样拥有大气层，且75%的表面区域被水覆盖，但由于温度太高，它无法支持地球型生命的存在。

据此完成5～6题。

5．“水世界”类地行星所在的天体系统是( )A．河外星系B．银河系C．太阳系D．地月系6．天文学家推测“水世界”类地行星可能没有地球型生命存在的主要原因是该行星( )A．水域面积大B．大气层太薄C．距离太阳太远D．距离恒星太近5．B 6．D[第5题，根据材料可知，该行星“绕昏暗恒星运转，距地球仅40光年”，这表明该恒星不是太阳，但距离地球、太阳都比较近，因此，它属于与太阳并列的其他恒星系统，属于银河系，选B。

原电池的工作原理1.锌铜原电池装置如图所示，下列说法正确的是（ )A 。

铜片作负极 B.电流方向:锌片→铜片C 。

盐桥的作用是传递电子 D.锌电极上的反应为2Zn 2eZn -+-=2。

某兴趣小组设计的水果电池装置如图所示.该电池工作时，下列说法正确的是（ ）A 。

铜片为负极 B.锌片发生还原反应C.将电能转化为化学能 D 。

电子由锌片经导线流向铜片 3.如图所示各种装置中能构成原电池的是（ ）A。

①②③B。

④⑤⑥ C. ①③⑤D. ②④⑥4.某兴趣小组设计了如图所示原电池装置(盐桥中吸附有饱和K SO溶液）。

下列说法正确的是( ）24A。

该原电池的正极反应是2Cu2e Cu+-+=B。

甲烧杯中溶液的红色逐渐变浅C.盐桥中的24SO-流向甲烧杯D。

若将甲烧杯中的溶液换成稀硝酸，电流表指针反向偏转5.a、b、c、d四块金属片浸入稀硫酸中，用导线两两相连组成原电池.a、b相连时，电流由a经导线流向b；c、d相连时，电子由d到c；a、c相连时，a极上产生大量气泡；b、d相连时，H+移向d极.则四种金属的活动性由强到弱的顺序为( )A.a>b>c 〉d B。

a>c>d〉b C。

c〉a>b>d D.b〉d 〉c 〉a6.某种利用垃圾渗透液发电的装置示意图如下.工作时，下列说法中不正确的是( ）A 。

盐桥中-Cl 向Y 极移动B.化学能转变为电能C.电子由X 极沿导线流向Y 极 D 。

Y 极发生的反应为--+3222NO+10e +12HN +6H O=, 周围pH 增大7。

结合图Ⅰ、Ⅱ判断，下列叙述正确的是( ）A.Ⅰ和Ⅱ中正极材料均未被腐蚀 B 。

Ⅰ和Ⅱ中负极反应均是2Fe 2e Fe -+-=C.Ⅰ和Ⅱ中正极反应均是22O2H O 4e 4OH --++=D 。

Ⅰ和Ⅱ电解质溶液中的阳离子均向负极作定向移动8.有如图所示的装置，当电流表中产生持续电流时，下列说法正确的是（ ）A 。

第一次作业中文教材：1-14 氮气在273.2K 时的摩尔体积为70.3×10-6m 3，试计算其压力。

（1）用理想气体状态方程式；（2）用范德华方程式； （3）用压缩因子图法。

将上述结果与实验值比较（实验值为40530kPa ） 解答：（1）据pV nRT = p=68.314273.270.310-⨯⨯Pa=3.23×106Pa (2) N 2的范德华参量据课本34页表1-7查得620.1368..a Pa m mol -= 63138.610.b m mol --=⨯p=2m m RT a V b V --=62128.314273.20.1368(70.338.6)1070.310Pa Pa --⨯--⨯⨯=4.40×107Pa (3) 由课本31页表1-6查得：T c =126.3K p c =3394.4kPa V c,m =90.1×10-3dm 3.mol -1 T r =c T T =273.2 2.165126.3= 压缩因子定义m pV Z RT=p=Z m RT V =3.23×107Z.Pa p r =9.52c pZ p = 在T r =2.165附近，作p r ~Z 直线，此直线交T r 于Z=1.24处，此Z 值即为同时满足T r =2.165和P r =9.52Z 的对应态的压缩因子值，以之代入公式得 P=3.23×107×1.24Pa=40.4MPa1-17 （1）若以下方程式中的a 具有范德华常数a 的量纲，试由量纲分析确定以下两方程式中哪一个属量纲上正确的？哪一个属量纲上不正确的？ (a) 1V m p p a T T V RT ⎛⎫∂⎛⎫=+ ⎪⎪∂⎝⎭⎝⎭ (b) 21V m p p a T T V RT ⎛⎫∂⎛⎫=+ ⎪⎪∂⎝⎭⎝⎭(2) 某生于考试中对算术平均速度公式记忆已模糊不清，仿佛是u =其中x 为待定的物理量，试用量纲分析帮助他确定下来。

GAMES103动画基础作业1impulse浅浅解析简介impulse 简单⽽⾔就是脉冲. 脉冲就是, 在碰撞的时候给⼀个脉冲. 导致其速度和⾓速度改变.pipelineQ&A简述Vi 和 ViNewVi 就是碰撞点速度的均值ViNew 就是碰撞点速度的改变.J 有什么⽤通过 ViNew 和 Vi 计算除了 J. 然后通过J 计算出整个模型的速度v和⾓速度w. TIPS通过⾓速度的更新来更新, 物体的四元数codeusing UnityEngine;using System.Collections;public class Rigid_Bunny : MonoBehaviour{bool launched = false;float dt = 0.015f;Vector3 v = new Vector3(0, 0, 0); // velocityVector3 w = new Vector3(0, 0, 0); // angular velocityfloat mass; // massMatrix4x4 I_ref; // reference inertiafloat linear_decay = 0.999f; // for velocity decayfloat angular_decay = 0.98f;float restitution = 0.5f; // for collisionfloat mu_T = 0.5f;// may be coefficient of air resistanceVector3 G = new Vector3(0.0f, -9.8f, 0.0f);// Use this for initializationvoid Start (){Mesh mesh = GetComponent<MeshFilter>().mesh;Vector3[] vertices = mesh.vertices;float m=1;mass=0;for (int i=0; i<vertices.Length; i++){mass += m;float diag=m*vertices[i].sqrMagnitude;I_ref[0, 0]+=diag;I_ref[1, 1]+=diag;I_ref[2, 2]+=diag;I_ref[0, 0]-=m*vertices[i][0]*vertices[i][0];I_ref[0, 1]-=m*vertices[i][0]*vertices[i][1];I_ref[0, 2]-=m*vertices[i][0]*vertices[i][2];I_ref[1, 0]-=m*vertices[i][1]*vertices[i][0];I_ref[1, 1]-=m*vertices[i][1]*vertices[i][1];I_ref[1, 2]-=m*vertices[i][1]*vertices[i][2];I_ref[2, 0]-=m*vertices[i][2]*vertices[i][0];I_ref[2, 1]-=m*vertices[i][2]*vertices[i][1];I_ref[2, 2]-=m*vertices[i][2]*vertices[i][2];}I_ref [3, 3] = 1;}Quaternion addTwoQuaternion(Quaternion q0, Quaternion q1){Quaternion result = new Quaternion(q0.x + q1.x, q0.y + q1.y,q0.z + q1.z, q0.w + q1.w);return result;}Matrix4x4 Get_Cross_Matrix(Vector3 a){//Get the cross product matrix of vector aMatrix4x4 A = Matrix4x4.zero;A [0, 0] = 0;A [0, 1] = -a [2];A [0, 2] = a [1];A [1, 0] = a [2];A [1, 1] = 0;A [1, 2] = -a [0];A [2, 0] = -a [1];A [2, 1] = a [0];A [2, 2] = 0;A [3, 3] = 1;return A;}Matrix4x4 multiplyScalar(Matrix4x4 a, float b){Matrix4x4 rlt = Matrix4x4.zero;for(int i=0; i<4; i++){for(int j = 0; j<4; j++){rlt[i, j] = a[i, j] * b;}}return rlt;}Matrix4x4 addTwoMatrix(Matrix4x4 a, Matrix4x4 b){Matrix4x4 rlt = Matrix4x4.zero;for(int i=0; i<4; i++){for (int j = 0; j<4; j++){rlt[i, j] = a[i, j] + b[i, j];}}return rlt;}Matrix4x4 minusTwoMatrix(Matrix4x4 a, Matrix4x4 b){return addTwoMatrix(a, multiplyScalar(b, -1));}// In this function, update v and w by the impulse due to the collision with //a plane <P, N>void Collision_Impulse(Vector3 P, Vector3 N){Mesh mesh = GetComponent<MeshFilter>().mesh;Vector3[] vertices = mesh.vertices; // may be this is local positionint[] vid_collision = new int[vertices.Length];int num_collision = 0;Matrix4x4 R = Matrix4x4.Rotate(transform.rotation);for(int i=0; i<vertices.Length; i++){Vector3 xi = transform.position + R.MultiplyVector(vertices[i]);if(Vector3.Dot(xi - P, N) < 0){vid_collision[num_collision] = i;num_collision++;}}if(num_collision == 0){return;}Vector3 ri = new Vector3(0, 0, 0);for(int i = 0; i<num_collision; i++){ri += vertices[vid_collision[i]];}ri = ri / (float)(num_collision);Vector3 Rri = R.MultiplyVector(ri);Vector3 Vi = v + Vector3.Cross(w, Rri);if (Vector3.Dot(Vi, N) > 0) return; // it may be in the state of Rebound ??// calc Compute the wanted _ ^newVector3 VN = Vector3.Dot(Vi, N) * N;Vector3 VT = Vi - VN;restitution = Mathf.Max(restitution - 0.0005f, 0); // We can decrease the restitution _ to reduce oscillation float a = Mathf.Max(0, 1.0f - mu_T * (1.0f + restitution)) * Vector3.Magnitude(VN) / Vector3.Magnitude(VT); Vector3 ViNew = -1.0f * restitution * VN + a * VT;// Compute the impulse jMatrix4x4 I_rot = R * I_ref * Matrix4x4.Transpose(R);Matrix4x4 I_inverse = Matrix4x4.Inverse(I_rot);Matrix4x4 Rri_star = Get_Cross_Matrix(Rri);Matrix4x4 K = minusTwoMatrix(multiplyScalar(Matrix4x4.identity , (1.0f / mass)) ,Rri_star * I_inverse * Rri_star);Vector3 J = K.inverse.MultiplyVector(ViNew - Vi);// update v and wv = v + 1 / mass * J;w = w + I_inverse.MultiplyVector(Vector3.Cross(Rri, J));}// Update is called once per framevoid Update (){//Game Controlif(Input.GetKey("r")){transform.position = new Vector3 (0, 0.6f, 0);restitution = 0.5f;launched=false;}if(Input.GetKey("l")){v = new Vector3 (5, 2, 0);launched=true;}// Part I: Update velocitiesif (launched == false) return;v = v + dt * G;v = v * linear_decay;w *= angular_decay;// Part II: Collision ImpulseCollision_Impulse(new Vector3(0, 0.01f, 0), new Vector3(0, 1, 0));Collision_Impulse(new Vector3(2, 0, 0), new Vector3(-1, 0, 0));// Part III: Update position & orientation//Update linear statusVector3 x = transform.position;x += dt * v;//Update angular statusQuaternion q = transform.rotation;Vector3 dw = 0.5f * dt * w;Quaternion qua_rotate = new Quaternion(dw.x, dw.y, dw.z, 0.0f);q = addTwoQuaternion(q, qua_rotate * q);// Part IV: Assign to the objecttransform.position = x;transform.rotation = q;}}Image。

反应热焓变1.“焓”是指（)A.物质所具有的内能B.反应热的变化C.化学键所具有的能量D.物质的一种化学性质2.下列关于化学反应与能量变化的说法正确的是( ）A。

燃烧属于放热反应 B.中和反应是吸热反应C。

断裂化学键放出能量 D.反应物总能量与生成物总能量一定相等3.下列说法正确的是（）A.焓变单位为1⋅，是指1mol物质参加反应时的能量变化kJ mol-B。

当反应放热时0H∆<∆>，反应吸热时0HC.一个化学反应中，当反应物的总能量大于生成物的总能量时，反应放热，H∆为“—”D。

一个化学反应中，生成物总键能大于反应物的总键能时,反应吸热，H∆为“+”4。

下列说法正确的是( ）A。

中和热一定是强酸跟强碱反应放出的热量B。

1mol酸与1mol碱完全反应放出的热量是中和热C。

在稀溶液中，酸与碱发生中和反应生成1mol 2H O(l)时所放出的热量叫做中和热D。

测定中和热时可用稀硫酸和稀2Ba(OH)溶液5.下列对能量变化的认识不正确的是（）A。

电解水生成氢气和氧气时，电能转化为化学能B。

绿色植物进行光合作用时，太阳能转化为化学能C.煤燃烧时,化学能主要转化为热能D。

白炽灯工作时，电能全部转化为光能6。

中和热测定实验中，用50 mL 0。

50mol/ L盐酸和50 mL 0.55mol/ L NaOH溶液进行实验,下列说法不正确的是( ）A。

改用60 mL 0.50mol/ L盐酸跟50 mL 0.55 mol/ L NaOH溶液进行反应，求出的中和热数值和原来相同B。

用50 mL 0。

5mol/ L盐酸和50 mL 0.55mol/ L NaOH溶液进行实验比用50 mL 0.50mol/ L盐酸和50 mL 0.50mol/L.NaOH溶液测得的数值准确C。

酸、碱溶液混合时，量筒中NaOH溶液应缓缓倒入小烧杯中，不断用玻璃棒搅拌D.装置中的大、小烧杯之间填满碎泡沫塑料的作用是保温隔热、减少热量损失7.已知化学反应X(g)+2Y(g)=2Z(g)的能量变化如图所示,下列有关该反应的说法正确的是（）A。

1.2 等差数列（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．在等差数列{}n a 中，若25=a ，43=a ，则6=aA. －1B. 0C. 1D. 6 【答案】C【解析】（解法一）因为25a =，43=a ，有2642+=a a a ，得6a =1，故选C ．（解法二）因为25a =，43=a ，所以2224-=-=a a d ，6421a a d ∴=+=，故选C ． 2．在等差数列{}n a 中，若34830a a a ++=，则19a a +=A ．15B ．20C ．25D ．30 【答案】B【解析】由34830a a a ++=，得5330a =，则195220a a a +==，故选B ． 3．等差数列{}n a 的前m 项和为30，前m 2项和为100，则它的前m 3项和为A ．130B ．170C ．210D ．260 【答案】C【解析】（解法一）m m m m m S S S S S 232--，， ，即10070 303-m S ，，成等差，1101003=-∴m S ，2103=∴m S ．故选C ．（解法二）特值法：取1=m 则100,3021211=+===a a S a S ，702=∴a ，1103=∴a ， 2103213=++=∴a a a S ．故选C ．4．设{}n a 是等差数列，则下列结论中正确的是A ．若021>+a a ，则032>+a aB ．若031<+a a ，则021<+a aC ．若210a a <<，则312a a a >D ．若01<a ，则0))((3212>--a a a a 【答案】C【解析】反例 A ： 2，-1，-4 B ：2，-1，-4 D:-3，-2，-1 或 02>-d 不成立．C ：210a a << ，3210a a a <<<∴，313122a a a a a >+=∴．故选C ．5．在等差数列{}n a 中，135105a a a ++=，24699a a a ++=，以n S 表示{}n a 的前n 项和， 则使n S 达到最大值的n 是A ．21B ．20C ．19D ．18 【答案】B【解析】（解法一） 135105a a a ++=，24699a a a ++=，∴335a =,433a =， ∴432d a a =-=-， ∴139a =，∴2240(20)400n S n n n =-+=--+， ∴当20n =时n S 取最大值20．故选B ．（解法二） 135105a a a ++=，24699a a a ++=，两式相减得：63=-d ，2-=∴d ． 又13533105a a a a ++==，335a ∴=，3(3)241n a a n d n ∴=+-=-+． 令0n a >,得412n <,∴当20n =时n S 取最大值20．故选B ． 6．数列{}n a 的首项为3，{}n b 为等差数列且n n n a a b -=+1．若23-=b ，1210=b ，则=8a A ．0 B ．3 C ．8 D ．11 【答案】B【解析】d b b 7310=- 且23-=b ，1210=b ,2=∴d,82622)3(3-=-+-=-+=∴n n d n b b n ,821-=-∴+n a a n n ,)()(.....)()(7867231218a a a a a a a a a a -+-++-+-+=∴36420)2()4()6(3=++++-+-+-+=．故选B ．二、填空题7．记n S 为等差数列{}n a 的前n 项和，10a ≠，213a a =，则105S S =___________． 【答案】4【解析】因为213a a =，所以113a d a +=，即12a d =，所以105S S =11111091010024542552a d a a a d⨯+==⨯+．8．已知n S 是等差数列{}n a 的前n 项和，且27S S =,6k S S =（6k ≠），则k = ．【答案】3【解析】（解法一）由27S S =,得1176272a d a d ⨯+=+, 所以14a d =-． 因为6k S S =，所以()11165622k k a d ka d -⨯+=+，所以()1241542k k d d kd d --+=-+，整理得，29180k k -+=，解得3k =，或6k =（舍去）． （解法二）因为()2111)222n n n d dS na d n a n -=+=--(， 所以对应的函数()21()22d df x x a x =--的图象是一条抛物线，因为27S S =， 所以()fx 的图象关于27922x +==对称． 又因为6k S S =，所以6922k +=，解得3k =． 9．已知}{n a 为等差数列，n S 表示}{n a 的前n 项和，}{n a 满足4560a a a ++>，100S <， 则n S 取得最大值时n 的取值为：___________． 【答案】5【解析】因为0)(510110<+=a a S ，所以065101<+=+a a a a ，又456530a a a a ++=>， 即05>a ， 所以06<a ，所以当5=n 时，n S 取得最大值．10．已知数列{}n a 的首项为1，其余各项为1或2，且在第k 个1和第1+k 个1之间有12-k 个2，即数列{}n a 为：1，2，1，2，2，2，1，2，2，2，2，2，1，…，记数列{}n a 的 前n 项和为n S ，则2019S =__________．（用数字作答） 【答案】3993【解析】（解法一）第1k +个1为数列{}n a 的第21(13521)1k k k k ++++++-=++项当44k =时211981k k ++=；当45k =时212071k k ++=； 所以前2019项有45个1和244(20191981)+-个2，所以22019452[44(20191981)]3993S =+⨯+-=．（解法二）把该数列排成如下格式 1，2 1，2，2，2 1，2，2，2，2，2 1，2，2，2，2，2，2，2 …设其前m 行共有m T 项，则)1(2642+=+⋯⋯+++=m m m T m , 令2019)1(≤+m m 则44≤m 又1980454444=⨯=T , 即前44行共有1980项，其中有44个1，1936441980=-个2,所以第2019项为第45行第3919802019=-项（其中有1个1，38个2）, 即前2019项共有45144=+个1，1974381936=+个2, 所以2019451197423993S =⨯+⨯=．三、解答题：解答应写出文字说明，证明过程或演算步骤．11．记n S 为数列{}n a 的前n 项和，已知0n a >，213a a =，且数列是等差数列，证明：{}n a 是等差数列．【解析】因为数列是等差数列，设公差为d ===(n -=，()n *∈N ，所以12n S a n =，()n *∈N所以当2n ≥时，()221111112n n n a S S a n a n a n a -=-=--=-， 当1n =时，11121=a a a ⨯-，满足112n a a n a =-，所以{}n a 的通项公式为112n a a n a =-，()n *∈N所以()()111111221=2n n a a a n a a n a a --=----⎡⎤⎣⎦，所以{}n a 是等差数列． 12．已知数列{}n a 的前n 项和为n S ，11=a ，0≠n a ，11-λ=+n n n S a a ，其中为常数，（I ）证明：λ=-+n n a a 2；（II ）是否存在λ，使得{}n a 为等差数列？并说明理由．【解析】（I ）11-λ=+n n n S a a ， 1121-λ=∴+++n n n S a a ，1121++++λ=-∴n n n n n a a a a a ， 又01≠+n a ， λ=-∴+n n a a 2．（II ）由（I ）可知：{}n a 的奇数项和偶数项均为等差数列． 若{}n a 为等差数列，则122++=+n n n a a a ，又λ=-+n n a a 2，λ+=∴++1222n n a a ，即212λ=-++n n a a ． 由11=a ，11-λ=+n n n S a a ，可得:12-λ=a ,13+λ=a ．3122a a a += ，即11)1(2+λ+=-λ，解得4=λ，212=-∴a a ，又2212=λ=-++n n a a ， ∴当4=λ时，{}n a 是以2为公差的等差数列．1．3 等比数列（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．等比数列t ，33+t ，66+t ，…的第四项等于A ．24-B ．0C ．12D ．24 【答案】A【解析】（解法一）23366=++=t t q ， t t 233=+∴，3-=∴t ， ∴第四项为：24233-=⨯-．故选A ．（解法二）依题意：)66()33(2+=+t t t ，091232=++∴t t ，即0)1)(3(32=++t t ，3-=∴t 或1-=t （舍去），所以该等比数列各项依次为：3-，6-，12-，24-． 即第四项为：24233-=⨯-．故选A ．2．我国古代数学著作（算法统宗》中有这样一个问题（意为）：“有一个人要走378里路， 第一天健步行走，从第二天起因脚痛每天走的路程为前一天的一半，走了6天后到达目 的地．”那么，此人第4天和第5天共走路程是A ． 24里B ． 36里C ． 48里D ． 60里 【答案】B【解析】记每天走的路程里数为{}n a ，可知{}n a 是公比12q =的等比数列． 由6378S =，得16611)2378112(a S -==-，解得：1192a =，344511192()192()24123622a a ∴+=⨯+⨯=+=，所以此人第4天和第5天共走了241236+=里．故选B ． 3．已知正项等比数列{}n a 的前n 项和为n S ，已知374S =，6634S =，则=8a A ．8 B ．16 C ．32 D ． 64 【答案】C【解析】设等比数列{}n a 的公比为q )0(>q ，显然1≠q ，则有：⎪⎪⎩⎪⎪⎨⎧=--==--=4631)1(471)1(616313q q a S q q a S ，两式相除可得：91136=--q q ，即911)1)(1(3333=+=-+-q q q q ，2=∴q ，411=∴a ，3224178=⨯=∴a ．故选C ． 4．已知等比数列{}n a 中，各项都是正数，且1a ，312a ，22a 成等差数列，则91078a a a a +=+A．3+ B．1 C．1+ D．3- 【答案】A【解析】 1321,,22a a a 成等差数列，3122a a a ∴=+，∴2210q q --=，解得1q =± 又0>n a ，0>∴q，1q ∴=+∴2910783a a q a a +==++A ． 5．已知正项等比数列{}n a 的前n 项和为n S ，11=a ，且3a -，2a ，4a 成等差数列，则2021S与2021a 的关系是A. 2021202141S a =+ B ．2021202143S a =- C ．2021202121S a =- D ．2021202121S a =+ 【答案】C【解析】设等比数列的公比为)0(>q q ，由423,,a a a -成等差数列，得4322a a a +-=，又11=a ， 322q q q +-=∴， 即022=--q q ，0)1)(2(=+-∴q q ．又0>q ，2=∴q ，202020212=∴a ，122121202120212021-=--=S ，2021202121S a ∴=-．故选C ． 6．正项等比数列{}n a 中，463718+=a a a a ，则31323339log log log log ++++a a a a =A ．4B ．5C ．8D ．9 【答案】D【解析】因为246375218+==a a a a a 且{}n a 各项均为正数， ∴53=a ．所以()3132333931289log log log log log a a a a a a a a ++++=()()()()()423192837465355log log a a a a a a a a a a a ⎡⎤=⋅⋅⋅⋅=⋅⎡⎤⎣⎦⎢⎥⎣⎦99353log log 39a ===． 故选D ． 二、填空题7．等比数列{}n a 的前n 项和22nn S a a =⋅+-，则=a ________．【答案】1【解析】因为11()2211n n n a aS q a a q q=+-=⋅+---，所以20a a +-=，解得1a =． 8．记n S 为等比数列{}n a 的前n 项和．若24S =，46S =，则6S = ． 【答案】7【解析】因为n S 为等比数列{}n a 的前n 项和，所以2S ，42S S -，64S S -成等比数列， 所以24S =，42642S S -=-=，所以641S S -=，所以641167S S =+=+=． 9．已知{}n a 为等比数列，且334,12a S ==，则=q ． 【答案】1=q 或21-=q 【解析】（解法一）当1=q 时，31333a a S ==，显然1=q 符合题意；当1≠q 时，4213==q a a 214qa =∴．又12)1(1)1(21313=++=--=q q a q q a S ， 解得 21-=q ．∴综上可得：1=q 或21-=q ． （解法二）4213==q a a ，214q a =∴．又123113=++=a q a a S ， 可得：84422=+q q q ，即0122=--q q ，0)1)(12(=-+∴q q ，21-=∴q 或1=q ． 10．设等比数列{}n a 满足13+=10a a ，24+=5a a ，则123n a a a a ⋅⋅⋅⋅⋅的最大值为_________． 【答案】64【解析】设等比数列的公比为q ，由1324105a a a a +=+=⎧⎨⎩得，2121(1)10(1)5a q a q q +=+=⎧⎨⎩，解得1812a q =⎧⎪⎨=⎪⎩． 所以2(1)1712(1)22212118()22n n n n n n nn a a a a q--++++-==⨯=， 于是当3n =或4时，12n a a a 取得最大值6264=．三、解答题：解答应写出文字说明，证明过程或演算步骤． 11．设等比数列{}n a 满足124a a +=，318a a -=．（1）求{}n a 的通项公式；（2）记n S 为数列{}3log n a 的前n 项和．若13m m m S S S +++=，求m ． 【答案】（1）13n n a -=；（2）6m =．【解析】（1）设等比数列{}n a 的公比为q ，则1121148a a q a q a +=⎧⎨-=⎩，解得113a q =⎧⎨=⎩，所以13n n a -=． （2）令313log log 31n n n b a n -===-，所以(01)(1)22n n n n n S +--==，根据13m m m S S S +++=，可得(1)(1)(2)(3)222m m m m m m -++++=， 整理得2560m m --=，因为0m >，所以6m =． 12．已知为数列{}n a 的前项和，11=a ，241+=+n n a S ．（1）设数列{}n b 中，n n n a a b 21-=+，求证：{}n b 是等比数列； （2）求数列{}n a 的通项公式及前n 项和．【答案】（1）证明详见解析；（2）22)43(1+-=-n n n S ．【解析】（1）（解法一）241+=+n n a S ， 2,241≥+=∴-n a S n n 两式相减可得：1144-+-=n n n a a a ，)2(2211-+-=-∴n n n n a a a a ，即2,21≥=-n b b n n ， ∴{}n b 是以2为公比的等比数列．（解法二）241+=+n n a S ，2,241≥+=∴-n a S n n 两式相减可得：1144-+-=n n n a a a ，22422244221111111=--=---=--=∴-----+-n n n n n n n n n n n n n n n a a a a a a a a a a a a a b b ，2≥n ， ∴{}n b 是以2为公比的等比数列．（2）241212+=+=a a a S 且11=a ，52=∴a ，32121=-=∴a a b ，11232-+⨯=-=∴n n n n a a b ，432211=-∴++n n n n a a ， ⎭⎬⎫⎩⎨⎧∴n n a 2是以2121=a 为首项，以43为公差的等差数列， )13(41)1(43212-=-+=∴n n a n n ，22)13(--=∴n n n a ． 当2≥n 时，312)43(---=n n n a ，∴241+=-n n a S 22)43(1+-=-n n ，又111==a S 符合上式，∴数列{}n a 的通项公式及前n 项和22)43(1+-=-n n n S ．n2.1 直线的斜率（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．下列命题中正确的是A ．若两直线的倾斜角相等，则它们的斜率也一定相等B ．若两直线的斜率相等，则它们的倾斜角也一定相等C ．若两直线的倾斜角不相等，则它们中倾斜角越大的，斜率也越大D ．若两直线的斜率不相等，则它们中斜率越大的，倾斜角也越大 【答案】B【解析】当倾斜角都为2π时，斜率都不存在，所以A 项不正确； 钝角的正切是负值，锐角的正切是正值，不是角越大斜率越大，所以C 、D 都不正确； 因为直线的斜率确定，则倾斜角就确定了，直线的斜率相等，倾斜角一定相等，故选B ． 2．若图中的直线123l l l ，，的斜率分别为123k k k ，，，则A ．123k k k <<B ．312k k k <<C ．321k k k <<D ．132k k k << 【答案】D【解析】直线1l 的倾斜角α是钝角，故10k <．直线2l 与3l 的倾斜角β与γ均为锐角，且<γβ，所以320k k <<，因此132k k k <<．故选D ．3．已知直线过)4 2(，A ，)1(mB ，两点，且倾斜角为 45，则=m A ．0 B ．2C ．3D ．5 【答案】C【解析】因为直线过)4 2(，A ，)1(m B ，两点，所以直线的斜率为m m -=--4214， 又直线的倾斜角为 45，所以直线的斜率为145tan =，即14=-m ，所以3=m ．故选C ．4．已知三点)1 2(-，A ，)3 4(，B ，) 5(kC ，在同一条直线上，则k 的值为 A ．4 B ．5 C ．6D ．7 【答案】B【解析】因为)1 2(-，A ，)3 4(，B ，) 5(k C ，三点共线，所以BC AB k k =，即45324)1(3--=---k ， 解得5=k ．故选B ．5．直线02sin =++⋅y x α的倾斜角的范围是A ．)0[π，B ．]40[π，C ．)43[]40[πππ，， D ．)2[]4 0[πππ，， 【答案】C【解析】因为02sin =++⋅y x α，可化为2sin -⋅-=x y α，所以直线的斜率为αsin -． 设直线的倾斜角为θ，则有]1 1[sin tan ，-∈-=αθ， 又)0[πθ，∈，所以)43[]40[πππθ，， ∈．故选C ． 6．直线l 过点)0,1(P ，且与以)1,2(-A ，)3,0(B 为端点的线段有公共点，则直线l 斜率 的取值范围是A ．]31,3[--B ．]3,31[ C ．),31[]3,(+∞---∞ D ．),3[]31,(+∞-∞ 【答案】A【解析】如图，311201-=---=AP k ，31003-=--=BP k所以]31,3[--∈k ．故选A ． 二、填空题7．直线2-=x y 的倾斜角的大小为_______． 【答案】4π 【解析】由一次函数的图像及直线的斜率公式可知，直线2-=x y 的斜率为1， 设倾斜角为θ，则)0[πθ，∈，由1 tan =θ可得4πθ=．8． 直线l 经过点)1,3(A ，),2(2m B -，R m ∈两点，则直线l 的倾斜角α的取值范围是______． 【答案】)2,4[ππ【解析】直线l 的斜率1123122≥+=-+=m m k ，即1tan ≥α，又),0[πα∈，所以)2,4[ππα∈． 9．直线l 过点)0,1(P ，且与以)1,2(A ，)3,0(B 为端点的线段有公共点，则直线l 斜率的取值范围为________． 【答案】),1[]3,(+∞--∞ 【解析】如图，11201=--=AP k ，31003-=--=BP k ， 所以),1[]3,(+∞--∞∈ k ．10．已知0>ab ，且)0 (，a A ，) 0(b B ，，)2 2(--，C 三点共线，则ab 的最小值为________． 【答案】16【解析】因为)0 (，a A ，) 0(b B ，，)2 2(--，C 三点共线，所以BC AC k k =， 所以)2(0)2()2()2(0----=----b a ，即2222+=+b a ，所以)(2b a ab +-=． 又因为0>ab ，故0<a ，0<b ，所以ab b a b a ab 4)]()[(2)(2≥-+-=+-=． 从而0≤ab (舍去)或4≥ab ，故16≥ab ，当且仅当4-==b a 时取等号， 即ab 的最小值为16．三、解答题：解答应写出文字说明，证明过程或演算步骤．11．a 为何值时，过点(2,3)A a ，(2,1)B -的直线的倾斜角是锐角？是钝角？是直角？ 【答案】当1a >时，直线的倾斜角为锐角；当1a <时，直线的倾斜角为钝角；当1a =时，直线的倾斜角为直角.．【解析】当22a =，即1a =时，直线AB 的斜率不存在，直线的倾斜角为直角． 当1a ≠时，132221AB k a a --==--，若直线的倾斜角α是锐角，则2tan 01AB k a α==>-，即10a ->，得1a >； 若直线的倾斜角α是钝角，则2tan 01AB k a α==<-，即10a -<，得1a <． 综上，当1a >时，直线的倾斜角为锐角；当1a <时，直线的倾斜角为钝角； 当1a =时，直线的倾斜角为直角．12．在平面直角坐标系内，)32 1(，A ，)3 4(，B ． （1）求直线AB 的倾斜角θ的值；（2）若一束光线通过点A ，经x 轴反射，反射光线通过点B ，求入射光线与x 轴的交点P 的坐标．【答案】（1）65πθ=； （2） )0 3(，【解析】（1）因为)32 1(，A ，)3 4(，B ，所以直线AB 的斜率为3314323-=--=AB k ．又)0[πθ，∈，所以65πθ=． （2）依题意，有BPx APO ∠=∠，即直线AP 与直线BP 的倾斜角互补，所以BP AP k k -=． 设)0 (，a P ，则4301320---=--a a ，解得3=a ，即点P 的坐标为)0 3(，．13．如图，在矩形ABCD 中，2BC AB =，直线AC 的斜率为1，求直线BC 的斜率．【答案】3【解析】由题意，在Rt ABC ∆中，2ABC π∠=，2BC AB =，所以1tan 2AB ACB BC ∠==． 设直线AC 的倾斜角为θ，则tan 1θ=， 且直线BC 的倾斜角为ACB θ+∠， 所以tan()BC k ACB θ=+∠11tan tan 2311tan tan 112ACB ACB θθ++∠===-∠-⨯．2.2 直线的方程（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知直线022:=--y x l 的方向向量可以是A ．)2 1(-，B ．)2 1(，C ．)1 2(，-D ．)1 2(， 【答案】D【解析】（解法一）因为022=--y x ，可化为121-=x y ，所以直线l 的斜率为21， 所以直线l 所有的方向向量为)211(，λ，其中λ是不为零的任意实数， 又)1 2(，)21 1(2，=，所以)1 2(，是直线l 的一个方向向量．故选D ． （解法二）由0=++C By Ax 的一个方向向量为) (A B -，， 可知直线022=--y x 的一个方向向量为)1 2(--，， 又)1 2(，)1 2(---=，，所以)1 2(，是直线l 的一个方向向量．故选D ． 2．已知直线0=++c by ax 经过第一、第二、第四象限，则a ，b ，c 应满足A ．0>ab ，0<bcB ．0>ab ，0>bcC ．0<ab ，0>bcD ．0<ab ，0<bc 【答案】A【解析】由于直线0=++c by ax 经过第一、二、四象限， 所以直线存在斜率，将方程变形为bc x b a y --=， 如图，易知0<-b a 且0>-bc，故0>ab ，0<bc ．故选A ． 3．已知直线l 的一个法向量为)2 1(-，，且经过点)4 1(，，则直线l 的方程为 A ．092=-+y x B ．012=++y x C ．072=+-y x D ．012=--y x 【答案】C【解析】因为直线l 的法向量为)2 1(-，，可设直线的方程为02=+-C y x ． 又直线l 经过点)4 1(，，所以081=+-C ，即7=C ， 所以直线l 的方程为072=+-y x ．故选C ．4．如图，直线0:1=+-n y mx l 和0:2=+-m y nx l 在同一坐标系中正确的图形可能为A B C D 【答案】B【解析】0:1=+-n y mx l 和0:2=+-m y nx l 可分别化为n mx y +=和m nx y +=． 当00>>n m ，时，直线1l 和2l 的斜率都大于零，纵截距也都大于零，四个选项均不满足； 当0<mn 时，直线1l 和2l ，有一条直线的斜率大于零，纵截距小于零，而另一条直线的斜率小于零，纵截距大于零，选项B 满足；当00<<n m ，时，直线1l 和2l 的斜率都小于零，纵截距也都小于零，四个选项均不满足； 当0=mn 时，直线1l 和2l 至少一条经过原点，四个选项均不满足．故选B ． 5．直线l 经过点)4,3(，且与两坐标轴围成一个等腰直角三角形，则直线l 的方程为 A ．07=-+y x B ．01=--y xC ．07=-+y x 或01=+-y xD ．07=-+y x 或01=--y x 【答案】C【解析】设直线l 的方程为:1=+b y a x ，因为直线l 过点)4,3(，所以有143=+ba ． 因为直线l 与两坐标轴围成一个等腰直角三角形，所以b a =，即b a ±=． 当b a =时，有143=+aa ，故7==b a ； 当b a -=时，有143=-aa ，故1,1=-=b a ． 所以直线l 的方程为:177=+yx 或1=+-y x ，即07=-+y x 或01=+-y x ．故选C ． 6．已知直线1l ：422-=-a y ax ，2l ：42222+=+a y a x ，若20<<a 时，直线1l ，2l 与两坐标轴围成一个四边形，当四边形的面积最小时，实数=a A ．1- B ．21C ．1D ．2 【答案】B【解析】直线1l 可写成)2(22-=-x a y ，直线2l 可写成)2(222--=-x ay ，所以直线1l ，2l 恒过定点)2 2(，P ，直线1l 的纵截距为a -2，直线2l 的横截距为22+a ，又20<<a ，所以四边形的面积222111152(2)2(2)4()2224S a a a a a =⨯⨯-+⨯⨯+=-+=-+， 故当21=a 时，四边形的面积最小．故选B ． 二、填空题7．若直线过点)1 3(，和点)4 32(，，则该直线的方程为 ． 【答案】023=--y x【解析】（解法一）因为直线过点)1 3(，和点)4 32(，，所以直线的方程为0)1)(332()3)(14(=-----y x ，整理得；023=--y x ．（解法二）因为直线过)1 3(，和点)4 32(，，所以直线的斜率为333214=--=k ，所以直线的方程为)3(31-=-x y ，整理得023=--y x ．8．已知直线0322=-+-m my x ，当m 变化时，直线都通过定点 ．【答案】)3 1(--， 【解析】（解法一）当0≠m 时，0322=-+-m my x ，可化为)1(23+=+x my ， 即))1((2)3(--=--x my ，所以直线过定点)3 1(--，． 又当0=m 时，0322=-+-m my x ，可化为1-=x ，也过点)3 1(--，． 综上所述，当m 变化时，直线0322=-+-m my x 都通过定点)3 1(--，． （解法二）0322=-+-m my x 可化为)1(2)3(+=+x y m ,令03=+y ，得13-=-=x y ，，所以直线过定点)3 1(--，．9．已知直线l 经过点)3,1(--A ，且倾斜角等于直线x y 3=的倾斜角的2倍，则直线l 的方 程为 ． 【答案】01543=++y x【解析】设直线l 倾斜角为α，直线x y 3=的倾斜角为θ，则θα2=． 又因为直线x y 3=的斜率为3，即3tan =θ，所以直线l 的斜率为43tan 1tan 22tan tan 2-=-===θθθαk ． 又直线l 过点)3,1(--A ，所以其方程为：)1(433+-=+x y ，即01543=++y x ． 10．已知过点)2 2(，-P 的直线l 在第二象限与两坐标轴围成一个三角形，当该三角形的面积最小时直线l 的方程为 ． 【答案】04 =+-y x【解析】显然，直线l 的斜率存在且大于零，设直线l 的方程为)2 (2+=-x k y ，0>k ， 令0=x 得，22+=k y ；令0=y 得，)22(+-=kx ； 所以三角形的面积为8224)22)(22(21)22(2221≥++=++=+-+=k kk k k k S ， 当且仅当k k22=，即1=k 时取等．故三角形的面积的最小值为8． 此时直线l 的方程为2 2+=-x y ，即04 =+-y x ． 三、解答题：解答应写出文字说明，证明过程或演算步骤． 11．已知直线l 过点)2 3(，P ．（1）若直线l 在两坐标轴上的截距互为相反数，求直线l 的方程；（2）若直线l 分别交x 轴的正半轴和y 轴的正半轴于A 、B 两点，当OAB ∆的面积为12时求直线l 的方程．【答案】（1）032=-y x 或01=--y x ；（2）01232=-+y x ．【解析】（1）设若直线l 在x 轴和y 轴上的截距分别为a ，b 当0=-=b a 时，直线l 过原点，斜率为320302=--， 所以直线l 的方程为x y 32=，即032=-y x ； 当0≠-=b a 时，直线l 的方程为1=+b y a x ．又直线l 过点)2 3(，P ，所以123=+ba ． 因为b a -=，所以123=-aa ，故1=a ，1-=b ． 所以直线l 的方程为1=-y x ，即01=--y x ； 综上，直线l 的方程为032=-y x 或01=--y x ． （2）设直线l 的方程为)3(2-=-x k y ，0<k ， 令0=x 得，k y 32-=；令0=y 得，kx 23-=；因为直线l 与x 轴和y 轴交于正半轴，所以032>-k ，023>-k， 所以OAB ∆的面积12)23)(32(21=--=k k S ，解得32-=k ． 所以直线l 的方程为)3(322--=-x y ，即01232=-+y x ． 12．过点)1 2(，P 作直线l 分别交x 轴的正半轴和y 轴的正半轴于A 、B 两点． （1）求的最小值及此时直线l 的方程； （2）求最小值及此时直线l 的方程． 【解析】（1）根据题意可设直线l 的方程为，则， 直线l 过点，， 又(当且仅当，即时取等号)， ，即， 的最小值为8，此时直线l 的方程为；（2）由（1）可知，，则，(当且仅当，即时取等号)． 的最小值为4，此时直线l 的方程为．||||OA OB ⋅||||PA PB ⋅1(0,0)x ya b a b+=>>(,0),(0,)A a Bb (2,1)P 211(0,0)a b a b∴+=>>21a b +≥21a b =4,2a b ==1∴≤8ab ≥||||=OA OB ab ∴⋅240x y +-=211a b +=02ab a ∴=>-2a>||||PA PB ∴⋅4≥=221(2)=(2)a a --3a =||||PA PB ∴⋅30x y +-=2.3 两条直线的位置关系（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．若直线()120x m y ++-=和直线240mx y ++=平行，则m 的值为 A ．1 B ．2- C ．1或2- D ．23- 【答案】A【解析】直线()120x m y ++-=和240mx y ++=平行，可得11224m m +-=≠， 得1m =．故选A ．2．已知0b >，直线2(1)20b x ay +++=与直线210x b y --=垂直，则ab 的最小值为 A ．1 B ．2 C ．22 D ．23 【答案】B【解析】由已知两直线垂直，得22(1)0b ab +-=，即221ab b =+，又0b >，所以12ab b b=+≥，当且仅当1b =时等号成立，所以ab 的最小值为2．故选B ． 3．若直线:3l y kx =-与直线30x y +-=的交点在第一象限，则直线l 的倾斜角α的取 值范围为A ．(0 )30，B ．(30 )90，C ．(90 )135，D ．(135 )180， 【答案】B【解析】（解法一）已知直线:3l y kx =-过定点(03) P -，， 直线30x y +-=与x 轴，y 轴分别交于(30) A ，，(03) B ，，如图． 又33PA k =，通过数形结合可得， 33k >，即3tan 3α>，故3090α<< ，选B ．（解法二）由330y kx x y ⎧=-⎪⎨+-=⎪⎩得交点坐标为3333,)1+1+k k k +-（，又交点在第一象限， 所以3301+3301+kk k⎧+>⎪⎪⎨-⎪>⎪⎩，解得33k > ，即3tan 3α>，故3090α<< ，选B ．4．已知0a >，若y a x =与y x a =+的图象有两个交点，则a 的取范围为A ．0a >B ．01a <<C ．1a >D ．1a ≥ 【答案】C【解析】y a x =表示关于y 轴对称的两条射线，y x a =+表示斜率为1，在y 轴上的截距为a 的直线，根据题意，画出大致图形，如下图，若y a x =与y x a =+的图象有两个交点，且0a >，则根据图形可知1a >．故选C ．5．若(2 3)P ，既是11()A a b ，，22()B a b ，的中点，又是直线111:130l a x b y +-=与直线 222:130l a x b y +-=的交点，则线段AB 的垂直平分线的方程是A ．23130x y +-=B ．32120x y +-=C ．2350x y -+=D ．320x y -= 【答案】D【解析】将P 点坐标代入12,l l 的方程得1123130a b +-=，2223130a b +-=，所以,A B 两点在直线23130x y +-=上，故23AB k =-，所以线段AB 的垂直平分线的斜率为32，又AB中点为(2 3)P ，，所以线段AB 的垂直平分线的方程是()3322y x -=-，即320x y -=． 故选D ．6．已知直线1:310l x y --=，2:250l x y +-=，3:30l x ay --=不能围成三角形，则 实数a 的取值不可能为 A ．1 B ．13C ．1-D ．2- 【答案】A【解析】因为直线1l 的斜率为3，直线2l 的斜率为12-，所以直线1l ，2l 一定相交， 由3125x y x y -=⎧⎨+=⎩解得交点坐标为：(1,2)．当0a =时，3l 与横轴垂直，方程为：3x =不经过点(1,2)，所以三条直线能构成三角形；当0a ≠时，3l 的斜率为：1a． 当1l 与3l 的斜率相等即13a =，时，13a =，此时这两直线平行，这三条直线不能三角形； 当2l 与3l 的斜率相等即112a =-时，2a =-，此时这两直线平行，这三条直线不能三角形； 当3l 过12,l l 交点(1,2)即1230a --=时，1a =-，此时三条直线不能构成三角形；故选A ． 二、填空题7．过点()4,2P －与直线370l x y --=：平行的直线方程为： ． 【答案】3140x y -+=【解析】设所求直线的方程是()307x y m m -+=≠-， 因为点()4,2P －在直线上， 所以()3420m ⨯-+－＝，解得14m =，即所求直线方程是3140x y -+=． 8．已知ABC ∆三条边所在的直线方程分别为02:=+-y x l AB ，022:=++y x l AC ，1:=x l BC ，则AC 边上的高所在直线方程为： ．【答案】012=+-y x 【解析】由201x y x -+=⎧⎨=⎩，解得点B 坐标为(1 3)，． 因为直线AC 的斜率为12-，所以AC 边上的高所在直线的斜率为2， 所以AC 边上的高所在直线的方程为)1(23-=-x y ，即012=+-y x ．9．直线:(21)(31)730l x y λλλ+++--=恒过定点，则该定点的坐标为： ． 【答案】(2 1)，【解析】（解法一）将(21)(31)730x y λλλ+++--=化成(237)(3)0x y x y λ+-++-=，要使直线恒过定点，必须237030x y x y +-=⎧⎨+-=⎩，解得21x y =⎧⎨=⎩，即直线l 恒过定点(2 1)，．（解法二）将(21)(31)730x y λλλ+++--=化成21733131y x λλλλ++=-+++，即212(21)13131y x λλλλ++=-++++，即211(2)31y x λλ+-=--+，所以直线l 恒过定点(2 1)，． 10．已知m R ∈，动直线110l x my +-=：过定点A ，动直线2:230l mx y m --+=过定点B ，若1l 与2l 交于点P （异于A ，B 两点），则PA PB +的最大值为： ．【答案】【解析】由题意可得()()1,0,2,3A B ，因为1(1)0m m ⨯+⨯-=， 所以直线10x my +-=和直线230mx y m --+=垂直， 则()2222102PA PB PA PB AB++==≥，当且仅当PA PB ==时取等号，所以PA PB +≤PA PB +的最大值为 三、解答题：解答应写出文字说明，证明过程或演算步骤．11．在ABC ∆中，已知角C 的角平分线所在的直线方程为2y x =，顶点A ，B 的坐标分别是(4 2)-，，(3 1)，，求顶点C 的坐标． 【答案】(2 4)，．【解析】设(4 2)A -，关于直线2y x =的对称点为00( )A x y '，， 则0024AA y k x '-=+，AA '的中点坐标为0042( )22x y -+，，所以0000221424222y x y x -⎧⨯=-⎪+⎪⎨+-⎪=⨯⎪⎩， 解得0042x y =⎧⎨=-⎩，所以(4 2)A '-，，因为点A '在直线BC 上，且(3 1)B ，，所以BC 所在的直线方程为211(3)43y x ---=--，即3100x y +-=． 因为C 为直线BC 与直线2y x =的交点， 所以由31002x y y x +-=⎧⎨=⎩，31003100x y x y +-=⎧⎨-+=⎩，即(2 4)C ，．12．已知ABC ∆的顶点(5 1)A ，，AB 边上的中线CM 所在直线方程为250x y --=，AC 边上的高BH 所在直线方程为250x y --=． （1）求顶点C 的坐标； （2）求直线BC 的方程． 【答案】（1）(4 3)C ，； （2）6590x y --=．【解析】（1）由AC 边上的高BH 所在直线方程为250x y --=，得21=BH k ， 所以2-=AC k ，又(5 1)A ，，所以AC 边所在直线方程为2110x y +-=， 联立直线AC 与直线CM 方程得2110250x y x y +-=⎧⎨--=⎩，解得43x y =⎧⎨=⎩，即顶点C 的坐标为(4 3)，．（2）设00( )B x y ，，则AB 的中点M 为0051( )22x y ++，，由M 在直线250x y --=上，得005125022x y ++⨯--=，即00210x y --=， 由点B 在直线250x y --=上，得00250x y --=， 联立0000210250x y x y --=⎧⎨--=⎩，解得0013x y =-⎧⎨=-⎩，所以顶点B 的坐标为(1 3)--，．又(4 3)C ，，所以直线BC 的方程为333(1)14y x --+=+--，即6590x y --=．2.4 点到直线的距离（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．点 0)F0=的距离为 ABC ．3D ．m 3 【答案】A【解析】点F0=的距离d ==．故选A ．2．直线1:330l x y +-=与直线2:610l x my ++=平行，则1l 与2l 之间的距离为 A ．4 BCD【答案】D【解析】直线1:330l x y +-=可化为6260x y +-=，因为1l 与直线2:610l x my ++=平行，所以2=m ，即2:6210l x y ++=， 所以1l 与2l之间的距离为d ==故选D ． 3．已知12=+y x ，则22y x +的最小值为 A ．1 B ．14 C ．15 D ．110【答案】C【解析】22y x +表示)0,0(到12=+y x 上点的距离的平方， 所以22y x +的最小值是（0，0）到012=-+y x 的距离d 的平方，据点到直线的距离公式得d ==22y x +的最小值为15．故选C ． 4．直线1:320l x y --=和直线2:3100l x y +-=的夹角平分线的方程为 A ．240x y +-= B ．260x y --=C ．240x y +-=或260x y --=D ．240x y +-=或260x y --= 【答案】D【解析】设(,)P x y 为角平分线上的任意一点，由该点到两直线的距离相等，即可得：=32310x y x y --=+-，整理得240x y +-=或260x y --=．故选D ．5．知两点()1,2A ，()3,6B ，动点M 在直线y x =上运动，则MA MB +的最小值为 A ．25 B ．26 C ．4 D ．5 【答案】B【解析】根据题意画出图形，如图所示： 设点A 关于直线y x =的对称点()2,1A '， 连接A B '，则A B '即为MA MB +的最小值， 且()()22=32+61=26A B '--． 故选B ．6．已知点P 为直线013:=--y x l 上的动点，当点P 到(4 1)A ，和(0 4)B ，的距离之差最 大时，点P 坐标为A ．(1 2，）B ．4( 33，） C ．(2 5，）D ．(3 8，） 【答案】C【解析】如图，作点B 关于l 的对称点为B '，AB '的延长线交l 于0P ，在l 上任取一点P ，则00PA PB PA PB AB P A P B '''-=-≤=-，则点0P 即为所求．设(0 4)B ，关于直线l 的对称点为00( )B x y '，， 则004BB y k x '-=，BB '的中点坐标为004( )22x y +，， 所以0000431431022y x x y -⎧⨯=-⎪⎪⎨+⎪⨯--=⎪⎩，解得0033x y =⎧⎨=⎩，所以(3 3)B '，．所以直线AB '的方程为092=-+y x ．由290310x y x y +-=⎧⎨--=⎩，可得0P (2 5，）．故选D ．二、填空题7．若点Q P ，分别为直线01243=-+y x 与0343=++y x 上的动点，则PQ 的最小值 为： ． 【答案】3【解析】依题意知，两直线平行．所以PQ 的最小值为这两条平行直线间的距离， 即=min PQ 22|123|334--=+．8．若两条平行直线()1:200l x y m m -+=>与2:260l x ny +-=之间的距离是25m n += ．【答案】3【解析】由题意直线()1:200l x y m m -+=>与2:260l x ny +-=平行，则1226m n -=≠-， 即4n =-且3m ≠，所以2:2460l x y --=，化为2:230l x y --=，所以1l 与2l 之间的的距离为22(3)251(2)m --=+-，又0m >，所以7m =，所以3m n +=．9．已知点(1 2)A -，，(3 4)B ，．点P 在x 轴上，且PA PB =，则PAB ∆的面积为________． 【答案】152【解析】设AB 的中点坐标为M ，则(13)M ，， 因为241132AB k -==--，所以AB 的中垂线方程为)1(23--=-x y ，即052=-+y x ． 令=0y ，则52x =，即P 点的坐标为5( 0)2，，所以22(13)(24)25AB =--+-=， 点P 到AB 的距离为22535(1)(30)2PM =-+-= 所以113515252222PAB S AB PM ==⨯=△． 10．函数2291041y x x x =+-+_________． 74 【解析】()22222291041354y x x x x x =+-+=+-+设()0,3A ，()5,4B ，(),0C x ，则()2222354y x x AC BC =+-+=+，即x 轴上的一动点(),0C x 到()0,3A ，()5,4B 的距离之和．作()0,3A 点关于x 轴的对称点()10,3A -， 连接1BA ，则1BA 即为距离和的最小值， ()22153474BA =+--=min 74y ．三、解答题：解答应写出文字说明，证明过程或演算步骤．11．已知直线l 经过直线052=-+y x 与02=-y x 的交点．（1）若点)0 5(，A 到l 的距离为3，求l 的方程；（2）若直线l '经过原点O ，且与直线l 平行，求l '与l 的距离最大值时直线l '的方程．【答案】（1）2=x 或0534=--y x ；（2）02=+y x ．【解析】（1）（解法一）设经过两已知直线交点的直线方程为0)2(52=-+-+y x y x λ， 即05)21()2(=--++y x λλ3=．即02522=+-λλ，所以0)2)(12(=--λλ，解得21=λ或2-=λ．故l 的方程为2=x 或0534=--y x ． （解法二）由25020x y x y +-=-=⎧⎨⎩，解得交点)1 2(，P ． 当直线l 斜率不存在时，方程为：2=x ，此时点)0 5(，A 到l 的距离为3，故2=x 符合题意； 当直线l 斜率存在时，设其方程为：)2(1-=-x k y ，即021=-+-k y kx ，所以点)0 5(，A 到l 的距离为：31132=++k k ，解得34=k ， 所以直线l 的方程为：)2(341-=-x y ，即0534=--y x ． 综上，直线l 的方程为2=x 或0534=--y x ．（2）当两条平行直线l '，l 与P ，O 两点连线垂直时，两条平行直线间的距离最大． 又101202OP k -==-，所以两条平行直线的斜率为2-， 所以直线l '的方程是x y 2-=，即02=+y x ．12．已知直线方程为()()221340m x m y m -++++=．（1）证明：直线恒过定点；（2）当m 为何值时，点()3,4Q 到直线的距离最大，最大值为多少？（3）若直线分别与x 轴，y 轴的负半轴交于,A B 两点，求AOB ∆面积的最小值及此时直线的方程．【答案】（1）详见解析；（2）47m =； （3）AOB ∆面积的最小值为4，此时直线的方程240x y ++=．【解析】（1）证明：直线方程为()()221340m x m y m -++++=，可化为()()24230x y m x y +++-++=，对任意m 都成立，所以230240x y x y -++=⎧⎨++=⎩，解得12x y =-⎧⎨=-⎩，所以直线恒过定点()1,2--；（2）点()3,4Q 到直线的距离最大，可知点Q 与定点()1,2P --的连线的距离就是所求最=． 又 423312PQ k +==+， 且()()221340m x m y m -++++=的斜率为23-，故22321m m --=-+，解得47=m ． （3）由（1）可知，直线过定点，且分别与x 轴，y 轴的负半轴交于,A B 两点， 设直线方程为()21y k x +=+，0<k ，分别令=0x ，=0y ，可得2(1,0)A k -，()0,2B k -，则1212212(1)(2)2()24222AOB k S k k k k k -=--=--=++≥+=-△， 当且仅当2k =-时取等号，面积的最小值为4． 此时直线的方程240x y ++=．2.5 圆的方程（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．在平面内，,A B 是两个定点，C 是动点．若1AC BC ⋅=，则点C 的轨迹为A ．圆B ．椭圆C ．抛物线D ．直线【答案】A【解析】设()20AB a a =>，以AB 中点为坐标原点建立平面直角坐标系，则：( 0)( 0)A a B a -，，，，设(),C x y ，则()(),,,AC x a y BC x a y →→=+=-，所以()()21AC BC x a x a y →→⋅=+-+=，整理可得：22210x y a +=+>，即点C 的轨迹是以AB 为半径的圆．故选A ．2．已知点(1,1)a a +-在圆22240x y ay +--=的外部（不含边界），则实数a 的取值范围为A ．1a <B ．01a <<C ．15a >D ．1a > 【答案】D【解析】因为圆22240x y ay +--=，可化为()2224x y a a +-=+， 所以圆心()0,a ，半径24ra ． 因为点(1,1)a a +-在圆22240x y ay +--=的外部，所以点(1,1)a a +-到圆心()0,a 的距离大于半径，>1a >．故选D ． 3．若过点(2 1)，的圆与两坐标轴都相切，则圆心到直线032=--y x 的距离为 A ．55 B ．552 C ．553 D ．554 【答案】B【解析】由于圆上的点(2 1)，在第一象限，所以圆心必在第一象限， 因为圆与两坐标轴都相切，所以设圆的半径为a ，则圆心的坐标为()a a ，，故圆的标准方程为222()()x a y a a -+-=．由题意可得()()22221a a a -+-=，可得2650a a -+=，解得1a =或5a =，所以圆心的坐标为(11)，或(5 5)，，圆心到直线230x y --=的距离均为d ==，所以圆心到直线230x y --=．故选B ． 4．若方程22220x y kx y k ++++=所表示的圆取得最大面积，则直线(1)2y k x =-+的 倾斜角α等于A ．45B ．60C ．120D ．135【答案】D【解析】方程22220x y kx y k ++++=的标准方程为2223()(1)124k k x y +++=-， 则22314k r =-，当所表示的圆取得最大面积时，0k =，此时1r =， 则直线()12y k x =-+为2y x =-+，所以tan 1α=-，因为[0 180)α∈，，所以135α=︒．故选D ． 5．已知圆1C ：22(1)(1)1x y ++-=，圆1C 与圆2C 关于直线10x y --=对称，则圆2C 的 方程为A ．22(2)(2)1x y ++-=B ．22(2)(2)1x y +++=C ．22(2)(2)1x y -++=D ．22(2)(2)1x y -+-=【答案】C【解析】圆1C 的圆心为(11)-，，半径长为1，设圆2C 的圆心为( )a b ，， 由题意得111022a b -+--=且1=1+1b a --，解得22a b ==-，，即圆2C 的圆心为(2 2)-，， 又圆2C 的半径长为1，故圆2C 的方程为22(2)(2)1x y -++=．故选C ．6．设m R ∈，过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于 点P ，则||||PA PB +（异于A ，B 两点）的取值范围是A ．B ．C ．D ．【答案】B【解析】由题意可得(0,0)A ，(1,3)B ，因为1(1)0m m ⨯+⨯-=，所以直线0x my +=和直线230mx y m --+=垂直，故点P 在以AB 为直径的圆上运动，故||||||cos ||sin PA PB AB PAB AB PAB +=∠+∠)4PAB π=∠+，因为(0 )2PAB π∠∈，，所以3( )444PAB πππ∠+∈，，所以2sin()(1]42PAB π∠+∈， 所以||||PA PB +(10,25]∈．故选B ．二、填空题7．已知圆C 经过(5 1)A ，，(1 3)B ，两点，圆心在x 轴上，则C 的方程为 ．【答案】22(2)10x y -+=【解析】依题意设圆C 的方程为222()x a y r -+=，把所给的两点坐标代入方程得2222(5)1(1)9a r a r⎧-+=⎨-+=⎩，解得2210a r =⎧⎨=⎩，所以圆C 的方程为：22(2)10x y -+=． 8．若方程222(2)4850a x a y x y a +++++=表示圆，则圆心坐标是_____，半径长为____．【答案】(2,4)--； 5．【解析】由题意22a a =+，即1a =-或2a =．当1a =-时，方程为224850x y x y +++-=，即22(2)(4)25x y +++=，圆心为(2,4)--，半径为5，当2a =时，方程为224448100x y x y ++++=，2215()(1)24x y +++=-不表示圆． 9．由曲线2222x y x y +=+围成的图形面积为 ．【答案】84π+【解析】由题意，作出如图的图形，由曲线关于原点对称，当0x ，0y 时，解析式为22(1)(1)2x y -+-=，故可得此曲线所围的力图形由一个边长为22的正方形与四个半径为2的半圆组成， 所围成的面积是2122224(2)842ππ⨯+⨯⨯⨯=+． 10．已知点(, )P x y 是圆22:4230C x y x y ++-+=上的动点，则22(1)(2)-++x y 的取值范围为 ．【答案】[8 32]，【解析】圆22:4230C x y x y ++-+=可化为22(2)(1)2x y ++-=，则圆心(2,1)C -，半径2r =， 故22(1)(2)-++x y 表示圆上的点(,)P x y 到点(1,2)Q -的距离的平方，因为22(21)(12)32QC =--++=，所以22QC PQ QC -≤≤+，即2242PQ ≤≤，所以2832PQ ≤≤，所以22(1)(2)-++x y 的取值范围为[8 32]，． 三、解答题：解答应写出文字说明，证明过程或演算步骤．11．直角三角形ABC 的顶点坐标(2,0)A -，直角顶点(0,22)B -，顶点C 在x 轴上．（1）求BC 边所在直线的方程；（2）圆M 是三角形ABC 的外接圆，求圆M 的方程．【答案】（1）240x y --=；（2）22(1)9x y -+=．【解析】（1）直线AB 的斜率为022220AB k +==---， 由题意可知AB BC ⊥，则直线BC 的斜率为122BC AB k k =-=． 因此，BC 边所在直线的方程为2222y x +=，即240x y --=； （2）直线BC 的方程为240x y --=，由于点C 在x 轴上，令0y =得，点()4,0C ． 由于ABC ∆是以ABC ∠为直角的直角三角形，则该三角形的外接圆圆心M 为线段AC 的中点()1,0M ，半径长为132AC ．因此，圆M 的标准方程为22(1)9x y -+=． 12．在平面几何中，通常将完全覆盖某平面图形且直径最小的圆，称为该平面图形的最小覆盖圆．最小覆盖圆满足以下性质：①线段AB 的最小覆盖圆就是以AB 为直径的圆；①锐角△ABC 的最小覆盖圆就是其外接圆．已知曲线W ：2416x y +=，(0,)A t ，(4,0)B ， (0,2)C ，(4,0)D -为曲线W 上不同的四点．（1）求实数t 的值及△ABC 的最小覆盖圆的方程；（2）求四边形ABCD 的最小覆盖圆的方程；（3）求曲线W 的最小覆盖圆的方程．【答案】（1）2t =-，22340x y x +--=；（2）2216x y +=；（3）22654x y +=． 【解析】（1）因为(0,)A t 在曲线W ：2416x y +=上，所以令0x =得，2t =-． 由于△ABC 为锐角三角形，外接圆就是△ABC 的最小覆盖圆．设△ABC 外接圆方程为220x y Dx Ey F ++++=， 则4201640420E F D F E F -+=⎧⎪++=⎨⎪++=⎩， 解得304D E F =-⎧⎪=⎨⎪=-⎩．。

蛋白质是生命活动的主要承担者错误!一、选择题(每小题2分，共24分）1．人体免疫球蛋白由4条肽链构成,共有764个氨基酸，则此蛋白质分子中至少含有游离的氨基和羧基数分别是(D）A．764和764B．760和760C．762和762 D．4和4解析:根据氨基酸的通式我们知道，每个氨基酸分子都至少有一个氨基和一个羧基连接在同一个碳原子上，每一条肽链至少含有一个氨基和一个羧基，则该蛋白质至少含有4个游离的氨基和4个游离的羧基。

2．下列关于肽和蛋白质的叙述，正确的是(A）A．α.鹅膏蕈碱是一种环状八肽，分子中含有8个肽键B．蛋白质是由2条或2条以上多肽链构成的C．蛋白质变性是由于肽键的断裂造成的D．变性蛋白质不能与双缩脲试剂发生反应解析：α.鹅膏蕈碱是环状八肽，是由8个氨基酸脱去8分子水形成的，因而肽键的数目和脱去的水分子数目相同，A正确;蛋白质不一定是由2条或2条以上多肽链构成的,B错误；蛋白质变性是其空间结构被破坏造成的，肽键并没有断裂，C错误;变性蛋白质中仍含有肽键，能与双缩脲试剂发生反应，D错误。

3．已知氨基酸的平均相对分子质量为128，现有一个蛋白质分子由2条多肽链组成，共有肽键98个，此蛋白质的相对分子质量为（C）A．12 800 B．12 544C．11 036 D．12 288解析:蛋白质中的肽键数＝组成蛋白质的氨基酸分子数－蛋白质中的肽链数，可以推出该蛋白质由98(肽键数)＋2(肽链数）＝100个氨基酸分子缩合而成。

此蛋白质在形成过程中失去的水分子数＝形成的肽键数＝98个。

氨基酸的平均相对分子质量为128，水的相对分子质量为18。

因此，此蛋白质的相对分子质量＝128×100(缩合前100个氨基酸的相对分子质量之和)－18×98(失去98个水的相对分子质量之和)＝11 036。

故选C。

4．下面关于蛋白质分子结构与功能的叙述,错误的是(D）A．不同蛋白质含有的氨基酸数量不尽相同B．有些结构不同的蛋白质具有相似的功能C．组成蛋白质的氨基酸可按不同的排列顺序脱水缩合D．组成蛋白质的氨基酸之间可按不同的方式脱水缩合解析:本题考查蛋白质的结构和功能。