当前位置：文档之家 › 结构动力学第二讲

结构动力学第二讲

  • 格式：pps
  • 大小：838.00 KB
  • 文档页数：49

下载文档原格式

  / 49

合集下载

清华大学结构动力学2-2

清华大学结构动力学2-2

2.6 多自由度体系的Lagrange运动方程
我们在第二章中介绍了Lagrange运动方程，但没有实际应 用。用Lagrange运动方程来建立结构体系的运动控制方 程对那些不易直接用动平衡方法建立运动方程的问题 有时是特别有效的，特别是当结构动力分析时采用了 不易直观判断的广义坐标时更是如此。例如，用幂级 数展开烟囱或等效高层结构的横向位移
2.5 直接平衡法
若采用粘性阻尼假设，采用与弹性恢复力相似的方法也可 以建立如下阻尼力向量的计算公式： & ⎧ f D1 ⎫ ⎡ c11 c12 L c1N ⎤ ⎧ u1 ⎫ ⎪ f ⎪ ⎢c c 22 L c 2 N ⎥ ⎪ u 2 ⎪ ⎪ D 2 ⎪ ⎢ 21 ⎪& ⎪ ⎥ ⎨ ⎬ = [C ]{u} & {f D } = ⎨ ⎬ = ⎢ M M ⎥⎪ M ⎪ ⎪ M ⎪ ⎢ M ⎥⎪ ⎪ ⎪ f DN ⎪ ⎣c N 1 c N 2 L c NN ⎦ ⎩u N ⎭ & ⎩ ⎭ & 其中{fD}称为阻尼力向量，[C]称为阻尼矩阵，{u} 为速度 向量。系数cij称为阻尼影响系数，简称阻尼系数，其物 理意义： cij—由j自由度的单位速度引起的相应于i自由度的力 结构阻尼矩阵的计算很难，一般都给予一定的假设，例如 与刚度阵或质量阵成正比等。
2.5 多自由度体系运动方程的建立：直接平衡法
假设一N层层间结构，自由度为N，各楼层集中质量mi， 外荷载pi, 层间刚度ki, 各层的水平运动为ui, i=1, …, N。 这个层间模型也可以转化成串连的弹簧—质点模型。
2.5 直接平衡法
应用D’Alember原理：
f I i + f D i + f s i = pi (t ), i = 1, 2, L, N

结构动力学-2-2

结构动力学-2-2

2 bn = TP
∫
TP
0
P(t) sin nθtdt
位移反应 无阻尼时 在a0/2作用下 /2作用下
y0 = a0 / 2k
a n
在 an cos nθt 作用下
µn =
1 2 1− βn
an y (t) = µn cos nθt k
βn = nθ / ω
b a yn (t) = n µn sin nθt 在 bn sin nθt 作用下 k 合并后， 合并后，得 ∞ 1 a0 1 y(t) = [ + ∑ (an cos nθt + bn sin nθt)] 2 k 2 n=1 1− βn
& y (0) = v0
y * (t ) = D1 cos θ t + D 2 sin θ t
2
y(t) = Ae−ξωtsin( ωDt +ϕ1) + 1 + A e−ξωtsin( ωDt +ϕ2 ) 2 + Asin(θt −ϕ)
A = y +( 1
2 0
P 2ξωθ D1 = − m (ω 2 − θ 2 ) 2 + 4ξ 2ω 2θ ω 2 −θ 2 P D2 = m (ω 2 − θ 2 ) 2 + 4ξ 2ω 2θ 2
βn = nθ / ω
= nT / TP = n / 2
β1 =1/ 2; β12 =1/ 4
2 β 2 = 9 / 4; β5 = 25/ 4
3
y(t) =
P 1 8 1 2π 1 6π 1 10π 0 [ + ( sin t − sin t− sin t +L ] k 2 π 3 TP 15 TP 105 TP

结构力学

结构力学

自由振动的解
比较两式得：
A ( y 0 ) (v 0 / w )
2 2
arctan
wy0
v0
（a）没有初始速度，仅由初始位移引起的振动按 的 y0 coswt 的规律变化； （b）没有初始位移，仅由初始速度引起的振动按 的 v 0 sin wt 的规律变化; w （c）既有初始位移，又有初始速度引起的振动形态按 方程 y(t ) A sin(wt ) 进行。
能相差很大；
b、两个外表看来并不相同的结构，如果其自振周期相
近，则在动荷载作用下其动力性能基本一致。地震中常 出现这样的现象。
2009-12-3
单自由度系统的动力特性
圆频率的计算公式：
w
k m 1 m g W g st
圆频率也仅与结构参数k和m有关，即仅与结构体 系本身的固有性质有关，而与初始干扰无关，故称 为固有频率或自振频率。
y A sin(wt v)
则，系统振幅和初相角为：
A y
2 0
w
2 0 y 2
,
v arc tg
w y0
0 y
因物体落到C点后才开始振动，所以
y0 yst , 0 2gh y
2009-12-3
课后练习
于是
2 gh 2 A y yst 2hyst g / yst
2009-12-3
单自由度系统的动力特性
（3）工程频率f ：
w， 单位为Hz。 f 2
计算自振周期的几种形式：
（1）由周期和圆频率的定义可知：
m T 2 k
（2）将
1 k
代入上式，得：
T 2 m
2009-12-3

结构动力学第二章结构运动方程的建立

结构动力学第二章结构运动方程的建立

第2章 结构运动方程的建立结构动力分析的目的,是求出动荷载作用下结构的动位移和动内力,并研究它们随时间的响应历程。

在大多数情况下，应用包含有限个自由度的近似分析方法，计算结果就足够精确了。

通常情况下，独立的几何参数取的是位移，为了求出各种动力响应，应先列出结构动力位移方程，描述结构动力位移的数学方程，称为结构的运动方程。

运动方程的解，提供了位移过程，从而可求出其他各种所需的结构动力响应。

运动方程的建立，是结构动力学的核心问题，只有运动方程建立正确，整个求解过程才可能正确。

建立振动体系的运动方程有多种方法,一般常用的方法有直接平衡法（达朗贝尔原理）、虚位移原理（拉格朗日法）、变分原理（哈密尔顿原理）3种，但不管采用何种方法建立运动方程,其结果都是一致的，本章将综述建立方程的原理和基本概念。

§2.1达朗贝尔(d’Alembert)原理根据牛顿第二定律：任何质量m 的动量变化率等于作用在这个质量上的力()F t ，力()F t 包括恢复力()R t 、阻尼力()D t 、外力()P t ，即：()()dF t my t dt =⎡⎤⎣⎦ （2.1） 当质量m 不随时间变化时，上式变成：()F t my =即：()0F t my -= （2.2）式()0F t my -=（2.2）表示，作用在质量m 上的力()F t ，与加速度方向相反的惯性力my -平衡。

换句话说，如果我们把my -加到原来受力的质量上，则动力问题就可作为静力平衡问题来处理，这就是达朗贝尔原理。

按达朗贝尔原理，如果我们将惯性力my -沿自由度方向加到质量上，则动力问题可按静力问题来处理，当然在振动问题中，尚需考虑阻尼的存在。

按达朗贝尔原理建立质点系运动方程的一般步骤为： 1.确定体系振动分析的自由度的数目，建立计算模型； 2.建立坐标系，给出各自由度的位移参数；3.按达朗贝尔原理和所采用的阻尼理论，沿质量各自由度方向加上惯性力和阻尼力；4.通过分析质量平衡条件或考虑变形协调条件，建立体系运动方程。

结构动力学第二章

结构动力学第二章

∂T ∂V d ∂T ( )− + = Pncj (t ), & dt ∂u j ∂u j ∂u j
其中： T —— 体系的动能；
j = 1,2,L , N
V —— 体系的位能，包括应变能及任何保守力的势能； Pncj ——与 uj 相应的非保守力（包括阻尼力及任意外荷载）。
– 红色部分为引入动力自由度概念的目的，蓝色部分为实 现此目的的手段。 – 概念中的“全部”、“独立”两个条件非常关键。
• 严格来说，所以结构体系质量都是连续分布的，为无限自 由度体系，研究比较困难。但许多情况下，可以作一定的 简化，变为有限自由度体系。 • 简化并确定结构动力自由度最典型的方法：集中质量法
动能
1 & mu 2 转动质量 2
T =
1 &2 Jθ 2
1 2 V = ku 转动弹簧 2
1 &2 V = kθ θ 2
位能
1 1 & & &j T = ∑ ∑ mij u i u j = ∑ m j u 2 2 i j 2 j
V =
1 ∑ ∑ kij ui u j 2 i j
∫
1 体系的动能：T = mu 2 & 2
粘滞(性)阻尼力可表示为：
& f D = -cu
D — 表示阻尼（damping） c — 阻尼系数（Damping coefficient）
k c
u m
f S(t) m f D(t) f I (t)
& u — 质点的运动速度
阻尼系数 c 的确定：
• 不能像结构刚度 k 那样可通过结构几何尺寸、构件尺寸等 来获得，因为 c 是反映了多种耗能因素综合影响的系数， 阻尼系数一般是通过结构原型振动试验的方法得到。 • 粘性（滞）阻尼理论仅是多种阻尼中最为简单的一种。 • 其它常用的阻尼：

结构动力学课件—2dyanmics of structures-ch3

结构动力学课件—2dyanmics of structures-ch3
The ratio of the resultant harmonic response amplitude to the static displacement which
would be produced by the force p 0 will be called the dynamic magnification factor D; thus
the above equation with respect to and solve the resulting expression for obtaining
CHAPTER 3. RESPONSE TO HARMONIC LOADING
For typical values of structural damping, say < 0.10, the difference between And
FIGURE 3-4 Rate of buildup of resonant response from rest.
CHAPTER 3. RESPONSE TO HARMONIC LOADING
34 ACCELEROMETERS AND DISPLACEMENT METERS
At this point it is convenient to discuss the fundamental principles on which the operation of an important class of dynamic measurement devices is based. These are seismic instruments, which consist essentially of a viscously damped oscillator as shown in Fig. 35. The system is mounted in a housing which may be attached to the surface where the motion is to be measured. The response is measured in terms of the motion v(t) of the mass

第二讲材料与结构的动态行为ppt选优文档

第二讲材料与结构的动态行为ppt选优文档
Wilson－）。最新的程序采用更多的隐式格式类型以
及显式方法。
5）典型程序 DYNA，MARC，ADINA，ANSYS， ABAQUS，START－DYNA，NIKE，更多
4. 波传播
❖ 何谓“波”？ ✓ 扰动状态的传播
4. 波传播 （续）
❖ 波传播现象
✓ 月球及行星碰撞 ✓ 爆炸焊接 ✓ 爆炸成型 ✓ 爆炸硬化 ✓ 冲击波烧结与合成 ✓ 侵彻（化学能与动能）
p13(112233)
3.结构动力学问题（续）
❖ 结构动力学问题基本特征 （续）
5）结构动力学问题包含主要由系统最低谐波产生的全 局变形
6）在很多情况下，全局变形引发材料和结构破坏。
3.结构动力学问题（续）
❖ 结构动力学计算程序基本特征
1）由于变形有限且是全局性的，常用Lagrangian描述 2）如果变形较大，常用ALE方法来适应局部速度梯度 3）许多程序采用小变形，大旋转表述 4）最初采用隐式时间积分格式（Newmark－ ，Houbolt，
4. 波传播 （续）
❖ 波传播问题基本特征（续）
6）多种机理使得材料由破坏导致物理分离。如： 脆性断裂、径向断裂、延性空洞增长、层裂、开 瓣、冲塞等。
高率加载条件下材料破坏四阶段过程：
材料中许多位置处微裂纹的快速成核。 以相当对称的方式裂纹成长。 相邻裂纹级联 一条或多条连续裂纹形成，贯串材料形成层裂或碎块。
爆源：高能炸药，燃料－空气或蒸气 ❖5）由于加载和响应时间非常短，变形的范围高度局部化。
❖动力学问题成功模拟的基础
云爆炸，颗粒和粉尘爆炸，压力容器 ❖有一些特殊技术的Lagragian程序，如重新分区，破坏材料去除，碰撞面的动态重定义以及无网格方法等。

结构动力学_2

结构动力学_2

初相位
4、振幅C和初相位
x0 C sin
x0 Ccos
C
x02
x02
2
arctan x0
x0
——振幅 ——初相位
第2章 单自由度系统
x
3
x02
x02
2
sin(t
)
x
x02 2
x02
T 2
x0 0
t
图2.7 无阻尼系统自由振动位移曲线
-3
0
3
第2章 单自由度系统
x x02 x022 cos(t )
mx cx kx 0
设：
x Aept
第2章 单自由度系统
mp2 cp k 0
p1,2 c
c2 4mk 2m
c2 4mk
1、过阻尼系统
0 x A1e p1t A2e p2t
第2章 单自由度系统
2、临界阻尼系统
0
c2 4mk 0
cc 2 mk 2m
x
e
c 2m
t
第2章 单自由度系统
3、解的形式
x Asint x Bcost x Asint Bcost
x A2 B2 ( A sint B cost)
A2 B2
A2 B2
A2 B2 (cos sint sincost)
C sin(t )
第2章 单自由度系统
x C sin(t )
振幅
剪切变形
第2章 单自由度系统
3EI
ml 3
——弯曲频率
2 3EI
ml 3
——剪切频率
第2章 单自由度系统
图2.5 框架的剪切变形
第2章 单自由度系统
③摆问题

于开平-结构动力学第二讲

于开平-结构动力学第二讲

(2) 阻尼力的功：
Wd A cos t dt c 2 / 1 cos 2 t cA2 2 dt 0 2 1 2 1 2 2 2 / cA2 2 cA cos 2 t dt 0 2 2
5 稳态响应振幅和相位
5.2 初始相位角 根据初相位角表达式
2 tg 1 2
可以画出初相位角随频率比的变化曲线，简称相频曲线：
在共振点，不管阻尼比多大，初相位角均为90度。
6 稳态响应复数解法及频响函数
之前将外载荷假设为正弦形式，其运动控制方程为：
������������ሷ 1 + ������������ሶ 1 + ������������1 = ������0 sin������������ 简谐激励的另一种典型形式为余弦形式，其运动控制方程写作： ������������ሷ 2 + ������ ������ሶ 2 + ������������2 = ������0 cos������������ （2） （1）
o o o
o
1 2 Fo A sin Fo A sin 2
6 稳态响应复数解法及频响函数
令方程特解为������ ������ = ������������ ������ ������������������ ，代入运动控制方程得： (−������2 ������������������ + ������������������������������ + ������������������ )������ ������������������ = ������0 ������ ������������������ 方程对任意时刻t恒等，则方程两边指数函数������ ������������������ 前系数相等，由此可得： ������������ = ������0 ������ − ������������ 2 + ������������������

结构力学之结构动力学2

结构力学之结构动力学2

4EIa2
2l3
4EI
ma2l 2
ml4 学习文档
29.0l80lE62m9I[[6YY
E( xI )]2 精确d x (mx)]2 d解x
例13 求楔形悬臂梁的自振频率。 设梁截面宽度为 1，高度为 h0x 3 12 l
单位长度的质量： m h0 x
2
5
2
ml4
EI ml4
4 6
2 ml4 6
6
2
EI ml4
0 12
求得最 初两个 频率近 似值：
6 EI 7 EI
学习文档
1
3.533 l2
EI m
2
34.81 l2
EI m
（0.48%）
（58%） 说明
2、集中质量法
在计算无限自由度体系的自振频率时，可以用若干个集中质量来代 替连续分布的质量。关于质量的集中方法有多种，最简单的是静力等效 的集中质量法。
定律得：
Umax=Tmax
ω
※求Umax ，Tmax 位移幅值
设： y(x,t) Y(x)sin(t )
v y. Y(x) cos(t )
U如TUmm梁aaxx上12120l还1212m0l0l有EE(x2II集)0[lvYm中2d((x2x质x2y))Y]量21222dm(dxxi，2)xdcxo12s学2习s(※Y文ii为n档t求22集频(中)0率lt0lm质m[Y0(l量Ex)()0lxmIYE[)Yi2]处I2([xd(Y的)xxd)位x](2x移d)mx]幅2iYdi值2x。
(k11 2m1)Y1 k12Y2 P1
y2 (t)Y2 sint
Y1=D1/D0
k21Y1 (k22 2m2 )Y2 P2 Y2=D2/D0

结构动力学2PPT课件

结构动力学2PPT课件
可见质量 mi 的惯性力幅值为
Ii mi Ai 2 (i 1,2,n)
3.动内力幅值计算
位移、惯性力、动荷载频率相同，对于无阻尼体系三者同时达到幅值。故，可 将荷载幅值和惯性力幅值加在结构上，按静力学方法体系的最大动内力和最大 动位移。
例1 试求图示体系质量的最大动位移，并绘制结构的最大动力弯矩图。已知＝
3
EI 。 m l3
A m1 m
l2
EI
q sin t
B
C m2 2m EI
l2
l2
2021/5/25
第10页/共32页
10
解 本例静定结构，选择柔度法求解。
1 A m1 m
l2
EI
q sin t
B
C m2 2m EI
l/2
l2
l2
M1图
M图21源自l/4M图
P
q
ql2/8
用图乘法求得，11
l3 8E
小到大排列，称为频率谱。
➢将求得的 1 2 回代入(2)，由于系数行列式等于零，n个方程是相关的，只
能由其中的n-1个方程解得各自由度动位移之间的比值。可见，体系按某一频
率振动的形状是不变的，称之为振型。
✓ 振型向量 Ai A1i A2i
Ani T
✓ 振型向量常用表述方法一：令某自由度位移为1，例 Ai 1 2i
k 是对称矩阵，k k T
M 也是对称矩阵，同理，有 A jT M Ai AiT M A j
(3)-(4)，有
i2
2 j
AiT M A j 0
因为 i j ，所以 AiT M A j 0 i j
振型第一正交性：多自由度体系任意两个不同振型关于质量矩阵正交。

刘晶波结构动力学课件2-2w

刘晶波结构动力学课件2-2w

2.5 多自由度体系 运动方程的建立 —直接平衡法
15/78
16/78
4
2.5 多自由度体系运动方程的建立：直接平衡法
假设一 N层层间结构，自由度为 N，各楼层集中质量mi， 外荷载pi, 层间刚度ki, 各层的水平运动为ui, i=1, …, N。 这个层间模型也可以转化成串连的弹簧—质点模型。
u =u g+u u
t
☀ 牛顿第二定律； 直接平衡法 (D’Alember) ；虚位移原 理；Hamilton方程； 运动的Lagrange方程。 ☀ 基于矩阵位移法的 直接平衡方法 和基于变分原理的 Lagrange方程方法应用更广泛一些。 ① 直接平衡方法应用动平衡的概念以矩阵的形式建立多 自由度体系的运动方程，概念直观，易于通过各个结 构单元矩阵(刚度矩阵、质量矩阵、阻尼矩阵)建立整 个结构体系的相应矩阵，进而建立体系的运动方程， 便于计算机编程。 ② 而对于一些特殊的问题，例如，大变形(位移)问题， 运动的Lagrange方程可能更有效。且具有唯一性。
其中{fD}称为阻尼力向量，[C]称为阻尼矩阵；
}为速度向量。 {u
25/78 26/78
2.5 直接平衡法
f D1 c11 f c D2 21 f D c N 1 f DN c12 c 22 cN 2 1 c1N u u 2 c2 N C u N c NN u
f D C u
f I f D f s p(t )
18/78
2.5 直接平衡法
弹性恢复力fsi可以用结构的层间(单元)刚度来表示，其一 般表达式为：
2.5 直接平衡法

结构动力学-2.

结构动力学-2.

6.若质量增加800kg体系
的周期和阻尼比为多少
PROBLEMS：
1.A heavy table is supported by flat steel legs.Its natural period in lateral vibration is 0.5sec.When a 50kg plate is clamped to its surface.the natural period in lateral vibration is lengthened to 0.75sec.What are the weight and the effective lateral stiffness of the table?
mJ
二. 阻尼体系
阻尼:使振动衰减的作用. 阻尼产生原因：材料的内摩擦,连接点、支承面等处的外
摩擦及介质阻力等. 阻尼力：在振动分析当中用于代替阻尼作用的阻碍振动的力。 粘滞阻尼理论假定阻尼力大小与速度成正比,方向与速度相反。
R(t) cy(t)
c-----阻尼系数 (damping coefficient ）
eTD

ln
Ai Ai 1
TD
对数衰减率
计算频率和周期可不计阻尼 2 2 D
阻尼测量

ln
Ai Ai 1
TD
2 D
2
1 ln Ai 2 Ai1
1 ln Ai 2n Ain
例: 对图示体系作自由振动试验.用钢 丝绳将上端拉离平衡位置2cm,用 解: 1.阻尼比
运动方程及其解
m y(t)
cy(t)
my(t) k11 y(t )
运动方程 my cy k11y 0

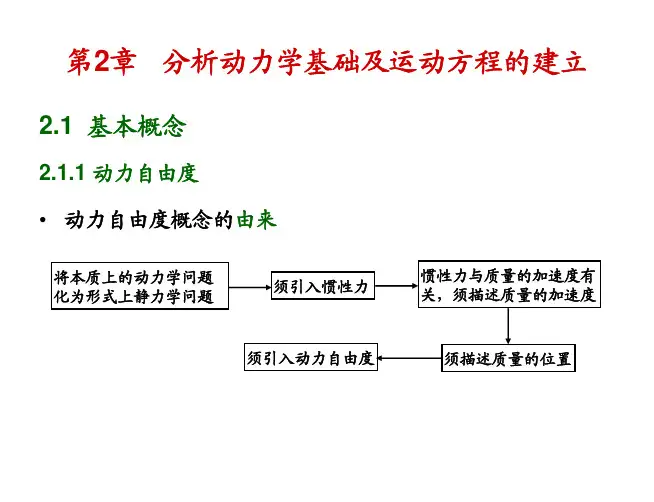
振动力学与结构动力学第二章21PPT课件

振动力学与结构动力学第二章21PPT课件

k2
12 EI h3
,
k 28 .284 rad / s, m
f 1 4 10 6 4 .502 Hz
2 5000
-
5
求图示系统的固有频率 （a）弹簧串联情况； （b）弹簧并联情况。
(a)串联情况
k1 yst1 k2 yst 2 mg ,
y st
yst1
yst 2
mg k1
mg k2
arctg(y0/ y0)
-
1
其通解为 y(t) c 1cot sc 2sitn 令 y0 Asinv
由初始条件 y(0)y0
y0/Acovs
y(0) y0
y(t)A si n t (v)
可得 c1 y0 c2 y0 /
y(t)y0cots y0si nt
其中
A
y02
y02
2
tan
y0
y0
mg ( k1 k2 ), k1k 2
k mg k1k2 , yst k1 k2
k1k 2
m(k1 k2 )
思考题：串联后系统频率与单 个弹簧系统相比有何变化？
-
6
(b) 并联情况
y st 1 y st 2 y st ,
k 1 y st 1 k 2 y st 2 mg ,
y st
mg k1
, k2
k k1 k2,
k1 k2 m
思考题：并联后系统频率与 单个弹簧系统相比有何变化？
-
7
例：简支梁AB，重量不计。在梁的中点位置放一重为W 的物体M时，其静挠度为yst。现将物体M从高度h处自由
释放，落到梁的中点处，求该系统振动的规律。
当物体落到梁上后，梁、物体系统作简谐振动，只要定 出简谐振动的三个参数：圆频率、振幅和初相角即可。

结构动力学第二章 运动方程的建立

结构动力学第二章 运动方程的建立

惯性：保持物体运动状态的能力 惯性力： 大小等于物体的质量与加速度的乘积，
方向与加速度的方向相反。
fI mu
I — 惯性（Inertial）； m— 质量（mass） ； ü — 质点的加速度。
坐标方向：向右为正
2.1 基本动力体系
2. 恢复力（Resisting Force of Spring）
D’Alembert原理的贡献：建立了动力平衡概念
2.2 运动方程的建立
3. 虚位移原理
虚位移原理：在一组外力作用下的平衡系统发生一个虚位移时， 外力在虚位移上所做的虚功总和恒等于零。
虚位移是指满足体系约束条件的无限小位移。
设体系发生一个虚位移δu，则平衡力系在δu 上做的总虚功为:
p(t)u fIu fDu fsu 0
h—框架结构的高度 E—弹性模量 Ib和Ic—梁和柱的截面惯性矩
ρ→∞：
k
24EIc h3
ρ→0
：
k
6EIc h3
2.1 基本动力体系
3. 阻尼力（Damping Force）
阻尼：引起结构能量的耗散，使结构振幅逐渐变小的一种作用 阻尼来源（物理机制）： (1)固体材料变形时的内摩擦，或材料快速应变引起的热耗散； (2)结构连接部位的摩擦，结构构件与非结构构件之间的摩擦； (3)结构周围外部介质引起的阻尼。例如，空气、流体等。
虚位移原理部分避免了矢量运算，在获得体系虚功后，可以采用标量运算建立体系 的运动方程，简化了运算。
Hamilton原理是一种建立运动方程的能量方法（积分形式的变分原理） ，如果不考 虑非保守力作的功（主要是阻尼力），它是完全的标量运算，但实际上直接采用 Hamilton原理建立运动方程并不多。Hamilton原理的美妙在于它以一个极为简洁 的表达式概括了复杂的力学问题。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

结构的动力特性kcm( )y t( )F t▪承受动力荷载的结构体系的主要物理特性：▪质量m = 结构的惯性；▪弹簧k = 结构的刚度；▪阻尼器c = 结构的能量耗散.质量、弹性特性、阻尼特性、外荷载▪在最简单的单自由度体系模型中，所有特性都假定集结于一个简单的基本动力体系模型内，每一个特性分别由一个具有相应物理特性的元件表示：数学模型ty表征结构动力响应特性的一些固有量称为结构的动力特性，又称自振特性。

定义结构的动力响应▪结构的动力特性与结构的质量、刚度、阻尼及其分布有关。

ty定义▪结构受外部干扰后发生振动，而在干扰消失后继续振动，这种振动称为结构的自由振动。

▪如果结构在振动过程中不断地受到外部干扰力作用，这种振动称为结构的强迫振动，又称受迫振动。

t y结构的自由振动与受迫振动固有频率▪质点在运动过程中完成一个完整的循环所需要的时间称为周期，单位时间内完成的循环次数称为频率。

▪结构在自由振动时的频率称为结构的自振频率或固有频率。

▪对大部分工程结构，结构的自振频率的个数与结构的动力自由度数相等。

▪结构的自振频率与结构的质量和刚度有关。

tyT阻尼▪结构在振动过程中的能量耗散作用称为阻尼。

▪结构的自由振动会因为阻尼作用而随时间衰减并最终停止。

▪由于阻尼而使振动衰减的结构系统称为有阻尼系统。

▪阻尼原因复杂：内摩擦、连接摩擦、周围介质阻力等。

yc F D ▪等效粘滞阻尼：以阻尼器表示结构阻尼作用：c 为阻尼系数，为质量的速度。

ytyTt yT结构体系运动方程的建立定义在结构动力分析中，描述体系质量运动规律的数学方程，称为体系的运动微分方程，简称运动方程。

▪运动方程的解揭示了体系在各自由度方向的位移随时间变化的规律。

▪建立运动方程是求解结构振动问题的重要基础。

▪常用方法：直接平衡法、虚功法、变分法。

kcm( )y t( )F t单自由度体系模型▪质量块m ，用来表示结构的质量和惯性特性▪自由度只有一个：水平位移y(t)▪无重弹簧，刚度为k ，提供结构的弹性恢复力▪无重阻尼器，阻尼系数c ，表示结构的能量耗散，提供结构的阻尼力▪随时间变化的荷载F(t)单自由度体系运动方程的建立[例2-0]单自由度体系运动方程的建立kcm( )y t( )F t( )y t建立计算模型)(t F F F F S D I 取质点为隔离体画平衡力系建立平衡方程IF DF SF )(t F)(t F F F F S D I 平衡方程：ym F I yc F D kyF S 根据d’Alembert 原理，等于质量与加速度的乘积：等于弹簧刚度与位移的乘积：阻尼力等于阻尼系数与速度的乘积：由此得到体系的运动方程：)(t F ky y c y m （2-0）惯性力：弹性力：阻尼力：( )y t( )F tSF D F IF建立体系运动方程的方法▪直接平衡法，又称动静法，将动力学问题转化为任一时刻的静力学问题：根据达朗贝尔原理，把惯性力作为附加的虚拟力，并考虑阻尼力、弹性力和作用在结构上的外荷载，使体系处于动力平衡条件，按照静力学中建立平衡方程的思路，直接写出运动方程。

▪虚功法: 根据虚功原理，即作用在体系上的全部力在虚位移上所做的虚功总和为零的条件，导出以广义坐标表示的运动方程。

▪变分法: 通过对表示能量关系的泛函的变分建立方程。

根据理论力学中的哈密顿原理或其等价形式的拉格朗日方程导出以广义坐标表示的运动方程。

•对于不同的结构体系建立运动方程时，三种方法的应用各有所长。

本课程仅讨论直接平衡法。

直接平衡法直接平衡法，又称动静法，将动力学问题转化为任一时刻的静力学问题：根据达朗贝尔原理，把惯性力作为附加的虚拟力，并考虑阻尼力、弹性力和作用在结构上的外荷载，使体系处于动力平衡条件，按照静力学中建立平衡方程的思路，直接写出运动方程。

根据所用平衡方程的不同，直接平衡法又分为刚度法和柔度法。

[例2-0]刚度法: 取每一运动质量为隔离体，通过分析所受的全部外力，建立质量各自由度的瞬时力平衡方程，得到体系的运动方程。

kcm( )y t( )F t( )y tIF DF SF )(t F )(t F F F F S D I 平衡方程：刚度法取每一运动质量为隔离体，通过分析所受的全部外力，建立质量各自由度的瞬时力平衡方程，得到体系的运动方程。

柔度法以结构整体为研究对象，通过分析所受的全部外力，利用结构静力分析中计算位移的方法，根据位移协调条件建立体系的运动方程。

[例1] 试用刚度法建立图示刚架的运动方程m1EI EIEI 2l 1l P F (t)[解]1）确定自由度数: 横梁刚性，柱子无轴向变形。

)(t y )(t F P IF DF 2S F 1S F 2）确定自由度的位移参数。

3）质量受力分析：取刚梁为隔离体，确定所受的所有外力！4）列动平衡方程：1个自由度。

21 S S D I P F F F F t F )(（2-1）)(t yym F I y c F D yl EI F S 32212 其中各力的大小：位移法：柱子一端产生单位平移时的杆端剪力等效粘滞阻尼力：212li柱端发生平移y 时产生的梁-柱间剪力：y l EI F S 31112 EI l1由此得到体系的运动方程：)(t F y l EI l EI y c y m P32311212 （2-2’）惯性力：021 S S D I P F F F F t F )(（2-1）弹性力: F s =F s1+F s2：由此得到体系的运动方程：)(t F ky y c y m P （2-2）比较：kcm( )y t( )F t)(t F ky y c y m （2-0）m1EI EIEI 2l 1l P F (t))(t y )(t F y l EI l EI y c y m P32311212 （2-2’）；k 为（等效）刚度系数。

3231211212l EIl EI F F k S S 令：运动方程(2-2)与(2-0)的形式是一样的！[例2] 试用柔度法建立图示简支梁的运动方程q t ( )m EIl[解]1）确定自由度数: 集中质量，仅竖向位移：)(t y 2）确定自由度的位移参数：质量m 的位移：3）体系受力分析：取梁整体为隔离体，确定所受的所有外力！1个自由度。

q t ( )D F IF 4）列位移方程：)(D I P F F y （2-3）改写成：PD I y F F1（2-3’）)(t y)(t q EI lP 38454D p 为动荷载q(t)引起的质量沿y 方向的位移：其中：d 为自由度方向加单位力所引起的位移，即柔度：EI l483惯性力：y m F I 阻尼力：yc F DPD I y F F1由此得到体系的运动方程：)(t q ly y c y m 851（2-4）q t ( )位移方程：)(t y比较：kcm( )y t( )F tq t ( )m EIl（2-5）)(t F y y c y m E1含义：等效动荷载直接作用在质量自由度上产生的动位移与实际动荷载产生的位移相等！)(t q ly y c y m 851)(t F ky y c y m 令：)()(t q l t F E85 F E (t )定义为体系的等效动荷载或等效干扰力。

其通用表达式PE t F)(（0）（2-4）)(t F ky y c y m E （2-6）已经知道柔度d 和刚度k 之间的关系为：1k 式（2-4）成为：结论：任何一个单自由度体系的运动方程都可以抽象成为一质量、弹簧、阻尼器体系的运动方程，一般形式为：)(t F ky y c y m P （2-7）（2-2）比较：)(t F ky y c y m P 刚架：)(t F ky y c y m （2-0）基本质量弹簧体系：简支梁：[练习题] 试建立图示简支梁的运动方程EI l llm1F ( )t P21P=12121P=121112yy m F IF ( )t P[解]1）确定自由度数: 1个自由度。

2）位移参数：质量m 的位移y(t)。

3）用柔度法：梁整体分析。

任一时刻m 的惯性力ym F I )()()(t F y m t F F y P P I 12111211 )(t F y y m P 1112111 则m 的位移方程为：整理得：)(t F P P12)()(t F t F P PE 11∵)(t F y y m E 11132l 32lEIl94311EIl 187312位移方程：EI l llm1F ( )t P2)(t F y y m P 1112111 作单位弯矩图，如右图：代入位移方程，整理得：)(t F y l EI y m P 87493 或：)(t F ky y m E 311491lEIk )()(t F t F P E 87用图乘法求 11、 12：单自由度体系的振动分析单自由度体系的自由振动分析▪最简单的由刚体、弹簧和阻尼器组成的单自由度体系.已经得到单自由度体系的运动方程：kcm( )y t( )F t)(t F ky y c y m P （3-1）▪这个运动方程也适用于可转换为单自由度体系的任何复杂结构体系的广义坐标反应。

ky y c y m （3-2）▪运动方程：等效动荷载为零的情况下的振动称为自由振动。

定义▪自由振动产生的原因：初始时刻的干扰！初始位移；初始速度；初始位移+初始速度▪结构受外部干扰后发生振动，而在干扰消失后继续振动，这种振动称为结构的自由振动。

如果去掉外荷载F P (t )=0!kcm( )y t( )F t▪（3-2）称为（二阶线性常系数）齐次方程；ky y c y m （3-2）▪齐次方程的求解：▪可设齐次方程解的形式为：stGet y )(（3-3）02stGe k cs ms )(▪其特征方程为：22s mc s 或：▪代入（3-2）可得：02)(k cs ms （3-4）stGset y )( steGs t y 2 )( ▪（3-2）称为（二阶线性常系数）齐次方程；▪式中w 2=k /m ，w 是体系振动的圆频率。

▪根据阻尼系数c 值的不同，解出的特征参数s 值将具有不同的特性。

无阻尼自由振动▪If c =0：▪特征方程：22s m c s 0ky y c y m （3-2）▪自由振动方程：i s （3-9）ti ti eG eG t y 21)(▪引入Euler 方程：▪代入(3-2)得：ti t eti sin cos （3-10）▪A 和B 是由初始条件决定的常数。

得无阻尼自由振动的位移反应：tB t A t y cos sin )( （3-12）▪设t =0时：00y y )(00y y )(tB t A t y cos sin )( ▪代入：t B t A t y sin cos )( 0y 0B 0y A 0y B ▪代入：y A▪单自由度无阻尼体系运动方程的解：ty t y t ycos sin )(00（3-13）▪或写成：)sin()( t t y （3-14）▪位移反应：tB t A t y cos sin )( （3-12）ty t y t ycos sin )(00（3-13）ba b a b a cos sin sin cos )sin( ▪三角关系：▪对比(3-13)：b — t; a —yy▪显然有：cos 0ysin 0y ▪(3-13)成为：tt t y cos sin sin cos )( ▪即：)sin()( t t y （3-14）2020y yy y arctant y 0.y 0 I 0.y 0y 0.y 0ty 0.y 0t y 0ty 0.y 0Ry 0.0y 0.y 0y 0.y 0ty 0.y 0t y 0.y 0t y 0.y 0.y 0R I t y 0 .y 0y .y 0.y 0It.y 0.y 0t 00y 0 .y 000y 0.y 0R I.y 00)sin()( t t y （3-14）0)sin()( t t y （3-14）2-tcos( )t-cos ty 0sin ty 0.y 0.y 0.y 0RIttty 0.y 02-T= 2T= 2T= 2定义•对于无阻尼体系，运动完全是反复进行的。