直角三角形斜边中线练习教学文案

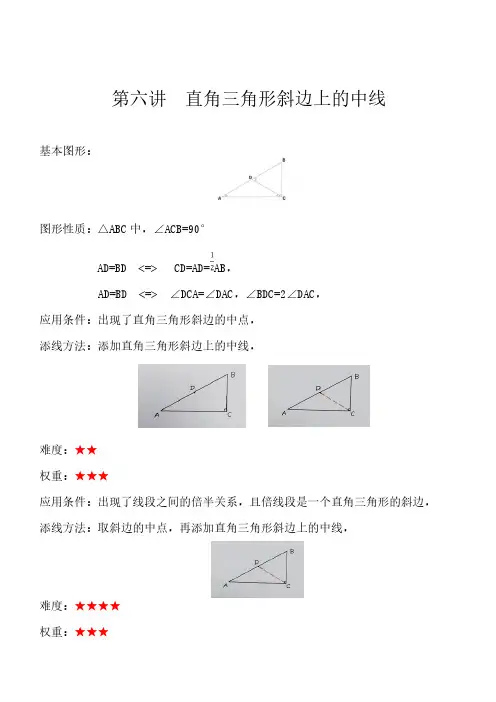
第六讲直角三角形斜边上的中线基本图形：图形性质：△ABC中，∠ACB=90°AD=BD<=>CD=AD=AB，AD=BD<=>∠DCA=∠DAC，∠BDC=2∠DAC，应用条件：出现了直角三角形斜边的中点，添线方法：添加直角三角形斜边上的中线，难度：★★权重：★★★应用条件：出现了线段之间的倍半关系，且倍线段是一个直角三角形的斜边，添线方法：取斜边的中点，再添加直角三角形斜边上的中线，难度：★★★★权重：★★★应用条件：出现了一个等腰三角形的底边再一个直角的直角边上，添线方法：将等腰三角形的一条腰延长到与另一条直角的边相交，难度：★★★★★★权重：★★★★★应用条件：出现了由线段的中点发出的两条相等线段，添线方法：将相等线段中的一条延长一倍后，联结成直角三角形斜边上中线的基本图形，难度：★★★★★★权重：★★例1，已知：△ABC中，∠ACB=90°，延长AB到D，AB=2CD，过D作DE∥CA交CB的延长线于E．求证：∠CDE=3∠ADE，分析：本题的条件中给出了AB=2CD，是两条线段之间的倍半关系，又因为∠ACB=90°，所以其中的倍线段AB就是直角△ABC的斜边，从而可应用直角三角形斜边上的中线的基本图形的性质进行证明，这是本题的第一个关键思维节点，就是由出现的两条线段之间的倍半关系，且的倍线段是一个直角三角形的斜边，就要想到应用或添加直角三角形斜边上的中线的基本图形进行证明，添加的方法就是将直角三角形斜边上的中线添上，由于图形中是有直角三角形而没有出现斜边上的中线，所以应将斜边上的中线添上，也就是取AB的中点F，联结CF，就可得AB=2CF，由条件AB=2CD，就有CD=CF，这是两条具有公共端点C的相等线段，它们可组成一个等腰三角形，应用等腰三角形的性质可得∠CDF=∠CFD，这是本题的第二个关键思维节点，就是由出现的两条具有公共端点的相等线段，想到要应用等腰三角形的性质进行证明，而由直角三角形斜边上的中线的基本图形的性质又可得∠CFD=2∠BAC，所以∠CDF=2∠BAC，又因为ED∥CA，这两条平行线可以看作是被AD所截，∠EDA和∠BAC是一组同位角，所以可应用与同位角有关的平行线的基本图形进行证明，所以∠EDA=∠BAC，∠CDA=2∠EDA，从而就可得∠CDE=∠CDA+∠EDA=3∠ADE.例2，已知：△ABC中，∠ABC=2∠ACB，AD⊥BC垂足是D，E是BC的中点．求证：DE=AB，分析一：本题给出了条件AD⊥BC，而要证明的结论DE=AB是两条线段之间的倍半关系，且其中的倍线段AB是直角△ABD的斜边，所以就可应用直角三角形斜边上的中线的基本图形的性质进行证明，现在图形中是有直角三角形，而没有斜边上的中线，于是要将斜边上的中线添上，这是本题的第一个关键思维节点，就是由出现的两条线段之间的倍半关系，且的倍线段是一个直角三角形的斜边，就要想到应用或添加直角三角形斜边上的中线的基本图形进行证明，添加的方法就是将直角三角形斜边上的中线添上，也就是取AB的中点F，联结DF，可得DF=AB，从而问题就转化成为应证DF=DE，而由所作的F是AB的中点和条件中给出的E是BC的中点，出现了两个中点，是多个中点问题，从而可应用三角形的中位线的基本图形的性质进行证明，这是本题的第二个关键思维节点，就是由出现的两个中点，是多个中点问题，从而想到可应用三角形的中位线的基本图形的性质进行证明，由于中点E、F所在线段BC、BA有公共端点B，可以组成三角形，所以E、F这两个中点的连线就是三角形的一条中位线，但现在图形中是有三角形而没有中位线，从而需将中位线添上，也就是联结EF，可得EF∥CA，这就是具体的添线方法，现在我们要证的性质是DF=DE，是两条具有公共端点D的相等线段，就可以组成一个等腰三角形，问题也就成为一个等腰三角形的判定问题，又因为E、D、B成一直线，图形中出现了这个要证明的等腰三角形的顶角的外角，所以要证明DE=DF，就可以转化成要证它的等价性质∠FDB=2∠FEB，这是本题的第三个关键思维节点，就是由出现的两条具有公共端点的相等线段，想到要应用等腰三角形的性质进行证明，又因为由直角三角形斜边上的中线的基本图形的性质，可得FD=FB，∠FDB=∠FBD，而由条件∠ABC=2∠ACB，所以问题就成为要证∠ACB=∠FEB，由于这两个角是FE、AC被BC所截得到的同位角，所以可应用与同位角有关的平行线的基本图形进行证明，由于已证EF∥CA，所以分析可以完成。

直角三角形斜边上中线定理
学习目标
知识与技能：探索并掌握直角三角形斜边上中线定理．
过程与方法：经历探索斜边上中线定理的过程，在证明中学会简单说理，发展初步的合
情推理能力和主动探究习惯，逐步掌握说理的基本方法．
情感态度与价值观：形成良好的几何感知，体会几何学的逻辑内涵，发展思维． 学习难点
理解和掌握直角三角形斜边上中线定理,并能应用该定理进行简单的计算证明．
一、情景导课
1.关于直角三角形，我们学习过哪些定理？
2.如图，在直角△ABC 中，
∠C=90°，∠B=30°，AC=2，
求BC
二、新知探究
1.如图，在矩形ABCD 中，对角线AC 、BD
相交于点O ，试说明BO=21AC 。

2.我们现在观察△ABC ，则BO 为斜边AC 上的中线，得到结论是什么？ 请把定理叙述一遍。

A B C A D CA B O
C
B D 三、巩固练习 1.如图，在△AB
C 中，∠C=90°，
点M 为AB 中点.
(1)若AB=8，求CM
(2)若∠A=60°，△ABC 是什么三角形
三、典例精讲：
1、如图，在Rt △ABC 中，CD 是斜边AB 上的中线， ∠CDA=80°，则∠A=_____ ∠B=_____
2、如图，已知△ABC 和△ABD 均为直角三角形， 其中∠ACB=∠ADB=90°，E 为AB 的中点， 求证：CE=DE ．
B C A M。

基本图形分析法：详细分析直角三角形斜边的中线问题（二）【分析方法导引】当几何问题中出现了直角三角形斜边上的中点时，就应想到要应用直角三角形斜边上的中线的基本图形的性质进行证明。

接下来就应将斜边上的中线添上。

进一步的分析就是：若斜边上的中点是条件，则直接推得斜边上的中线等于斜边的一半，并可直接应用两等腰三角形推得角之间的等量关系。

若斜边上的中点是要证明的结论，则应转而证明要证相等的这两条线段都和这条斜边上的中线相等，也就是转化为等腰三角形的判定问题或者也就是证明角相等的问题。

进一步也就是应用线段相等与角相等之间的等价关系来完成分析。

当几何问题中出现了线段之间的倍半关系，且倍线段是直角三角形的斜边时，就应想到要应用直角三角形斜边上的基本图形进行证明。

接下来就应将斜边上的中线添上，得到这条斜边上的中线等于斜边的一半，和相应的角之间的等量关系和倍半关系，问题就转化成要证明问题中出现的倍半关系中的半线段与这条斜边上的中线相等。

当几何问题中出现了两个角之间的倍半关系，且其中的半角是一个直角三角形的锐角时，就可想到要应用直角三角形斜边上的中线的基本图形进行证明。

接下来的问题也是将斜边上的中线添上，然后可应用两个等腰三角形的顶角的外角等于底角的两倍的性质来完成分析。

例4 如图3-198，已知：△ABC中，∠ABC=2∠C，AD 是高，延长AB到E使BE=BD，ED的延长线交AC于F。

求证:(1)AF=CF；(2)AB=DC-DB。

图3-198分析：(1)本题要证明AF=CF，而已知∠ADC=90°，就出现了F是直角△ACD的斜边的中点，从而就要应用直角三角形斜边上的中线这个基本图形的性质进行证明(如图3-199)。

这样要证明AF=CF，就应证明AF、CF都与DF相等，也就是要证明AF=CF的等价性质∠FDC=∠C成立。

因∠FDC=∠BDE，所以问题就成为要证明∠BDE=∠C，而已知∠ABC=2∠C，则又应证∠ABC=2∠BDE。