现代信号处理第3章最优滤波

69第3章 Wigner 分布3.1 Wigner 分布的定义我们在第一章讨论了对非平稳信号作时－频联合分析的必要性，在第二章介绍了具有线性形式的时－频分布，如STFT 及Gabor 变换。

这一类形式的时－频分布还有小波变换，我们将在第九章以后详细讨论。

本章及下一章集中讨论具有双线性形式的时－频分布，主要是Wigner 分布及具有更一般形式的Cohen 类分布。

所谓双线性形式，是指所研究的信号在时－频分布的数学表达式中以相乘的形式出现两次。

在有的文献中又称为非线性时－频分布。

令信号()t x ，()t y 的傅立叶变换分别是()Ωj X ，()Ωj Y ，那么，()t x ，()t y 的联合Wigner分布定义为：()()(),,22j x y W t x t y t e d ττττ∞-Ω-∞Ω=+-⎰＊ （3.1.1）信号()t x 的自Wigner 定义为 ()()(),22j x W t x t x t e d ττττ∞-Ω-∞Ω=+-⎰＊ （3.1.2）Wigner 于1932年首先提出了Wigner 分布的概念［120］，并把它用于量子力学领域。

在之后的一段时间内并没有引起人们的重视。

直到1948年，首先由Ville 把它应用于信号分析。

因此，Wigner 分布又称Wigner －Ville 分布，简称为WVD 。

1973年，DE ．Bruijn 对WVD分布作了评述，并给出了把WVD 用于信号变换的新的数学基础［32］。

1966年，Cohen 给出了各种时－频分布的统一表示形式［46］，1980年，Classen 在Philips ．J ．Res ．上连续发表了三篇关于WVD 的文章［38,39,40］，对WVD 的定义、性质等作了全面的讨论。

由于这些工作，使得80年代后对WVD 的研究骤然引起了人们的兴趣，发表的论文很多，也取得了一些可喜的成果。

由下面的讨论可知，在已提出的各种时－频分布中，WVD 具有最简单的形式，并具有很好的性质。

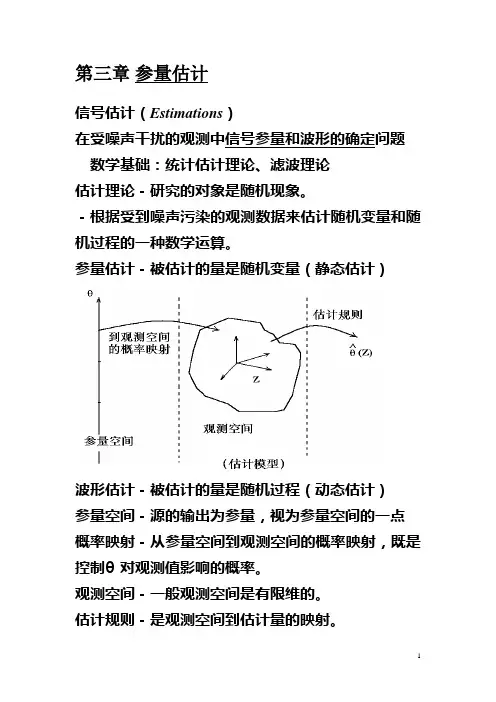
第三章参量估计信号估计（Estimations）在受噪声干扰的观测中信号参量和波形的确定问题数学基础：统计估计理论、滤波理论估计理论－研究的对象是随机现象。

－根据受到噪声污染的观测数据来估计随机变量和随机过程的一种数学运算。

参量估计－被估计的量是随机变量（静态估计）波形估计－被估计的量是随机过程（动态估计）参量空间－源的输出为参量，视为参量空间的一点概率映射－从参量空间到观测空间的概率映射，既是控制θ对观测值影响的概率。

观测空间－一般观测空间是有限维的。

估计规则－是观测空间到估计量的映射。

若接收机判决某一假设为真，但与信号有关的某个参量是未知的。

参量估计的目的：在有限个信号观测样值中，以最佳方式估计该参量。

设z 1,z 2,...,z N 为随机变量z 的独立同分布的N 个观测样值，而f(z 1,z 2,...,z N )是用来估计参量θ的观测样值函数（统计量），称：∧θ＝f(z 1,z 2,...,z N ) （3－1）为参量θ的估计量。

用∧θ表示对参量θ的估值。

∧θ的均值即为E[∧θ]=E[f(z 1,z 2,...,z N )]。

最佳估计－最优估计准则；随机参量－其特性用概率密度来表征－贝叶斯估计 非随机参量－仅为一般的未知量－最大似然估计 §3－1、非随机参量的最大似然估计(Maximum Likelihood Estimation--MLE)设z 1,z 2,...,z N 为随机变量z 的独立同分布的N 个观测样值，p(z|θ)为z 的依赖参量θ分布密度函数， 参量θ为待估计的量。

则似然函数为：())23)..(()()z ,..,z ,z (1N 21-===∏=θθθθNi i z p z p p L 选取使似然函数L (θ)为最大的∧θ作为θ的估计量，称为θ的最大似然估计。

L (θ)最大等效Ln L (θ)最大。

要求θ的最大似然估计∧θ，必需解似然方程：)33....(0)(-=∂∂θθz Lnp 此式为必要条件，而不是充分条件。

一：采用不同的积分变换的实质是应用不同的基函数，属于频域滤波器。

变换将难以处理的时域信号转换成了易于分析的频域信号频域滤波器的特点是将信号与噪声在频率上进行分离，抑制有用信号频带以外的噪声，是有用信号通过，但不能抑制与有用信号占据相同频带的噪声，这一点与维纳滤波与卡尔曼滤波从根本上是不同的。

器设计的中心任务是求得系统函数，即求一组零极点使得在规定意义上滤波器的响应逼近一给定的特性。

维纳滤波与卡尔曼滤波是统计滤波的方法。

属于时域滤波器。

不需要从频域设计转换到时域实现。

估计方差在某种统计意义下尽可能小的滤波器称为这一统计意义下的最优滤波器。

维纳滤波器在最小均方误差的准则下是最优的。

仅在理论上有意义，实际应用不多。

卡尔曼滤波器是一种自适应滤波器，kalman滤波是一种递推的数据处理算法，提供了针对离散线性系统状态的线性最小估计方法的有效计算方法。

其有效性体现在它提供了过去、现在、未来状态的估计，甚至当系统的精细特性未知的情况下也能如此。

采用kalman滤波算法通过对观测数据的处理来得到系统状态变量的估计。

它不仅可以处理平稳随机信号，还可以用来处理非平稳随机信号，而且物理可实现。

版本二：//滤波的计算方法有很多，有线性滤波方法、非线性滤波方法和统计滤波方法等。

线型滤波方法是对信号进行时域、频域或两者的变换来实现滤波，如中值滤波、基于傅里叶变换的滤波、小波变换等；统计滤波方法则利用统计学的方法来处理信号中的各种噪声而达到滤波的目的，如卡尔曼滤波、维纳滤波等。

线性滤波器经常用于剔除输入信号中不想要的频率或者从许多频率中选择一个想要的频率。

而采用不同的积分变换的实质是应用不同的基函数，基函数决定变换的性质。

傅里叶变换的缺点是失去时间，短时傅里叶变换通过加不同的时间窗函数可以克服这一缺点。

小波变换相当于滤波器组，将频谱按频带分割，能够同时具有时间分辨率和频率分辨率。

所有类型的线性滤波器都可以完全用频率响应和相位响应来描述，它们唯一地定义了脉冲响应，反之亦然。