专题9 方程根的存在性及个数--考研数学

方程根的定义方程根是指能够满足给定方程的解的数值或数值集合。

在数学中，方程是描述数值关系的等式，方程的根是能够使方程成立的数值。

方程根的概念广泛应用于各个数学分支以及实际问题中，如代数方程、微分方程、概率方程等。

一元一次方程是最简单的方程形式，其一般形式为ax + b = 0，其中a和b是已知常数，x是未知数。

一元一次方程的解即为方程的根，通过对方程进行变形和求解，可以得到方程的根。

例如，对于方程2x + 3 = 0，通过移项和化简可以得到x = -3/2，-3/2即为方程的根。

一元二次方程是一种更复杂的方程形式，其一般形式为ax^2 + bx + c = 0，其中a、b、c是已知常数，x是未知数。

一元二次方程的解也是方程的根，通过应用求根公式或配方法等求解技巧，可以得到方程的根。

例如，对于方程x^2 - 5x + 6 = 0，通过因式分解或求根公式可以得到x = 2，3，2和3即为方程的根。

方程根的存在性和唯一性是方程理论中的重要问题。

对于一元一次方程来说，存在且唯一的根，即使方程无解也可以看作是存在一个复数根。

而对于一元二次方程来说，根的情况则有所不同。

如果方程的判别式b^2 - 4ac大于0，方程有两个不相等的实数根；如果判别式等于0，方程有两个相等的实数根；如果判别式小于0，方程有两个共轭复数根。

在实际问题中，方程根的求解常常涉及到数学建模和计算机算法等领域。

例如，在物理学中，通过建立方程模型可以描述物体运动的规律，求解方程的根可以得到物体的位置、速度等信息。

在工程学中，通过建立方程模型可以分析电路、结构等问题，求解方程的根可以得到电流、应力等参数。

在计算机科学中，通过建立方程模型可以解决搜索、优化等问题，求解方程的根可以得到最优解或满足特定条件的解。

方程根的求解方法不仅限于代数方法，还可以通过数值计算的方法进行近似求解。

数值方法通过迭代计算，逐步逼近方程的根。

例如，牛顿迭代法、二分法等都是常用的数值求根方法。

第13讲一元二次方程的根与系数的关系模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．熟记一元二次方程的根与系数的关系；2．掌握一元二次方程的根与系数的关系以及在各类问题中的运用；知识点一.一元二次方程的根与系数的关系如果一元二次方程)0(02≠=++a c bx ax 的两个实数根是21x x ，，那么a b x x -=+21，acx x =21.注意它的使用条件为a≠0，Δ≥0.也就是说，对于任何一个有实数根的一元二次方程，两根之和等于方程的一次项系数除以二次项系数所得的商的相反数；两根之积等于常数项除以二次项系数所得的商.知识点二.一元二次方程的根与系数的关系的应用(1)验根．不解方程，利用根与系数的关系可以检验两个数是不是一元二次方程的两个根；(2)已知方程的一个根，求方程的另一根及未知系数；(3)不解方程，可以利用根与系数的关系求关于x 1、x 2的对称式的值．此时，常常涉及代数式的一些重要变形；如：①222121212()2x x x x x x +=+-；②12121211x x x x x x ++=；③2212121212()x x x x x x x x +=+；④2221121212x x x x x x x x ++=2121212()2x x x x x x +-=；⑤22121212()()4x x x x x x -=+-；⑥12()()x k x k ++21212()x x k x x k =+++；⑦12||x x -=；⑧22212121222222121212()211()x x x x x x x x x x x x ++-+==；⑨12x x -==⑩12||||x x +===．(4)已知方程的两根，求作一个一元二次方程；以两个数为根的一元二次方程是.(5)已知一元二次方程两根满足某种关系，确定方程中字母系数的值或取值范围；（6）利用一元二次方程根与系数的关系可以进一步讨论根的符号.设一元二次方程20(0)ax bx c a ++=≠的两根为1x 、2x ，则①当△≥0且120x x >时，两根同号．当△≥0且120x x >，120x x +>时，两根同为正数；当△≥0且120x x >，120x x +<时，两根同为负数．②当△＞0且120x x <时，两根异号．当△＞0且120x x <，120x x +>时，两根异号且正根的绝对值较大；当△＞0且120x x <，120x x +<时，两根异号且负根的绝对值较大．要点：（1）利用根与系数的关系求出一元二次方程中待定系数后，一定要验证方程的∆．一些考试中，往往利用这一点设置陷阱；（2）若有理系数一元二次方程有一根a +a -a ，b为有理数）．考点一：利用一元二次方程根与系数的关系求值例1．（2024·湖南岳阳·二模）已知关于x 的一元二次方程210x x +-=两个根12x x 、，则12x x +=．【变式1-1】（2024·江西吉安·一模）已知方程2430x x --=的两个根分别为1x ，2x ，则12x x 的值为．【变式1-2】（2024·广东深圳·模拟预测）若1，2是方程210x x --=1212的值为．()αβαβ+=．考点二：通过化简、变形利用一元二次方程根与系数的关系求值例2.（2024·湖南长沙·三模）已知关于x 的一元二次方程2420x x -+=的两个实数根分别为1x 和2x ，则1212x x x x ++的值为．【变式2-1】（2024·江苏南京·三模）设12是方程320210x x --=112．【答案】2024【分析】本题主要考查一元二次方程根与系数关系，方程解的定义，掌握一元二次方程根与系数关系，方程解的定义是解题的关键．根据根与系数关系得到123x x +=，之后将1x 代入方程中得到211320210x x -=-，变形为21132021x x -=，两式相加即可得到答案．【详解】解： 12x x 、是方程2320210x x --=的两个根，∴123x x +=，211320210x x -=-，∴21132021x x -=，∴22112111220213230224x x x x x x x -+=-+=+=+．故答案为：2024．【变式2-2】（2024·山东济宁·一模）设α，β是一元二次方程23170x x +-=的两个根，则252a αβ++=.【答案】11【分析】此题主要考查了根与系数的关系，由α，β是一元二次方程23170x x +-=的两个根，得出3αβ+=-，23170αα+-=，再把252a αβ++变形为()232αααβ+++，即可求出答案．【详解】解：∵α，β是一元二次方程23170x x +-=的两个根，∴3αβ+=-，23170αα+-=，∴2317αα+=，∴()()225232172311ααβαααβ++=+++=+⨯-=，故答案为：11．【变式2-3】（2024·四川泸州·中考真题）已知1x ，2x 是一元二次方程2350x x --=的两个实数根，则()212123x x x x -+的值是．【答案】14考点三：利用一元二次方程根与系数的关系求参数例3.（2024·山东临沂·二模）关于x 的一元二次方程210x kx k +++=的两实数根分别为1x ，2x ，且22121x x +=，则k 的值为．【变式3-1】（2024·四川广元·二模）已知关于x 的一元二次方程1、2x ，且()()1210m x x m --=，则m 的值为．【答案】2-【分析】本题主要一元二次方程根与系数的关系，根的判别式．由一元二次方程根与系数的关系可知()1244x x +=--=，12x x m ⋅=，再整体代入()()1210m x x m --=中，求出m 的值，代入原方程，判断是否有两个实数根即可．【详解】解： 1x 、2x 是240x x m -+=的两个实数根，∴()1244x x +=--=，12x x m ⋅=，()()()212121210x mxm x x x x m m --=×-++=，∴2410m m m +=-，∴23100m m --=，∴()()520m m -+=，∴15m =，22m =-，当5m =时，原方程为2450x x -+=，()2441540∆=--⨯⨯=-<，∴5m =不合题意，应舍去；当2m =-时，原方程为2420x x --=，()()24412240∆=--⨯⨯-=>，∴2m =-符合题意；即m 的值为2-．故答案为：2-．【变式3-2】（2024·江西景德镇·二模）已知关于x 的一元二次方程220x mx --=的两根分别是1x ，2x ，若12111x x +=，则m 的值为.【变式3-3】（2024·江西南昌·二模）已知1，2为关于的方程20x x k -+=2111222x x x x --=，则k =．考点四：利用一元二次方程根与系数的关系分析、判断命题真假例4.（23-24八年级下·浙江杭州·期中）对于一元二次方程()200ax bx c a --=≠，下列说法其中正确的是（）①若方程的两个根是1-和2，则20a c -=；②若c 是方程的一个根，则一定有10ac b --=成立；③若0a b c +-=，则它有一个根是=1x -；④若方程有一个根是()0x m m =≠，则方程20cx bx a +-=一定有一个实数根1m．A ．①②③④B ．②③④C ．①③④D ．①②③【变式4-1】（2024·江苏宿迁·三模）关于x 的一元二次方程有以下命题：①若0a b c -+=，则²40b ac -≥②若方程的两根为3-和1，则30a c +=③若上述方程有两个相等的实数根，则²1ax bx c ++=-必有实数根；④若m 是该方程的一个根，则1m一定是²0cx bx a ++=的一个根．其中真命题的个数（）A ．4B ．3C ．2D ．1【答案】B【分析】本题考查了一元二次方程的知识，掌握一元二次方程解的概念和计算方法，根与系数的关系是解题的关键．根据一元二次方程的解，把131x x x =-==，，代入可判定命题①②；根据根的判别式240b ac ∆=-≥可判定命题③；根据方程的根进行验证即可判断命题④；由此即可求解．【详解】解：命题①，当1x =-时，一元二次方程为0a b c -+=，∴1x =-是方程的解，即方程有实数解，∴240b ac -≥，原命题为真命题；命题②，当3x =-时，一元二次方程为930a b c -+=，当1x =时，一元二次方程为0a b c ++=，∴联立方程组得9300a b c a b c -+=⎧⎨++=⎩，∴解得，1240a c +=，∴30a c +=，原命题为真命题；【变式4-2】（23-24七年级下·安徽马鞍山·期中）对于一元二次方程，下列说法：①若0a b c ++=，则方程必有一根为1x =；②若方程20ax bx c ++=无实根，则方程20ax c +=有两个不相等的实根；③若方程()200ax bx c a ++=≠两根为1x 、2x ，且满足120x x ≠≠，则方程()200cx bx a c ++=≠，必有实根11x ，21x ；④若c 是方程()200ax bx c a ++=≠的一个根，则一定有10ac b ++=；⑤若0x 是一元二次方程20ax bx c ++=的根，则()22042b ac ax b -=+．其中正确的是（）A ．①②③B ．②③④C ．①②④⑤D ．①③⑤【答案】D【分析】本题主要考查一元二次方程的根、一元二次方程的根的判别式、等式的性质．按照方程的解的含义、一元二次方程的实数根与判别式的关系、等式的性质、一元二次方程的求根公式等对各选项分别讨论，可得答案．如：[3,2]*[5,1]352117=⨯+⨯=．①已知[,1]*[,2]0x x x -+=，则12x =，21x =-；②若关于x 的方程[,21]*[1,]0x x mx m ++=有实数根，则14m ≥-且0m ≠；③若实数s 、()t s t ≠满足1[2,3]*,03s s s ⎡⎤-=⎢⎣⎦，1[2,3]*,03t t t ⎡⎤-=⎢⎥⎣⎦，则11s t -以上结论正确的个数有（）个．A ．0B ．1C ．2D ．3【答案】B【分析】此题考查了解一元二次方程、一元二次方程根与系数关系、一元二次方程根的判别式等知识，利用因式分解法解①得到的方程，即可判断①，利用分类讨论即可判断②，利用一元二次方程的根与系数关系和公式法解方程即可判断③．【详解】解：①∵[,1]*[,2]0x x x -+=，考点五：利用一元二次方程根与系数的关系比较根的大小例5.（23-24九年级上·广东深圳·期中）已知1x ，2x 是关于x 的方程230x bx +-=的两根，则下列结论一定正确的是（）A ．12x x ≠B ．120x x +<C ．120x x ⋅>D ．1>0x ，20x >【答案】A【分析】本题考查了根的判别式以及根与系数的关系，解题的关键是A 、根据方程的系数结合根的判别式，可得出0∆>，由此即可得出12x x ≠，结论A 正确；B 、根据根与系数的关系可得出12x x b +=-，结合b 的值不确定，可得出B 结论不一定正确；C 、根据根与系数的关系可得出213x x ⋅=-，结论C 错误；D 、由213x x ⋅=-，可得出1x 、2x 异号，结论D 错误．综上即可得出结论．【详解】解：A 、 2241(3)120b b ∆=-⨯⨯-=+>，12x x ∴≠，结论正确，符合题意；B 、1x 、2x 是关于x 的方程230x bx +-=的两根，12x x b ∴+=-，b 的值不确定，∴结论不一定正确，不合题意；C 、1x 、2x 是关于x 的方程230x bx +-=的两根，123x x ∴⋅=-，结论错误，不合题意；D 、123x x ⋅=- ，1x ∴、2x 异号，结论D 错误，不合题意．故选：A ．【变式5-1】（23-24九年级下·湖南娄底·阶段练习）关于x 的方程2224x mx m -+=的两个根1x ，2x 满足1223x x =+，且12x x >，则m 的值为（）A ．3-B ．1C ．3D ．9【变式5-2】（23-24八年级下·浙江嘉兴·期末）已知关于的一元二次方程有两个不相等的实数根12,x x ，且121x x <<，则实数a 的取值范围为．【变式5-3】（23-24九年级上·福建泉州·阶段练习）设方程有两个根1x 和2，且12124x x <<<<，那么方程20cx bx a -+=的较大根3x 的范围为（）A ．3112x <<B ．342x -<<-C ．31124x -<<-D ．3112x -<<-考点六：与一元二次方程根与系数有关的解答证明题例6.（23-24八年级下·四川成都·期中）已知关于x 的方程2210x x k -+-=有两个实数根．(1)求k 的取值范围；(2)若221121221x x x x x x +=+-，求k 的值．由（1）知2k ≤，则2k =．【点睛】本题考查一元二次方程综合，涉及由一元二次方程根的情况求参数范围、解不等式、一元二次方程根与系数的关系、解一元二次方程等知识，熟练掌握一元二次方程的相关知识是解决问题的关键．【变式6-1】（2024·四川南充·三模）已知关于x 的一元二次方程()221230x k x k -+--=有两个不相等的实数根．(1)求实数k 的取值范围，(2)当2k =时，设方程的两个实数根分别为12,x x ，求32221121243x x x x x -+++的值．【变式6-2】（23-24八年级下·山东淄博·期中）已知关于x 的一元二次方程(1)求证：不论m 取何值，方程总有两个不相等的实数根；(2)若方程有两个实数根为12,x x ，且121231x x x x ++=，求m 的值．【答案】(1)见详解(2)6m =-【分析】（1）根据根的判别式得出22[(21)]41(2)4890m m m m ∆=-+-⨯⨯--=++>，据此可得答案；（2）根据根与系数的关系得出1221x x m +=+，122x x m =--，代入121231x x x x ++=得出关于m 的方程，解之可得答案．本题主要考查根与系数的关系、根的判别式，解题的关键是掌握1x ，2x 是方程20x px q ++=的两根时，12x x p +=-，12x x q =．【详解】（1）证明： 2[(21)]41(2)m m ∆=-+-⨯⨯--244148m m m =++++2489m m =++()2415m =++，∵()()220414105m m +++≥>，∴无论m 取何值，此方程总有两个不相等的实数根；（2）解：由根与系数的关系，得1221x x m +=+，122x x m =--，由121231x x x x ++=，得213(2)1m m ++--=，解得6m =-．【变式6-3】（23-24八年级下·广西贺州·期中）阅读材料：材料：关于x 的一元二次方程()200ax bx c a ++=≠的两个实数根1x ，2x 和系数a ，b ，c 有如下关系：12b x x a+=-，12cx x a =；根据上述材料，结合你所学的知识，完成下列问题：(1)类比：一元二次方程22310x x +-=的两个实数根为m ，n ，则m n +=；mn =；(2)应用：已知一元二次方程22310x x +-=的两个实数根为m ，n ，求22m n +的值；(3)提升：已知实数s ，t 满足22310s s +-=，22310t t +-=且s t ≠，求11s t -的值．一、单选题1．（2023·西藏日喀则·一模）如果12,x x 是一元二次方程2230x x +-=的解，则12x x ⋅的值为（）A ．3-B ．3C ．2D ．1-【答案】A【分析】本题主要考查了一元二次方程根与系数的关系，对于一元二次方程()200ax bx c a ++=≠，若12x x ，是该方程的两个实数根，则1212b ca x x x x a+=-=，，据此求解即可．【详解】解：∵12,x x 是一元二次方程2230x x +-=的解，∴213x x ⋅=-，故选：A ．．（八年级下浙江湖州阶段练习）关于x 一个实数根为，则另一实数根和m 的值分别为（）A ．6，4-B ．6-，4-C ．6，4D ．6-，4【答案】D【分析】本题考查了一元二次方程根与系数的关系，熟练掌握根与系数的关系是解题的关键．设该方程的两个实数根为12x =和2x ，由根与系数的关系得，12b x x m a +=-=-，1212cx x a==-，将12x =代入即可求解．【详解】解：设关于x 的一元二次方程2120x mx +-=实数根为12x =和2x ，则：12b x x m a +=-=-，1212cx x a==-，∴2212x =-，解得26x =-，∴12264m x x -=+=-=-，解得4m =，故选：D ．3．（23-24八年级下·安徽六安·阶段练习）已知正方形ABCD 的两邻边AB ，AD 的长度恰为方程的两个实数根，则正方形ABCD 的周长为（）A ．2B ．4C ．6D ．8【答案】B【分析】此题考查了正方形的性质，一元二次方程根与系数的关系.首先根据正方形的性质得到AB AD =，然后根据一元二次方程根与系数的关系得到1AB CD ⋅=，进而求出1AB CD ==，即可得到正方形ABCD 的周长．【详解】∵四边形ABCD 是正方形∴AB AD=∵正方形ABCD 的两邻边AB ，AD 的长度恰为方程210x mx -+=的两个实数根，∴1AB CD ⋅=，∴1AB CD ==∴正方形ABCD 的周长为4．故选：B ．4．（2024·江苏无锡·一模）设12,x x 是关于x 的一元二次方程()222120x m x m -+++=的两个实数根，且()()12118x x ++=，则m 的值为（）A ．1B ．3-C ．3或1-D ．1或3-（1）当1k ≥-，方程有两个实数根；（2）如果方程的两实数根是1x ，2x ，那么122x x +=；（3）如果方程的两实数根是1x ，2x ，那么221224x x k +=+；（4）如果方程的两实数根是1x ，2x ，那么12x x -=A ．1个B ．2个C ．3个D ．4个二、填空题6．（23-24九年级下·四川成都·阶段练习）若12,x x 是一元二次方程2260x x --=的两个实数根，则1212x x x x +=231x x -=-1和2，则1212x x x x +-的值为．1，2若1212则实数k =．【答案】7-【分析】本题考查了一元二次方程的根与系数的关系，熟练掌握一元二次方程根与系数的关系是解题的关键．根据一元二次方程的根与系数的关系，得出12123,x x x x k +=-=，代入12122213x x x x ++=-，即可求解．【详解】解：∵一元二次方程230x x k ++=的两个实数根为1x ，2x ，∴12123,x x x x k +=-=∵12122213x x x x ++=-，∴613k -=-，解得：7k =-，故答案为：7-．9．（23-24九年级下·广东汕头·期中）对于字母m 、n ，定义新运算22m n m mn n =++★，若方程2310x x ++=的解为a 、b ，则2a b +★的值为．【答案】10【分析】本题考查定义新运算，一元二次方程根与系数的关系，根据根与系数的关系，得到3,1a b ab +=-=，根据新运算，列出代数式，整体代入法求值即可．【详解】解：∵方程2310x x ++=的解为a 、b ，∴3,1a b ab +=-=，∵22m n m mn n =++★，∴2222a b a ab b +=+++★2222a ab b ab =++-+()22a b ab =+-+()2312=--+912=-+10=．故答案为：10．10．（2024·浙江杭州·二模）关于一元二次方程()200ax bx c ac ++=≠，有以下命题：①若0a b c -+=，则240b ac -≥；②若该方程的两根为3-和1，则30a c +=；③若上述方程有两个相等的实数根，则21ax bx c ++=-必有实数根；④若r 是该方程的一个根，则1r一定是方程20cx bx a ++=的一个根．其中真命题是．（只需填写序号）三、解答题11．（23-24八年级下·安徽亳州·期中）若12,x x 是关于x 的一元二次方程2240kx x -+=的两个实数根．(1)求k 的取值范围；(2)若112x =，求()()1233x x --的值．(1)如果方程有实数根，求k 的取值范围；(2)如果12,x x 是这个方程的两个根，且221212324x x x x ++=，求k 的值．【答案】(1)10k ≤(2)11-【分析】本题考查了一元二次方程根的判别式，一元二次方程的根与系数的关系，完全平方公式等知识．熟练掌握一元二次方程根的判别式，一元二次方程的根与系数的关系，完全平方公式是解题的关键．（1）由题意知()()26410k ∆=---≥，计算求解即可；（2）由题意知，126x x +=，121x x k ⋅=-，由221212324x x x x ++=，可得()2121224x x x x ++=，即26124k +-=，计算求解即可．【详解】（1）解：∵2610x x k -+-=，∴()()26410k ∆=---≥，解得，10k ≤；（2）解：由题意知，126x x +=，121x x k ⋅=-，∵221212324x x x x ++=，∴()2121224x x x x ++=，∴26124k +-=，解得，11k =-，∴k 的值为11-．13．（23-24八年级下·浙江杭州·期中）已知关于x 的一元二次方程2243210x tx t t -++-=.(1)当3t =时，解这个方程；(2)试判断这个一元二次方程根的情况，并说明理由；(3)1x ，2x 是这个方程的两个实数根，若n 、t 为正整数，且12x nx =，求n 的值.【答案】(1)18x =，24x =(2)方程有两个实数解．理由见详解(3)n 的值为1或2．(1)求证：该方程总有两个实数根；(2)记该方程的两个实数根为12,x x 求代数式()()1222--x x 的值；(3)若221212,3M x x N x x =+=-，比较M 与N 的大小．【答案】(1)见解析；满足2121x x x x -=⋅，则称此类方程为“差积方程”．例如：()1102x x ⎛⎫--= ⎪⎝⎭是差积方程．(1)判断方程26510x x -+=是否为“差积方程”？并验证；(2)若方程()2220x m x m -++=是“差积方程”，直接写出m 的值；(3)当方程(()²00ax bx c a ++=≠为“差积方程”时，求a 、b 、c 满足的数量关系．(1)求证：不论m为何实数，方程总有实数根；(2)当方程的两个根12,x x均为正数时，①求m的取值范围；②若12,x x分别是菱形ABCD的两条对角线的长，求菱形ABCD的边长（用含m的代数式表示）．。

高中数学多项式方程与根的性质分析在高中数学中，多项式方程是一个重要的概念，也是学习代数的基础。

多项式方程的解，即方程的根，具有一些特殊的性质，我们将在本文中对这些性质进行详细的分析和说明。

一、多项式方程的根的性质1. 多项式方程的根的个数与次数的关系对于一个n次多项式方程，其最多有n个根。

这是因为多项式方程的次数决定了方程的最多解数。

例如，一个二次方程最多有两个根，一个三次方程最多有三个根，以此类推。

2. 多项式方程的根与系数的关系对于一个n次多项式方程，其根与系数之间有着密切的联系。

根据代数基本定理，一个n次多项式方程在复数域上一定有n个根。

这意味着，如果我们知道了一个n次多项式方程的n-1个根，就可以通过系数与根的关系求出最后一个根。

例如，对于一个二次方程ax^2 + bx + c = 0，已知其中一个根为x1，根据二次方程的求根公式可得：x2 = (-b - √(b^2 - 4ac))/(2a)这样，我们就可以通过已知的一个根和方程的系数求出另一个根。

3. 多项式方程的根的性质多项式方程的根具有一些重要的性质。

首先，多项式方程的根可以是实数或者复数。

其次，如果一个多项式方程的系数都是实数，且有一个复数根，那么它的共轭复数也是它的根。

例如，对于一个二次方程ax^2 + bx + c = 0，如果其中一个根是复数a + bi，那么它的共轭复数a - bi也是它的根。

这是因为复数的性质决定了方程的系数都是实数时，方程的解是成对出现的。

二、多项式方程根的应用举例1. 求解方程的根考虑一个一次方程2x + 3 = 0，我们可以通过移项得到x = -3/2，这就是方程的根。

2. 利用已知根求解方程考虑一个二次方程x^2 - 5x + 6 = 0，已知其中一个根为2，我们可以利用已知根与系数的关系求解另一个根。

根据二次方程的求根公式，我们可以得到：x2 = 5 - 2 = 3所以方程的另一个根为3。

3. 复数根的应用考虑一个三次方程x^3 + 2x^2 + 2x + 1 = 0，我们可以通过求解方程的根来解决问题。

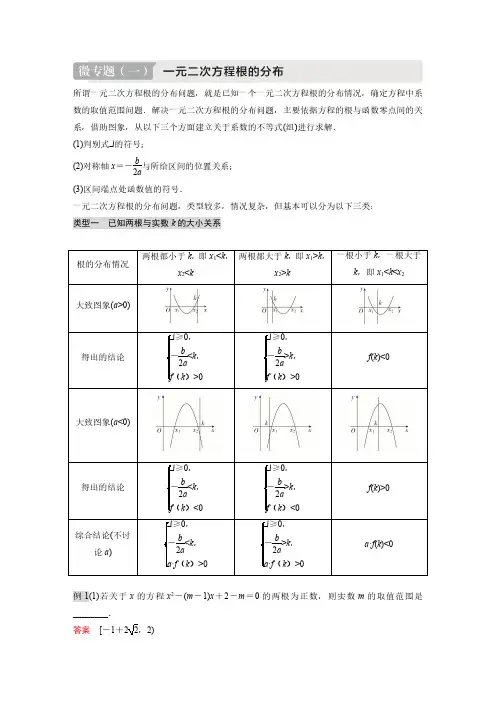
所谓一元二次方程根的分布问题，就是已知一个一元二次方程根的分布情况，确定方程中系数的取值范围问题．解决一元二次方程根的分布问题，主要依据方程的根与函数零点间的关系，借助图象，从以下三个方面建立关于系数的不等式(组)进行求解．(1)判别式Δ的符号；(2)对称轴x ＝－b 2a与所给区间的位置关系；(3)区间端点处函数值的符号．一元二次方程根的分布问题，类型较多，情况复杂，但基本可以分为以下三类：类型一已知两根与实数k 的大小关系根的分布情况两根都小于k ，即x 1<k ，x 2<k 两根都大于k ，即x 1>k ，x 2>k 一根小于k ，一根大于k ，即x 1<k <x 2大致图象(a >0)得出的结论Δ≥0，－b 2a<k ，f （k ）>0Δ≥0，－b 2a >k ，f （k ）>0f (k )<0大致图象(a <0)得出的结论Δ≥0，－b 2a<k ，f （k ）<0Δ≥0，－b 2a >k ，f （k ）<0f (k )>0综合结论(不讨论a )Δ≥0，－b 2a<k ，a ·f （k ）>0Δ≥0，－b 2a >k ，a ·f （k ）>0a ·f (k )<0例1(1)若关于x 的方程x 2－(m －1)x ＋2－m ＝0的两根为正数，则实数m 的取值范围是________．答案[－1＋22，2)解析设f(x)＝x2－(m－1)x＋2－m，m－1）2－4（2－m）≥0，，2－m>0，解得－1＋22≤m<2.(2)(2024·湖北武汉华师第一附中模拟)若关于x的方程ax2＋(a＋2)x＋9a＝0有两个不相等的实数根x1，x2，且x1<1<x2，那么实数a的取值范围是________．答案－211，解析由于方程ax2＋(a＋2)x＋9a＝0有两个不相等的实数根，故a≠0，则ax2＋(a＋2)x＋9a ＝0可化为x2＋9＝0，令f(x)＝x2＋9，则f(1)＝1＋9<0，解得－211<a<0.当方程中二次项系数含有参数时，为避免讨论对应二次函数图象的开口方向，可将方程两边同时除以二次项系数，从而只需研究开口向上的情况，当然需要先判断二次项系数能否为0.1．(2023·黑龙江哈尔滨六中模拟)关于x的方程x2＋(m－2)x＋6－m＝0的两根都大于2，则实数m的取值范围是________．答案(－6，－25]解析令f(x)＝x 2＋(m－2)x＋6－m，＝（m－2）2－4（6－m）≥0，－m－22>2，2）＝4＋2（m－2）＋6－m>0，即≥25或m≤－25，<－2，>－6，解得－6<m≤－2 5.2．已知二次方程(2m＋1)x2－2mx＋(m－1)＝0有一正根和一负根，则实数m的取值范围是________．答案－12，解析解法一：显然2m＋1≠0，令f(x)＝x2－2m2m＋1x＋m－12m＋1，则f(0)<0，即m－12m＋1<0，所以(2m ＋1)(m－1)<0，解得－12<m<1.解法二：设x1，x2是方程(2m＋1)x2－2mx＋(m－1)＝0的两个根，则x1x2＝m－12m＋1<0，解得－12<m<1.类型二已知两根所在的区间f（m）<0，另外，根在区间上的分布还有一种情况：两根分别在区间(m，n)外，即在区间两侧x1<m，x2>n(图形分别如下)，需满足的条件是：(1)当a >0f m ）<0，f n ）<0；(2)当a <0f m ）>0，f n ）>0.例2已知关于x 的二次方程x 2＋2mx ＋2m ＋1＝0.若方程有两根，其中一根在区间(－1，0)内，另一根在区间(1，2)内，则实数m 的取值范围为________；若方程两根均在区间(0，1)内，则实数m 的取值范围为________．答案－56，－12－12，1－2解析设函数f (x )＝x 2＋2mx ＋2m ＋1，则其图象与x 轴的交点分别在区间(－1，0)和(1，2)内，画出示意图如图1，由题意，得f 0）＝2m ＋1<0，f 1）＝2>0，f 1）＝4m ＋2<0，f 2）＝6m ＋5>0，m <－12，m ∈R ，m <－12，m >－56，解得－56＜m ＜－12.由题意知函数f (x )＝x 2＋2mx ＋2m ＋1的图象与x 轴的交点落在区间(0，1)内，画出示意图如图2，由题意，得0）＝2m＋1>0，1）＝4m＋2>0，＝4m2－4（2m＋1）≥0，－m<1，>－12，>－12，≥1＋2或m≤1－2，1<m<0，解得－12＜m≤1－ 2.求解二次方程根的分布问题，最重要的是数形结合，即结合对应二次函数的图象，从以下角度考虑：①开口方向；②对称轴；③判别式；④在区间端点的函数值．注意以下两点：一是特殊点(含参的二次函数过的一些定点(比如与x，y轴的交点)或某些函数值的正负)的应用；二是对于一些特殊情况，还可以利用根与系数的关系、因式分解求出根再求解等方法．3．已知方程x2－(2a＋1)x＋a(a＋1)＝0的两根分别在区间(0，1)，(1，3)内，则实数a的取值范围为________．答案(0，1)解析解法一：设f(x)＝x2－(2a＋1)x＋a(a＋1)，则0）>0，1）<0，3）>0，即（a＋1）>0，2a＋a（a＋1）<0，－3（2a＋1）＋a（a＋1）>0，>0或a<－1，a<1，>3或a<2，所以0<a<1.解法二：由x2－(2a＋1)x＋a(a＋1)＝0，得(x－a)[x－(a＋1)]＝0，所以方程两根为x1＝a，x2＝a＋1，a<1，a＋1<3，解得0<a<1.4．已知关于x的方程ax2＋x＋2＝0的两个实根一个小于0，另一个大于1，则实数a的取值范围是________．答案(－3，0)解析显然a≠0，则方程ax2＋x＋2＝0可化为x2＋xa＋2a＝0，设f(x)＝x2＋xa＋2a，则0）<0，1）<0，，＋1a＋2a<0，解得－3<a<0，所以实数a的取值范围是(－3，0)．类型三可转化为一元二次方程根的分布的问题一元二次方程根的分布问题是高中数学的重要知识点之一，很多涉及函数零点个数问题或方程根的个数问题，经过换元后都能转化为根的分布问题求解．(2023·河北石家庄藁城一中模拟)设函数f (x )＝－32cos2x ＋a sin x ＋a ＋92，若方程f (x )＝0在(0，π)上有4个不相等的实数根，则实数a 的取值范围是________．答案(－3，6－62)解析f (x )＝－32(1－2sin 2x )＋a sin x ＋a ＋92＝3sin 2x ＋a sin x ＋a ＋3，x ∈(0，π)，令sin x ＝t ，t ∈(0，1]，h (t )＝3t 2＋at ＋a ＋3，当0<t <1时，sin x ＝t 有两个不相等的实数根，当t ＝1时，sin x ＝t 有且仅有一个实数根，因为方程f (x )＝0在(0，π)上有4个不相等的实数根，所以原问题等价于h (t )＝3t 2＋at ＋a ＋3＝0在区间(0，1)上有两个不相等的实数根，所以－a 6<1，＝a 2－12（a ＋3）>0，（0）＝a ＋3>0，（1）＝2a ＋6>0，解得－3<a <6－6 2.本题中，令sin x ＝t ，将原问题转化为3t 2＋at ＋a ＋3＝0在区间(0，1)上有两个不相等的实数根，进而转化为一元二次方程根的分布问题是解决问题的关键，同时要注意区间端点是否满足题意．5．(2024·黑龙江哈尔滨南岗实验中学模拟)设函数f (x )x ＋1，x ≤0，4x |，x >0，若关于x 的函数g (x )＝[f (x )]2－(a ＋2)f (x )＋3恰好有六个零点，则实数a 的取值范围是________．答案23－2，32解析作出函数f (x )x ＋1，x ≤0，4x |，x >0的图象如图，令f (x )＝t ，则当t ∈(1，2]时，方程f (x )＝t 有3个不同的实数解，所以使关于x 的方程[f (x )]2－(a ＋2)f (x )＋3＝0恰好有六个不同的实数解，则方程t 2－(a ＋2)t ＋3＝0在(1，2]上有两个不同的实数根，令g (t )＝t 2－(a ＋2)t ＋3，则＝（a ＋2）2－12>0，1<a ＋22<2，（1）＝2－a >0，（2）＝3－2a ≥0，解得23－2<a ≤32，故实数a 23－2，32.。

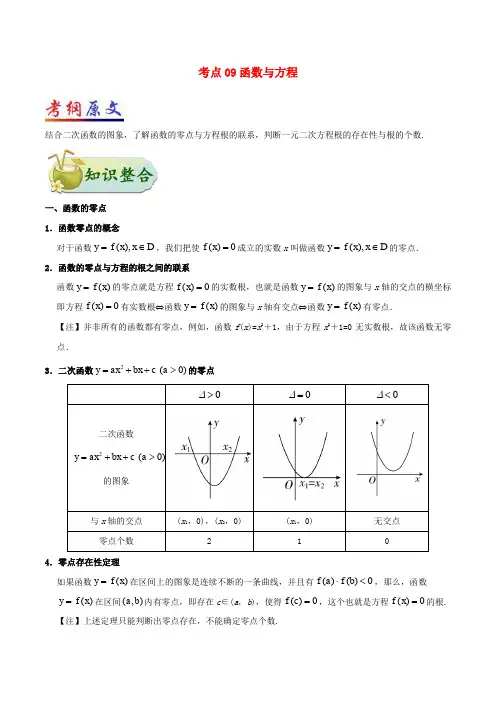
考点09函数与方程结合二次函数的图象，了解函数的零点与方程根的联系，判断一元二次方程根的存在性与根的个数.一、函数的零点 1．函数零点的概念对于函数(),y f x x D =∈，我们把使()0f x =成立的实数x 叫做函数(),y f x x D =∈的零点． 2．函数的零点与方程的根之间的联系函数()y f x =的零点就是方程()0f x =的实数根，也就是函数()y f x =的图象与x 轴的交点的横坐标即方程()0f x =有实数根⇔函数()y f x =的图象与x 轴有交点⇔函数()y f x =有零点．【注】并非所有的函数都有零点，例如，函数f (x )=x 2＋1，由于方程x 2＋1=0无实数根，故该函数无零点．3．二次函数2)( 0y ax bx c a =++>的零点)4．零点存在性定理如果函数()y f x =在区间上的图象是连续不断的一条曲线，并且有()()0f a f b ⋅<，那么，函数()y f x =在区间(,)a b 内有零点，即存在c ∈(a ，b )，使得()0f c =，这个也就是方程()0f x =的根.【注】上述定理只能判断出零点存在，不能确定零点个数.5．常用结论(1)若连续不断的函数()f x 是定义域上的单调函数，则()f x 至多有一个零点； (2)连续不断的函数，其相邻两个零点之间的所有函数值保持同号；(3)函数()()()F x f x g x =-有零点⇔方程()0F x =有实数根⇔函数()y f x =与()y g x =的图象有交点；(4)函数()()F x f x a =-有零点⇔方程()0F x =有实数根⇔函数()y f x =与y a =的图象有交点⇔{|()}a y y f x ∈=，其中为常数.二、二分法 1．二分法的概念对于在区间上连续不断且()()0f a f b ⋅<的函数()y f x =，通过不断地把函数()f x 的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法． 2．用二分法求函数()f x 零点近似值的步骤给定精确度ε，用二分法求函数()f x 零点近似值的步骤如下： ①确定区间，验证()()0f a f b ⋅<，给定精确度ε； ②求区间(a ，b )的中点c ； ③计算f (c )；a ．若f (c )=0，则c 就是函数的零点；b ．若f (a )·f (c )<0，则令b =c (此时零点x 0∈(a ，c ))； c ．若f (c )·f (b )<0，则令a =c (此时零点x 0∈(c ，b ))．④判断是否达到精确度ε：即若|a −b |<ε，则得到零点近似值a (或b )；否则重复②③④. 【速记口诀】定区间，找中点；中值计算两边看， 同号丢，异号算，零点落在异号间． 重复做，何时止，精确度来把关口．考向一函数零点（方程的根）所在区间的判断函数零点的判定方法(1)定义法（定理法）：使用零点存在性定理，函数()y f x =必须在区间上是连续的，当()()f a f b ⋅0<时，函数在区间(a ，b )内至少有一个零点．(2)方程法：判断方程()0f x =是否有实数解．(3)图象法：若一个函数(或方程)由两个初等函数的和(或差)构成，则可考虑用图象法求解，如()()()f x g x h x -=，作出()y g x =和()y h x =的图象，其交点的横坐标即为函数f (x )的零点.典例1 函数21()ln1f x x x =+-的零点所在的大致区间是 A ．(1,2) B ．(2,3) C ．(3,4) D ．(1,2)与(2,3)【答案】B【规律总结】判断函数零点所在区间的方法：一般而言判断函数零点所在区间的方法是将区间端点代入函数求出函数的值，进行符号判断即可得出结论．此类问题的难点往往是函数值符号的判断，可运用函数的有关性质进行判断．1．方程log 3x ＋x =3的解所在的区间为A ．(0,2)B ．(1,2)C ．(2,3)D ．(3,4)考向二函数零点个数的判断判断函数零点个数的方法(1)解方程法：令f (x )=0，如果能求出解，则有几个解就有几个零点．学%(2)零点存在性定理法：利用定理不仅要求函数在区间上是连续不断的曲线，且f (a )·f (b )<0，还必须结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有多少个零点或零点值所具有的性质．(3)数形结合法：转化为两个函数的图象的交点个数问题，先画出两个函数的图象，看其交点个数，其中交点的横坐标有几个不同的值，就有几个不同的零点.典例2函数f (x )=2x＋lg(x ＋1) −2的零点有A ．0个B ．1个C ．2个D ．3个【答案】B解法二：在同一坐标系中作出h (x )=2−2x和g (x )=lg(x ＋1)的图象，如图所示，由图象可知h (x )=2−2x和g (x )=lg(x ＋1)有且只有一个交点，即f (x )=2x＋lg(x ＋1)−2与x 轴有且只有一个交点，即函数f (x )仅有一个零点．2．函数223,0()=2ln ,0x x x f x x x ⎧+-≤⎨-+>⎩的零点个数为A ．0B ．1C ．2D ．3考向三函数零点的应用问题高考对函数零点的考查多以选择题或填空题的形式出现，有时也会出现在解答题中．常与函数的图象及性质相结合，且主要有以下几种常见类型及解题策略． 1．已知函数零点所在区间求参数或参数的取值范围根据函数零点或方程的根求解参数的关键是结合条件给出参数的限制条件，此时应分三步： ①判断函数的单调性；②利用零点存在性定理，得到参数所满足的不等式；③解不等式，即得参数的取值范围．在求解时，注意函数图象的应用． 2．已知函数零点的个数求参数或参数的取值范围一般情况下，常利用数形结合法，把此问题转化为求两函数图象的交点问题． 3．借助函数零点比较大小或直接比较函数零点的大小关系要比较f (a )与f (b )的大小，通常先比较f (a )、f (b )与0的大小．若直接比较函数零点的大小，则可有以下三种常用方法： ①求出零点，直接比较大小； ②确定零点所在区间；③同一坐标系内画出函数图象，由零点位置关系确定大小.典例3对任意实数a ，b 定义运算“⊗”：,1,1b a b a b a a b -≥⎧⊗=⎨-<⎩,设()21()(4)f x x x =⊗+-，若函数()y f x k =+恰有三个零点，则实数k 的取值范围是A ．(−2,1)B ．C ．时，f (x )=x ，则方程f (x )=log 3|x |的解有 A ．2个 B ．3个 C ．4个D ．多于4个5．已知三个函数()()()32,1,log xf x xg x xh x x x =+=-=+的零点依次为,,a b c ，则 A ．a b c << B ．b a c << C ．c a b <<D ．a c b <<6．若函数f (x )=x 3＋ax 2＋bx ＋c 有极值点x 1，x 2，且f (x 1)=x 1，则关于x 的方程3(f (x ))2＋2af (x )＋b =0的不同实根个数是 A ．3 B ．4 C ．5D ．67．已知函数2,0(),0x x f x x x x ≤⎧=⎨->⎩，若函数g (x )=f (x )−m 有三个不同的零点，则实数m 的取值范围为A ．1[,1]2-B ．1[,1)2-C ．1(,0)4-D ．1(,0]4-8．已知12,x x 是函数()2sin cos f x x x m =+-在[]0,π内的两个零点，则()12sin x x +=A ．12 B ．35 C ．45D ．349．若函数12)2()(2+++=ax x a x f 有零点，但不能用二分法求其零点，则的值为______．10．已知函数()3f x x x =+，函数()g x 满足()()20g x g x +-=，若函数()()()1h x g x f x =--有10个零点，则所有零点之和为___________．1．（2017年高考新课标Ⅲ卷）已知函数211()2(e e )x x f x x x a --+=-++有唯一零点，则a =A ．12- B ．13C ．12D ．12．（2015年高考安徽卷）下列函数中，既是偶函数又存在零点的是 A ．y =ln x B ．21y x =+ C ．y =sin xD ．y =cos x3．（2015年高考天津卷）已知函数222()(2)2x x f x x x ⎧-≤=⎨->⎩,,，函数3())(2g x f x =--，则函数()()y f x g x =-的零点个数为A ．2B ．3C ．4D ．54．（2015年高考湖北卷）函数2π()2sin sin()2f x x x x =+-的零点个数为_________.5．（2017年高考江苏卷）设()f x 是定义在R 上且周期为1的函数，在区间[0,1)上，2,,(),,x x D f x x x D ⎧∈⎪=⎨∉⎪⎩其中集合1{n D x x n-==，*}n ∈N ，则方程()lg 0f x x -=的解的个数是． 6．（2016年高考山东卷）已知函数2()24x x mf x x mx m x m ⎧≤=⎨-+>⎩||,,，其中0m >．若存在实数b ，使得关于x 的方程()f x b =有三个不同的根，则m 的取值范围是_________.1．【答案】C2．【答案】C 【解析】由2230x x x ≤⎧⎨+-=⎩得3x =-，又02ln 0x x >⎧⎨-+=⎩得x =e 2，∴f (x )的零点个数为2.3．【答案】123x x x <<【解析】令x ＋2x=0，得2x=−x ；令x ＋ln x =0，得ln x =−x ； 在同一坐标系内画出y =2x，y =ln x ，y =−x 的图象．如图可知x 1<0<x 2<1.令()10h x x ==，则201=12+=，即3312x +=>. 所以123x x x <<.1．【答案】C【解析】由零点存在性定理易知C 正确. 2．【答案】C【解析】如图所示，易知y =ln x 与11y x =-的图象有两个交点．3．【答案】B4．【答案】C【解析】函数f (x )满足f (x ＋2)=f (x )，则函数f (x )是以2为周期的周期函数，在同一坐标系中画出函数y =f (x )与函数y =log 3|x |的图象，如图所示：由图可知函数y =f (x )与函数y =log 3|x |的图象共有4个交点，即方程f (x )=log 3|x |的解有4个，故选C. 5．【答案】D【解析】()()(),,f x g x h x 均为R 上的增函数，有唯一零点，因为所以10a -<<.由()0g x =可得1x =，所以1b =.因为()11210,110333h h ⎛⎫=-+=-<=> ⎪⎝⎭，所以113c <<，所以a c b <<，故选D. 6．【答案】A若x 2＜x 1，如图所示：由图象可知1()f x x =有2个解，2()f x x =有1个解，因此23(())2()0f x af x b ++=的不同实根个数为3.【名师点睛】本题的关键是把求方程23(())2()0f x af x b ++=的根的个数转化成求解方程1()f x x =或2()f x x =的根的个数．7．【答案】C【解析】由g (x )=f (x )−m =0得f (x )=m ，作出函数y =f (x )的图象．当x >0时，()221()21144f x x x x --=≥--=，所以要使函数g (x )=f (x )−m 有三个不同的零点，则14-<m <0，即m ∈1(,0)4-，故选C. 8．【答案】C9．【答案】2或−1【解析】二次函数不能用二分法求零点，则244(2)0,2a a a D =-+==或1a =-． 10．【答案】10【解析】易知函数()f x 为奇函数，其对称中心为(0,0)，所以函数(1)y f x =-的对称中心为(1,0)．由函数()g x 满足()()20g x g x +-=，知函数()g x 的对称中心为(1,0)，函数()()()1h x g x f x =--有10个零点，即函数()y g x =与(1)y f x =-的图象有10个交点，并且关于点(1,0)对称，所以函数()()h x g x =−()1f x -有10个零点，则所有零点之和为10．1．【答案】C当()0g x '=时，1x =；当1x <时，()0g x '<，函数()g x 单调递减；当1x >时，()0g x '>，函数()g x 单调递增，当1x =时，函数()g x 取得最小值，为()12g =.设()22h x x x =-，当1x =时，函数()h x 取得最小值，为1-， 若0a ->，函数()h x 与函数()ag x -没有交点；若0a -<，当()()11ag h -=时，函数()h x 和()ag x -有一个交点，即21a -⨯=-，解得12a =.故选C. 【名师点睛】利用函数零点的情况求参数的值或取值范围的方法：（1）利用零点存在性定理构建不等式求解.（2）分离参数后转化为函数的值域(最值)问题求解.（3）转化为两个熟悉的函数图象的上、下关系问题，从而构建不等式求解.2．【答案】D【解析】选项A ：x y ln =的定义域为(0,+∞)，故x y ln =不具备奇偶性，故A 错误；选项B ：12+=x y 是偶函数，但012=+=x y 无解，即不存在零点，故B 错误； 选项C ：x y sin =是奇函数，故C 错；选项D ：x y cos =是偶函数，且0cos ==x y 2x k π⇒=+π，k ∈Z ，故D 项正确. 3．【答案】A【解析】方法一：分别画出函数(),()f x g x 的草图，观察发现有2个交点.学/方法二：当0x <时，22x ->,所以()22f x x x =-=+,()22f x x -=,此时函数()()f x g x -=()()2231f x f x x x +--=+-的小于零的零点为12x +=- ; 当02x ≤≤时，()22f x x x =-=-,()222f x x x -=--=,函数()()23f x g x x x -=-+-= 1-无零点;当2x >时, ()()22f x x =-,()2224f x x x -=--=-,函数()()()224f x g x x x -=-+--2355x x =-+大于2的零点为x =综上可得函数()()y f x g x =-的零点的个数为2.故选A.4．【答案】5．【答案】8【解析】由于()[0,1)f x ∈，则需考虑110x ≤<的情况，在此范围内，x ∈Q 且x D ∈时，设*,,,2q x p q p p=∈≥N ，且,p q 互质， 若lg x ∈Q ，则由lg (0,1)x ∈，可设*lg ,,,2n x m n m m =∈≥N ，且,m n 互质，因此10nm q p=，则10()n m q p =，此时左边为整数，右边为非整数，矛盾，因此lg x ∉Q ， 因此lg x 不可能与每个周期内x D ∈对应的部分相等，只需考虑lg x 与每个周期x D ∉的部分的交点，画出函数图象，图中交点除外(1,0)其他交点横坐标均为无理数，属于每个周期x D ∉的部分， 且1x =处11(lg )1ln10ln10x x '==<，则在1x =附近仅有一个交点， 因此方程()lg 0f x x -=的解的个数为8．【名师点睛】对于方程解的个数(或函数零点个数)问题，可利用函数的值域或最值，结合函数的单调性、草图确定其中参数范围．从图象的最高点、最低点，分析函数的最值、极值；从图象的对称性，分析函数的奇偶性；从图象的走向趋势，分析函数的单调性、周期性等．6．【答案】(3，＋∞)【解析】函数()f x 的大致图象如图所示，根据题意知只要24m m m >-即可，又m ＞0，解得m ＞3，故实数m 的取值范围是(3，＋∞)．。

专题04 一元二次方程根的分布二次方程()200ax bx c a ++=≠的根从几何意义上来说就是二次函数()c bx ax x f ++=2与x 轴交点的横坐标，所以研究02=++c bx ax 的实根的情况，可从函数()c bx ax x f ++=2的图象上进行研究.若在()+∞∞-,内研究方程02=++c bx ax 的实根情况，只需考查()c bx ax x f ++=2与x 轴交点的个数以及交点横坐标的符号，根据判别式以及韦达定理，由∆、21x x +、21x x ⋅的值与符号，从而判断出实根的情况.若在区间()n m ,内研究二次方程02=++c bx ax ，则需由二次函数图象与区间关系来确定.知识梳理分布情况两个负根即两根都小于0 ()120,0x x << 两个正根即两根都大于0 ()120,0x x >>一正根一负根即一个根小于0，一个大于0()120x x <<大致图象（0>a ）知识结模块一：得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩()00<f大致图象（0<a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩()00>f综合结论（不讨论）()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩()00<⋅f a【例1】已知方程()2210x m x m -++=有两个不等正实根，求实数m 的取值范围． 【难度】★★ 【答案】见解析 【解析】由典例剖析()()0102200m f ∆>⎧⎪-+⎪->⎨⎪>⎪⎩⇒()218010m m m m ⎧+->⎪>-⎨⎪>⎩⇒330m m m ⎧<->+⎪⎨>⎪⎩⇒03m <<-3m >+即为所求的范围．【例2】若方程05)2(2=-+-+m x m x 的根满足下列条件，分别求出实数m 的取值范围． （1） 方程两实根均为正数； （2） 方程有一正根一负根． 【难度】★★ 【答案】见解析【解析】分析 讨论二次方程根的分布，应在二次方程存在实根的条件下进行．代数方法与图象法是研究二次方程根的分布问题的主要方法．解1 （1）由题意，得.45244050)2(0)5(4)2(00022121-≤⇒⎪⎩⎪⎨⎧<<≥-≤⇒⎪⎩⎪⎨⎧>->--≥---⇒⎪⎩⎪⎨⎧>>+≥∆m m m m m m m m m x x x x 或所以，当4-≤m 时，原方程两实根均为正数；（2）由题意，得.5050021>⇒<-⇒⎩⎨⎧<≥∆m m x x所以，当5>m 时，原方程有一正根一负根．解2 二次函数m x m x y -+-+=5)2(2的图象是开口向上的抛物线． （1）如图，由题意，得4052)2(4)2(022050)2(020)0(22-≤⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧≤-+--->-->-⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧≤->->m m m m m m a b f a b f 。

讨论函数零点或方程根的个数问题-高考数学专练【方法总结】判断、证明或讨论函数零点个数的方法利用零点存在性定理求解函数热点问题的前提条件为函数图象在区间[a ，b ]上是连续不断的曲线，且f (a )·f (b )<0．①直接法：判断一个零点时，若函数为单调函数，则只需取值证明f (a )·f (b )<0；②分类讨论法：判断几个零点时，需要先结合单调性，确定分类讨论的标准，再利用零点存在性定理，在每个单调区间内取值证明f (a )·f (b )<0．【例题选讲】[例1]已知f (x )＝e －x (ax 2＋x ＋1)．当a >0时，试讨论方程f (x )＝1的解的个数．[破题思路]讨论方程f (x )＝1的解的个数，想到f (x )－1的零点个数，给出f (x )的解析式，用f (x )＝1构造函数，转化为零点问题求解(或分离参数，结合图象求解)．[规范解答]法一：分类讨论法方程f (x )＝1的解的个数即为函数h (x )＝e x －ax 2－x －1(a >0)的零点个数．而h ′(x )＝e x －2ax －1，设H (x )＝e x －2ax －1，则H ′(x )＝e x －2a ．令H ′(x )>0，解得x >ln 2a ；令H ′(x )<0，解得x <ln 2a ，所以h ′(x )在(－∞，ln 2a )上单调递减，在(ln 2a ，＋∞)上单调递增．所以h ′(x )min ＝h ′(ln 2a )＝2a －2a ln 2a －1．设m ＝2a ，g (m )＝m －m ln m －1(m >0)，则g ′(m )＝1－(1＋ln m )＝－ln m ，令g ′(m )<0，得m >1；令g ′(m )>0，得0<m <1，所以g (m )在(1，＋∞)上单调递减，在(0，1)上单调递增，所以g (m )max ＝g (1)＝0，即h ′(x )min ≤0(当m ＝1即a ＝12时取等号)．①当a ＝12时，h ′(x )min ＝0，则h ′(x )≥0恒成立．所以h (x )在R 上单调递增，故此时h (x )只有一个零点．②当a >12时，ln 2a >0，h ′(x )min ＝h ′(ln 2a )<0，又h ′(x )在(－∞，ln 2a )上单调递减，在(ln 2a ，＋∞)上单调递增，又h ′(0)＝0，则存在x 1>0使得h ′(x 1)＝0，这时h (x )在(－∞，0)上单调递增，在(0，x 1)上单调递减，在(x 1，＋∞)上单调递增．所以h (x 1)<h (0)＝0，又h (0)＝0，所以此时h (x )有两个零点．③当0<a <12时，ln 2a <0，h ′(x )min ＝h ′(ln 2a )<0，又h ′(x )在(－∞，ln 2a )上单调递减，在(ln 2a ，＋∞)上单调递增，又h ′(0)＝0，则存在x 2<0使得h ′(x 2)＝0．这时h (x )在(－∞，x 2)上单调递增，在(x 2，0)上单调递减，在(0，＋∞)上单调递增，所以h (x 2)>h (0)＝0，h (0)＝0，所以此时f (x )有两个零点．综上，当a ＝12时，方程f (x )＝1只有一个解；当a ≠12且a >0时，方程f (x )＝1有两个解．法二：分离参数法方程f (x )＝1的解的个数即方程e x －ax 2－x －1＝0(a >0)的解的个数，方程可化为ax 2＝e x －x －1．当x ＝0时，方程为0＝e 0－0－1，显然成立，所以x ＝0为方程的解．当x ≠0时，分离参数可得a ＝e x －x －1x2(x ≠0)．设函数p (x )＝e x －x －1x 2(x ≠0)，则p ′(x )＝(e x －x －1)′·x 2－(x 2)′·(e x －x －1)(x 2)2＝e x (x －2)＋x ＋2x 3．记q (x )＝e x (x －2)＋x ＋2，则q ′(x )＝e x (x －1)＋1．记t (x )＝q ′(x )＝e x (x －1)＋1，则t ′(x )＝x e x ．显然当x <0时，t ′(x )<0，函数t (x )单调递减；当x >0时，t ′(x )>0，函数t (x )单调递增．所以t (x )>t (0)＝e 0(0－1)＋1＝0，即q ′(x )>0，所以函数q (x )单调递增．而q (0)＝e 0(0－2)＋0＋2＝0，所以当x <0时，q (x )<0，即p ′(x )>0，函数p (x )单调递增；当x >0时，q (x )>0，即p ′(x )>0，函数p (x )单调递增．而当x →0时，p (x →0＝e x －12xx →0＝(e x －1)′(2x )′x →0＝e x 2x →0＝12(洛必达法则)，当x →－∞时，p (x －∞＝e x －12xx →－∞＝0，故函数p (x )的图象如图所示．作出直线y ＝a ．显然，当a ＝12时，直线y ＝a 与函数p (x )的图象无交点，即方程e x －ax 2－x －1＝0只有一个解x ＝0；当a ≠12且a >0时，直线y ＝a 与函数p (x )的图象有一个交点(x 0，a )，即方程e x －ax 2－x －1＝0有两个解x ＝0或x ＝x 0．综上，当a ＝12时，方程f (x )＝1只有一个解；当a ≠12且a >0时，方程f (x )＝1有两个解．[注]部分题型利用分离法处理时，会出现“0”型的代数式，这是大学数学中的不定式问题，解决这类问题有效的方法就是洛必达法则．法则1若函数f (x )和g (x )满足下列条件：(1)li m x →a f (x )＝0及li m x →a g (x )＝0；(2)在点a 的去心邻域内，f (x )与g (x )可导且g ′(x )≠0；(3)li m x →af ′(x )g ′(x )＝l ．那么li m x →a f (x )g (x )＝li m x →a f ′(x )g ′(x )＝l ．法则2若函数f (x )和g (x )满足下列条件：(1)li m x →a f (x )＝∞及li m x →a g (x )＝∞；(2)在点a 的去心邻域内，f (x )与g (x )可导且g ′(x )≠0；(3)li m x →a f ′(x )g ′(x )＝l ．那么li m x →af (x )g (x )＝li m x →a f ′(x )g ′(x )＝l ．[题后悟通]对于已知参数的取值范围，讨论零点个数的情况，借助导数解决的办法有两个．(1)分离参数：得到参数与超越函数式相等的式子，借助导数分析函数的单调区间和极值，结合图形，由参数函数与超越函数的交点个数，易得交点个数的分类情况；(2)构造新函数：求导，用单调性判定函数的取值情况，再根据零点存在定理证明零点的存在性．[例2]设函数f (x )＝x 22－k ln x ，k >0．(1)求f (x )的单调区间和极值；(2)证明：若f (x )存在零点，则f (x )在区间(1，e]上仅有一个零点．[规范解答](1)函数的定义域为(0，＋∞)．由f (x )＝x 22－k ln x (k >0)，得f ′(x )＝x －k x ＝x 2－kx．由f ′(x )＝0，解得x ＝k (负值舍去)．f ′(x )与f (x )在区间(0，＋∞)上随x 的变化情况如下表：x (0，k )k (k ，＋∞)f ′(x )－0＋f (x )↘k (1－ln k )2↗所以，f (x )的单调递减区间是(0，k )，单调递增区间是(k ，＋∞)．f (x )在x ＝k 处取得极小值f (k )＝k (1－ln k )2，无极大值．(2)由(1)知，f (x )在区间(0，＋∞)上的最小值为f (k )＝k (1－ln k )2．因为f (x )存在零点，所以k (1－ln k )2≤0，从而k ≥e ，当k ＝e 时，f (x )在区间(1，e]上单调递减且f (e)＝0，所以x ＝e 是f (x )在区间(1，e]上的唯一零点；当k >e 时，f (x )在区间(1，e]上单调递减且f (1)＝12>0，f (e)＝e －k 2<0，所以f (x )在区间(1，e]上仅有一个零点．综上可知，若f (x )存在零点，则f (x )在区间(1，e]上仅有一个零点．[例3]已知函数f (x )＝a ln x ＋bx(a ，b ∈R ，a ≠0)的图象在点(1，f (1))处的切线斜率为－a .(1)求f (x )的单调区间；(2)讨论方程f (x )＝1根的个数．[规范解答](1)函数f (x )的定义域为(0，＋∞)，f ′(x )＝a －b －a ln xx 2，由f ′(1)＝a －b ＝－a ，得b ＝2a ，所以f (x )＝a (ln x ＋2)x ，f ′(x )＝－a (ln x ＋1)x2.当a >0时，由f ′(x )>0，得0<x <1e ；由f ′(x )<0，得x >1e .当a <0时，由f ′(x )>0，得x >1e ；由f ′(x )<0，得0<x <1e.综上，当a >0时，f (x )a <0时，f (x )的单调递增(2)f (x )＝1，即方程a ln x ＋2a x ＝1，即方程1a ＝ln x ＋2x ，构造函数h (x )＝ln x ＋2x，则h ′(x )＝－1＋ln x x 2，令h ′(x )＝0，得x ＝1e ，h ′(x )>0，h ′(x )<0，即h (x )h (x )max ＝ e.h (x )单调递减且h (x )＝ln x ＋2x >0，当x 无限增大时，h (x )无限接近0；h (x )单调递增且当x 无限接近0时，ln x ＋2负无限大，故h (x )负无限大．故当0<1a <e ，即a >1e 时，方程f (x )＝1有两个不等实根，当a ＝1e 时，方程f (x )＝1只有一个实根，当a <0时，方程f (x )＝1只有一个实根．综上可知，当a >1e 时，方程f (x )＝1有两个实根；当a <0或a ＝1e 时，方程f (x )＝1有一个实根；当0<a <1e 时，方程f (x )＝1无实根．[例4]已知函数f (x )＝e x ，x ∈R .(1)若直线y ＝kx 与f (x )的反函数的图象相切，求实数k 的值；(2)若m <0，讨论函数g (x )＝f (x )＋mx 2零点的个数．[规范解答](1)f (x )的反函数为y ＝ln x ，x >0，则y ′＝1x．设切点为(x 0，ln x 0)，则切线斜率为k ＝1x 0＝ln x 0x 0，故x 0＝e ，k ＝1e.(2)函数g (x )＝f (x )＋mx 2的零点的个数即是方程f (x )＋mx 2＝0的实根的个数(当x ＝0时，方程无解)，等价于函数h (x )＝e xx 2(x ≠0)与函数y ＝－m 图象交点的个数．h ′(x )＝e x (x －2)x 3.当x ∈(－∞，0)时，h ′(x )>0，h (x )在(－∞，0)上单调递增；当x ∈(0,2)时，h ′(x )<0，h (x )在(0,2)上单调递减；当x ∈(2，＋∞)时，h ′(x )>0，h (x )在(2，＋∞)上单调递增．∴h (x )的大致图象如图：∴h (x )在(0，＋∞)上的最小值为h (2)＝e 24.∴当－m m －e 24，h (x )＝e xx 2与函数y ＝－m 图象交点的个数为1；当－m ＝e 24，即m ＝－e 24时，函数h (x )＝e xx2与函数y ＝－m 图象交点的个数为2；当－m m ∈－∞，－e 24时，函数h (x )＝e xx 2与函数y ＝－m 图象交点的个数为3.综上所述，当m ∞g (x )有三个零点；当m ＝－e 24时，函数g (x )有两个零点；当m ∈－e 24，0时，函数g (x )有一个零点．[例5]已知函数f (x )＝－x 3＋ax －14，g (x )＝e x －e(e 为自然对数的底数)．(1)若曲线y ＝f (x )在(0，f (0))处的切线与曲线y ＝g (x )在(0，g (0))处的切线互相垂直，求实数a 的值；(2)设函数h (x )x )，f (x )≥g (x )，(x )，f (x )<g (x )，试讨论函数h (x )零点的个数．[规范解答](1)f ′(x )＝－3x 2＋a ，g ′(x )＝e x ，所以f ′(0)＝a ，g ′(0)＝1，由题意，知a ＝－1．(2)易知函数g (x )＝e x －e 在R 上单调递增，仅在x ＝1处有一个零点，且x <1时，g (x )<0，又f ′(x )＝－3x 2＋a ，①当a ≤0时，f ′(x )≤0，f (x )在R f (－1)＝34－a >0，即f (x )在x ≤0时必有一个零点，此时y ＝h (x )有两个零点；②当a >0时，令f ′(x )＝－3x 2＋a ＝0，得两根为x 1＝－a3<0，x 2＝a3>0，则－a3是函数f (x )的一个极小值点，a3是函数f (x )的一个极大值点，而＋－14＝－2a 3a 3－14<0．现在讨论极大值的情况：＋aa 3－14＝2a 3a 3－14，当，即a <34时，函数y ＝f (x )在(0，＋∞)上恒小于零，此时y ＝h (x )有两个零点；当0，即a ＝34时，函数y ＝f (x )在(0，＋∞)上有一个零点x 0＝a 3＝12，此时y ＝h (x )有三个零点；当，即a >34时，函数y ＝f (x )在(0，＋∞)上有两个零点，一个零点小于a3，一个零点大于a 3，若f (1)＝a －54<0，即a <54时，y ＝h (x )有四个零点；若f (1)＝a －54＝0，即a ＝54时，y ＝h (x )有三个零点；若f (1)＝a －54>0，即a >54时，y ＝h (x )有两个零点．综上所述：当a <34或a >54时，y ＝h (x )有两个零点；当a ＝34或a ＝54时，y ＝h (x )有三个零点；当34<a <54时，y ＝h (x )有四个零点．[例6]已知函数f (x )＝12ax 2－(a ＋2)x ＋2ln x (a ∈R )．(1)若a ＝0，求证：f (x )<0；(2)讨论函数f (x )零点的个数．[破题思路](1)当a ＝0时，f (x )＝－2x ＋2ln x (x >0)，f ′(x )＝－2＋2x ＝2(1－x )x，设g (x )＝1－x ，根据g (x )的正负可画出f (x )的图象如图(1)所示．(2)f ′(x )＝(x －1)(ax －2)x (x >0)，令g (x )＝(x －1)(ax －2)，当a ＝0时，由(1)知f (x )没有零点；当a >0时，画g (x )的正负图象时，需分2a ＝1，2a >1，2a <1三种情形进行讨论，再根据极值、端点走势可画出f (x )的图象，如图(2)(3)(4)所示；当a <0时，同理可得图(5)．综上，易得f (x )的零点个数．[规范解答](1)当a ＝0时，f ′(x )＝－2＋2x ＝2(1－x )x，由f ′(x )＝0得x ＝1.当0<x <1时，f ′(x )>0，f (x )在(0,1)上单调递增；当x >1时，f ′(x )<0，f (x )在(1，＋∞)上单调递减．所以f (x )≤f (x )max ＝f (1)＝－2，即f (x )<0.(2)由题意知f ′(x )＝ax －(a ＋2)＋2x ＝ax 2－(a ＋2)x ＋2x ＝(x －1)(ax －2)x (x >0)，当a ＝0时，由第(1)问可得函数f (x )没有零点．当a >0时，①当2a ＝1，即a ＝2时，f ′(x )≥0恒成立，仅当x ＝1时取等号，函数f (x )在(0，＋∞)上单调递增，又f (1)＝－12a －2＝－12×2－2<0，当x →＋∞时，f (x )→＋∞，所以函数f (x )在区间(0，＋∞)上有一个零点．②当2a >1，即0<a <2时，若0<x <1或x >2a ，则f ′(x )>0，f (x )在(0,1)若1<x <2a ，则f ′(x )<0，f (x )又f (1)＝12a －(a ＋2)＋2ln 1＝－12a －2<0，则f (1)<0，当x →＋∞时，f (x )→＋∞，所以函数f (x )③当0<2a <1，即a >2时，若0<x <2a x >1，则f ′(x )>0，f (x )(1，＋∞)上单调递增；若2a<x <1，则f ′(x )<0，f (x )因为a >2，所以＝－2a －2＋2ln 2a <－2a －2＋2ln 1<0，又x →＋∞时，f (x )→＋∞，所以函数f (x )仅有一个零点在区间(1，＋∞)上．当2a<0，即a <0时，若0<x <1，f ′(x )>0，f (x )在(0,1)上单调递增；若x >1，f ′(x )<0，f (x )在(1，＋∞)上单调递减．当x →0时，f (x )→－∞，当x →＋∞时，f (x )→－∞，又f (1)＝12a －(a ＋2)＋2ln 1＝－12a －2＝－a －42.当f (1)＝－a －42>0，即a <－4时，函数f (x )有两个零点；当f (1)＝－a －42＝0，即a ＝－4时，函数f (x )有一个零点；当f (1)＝－a －42<0，即－4<a <0时，函数f (x )没有零点．综上，当a <－4时，函数f (x )有两个零点；当a ＝－4时，函数f (x )有一个零点；当－4<a ≤0时，函数f (x )没有零点；当a >0时，函数f (x )有一个零点．[题后悟通]解决本题运用了分类、分层的思想方法，表面看起来非常繁杂．但若能用好“双图法”处理问题，可回避不等式f ′(x )>0与f ′(x )<0的求解，特别是含有参数的不等式求解，而从f ′(x )抽象出与其正负有关的函数g (x )，画图更方便，观察图形即可直观快速地得到f (x )的单调性，大大提高解题的效率．[对点训练]1．(2018·全国Ⅱ)已知函数f (x )＝13x 3－a (x 2＋x ＋1)．(1)若a ＝3，求f (x )的单调区间；(2)证明：f (x )只有一个零点．1．解析(1)当a ＝3时，f (x )＝13x 3－3x 2－3x －3，f ′(x )＝x 2－6x －3．令f ′(x )＝0解得x ＝3－23或x ＝3＋2 3.当x ∈(－∞，3－23)∪(3＋23，＋∞)时，f ′(x )>0；当x ∈(3－23，3＋23)时，f ′(x )<0.故f (x )在(－∞，3－23)，(3＋23，＋∞)单调递增，在(3－23，3＋23)单调递减．(2)由于x 2＋x ＋1>0，所以f (x )＝0等价于x 3x 2＋x ＋1－3a ＝0.设g (x )＝x 3x 2＋x ＋1－3a ，则g ′(x )＝x 2（x 2＋2x ＋3）（x 2＋x ＋1）2≥0，仅当x ＝0时g ′(x )＝0，所以g (x )在(－∞，＋∞)单调递增．故g (x )至多有一个零点，从而f (x )至多有一个零点．又f (3a －1)＝－6a 2＋2a －13＝－－16<0，f (3a ＋1)＝13>0，故f (x )有一个零点．综上，f (x )只有一个零点．2．已知函数f (x )＝e x －1，g (x )＝x ＋x ，其中e 是自然对数的底数，e ＝2.71828…．(1)证明：函数h (x )＝f (x )－g (x )在区间(1，2)上有零点；(2)求方程f (x )＝g (x )的根的个数，并说明理由．2．解析(1)由题意可得h (x )＝f (x )－g (x )＝e x －1－x －x ，所以h (1)＝e －3＜0，h (2)＝e 2－3－2＞0，所以h (1)h (2)＜0，所以函数h (x )在区间(1，2)上有零点．(2)由(1)可知h (x )＝f (x )－g (x )＝e x －1－x －x ．由g (x )＝x ＋x 知x ∈[0，＋∞)，而h (0)＝0，则x ＝0为h (x )的一个零点．又h (x )在(1，2)内有零点，因此h (x )在[0，＋∞)上至少有两个零点．h ′(x )＝e x －12x －12－1，记φ(x )＝e x －12x －12－1，则φ′(x )＝e x ＋14x －32．当x ∈(0，＋∞)时，φ′(x )＞0，因此φ(x )在(0，＋∞)上单调递增，易知φ(x )在(0，＋∞)内只有一个零点，则h (x )在[0，＋∞)上有且只有两个零点，所以方程f (x )＝g (x )的根的个数为2．3．设函数f (x )＝ln x ＋mx，m ∈R ．(1)当m ＝e(e 为自然对数的底数)时，求f (x )的极小值；(2)讨论函数g (x )＝f ′(x )－x3零点的个数．3．解析(1)由题设，当m ＝e 时，f (x )＝ln x ＋ex ，则f ′(x )＝x －e x2，∴当x ∈(0，e)时，f ′(x )<0，f (x )在(0，e)上单调递减；当x ∈(e ，＋∞)时，f ′(x )>0，f (x )在(e ，＋∞)上单调递增，∴当x ＝e 时，f (x )取得极小值f (e)＝ln e ＋ee ＝2，∴f (x )的极小值为2．(2)由题设g (x )＝f ′(x )－x 3＝1x －m x 2－x 3(x >0)，令g (x )＝0，得m ＝－133＋x (x >0)．设φ(x )＝－13x 3＋x (x >0)，则φ′(x )＝－x 2＋1＝－(x －1)(x ＋1)．当x ∈(0，1)时，φ′(x )>0，φ(x )在(0，1)上单调递增；当x ∈(1，＋∞)时，φ′(x )<0，φ(x )在(1，＋∞)上单调递减．∴x ＝1是φ(x )的唯一极值点，且是极大值点，因此x ＝1也是φ(x )的最大值点，∴φ(x )的最大值为φ(1)＝23．又φ(0)＝0，结合y ＝φ(x )的图象(如图)，可知，①当m >23时，函数g (x )无零点；②当m ＝23时，函数g (x )有且只有一个零点；③当0<m <23时，函数g (x )有两个零点；④当m ≤0时，函数g (x )有且只有一个零点．综上所述，当m >23时，函数g (x )无零点；当m ＝23或m ≤0时，函数g (x )有且只有一个零点；当0<m <23时，函数g (x )有两个零点．4．已知函数f (x )＝ln x ＋1ax －1a，a ∈R 且a ≠0.(1)讨论函数f (x )的单调性；(2)当x ∈1e ，e时，试判断函数g (x )＝(ln x －1)e x ＋x －m 的零点个数．4．解析(1)f ′(x )＝ax －1ax 2(x >0)，当a <0时，f ′(x )>0恒成立，∴函数f (x )在(0，＋∞)上单调递增；当a >0时，由f ′(x )>0，得x >1a ；由f ′(x )<0，得0<x <1a ，∴函数f (x )综上所述，当a <0时，函数f (x )在(0，＋∞)上单调递增；当a >0时，函数f (x )(2)∵当x ∈1e ，e时，函数g (x )＝(ln x －1)e x ＋x －m 的零点，即当x ∈1e ，e时，方程(ln x －1)e x ＋x ＝m 的根．令h (x )＝(ln x －1)e x ＋x ，则h ′(x )ln x －x＋1.由(1)知当a ＝1时，f (x )＝ln x ＋1x －1(1，e)上单调递增，∴当x ∈1e ，e 时，f (x )≥f (1)＝0．∴1x＋ln x －1≥0在x ∈1e ，e 上恒成立．∴h ′(x )ln x －x ＋1≥0＋1>0，∴h (x )＝(ln x －1)e x ＋x 在x ∈1e ，e上单调递增．∴h (x )min ＝2e 1e ＋1e，h (x )max ＝e.∴当m <－2e 1e＋1e或m >e 时，函数g (x )在1e ，e 上没有零点；当－2e 1e＋1e≤m ≤e 时，函数g (x )在1e ，e 上有且只有一个零点．5．设函数f (x )＝e x －2a －ln(x ＋a )，a ∈R ，e 为自然对数的底数．(1)若a >0，且函数f (x )在区间[0，＋∞)内单调递增，求实数a 的取值范围；(2)若0<a <23，试判断函数f (x )的零点个数．5．解析(1)∵函数f (x )在[0，＋∞)内单调递增，∴f ′(x )＝e x －1x ＋a≥0在[0，＋∞)内恒成立．即a ≥e －x －x 在[0，＋∞)内恒成立．记g (x )＝e －x －x ，则g ′(x )＝－e －x －1<0恒成立，∴g (x )在区间[0，＋∞)内单调递减，∴g (x )≤g (0)＝1，∴a ≥1，即实数a 的取值范围为[1，＋∞)．(2)∵0<a <23，f ′(x )＝e x －1x ＋a (x >－a )，记h (x )＝f ′(x )，则h ′(x )＝e x ＋1(x ＋a )2>0，知f ′(x )在区间(－a ，＋∞)内单调递增．又∵f ′(0)＝1－1a <0，f ′(1)＝e －1a ＋1>0，∴f ′(x )在区间(－a ，＋∞)内存在唯一的零点x 0，即f ′(x 0)＝0e x－1x 0＋a ＝0，于是0e x＝1x 0＋a，x 0＝－ln (x 0＋a )．当－a <x <x 0时，f ′(x )<0，f (x )单调递减；当x >x 0时，f ′(x )>0，f (x )单调递增．∴f (x )min ＝f (x 0)＝0e x －2a －ln (x 0＋a )＝1x 0＋a －2a ＋x 0＝x 0＋a ＋1x 0＋a－3a ≥2－3a ，当且仅当x 0＋a ＝1时，取等号．由0<a <23，得2－3a >0，∴f (x )min ＝f (x 0)>0，即函数f (x )没有零点．6．已知函数f (x )＝ln x －12ax 2(a ∈R )．(1)若f (x )在点(2，f (2))处的切线与直线2x ＋y ＋2＝0垂直，求实数a 的值；(2)求函数f (x )的单调区间；(3)讨论函数f (x )在区间[1，e 2]上零点的个数．6．解析(1)f (x )＝ln x －12ax 2的定义域为(0，＋∞)，f ′(x )＝1x －ax ＝1－ax 2x ，则f ′(2)＝1－4a2．因为直线2x ＋y ＋2＝0的斜率为－2，所以(－2)×1－4a2＝－1，解得a ＝0．(2)f ′(x )＝1－ax 2x ，x ∈(0，＋∞)，当a ≤0时，f ′(x )>0，所以f (x )在(0，＋∞)上单调递增；当a >0′(x )>0，>0得0<x <aa ；由f ′(x )<0得x >aa ，所以f (x )综上所述：当a ≤0时，f (x )的单调递增区间为(0，＋∞)；当a >0时，f (x )(3)由(2)可知，(ⅰ)当a <0时，f (x )在[1，e 2]上单调递增，而f (1)＝－12a >0，故f (x )在[1，e 2]上没有零点．(ⅱ)当a ＝0时，f (x )在[1，e 2]上单调递增，而f (1)＝－12a ＝0，故f (x )在[1，e 2]上有一个零点．(ⅲ)当a >0时，①若aa ≤1，即a ≥1时，f (x )在[1，e 2]上单调递减．因为f (1)＝－12a <0，所以f (x )在[1，e 2]上没有零点．②若1<aa ≤e 2，即1e 4≤a <1时，f (x )在1，a a 上单调递增，在a a ，e 2上单调递减，而f (1)＝－12a <0，f ＝－12ln a －12，f (e 2)＝2－12a e 4，若f＝－12ln a－12<0，即a>1e时，f(x)在[1，e2]上没有零点；若f＝－12ln a－12＝0，即a＝1e时，f(x)在[1，e2]上有一个零点；若f＝－12ln a－12>0，即a<1e时，由f(e2)＝2－12a e4>0，得a<4e4，此时，f(x)在[1，e2]上有一个零点；由f(e2)＝2－12a e4≤0，得a≥4e4，此时，f(x)在[1，e2]上有两个零点；③若aa≥e2，即0<a≤1e4时，f(x)在[1，e2]上单调递增，因为f(1)＝－12a<0，f(e2)＝2－12a e4>0，所以f(x)在[1，e2]上有一个零点．综上所述：当a<0或a>1e时，f(x)在[1，e2]上没有零点；当0≤a<4e4或a＝1e时，f(x)在[1，e2]上有一个零点；当4e4≤a<1e时，f(x)在[1，e2]上有两个零点．。

方程根知识点总结1. 一元一次方程的根一元一次方程的一般形式为ax+b=0，其中a和b是已知的实数，x是未知数。

求解一元一次方程的根的基本步骤是通过移项和化简，将方程化为x=的形式。

例如，对于方程2x+1=0，我们首先将式子中的1移项变为2x=-1，然后再将2移项变为x=-1/2，得到方程的根x=-1/2。

2. 一元二次方程的根一元二次方程的一般形式为ax^2+bx+c=0，其中a、b和c是已知的实数，x是未知数。

一元二次方程的根可以通过求解二次方程的根公式来得到。

对于一元二次方程ax^2+bx+c=0，它的根可以通过求解x= (-b±√(b²-4ac))/(2a)来得到。

根的个数取决于b²-4ac的大小，当b²-4ac>0时，方程有两个实数根；当b²-4ac=0时，方程有一个实数根；当b²-4ac<0时，方程没有实数根，但可能有复数根。

3. 一元高次方程的根一元高次方程的根是一个更加广泛的概念，它包括了一元一次方程和一元二次方程的根。

一元高次方程的根的求解通常是通过因式分解、配方法、换元法、降次法等方法来得到。

例如，对于一元高次方程x^3+2x^2-5x-6=0，它的根可以通过因式分解或者配方法来得到。

对于一元高次方程的根的求解，学生需要掌握已知根的性质，如根的数量、根的和与积等。

4. 方程根的性质方程根有一些基本的性质，如根的数量、根的性质、根的关系等。

学生需要掌握这些性质，从而更好地求解方程的根。

例如，一元二次方程的根的性质包括：根的和为-x₁/x₂，根的积为c/a。

掌握这些性质对于求解方程的根至关重要。

综上所述，方程根是代数学中一个重要的概念，对于学生来说，掌握方程根的求解方法和性质是学习数学的关键。

通过对方程根的学习与掌握，可以帮助学生提高数学解题的能力，也可以为学生今后学习更高级的数学知识打下坚实的基础。

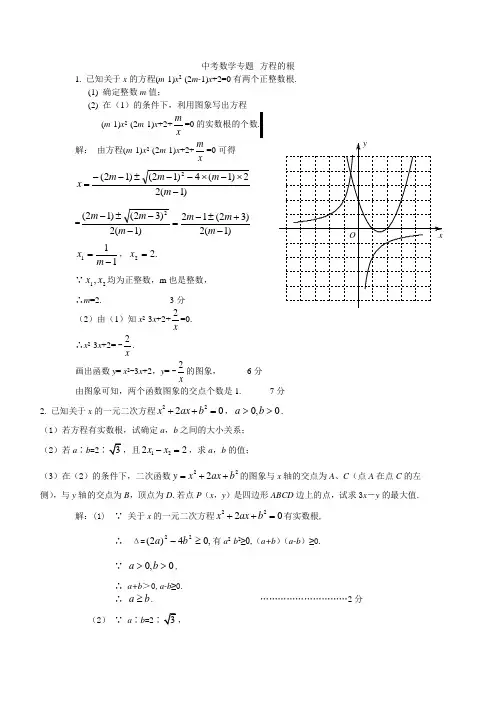
中考数学专题--方程的根1. 已知关于x 的方程(m -1)x 2-(2m-1)x +2=0有两个正整数根.(1) 确定整数m 值；(2) 在（1）的条件下，利用图象写出方程(m -1)x 2-(2m -1)x +2+xm =0的实数根的个数. 解： 由方程(m -1)x 2-(2m -1)x +2+x m =0可得 )1(22)1(4)12()12(2-⨯-⨯--±--=m m m m x =)1(2)32(12)1(2)32()12(2-+±-=--±-m m m m m m 111-=m x ，.22=x ∵21,x x 均为正整数，m 也是整数，∴m =2. ----------3分（2）由（1）知x 2-3x +2+x 2=0. ∴x 2-3x +2= -x2. 画出函数y = x 2-3x +2，y = -x2的图象，---------6分 由图象可知，两个函数图象的交点个数是1. ---------7分 2. 已知关于x 的一元二次方程2220x ax b ++=，0,0>>b a .（1）若方程有实数根，试确定a ，b 之间的大小关系；（2）若a ∶b =2，且1222x x -=，求a ，b 的值；（3）在（2）的条件下，二次函数222y x ax b =++的图象与x 轴的交点为A 、C （点A 在点C 的左侧），与y 轴的交点为B ，顶点为D .若点P （x ，y ）是四边形ABCD 边上的点，试求3x －y 的最大值.解：(1) ∵ 关于x 的一元二次方程2220x ax b ++=有实数根,∴ Δ=,04)2(22≥-b a 有a 2-b 2≥0,（a+b ）（a-b ）≥0.∵ 0,0>>b a ,∴ a+b ＞0,a-b ≥0.∴ b a ≥. …………………………2分（2） ∵ a ∶b =2∴ 设2,a k b ==(k ＞0).解关于x 的一元二次方程22430x kx k ++=，得 -3x k k =-或.当12,= -3x k x k =-时，由1222x x -=得2k =.当123,= -x k x k =-时，由1222x x -=得25k =-（不合题意，舍去）.∴ 4,a b ==. …………………………5分（3） 当4,a b ==时，二次函数2812y x x =++与x 轴的交点为、C 的交点坐标分别为A （－6，0）、（－2，0），与y 轴交点坐标为（0，12），顶点坐标D 为（－4，－4）.设z ＝3x －y ，则3y x z =-.画出函数2812y x x =++和3y x =的图象，若直线3y x =平行移动时，可以发现当直线经过点C 时符合题意，此时最大z 的值等于－6 ……………7分3. 已知：关于x 的方程2(23)30+-+-=kx k x k .（1）求证：方程总有实数根；（2）当k 取哪些整数时，关于x 的方程2(23)30+-+-=kx k x k 的两个实数根均为负整数？解：（1）分类讨论：若k =0，则此方程为一元一次方程，即033=--x ，∴1-=x 有根，……1分 若k ≠0，则此方程为一元二次方程，∴△=()()934322=---k k k ＞0， …………………………………………2分 ∴方程有两个不相等的实数根，…………………………………………………3分 综上所述，方程总有实数根.（2）∵方程有两个实数根 ∴方程为一元二次方程. ∵利用求根公式()k k x 2932±--=， ………………………………………4分 得132261-=-=kk k x ；12-=x ，……………………………………………5分 ∵方程有两个负整数根 ∴13-k是负整数，即k 是3的约数 ∴k =1±，3±但k =1、3时根不是负整数，∴k =1-、3-.…………………………………7分4. 已知关于x 的一元二次方程22(41)30x m x m m -+++=.（1）求证：无论m 取何实数时，原方程总有两个实数根；（2）若原方程的两个实数根一个大于2，另一个小于7，求m 的取值范围；（3）抛物线22(41)3y x m x m m =-+++与x 轴交于点A 、B ，与y 轴交于点C ，当m 取（2）中符合题意的最小整数时，将此抛物线向上平移n 个单位，使平移后得到的抛物线顶点落在△ABC 的内部（不包括△ABC 的边界），求n 的取值范围（直接写出答案即可） 解：(1)证明： Δ=[]22(41)4(3)m m m -+-+=2441m m ++=2(21)m +∵ 2(21)m +≥0，∴ 无论m 取何实数时，原方程总有两个实数根. ………………2分（2） 解关于x 的一元二次方程22(41)30x m x m m -+++=，得 1231,= x m x m =+. ………………3分由题意得 312,317,7. 2.m m m m +>+>⎧⎧⎨⎨<<⎩⎩或 ………………4分 解得 173m <<. ………………5分 （3）符合题意的n 的取值范围是 91544n <<. ……………7分 5. 已知：关于x 的一元二次方程：22240x mx m -+-=.（1）求证：这个方程有两个不相等的实数根；（2）当抛物线2224y x mx m =-+-与x 轴的交点位于原点的两侧，且到原点的距离相等时，求此抛物线的解析式；（3）将（2）中的抛物线在x 轴下方的部分沿x 轴翻折，其余部分保持能够不变，得到图形C 1,将图形C 1向右平移一个单位,得到图形C 2，当直线y=x b +(b <0)与图形C 2恰有两个公共点时，写出b 的取值范围.（1）证明∵016)4(4)2(22>=---=∆m m ．…………1分∴该方程总有两个不相等的实数根．. ………2分（2）由题意可知y 轴是抛物线的对称轴， ∴02=-m ，解得0=m ．………4分 ∴此抛物线的解析式为42-=x y ．.……5分（3）-3<b <1．………7分6. 已知关于x 的方程 03)13(2=+++x m mx .（1）求证: 不论m 为任何实数, 此方程总有实数根；（2）若抛物线()2313y mx m x =+++与x 轴交于两个不同的整数点，且m 为正整数，试确定此抛物线的解析式；（3）若点P ),(11y x 与Q ),(21y n x +在（2）中抛物线上 (点P 、Q 不重合), 且y 1=y 2, 求代数式81651242121++++n n n x x 的值.解：（1）当m =0时，原方程化为,03=+x 此时方程有实数根 x = -3. 1分当m ≠0时，原方程为一元二次方程.∵()()222311296131m m m m m ∆=+-=-+=-≥0.∴ 此时方程有两个实数根. ………………………………2分综上, 不论m 为任何实数时, 方程 03)13(2=+++x m mx 总有实数根.（2）∵令y =0, 则 mx 2+(3m +1)x +3=0.解得 13x =-，21x m=-. …………………………3分 ∵ 抛物线()2313y mx m x =+++与x 轴交于两个不同的整数点，且m 为正整数， ∴1m =.∴抛物线的解析式为243y x x =++. ………………4分（3）法一：∵点P ),(11y x 与Q ),(21y n x +在抛物线上,∴2211121143,()4()3y x x y x n x n =++=++++.∵,21y y =∴22111143()4()3x x x n x n ++=++++.可得 04221=++n n n x .即 0)42(1=++n x n .∵ 点P , Q 不重合,∴ n ≠0.∴ 124x n =--. …………………………5分∴ 222211114125168(2)265168x x n n n x x n n n ++++=+⋅+++ 22(4)6(4)516824.n n n n n =++--+++= ………………7分。

判别代数方程根的存在性的几种方法摘要：代数方程通常指整式方程，即由多项式组成的方程。

有时也泛指由未知数的代数式所组成的方程，包括整式方程、分式方程和无理方程。

在数学学习中，常常要计算一些代数方程的解，然而在解代数方程时，我们首先就要判断这类方程的解的存在性。

本文从复变函数论、连续函数零点、多项式根的判别式、不动点定理、Kronecker定理方面判别代数方程根的存在性。

总结前人的研究成果，并略作一些整理，使分散的知识点汇聚在一起，以方便阅读。

关键词：代数方程；根；存在性Several methods ofdetermining the existence of Algebraic EquationWang Sheng-feng，College of Mathematics and Computer Science Abstract：Algebraic equations usually mean equations of integral expression, that is composed of polynomial equations. Sometimes it also refers to the unknown algebraic equations, including equation of integral expression, fractional equation and irrational equation. During learning mathematics, often to calculate the number of algebraic equation, but in solving algebraic equations, we must first determine the existence of solutions of these equations. From the theory of complex functions, continuous functions’zero, polynomial root discriminant, fixed point theorem, Kronecker theorem of algebraic equations determine the root of the problem. We summarize previous research results, and slightly up a bit, so that brings together scattered knowledge points to facilitate reading.Key words：Algebraic equations；Root；Existence1 引言中世纪的阿拉伯数学家把代数学看成是解代数方程的学问。