下载文档原格式
导体半导体和绝缘体的能带论解释篇一：嘿，朋友！你知道吗？在神奇的物理世界里，导体、半导体和绝缘体可有着超级有趣的秘密，而能带论就是解开这些秘密的关键钥匙！咱先来说说导体。
你想想看，导体就像是一条畅通无阻的高速公路，电子在上面能自由地奔跑，毫无阻碍。
为啥呢？因为导体的能带结构就决定了这一点！导体的价带和导带是部分重叠的，这意味着电子不需要额外的能量就能轻松地从价带跃迁到导带，然后欢快地流动起来，形成电流。
这难道不神奇吗？就好像你在游乐场里，不需要排队等待，直接就能坐上最刺激的过山车一样！再看看半导体，它就像是一个有点小脾气的家伙。
半导体的价带和导带之间有个能隙，不过这个能隙比较小。
这就像是有一道小门槛，电子要费点劲才能跨过去。
在常温下，只有一小部分电子有足够的能量跨越这个能隙，进入导带参与导电。
这是不是有点像一群小伙伴要翻过一个不太高的墙去探险，只有几个勇敢又有力气的能翻过去？而绝缘体呢，那简直就是一堵高高的围墙！绝缘体的能隙非常大，电子几乎没办法跨越这个巨大的鸿沟。
所以在一般情况下，电流在绝缘体中几乎无法通过，就好像你想翻过一座高耸入云的山峰，那几乎是不可能的事儿！有一次，我和几个物理爱好者朋友一起讨论这个话题。
小李就说：“这导体就像是个热情奔放的舞者，随时都能展现出灵动的舞姿。
”小王接着道：“那半导体岂不是个犹豫不决的孩子，有时候能勇敢地迈出一步，有时候又缩回去了。
”我笑着回应：“哈哈，那绝缘体就是个顽固的老头，把一切都拒之门外！”咱再深入想想，这导体、半导体和绝缘体的能带特性，在我们的日常生活中可有着大用处呢！比如半导体，它被广泛应用在各种电子设备里，像手机、电脑的芯片，不就是利用了半导体的特性嘛！所以啊，通过能带论来理解导体、半导体和绝缘体，就像是打开了一扇通往微观世界的神奇大门。
我们能更清楚地看到物质内部的奥秘，也能更好地利用这些特性来创造更美好的科技生活。
总之，导体、半导体和绝缘体的能带论解释让我们对物质的导电性能有了更深刻的认识，也为我们探索和利用材料的特性提供了有力的理论支持。
绝缘体半导体导体的能带结构差异1. 引言大家好，今天我们要聊聊一个听起来可能有点儿复杂，但其实很有趣的话题——绝缘体、半导体和导体的能带结构差异。
乍一听，这些名词可能让人觉得像是看了一部科学电影的开头，满脑子都是“什么鬼？”，但别担心，我们会把它拆得简单明了，让你轻松懂得透透的。
2. 能带结构的基础知识在我们深入之前，先来了解一下什么是能带结构。
简单来说，能带就是电子在材料中可占据的能量状态。
想象一下，你在一个音乐会上，有些区域人声嘈杂，有些区域却安静得像个图书馆。
能带结构就是这个“音乐会”的场地安排，不同的材料在这个“会场”上，电子可以在不同的区域里“舞动”。
2.1 绝缘体的能带结构好啦，咱们先从绝缘体说起。
绝缘体就像一个不让你进门的高冷明星，里面的电子都懒得动，跟死水一潭似的。
为什么呢？因为在绝缘体中，价带（电子的低能量状态）和导带（电子的高能量状态）之间有着巨大的能量间隙，通常超过4电子伏特（eV）。
这就意味着，电子要想跳到导带去“嗨”，需要付出不少的“门票”，所以绝缘体一般不导电。
你可以想象一下，绝缘体就像一座封闭的大厦，里面的电子们各自待着，不会随便走出门。
2.2 半导体的能带结构接下来是半导体。
半导体就像是一个热情的派对，虽然有些电子在低能量的价带里，但是只要给它们点儿小刺激，比如增加温度或者用光照射，它们就会兴奋地跳到导带。
半导体的能量间隙相对较小，一般在1到3 eV之间，这让电子们能够在适当的条件下“出门”。
所以，半导体被广泛应用在电子设备上，比如手机、电脑这些日常必备的高科技产品上。
3. 导体的能带结构最后，我们来看看导体。
导体就像一个随时欢迎你的舞会，电子们随时都可以在价带和导带之间自由移动。
它们的能带结构非常特别，价带和导带之间没有能量间隙，或者间隙极小，几乎可以忽略不计。
这就意味着，只要你一给导体通电，电子们就会如同鱼儿入水，尽情游动，发出“咔咔咔”的导电声音。
3.1 导体的日常例子我们日常生活中常见的导体材料有铜、铝等。
导体半导体和绝缘体的能带论解释导体、半导体和绝缘体的能带论解释在我们日常生活和现代科技中，导体、半导体和绝缘体是非常重要的概念。
从电线中的铜到计算机芯片中的硅，材料的导电性能决定了它们的用途和应用场景。
而要深入理解这些材料的导电特性，能带论是一个关键的理论工具。
让我们先从最基本的概念说起。
在原子物理学中，每个原子都有一系列离散的能级，电子只能占据这些特定的能级。
当大量的原子聚集在一起形成固体时，这些离散的能级会扩展形成能带。
导体之所以能够良好地导电，是因为其能带结构具有一些独特的特征。
在导体中，存在着部分被填满的能带，这被称为导带。
导带中的电子能够在外界电场的作用下自由移动，从而形成电流。
打个比方，想象一个充满人的体育场，导带就像是其中没有坐满人的区域，人们（电子）可以在这个区域内自由移动找到空位。
而且，导体的价带和导带之间通常没有能隙，或者能隙非常小。
这意味着电子很容易从价带跃迁到导带，参与导电过程。
接下来看看半导体。
半导体的能带结构比较特殊。
它的价带是填满的，而导带是空的，但是价带和导带之间存在一个相对较小的能隙，也被称为禁带。
在常温下，只有少量的电子能够获得足够的能量从价带跃迁到导带，从而导电。
但如果我们对半导体进行掺杂，也就是有意地引入一些杂质原子，就能够显著改变其导电性能。
比如，在纯净的半导体中掺入少量的五价杂质原子，就会形成 N 型半导体；掺入少量的三价杂质原子，则会形成 P 型半导体。
以硅为例，它是一种常见的半导体材料。
在纯净的硅中，电子很难跃过禁带进入导带。
但当掺入磷等五价元素时，磷原子在硅晶体中会多出一个自由电子，这个电子很容易在电场作用下移动，从而增加了导电性。
而当掺入硼等三价元素时，会形成空穴，周围的电子可以填补这个空穴，从而也能实现导电。
绝缘体与导体和半导体有很大的不同。
绝缘体的价带是填满的，并且其价带和导带之间存在一个非常大的能隙。
这使得在一般条件下，电子几乎无法从价带跃迁到导带，因此绝缘体几乎不能导电。
§5-6 导体、绝缘体与半导体得能带模型尽管所有得固体都包含大量有电子，但有些固体具有很好得电子导电性能,而另一些固体则观察不到任何电子得导电性。
对于固体为什么分为导体、绝缘体与半导体呢?这一基础事实曾长期得不到解释,能带论对这一问题给出了一个理论说明，并由此逐步发展成为有关导体、绝缘体与半导体得现代理论。
晶体中电子有能量本征值分裂成一系列能带,每个能带均由N 个准连续能级组成（N 为晶体原胞数),所以，每个能带可容纳２N 个电子。
晶体电子从最低能级开始填充,被电子填满得能带称作满带,被电子部分填充得能带称为不满带,没有电子填充得能带称为空带。
能带论解释固体导电得基本观点就是:满带电子不导电,而不满带中得电子对导电有贡献。
5. 6. 1 满带电子不导电从前面得知识中，已经知道,晶体中电子能量本征值E (k )就是k 得偶函数,则利用(５-５-１1），可以证明v (－k )=-ｖ（k ),即v (k )就是ｋ得奇函数。
一个完全填满得电子能带,电子在能带上得分布,在ｋ空间具有中心对称性，即一个电子处于k 态,其能量为E(k ),则必有另一个与其能量相同得E (－ｋ)=Ｅ(k ）电子处于-ｋ态。
当不存在外电场时，尽管对于每一个电子来证,都带有一定得电流-e v ,但就是ｋ态与－k 态得电子电流-e ｖ(ｋ)与-e v (-k )正好一对对相互抵消,所以说没有宏观电流。
当存在外电场或外磁场时,电子在能带中分布具有k 空间中心对称性得情况仍不会改变。
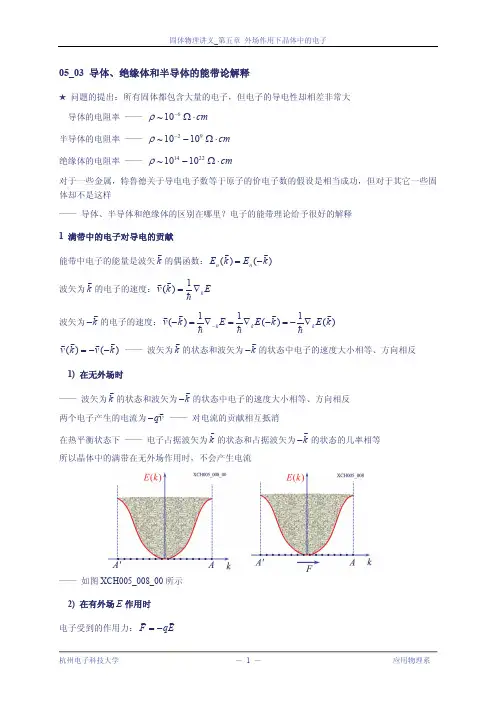
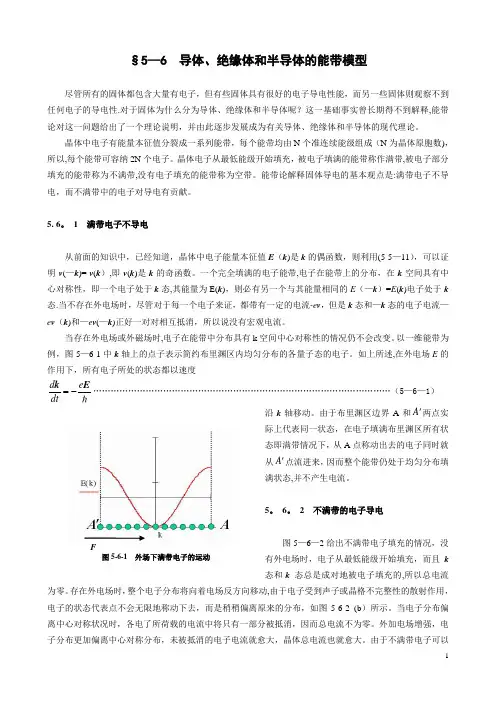
以一维能带为例,图5-６-1中k 轴上得点子表示简约布里渊区内均匀分布得各量子态得电子。
如上所述，在外电场E 得作用下,所有电子所处得状态都以速度…………………………………………………………………………………………(5-6-1）沿k 轴移动。
由于布里渊区边界A 与两点实际上代表同一状态,在电子填满布里渊区所有状态即满带情况下,从Ａ点称动出去得电子同时就从点流进来,因而整个能带仍处于均匀分布填满状态，并不产生电流。
§5—6 导体、绝缘体和半导体的能带模型尽管所有的固体都包含大量有电子，但有些固体具有很好的电子导电性能，而另一些固体则观察不到任何电子的导电性.对于固体为什么分为导体、绝缘体和半导体呢？这一基础事实曾长期得不到解释,能带论对这一问题给出了一个理论说明，并由此逐步发展成为有关导体、绝缘体和半导体的现代理论。
晶体中电子有能量本征值分裂成一系列能带，每个能带均由N 个准连续能级组成（N 为晶体原胞数)，所以,每个能带可容纳2N 个电子。
晶体电子从最低能级开始填充，被电子填满的能带称作满带,被电子部分填充的能带称为不满带,没有电子填充的能带称为空带。
能带论解释固体导电的基本观点是:满带电子不导电，而不满带中的电子对导电有贡献。
5. 6。
1 满带电子不导电从前面的知识中，已经知道，晶体中电子能量本征值E （k )是k 的偶函数，则利用(5-5—11），可以证明v (—k )=-v (k ）,即v (k )是k 的奇函数。
一个完全填满的电子能带,电子在能带上的分布，在k 空间具有中心对称性，即一个电子处于k 态,其能量为E(k )，则必有另一个与其能量相同的E （—k ）=E (k )电子处于-k 态.当不存在外电场时，尽管对于每一个电子来证，都带有一定的电流-e v ，但是k 态和—k 态的电子电流—e v （k )和—e v (—k )正好一对对相互抵消，所以说没有宏观电流。
当存在外电场或外磁场时,电子在能带中分布具有k 空间中心对称性的情况仍不会改变。
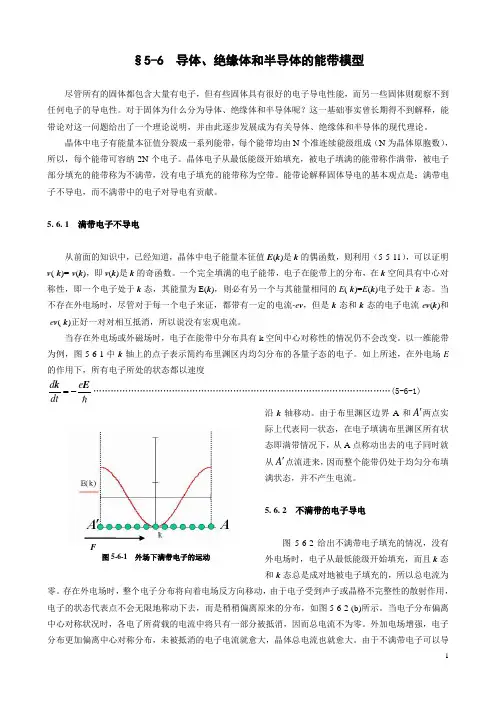
以一维能带为例，图5—6-1中k 轴上的点子表示简约布里渊区内均匀分布的各量子态的电子。
如上所述,在外电场E 的作用下，所有电子所处的状态都以速度d e dt=-k E …………………………………………………………………………………………（5—6—1） 沿k 轴移动。
由于布里渊区边界A 和A '两点实际上代表同一状态，在电子填满布里渊区所有状态即满带情况下，从A 点称动出去的电子同时就从A '点流进来，因而整个能带仍处于均匀分布填满状态,并不产生电流。
§ 5-6 导体、绝缘体和半导体的能带模型
尽管所有的固体都包含大量有电子，但有些固体具有很好的电子导电性能，而另一些固体则观察不到任何电子的导电性。
对于固体为什么分为导体、绝缘体和半导体呢？这一基础事实曾长期得不到解释，能带论对这一问题给出了一个理论说明，并由此逐步发展成为有关导体、绝缘体和半导体的现代理论。
每个能带均由N个准连续能级组成(N为晶体原胞数)，所以，每个能
带可容纳2N个电子。
晶体电子从最低能级开始填充，被电子填满的能带称作满带，被电子
部分填充的能带称为不满带，没有电子填充的能带称为空带。
能带论解释固体导电的基本观点是：满带电子不导电，而不满带中的电子对导电有贡献。
5. 6. 1 满带电子不导电
从前面的知识中，已经知道，晶体中电子能量本征值E(k)是k的偶函数，则利用(5-5-11)，可以证明
k空间具有中心对
v(-k)=-v(k)，即v(k)是k的奇函数。
一个完全填满的电子能带，电子在能带上的分布，在
称性，即一个电子处于k态，其能量为E(k)，则必有另一个与其能量相同的E(-k)=E(k)电子处于-k态。
当
不存在外电场时，尽管对于每一个电子来证，都带有一定的电流-ev,但是k态和-k态的电子电流-ev(k)和
-ev(-k)正好一对对相互抵消，所以说没有宏观电流。
当存在外电场或外磁场时，电子在能带中分布具有k空间中心对称性的情况仍不会改变。
以一维能带
为例，图5-6-1中k轴上的点子表示简约布里渊区内均匀分布的各量子态的电子。
如上所述，在外电场
的作用下，所有电子所处的状态都以速度
dk dt eE
h
(5-6-1)
沿k轴移动。
由于布里渊区边界A和A两点实
F
图5-6-1外场下满带电子的运动
际上代表同一状态，在电子填满布里渊区所有状
态即满带情况下，从A点称动出去的电子同时就
从A点流进来，因而整个能带仍处于均匀分布填
满状态,
5. 6.
2
并不产生电流。
不满带的电子导电
5-6-2给出不满带电子填充的情况，没有
外电场时，电子从最低能级开始填充，而且k态
和-k态总是成对地被电子填充的，所以总电流为
零。
存在外电场时，整个电子分布将向着电场反方向移动, 由于电子受到声子或晶格不完整性的散射作用,
5-6-2 (b)所示。
当电子分布偏离中心对称状况时，各电了所荷载的电流中将只有一部分被抵消，因而总电流不为零。
外加电场增强，电子
电子的状态代表点不会无限地称动下去，而是稍稍偏离原来的分布，如图
分布更加偏离中心对称分布，未被抵消的电子电流就愈大，晶体总电流也就愈大。
由于不满带电子可以导晶体中电子有能量本征值分裂成一系列能带,
电，因而将不满带称作导带。
5. 6. 3导体、绝缘体与半导体的能带模型
我们可以通过考察晶体电子填充能带的状况来判断晶体的导电性能。
如果晶体电子恰好填满了最低的
一系列能带，能量再高的能带都是空的，而且最高的满带与最低的空带之间存在一个很宽的禁带（如
E g 5eV ）,那么，这种晶体就是绝缘体。
图5-6-3 （C）给出了这种晶体电子填充能带的状况。
如果晶体
的能带中，除了满带外，还有不满带，那么，这种晶体就是金属。
半导体晶体电子填充能带的状况与绝缘
体的没有本质不同，只是最高满带与最低空带之间的带隙较窄（为E g 1~3eV ),这样，在T=0K 时,
晶体是不导电的，在T M OK时，将有部分电子从满带顶部被激发到空带的底部，使最高的满带及最低的空
带都变成部分填充电子的不满带，晶体因而具有一定的导电能力。
图5-6-3画出导体、绝缘体与半导体电
子填充能带的模型。
碱金属（如锂、钠、钾等）及贵金属（如金、银等）每个原胞只含一个价电子。
当N个这类原子结合
成固体时，N个电子就占据着能带中N个最低的量子态。
其余N个能量较高的量子态则是空的，即能带
是半满的（每个能带可容纳2N个电子）。
因此，所有碱金属、贵金属晶体都是导体。
惰性气体原子的电子
壳层是闭合的，电子数是偶数，所以总是将最低能带填满，而较高的能带空着。
这些元素形成的固体是绝
缘体的典型例子。
金刚石、硅和锗的原胞含有两个四价原子，故每个原胞含有八个价电子，正好填满价电
子所形成的能带。
所以，这些纯净的晶体在T=0K时是绝缘体。
碱土金属（如钙、锶、钡等）的每个原胞
含有两个s电子，正好填满s带，碱土金属晶体似乎应该是绝缘体，实际上却是良导体。
原因在于s带与上面的能带发生交叠（如图5-6-3 （b）的情况），2N个s电子在未完全填满s带时，就开始填充上面那个能带，造成两个不满带。
因此，碱土金属晶体是导体。
五族元素铋、锑、砷等的晶体，每个原胞内含有两
个电子，所以原胞内含有偶数个电子。
这些晶体也应该是绝缘体，但它们却有一定的导电性。
原因在于这
些晶体的能带有交叠，只是交叠部分较少，使能对与导电的电子浓度远远小于正常金属中的电子浓度，电
考虑m x m y m z 球形等能面的简单情况，上式变为:
阻率比正常金属大约105倍，因而被称作半金属。
由此可见，若晶体的原胞含有奇数个价电子，这种晶体 必是导体；原胞含有偶数个价电子的晶体， 如果 能带交叠，则晶体是导体或半金属， 如果能带没有交叠,
禁带窄的晶体就是半导体，禁带宽的则是绝缘体。
T^nr
速度v (k)所产生的。
在电场E 的作用下，近满带中所有电子的状态都以式( 5-5-14)的规律变化，空状态也按同样规律变
化。
因而空状态的加速度为
dv(k) dt
5. 6. 4 空穴
满带中如缺了少数电子就会产生一定的导电性，这种近满带的情形在半导体的问题中特别重要。
要描 述近满带中电子的运动，由于涉及到数目很大的电子集体运动，因而在表述上十分不便。
为此，我们引入 空穴的概念，将大量电子的集体运动等价地变为描述少数空穴的概念,
从而大大简化了有关近满带的问题。
为了说明空穴的概念并证明用电子和空穴两种描述方法的等价性，我们不妨假设满带中只有某一个状 态k 未被电子占据，此时能带是不满的，因而应有电流产生，以
j (k)表示。
为计算j (k)，我们假想在空的
k 态中放入一个电子，这个电子的电流等于 -ev (k)。
但是k 态加入这个电子后，能带又成为满带，所以，总 的电流应为
零，从而有：
j(k) [ ev(k)] 0
(5-6-2)
j(k) ev(k)
(5-6-3)
上式表明，当k 态缺少一个电子时，近满带的总电流就如同一个具有正电荷
e 的粒子, 以空状态 k 的电子
(5-6-4)
(0
由于满带顶的电子比较容易受热而激发到导带，因此空状态多位于能带顶附近。
在能带顶附近 负值，为此我们定义空穴有效质量为:
样一个假想的粒子称为空穴。
空穴概念的引入，使得满带顶附近缺少一些电子的问题和导带底有少数电子的问题十分相似。
然而应 该强调指出，我们虽然赋于空穴有效质量、电荷等属性，但它并不是客观存在的一种实物闻子，而只是客
观物质一一电子集体运动的一种等价描述。
正如前面所提到的声子概念一样， 它也不是一个客观物质粒子, 而是晶格中原子集体振动的一种等价描述，我们常把声子、空穴等称为准粒子或元激发。
在固体物理学中 处理多粒子体系的集体运动时常常引入各种元激发，以使多体问题简化。
dv(k) dt
eE m e (k)
(5-6-5)
m e 为
m h k
m e k
(5-6-6)
则有
dv(k) dt
eE m h (k)
(5-6-7)
由上面的讨论我们得到下列结论：当满带顶附近有空状态 k 时，整个能带中的电子运动，以及电流在
外场作用下的变化，完全如同存在一个带正电荷 e ,具有正有效质量 m 、速度v(k)的粒子情况一样，这。
