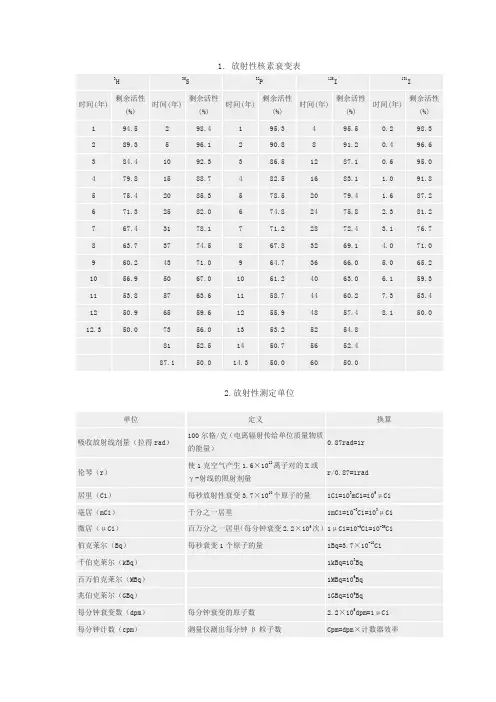
衰变表

Bk
97
(247)
铍（beryllium）
Be
4
9.01
铋（bismuth）
Bi
83
208.98
硼（boron）
B
5
10.81
溴（bromine）
Br
35
79.90
镉（cadmium）
Cd
48
112.41
钙（calcium）
Ca
20
40.08
锎（californium）
Cf
98
(251)
碳（carbon）
1．放射性核素衰变表
3H
35S
32P
125I
131I
时间(年)
剩余活性(%)
时间(年)
剩余活性(%)
时间(年)
剩余活性(%)
时间(年)
剩余活性(%)
时间(年)
剩余活性(%)
1
94.5
2
98.4
1
95.3
4
95.5
0.2
98.3
2
89.3
5
96.1
2
90.8
8
91.2
0.4
96.6
3
84.4
10
92.3
U
92
238.02
钒（vanadium）
V
23
50.94
氙（xenon）
Xe
54
131.29
镒（ytterbium）
Yb
70
173.04
钇（yttrium）
Y
39
88.90
锌（zinc）
Zn
30
65.38

λ: decay constant t: decay time e: base of natural logarithm
25
1、衰变规律
指数衰减规律 N = N0e-t
N0: （t = 0）时放射性原子 核的数目
N: 经过t时间后未发生衰变的放射性原子核 数目
:放射性原子核衰变常数（单位时间内一个原 子核衰变的几率）
子核（基态） （0.0）
射线是什麽？ 射线就是高能量的光子：几百keV-MeV 量级 衰变发生由于原子核能量态高，从高能态向低能态跃
迁，在这个过程中发射 射线，原子核能态降低。 射线是高能量的电磁辐射—— 光子
21
衰变特点：
1.从原子核中发射出光子 2.常常在 或 衰变后核子从激发态退激时发生 3.产生的射线能量离散 4.可以通过测量光子能量来区分母体的核素类别
5
放射性来源于原子核的衰变：
不稳定的核素
衰变
稳定的核素
• 原子核自发地放射出某种粒子或射线的现象，称为放射性。
• 放射性不受物理、化学等环境条件的影响，是原子核的内在
特征。
6
射线在电场中的偏转
： 在电/磁场中偏转，与带正电荷离子流相同； ： 在电/磁场中偏转，与带负电荷粒子流相同； ： 在电/磁场中不偏转，电中性。
T1
2
ln 2
0.639
半衰期是放射性原子核的重要特征常数之一
不同放射性核有不同的半衰期
27
3. 平均寿命τ
放射性原子核的每一个原子核生存时间的平均值
有的核在 t 0 时刻就衰变了
有的核在 t 时才衰变
所有核的总寿命： 0 Ntdt
t N 0e t dt
0
1

元素半衰期清单计算公式在核物理学中，半衰期是指某种放射性元素衰变到其原始数量的一半所需的时间。

半衰期是放射性元素衰变速率的重要参数，对于研究核物理和放射性同位素的应用具有重要意义。

在本文中，我们将介绍一些常见的放射性元素的半衰期清单，并探讨计算半衰期的公式。

首先，让我们来看一下一些常见的放射性元素及其半衰期：1. 钍-232（Th-232），14.05亿年。

2. 铀-238（U-238），4.468亿年。

3. 钍-230（Th-230），75,380年。

4. 铀-235（U-235），703.8万年。

5. 钍-234（Th-234），24.10天。

6. 铀-234（U-234），245,500年。

7. 钍-228（Th-228），1.911年。

8. 铀-233（U-233），159,200年。

以上是一些常见的放射性元素及其半衰期。

这些放射性元素在自然界中广泛存在，它们的半衰期不仅对核物理学研究具有重要意义，也对地质学、考古学和医学等领域有着重要的应用价值。

接下来，让我们来看一下计算放射性元素半衰期的公式。

放射性元素的衰变过程是一个随机的过程，但是可以用指数函数来描述。

放射性元素的衰变速率与其数量成正比，即：N(t) = N0 e^(-λt)。

其中，N(t)是时间t时放射性元素的数量，N0是初始时刻放射性元素的数量，λ是衰变常数，t是时间。

衰变常数λ与半衰期T1/2之间有如下关系：λ = ln(2) / T1/2。

将λ代入放射性元素数量的指数函数中，可以得到放射性元素的数量随时间的变化规律。

通过这个指数函数，我们可以计算出放射性元素的半衰期。

以铀-238（U-238）为例，其半衰期为4.468亿年。

假设初始时刻铀-238的数量为N0，那么在经过一个半衰期后，其数量将减少到N0的一半。

根据指数函数的表达式，可以得到：N(2T1/2) = N0 e^(-ln(2))。

化简后得到：N(2T1/2) = N0 / 2。

（2-1） （2-2）
②β -衰变: 放射性核素内一个中子转变为 质子并放出β 粒子和中微子的核衰变。 β 粒子是电子，电荷=-1，质量≈0
如 23490Th —— 23491Pa + β + ν （2-3）
AZX —— AZ+1Y + β + ν
（2-4）
③β +衰变: 放射性核素内一个质子转变为 中子并放出β +粒子和中微子的衰变。 β +是正电子，质量≈0，电荷=+1，
反应通式：A1Z1X + A2Z2a – A3Z3b + A4Z4Y A1Z1X(a, b)A4Z4Y
举例见P15.
3、铀核自发裂变的产物
由于铀的自发裂变，产生了原子序数在30 至65之间的200多种放射性核素，其中重 要的集中高产额核素是：90Sr(19.9a), 99Tc(2.12×105a), 137Cs(33a) 和 147Pm(2.26a)
人工放射性元素：指最初用人工方法制得并被鉴定、 命名，没有稳定同位素的元素。周期表中：
元素名称 符号 英文名 原子序数
锝
Tc Technetium 43
钷
Pm Promethium 61
砹
At Astatine
85
超铀元素 TrU Transuranium ≥93
一、锝 Tc Technetium 希腊语 “人造”
二、由加速器生产放射性核素
1945年以前，带电粒子加速器是生产放射性核素的 重要设施。1945年以后，主要用反应堆生产放射 性核素。上世纪60年代以后，由于对各种特殊性 能放射性核素的需要以及加速器技术的发展，由 加速器生产短寿命、缺中子的医用放射性核素又 受到重视。

1Ci=103mCi=1CF口Ci
毫居（mCi）
千分之一居里
1mCi=1O3Ci=103uCi
微居（nCi）
百万分之一居里（每分钟衰变2.2X106次）
1nCi=10-6Ci=10-3MCi
伯克莱尔（Bq）
每秒衰变1个原子的量
1Bq=3.7X10-10Ci
千伯克莱尔（kBq）
1kBq=103Bq
百万伯克莱尔（MBq
P
15
30.94
铂(platium)
Pt
78
195.08
钚(piutonium)
Pu
94
(244)
钋(polonium)
Po
84
(209)
钾(potassium)
K
19
39.09
镨(praseodymium)
Pr
59
140.90
钜(promethium)
Pm
61
(145)
镤(protactinium)
Ge
32
72.59
金(gold)
Au
79
196.96
铪(hafnium)
Hf
72
178.49
氦(helium)
He
2
4.00
钦(holmium)
Ho
67
164.93
氢(hydrogen)
H
1
1.00
铟1(indium)
In
49
114.82
碘(iodine)
I
53
126.90
铱(iridium)
Ir
77பைடு நூலகம்
58
140.12

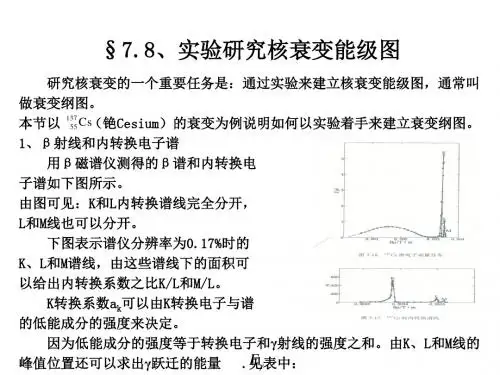
⼆、β衰变原⼦核⾃发地放射出β粒⼦（电⼦）或俘获⼀个轨道电⼦⽽发⽣的转变，称为β衰变。

主要有三种⽅式：β¯衰变、β+衰变和轨道电⼦俘获。

在β衰变中，原⼦核的质量数不变，只是电荷数改变了⼀个单位。

β衰变的半衰期在10秒到10年之间，发射出粒⼦的能量最⼤为⼏兆电⼦伏。

1、β衰变的主要⽅式 （1）β¯衰变，原⼦核⾃发地放射出⼀个电⼦的核转变过程。

⼀般表⽰为：AZ X→AZ+1Y + e¯； 原⼦序数为Z的核素放射出电⼦后，原⼦序数变为（Z+1）的新核素，在元素周期表中的位置右移⼀格，这就是β¯衰变的位移定则。

（2）β+衰变，原⼦核⾃发地放射出⼀个正电⼦的核转变过程。

⼀般表⽰为：AZ X→AZ-1Y + e+； 经β+衰变以后，新核素在在元素周期表中的位置左移⼀格，称为β+衰变的位移定则。

（3）轨道电⼦俘获，原⼦核俘获⼀个核外电⼦，转变成新核素的过程。

⼀般表⽰为：AZ X + e¯→AZ-1Y； 由于核外K壳层的电⼦距离原⼦核最近，被原⼦核俘获的⼏率最⼤，因此，轨道电⼦俘获常称为K俘获。

同样有L俘获、M俘获等，⽤符号EC表⽰。

通过K俘获形成的新核素，在元素周期表中的位置左移⼀格。

例如：74Be + e¯→ 73Li 其中：式中X和Y分别代表母核和⼦核，A和Z是母核质量数（核⼦数）和电荷数（质⼦数），e¯、e+为电⼦和正电⼦。

2、β衰变的机制 传统理论认为，β衰变中放出的电⼦并不是原⼦核中固有的，⽽是在衰变过程中产⽣的，如同光⼦是原⼦从⼀个激发态跃迁到另⼀个状态时产⽣的⼀样。

费⽶曾经指出，β¯衰变的本质是原⼦核内⼀个中⼦变为质⼦，β+衰变核和EC的本质是⼀个质⼦变为中⼦。

⽽中⼦和质⼦可视为核⼦的两个不同状态，它们之间的转换相当于⼀个量⼦态到另⼀个量⼦态的跃迁，在跃迁过程中放出电⼦和中微⼦（ν），它们事先并不存在于核内。

(2)α 衰变：放射性元素放出 α 粒子的衰变叫作 α 衰变． (3)β 衰变：放射性元素放出 β 粒子的衰变叫作 β 衰变． 2．(1)衰变规律：原子核衰变时，衰变前后的电荷数和 质量数都守恒． (2)衰变方程：α 衰变：AZX→AZ－－24Y＋24He； β 衰变：AZX→Z＋A1Y＋－0 1e.
个质子结合得比较紧密，有时会作为一个整体从较大的原子核中抛
射出来，这就是放射元素的_α_衰___变___现象；原子核里虽没有电子， 但核内的___中__子___可转化成质子和电子，产生的电子从核内发射出 来，这就是__β_衰__变___．
(4)γ 射线产生的本质：原子核的能量只能取一系列不连续数
值，当原子核发生 α 衰变、β 衰变后，新核往往处于高能级．这时
2．公式．
N
余＝N
原21Tt ，m
余＝m
1 t 原2T
式中 N 原、m 原表示衰变前的放射性元素的原子数或质量，N 余、
m 余表示衰变后尚未发生衰变的放射性元素的原子数或质量，t 表示
衰变时间，T 表示半衰期．
注：半衰期由放射性元素的原子核内部本身的因素决定，跟原子
所处的物理状态(如压强、温度、环境)或化学状态(如单质、化合物)
放射性元素的衰变
1．原子核的衰变． (1)原子核的衰变：原子核放出 α 粒子或 β 粒子，由于 _核__电__荷__数_ 变 了 ， 它 在 周 期 表 中 的 位 置 变 了 ， 变 成 另 一 种 ___原__子__核_．这种变化称为原子核的___衰__变___． (2)衰变规律：原子核衰变时，衰变前后的电荷数和质 量数都___守__恒___． α 衰变：质量数减少 4，电荷数减少 2，衰变方程为：AZ
解析：原子核的衰变是由原子核内部因素决定 的，与一般外界环境无关．原子核的衰变有一定的 速率，每隔一定的时间即半衰期，原子核就衰变了 总数的一半．不同种类的原子核，其半衰期也不 同．若开始时原子核数目为 N0，经时间 t 剩下的原 子核数目为 N，半衰期为 T，则有如下关系式：N＝ N012Tt .若能测定出 N 与 N0 的比值．则就可求出时间 t 值，依此公式就可测定地质年代、生物年代或考察 出土文物存在年代等．

6
二、基本衰变类型
1. 衰变
+ +
+
++
+
+
+ +
放射性母核
238U → 234Th + 4He + Q 粒子得到大部分衰变能， 粒子含2个质子，
2个中子
238U4He + 234Th
从母核中射出 的4He原子核
7
AX AY 4 Z X ZY -2
α衰变表达式：
元素周期表 左移2格
A Z
X
21
α 衰变 β+ 衰变
β- 衰变 衰变
22
第二节 衰变纲图
Decay scheme用以综合反映某核素放射性衰变的主要特征和数的示意图
23
第三节 衰变的基本规律
➢ 对于由大量原子组成的放射源，每个原子核都可能发生衰变，但不是所 有原子在同一时刻都发生衰变，某一时刻仅有极少数原子发生衰变。放 射性核素衰变是随机的、自发的按一定的速率进行，各种放射性核素都 有自己特有的衰变速度。放射性核素原子随时间而呈指数规律减少，其 表达式为： N=N0e-λt
λ: decay constant t: decay time e: base of natural logarithm
24
1、衰变规律
指数衰减规律 N = N0e-t
N0: （t = 0）时放射性原子 核的数目
N: 经过t时间后未发生衰变的放射性原子核 数目
:放射性原子核衰变常数（单位时间内一个原 子核衰变的几率）
正电子衰变 137N → 136C + β+ + υ + 1.190MeV
β射线本质是高速运动的电子流

2.6 min .
3、衰变纲图的建立
∵β谱的最大能量为1176KeV
正好等于低能成分的最大能量514KeV和γ射线的能量661.6KeV之和。
∴高能成分的 跃迁是在用母核 15357Cs
至子核
137 56
Ba
的基态之间的跃迁。
低能成分的 跃迁是在母核 15357Cs 到
137 56
下图表示谱仪分辨率为0.17%时的
K、L和M谱线，由这些谱线下的面积可
以给出内转换系数之比K/L和M/L。
K转换系数ak可以由K转换电子与谱 的低能成分的强度来决定。
因为低能成分的强度等于转换电子和γ射线的强度之和。由K、L和M线的
峰值位置还可以求出γ跃迁的能量 .见E表中：
内转换系数的理论值见上表，由表所列结果可见，分支比K/L的实验值
与M4的理论值很好的符合，所以断定此跃迁的多极性是M4，另外，从 ak 的
实验值与理论值的比较也得出M4的结论。
β谱的组成： 低能部分，强度高 高能部分，强度低
高能成分的动量谱分布如下图的黑点所 示，其纵坐标标尺放大了1000倍。
高能成分中的低能部分被高强度的低能 成分和内转换电子所掩盖，所以无法测出。 经β谱的分解获得高低能成分的强度之比约 为7:93。
实验值：
Texp

ln 2
r

[
(1

)]ln
2

T1 2
(1
)
2.6 60 (1 0.12) 1.75102 s
其中:

K
L
M


K
(
K L
1
M L
) /( K ) L

用辽大教辅
考名牌大学
【解析】 (1)设238U 衰变为206Pb 经过 x 次 α 衰变和 y 次 92 82 β 衰变．由质量数守恒和电荷数守恒可得 238＝206＋4x① 92＝82＋2x－y② 联立①②解得 x＝8，y＝6 即一共经过 8 次 α 衰变和 6 次 β 衰变．


用辽大教辅
考名牌大学
思考讨论 在 α 和 β 衰变中，新核的质量数与原来的核的质量数有 什么关系？相对于原来的核在周期表中的位置，新核在周期 表中的位置应该向前移还是向后移？要移动几位？
提示：在 α 衰变中新核的质量数比原来的核的质量数少 4，相对于原来的核在周期表中的位置，新核在周期表中的位 置将向前移动两位，每经过一次 α 衰变，质量数减少 4，核电 荷数减少 2，在 β 衰变中新核的核电荷数增加 1，原子序数增 加 1，质量数不变，在元素周期表中的位置向后移动 1 位.
232 Th→208Pb＋64He＋4－0e 90 82 2 1

用辽大教辅
考名牌大学
【解析】 本题主要考查对衰变规律的应用和计算能力． 解法一：由于 β 衰变不会引起质量数的减少，故可先根 据质量数的减少确定 α 衰变的次数， 因为每进行一次 α 衰变， 232－208 质量数减 4，所以 α 衰变的次数为：x＝ 次＝6 次 4 再结合核电荷数的变化情况和衰变规律来判断 β 衰变的 次数.6 次 α 衰变，电荷数减少 2×6＝12 个，而每进行一次 β 衰变，电荷数增加 1，所以 β 衰变的次数为：y＝[12－(90－ 82)]次＝4 次．

用辽大教辅
考名牌大学
要点 2 半衰期 1．半衰期的理解：半衰期是表示放射性元素衰变快慢的 物理量，同一放射元素具有的衰变速率一定，不同元素半衰 期不同，有的差别很大．

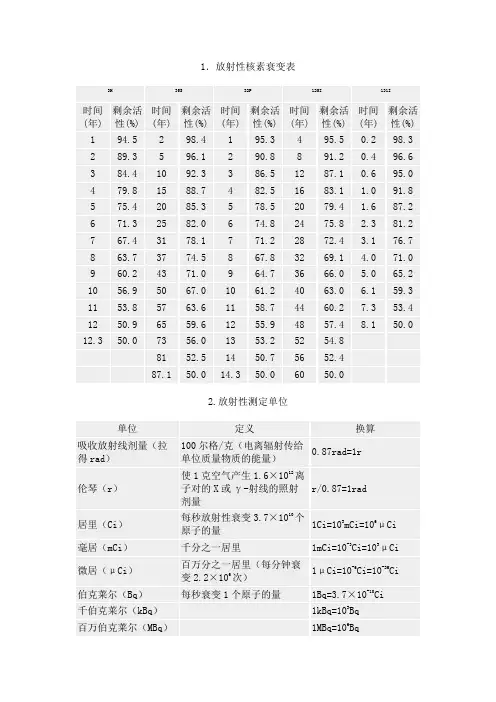
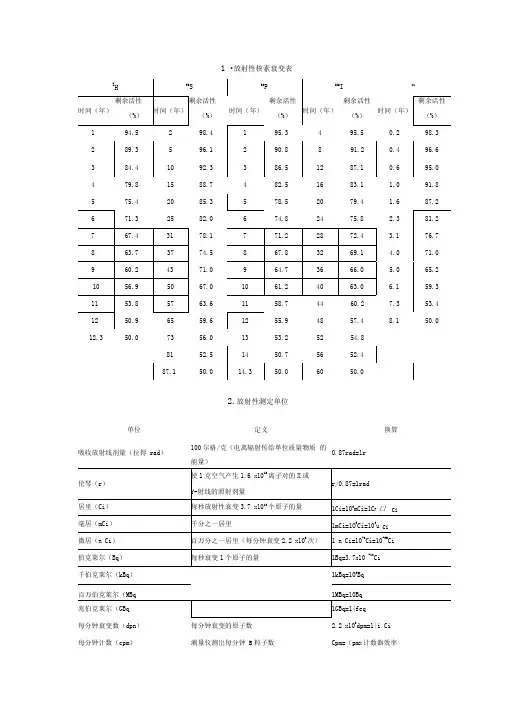
1．放射性核素衰变表3H 35S 32P 125I 131I时间(年) 剩余活性(%)时间(年)剩余活性(%)时间(年)剩余活性(%)时间(年)剩余活性(%)时间(年)剩余活性(%)1 94.52 98.4 1 95.34 95.5 0.2 98.32 89.3 5 96.1 2 90.8 8 91.2 0.4 96.63 84.4 10 92.3 3 86.5 12 87.1 0.6 95.04 79.8 15 88.7 4 82.5 16 83.1 1.0 91.85 75.4 20 85.3 5 78.5 20 79.4 1.6 87.26 71.3 25 82.0 6 74.8 24 75.8 2.3 81.27 67.4 31 78.1 7 71.2 28 72.4 3.1 76.78 63.7 37 74.5 8 67.8 32 69.1 4.0 71.09 60.2 43 71.0 9 64.7 36 66.0 5.0 65.210 56.9 50 67.0 10 61.2 40 63.0 6.1 59.311 53.8 57 63.6 11 58.7 44 60.2 7.3 53.412 50.9 65 59.6 12 55.9 48 57.4 8.1 50.0 12.3 50.0 73 56.0 13 53.2 52 54.881 52.5 14 50.7 56 52.487.1 50.0 14.3 50.0 60 50.02.放射性测定单位单位定义换算吸收放射线剂量（拉得rad）100尔格/克（电离辐射传给单位质量物质的能量）0.87rad=1r伦琴（r）使1克空气产生1.6×1012离子对的X或γ-射线的照射剂量r/0.87=1rad居里（Ci）每秒放射性衰变3.7×1010个原子的量1Ci=103mCi=106μCi毫居（mCi）千分之一居里1mCi=10-3Ci=103μCi微居（μCi）百万分之一居里（每分钟衰变2.2×106次）1μCi=10-6Ci=10-3M Ci伯克莱尔（Bq）每秒衰变1个原子的量1Bq=3.7×10-10Ci 千伯克莱尔（kBq）1kBq=103Bq百万伯克莱尔（MBq）1MBq=106Bq兆伯克莱尔（GBq）1GBq=109Bq每分钟衰变数（dpm）每分钟衰变的原子数 2.2×106dpm=1μCi每分钟计数（cpm）测量仪测出每分钟β粒子数Cpm=dpm×计数器效率十一、原子量符号原子序数原子量锕（actinium）Ac 89 227.02铝（aluminium）Al 13 26.98镅（americium）Am 95 (243)锑（antimony）Sb 51 121.75氩（argon）Ar 18 39.94砷（arsenic）As 33 74.92砹（astatine）At 85 (210)钡（barium）Ba 56 137.33锫（berkelium）Bk 97 (247)铍（beryllium）Be 4 9.01铋（bismuth）Bi 83 208.98硼（boron） B 5 10.81溴（bromine）Br 35 79.90镉（cadmium）Cd 48 112.41钙（calcium）Ca 20 40.08锎Cf 98 (251) （californium）碳（carbon） C 6 12.01铈（cerium）Ce 58 140.12铯（cesium）Cs 55 132.90氯（chlorine）Cl 17 35.45铬（chromium）Cr 24 51.99钴（cobalt）Co 27 58.93铜（copper）Cu 29 63.54锔（curium）Cm 96 (247)镝（dysprosium） Dy 66 162.50锿Es 99 (252) （einsteinium）铒（erbium）Er 68 167.26铕（euroqium）Eu 63 151.96镄（fermium）Fm 100 (257)氟（fluorine） F 9 18.99钫（francium）Fr 87 (223)钆（gadolinium） Gd 64 157.52镓（galium）Ga 31 69.72锗（germanium）Ge 32 72.59金（gold）Au 79 196.96铪（hafnium）Hf 72 178.49氦（helium）He 2 4.00钬（holmium）Ho 67 164.93氢（hydrogen）H 1 1.00铟（indium）In 49 114.82碘（iodine）I 53 126.90铱（iridium）Ir 77 192.22铁（iron）Fe 26 55.84氪（krypton）Kr 36 83.80镧（lanthanum）La 57 139.90铹（Lawrencium） Lr 103 (260)铅（lead）Pb 82 207.2锂（lithium）Li 3 6.94镥（lutetium）Lu 71 174.96镁（Magnesium）Mg 12 24.30锰（manganse）Mn 25 54.93钔Md 101 (258) （mendelevium）汞（molybdenum） Hg 80 200.59钼（molybdenum） Mo 42 95.94钕（neodymium）Nd 60 144.24氖（neon）Ne 10 20.17镎（neptunium）Np 93 237.04镍（nickel）Ni 28 58.69铌（niobium）Nb 41 92.00氮（nitrogen）N 7 14.00锘（nobelium）No 102 (259)锇（osmium）Os 76 190.2氧（oxygen）O 8 15.99钯（palladium）Pd 46 106.42磷（phosphorus） P 15 30.94铂（platium）Pt 78 195.08钚（piutonium）Pu 94 (244)钋（polonium）Po 84 (209)钾（potassium）K 19 39.09镨Pr 59 140.90 （praseodymium）钜（promethium） Pm 61 (145)镤Pa 91 231.03 （protactinium）镭（radium）Ra 88 226.02氡（radon）Rn 86 (222)铼（rhenium）Re 75 186.20铑（rhodium）Rh 45 102.90铷（rubidium）Rb 37 85.46钌（ruthenium）Ru 44 101.07钐（samarium）Sm 62 150.36钪（scandium）Sc 21 44.95硒（sillicon）Se 34 78.96硅（sillicon）Si 14 28.08银（sliver）Ag 47 107.86钠（sodium）Na 11 22.98锶（strontium）Sr 38 87.62硫（sulfur）S 16 32.06钽（tantalum）Ta 73 180.94锝（technetium） Tc 43 (98)碲（tellurium）Te 52 127.60铽（terbium）Tb 65 158.92铊（thallium）Tl 81 204.38钍（thorium）Th 90 232.03锡（tin）Sn 50 118.69铥（thulium）Tm 69 168.93钛（titanium）Ti 22 47.88钨（tungsten）W 74 183.85 unhilhexium (Unh) 106 (263) unnilpentium (Unp) 105 (262) unnilquadium (Unq) 104 (261) unnilseptium (Uns) 107 (262)铀（uranium）U 92 238.02钒（vanadium）V 23 50.94氙（xenon）Xe 54 131.29镒（ytterbium）Yb 70 173.04钇（yttrium）Y 39 88.90锌（zinc）Zn 30 65.38锆（zirconium）Zn 40 91.22 圆括号中的数字是该元素最稳定的同位素的质量数。

原子核衰变是指原子核内部发生变化，从而释放出放射性粒子的过程。

这个过程是不可逆的，因此可以用一些参数来表征原子核衰变的快慢。

本文将介绍一些常见的参数，并举例说明它们的应用。

一、半衰期半衰期是指在一定时间内，放射性物质衰变一半所需的时间。

例如，铀-238的半衰期是45. 7亿年，这意味着在45.7亿年后，铀-238的数量会减少一半。

半衰期越长，说明放射性物质衰变越慢，反之亦然。

二、衰变常数衰变常数是指单位时间内放射性物质衰变的概率。

它与半衰期之间存在以下关系式：λ=l n2/t1/2。

其中，λ为衰变常数，t1/2为半衰期。

例如，铀-238的衰变常数为1.52×10^-10年^-1，这意味着每年铀-238会衰变1.52×10^-10的比例。

三、放射性能量释放放射性物质衰变时会释放出能量，这个能量可以用来表征放射性物质衰变的强弱。

例如，放射性同位素碘-131的能量释放为364keV，而钴-60的能量释放为1.17MeV和1.33MeV。

可以看出，钴-60的能量释放比碘-131大很多，因此钴-60的放射性更强。

四、放射性衰变方式放射性物质衰变的方式有α衰变、β衰变、γ衰变等。

其中，α衰变是指放射性核子释放出一个α粒子，β衰变是指放射性核子释放出一个β粒子，γ衰变是指放射性核子释放出一个γ光子。

不同的衰变方式会对放射性物质的性质产生影响。

例如，α粒子的能量释放比β粒子大很多，因此α衰变的放射性更强。

五、放射性毒性放射性物质的毒性是指它对人体健康的危害程度。

放射性物质的毒性与它的放射性强度、放射性衰变方式、放射性能量释放等因素有关。

例如，镭-226的放射性强度很高，它可以通过α衰变释放出高能量的α粒子，因此对人体的伤害很大。

总之，以上这些参数可以用来表征放射性物质衰变的快慢、强弱、方式、毒性等方面。

在实际应用中，人们可以根据这些参数来评估放射性物质对人体健康的危害程度，从而采取相应的防护措施。