人教版高中物理必修2：《重力势能》

三、重力做的功与重力势能的关系
WG = EP1 − E P 2
= −( EP 2 − EP1 ) = −∆E P
结论： 结论： 当物体由高处运动到低处 高处运动到低处时 重力做正功 ①当物体由高处运动到低处时，重力做正功 ），重力势能减少（ 重力势能减少 （WG > 0），重力势能减少（ EP1 > E P 2 ）； 当物体由低处运动到高处 低处运动到高处时 重力做负功 ②当物体由低处运动到高处时，重力做负功 ），重力势能增加（ 重力势能增加 （WG < 0），重力势能增加（ E P1 < E P 2 ）。
下列关于重力势能的说法， 2．下列关于重力势能的说法，正确的是 AB
A．重力做功只跟物体所处的初末位置有关，与 ．重力做功只跟物体所处的初末位置有关， 物体实际经过的路径无关 B．重力势能的变化，只跟重力做功有关，和其 ．重力势能的变化，只跟重力做功有关， 他力做功多少无关 C．重力势能是矢量，在地球表面以上为正，在 ．重力势能是矢量，在地球表面以上为正， 地球表面以下为负 D．重力势能的变化量等于重力对物体做的功 ．
二、重力势能
E P = mgh
物体的重力势能等于它所受重力与所处高度 的乘积。 的乘积。 重力势能是机械能的一种具体形式。 重力势能是机械能的一种具体形式。 关于重力势能的几点说明： 关于重力势能的几点说明： 重力势能的几点说明
①重力势能是标量，单位是焦耳 重力势能是标量，单位是焦耳——J。 标量 焦耳 。 ②重力势能的大小依赖于参考面，因此，具有相 重力势能的大小依赖于参考面，因此，具有相 对性，是个不定值！ 对性，是个不定值！ ③物体在参考面之上，其重力势能为正值；在参 物体在参考面之上 其重力势能为正值； 正值 考面之下 其重力势能为负值 在参考面上， 负值； 考面之下，其重力势能为负值；在参考面上，其 重力势能为零。 重力势能为零。 ④比较重力势能的大小，要考虑正负，并且必须选 比较重力势能的大小，要考虑正负，并且必须选 择同一个参考面！ 择同一个参考面！ ⑤重力势能是物体和地球组成的“系统”所共有的！ 重力势能是物体和地球组成的“系统” 共有的！ ⑥

2. 标矢性： 标量
3. 单位： 焦耳
4. 功能关系： WG = Ep1 － Ep2 = -ΔEP
P60 图7.4—4 重力做正功，重力势能减少；
P60图7.4—5 克服重力做功，重力势能增加；[z x x k
学科网]
5. 重力势能的相对性 脑筋急转弯
[z x x k 学科网]
例：如图，质量为1 kg的小球，从桌面以上h1=1.2m的A 点落到地面的B点，桌面高h2=0.8m．请按要求填写下 表．(g=10m/s2)
（2）设挺举过程用了1s，张国政 在短时间内爆发出的功率有多大？
恐惧
挑战
征服
雪崩
攀岩
பைடு நூலகம்过山车
高中物理课件
灿若寒星整理制作
4 重力势能
一、知识回顾
1. 重力势能： 受重力作用的物体具有的
与它的高度有关的能量.
“蓄势待发”
2. 相关因素：经验物: 体的质量越大，高度越大，重力势能就越大。
美国内华达州亚利桑那 陨石坑。
这个陨石坑是5万年前，一颗直径 约为30～50m的铁质流星撞击地面 的结果。这颗流星重约500 t、速 度达到20km/s，爆炸力相当于 20000 t梯恩梯(TNT)，超过美国轰 炸日本广岛那颗原子弹的一千倍。
h1
h2
over
h3
on
h4
under
•注意: 势能的正、负不是表示方向。 而是用来表示大小的。 状态量
北京时间8月19日凌晨，雅典（ 2004年）奥运会男子举 重69公斤级比赛在雅典尼凯亚奥林匹克举重馆结束，中 国选手张国政以抓举160公斤，挺举187.5公斤，总成绩 347.5公斤获得金牌。
（1）在抓举过程中 杠铃的重力 势能变化了多少？

1. 定义: 物体由于被举高而具有的能量 E =
p减 EpA-EpB
2. 表达式: Ep=mgh
Ep的变化量 E = E -E
p减
pA
pB
与什么有关？ m=1kg
3. 单位： 焦耳(J)
4. 标矢性： 标量，状态量。
EpA=8J A
EpA= 4J
注意: ①Ep是个相对值，先要选取参考平面。
②Ep有正负，表示大小。
放起来，那么人至少做功(
A．n(n－1)mgh
1
B. n(n－1)mgh
2
C．n(n＋1)mgh
1
D. n(n＋1)mgh
2
B
)
【典例3】如图6所示，有一质量为m、长为L的均匀金属链条，一
半长度在光滑斜面上，斜面倾角为θ，另一半长度沿竖直方向下垂
在空中，当链条从静止开始释放后链条滑动，以斜面顶点为重力势
）
课堂练习
【练习4】如图所示，质量为m的物体用轻绳AB悬挂于天花板上。现用水
平向左的力F拉动轻绳的中点O，使物体静止于图示位置，此时力F的大小
小于mg。若保持力F的大小不变，沿顺时针方向缓慢转动力F到竖直向上的
过程中，下列说法正确的是（
D
）
A．OA段轻绳的张力FOA逐渐变大
B．物体受到的合力增大
C．轻绳中点O的位置升高
发生形变的物体能够对外做功 , 则说此物体具有能量
原长
x
发生弹性形变的竹竿
能够对人做功
F弹
发生弹性形变的弹簧
能够对球做功
三、弹性势能(elastic potential energe)
1.定义: 发生弹性形变的物体拥有的一种势能
①势能由相互作用的两物体共同拥有。

《重力势能》知识全解【教学目标】1．通过不同路径重力做功的分析，归纳出重力做功与路径无关的特点。

2．理解重力势能的表达式。

通过重力做功与重力势能变化的关系体会功能关系。

3．知道重力势能的大小与参考平面的选取有关，即重力势能具有相对性，但重力势能的变化量与参考平面的选取无关。

4．了解弹性势能的决定因素。

【内容解析】1．什么是弹性势能？发生弹性形变的物体的各部分之间，由于有弹力的相互作用，也具有势能，这种势能叫做弹性势能。

可见，物体具有弹性势能的条件是发生了弹性形变。

卷紧的发条、拉长或压缩的弹簧、拉开的弓、正在击球的网球拍、撑杆运动员手中弯曲的杆，等等，都发生了弹性形变，都具有弹性势能。

2．研究弹性势能的出发点弹性势能与重力势能都是物体凭借其位置而具有的能。

在讨论重力势能的时候，我们从重力做功的分析入手。

同样，在讨论弹性势能的时候，则要从弹力做功的分析入手，弹力做功应是我们研究弹性势能的出发点。

3．弹性势能的表达式可能与哪些物理量有关呢？（1）可能与弹簧被拉伸（或压缩）的长度有关。

这是因为，与重力势能相类比，重力势能与物体被举起（或下降）的高度有关，所以弹性势能很可能与弹簧被拉伸（或压缩）的长度有关。

重力势能与高度成正比，但是弹性势能与弹簧被拉伸（或压缩）的长度则不一定成正比，在地球表面附近可认为重力不随高度变化，而弹力在弹簧形变过程中则是变力。

（2）可能与弹簧的劲度系数有关。

这是因为，不同弹簧的“软硬”程度不同，即劲度系数不同，使弹簧发生相同长度的形变所需做的功也不相同。

4．弹性势能与拉力做功的关系当弹簧的长度为原长时，我们设它的弹性势能为0，弹簧被拉长或缩短后就具有了弹性势能。

我们研究弹簧被拉长的情况，那么弹簧的弹性势能应该与拉力所做的功相等。

可见，研究弹性势能的表达式，只需研究拉力做功的表达式。

5．如何计算拉力所做的功？在拉伸弹簧的过程中，拉力是随弹簧的形变量的变化而变化的，拉力还因弹簧的不同而不同。

课后作业
P66 1、4
谢谢
课堂小结
特点：跟起点和终点的 位置有关,跟路径无关
WG=mgh=mgh1-mgh2
重力势能
Ep=mgh 标量 相对性 系统性
重力做功
关系
WG = Ep1 － Ep2
课后探究
如果重力做的功与路径有关，即对应于同 样的起点和终点，重力对同一物体所做的功， 随物体运动路径的不同而不同，我们还能把 mgh叫做物体的重力势能吗？为什么？
A
A
A
mg B
l θ mg B
mg
B
h h1
h2
课堂探究
如图，质量m=0.5kg的小球，从桌面以上h1=1.2m的A点
下落到地面的B点，桌面高h2=0.8m。(g=10m/s2)
A h1
参考 小球在 小球在 下落过程 下落过程小 平面 A点重 B点重 小球重力 球重力势能
力势能 力势能 做的功 的变化
地面 10J
0
10J 减少 10J
h2
桌面 6J
-4J 10J 减少 10J
B
选取不同的参考平面,物体的重力势能的数值不同
对一个确定的过程， WG 和△EP与参考面的选择无关
如果下落时有空气阻力，表格中的数据是否应该改变？
课堂检测
如图，质量为m的足球在地面1的位置被踢出后落到地面3 的位置，在空中达到的最高点2的高度为h。 (1)足球由位置1运动到位置2时，重力做了多少功？足球 克服重力做了多少功？足球的重力势能增加了多少？ (2)足球由位置2运动到位置3时，重力做了多少功？足球 重力势能减少了多少？ (3)足球由位置1运动到位置3时，重力做了多少功？足球 重力势能变化了多少？
=mgh1-mgh2

高中物理（人教版）必修第二册讲义— 重力势能
【学习目标】
1．理解重力势能的概念，会用重力势能的定义进行计算；
2．理解重力势能的变化和重力做功的关系，知道重力做功与路径无关；
3．知道重力势能的相对性；
4．理解弹性势能的概念及其物理意义；
5．知道弹性势能具有相对性。
【学习重点】
重力势能的概念及重力做功跟物体重力势能改变的关系。
A. 0B. - mgLC. - mgLD. - mgL
【答案】D
【解析】
【详解】将链条分成水平部分和竖直部分两段，水平部分的重力势能为零，竖直部分的重心中竖直段的中间，高度为 ，而竖直部分的重力为 ，这样竖直部分的重力势能为
这样链条总的重力势能为 。
故选D。
知识点二、重力势能
1．重力势能
(1)重力势能Ep＝mgh具有相对性，与参考平面的选取有关，其中h是相对参考平面的高度．当物体在参考平面下方h处，重力势能Ep＝－mgh.
(3)比较以上计算结果，说明什么问题？
答案(1)7.84 J23.52 J(2)23.52 J23.52 J
(3)见解析
解析(1)以桌面为参考平面，物体距参考平面的高度为h1＝0.4 m，
因而物体具有的重力势能为
1．做功表达式
WG＝mgh＝mgh1－mgh2，式中h指初位置与末位置的高度差；h1、h2分别指初位置、末位置的高度。
2．做功的正负
物体下降时重力做正功；物体被举高时重力做负功。
3．做功的特点
物体运动时，重力对它做的功只跟它的_起点和终点的位置有关，而跟物体运动的路径无关。
4.重力做功与重力势能变化关系的理解
【变式训练1】如图所示，桌面距地面的高度为0.8 m，一物体(可看成质点)质量为2 kg，放在桌面上方0.4 m的支架上，则：(g取9.8 m/s2)

表达式
EP mgh
三、重力做功与重力势能变化的关系
重力做正功，重力势能减少；重力做负功，重力势能增加
四、重力势能是相对的 ，正负表示大小。
一般不加说明是以地面或题目中的最低点所在的平面作为
零势能参考面。
参考 小球在A 小球在B A到B过程 初重力势能
平面 点重力势 点重力势 小球重力 减去末重力
能
能
做功

h1 地面 10J
0
10J 10J
10J
10J
选取不同的参考平面,物体的重力势能的数值不同
h2 对一个确定的过程，WG和△EP与参考面的选择无关 B
WG=Ep1—Ep2
20
•1、纪律是集体的面貌，集体的声音，集体的动作，集体的表情，集体的信念。 •2、知之者不如好之者，好之者不如乐之者。 •3、反思自我时展示了勇气，自我反思是一切思想的源泉。 •4、在教师手里操着幼年人的命运，便操着民族和人类的命运。一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人。 •5、诚实比一切智谋更好，而且它是智谋的基本条件。 •6、做老师的只要有一次向学生撒谎撒漏了底，就可能使他的全部教育成果从此为之失败。2021年11月2021/11/22021/11/22021/11/211/2/2021 •7、凡为教者必期于达到不须教。对人以诚信，人不欺我;对事以诚信，事无不成。2021/11/22021/11/2November 2, 2021 •8、教育者，非为已往，非为现在，而专为将来。2021/11/22021/11/22021/11/22021/11/2
③势能是状态量、标量．+、–表示大小．
④参考平面的选取是任意的 .
重力势能属于物体和地球组成的系统 .

第四节重力势能1.重力做的功(1)表达式W G＝mgh＝mg(h1－h2)，其中h表示物体起点和终点的高度差，h1、h2分别表示物体起点和终点的高度。

(2)正负物体下降时重力做正功；物体被举高时重力做负功，也可以说成物体克服重力做功。

(3)特点物体运动时，重力对它做的功只跟它的起点和终点的位置有关，而跟物体运动的路径无关。

2．重力势能(1)定义：物体由于位于高处而具有的能量。

(2)大小：等于物体所受重力与所处高度的乘积，表达式为E p＝mgh，其中h 表示物体所在位置的高度。

(3)单位：焦耳，与功的单位相同。

重力势能是标量，正负表示大小。

(4)重力做功与重力势能变化的关系①表达式：W G＝E p1－E p2。

②重力做正功，重力势能减小；重力做负功，重力势能增大。

3．重力势能的相对性和系统性(1)相对性①参考平面：物体的重力势能总是相对于某一水平面来说的，这个水平面叫做参考平面，在参考平面，物体的重力势能取作0。

②重力势能的相对性选择不同的参考平面，物体重力势能的数值是不同的。

对选定的参考平面，上方物体的重力势能是正值，下方物体的重力势能是负值，负值的重力势能，表示物体在这个位置具有的重力势能要比在参考平面上具有的重力势能小。

(2)系统性重力势能是地球与物体所组成的系统共有的。

判一判(1)重力势能E p1＝2 J，E p2＝－3 J，则E p1与E p2方向相反。

()(2)同一物体的重力势能E p1＝2 J，E p2＝－3 J，则E p1>E p2。

()(3)在同一高度的质量不同的两个物体，它们的重力势能一定不同。

()提示：(1)×重力势能是标量，没有方向。

(2)√重力势能为正值，表示物体处于参考平面的上方，为负值表示物体处于参考平面的下方，而同一物体在越高的地方重力势能越大。

(3)×若选定两物体所处的水平面为参考平面，则两物体的重力势能均为0。

说明：(1)重力做功与路径无关，只与始末位置的高度差有关。

前需要先选定0势能参考平面。参考平面（零势能面）的选取是任意的，
通常选择地面作为参考平面。
高度h
重力势能EP
零势能面
A hA > 0 EpA > 0 A
参考平面
正负表示大小
0
0
B hB < 0 EpB < 0 B
【例题3】如图，质量 0.5 kg 的小球，从桌面以上 h1 = 1.2 m 的 A 点落到地面的 B 点，桌面高 h2 = 0.8 m。关于小球的重力势能，请按要求填写下表。( g = 10 m/s2 )
说明： (1)物体由高处运动到低处时，重力做正功，重力势能减少，即 WG>0，则EP1>EP2 ,重力势能减少的数量等于重力做的功。 (2)物体由低处运动到高处时，重力做负功，WG<0，则EP1<EP2 ，重 力势能增加，重力势能增加的数量等于物体克服重力所做的功(重 力做负功)。
例2（P82 第2题）：质量为m的足球在地面1的位置被踢出后落到地面
第八章 机械能守恒定律
第2节 重力势能
新课导入
初中我们已经定性地学习了重 力势能（物体由于被举高而具有的 能量），物体的质量越大、所处的 位置越高，重力势能就越大。这一 节我们来进一步定量地研究重力势 能。你认为重力势能的表达式应该 是怎样的呢？
重力势能的表达式是什么？
一、重力做功
思考：观察小球的运动情况并求出三种情况下小球重力做的功？
（1）与重力做功密切相关 （2）随高度的变化而变化．
A Δh
可见,重力做的功等于mgh这个量的变化.在物理 学中， mgh 是一个由特殊意义的物理量.就用这个 物理量表示物体的重力势能。
B
h1
h2

•谢谢大家！
。2. 一份耕耘，份收获，努力越大，收获越多，奋斗!奋斗!奋斗!3. 让我们将事前的忧虑，换为事前的思考和计划吧！4. 世界上那些最容易的事情中，拖延时间最不费力5. 不管现在有多么艰辛，我们也要做个生活的舞者。6. 奋斗是万物之父。— —陶行知7. 上帝制造人类的时候就把我们制造成不完美的人，我们一辈子努力的过程就是使自己变得更加完美的过程，我们的一切美德都来自于克服自身缺点的奋斗。8. 不要被任何人打乱自己的脚步，因为没有谁会像你一样清楚 和在乎自己的梦想。9. 时间不在于你拥有多少，只在于你怎样使用10. 水只有碰到石头才能碰出浪花。11. 嘲讽是一种力量，消极的力量。赞扬也是一种力量，但却是积极的力量。12. 在我们成长的路上也会遇到一些挫折，一些困 难，那韩智华就是我们的榜样，永不认输，因为我知道挫折过后是一片晴朗的天空，瞧，成功就在挫折背后向我们招手，成功就是在努力的路上，“成功就在努力的路上”！让我们记住这句话，向美好的明天走去。13. 销售世界上 第一号的产品——不是汽车，而是自己。在你成功地把自己推销给别人之前，你必须百分之百的把自己推销给自己。14. 不要匆忙的走过一天又一天，以至于忘记自己从哪里来，要到哪里去。生命不是一场速度赛跑，她不是以数量 而是以质量来计算，知道你停止努力的那一刻，什么也没有真正结束。15. 也许终点只有绝望和失败，但这绝不是停止前行的理由。16. 有事者，事竟成；破釜沉舟，百二秦关终归楚；苦心人，天不负；卧薪尝胆，三千越甲可吞吴。 17. 我颠覆了整个世界。只为了摆正你的倒影18. 好的想法是十分钱一打，真正无价的是能够实现这些想法的人。19. 伤痕是士兵一生的荣耀。20. 只有一条路不能选择——那就是放弃的路；只有一条路不能拒绝——那就是成长的路。 21. 多对自己说“我能行，我一定可以”，只有这样才不会被“不可能”束缚，才能不断超越自我。22. 人生本来就充满未知，一切被安排好反而无味——坚信朝着目标，一步一步地奋斗，就会迈向美好的未来。23. 回避现实的人， 未来将更不理想。24. 空想会想出很多绝妙的主意，但却办不成任何事情。25. 无论什么思想，都不是靠它本身去征服人心，而是靠它的力量；不论靠思想的内容，而是靠那些在历史上某些时期放射出来的生命的光辉。——罗曼·罗 兰《约翰·克利斯朵夫》26. 上帝助自助者。27. 你的爸妈正在为你奋斗，这就是你要努力的理由。28. 有很多人都说：平平淡淡就福，没有努力去拼博，又如何将你的人生保持平淡?又何来幸福?29. 当事情已经发生，不要抱怨，不 要沮丧，笑一笑吧，一切都会过去的。30. 外在压力增加时，就应增强内在的动力。31. 我们每个人都应微笑面对人生，没有了怨言，也就不会有哀愁。一个人有了希望，就会对生活充满信心，只要你用美好的心灵看世界，总是以 乐观的精神面对人生。32. 勇敢的人。——托尔斯泰《袭击》33. 昨天下了雨，今天刮了风，明天太阳就出来了。34. 是的，成功不在于结果，更重要的是过程，只要你努力过，拼搏过，也许结果不一定是最好的那也走过了精彩的过 程，至少，你不会为此而后悔。35. 每一天的努力，以后只有美好的未来。每一天的坚持，换来的是明天的辉煌。36. 青年最要紧的精神，是要与命运奋斗。——恽代英37. 高峰只对攀登它而不是仰望它的人来说才有真正意义。38. 志不可立无可成之事。如无舵之舟，无衔之马，飘荡奔逸，何所底乎？--王守仁39. 拿望远镜看别人，拿放大镜看自己。40. 顽强的毅力可以征服世界上任何一座高峰。——狄更斯41. 士人第一要有志，第二要有识，第三要有恒。— —曾国42. 在我们能掌控和拼搏的时间里，去提升我们生命的质量。43. 我们不是等待未来，我们是创造未来，加油，努力奋斗。44. 人生如画，一笔一足迹，一步一脚印，有的绚丽辉煌，有的却平淡无奇。45. 脚跟立定以后，你必 须拿你的力量和技能，自己奋斗。——萧伯纳46. 一个能从别人的观念来看事情，能了解别人心灵活动的人，永远不必为自己的前途担心。

练习二：将一个物体由A点移动到B点，重力做功（ D ）
A．与运动过程中是否存在阻力有关 B．与物体运动的路径有关 C．与物体所处的运动状态有关 D．与物体运动过程的始、末位置有关
练习三：如图,质量0.5kg的小球,从桌面以上h1=1.2m的A点落到地 面的B点，桌面高h2=0.8m．请按要求填写下表．（g = 10m/s2）
作
业
1.书面作业： 课本第66页 2题、3题
2.课外作业： 试举例说明，实际生活中对重力势能的应用。
谢谢
15、总不能流血就喊痛，怕黑就开灯，想念就联系，疲惫就放空，被孤立就讨好，脆弱就想家，不要被现在而蒙蔽双眼，终究是要长大，最漆黑的那段路终要自己走完。 16、人生在世：可以缺钱，但不能缺德;可以失言，但不能失信;可以倒下，但不能跪下;可以求名，但不能盗名;可以低落，但不能堕落;可以放松，但不能放纵;可以虚荣，但不能虚伪;可以平凡，但 不能平庸;可以浪漫，但不能浪荡;可以生气，但不能生事。 34、心作良田耕不尽，善为至宝用无穷。我们应有纯洁的心灵，去积善为大众。就会获福无边。 37、世间上最美好的爱恋，是为一个人付出时的勇敢，即使因此被伤得体无完肤，也无悔无怨。 19、积极的人在每一次忧患中都看到一个机会，而消极的人则在每个机会中看到了某种忧患。莫找借口失败，只找理由成功。 2、如果放弃太早，你永远都不知道自己会错过什么。 50、生活中的许多事，并不是我们不能做到，而是我们不相信能够做到。 13、不同的人生，有不同的幸福。去发现你所拥有幸运，少抱怨上苍的不公，把握属于自己的幸福。你，我，我们大家都可以经历幸福的人生。 3、起点低怕什么，大不了加倍努力。人生就像一场马拉松比赛，拼的不是起点，而是坚持的耐力和成长的速度。只要努力不止，进步也会不止。 1、这世上，没有谁活得比谁容易，只是有人在呼天抢地，有人在默默努力。 27、一份耕耘，份收获，努力越大，收获越多。 18、自己想要的东西，要么奋力直追，要么干脆放弃。别总是逢人就喋喋不休的表决心或者哀怨不断，做别人茶余饭后的笑点。 3、你特么的看看你现在的样子?还是我爱的那个你么?

高中物理人教版必修2《重力势能》教学设计第一篇：高中物理人教版必修2《重力势能》教学设计§7.4 重力势能本节知识点是人教版高一物理第七章第四节的内容，在此之前，学生已初步认识到处理动力学问题可以从两个方面去思考：1、牛顿运动定律和运动学的相关规律；2、力做功与能量变化之间的关系。

本章节主要是从第二方面着手探究动力学问题。

本节强化的一个思想是从定性到定量地探究重力做功与重力势能变化的关系。

同时本节中重力做功与重力势能的变化之间的关系也是“机械能守恒定律”的必备知识。

本节的讲解思路也为学生学习电势能打下坚实的基础。

一、教学目标: 1.知识与技能1)．理解重力势能的概念，会用重力势能的定义进行计算。

2)．理解重力势能的变化和重力做功的关系，知道重力做功与路径无。

3)．知道重力势能的相对性。

2.过程与方法用所学功的概念推导重力做功与路径的关系，亲身感受知识的建立过程。

3.情感、态度与价值观渗透从对生活中有关物理现象的观察，得到物理结论的方法，激发和培养学生探索自然规律的兴趣。

二、教学重点、难点：重点：重力势能的概念及重力做功跟物体重力势能改变的关系。

难点：重力势能的系统性和相对性。

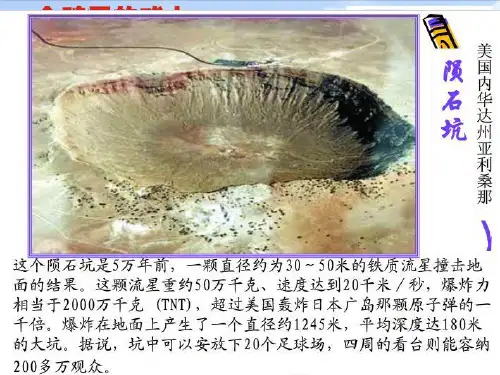
三、教学方法：探究、讲授、讨论、练习四、教学手段：多媒体辅助教学课型：新授课（1课时）五、教学活动：[新课导入](多媒体投影演示．引发学生有意注意，引导学生进入状态)雪崩；陨石坑等等。

师：从刚才的画面中，同学们想到了什么，从做功和能量转化的角度分析问。

生：雪，陨石等物体下落过程中它们受到的重力对它们做了功。

据功和能的关系，既然重力做了功，表明这些物体在没有下落之前具有。

因为一个物体能够对外做功，所以这个物体具有能。

师：由于物体被举高而使物体具有的能量是什么能？生：在初中我们已经学过：物体由于被举高而具有的能量叫重力势能。

师：那么重力势能的大小与什么有关？学生探究：1）同一课本从不同高度下落到自己手上，感觉• • • 2）不同质量的课本从同一高度下落到自己手上，感觉• • • 师生分析：重力势能的大小与物体的高度和质量有关 [新课教学]一、重力的功师：重力做功与什么因素有关呢？我们现在就通过几个例子来探究一下。

变化
桌面 6J -4J
h2 地面 10J
0
B
18
例：
如图，质量5kg的小球，从桌面以上h1=1.2m的 A点落到地面的B点，桌面高h2=0.8m．请按要 求填写下表．(g=10m/s2)
A h1
参考 小球在 小球在 下落过程 平面 A点重 B点重 小球重力
力势能 力势能 势能变化
桌面 6J -4J
以下关于重力势能的说法中，正确的是（ D ）
A.地面上的物体的重力势能一定为零 B.质量大的物体重力势能一定大 C.高处物体的重力势能一定大 D.重力做正功时，物体的重力势能一定变化
桌面距地面0.8m，一物体质量为2kg，放在距桌 面0.4m的支架上．
（1）以地面为零势能位置，计算物体具有的势能， 并计算物体由支架下落到桌面过程中，势能减 少多少？
质量为m的小球，从离桌面H高处由静止下落， 桌面离地面的高度为h，如图所示，若以桌面 为参考面，那么小球落地时的重力势能及整个 过程中重力势能的变化是：( D )
A.mgh，减少mg(H-h)
H
B.mgh，增加mg(H+h)
C.-mgh，增加mg(H-h)
h
D.-mgh，减少mg(H+h)
巩固练习：
小结
一、重力势能：物体由于举高而具有 的能。表达式: Ep=mgh 二、重力势能的大小具有相对性，与 参考平面的选取有关，而重力势能的 改变量△EP与参考平面选取无关，重 力势能改变量具有绝对性。 三、重力势能是地球与物体所组成的 “系统”所共有的，而不是地球上的 物体单独具有的。
17
重力势能
一、水电站
水电站为什么要建高高的大坝?
打桩机
打

A．沿路径 ACB 重力做的功多一些 B．沿路径 ADB 重力做的功多一些 C．沿路径 ACB 和路径 ADB 重力做功一样多 D．无法判断沿哪条路径重力做功多一些
参考面下方的物体的重力势能是负数。
说 明
1、参考面（0势能面）的选取是任意的。
2、选不同的参考面物体的重力势能各不 相同,但重力势能的变化和重力做功与参 考平面无关。 3、通常选地面为参考面。
例： 如图，质量0.5kg的小球，从桌面以
上h1=1.2m的A点落到地面的B点，桌面高 h2=0.8m．请按要求填写下表．(g=10m/s2)
重力做功的特点：物体运动时，重力对它 做的功只跟它的起点和终点的位置有关（只跟 它的初末位置的高度差有关），而跟物体运动 的路径无关。（无论路径是直线还是曲线、光 滑还是粗糙）
WG＝mgh1－mgh2
初态和末态的表达式均为“mgh”，可见
“mgh”是一个具有特殊意义的物理量。
二
、
重 力
我们把物理量mgh叫做物体的重力势能．
答案：D
4．一个实心铁球与一个实心木球质量相等，将它们放在同一水平地面上， 下列结论中正确的是(选地面为参考平面)( C )
A．铁球的重力势能大于木球的重力势能 B．铁球的重力势能等于木球的重力势能 C．铁球的重力势能小于木球的重力势能 D．上述三种情况都有可能
5.如图所示，A 点距地面高为 h，B 点在地面上，一物体沿两条不同的路径 ACB 和 ADB 由 A 运动到 B，则( )
解析：将物体由 A 移至 B，重力做功只与物体初、末位置高度差有关，A、 B、C 错，D 对．
答案：D
2．关于重力势能，下列说法中正确的是( ) A．重力势能的大小只由物体本身决定 B．重力势能恒大于零 C．在地面上的物体，它具有的重力势能一定等于零 D．重力势能是物体和地球所共有的

二、重力势能
• 打桩机的重锤从
高处落下时，可 以把水泥打进地 里，为什么？
雪 崩
2002年９月２１日上午，俄罗斯高加索 北奥塞梯地区的一个村庄发生雪崩，造成至少 １００人失踪。
2
美
陨国 内
石华 达 州
坑亚 利 桑 那
美国内华达州亚利桑那陨石坑。这个陨石坑是5万年前，一颗 直径约为30～50米的铁质流星撞击地面的结果。这颗流星重约50万 千克、速度达到20千米／秒，爆炸力相当于2000万千克梯恩梯 (TNT)，超过美国轰炸日本广岛那颗原子弹的一千倍。爆炸在地面 上产生了一个直径约1245米，平均深度达180米的大坑。据说，坑 中可以安放下20个足球场，四周的看台则能容纳200多万观众。
A Δh
h1
B
A
θ
Δh
C
h2
A Δh
C
ΔΔΔhhh123 C
结论：
⑴ WG = mgΔh
重力做功
与路径无关,只跟始末位置的高度差有关
⑵ WG = mgΔh = mgh1- mgh2 = -（mgh2- mgh
即：WG = -Δ EP
重力做正功时，重力势能减少，减少的重力势能等于 重力所做的功；重力做负功即物体克服重力做功时，重力 势能增加，增加的重力势能等于物体克服重力所做的功．
面上时，哪个重力势能较大？为什么？
⒋重力势能与重力做功的关系
用Ep1 = mgh1来表示物体在初位置的重力势能；用Ep2 = mgh2来表示物体在末位置的重力势能
讨论：如图所示，质量为m的小物体从A处运动 到C处，运动的路径有无数条，请利用功的概念和 重力作功与重力势能的变化之间的关系这两个不同 的角度来讨论，在这些运动过程中，求重力所做的 功是多少？是否相同？（已知AC的高度为h）

▪
Байду номын сангаас
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
24
人教版高中物理课件必修二：《重力势能》
11、获得的成功越大，就越令人高兴 。野心 是使人 勤奋的 原因， 节制使 人枯萎 。 12、不问收获，只问耕耘。如同种树 ，先有 根茎， 再有枝 叶，尔 后花实 ，好好 劳动， 不要想 太多， 那样只 会使人 胆孝懒 惰，因 为不实 践，甚 至不接 触社会 ，难道 你是野 人。(名 言网) 13、不怕，不悔(虽然只有四个字，但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己， 我用清 洁与节 制来珍 惜我的 身体， 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米，如 果他不 曾希望 它长成 种籽； 单身汉 不会娶 妻，如 果他不 曾希望 有小孩 ；商人 或手艺 人不会 工作， 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇