2003年中考试题精选

甘肃省2003年中考试卷一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的，将此选项的代号填入括号内） 1．下列方程中，关于x 的一元二次方程是（ ）． A ．1) 2(1)3(2＋x x =+ B ．02112＝－＋xx C ．0 2=c bx ax ＋＋ D ．1 2 22－＋x x x =2．在Rt △ABC 中，∠C ＝90°，AB ＝10，AC ＝6，则cos A 的值是（ ）． A ．53 B ．54 C ．43 D ．343．⊙1O 与⊙2O 的半径分别为2和5，当 2.521=O O 时，两圆的位置关系是（ ）． A ．外切 B ．相交 C ．内切 D ．内含4．点M （3，－4）关于x 轴的对称点M ′的坐标是（ ）． A ．（3，4） B ．（－3，－4） C ．（－3，4） D ．（－4，3） 5．已知正六边形的外接圆的半径是a ，则正六边形的周长是（ ）． A ．3a B ．6a C ．12a D ．24a6．结合正比例函数y ＝4x 的图象回答：当x ＞1时，y 的取值范围是（ ）． A ．y ＜1 B ．1≤y ＜4 C ．y ＝4 D ．y ＞47．为了判断甲、乙两个小组学生英语口语测验成绩哪一组比较整齐，通常需要知道两组成绩的（ ）．A ．平均数B ．方差C ．众数D ．频率分布8．已知h 关于t 的函数关系式为221gt h ＝(g 为正常数，t 为时间)，则函数图象为（ ）．9．在地表以下不太深的地方，温度y （℃）与所处的深度x （km ）之间的关系可以近似用关系式y ＝35x ＋20表示，这个关系式符合的数学模型是（ ）．A ．正比例函数B ．反比例函数C ．二次函数D ．一次函数10．如图，ABCD 为圆内接四边形，E 为DA 延长线上一点．若∠ C ＝45°，则∠BAE 等于（ ）．A ．90°B ．30°C ．135°D ．45° 11．已知3是关于x 的方程012342＝＋－a x 的一个解，则2a 的值是（ ）． A ．11 B ．12 C ．13 D ．1412．如图，△ABC 为等腰直角三角形，∠A ＝90°，AB ＝AC ＝2，⊙A 与BC 相切，则图中阴影部分的面积为（ ）．A ．2π1－B ．3π1－C ．4π1－D ．5π1－二、填空题（本大题共8小题，每小题3分，共24分．把答案填在题中的横线上）13．分解因式：1452－－x x ＝________． 14．一个函数的图象过点（1，2），且y 随x 的增大而增大，则这个函数的解析式是________．（任写一个）．15．关于x 的一元二次方程0122=＋＋kx x 有两个相等的实根，则k ＝________． 16．用一张面积为9002cm 的正方形硬纸片围成一个圆柱的侧面，则这个圆柱的底面直径为________cm ．（用含π的式子表示）17．据资料记载，位于意大利的比萨斜塔1918－1958这41年间，平均每年倾斜1.1毫米；1959－1969这11年间，平均每年倾斜1.26毫米，那么1918－1969这52年间，平均每年倾斜约________毫米．（保留两位小数） 18．为了解中学生的身体发育情况，对某中学同年龄的60名同学的身高进行了测量．经统计，身高在148.5～151.5之间的频数为3，则这一组的频率为________．19．已知抛物线c bx ax y ＋＋2=的图象与x 轴有两个交点，那么一元二次方程02=c bx ax ＋＋的根的情况是________________________．20．如图，A 、B 、C 是⊙O 上的三个点，当BC 平分∠ABO 时，能得出结论：_________ ________（任写一个）．三、画图题（本题5分）21．某地板厂要制作一批正六边形形状的地板砖，为适应市场多样化需求，要求在地板砖上设计的图案能够把正六边形6等分，请你帮他们设计等分图案（至少设计两种）．四、解答题（本大题共5小题，每小题7分，共35分．写出必要的文字说明及演算步骤）22．已知一次函数y ＝kx ＋k 的图象与反比例函数xy 8＝的图象在第一象限交于B （4，n ），求k ，n 的值．23．用换元法解方程71)3(63)1(2＝－＋＋＋－x x x x ．24．如图，在Rt △ABC 中，∠C ＝90°，AC ＝3 cm ，BC ＝4 cm ，以C 为圆心，r 为半径作圆．当r ＝2.4 cm 时，AB 与圆有怎样的位置关系?为什么?25．已知二次函数23)(2)(2＋＋＋＋－m x m x m y =的图象过点（0，5）．（1）求m 的值，并写出二次函数的解析式； （2）求出二次函数图象的顶点坐标、对称轴．26．右图为住宅区内的两幢楼，它们的高AB ＝CD ＝30 m ，两楼间的距离AC ＝24 m ．现需了解甲楼对乙楼的采光的影响情况，当太阳光与水平线的夹角为30°时，问甲楼的影子在乙楼上有多高?（精确到0.1m ，41.12≈，73.13≈）五、解答题（本大题共6小题，共50分．解答应写出必要的文字说明、证明过程或演算步骤）27．（本题满分8分）如图，AB为⊙O的直径，BC切⊙O于B，AC交⊙O于P，CE＝BE，E在BC上．求证：PE是⊙O的切线．28．（本题满分8分）如图，在梯形ABCD中，BC∥AD，∠A＝90°，AB＝2，BC＝3，AD＝4，E为AD的中点，F为CD的中点，P为BC上的动点（不与B、C重合）．设BP为x，四边形PE－FC 的面积为y，求y关于x的函数关系式，并写出x的取值范围．29．（本题满分8分）现需测量一井盖（圆形）的直径，但只有一把角尺（尺的两边互相垂直，一边有刻度，且两边长度都长于井盖半径）．请配合图形、文字说明测量方案，写出测量的步骤（要求写出两种测量方案）．30．（本题满分9分）某工厂生产某种产品，每件产品的出厂价为1万元，其原材料成本价（含设备损耗等）为0.55万元，同时在生产过程中平均每生产一件产品有1吨的废渣产生．为达到国家环保要求，需要对废渣进行脱硫、脱氮等处理，现有两种方案可供选择：方案一由工厂对废渣直接进行处理，每处理1吨废渣所用的原料费为0.05万元，并且每月设备维护及损耗费为20万元．方案二 工厂将废渣集中到废渣处理厂统一处理，每处理1吨废渣需付0.1万元的处理费．（1）设工厂每月生产x 件产品，每月利润为y 万元，分别求出方案一和方案二处理废渣时，y 与x 之间的函数关系式；（利润＝总收入－总支出）（2）若你作为工厂负责人，如何根据月生产量选择处理方案，既可达到环保要求又最合算．31．（本题满分9分） 已知抛物线bx ax y ＋2=经过点A （2，0），顶点为D （1，－1）．（1）确定抛物线的解析式；（2）直线y ＝3与抛物线相交于B 、C 两点（B 点在C 点左侧），以BC 为一边，原点O 为另一顶点作平行四边形，设平行四边形的面积为S ，求S 的值；（3）若以（2）小题中BC 为一边，抛物线上的任一点P 为另一顶点作平行四边形，当平行四边形面积为8时，试确定P 点的坐标； （4）当－2≤x ≤4时，（3）小题中平行四边形的面积是否有最大值?若有请求出，若无请说明理由．32．（本题满分8分） 阅读以下材料并填空． 平面上有n 个点（n ≥2），且任意三个点不在同一直线上，过这些点作直线，一共能作出多少条不同的直线?（1）分析：当仅有两个点时，可连成1条直线； 当有3个点时，可连成3条直线； 当有4个点时，可连成6条直线； 当有5个点时，可连成10条直线； ……（2）归纳：考察点的个数n 和可连成直线的条数n S ，发现：（3个点B 有（n －1）种取法，所以一共可连成n （n －1）条直线，但AB 与BA 是同一条直线，故应除以2，即2)1(－＝n n S n ． （4）结论：2)1(－＝n n S n ．试探究以下问题：平面上有n （n ≥3）个点，任意三个点不在同一直线上，过任意三点作三角形，一共能作出多少不同的三角形? （1）分析：当仅有3个点时，可作________个三角形； 当有4个点时，可作________个三角形； 当有5个点时，可作________个三角形； ……（2）归纳：考察点的个数n 和可作出的三角形的个数n S ，发现：（3）推理：_________________________________________________________________ _______________________________________________________________________________ _______________________________________________________________________________ _______________________________________________________________________________ _______________________________________________________________________________ （4）结论：___________________________参考答案一、选择题（每小题3分，共36分）1．A 2．A 3．D 4．A 5．B 6．D 7．B 8．A 9．D 10．D 11．C 12．C 二、填空题（每小题3分，共24分）13．（x ＋2）（x －7） 14．写出符合条件的一个即可，如y ＝2x ，y ＝x ＋1等 15．22 16．π3017．1.13 18．0.05 19．有两个不相等的实数根 20．写出符合条件的一个即可，如∠ABO ＝∠AOC ，∠AOC ＝2∠OBC 等． 三、画图题（5分）21．只要符合题目要求，即可得分，设计一种得3分，设计两种得5分．如：四、解答题（每小题7分）22．解：∵ B （4，n ）在反比例函数xy 8＝的图象上， ∴ 248＝＝n ．…………………………………………………………………………3分 又∵ B （4，2）在一次函数y ＝kx ＋k 的图象上，∴ 2＝4k ＋k ，52＝k ．…………………………………………………………………6分 答：k ，n 的值分别是52，2．……………………………………………………………7分 23．解：设y x x ＝＋－31，那么y x x 113＝－＋， 原方程变形为762＝＋yy ，……………………………………………………………2分整理得06722＝＋－y y ．解这个方程，得231＝y ，22＝y ．………………………………………………………4分当23＝y 时，2331＝＋－x x ，去分母，得3x ＋9＝2x －2，∴ x ＝－11．…………………………………………………………5分当2＝y 时，231＝＋－x x ，去分母，得 2x ＋6＝x －1，∴ x ＝－7．……………………………………………………………6分 检验，把x ＝－11，x ＝－7分别代入原方程的分母，各分母都不等于0，所以它们都是原方程的根．∴ 原方程的根是111＝－x ，72＝－x ．……………………………………………7分 24．解：过C 作CD ⊥AB ，垂足为D ，如图．…………………………………………1分 在Rt △ABC 中，522＝＋＝BC AC AB ．………………………………………………………………3分 根据三角形的面积公式有 BC AC AB CD ⋅⋅＝， ∴ cm 4.2＝＝ABBCAC CD ⋅．…………………………………………………………5分∵ r ＝2.4 cm∴ r ＝CD ．因此AB 与⊙O 相切．……………………………………………………7分25．解：（1）∵ 点（0，5）在二次函数2)3()2(2＋＋＋＋－＝m x m x m y 的图象上， ∴ 5＝m ＋2，解得m ＝3．……………………………………………………………2分 ∴ 二次函数的解析式为562＋＋＝x x y ．……………………………………………4分 （2）∵ 4)3(5622－＋＝＋＋＝x x x y ， ∴ 图象的顶点坐标为（－3，－4），对称轴为x ＝－3．……………………………7分 26．解：设甲楼的影子在乙楼上的最高点为E ，作EF ⊥AB ，垂足为F ，如图．…1分 ∵ ∠BEF ＝30°，∴ 在Rt △BFE 中，︒︒⋅⋅30tan 30tan AC EF BF ＝＝8.1384.1338≈≈＝（m ）．……………………………………………………………4分 ∴ CE ＝AF ＝AB －BF ≈16.2（m ）……………………………………………………6分 答：甲楼的影子在乙楼上的高度约为16.2米．………………………………………7分五、（本大题共6小题，共50分）27．如图，连接OP 、BP ．………………………………………………………………1分 AB 是⊙O 的直径…………………………………………………………………………1分EB EP BE CE APB =⇒⎭⎬⎫=︒=∠⇒90PE ⇒是⊙O 的切线．…………………………………………………………………8分28．解：过F 作FG ⊥AD ，G 为垂足．…………………………………………………1分 ∵ F 为CD 的中点，∠A ＝90°，AB ＝2， ∴ FG ＝1．∵ BC ＝3，BP ＝x ，∴ PC ＝3－x ．∵ AD ＝4，E 为AD 的中点，∴ ED ＝2．…………………………………………4分那么EFD PEDC PEFC S S S ∆－＝梯形四边形 122122]2)3[(⨯⨯⨯－＋－＝x＝5－x －1＝4－x ．………………………………………………………7分∴ y ＝4－x ，0＜x ＜3．…………………………………………………………………8分 29．解法一：如图（1），把井盖卡在角尺间，可测得AB 的长度．记井盖所在圆的圆心为O ，连接OB 、OC ，由切线的性质得OB ⊥AB ，OC ⊥AC ．又AB ⊥AC ，OB ＝OC ，则四边形ABOC 为正方形．那么井盖半径OC ＝AB ，这样就可求出井盖的直径．解法二：如图（2），把角尺顶点A 放在井盖边缘，记角尺一边与井盖边缘交于点B ，另一边交于点C （若角尺另一边无法达到井盖的边上，把角尺当直尺用，延长另一边与井盖边缘交于点C ），度量BC 长即为直径．解法三：如图（3），把角尺当直尺用，量出AB 的长度，取AB 中点C ，然后把角尺顶点与C 点重合，有一边与CB 重合，让另一边与井盖边缘交于D 点，延长DC 交井盖边于E ，度量DE 长度即为直径．解法四：如图（4），把井盖卡在角尺间，记录B 、C 的位置，再把角尺当作直尺用，可测得BC 的长度．记圆心为O ，作OD ⊥BC ，D 为垂足，由垂径定理得BC DC BD 21＝＝，且∠BOD ＝∠COD ．由作图知∠BOC ＝90°，∴ ︒︒⨯∠459021＝＝BOD ． 在Rt △BOD 中，︒45sin BDBO ＝，这样就可求出井盖的半径，进而求得直径．解法五：如图（5），把角尺当作直尺用，先测得AB 的长度，记录A 、B 的位置，再量AC ＝AB ，记录C 的位置，然后测得BC 的长度．作等腰三角形BAC 底边BC 上的高AD ，D 为垂足． ∵ AD 垂直平分BC ，∴ 由垂径定理的推论可知AD 一定过圆心O ． 由BC BD 21＝，可求出BD ．∵ AB 已测出．∴ 在Rt △BDA 中，根据勾股定理可求出AD ． 那么，在Rt △BDO 中，22222)(AO AD BD OD BD OB －＋＝＋＝． 设井盖半径为r ，则222)(r AD BD r －＋＝．∵ BD 、AD 都已知，∴ 解一元二次方程就可求出井盖的半径r ，这样就可求出井盖的直径．注：学生的其他测量方案只要符合题目要求，且是可行的都应得分．写出一种方案得4分，两种方案得8分．30．解：（1）因为工厂每月生产x 件产品，每月利润为y 万元，由题意得选择方案一时，月利润为204.02005.055.01－＝－－－＝x x x x y ．……………………………………………2分 选择方案二时，月利润为x x x x y 35.01.055.02＝－－＝．…………………………………………………………4分（2）若21y y ＞，即0.4x －20＞0.35x ．解得 x ＞400．……………………………………………………………………………6分则当月生产量大于400件时，选择方案一所获得利润较大；则当月生产量等于400件时，两种方案所获得利润一样大； 则当月生产量小于400件时，选择方案二所获得利润较大．…………………………9分31．解：（1）∵ 抛物线bx ax y +2＝过点A （2，0），D （1，－1），∴ ⎩⎨⎧.1.024＝－＋＝＋b a b a 解得 a ＝1，b ＝－2． 则抛物线的解析式为x x y 22－＝.………………………………………………………1分（2）在抛物线解析式为x x y 22－＝中，令y ＝3，即x x 232－＝．解得11＝－x ，32＝x …………………………………………………1分则B （－1，3）、C （3，3）．故 BC ＝4，那么S ＝4×3＝12．…………………………………………………………3分（3）当P 点在直线BC 下方时， S ＝4×（3－y ）＝12－4y ＝8，y ＝1． 由122＝－x x ，得211－＝x ，212＋＝x ． 则P 点的坐标为1P （21－，1），2P （21＋，1）．…………………………………………………5分当P 点在直线BC 上方时，S ＝4×（y －3）＝4y －12＝8，y ＝5．由522＝－x x ，得613－＝x ，614＋＝x ．则P 点的坐标为3P （61－，5），4P （61＋，5）．…………………………………………………7分（4）把x ＝－2代入x x y 22－＝，得y ＝8，把x ＝4代入x x y 22－＝，得y ＝8，当－2≤x ≤4时，顶点D 到BC 的距离为4，抛物线上与线段BC 距离最远的有两个点，坐标分别为（－2，8）、（4，8）与线段BC 的距离都为5．∴ S 有最大值，其最大值为S ＝4×（8－3）＝20．……………………………………………………………………9分32．（1）1，4，10…………………………………………………………………………3分（2）6123⨯⨯，6234⨯⨯，6345⨯⨯，6)2)(1(－n n n -…………………………… 5分 （3）平面上有n 个点，过不在同一条直线上的三点可以确定一个三角形，取第一个点A 有n 种取法，取第二个点B 有（n －1）种取法，取第三个点C 有（n －2）种取法，所以一共可以作n （n －1）（n －2）个三角形，但△ABC 、△ACB 、△BAC 、△BCA 、△CAB 、△CBA 是同一个三角形，故应除以6，即6)2)(1(-n n n S n －＝．……………………………7分 （4）6)2)(1(-n n n S n －＝………………………………………………………………8分。

黑龙江省2003年中考试卷一、单选题（共16分，每小题2分，每小题只有一个选项是正确的，请把正确选项的字母填在题后括号内）1．下列措施中，能防止蒸发的是（）．A．把粮食晒在朝阳的地方B．把酒精放在密封的瓶中C．将洒在地上的水用笤帚摊开D．将湿衣服晾在通风处2．下列说法中错误的是（）．A．潜望镜利用了平面镜成像的原理B．在光的反射现象中，光路是可逆的C．在漫反射现象中，反射角可能不等于入射角D．平面镜所成的像是由光的反射形成的3．小红用一水平的力去推水平地面上的桌子，但未推动，这是因为（）．A．推力小于此时桌子受到的摩擦力B．桌子受到的重力与地面对桌子的支持力平衡，所以桌子水平方向不动C．小红对桌子的推力等于桌子对小红的推力D．推力与地面对桌子的摩擦力平衡，合力为零4．下列事例中，能够增大压强的做法是（）．A．在铁路的钢轨下铺设枕木B．把书包带做得宽些C．菜刀钝了磨一磨，使它锋利些D．在拖拉机轮上安装履带5．在图1中，属于省力杠杆的是（）．图16．下列关于机械效率的说法正确的是（）．A．机械效率可以提高到100％B．机械效率总小于1C．功率大的机械，机械效率高D．机械效率越高，有用功就越多7．对于图2中的各种数据，说法不正确的是（）．A．每消耗1kW·h的电能，电能表的转盘转3000转B．额定电压为220V，额定电流为10AC．同时使用的用电器总功率不能超过2200WD．电能表读数的单位是kW·h图28．在下列现象中，不可能引起家中保险丝熔断的是（）．A．开关中的两个线头相碰B．电路中增加了大功率的用电器C．插座中的两个线头相碰D．室内电线绝缘皮损坏二、填空题（共18分，每题2分）9．我国上海建成世界第一条高速磁浮交通系统——上海磁浮示范运营线于2002年12月31日正式通车，磁浮列车从上海市龙阳地铁车站到蒲东国际机场全程30km，单程行驶只用8min，它的平均速度为________km/h，上海磁浮列车已达到设计的最高时速430km/h．它能悬浮在轨道上运行，是因为利用了__________________________的原理．10．我国“神舟”四号飞船于2002年12月30日凌晨在酒泉载人航天发射场发射升空，试验获得圆满成功．飞船在太空成功完成了数百个运行动作，是通过喷射燃气来实施变轨、姿态确定的（即改变运行高度、运行方向），这是应用了物理学中________的原理，而太阳能帆板展开，是为了__________________________________．11．我们通过实验探究知道：一切正在发声的物体都在振动．请你举出一个发声体在振动的事例：．________．12．摄影师在给某班照集体像后，又给一名同学照半身像．那么，应________（选填“减小”或“增大”）照相机镜头和这个同学的距离．13．体育运动与物理知识有着密切的联系，请说出一个利用惯性的体育项目:________．14．在水平地面上，用50N的水平推力推重为100N的箱子，在10s内前进了10m，如图3所示．推箱子的小朋友做功的功率为________W．图315．黑龙江省地处高寒地区，冬天室内的暖气用热水循环供热，而不用其他液体，是因为________；在降低相同温度时，水比等质量的其他液体放出的热量________．16．请说出一个你所知道的利用电磁继电器工作的电器：________．17．法拉第是一个伟大的实验物理学家，他以深刻的洞察力，针对奥斯特实验提出：既然电能生磁，那么，磁能不能生电呢?为此，他经过十年的坚持不懈的努力，终于在1831年发现了________现象．从此，人类实现了机械能向电能的大规模转化．三、实验探究（共14分，18题3分，19题6分，20题5分）18．如图4是某实验小组测量一种未知液体密度实验的正确操作情境，其中负责设计实验记录表格和填写实验数据的同学有三项没填完，请你帮他填上．图419．通过实验探究，同学们已经知道，浸入液体中的物体受到的浮力与液体的密度有关，也与物体排开液体的体积有关．但某些同学猜想，物体受到浮力的大小可能还与物体密度的大小有关．请你设计一个实验对此猜想进行检验．（1）现有器材：弹簧测力计、细线、烧杯、适量的水．你认为实验还需补充的器材是：．_______________________________________________________________________．（2）简述主要的实验步骤：20．如图5所示，是小强测量一只标有“2.5V ”字样小灯泡电功率的实验电路，但尚未连接完．（小灯泡电阻约为10Ω）图5（1）请你用笔画线代替导线帮他完成电路连接（画线不许交叉）．（2）连接电路时，应注意：开关要________；变阻器的滑片要移到________．（3）电路连接准确无误后，闭合开关，移动变阻器滑片P 使小灯泡正常发光．此时，电流表示数如图6所示，则小灯泡的额定功率为________W ．图6（4）另一小组在做此实验时，连完电路，闭合开关后，发现电流表的指针反向偏转，他们应采取的纠正方法是_________________________________________．四、创新与开放（共22分，21题8分，22题8分，23题6分）21．白炽灯是人们常用的照明用具，如图7所示．根据你对白炽灯的了解，请提出两个与物理知识有关的问题，并针对提出的问题作出简要回答．例如：问题：白炽灯的灯丝用久了为什么会变细?图7简答：在高温状态下工作灯丝升华造成的．（1）问题：__________________________________________________________ 简答：__________________________________________________________ （2）问题：__________________________________________________________ 简答：__________________________________________________________ 22．现有两根完全相同的电热丝（元件符号），电阻值均为60.5Ω，一个单刀单掷开关，一个单刀双掷开关（元件符号），电源电压220V，导线若干．（1）请用给出的电阻，画出所有阻值不同的连接方式．（2）在绿色证书教育活动中，某学生科技小组征集为养鸡场孵化室设计一个调温电路的方案，要求：用题中给出的电阻和开关设计一个调温电路，要有尽可能多档位的调温功能，在虚线框内画出你所设计的电路图（其中电源已给出）．（3）请计算你所设计的电路中各档位的发热功率是多少瓦?23．黑龙江《生活报》2003年5月2日在头版报道了这样一条科技新闻：由哈尔滨工业大学机电工程学院和哈尔滨医科大学的五位科研人员，研制出一间微型非典隔离监护室．这种隔离监护室最突出的设计特点就是室内用了负压原理设计（室内的气压比室外的气压低一些）．室壁设有进气孔和抽气孔，这样，保证为室内提供新鲜空气，还可以利用真空泵将病人呼出的携带病毒的气体抽出去……看过报道后，结合非典SARS病毒通过空气扩散而造成交互传染的特点，运用物理知识回答：（1）微型非典隔离室形成相对低压的作用是什么?（2）针对非典隔离室，为保护医护人员和医院周边群众的安全，为方便医护人员对非典病人的观察和护理，从物理学的角度还应采取哪些合理措施?（提出一条即可）参考答案一、单选题（共16分，每题2分）1．B 2．C 3．D 4．C 5．D 6．B 7．B 8．A二、填空题（共18分，每题2分）9．225 磁极间的相互作用（或“同名磁极相互排斥”或“异名磁极相互吸引”）（每空1分）10．力可以改变物体的运动状态（或“力的作用是相互的”）增大受光的面积，利用更多的太阳能转化为电能（每空1分）评分标准：只要联系太阳能即可给分．11．正在发声的琴弦在振动（或“正在发声的鼓面在振动”等）评分标准：答案中体现出物体发声时正在振动即可给分．12．减小 13．跳远（或“跳高”等）评分标准：只要说出的体育项目是利用惯性的即可给分．14．50 15．水的比热容大 多（每空1分） 16．电话（或“电铃”等） 17．电磁感应三、实验探究（共14分，18题3分，19题6分，20题5分）18．量筒中液体的质量 30 3100.83 （每空1分）19．方法一：（1）等体积的铜块和铝块 （2分）（2）A ．用细线分别系好铜块和铝块，并分别挂在弹簧测力计上，测出重力1G 和2G （1分）B ．再读出铜块和铝块分别浸没在水中时，弹簧测力计的示数1F 和2F （1分）C ．计算出111F G F －＝浮和222F G F －＝浮 （1分）D ．比较1浮F 和2浮F 的大小，即可检验上述猜想（1分）评分标准：（1）在这种方法中选择的两个固体，体积相同，密度不同，且两种物质的密度要大于水的密度，才能给分，其他方法参照给分．（2）在测量铜块和铝块浸在水中读取弹簧测力计的读数时，必须说出铜块和铝块浸没在水中，才能给1分，否则不给分（3）在C 和D 步骤中，必须有计算和比较过程才能给2分，若没有计算或比较过程，则各扣1分．（4）其他方案如果正确、合理即可参照给分．20．（1）电流表量程连0～0.6A ，正负接线柱接线正确，图略 （1分） 评分标准：接线柱和量程都选对才能给分．（2）断开 D 端（或“最大值”或“右端”）（每空各1分）（3）0.7 （1分）（4）立即断开开关，将接电流表“＋”、“－”接线柱的导线对调 （1分）四、创新与开放（共22分，21题8分，22题8分，23题6分）21．（1）铁螺扣套为什么有花纹？为了增大灯口螺套和灯头之间的摩擦（2）白炽灯的工作原理是什么？白炽灯是利用电流的热效应工作的 评分标准：（1）每个问题提问正确2分，简答2分．（2）答案很多，不能一一列出，其他答案，如果正确可参照给分．（3）类似“灯丝是由电阻率大，而熔点高的钨丝制作的吗？简答：是”．这样的提问和回答，价值比较低，给2分．22．（1）图略，每种联接方式1分，共3分（2）评分标准：（1）若设计成图B ，应强调1S 闭合时，2S 不能接a ，否则不能给满分．（2）其他画法只要正确，即可给分．（3）画出有三档的电路图，给2分，画出只有两档的电路图，给1分．（3）如图A ：当1S 断开，2S 接b 时，两电阻串联，为低温档．W 400121)V 220(222＝＝＝低ΩR U P （1分） 当1S 闭合，2S 接b 时，一个电阻接入，为中温档．W 8005.60)V 220(22=Ω＝＝中R U P （1分） 当1S 闭合，2S 接a 时，两个电阻并联，为高温档．W 160025.60)V 220(222=Ω＝＝高R U P （1分） 23．（1）作用：开病房门后，由于室内气压小于室外大气压，室外空气会向室内流动，室内空气不会向室外流动，这样可防止室内空气中的SARS 病毒扩散到室外，避免医院内非典病人与医护人员的交叉传染 （3分）（2）参考答案：①利用电能转化为内能，被真空泵抽出去的含SARS 病毒的空气通入密闭的电热丝容器进行高温消毒，杀死SARS病毒②利用电能转化为光能，被真空泵抽出去的含SARS病毒的空气通入密闭的紫外线消毒装置，杀死SARS病毒③为防止SARS病毒扩散，要求非典病人、疑似病人、医护人员，带有符合要求的口罩④利用光的直线传播，光的反射，在隔离室设置抗压强透明观察窗口评分标准：第二问答案可能有多种，只要提出“怎样杀死病毒”和“怎样防止病毒扩散”两条中的一条，即可给3分．。

陕西省2003年中考试卷一、选择题（共10小题，每小题3分，共30分．每小题只有一个选项是正确的） 1．今年我省元月份某一天的天气预报中，延安市最低气温为－6℃，西安市最低气温为2 ℃．这一天延安市的气温比西安市的气温低（ ）．A ．8℃B ．－8℃C ．6 ℃D ．2℃2．如果两圆半径分别为3和7，圆心距为4，那么这两圆的位置关系是（ ）． A ．内含 B ．内切 C ．相交 D ．外切 3．地球上的陆地面积约为2149000000千米，用科学记数法表示为（ ）． A ．2610149千米⨯ B ．2710149千米⨯ C ．28101.49千米⨯ D ．29101.49千米⨯4．方程91)(2=＋x 的解是（ ）．A ．x ＝2B ．x ＝－4C ．21=x ，4 2－=xD ．21－=x ，4 2=x5．把不等式组⎩⎨⎧≥01,01＜－＋x x 的解集表示在数轴上，正确的是（ ）．6．香港于1997年7月1日成为中华人民共和国的一个特别行政区，它的区徽图案（紫荆花）如图，这个图形（ ）．A ．是轴对称图形B ．是中心对称图形C ．既是轴对称图形，又是中心对称图形D ．既不是轴对称图形，也不是中心对称图形7．为保护生态环境，我省某山区县响应国家“退耕还林”号召，将该县某地一部分耕地改为林地．改变后，林地面积和耕地面积共有180平方千米，耕地面积是林地面积的25％，为求改变后林地面积和耕地面积各为多少平方千米，设耕地面积为x 平方千米，林地面积为y 平方千米，根据题意，列出如下四个方程组，其中正确的是（ ）． A ．⎩⎨⎧⋅%25180x y y x ＝＝＋ B ．⎩⎨⎧⋅%25180y x y x ＝＝＋C ．⎩⎨⎧%25180＝－＝＋y x y x D ．⎩⎨⎧%25180＝－＝＋x y y x8．将一张矩形纸对折再对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是（ ）．A ．矩形B ．三角形C ．梯形D ．菱形9．要做甲、乙两个形状相同（相似）的三角形框架，已有三角形框架甲，它的三边长分别为50 cm 、60 cm 、80 cm ，三角形框架乙的一边长为20 cm ，那么符合条件的三角形框架乙共有（ ）．A ．1种B ．2种C ．3种D ．4种10．星期天晚饭后，小红从家里出去散步，下图描述了她散步过程中离家的距离s （米）与散步所用时间t （分）之间的函数关系．依据图象，下面描述符合小红散步情景的是（ ）．A ．从家出发，到了一个公共阅报栏，看了一会儿报，就回家了B ．从家出发，到了一个公共阅报栏，看了一会儿报后，继续向前走了一段，然后回家了C ．从家出发，一直散步（没有停留），然后回家了D ．从家出发，散了一会儿步，就找同学去了，18分钟后才开始返回二、填空题（共6小题，每空3分，共24分）11．计算1023.14)(1－＋－－+＝________．12．在△ABC 中，∠C ＝90°，若21tan ＝A ，则sin A ＝________．13．如图，AB 是⊙O 的直径，C 、D 、E 都是⊙O 上的点，则∠1＋∠2________．14．华山鞋厂为了了解初中学生穿鞋的鞋号情况，对永红中学初二（1）班的20名男生所穿鞋号统计如下表：那么这20名男生鞋号数据的平均数是________，中位数是________；在平均数、中位数和众数中，鞋厂最感兴趣的是________．15．计算2003的算术平方根时，现有如下三个方案，请你只选择其中一个方案填空： 方案一：用双行显示科学计算器求：先按动键，再依次按键（或或按开平方键）、．方案二：用单行显示科学计算器求：先按动键，再依次按键（或或按开平方键）．方案三：查算表（数学用表）计算：下表是平方根表的一部分，依据下表，得2003＝________．16．如图，梯子AB 靠在墙上，梯子的底端A 到墙根O 的距离为2米，梯子的顶端B 到地面的距离为7米．现将梯子的底端A 向外移动到A ′，使梯子的底端A ′到墙根O 的距离等于3米，同时梯子的顶端B 下降至B ′，那么BB ′：①等于1米；②大于1米；③小于1米．其中正确结论的序号是________．三、解答题（本大题9小题，共66分．解答应写出过程） 17．（本题满分5分）先化简，再求值：131)1(11432＋－－－＋＋＋x x x x x x ，其中x ＝13＋．18．（本题满分6分）用换元法解方程08)1(2)1(2＝－＋＋x x x x -．19．（本题满分7分）设1x ，2x 是关于x 的方程01)(2=m x m x －－－（m ≠0）的两个根，且满足0321121＝＋＋x x ，求m 的值．20．（本题满分7分）如图，在梯形ABCD 中，已知AD ∥BC ，BC ＝BD ，AD ＝AB ＝4 cm ，∠A ＝120°，求梯形ABCD 的面积．21．（本题满分7分） 已知反比例函数xky ＝的图象经过点A （－2，3）． （1）求出这个反比例函数的解析式；（2）经过点A 的正比例函数y ＝k'x 的图象与反比例函数xky ＝的图象还有其他交点吗?若有，求出交点坐标；若没有，说明理由．22．（本题满分7分）为了学生的身体健康，学校课桌、凳的高度都是按一定的关系科学设计的．小明对学校所添置的一批课桌、凳进行观察研究，发现它们可以根据人的身高调节高度．于是，他测量了一套课桌、凳上相对应的四档高度，得到如下数据：（1）小明经过对数据探究，发现：桌高y 是凳高x 的一次函数，请你求出这个一次函 数的关系式；（不要求写出x 的取值范围）（2）小明回家后，测量了家里的写字台和凳子，写字台的高度为77 cm ，凳子的高度为43.5 cm ，请你判断它们是否配套?说明理由．23．（本题满分8分）如图，正方形ABCD 是⊙O 的内接正方形，延长BA 到E ，使AE ＝AB ，连结ED ．（1）求证：直线ED 是⊙O 的切线；（2）连结EO 交AD 于点F ，求证：EF ＝2FO ．24．（本题满分9分）如图，在直角坐标系中，以点A （3，0）为圆心，以32为半径的圆与x 轴交于B 、C 两点，与y 轴交于D 、E 两点．（1）求D 点的坐标；（2）若B 、C 、D 三点在抛物线c bx ax y ＋＋2上，求这个抛物线的解析式； （3）若⊙A 的切线交x 轴正半轴于点M ，交y 轴负半轴于点N ，切点为P ，且∠OMN ＝30°，试判断直线MN 是否经过所求抛物线顶点?说明理由．25．（本题满分10分）． 在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案．也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫做平面镶嵌）．这显然与正多边形的内角大小有关．当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角（360°）时，就拼成了一个平面图形．（1）请根据下列图形，填写表中空格：（2）如果限于用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形?（3）从正三角形、正四边形、正六边形中选一种，再在其他正多边形中选一种，请画出用这两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由．参考答案一、选择题（每小题3分，共30分）1．A 2．B 3．C 4．C 5．C 6．D 7．B 8．D 9．C 10．B 二、填空题（每空3分，共24分） 11．2112．55 13．90° 14．24.55，24.5，众数（或25） 15．44.75 16．③三、解答题（共66分．解答应写出过程）17．解：原式13)1()1)(1)(1(11322＋－－＋－＋＋＋＋x x x x x x x x ⋅=…………………………………2分 1311＋－－＋－＝x x x x …………………………………………………………3分 12＋＝x ．…………………………………………………………………4分当13＋＝x 时， 原式)23)(23()23(2232－＋＝＋＝- ＝324－．…………………………………………………………………………5分 18．解：设y x x＝＋1，则原方程变形为0822＝－－y y ．…………………………………2分解这个方程得：41＝y ，22＝－y ．……………………………………………………3分当y ＝4时，41＝＋x x ，34＝－x ； 当y ＝－2时，21＝－＋x x ，32＝－x ．………………………………………………5分经检验，341＝－x ，322＝－x 都是原方程的根．……………………………………6分19．解：∵ 0)1(4)]1([22≥∆＋＝＋－－＝m m m ， ∴ 对于任意实数m ，方程恒有两个实数根1x ，2x ．又∵ 121－＝＋m x x ，m x x ＝－21，且0≠m ，……………………………………4分 ∴0321＝＋－－m m ，即m ＝3．…………………………………………………………7分 20．解：如图，作AE ⊥BC 于E ，作DF ⊥BC 于F ．∴ AE ∥DF ．又∵ AD ∥BC ，且∠A ＝120°，∴ ∠ABC ＝60°，AE ＝DF ．………………………………………………………… 2分 ∵ AB ＝AD ＝4，∴ ∠ABD ＝∠ADB ＝∠DBC ＝30°．…………………………………………………4分在Rt △ABE 中，得32＝AE ．在Rt △BDF 中，3422＝＝＝AE DF BD ． ∴ 34＝＝BD BC ．∴ AE BC AD S ABCD ⋅)(21＋＝梯形2cm )3412(＋＝．………………………………………………………7分（其他解法参照以上评分标准评分）21．解：①∵ 点A （－2，3）在xky ＝的图象上， ∴ 23－＝k．……………………………………………………………………………2分 ∴ k ＝－6．∴ 反比例函数的解析式为xy 6＝－.…………………………………………………4分 ②有．∵ 正、反比例函数的图象均关于原点对称，且点A 在它们的图象上， ∴ A （－2，3）关于原点的对称点B （2，－3）也在它们的图象上． ∴ 它们相交的另一个交点坐标为（2，－3）．…………………………………… 7分 （其他解法参照以上评分标准评分） 22．解：（1）设一次函数为y ＝kx ＋b ，将表中的数据任取两组，不防取（37.0，70.0）和（42.0，78.0）代入，得………………………………………………………………………2分 ⎩⎨⎧;4278,3770b k b k ＋＝＋＝解得⎩⎨⎧.8.10,6.1＝＝b k∴ 一次函数关系式为y ＝1.6x ＋10.8．…………………………………………………4分（2）当x ＝43.5时，y ＝1.6×43.5＋10.8＝80.4．∵ 77≠80.4，∴ 不配套．……………………………………………………………7分 （其他解法参照以上评分标准评分） 23．证明：（1）连结OD ．∵ 四边形ABCD 为正方形，AE ＝AB ，∴ AE ＝AB ＝AD ，∠EAD ＝∠DAB ＝90°．∴ ∠EDA ＝45°，∠ODA ＝45°．……………………………………………………2分 ∴ ∠ODE ＝∠ADE ＋∠ODA ＝90°．∴ 直线ED 是⊙O 的切线．………………………………………………………4分 （2）作OM ⊥AB 于M ． ∵ O 为正方形的中心，∴ M 为AB 中点．………………………………………………………………………5分 ∴ AE ＝AB ＝2AM ，AF ∥OM ．∴2＝＝AMAEFO EF ．……………………………………………………………………7分 ∴ EF ＝2FO ．…………………………………………………………………………8分 （其他证法参照以上评分标准评分）24．解：（1）连结AD ．根据题意，得3＝OA ，32＝AD ．∴ OD ＝3．∴ D 点坐标为（0，－3）．……………………………………………………………2分 （2）根据题意，得：B （3－，0），C （33，0）．………………………………3分 ∵ B 、C 、D 三点在抛物线c bx ax y ＋＋＝2上，∴ ⎪⎪⎩⎪⎪⎨⎧=;3,33270,330c c b a c b a －＋＋＝＋－＝解得⎪⎪⎪⎩⎪⎪⎪⎨⎧--.3,332,31＝＝＝c b a ∴ 所求抛物线的解析式为：3332312－－＝x x y ．………………………………6分 （3）连结AP ．在Rt △APM 中，∠PMA ＝30°，32＝AP ， ∴ 34＝AM ．∴ M 点的坐标为（35，0）． ∴ 5333530tan ＝＝＝⋅⋅︒OM ON ．∴ N 点坐标为（0，－5）． ∴ 直线MN 的解析式为533－＝x y ．……………………………………………7分 又∵ 抛物线4)3(3133323122－－＝－－＝x x x y ， ∴ 顶点坐标为（3，－4）．…………………………………………………………8分∵45333533＝－－＝－⨯x ， ∴ 抛物线的顶点在直线MN 上．………………………………………………………9分25．解：（1）nn ︒⋅180)2(－．（2）正三角形、正四边形（或正方形）、正六边形． （说明：（1）、（2）填对一个给1分）． （3）如：正方形和正八边形，草图如右：（画出草图2分）…………………………8分设在一个顶点周围有m 个正方形的角，n 个正八边形的角，那以，m 、n 应是方程︒︒︒⋅⋅36013590＝＋n m 的整数解，即2m ＋3n ＝8的整数解．∵ 这个方程的整数解只有⎩⎨⎧2,1＝＝n m 一组，∴ 符合条件的图形只有一种．………………………………………………………10分（其他解法参照以上评分标准评分）。

2003年安徽省中考语文试题（含答案）第Ⅰ卷 (共76分) 一、（6分）1.下列句子中加点字的读音相同的一组是（）（2分）A.①鸟儿唱出宛转的曲子，跟轻风流水应和着。

②她洗完手，就舀水和面，做起窝窝头来。

B.①我军歼灭了抵抗之敌，控制了南下要塞。

②环卫工人及时疏通了堵塞的下水道。

C.①凡是不称职的人就看不见它，这个说法让他心里发慌。

②这座大桥结构匀称，和四周景色配合得十分和谐。

D.①大家得小心提防，千万不要让这些小东西溜出去撒欢。

②他从剩余的资金中提留了一部分，作为今后的活动基金。

2.下列句子中有两个错别字的一项是（）（2分）A.春风和熙，阳光灿烂，山谷里回荡着鸟儿们缭亮的歌声。

B.突然，蝉声戛然而止，树林里顿时一片寂静。

C.这小生灵虽然是缈小的，但是我们绝不能忽视它。

D.叶欣以身恂职的事迹见报后，人们无不为之感动。

3.依次填入下列各句横线处的成语，恰当的一组是（）（2分）①孙小龙模仿赵本山的表演真是________________，让大家不时地捧腹大笑。

②经过长时间的试验，主要问题一解决，其它问题就________________了。

③这部________________的艺术作品，为我们描绘了一幅情景交融的图画。

A.惟妙惟肖不攻自破得天独厚B.栩栩如生不攻自破匠心独运C.栩栩如生迎刃而解得天独厚D.惟妙惟肖迎刃而解匠心独运二、（45分）阅读下面文字，分别回答问题。

(一)阳光，是一种语言(23分)雷抒雁①早晨，阳光以一种最明亮、最透彻的语言和树叶攀谈，绿色的叶子，立即兴奋地颤抖，通体透亮，像是一页页黄金锻打的箔片，炫耀在枝头。

而当阳光微笑着与草地上的鲜花对语，花朵便立即昂起头来，那些蜷缩在一起的忧郁的花瓣，也迅即展开，像一个个恭听教诲的耳朵。

②晴朗的日子，走在街上，你不会留意阳光。

普照的阳光，有时像是在对大众演讲的平庸演说家，让人昏昏欲睡，到处是燥热的嘈杂。

③阳光动听的声音，响在暗夜之后的日出，严寒之后的春天，以及黑夜到来前的黄昏。

广东省2003年中考试卷一、选择题（每小题3分，共15分．每小题给出的四个选项中只有一个是正确的，请将所选选项的字母写在题目后面的括号内） 1．下列运算正确的是（ ）． A ．7232)(a a a＝⋅B ．310505.0－＝－⨯C ．4)2(22－＝－a aD ．2)12(1)21(01＝－－－＋－2．如图，某个反比例函数的图象经过点P ，则它的解析式为（ ）．A ．)0(1＞＝x xy B ．)0(1＞＝－x xy C ．)0(1＜＝x xy D ．)0(1＜＝－x xy3．下列说法中正确的是（ ）．A ．有两边和其中一边的对角对应相等的两个三角形全等B ．等腰三角形是轴对称图形，也是中心对称图形C ．对角线互相平分的四边形是平行四边形D ．有两边平行的四边形是梯形4．关于x 的方程2（x －1）－a ＝0的根是3，则a 的值为（ ）． A ．4 B ．－4 C ．5 D ．－55．如图，正方形的边长为a ，以各边为直径在正方形内画半圆，所围成的图形（阴影部分）的面积为（ ）．A ．22πa a -B ．222πa a - C ．22π21a a - D ． 22π41a a -二、填空题（每小题4分，共20分．请把正确答案填写在横线上） 6．若∠A 是锐角，23cos =A ，则∠A ＝________． 7．不等式组⎩⎨⎧≥x x x x 14,43＋＋＜的解集为________．8．当a ＋b ＝3，x －y ＝1时，代数式y x b ab a ＋－＋＋222的值等于________． 9．如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为P 、若AP ∶PB ＝1∶4，CD ＝8，则AB ＝________．10．与点P （3，－4）关于y 轴对称的点的坐标为________．；与点Q （－3，4）关于原点对称的点的坐标为________．三、解答下列各题（每小题6分，共30分） 11．先化简后求值：)252(23－－＋－－x x x x ÷，其中22＝x ． 12．如图，AB 、AC 分别是菱形ABCD 的一条边和一条对角线，请用尺规把这个菱形补充完整．（保留作图痕迹，不要求写作法和证明）13．如图，灯塔A 周围1000米水域内有礁石，一舰艇由西向东航行，在O 处测得灯塔A 在北偏东74°方向线上，这时O 、A 相距4200米，如果不改变航向，此舰艇是否有触礁的危险?（指定数学课使用科学计算器的地区的考生须使用计算器计算．以下数据供计算器未进入考场的地区的考生选用：cos 74°＝0.2756，sin 74°＝0.9613，cot 74°＝0.2867，tan 74°＝3.487） 14．在公式h b a S )(21+＝中，已知h 、S 、b ，求a ．15．某商场出售某种文具，每件可盈利2元，为了支援贫困山区，现在按原售价的7折出售给一山区学校，结果每件盈利0.2元（盈利＝售价－进货价）．问该文具每件的进货价是多少元?四、（每小题7分，共28分）16．已知二次函数c bx x y ＋＋＝2的图象经过A （0，1），B （2，－1）两点． （1）求b 和c 的值；（2）试判断点P （－1，2）是否在此函数图象上?17．为了了解中学生的身体发育情况，对某一中学同年龄的50名女学生的身高进行了测量，结果如下（单位：厘米）：165 155 160 166 157 171 151 163 161 167 169 162 155 148 162 163 156 167 159 171 150 153 156 167 165 164 163 164 161 161 148 160 155 165 155 164 159 153 156 156 164 162 156 162 157 162 165 151 163 157 完成下面的频率分布表．18．已知1x ，2x 为方程02＝＋＋q px x 的两根，且621＝x x ，202221＝＋x x ，求p 和q 的值．19．如图，在梯形ABCD 中，AD ∥BC ，AD ＝AB ＝DC ，BD ⊥DC ，求∠C 的度数．五、（每小题9分，共27分） 20．某人从A 城出发，前往离A 城30千米的B 城．现在有三种车供他选择：①自行车，其速度为15千米／时；②三轮车，其速度为10千米／时；③摩托车，其速度为40千米／时．（1）用哪些车能使他从A城到达B城的时间不超过2小时?请说明理由；（2）设此人在行进途中离B城的路程为s千米，行进时间为t小时．就（1）所选定的方案，试写出s与t的函数关系式（注明自变量t的取值范围），并在所给的平面直角坐标系中画出此函数的图象．21．如图，P A和PB分别与⊙O相切于A，B两点，作直径AC，并延长交BP于点D，连结OP，CB．（1）求证：OP∥CB；（2）若P A＝12，DB∶DC＝2∶1，求⊙O的半径．22．如图，在Rt△ABC中，AB＝AC，∠BAC＝90°，O为BC的中点．（1）写出点O到△ABC的三个顶点A、B、C的距离的关系式（不要求证明）；（2）如果点M、N分别在线段AB、AC上移动，在移动中保持AN＝BM，请判断△OMN 的形状，并证明你的结论．参考答案一、选择题（每小题3分，共15分）1．D 2．D 3．C 4．A 5．C二、填空题（每小题4分，共20分）6．30° 7．231<≤-x 8．8 9．10 10．)43(--，，)43(-， 三、解答下列各题（每小题6分，共30分）11．解：原式29232--÷--=x x x x …………………………………………………………2分 )3x )(3x (2x 2x 3x -+-⨯---=…………………………………………………………………3分 31+-=x ，………………………………………………………………………………4分 当22=x 时，原式3223221-=+-=． ……………………………………6分12．解：……………………………………6分[说明]本题画法很多，只要正确均给满分．13．解：过A 作AB 与正东方向线垂直，垂足为B ．在Rt △AOB 中， 1分 4200=OA ，︒=︒-︒=∠167490AOB ，A O BAO AB ∠=⋅sin …………………………………………………………………3分 ︒=︒=⋅⋅74cos 420016sin 4200 2756.04200⨯=≈1158（米）＞1000（米）………………………………………………………5分 答：此舰按原航向继续航行没有触礁的危险．………………………………………6分 [说明] 使用计算器进行计算的可略去“︒=⋅74cos 4200”这一步，不按规定使用计算器计算的扣1分．14．解：由h b a S )(21+=，得 bh ah S +=2，……………………………………………………………………………2分 bh S ha -=2，……………………………………………………………………………4分 ∴ hbhS a -=2．…………………………………………………………………… 6分 15．解：设该文具每件的进货价是x 元，依题意，得 ……………………………… 1分 2.0)2(%70=-+⋅x x ．…………………………………………………………………4分 解得 4=x ．……………………………………………………………………………5分 答：该文具每件的进货价为4元．………………………………………………………6分四、（每小题7分，共28分） 16．解：（1）依题意，得⎩⎨⎧-=++=.1241c b c ，……………………………………………2分解得3-=b ，1=c ．……………………………………………………………………4分（2）由（1）知二次函数为132+-=x x y ． ① …………………………5分把1-=x 代入①，得25131≠=++=y ．…………………………………………6分 ∴ 点)21(，-P 不在此函数图象上．…………………………………………………7分 17…………………………………………………………………………………………………7分 [说明]填对一格给1分．18．解：6)(21-=+-=x x p ．…………………………………………………………3分 [])()(21222122121x x x x x x q +-+== 8)2036(21=-=．………………………………………………………………………6分 0484)6(422>=⨯--=-=∆q p ，所给方程有实数根．…………………………7分19．解：设x CBD =∠． ∵ AD ∥BCC B DA DB ∠=∠．………………………………………………………………………1分 ∵ AD ＝AB ∴ A D B A B D ∠=∠． ∴ xCD B ABC 22=∠=∠．…………………………………………………………3分 又∵ AB ＝DC ，∴ x ABC C 2=∠=∠．………………………………………………………………4分 ∵ DC BD ⊥，∴ ︒=∠+∠90C CBD ．即︒=+902x x ．…………………………………………………………………………6分解得︒=30x ．∴ ︒=∠60C ．………………………………………………………7分五、（每小题9分，共27分） 20．解：（1）∵ 30215=⨯，3020210<=⨯，3080240>=⨯，……………………………………………………………………… 1分∴ 此人可选骑自行车或摩托车．………………………………………………………4分[说明]直接写出正确结果，无说明理由得3分，（2）)20(1530≤≤-=t t s 或)430(4030≤≤-=t t s ．…………………………………………………………7分 [说明]只写出其中一个式子得2分．对于)20(1530≤≤-=t t s ，①对于)430(4030≤≤-=t t s ，②……………………………………………………………………………………………9分 21．（1）证明：连结AB ．∵ P A ，PB 分别与⊙O 相切于A 、B 两点， ∴ P A ＝PB ，且BPO APO ∠=∠．∴ AB OP ⊥．①………………………………………………………………………2分 ∵ AC 是⊙O 的直径，CB AB ⊥．②由①和②，得OP ∥CB ，…………………………………………………………………4分（2）由（1）知OP ∥CB ，∴DCDBOC PB =又∵PB=PA=12，12=DC DB ，∴1212=OC ．……………………………………………………………………………8分 ∴ 6=OC ，即⊙O 的半径为6． ……………………………………………………9分22．解：（1）OC OB OA ==．………………………………………………………2分 （2）答：△OMN 是等腰直角三角形．……………………………………………… 4分 证明：连结OA ．∵ AB AC =，OB OC =，∴ BC AO ⊥，即︒=∠90AOB ，BAO CAO ∠=∠．又∵ ︒=∠90BAC ，∴ ︒=∠=∠4521BAC CAO ．………………………………………………………5分 ∵ AB AC =，︒=∠90BAC ，∴ ︒=∠45B ． ∴ B N A O ∠=∠．又∵ BM AN =，OB OA =，∴ △AON ≌△BOM ．…………………………………………………………………7分 ∴ OM ON =， ① M O B N O A ∠=∠． ∴ A O M M O B A O M N O A ∠+∠=∠+∠． ∴ ︒=∠=∠90AOB NOM ． ②由①和②可知△OMN 是等腰直角三角形．……………………………………………9分。

页脚内容12003年中考试题精选1、某种空调器经3次降价，价格比原来下降了30%。

则其平均每次下降的百分比（精确到0.1%）应该是（ ）A 、26.0%B 、33.1%C 、8.5%D 、11.2%2、北京故宫的占地面积约为721000m 2,用科学记数法表示其结果是（ ）A 、7.21×105m 2B 、7.21×104m 2C 、721×103m 2D 、0.721×106m 23、计算机是将信息转换成二进制进行处理的。

二进制即“逢二进一”如（1101）2表示二进制数，将它转化成十进制形式是321121202113⨯+⨯+⨯+=，那么将二进制的数（1111）2转化成十进制形式的数是（ ）A 、8B 、15C 、20D 、304、下列运算正确的是（ ）2234122239.220.(2)2.(23)36.()22A B C D -⨯==-⨯=-= 5）A 、1个B 、2个C 、3个D 、4个6、若▲表示最小的正整数，●表示最大的负整数，■表示绝对值最小的有理数，则（▲+●）×■= 。

页脚内容27、回收废纸用于造纸可以节约木材，据专家估计，每回收1吨废纸可节约3立方米木材，那么回收a 吨废纸可以节约 立方米木材。

8、有一大捆粗细均匀的电线，现要确定其长度的值，从中先取出1米长的电线，称出它的质量为a ，再称其余电线的总质量为b ，则这捆电线的总长度是 米。

9、下表给出的是2003年6月份的日历表，任意圈出一竖列上相邻的三个数，请你运用方程的思想来研究，你发现这三个数的和不可能是（ ）A 、69B 、54C 、40D 、2710、如果分式方程11x m x x =++无解，则m 等于（ ） A 、1 B 、0 C 、-1 D 、-2页脚内容311、花果山景区某一景点改造工程要限期完成，甲工程队独做可提前1天完成，乙工程队独做要误期6天，现由两工程队合做4天后，余下的由乙工程队独做，正好如期完成，若设工程期限为x 天，则下面所列方程正确的是（ ）4444.1..1.16161616x x x x A B C D x x x x x x x x x +==+=+=+--+-+-+ 12、不等式组1413422x x x ->-⎧⎪⎨≥-⎪⎩ 的解集在数轴上表示为 13、2002年世界杯足球赛的积分方法如下：赢一场得3分，平一场 得1分，输一场得0分，某小组四个队进行单循环赛，其中一队积7分，该队赢了x 场，平了y 场，则（x,y ）是（ ）A 、（1，4）B 、（2，1）C 、（0，7）D 、（3，1）14、解方程组7,(1)12(2)x y x y +=⎧⎪⎨=⎪⎩g 有两种方法：第一种方法是把方程（1）化为y=（或x= ），代入（2）转化为一元二次方程解之；第二种方法是根据一元二次方程根与系数的关系，把x,y 看作是方程 的两个根，通过解这个方程得原方程的解。

2003年“非典”真题精选一、默写1.（2003年陕西1题6分）根据下面提示默写。

(6分，每小题2分)（1）《观书有感》这首诗中用来比喻不断学习新知识、才能达到新境界的两句诗是：，。

（2）王老师已经退休五年了，还一直做我们的课外辅导员，他的这种退而不休的精神，正如龚自珍的诗句描写的样：，。

（3）在你读过的古诗词中，有许多表达作者理想抱负的名句，请写出连续的两句。

2.（2004年陕西2题4分）请你根据下面的提示或要求填空。

（4分）（1）温家宝总理在今年“两会”结束答记者问时，引用毛泽东同志长征时期所写《忆秦娥·娄山关》词中“雄关漫道真如铁，而今迈步从头越”的名句，抒发他不畏艰难、勇往直前的雄心壮志。

由此我们可以联想到唐代诗人杜甫《望岳》中的诗句：“，。

”（2）中国古代诗文中，有许多格言给人以教育和启迪。

请你写出一则关于品德修养方面的格言。

（2分）二、成语运用（2003福建福州2题3分）下列加点的词语运用不当．．的一项是（）。

（3分）A.2003年中国—福建项目成果交易会于6月20日在福州圆．满结束．．．。

B.记者在北京小汤山医院亲眼目睹．．．．了医务人员在抗击非典战斗中感人的工作场面。

C.有关部门高度重视防汛工作，加大宣传力度，将暴雨警报广而告之，做到家喻户晓．．．．。

D.神舟发射基地的广大官兵，个个身怀绝技，却因工作的机密而鲜为人知．．．．。

三、病句辨析1.（2003年湖南长沙3题）下列句子没有语病的一句是（）A.通过大家的共同努力，“非典”疫情慢慢地被控制住了。

B.要把我们的学生培养成为既有丰富的知识又有高尚的品质。

C.从他上学的那天起，语文对他就产生了浓厚的兴趣。

D.我将妈妈的一张张笑脸和一句句言语摄入镜头，制成相册。

2.（2003四川成都4题3分）下列句子中没有语病的一句是（）A.白衣天使奋战在抗击非典的第一线，他们动人的事迹和牺牲精神在广大人民心中传扬。

B.在阅读文学名著的过程中，使我明白了许多做人的道理，感悟了人生的真谛。

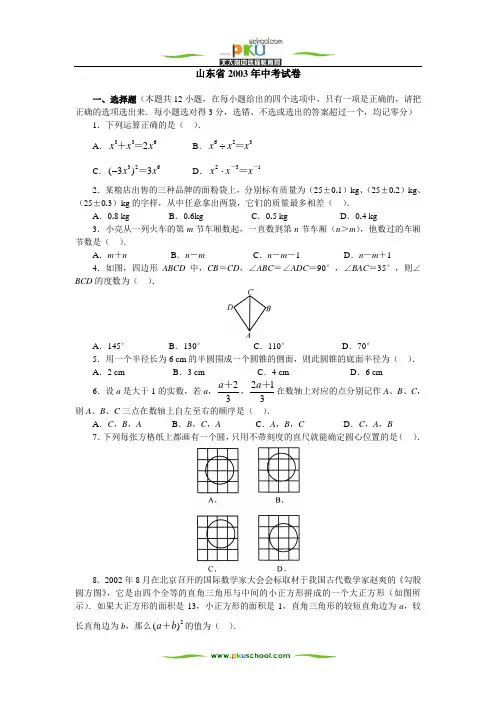
山东省2003年中考试卷一、选择题（本题共12小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个，均记零分） 1．下列运算正确的是（ ）． A ．6332x x x ＝＋ B ．326x x x ＝÷ C ．6233)3(x x ＝- D ．132－－＝x x x⋅2．某粮店出售的三种品牌的面粉袋上，分别标有质量为（25±0.1）kg 、（25±0.2）kg 、（25±0.3）kg 的字样，从中任意拿出两袋，它们的质量最多相差（ ）．A ．0.8 kgB ．0.6kgC ．0.5 kgD ．0.4 kg 3．小亮从一列火车的第m 节车厢数起，一直数到第n 节车厢（n ＞m ），他数过的车厢节数是（ ）．A ．m ＋nB ．n －mC ．n －m －1D ．n －m ＋14．如图，四边形ABCD 中，CB ＝CD ，∠ABC ＝∠ADC ＝90°，∠BAC ＝35°，则∠BCD 的度数为（ ）．A ．145°B ．130°C ．110°D ．70°5．用一个半径长为6 cm 的半圆围成一个圆锥的侧面，则此圆锥的底面半径为（ ）． A ．2 cm B ．3 cm C ．4 cm D ．6 cm 6．设a 是大于1的实数，若a ，32＋a ，312＋a 在数轴上对应的点分别记作A 、B 、C ，则A 、B 、C 三点在数轴上自左至右的顺序是（ ）．A ．C ，B ，A B ．B ，C ，A C ．A ，B ，CD ．C ，A ，B 7．下列每张方格纸上都画有一个圆，只用不带刻度的直尺就能确定圆心位置的是（ ）．8．2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图所示）．如果大正方形的面积是13，小正方形的面积是1，直角三角形的较短直角边为a ，较长直角边为b ，那么2)(b a ＋的值为（ ）．A．13 B．19 C．25 D．1699．如图是某蓄水池的横断面示意图，分深水区和浅水区．如果这个蓄水池以固定的流量注水，下面哪个图象能大致表示水的最大深度h和时间t之间的关系?（）．10．若A（a，6），B（2，a），C（0，2）三点在同一条直线上，则a的值为（）．A．4或－2 B．4或－1 C．－4或1 D．－4或211．工人师傅在一个长为25 cm，宽为18 cm的矩形铁皮上，剪去一个和三边都相切的圆A后，在剩余部分的废料上再剪出一个最大的圆B，则圆B的直径是（）．7cm B．8 cm C．7 cm D．4 cm A．212．在一列数1，2，3，4，…，1000中，数字“0”出现的次数一共是（）．A．182 B．189 C．192 D．194二、填空题（本题共4小题，每小题填对得4分，共16分．只要求填写最后结果）13．某市召集20名特级教师参加教改研讨会，与会的特级教师每两人之间都握手一次，那么他们之间一共握手________次．14．赵刚利用科学计算器计算0.15＋0.27时，虽然按键正确，但结果总是0，其原因是________．15．某工厂2002年的年产值为26948万元，比2001年增长8.2％．若年增长率保持不变，预计2005年该厂的年产值为________万元（结果精确到万元）．16．如图所示的曲边三角形可按下述方法作出：分别以正三角形的一个顶点为圆心，边长为半径，画弧使其经过另外两个顶点，然后擦去正三角形，三段圆弧所围成的图形就是一个曲边三角形．如果一个曲边三角形的周长为π，那么它的面积为________．三、解答题（本题共7小题，共68分．解答应写出文字说明、证明过程或演算步骤） 17．计算（本题满分8分，可用计算器计算）：＝＋＋1212222⨯________，＝＋＋12321333333++⨯________，＝＋＋123432144444444++++⨯________．由此你可以猜想出哪些类似的等式________________________________________． 18．（本题满分9分）给出两块相同的正三角形纸片（如图（1），图（2）），要求用其中一块剪拼成一个底面为正三角形的三棱锥模型，另一块剪拼成一个上下底面为正三角形的直三棱柱模型，使它们的表面面积都与原三角形的面积相等．请设计一种剪拼方法，分别用虚线标示在图（1）、图（2）中，并作简要说明：19．（本题满分9分）已知抛物线1C 的解析式是5422＋－＝x x y ，抛物线2C 与抛物线1C 关于x 轴对称，求抛物线2C 的解析式．20．（本题满分10分） 我省某城镇邮政局对甲、乙两个支局的报刊发行部2002年度报纸的发行量进行了统计，并绘成统计图如下：请根据上面统计图反映的信息，回答问题：（1）哪个支局发行《齐鲁晚报》的份数多?多多少?（2）分别写出上面两个统计图中提供的6个统计数据的中位数；（3）已知甲、乙两个支局所服务的居民区住户分别是11280户、8600户，哪个居民区平均每户订阅报纸的份数多?试说明理由．21．（本题满分10分）如图，割线ABC 与⊙O 相交于B 、C 两点，D 为⊙O 上一点，E 为弧BC 的中点，OE 交BC 于F ，DE 交AC 于G ，∠ADG ＝∠AGD ．（1）求证：AD 是⊙O 的切线；（2）如果AB ＝2，AD ＝4，EG ＝2．求⊙O 的半径．22．（本题满分10分）已知方程组⎩⎨⎧=ax y x y ＋＝2,42有两个实数解为⎩⎨⎧=11,y y x x ＝和⎩⎨⎧=,,22y y x x ＝且021≠⋅x x ，21x x ≠，设2111x x b ＋＝． （1）求a 的取值范围；（2）试用关于a 的代数式表示出b ；（3）是否存在使b ＝3的a 的值?若存在就求出所有这样的a 的值；若不存在，请说明理由．23．（本题满分12分）如图，正三角形ABC 的中心O 恰好为扇形ODE 的圆心，且点B 在扇形内．要使扇形ODE 绕点O 无论怎样转动，△ABC 与扇形重叠部分的面积总等于△ABC 的面积的31，扇形的圆心角应为多少度?说明你的理由．参考答案一、选择题（每小题选对得3分，选错、不选或选出的答案超过一个，均记零分） 1．D 2．B 3．D 4．C 5．B 6．B 7．A 8．C 9．C 10．A 11．B 12．C 二、填空题（只要求填写最后结果，每小题填对得4分）13．190 14．将小数点的位数设为0（或设定计算结果取整数） 15．34136 16．23π- 三、解答题 17．（本题满分8分）121，12321，1234321（每空1分）1234543211234543215555555555=++++++++⨯， 1123456543212345654321666666666666=++++++++++⨯， 3211234567654123456765432177777777777777=++++++++++++⨯ 5432112345678761234567876543218888888888888888=++++++++++++++⨯，7654321123456789812345678987654321999999999999999999=++++++++++++++++⨯． 每写对一个式子得1分，满分8分． 18．（本题满分9分）解：（1）如图，沿正三角形三边中点连结折起，可拼得一个底面为正三角形的三棱锥．………………………………………………………………………………………………4分 如图，在正三角形三个角上剪出三个相同的四边形，其较长的一组邻边边长为三角形边长的41，有一组对角为直角，余下部分按虚线折起，可成为一个缺上底而下底为正三角形的直三棱柱，而剪出的三个相同的四边形恰好拼成这个三棱柱的上底．…………………9分 19．（本题满分9分） 解：经检验，点A （0，5）、B （1，3）、C （－1，11）都在抛物线1C 上，点A 、B 、C 关于x 轴的对称点分别为1A （0，－5）、1B （1，－3）、1C （－1，－11），它们都在抛物线2C 上．抛物线2C 的解析式为c bx ax y ++=2，则⎪⎩⎪⎨⎧-=+--=++-=.1135c b a c b a c ，，，解得⎪⎩⎪⎨⎧-==-=.542c b a ，，所以抛物线解析式是5422-+-=x x y ． 评分要点：（1）选定抛物线1C 上的三点，得1分．（2）确定所求的抛物线2C 上的三点的坐标，得3分． （3）正确列出方程组并求出解，得4分． （4）写出解析式得1分．满分得9分． 20．（本题满分10分）解：（1）甲支局发行《齐鲁晚报》840份，乙支局发行《齐鲁晚报》880份，乙支局比甲支局多发行40份．…………………………………………………………………………4分 （2）甲图中6个统计数据的中位数是4.5，乙图中6个统计数据的中位数是3.6． …………………………………………………………………………………………………7分 （3）由统计图知，甲支局订阅报纸共2820份，平均每户订阅报纸的份数是2820÷11280＝0.25．乙支局订阅报纸2580份，平均每户订阅报纸的份数是2580÷8600＝0.3．所以乙支局所服务的居民区住户比甲支局服务的居民区住户平均每户多订阅报纸0.05份．……………………………………………………………………………………………10分 21．（本题满分10分） （1） 证明：∵ E 为弧BC 的中点， ∴ BC OE ⊥于F ．∴ ∠AGD ＋∠ODE ＝∠EGF ＋∠OED ＝90° 连结OD ，则OD ＝OE ． ∴ ∠ODE ＝∠OED ． ∵ ∠AGD ＝∠ADG ，∴ ∠ADG ＋∠ODG ＝90°，即OD ⊥AD ． ∴ AD 是⊙O 的切线．……………………………………………………………………5分 （2）由AD ＝4，AB ＝2，AC AB AD ⋅=2，得AC ＝8．∵ AD ＝AG ，∴ BG ＝2，CG ＝4．由EG ＝2，CG BG GD EG ⋅⋅=，得DG ＝4． ∴ AD ＝DG ＝GD ，∴∠ADG ＝60°，作OH ⊥ED 于H ，则∠EOH ＝60°，…………………………………………………8分在Rt △OEH 中，EH ＝21（EG ＋GD ）＝3， ∴ 23360sin =︒=EH OE ．即⊙O 的半径为233．…………………………………………………………………10分 22．（本题满分10分）（1） 由原方程组可得关于x 的二次方程：0)1(4422=+-+a x a x ．………………………………………………………………1分 ∵ 原方程组有两个不同的实数解，即上述二次方程有两个不等实根，∴ △016)]1(4[22>--=a a ，解得：21＜a ．………………………………………3分 （2） 由根与系数的关系得：a x x -=+121，4221a x x =⋅……………………………………………………………5分∴ 22121)1(4aa x x x xb -=+=⋅………………………………………………………………6分 （3） 当3=b 时，3)1(42=-aa ，解得： 21-=a ，21322>=a （舍去）．………………………………………………………9分 ∴ 所求a 的值为－2．…………………………………………………………………10分 23．（本题满分12分）解：当扇形圆心角为120°时，△ABC 与扇形重叠部分的面积，总等于△ABC 的面积的31．……………………………………………………………………………………………2分 证明如下：（1） 当扇形的圆心角与正三角形的中心角重合时，显然，△ABC 与扇形重叠部分的面积等△ABC 的面积的31．…………………………………………………………………4分 （2） 当扇形的圆心角与正三角形的中心角不重合时，如图，连结OA 、OB ，设OD 交AB 于F ，OE 交BC 于G ． ∵ O 是正三角形的中心，∴ OA ＝OB ，∠OAF ＝∠OBG ，∠AOB ＝120° ∴ ∠AOF ＝120°－∠BOF ， ∠BOG ＝120°－∠BOF ， ∠AOF ＝∠BOG ．∠AOF ≌△BOG ．…………………………………………………………………………8分 即ABC AOB OFBG S S S ∆∆==31四边形，即△ABC 与扇形重叠部分的面积，总等于△ABC 的面积的31．…………………………………………………………………………………10分 同理可证，当扇形ODE 旋转至其他位置时，结论仍成立．…………………………11分 由（1）、（2）可知，当扇形的圆心角为120°时，△ABC 与扇形重叠部分的面积，总等于△ABC 的面积的31．……………………………………………………………………12分。

山东省2003年中考试卷第Ⅰ卷（选择题共27分）一、选择题（本题共9个小题，每小题3分，共27分．每题给出的四个选项中，只有一项是符合题目要求的）1．我们经常提到的像：（1）小孔成像、（2）平面镜成像、（3）放大镜成像、（4）电影银幕上的像、（5）汽车观后镜中的像．其中（）．A．属于实像的是（1）（2）（3）B．属于虚像的是（2）（3）（4）C．由于反射而成的像是（2）（5）D．由于折射而成的像是（1）（3）（4）2．在举重比赛时，一运动员在第一阶段把150kg的杠铃很快举过头顶，第二阶段使杠铃在空中停留3s．下列关于运动员对杠铃做功的说法，正确的是（）．A．他在第一阶段内没有做功B．他在第二阶段内没做功C．他在两个阶段内都没做功D．他在两个阶段内都做了功3．安装家庭电路时，下列做法中错误的是（）．A．各电灯之间关联B．插座与电灯之间并联C．开关应控制火线D．火线、零线都要安装保险丝4．我们生活在声音的世界里，声音无处不在．下列声音：（1）工厂车间机器的轰鸣声、（2）剧场里京剧表演的演奏声、（3）清晨公园里小鸟的鸣叫声、（4）装修房子时的电钻声、（5）婚庆时的爆竹声、（6）山间小溪潺潺的流水声．其中属于噪声的是（）．A．（1）（3）（4）B．（1）（2）（5）C．（1）（4）（5）D．（1）（4）（5）（6）5．为了判断一段导线中是否有直流电通过，手边若有下列几组器材，其中最理想的一组是（）．A．被磁化的缝衣针和细棉线B．蹄型磁铁和细棉线C．小灯泡和导线D．带电的泡沫塑料球和细棉线6．一个重500N的物体，受到500N竖直向上的拉力时，则该物体（）．A．一定处于静止状态B．一定处于匀速上升状态C．一定处于匀速下降状态D．以上三种状态都有可能7．用一只量筒、水、一根细针做实验，来测木块的某些物理量．下列说法中正确的是（）．A．只能测木块的体积B．只能测木块所受的浮力C．只能测木块的体积、质量和密度D．木块的体积、所受的浮力、质量和密度都能测量8．把一个小球轻轻放入盛满水的杯子里，溢出了50g 水，则小球的质量（ ）． A ．一定等于50g B ．一定大于50g C ．大于或等于50g D ．小于或等于50g9．如图1所示，电源电压不变，闭合开关S ，当滑动变阻器的滑片P 由右向左移动时，三只电表1V 、2V 、A 的示数变化情况是（ ）． A ．1V 不变，2V 减小，A 不变 B ．1V 减小，2V 增大，A 减小 C ．1V 不变，2V 增大，A 不变 D ．1V 增大，2V 减小，A 增大图1第Ⅱ卷（非选择题 共43分）二、填空题（本题共8个小题，每小题1分，共8分） 10．原子核是由带正电的________和不带电的中子组成． 11．1kg 冰全部熔化成水后的体积是________3m ．12．使用电压表测电压时，在不能预先估计被测电压的情况下，可以用________法判断被测电压是否超过量程．13．运载火箭点火后向空中飞去，使火箭上升的力是________施加的． 14．在镊子、钳子、扳手和瓶盖起子当中，属于费力杠杆的是________． 15．滑动变阻器是用电阻率较大的合金线制成的，其原理是通过改变合金线在电路中的________来改变电阻的大小．16．2003年2月1日，美国“哥伦比亚”号航天飞机在返回大气层后，舱体温度急剧升高，最后导致航天飞机解体．这是通过________方式改变了它的内能．17．小强同学家住北园小区3号楼五楼．放学后，他从一楼上到五楼共用了20s ．若小强及书包总重为480N ，每层楼的高度为3m ，则他上楼的功率是________W ．三、作图、实验题（本题共5个小题，第18、19、20、21小题各3分，第22小题4分，共16分）18．如图2所示，一束光垂直射向一顶角为30°的玻璃三棱镜，请在图中画出光通过三棱镜的光路图．图219．今年春季在我国部分地区出现了SARS疫情，我国政府采取了强有力的措施有效地控制了该病的流行．学校为了防止SARS进入校园，规定学生每天要测量体温．小明用如图3所示的医用体温计测量体温时，他观察到体温计的初始状态如图3甲所示，然后他将体温计_________________，这样做的道理是___________________，取出体温计后观察到体温计的示数如图3乙所示，小明的体温是____________________℃．图320．在测平均速度的实验中，小车在斜面上由顶端滑过斜面的始、末位置如图4所示，小车通过的路程为________，若小车通过这段路程所用时间为2.5s，则小车在这段时间内的平均速度为________．图421．给你一个带铁芯的螺线管、蓄电池、开关、滑动变阻器，如图5所示．（1）用笔画线代替导线，把它们连接起来（连线不要交叉），要求满足以下两点要求：a．组成一个可以改变电磁铁磁性强弱的电路．b．当滑动变阻器的滑片向左滑动时，电磁铁的磁性增强．（2）标出通电电磁铁的N、S极．图522．如图6所示的电路盒，面板上有红、绿灯各一个，三个拨动开关1S 、2S 、3S ．为了在不打开盒子的情况下探究盒内的电路结构，小明做了多次实验并将实验结果填入下表．图6根据上述实验情况，在虚线框内画出盒内的电路图．四、计算题（本题共3个小题，第23小题5分，第24小题6分，第25小题8分，共19分．解答时应写出必要的文字说明、方程式和重要的演算步骤，只写出最后答案的不能得分，有数据计算的题，答案中必须写出数据和单位）23．在“观察水的沸腾”实验中，用酒精灯将烧杯中250g 、60℃的热水加热到沸腾，共用去2.5g 酒精．问：酒精完全燃烧放出的热量中，有百分之几被水吸收了？（已知实验室的气压为1标准大气压，酒精的热值为J/kg 103.07）24．在一根粗细均匀且长为20cm 的圆柱形细直木棒的表面涂上一层蜡，一端绕上适量的细铅丝（铅丝体积可以忽略不计），可以制成简易密度计．把它放入水中静止时的状态如图7所示．（1）求水对容器底面的压强．（2）当把它放入某种盐水中静止时，密度计露出水面的长度为7cm ，此盐水的密度是多少？图725．为研究某种植物在恒温下生长的规律，某中学物理兴趣小组的同学，设计制作了一台如图8所示的恒温箱．箱内安装了一根电热丝，按实际需要，电热丝每秒应向箱内提供539J 的热量（设电能全部转化为内能）．经选用合适的材料制成后，用220V 的恒压电源供电，测得该电热丝每秒实际供热1100J ．为使电热丝供热达到设计要求，在不改变电热丝阻值及电源电压的条件下，应在箱外怎样连接一个电阻元件？并通过计算确定这个电阻元件的阻值．图8参考答案一、选择题（本题共9个小题，每小题3分，共27分．每题给出的四个选项中，只有一项是符合题目要求的）1．C 2．B 3．D 4．C 5．A 6．D 7．D 8．C 9．A 二、填空题（本题共8个小题，每小题1分，共8分）10．质子 11．3101－ 12．试触 13．空气 14．镊子 15．长度 16．做功 17．288三、作图、实验题（本题共5个小题，第18、19、20、21小题各3分，第22小题4分，共16分）18．如图1所示图119．夹在腋窝中 使体温计的玻璃泡与人体充分接触36.2（或36.20） 20．0.587m （或58.7cm ） 0.235m/s （或23.5cm/s ） 注意：本题第一空的答案在0.585～0.588m 范围内；第二空的答案为0.234m/s 或0.235m/s 或0.23m/s 都算正确． 21．如图2所示注意：其他接法，只要符合题目要求都算正确．图222．如图3所示（或如图4所示）图3图4四、计算题（本题共3个小题，第23小题5分，第24小题6分，第25小题8分，共19分．解答时应写出必要的文字说明、方程式和重要的演算步骤，只写出最后答案的不能得分，有数据计算的题，答案中必须写出数据和单位）23．在1标准大气压下，沸水的温度为100℃，所以水升高的温度△t ＝100℃－60℃＝40℃水吸收的热量为 t m c Q ∆水水吸＝＝J 104.23⨯/（kg ·℃）×0.25kg ×40℃ ＝J 104.24⨯酒精燃烧放出的热量为 酒酒放＝m q QJ 107.5kg 102.5J/kg 103437⨯⨯⨯⨯＝＝－∴ ％％＝％＝＝放吸56100J105.7J 102.410044⨯⨯⨯⨯Q Q η24．（1）gh p 水＝ρ＝0.2m 9.8N/kg kg/m 10133⨯⨯⨯pa 101.963⨯＝（2）“密度计”在水中和在盐水中浸入的长度分别为15cm 和13cm ，都是漂浮，受到的浮力相等，有21浮浮＝F F ，21gSh gSh 盐水水＝ρρ，水盐水＝ρρ21h h 33kg/m 10113cmcm15⨯⨯＝33kg/m 1015.1⨯＝25．由“在220V 电压下，每秒实际供热1100J ”，根据焦耳定律，有t RU Rt I Q 2211＝= 则电热丝的电阻为Ω⨯44J1100s1)V 220(212＝＝＝Q t U R当满足设计要求时，电路中的电流为2I ，电热丝每秒供热539J ，由Rt I Q 222＝，得A 5.31s44J53922＝＝＝⨯ΩRt Q I 此时，电路中的总电阻为Ω29.623.5AV202＝＝＝总I U R 所以，应在箱外串联一个电阻'R ，其阻值为Ω=Ω-Ω9.18449.62'＝－＝总R R R。

2003年全国各地中考语文作文题精选三十一、济南市每个人的内心，都有着美好的期盼。

我们期盼学业的成功与进步，彼此的理解与信任，家庭的幸福与安康，社会的安定与发展……请以“期盼”为话题，写一篇文章。

要求：①自选角度。

②自定文体(诗歌除外)。

③自拟题目。

④不得抄袭。

⑤不少于600字。

三十二、兰州市一位著名的高空走钢索表演者，当表演取得成功时，有人问他：“高空走钢索如此危险，而你为何每次都能保证成功?”表演者说：“重要的是每次表演前，我都充分调整好自己的心态，使自己心态平和，想得多的是表演中如何集中注意力，如何把握技术要领，而不去多想表演后的一切。

”许多考试成功者，总结其“秘诀”：考前有一个良好的心态。

一位哲人曾言：你的心态失去平和，世界就倾斜了。

是啊，我们生活在二个纷繁变化的社会中，那么，我们做事、做人、学习、修性养生是否都要平和心态呢。

请以“平和心态”为话题，写篇文章。

要求：1，情感要真挚，思想要健康。

2，立意自定，题目自拟，文体不限(除诗歌外)，不少于600字。

三十三、上海闵行区从下面两个题目中任选一题，按要求写作：题目一；少年鲁迅喜欢百草园，流浪的高尔基喜欢读书，鲁彦喜欢海，陈祖芬夫妇喜欢木头和石头，而安徒生笔下的皇帝则喜欢穿新衣服……课文中提到的种种喜欢，折射出人物不同的生活经历、个性气质、审美情趣、志向追求。

请以“我喜欢”为题，写一篇六七百字的文章。

题目二；钱，是一个说不尽的话题，在生活的舞台上，演绎了无数的酸甜苦辣。

面对这个熟悉的字眼，你想起了哪些生活故事?或者，你想发表怎样的见解?请围绕这个话题，写一篇六、七百字的文章。

题目自拟。

三十四、吉林省下面两个题目任选其一。

（1）陶醉（2）阅读下面的诗句，选择你感受最深的一点，自拟题目，写一篇文章。

我们期待所有响亮的日子悄然降临我们的日子应该是花每一寸彩虹样清晰的阳光我们的日子应该是树枝繁叶茂最强壮地扎根土地我们的日子应该是天空辽阔的襟怀是飞鸟的梦想和天堂我们日子的天空一碧千里每一粒最善良的愿望在天空的温柔注目中悄声歌唱把美和善良、淳朴和真实的花子洒进每一缕细小亲热的芬芳充盈我们锐敏的呼吸(节选自丹好的《我们期待所有响亮的日子》) 作文提示：①选择你最擅长的文体抒写真情实感。