最新重庆中考数学第17题专题训练

2021级重庆中考17题行程问题专题练习（巴蜀试题集）1（巴蜀2020级初三下数学自主测试A、B 两地相距90km，甲、乙两人从两地出发相向而行，甲先出发．图中l1，l2 表示两人离A地的距离S（km）与时间t（h）的关系，结合图象，下列结论错误的是（）A.l1 是表示甲离A地的距离与时间关系的图象B.乙的速度是30km/ hC.两人相遇时间在t 1.2hD.当甲到达终点时乙距离终点还有45 k m2（巴蜀2020级初三下第三次模拟）在中考考试中，第一堂语文考试9:00开考，小恺8:00从家出发匀速步行去中考考场，5分钟后，弟弟小熙发现哥哥忘记带准考证，马上沿同一路线匀速送去给哥哥，哥哥到考场门口时发现忘带准考证，马上以之前的速度回家取，途中遇到赶来的弟弟，哥哥拿到准考证后以同样的速度赶往考场，弟弟则回到家中．哥哥与弟弟之间的距离y（米）与弟弟从家出发后步行的时间x（分）之间的关系如图所示（交接准考证的时间忽略不记）．则下列结论中，不正确的是（）A．弟弟出发20分钟时，将准考证拿给哥哥B．哥哥出发20分钟到达考场忘记拿准考证C．哥哥返回考场时，离开考还有30分钟D．哥哥返回考场时，弟弟离家还有300米3（巴蜀2020级初三上自主训练四）周末小明匀速步行从家赶往学校参加植树活动，出发30分钟后，发现忘带植树工具，于是马上掉头往回走，速度比之前每小时提高了1千米(仍保持匀速步行)，同时小明打电话给爸爸，请爸爸帮他把植树工具送过来，从小明开始打电话到爸爸出门一共用了4分钟，爸爸的速度与小明提速后的速度相同。

两人相遇后，小明接过工具立即赶往学校，爸爸则转身回家，两人速度均保持不变，爸爸在回家途中用了10分钟吃早餐，当爸爸到家时小明刚好到达学校，两人相距的路程y (千米)与小明从家出发的时间x (分钟)之间的函数关系如图所示，则小明从家到学校途中步行的总路程是千米。

4（巴蜀2020级初三下定时训练一）如图，小明和小亮同时从学校放学，两人以各自速度匀速步行回家，小明的家在学校的正西方向，小亮的家在学校的正东方向，小明准备一回家就开始做作业，打开书包时发现错拿了小亮的练习册，于是立即跑步去追小亮，终于在途中追上了小亮并交还了练习册，然后再以先前的速度步行回家，（小明在家中耽搁和交还作业的时间忽略不计）结果小明比小亮晚回到家中．如图是两人之间的距离y 米与他们从学校出发的时间x 分钟的函数关系图．则小明的家和小亮的家相距 米．5（巴蜀2020级初三下二诊考试）甲乙两地相距300km ，一辆货车和一辆轿车先后从甲地出发到乙地停止，货车先出发从甲地匀速开往乙地，货车开出一段时间后，轿车出发，匀速行驶一段时间后接到通知提速后匀速赶往乙地（提速时间不计），最后发现轿车比货车提前0.5小时到达，下图表示两车之间的距离y(km)与货车行驶的时间x(h)之间的关系，则货车行驶 小时．两车在途中相遇．6（巴蜀2020级初三下模拟考试一）甲骑自行车从A 地到B 地，甲出发1分钟后乙骑平衡车从A 第地沿同一条路线追甲，追上甲时，平衡车电量耗尽，乙立即手推平衡车返回A 地，速度变为原来的31，甲继续向B 地骑行，结果甲乙同时到达各自的目的地并停止行进.整个过程中，两人均保持各自的速度匀速行驶，甲乙两人相距的路程y （米）与甲出发的时间x （分钟）之间的部分关系如图所示，则A 、B 两地相距的路程为 米。

2020中考专题17——存在性问题之特殊三角形姓名____________ . 【方法解读】特殊二和形存化件问题L婪足指寻找符介条件的点使之构成等腰二角形、江用三角形、全第一;角形等特殊二用形.解决此类问题的美犍在于恰当地分类4M避免M籽.【例题分析】例L如图，直线产3x-3交x轴例点A,交y轴J点B,过A, B两点的他物线交x例J另一点C(3, 0).(1)求点A,B的坐标.(2)求旭物线对应的函数表认式.(3)在附物线的对称轴上是否存在点Q,使△ABQ皓笔腰三角形?若存在，求出符合条件的点Q的坐标: 若不存在.请说明毋山.例2.如凰tl知直线.kx 6与抛物线y』x'b乂，c相交十A, 3两点，口点A(l,⑷为抛物段的顶点, 点B 在x轴上.⑴求旭利线对应的函数及辽揖⑵任⑴中：次函数的第.拿限的图象上是否存在•点P,便△FOB与APOC全等?若存在，求出点P 的％标:若不存在,请说明理由.(3)若点Q是y轴上…点,HAABQ为直角三角形,求点Q的坐标.D.【巩固训练】1.（2019•止宾〉已刈抛物纹y = x'-l，j轴文于点A.。

宜纹/=代内为任总实数）出文于S , C两点.则下列结论不正确的是（）A.存在实数使得448C为等腰三角形民存在实数A ,使得&46C的内角中仃两角分别为3伊和60）C.任意实数A,伐得部为血角三角形D.存在实数4,使得M8c为等边三处形2. M图.在平行四边形ABCD中,AB 7 cm, BC 4 c0 NA-30' .点P从点A出发沿着AB边向燃B运劭, 速度为I cm/.连结印，若以运动时间为则当〔二 w时,AADP为等小」角形.3.（2019 •泰安）已知次函数】七公十）的图象。

反比例函数y =巴的图象大丁点T,与x他交丁x 点用 5.U）.若 08 二4 8, H.S^=y .（1）求反比例函数与一次函数的表达式，<2）苦点P为x粕上一点,是等股三角形.求点「的坐乐.1. （2D18・ F州）如图，池物线y = a/+bx-4经过,4（-3.0）.£（5.-4）两点, I j•地文于点C ,性接力&•4C. RC.（1）求抛物线的表达式，（2）求证，.48平分NO6（3）抛物线的对称轴卜.是否存在点M,使得M8W是以48为宜用边的汽角H角形，若存在，求山点M的坐标：苍不存在，请说刚理由.5.(2019•的卅)如图I.在平面直用坐标系中•点。

2021年重庆年中考17题一次函数图像与行程问题专题（重庆育才试题集）A、两地同时相向而行，并以各自的速度匀速行驶，途中1（育才2021级初三上定时训练二）小明和小亮分别从B会经过奶茶店C，小明先到达奶茶店C，并在C地休息了一小时，然后按原速度前往B地，小亮从B地直达A地，y（千米）与小亮出发时间x（时）的函数的图像，结果还是小明先到达目的地，下图是小明和小亮两人之间的距离请问当小明到达B地时，小亮距离A地千米.2（育才2020级初三下中考模拟5月份）一辆货车从A地匀速驶往相距350km的B地，当货车行驶1小时经过途中的C地时，一辆快递车恰好从C地出发以另一速度匀速驶往B地，当快递车到达B地后立即掉头以原来的速度匀速驶往A地．（货车到达B地，快递车到达A地后分别停止运动）行驶过程中两车与B地间的距离y（单位：km）与货车从出发所用的时间x（单位：h）间的函数关系如图所示．则货车到达B地后，快递车再行驶h到达A地．3（育才2020级初三下中考模拟二）快、慢车分别从相距180千米的甲、乙两地同时出发，沿同一路线匀速行驶，相向而行，快车到达乙地停留一段时间后，按原路原速返回甲地．慢车到达甲地比快车到达甲地早小时，慢车速度是快车速度的一半．快、慢两车到达甲地后停止行驶，两车距各自出发地的路程y（千米）与所用时间x（小时）的函数图象如图所示．在快车从乙地返回甲地的过程中，当慢车恰好在快车前，且与快车相距80千米的路程时，慢车行驶的总的时间是小时．4（育才2020级初三下中考模拟三））A、B两地之间路程为4500米，甲、乙两人骑车都从A地出发，已如甲先出发6分钟后，乙才出发，乙在A、B之间的C地追赶上甲，当乙追赶上甲后，乙立即返A地，甲继续向B地前行．甲到达B地后停止骑行．乙骑行到A地时也停止（假定乙在C地掉头的时间忽略不计），在整个骑行过程中，甲和乙均保持各自的速度匀速骑行，甲、乙两人相距的路程y（米）与甲出发的时间x（分钟）之间的关系如图所示，则乙到达A地时，甲与B地相距的路程是米．5（育才2019级初三下中考模拟一）甲乙沿着同一路线以各自的速度匀速从A地到B地，甲出发1分钟后乙随即出发，甲、乙到达B地后均立即按原路原速返回A地，甲、乙之间的距离y（米）与甲出发的时间x（分）之间的部分图象如图所示．当甲返回到A地时，乙距离B地米．6（育才2020级初三下中考模拟二练习）小刚从家出发匀速步行去学校上学．几分钟后发现忘带数学作业，于是掉头原速返回并立即打电话给爸爸，挂断电话后爸爸立即匀速跑步去追小刚，同时小刚以原速的两倍匀速跑步回家，爸爸追上小刚后以原速的倍原路步行回家．由于时间关系小明拿到作业后同样以之前跑步的速度赶往学校，并在从家出发后23分钟到校（小刚被爸爸追上时交流时间忽略不计）．两人之间相距的路程y（米）与小刚从家出发到学校的步行时间x（分钟）之间的函数关系如图所示，则小刚家到学校的路程为米．7（双福育才2020级初三下中考模拟一）小宁和弟弟小强分别从家和图书馆出发,沿同一条笔直的马路相向而行,小宁先出发5分钟后,小强骑自行车匀速回家,小宁出发时跑步，中途改为步行,且步行的速度为跑步速度的一半,到达图书馆恰好用了35分钟,两人之间的距离y(m)与小宁离开出发地的时间x(min)之间的函数图象如图所示，下列选项正确的是A.小强骑车的速度为250m/minB.小宁由跑步变为步行的时刻为15分钟C.小强到家的时刻为15分钟D.当小强到家时，小宁离图书馆的距离为1500m8（育才2020级初三下入学测试）一个阳光明媚的上午，小育和小才相约从学校沿相同的路线去学校旁边的公园写生，小育出发5分钟后小才出发，此时小育发现忘记带颜料，立即按原速原路回学校拿颜料，小育拿到颜料后，以比原速提高20%的速度赶去公园，结果还是比小才晚2分钟到公园（小育拿颜料的时间忽略不计）．在整个过程中，小才保持匀速运动，小育提速前后也分别保持匀速运动，如图所示是小育与小才之间的距离y（米）与小育出发的时间x（分钟）之间的函数图象，则学校到公园的距离为米．第17题图9（育才2020级初三上第二次月考）一条笔直的公路上顺次有A、B、C三地，甲车从B地出发往A地匀速行驶，到达A地后停止，在甲车出发的同时，乙车从B地出发往A地匀速行驶(乙车比甲上快），到达A地停留1小时后，调头按原速向C地行驶，甲乙两车相遇后，甲车速度提升至原速的1.5倍，乙车速变不变，若AB两地相距300千米，在两车行驶的过程中，甲，乙两车之间的距离y（千米）与乙车行驶时间x(时）之间的关系如图所示，则甲车到达A地后，经过时乙车到达C地.10（双福育才2020级初三下第二次诊断性测试）甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；乙车匀速前往A地，中途与乙相遇后休息了一会儿，然后以原来的速度继续行驶直到A地．设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时），y与x之间的函数图象如图所示，则乙车到达A地时甲车距B地的路程为千米．11（育才2020级初三下开学试卷）一条笔直的公路上顺次有A、B、C三地，甲车从B地出发往A地匀速行驶，到达A地后停止，在甲车出发的同时，乙车从B地出发往A地匀速行驶，到达A地停留1小时后，调头按原速向C 地行驶，若AB两地相距300千米，在两车行驶的过程中，甲、乙两车之间的距离y（千米）与乙车行驶时间x （小时）之间的函数图象如图所示，则在他们出发后经过小时相遇．12（育才2020级初三上期末试卷）自行车远动员甲准备参加一项国际自行车赛事，为此特地骑自行车从A地出发，匀速前往168千米外的B地进行拉练．出发2小时后，乙发现他忘了带某训练用品，于是马上骑摩托车从A 地出发匀速去追甲送该用品．已知乙骑摩托车的速度比甲骑自行车的速度每小时多30千米，但摩托车行驶一小时后突遇故障，修理15分钟后，又上路追甲，但速度减小了，乙追上甲交接了训练用品（交接时间忽略不计），随后立即以修理后的速度原路返回，甲继续以原来的速度骑行直至B地．如图表示甲、乙两人之间的距离S（千米）与甲骑行的时间t（小时）之间的部分图象，则当甲达到B地时，乙距离A地千米．13（育才2020级初三上开学测试）国防教育和素质拓展期间，某天小明和小亮分别从校园某条路的A，B两端同时相向出发，当小明和小亮第一次相遇时，小明觉得自己的速度太慢便决定提速至原速的倍，当他到达B端后原地休息，小亮匀速到达A端后，立即按照原速返回B端（忽略掉头时间）．两人相距的路程y（米）与小亮出发时间t（秒）之间的关系如图所示，当小明到达B端后，经过秒，小亮回到B端．14（育才2020级初三上期中试卷）小蒲家与学校之间是一条笔直的公路，小蒲从家步行前往学校的途中发现忘带作业本，便向路人借了手机打给妈妈，妈妈接到电话后，带上作业本马上赶往学校，同时小蒲沿原路返回，两人相遇后，小蒲立即赶往学校，妈妈沿原路返回家，小蒲到达学校刚好比妈妈到家晩了2分钟．若小蒲步行的速度始终不变，打电话和交接作业本的时间忽略不计，小蒲和妈妈之间的距离y米与小蒲打完电话后步行的时间x分钟之间的函数关系如图所示；则相遇后妈妈返回家的速度是每分钟米．15（育才2020级初三下入学测试）国防教育和素质拓展期间，某天小明和小亮分别从校园某条路的A，B两端同时相向出发，当小明和小亮第一次相遇时，小明觉得自己的速度太慢便决定提速至原速的32倍，当他到达B端后原地休息，小亮匀速到达A 端后，立即按照原速返回B 端（忽略掉头时间）．两人相距的路程y （米）与小亮出发时间t （秒）之间的关系如图所示，当小明到达B 端后，经过______秒，小亮回到B 端．16（育才2019级初三是哪个期末测试）甲、乙两车从A 地出发，沿同一路线驶向B 地。

专题17 圆中阴影部分的面积七种计算方法（解析版）第一部分典例剖析+针对训练方法一公式法典例1 （2022•凉山州）家具厂利用如图所示直径为1米的圆形材料加工成一种扇形家具部件，已知扇形的圆心角∠BAC＝90°，则扇形部件的面积为（ ）A．12π米2B．14π米2C．18π米2D．116π米2思路引领：连结BC，AO，90°所对的弦是直径，根据⊙O的直径为1米，得到AO＝BO=12米，根据勾股定理得到AB的长，根据扇形面积公式即可得出答案．解：连结BC，AO，如图所示，∵∠BAC＝90°，∴BC是⊙O的直径，∵⊙O的直径为1米，∴AO＝BO=12（米），∴AB=AO2+BO2=22（米），∴扇形部件的面积=90360π×（22）2=π8（米2），故选：C．总结提升：本题考查了扇形面积的计算，掌握设圆心角是n°，圆的半径为R的扇形面积为S，则S扇形=n360πR2是解题的关键．针对训练1．（2021•卧龙区二模）如图，△ABC中，D为BC的中点，以点D为圆心，BD长为半径画弧，交边BC 于点B，交边AC于点E，若∠A＝60°，∠B＝100°，BC＝6，则扇形BDE的面积为 ．思路引领：求出扇形的圆心角以及半径即可解决问题．解：∵∠A＝60°，∠B＝100°，∴∠C＝180°﹣60°﹣100°＝20°，∵DE＝DC，∴∠C＝∠DEC＝20°，∴∠BDE＝∠C+∠DEC＝40°，∴S扇形DBE=40π×32360=π．故答案为：π．总结提升：本题考查扇形的面积公式、三角形内角和定理等知识，解题的关键是记住扇形的面积公式．方法二和差法典例2（2022•荆州）如图，以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧，恰好与BC边相切，分别交AB，AC于D，E，则图中阴影部分的面积是（ ）A．3―π4B．23―πC．(6―π)33D．3―π2思路引领：作AF⊥BC，由勾股定理求出AF，然后根据S阴影＝S△ABC﹣S扇形ADE得出答案．解：由题意，以A为圆心、一定的长为半径画弧，恰好与BC边相切，设切点为F，连接AF，则AF⊥BC．在等边△ABC中，AB＝AC＝BC＝2，∠BAC＝60°，∴CF＝BF＝1．在Rt△ACF中，AF=AB2―AF2=3，∴S阴影＝S△ABC﹣S扇形ADE=12×2×3―60π×(3)2360=3―π2，故选：D．总结提升：本题主要考查了等边三角形的性质，求扇形面积，理解切线的性质，将阴影部分的面积转化为三角形的面积﹣扇形的面积是解题的关键．针对训练1．（2022•玉树市校级一模）如图，在扇形OAB中，已知∠AOB＝90°，OA＝2，过AB的中点C作CD⊥OA，CE⊥OB，垂足分别为点D，E，则图中阴影部分的面积为（ ）A．π﹣1B．π﹣2C．π﹣4D．π2―1思路引领：连接OC，求出∠AOC＝∠BOC＝45°，求出∠DCO＝∠AOC＝∠ECO＝∠COE＝45°，求出CD＝OD，CE＝OE，根据勾股定理求出CD＝OD＝OE＝CE=2，再求出阴影部分的面积即可．解：连接OC，∵OA＝2，∴OC＝0A＝2，∵∠AOB＝90°，C为AB的中点，∴∠AOC＝∠BOC＝45°，∵CD⊥OA，CE⊥OB，∴∠CDO＝∠CEO＝90°，∴∠DCO＝∠AOC＝∠ECO＝∠COE＝45°，∴CD＝OD，CE＝OE，∴2CD2＝22，2OE2＝22，即CD＝OD＝OE＝CE=2，∴阴影部分的面积S＝S扇形AOB﹣S△CDO﹣S△CEO=90π×22360―2×12×2×2=π﹣2，故选：B．总结提升：本题考查了等腰直角三角形的性质和判定，圆心角、弧、弦之间的关系，扇形面积的计算等知识点，把求不规则图形的面积转化成求规则图形的面积是解此题的关键，注意：如果扇形的圆心角为n°，半径为r，那么该扇形的面积为nπr2360．方法三等积变形法典例3（2020•朝阳）如图，点A，B，C是⊙O上的点，连接AB，AC，BC，且∠ACB＝15°，过点O作OD ∥AB交⊙O于点D，连接AD，BD，已知⊙O半径为2，则图中阴影面积为 ．思路引领：由圆周角定理可得∠AOB的度数，由OD∥AB可得S△ABD＝S△ABO，进而可得S阴影＝S扇形AOB，然后根据扇形面积公式计算即可．解：∵∠ACB＝15°，∴∠AOB＝30°，∵OD∥AB，∴S△ABD＝S△ABO，∴S阴影＝S扇形AOB=30π×22360=π3．故答案为：π3．总结提升：本题考查了圆周角定理、扇形面积公式和同底等高的两个三角形的面积相等等知识，属于常考题型，熟练掌握上述基本知识是解题的关键．针对训练1．（2022秋•天桥区期末）如图，菱形OABC的三个顶点A，B，C在⊙O上，对角线AC，OB交于点D，若⊙O的半径是23，则图中阴影部分的面积是（ ）A．2πB．6πC．33πD．3π思路引领：根据四边形OABC是菱形，得BC＝OC＝OB，即△COB是等边三角形，根据S△ADB＝S△OCD，所以图中阴影部分的面积＝S扇形COB．解：∵四边形OABC是菱形，∴BC＝OC＝OB，∴△COB是等边三角形，∴∠COB＝60°，∵S△ADB＝S△OCD，∴图中阴影部分的面积＝S扇形COB=60π×(23)2360=2π．故选：A．总结提升：本题考查的是扇形面积的计算和菱形的性质，掌握扇形的面积公式是解题的关键．方法四化零为整法（整体法）典例4（2021•天桥区二模）如图，已知正六边形的边长为4，分别以正六边形的6个顶点为圆心作半径是2的圆，则图中阴影部分的面积为 ．思路引领：先求出六边形的内角和，再根据扇形的面积公式即可求出．解：∵六边形的内角和＝（6﹣2）×180°＝720°，∴阴影面积＝6×π×22―720π×22360=16π．故答案为：16π．总结提升：本题主要考查了扇形的面积公式，学会把图中不规则图形的面积由几何关系转化为规则图形的面积．针对训练1．如图，分别以五边形的各个顶点为圆心，1cm长为半径作圆，则图中阴影部分的面积为　π　cm2．思路引领：根据多边形的外角和为360°可得阴影部分的面积为半径为1的圆的面积，再利用圆的面积计算公式可得答案．解：图中阴影部分的面积为π×12＝π．故答案为：π．总结提升：此题主要考查了多边形的外角，关键是掌握多边形的外角和为360°．方法五割补法（拼接法）典例5（2022•铜仁市）如图，在边长为6的正方形ABCD中，以BC为直径画半圆，则阴影部分的面积是（ ）A．9B．6C．3D．12思路引领：设AC与半圆交于点E，半圆的圆心为O，连接BE，OE，证明BE＝CE，得到弓形BE的面积＝弓形CE的面积，则S阴影=S△ABE=S△ABC―S△BCE=12×6×6―12×6×3=9．解：设AC与半圆交于点E，半圆的圆心为O，连接BE，OE，∵四边形ABCD是正方形，∴∠OCE＝45°，∵OE＝OC，∴∠OEC＝∠OCE＝45°，∴∠EOC＝90°，∴OE垂直平分BC，∴BE＝CE，∴弓形BE的面积＝弓形CE的面积，∴S阴影=S△ABE=S△ABC―S△BCE=12×6×6―12×6×3=9，故选：A．总结提升：本题主要考查了求不规则图形的面积，正方形的性质，等腰直角三角形的性质，圆的性质，熟知相关知识是解题的关键．针对训练1．（2021•郑州模拟）如图，在扇形CBA中，∠ACB＝90°，连接AB，以BC为直径作半圆，交AB于点D．若阴影部分的面积为（π﹣1），则阴影部分的周长为 ．思路引领：根据BC为直径可知∠CDB＝90°，在等腰直角三角形ABC中，CD垂直平分AB，CD＝DB，D为半圆的中点，设AC＝BC＝m，则AB=2m，CD＝AD＝BD=22m，阴影部分的面积可以看作是扇形ACB的面积与△ADC的面积之差，据此求得直角三角形的边长，进而求得AB和CD的长，进一步求得阴影部分的周长．解：设BC的中点为O，连接OD，连接CD，∵以BC为直径作半圆，交AB于点D．∴CD⊥AB，∵AC＝BC，∠ACB＝90°，∴AD＝BD，CD=12 AB，∴CD＝BD，∴CD=BD，∵AD＝BD，CO＝BO，∴OD∥AC，∴∠BOD＝90°，设AC＝BC＝m，则AB=2m，CD＝AD＝BD=22 m，∵阴影部分的面积为（π﹣1），∴S阴影部分＝S扇形ACB﹣S△ADC=14π•m2―12×（22m）2＝π﹣1．∴14πm2―14m2＝π﹣1，∴14m2＝1，∴m＝2，∴AC＝BC＝2，AB＝22，OC＝OB＝1，∴AB的长为：90⋅π×2180=π，BD的长为：90⋅π×1180=12π，∴阴影部分的周长为：π+2×12π+22+2＝2π+22+2故答案为：2π+22+2．总结提升：本题考查了扇形的面积和弧长的计算，等腰直角三角形的性质，正确的作出辅助线是解题的关键．方法6 图形变化法（旋转、平移、翻折）典例6（2022•武威模拟）在△ABC中，已知∠ABC＝90°，∠BAC＝30°，BC＝1．如图所示，将△ABC 绕点A按逆时针方向旋转90°后得到△AB'C'．则图中阴影部分的面积为 ．思路引领：解直角三角形得到AB=3BC=3，AC＝2BC＝2，然后根据扇形的面积公式即可得到结论．解：∵∠ABC＝90°，∠BAC＝30°，BC＝1，∴AB=3BC=3，AC＝2BC＝2，∴图中阴影部分面积＝S扇形ACC′﹣S扇形ADB′﹣S△AB′C′=90⋅π⋅22360―60⋅π⋅(3)2360―12×1×3=π―32，故答案为：π―32；总结提升：本题主要考查了图形的旋转，扇形的面积公式，解直角三角形，熟练掌握扇形的面积公式是解决问题的关键．针对训练1．（2022•西宁）如图，等边三角形ABC内接于⊙O，BC＝23，则图中阴影部分的面积是　4π3　．思路引领：根据内接于圆O的等边三角形的性质可得S△AOB＝S△AOC，∠AOC＝120°，将阴影部分的面积转化为扇形AOC的面积，利用扇形面积的公式计算可求解．解：∵△ABC为等边三角形，∴S△BOC＝S△AOC，∠AOC＝120°，在△OBC中，OB＝OC，∠BOC＝120°，BC＝23，∴OB＝OC＝2，∴S阴影＝S扇形AOC=120π×22360=4π3，故答案为：4π3．总结提升：本题主要考查扇形面积的计算，等边三角形的性质，掌握扇形面积公式是解题的关键．典例7（2022•九龙坡区自主招生）如图，正方形ABCD的边长为4，O为对角线的交点，点E，F分别为BC，AD的中点，以C为圆心，4为半径作圆弧BD，再分别以E，F为圆心，2为半径作圆弧BO，OD，则图中阴影部分的面积为 ．（结果保留π）思路引领：连接BD，根据在同圆或等圆中，相等的圆心角所对的弧，所对的弦分别相等，利用面积割补法可得阴影部分的面积等于弓形面积，即等于扇形CBD减去直角三角形CBD的面积之差．解：连接BD，EF，如图，∵正方形ABCD的边长为4，O为对角线的交点，由题意可得：EF，BD经过点O，且EF⊥AD，EF⊥CB．∵点E，F分别为BC，AD的中点，∴FD＝FO＝EO＝EB＝2，∴OB=OD，OB＝OD．∴弓形OB＝弓形OD．∴阴影部分的面积等于弓形BD的面积．∴S阴影＝S扇形CBD﹣S△CBD=90π×42360―12×4×4=4π﹣8．故答案为：4π﹣8．总结提升：本题主要考查了正方形的性质，扇形面积的计算．通过添加适当的辅助线将不规则的阴影部分的面积转化成规则图形的面积的差是解题的关键．针对训练1．（2021•重庆模拟）如图，在正方形ABCD中，扇形BAD的半径AB＝4，以AB为直径的圆与正方形的对角线BD相交于O，连接AO．则图中阴影部分的面积为 ．（结果保留π）思路引领：理由圆周角定理得出AO⊥BD，利用正方形的性质性质和等腰直角三角形的性质得出OD＝OA ＝OB，结合转化思想得出阴影部分面积＝S扇形ABD﹣S△ADC，进而得出答案．解：如图，∵AB是直径，∴∠AOB＝90°，∴AO⊥BD，∵AB＝AD＝4，∠BAD＝90°，∴OD＝OA＝OB，∴S弓形OA＝S弓形OB，∴阴影部分面积＝S扇形ABD﹣S△ADC=14π×42―12×4×4=4π﹣8，故答案为4π﹣8．总结提升：本题考查正方形的性质，扇形的面积等知识，解题的关键是学会把不规则图形转化为规则图形，属于中考常考题型．典例8（2019•招远市一模）如图，CD是⊙O的直径，AB是⊙O的弦，AB⊥CD，垂足为G，OG：OC＝3：5，AB＝8．点E为圆上一点，∠ECD＝15°，将CE沿弦CE翻折，交CD于点F，图中阴影部分的面积＝ ．思路引领：根据AB⊥CD，垂足为G，OG：OC＝3：5，AB＝8，可以求得⊙O的半径；要求阴影部分的面积只要做出合适的辅助线，然后利用锐角三角函数、扇形的面积和三角形的面积即可解答本题．解：如图，连接AO，将阴影部分沿CE翻折，点F的对应点为M，过点M作MN⊥CD于点N，∵CD为⊙O的直径，AB⊥CD，AB＝8，∴AG=12AB＝4，∵OG：OC＝3：5，AB⊥CD，垂足为G，∴设⊙O的半径为5k，则OG＝3k，∴（3k）2+42＝（5k）2，解得，k＝1或k＝﹣1（舍去），∴5k＝5，即⊙O的半径是5；∵∠ECD＝15°，由对称性可知，∠DCM＝30°，S阴影＝S弓形CBM，连接OM，则∠MOD＝60°，∴∠MOC＝120°，过点M作MN⊥CD于点N，∴MN＝MO•sin60°＝5×3 2，∴S阴影＝S扇形OMC﹣S△OMC=120×π×25360―2534=25π3―2534，即图中阴影部分的面积是：25π3―2534．总结提升：本题考查翻折变换、扇形的面积、垂径定理，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答问题．针对训练1．（如图，将半径为4cm的圆形纸片折叠后，圆弧恰好经过圆心O，折痕为AB，则图中阴影部分的面积为 ．思路引领：作OC⊥AB于C，交AB于点D，连接AO，BO，AD，BD，根据轴对称的性质可以得出CO＝CD，由三角函数值就可以求出∠AOB的度数，由扇形的面积﹣三角形AOB的面积就可以得出结论．解：作OC⊥AB于C，交AB于点D，连接AO，BO，AD，BD，∴∠ACO＝90°．∵△AOB与△ADB关于AB对称，∴△AOB≌△ADB∴AO＝AD，∠ACO＝∠ACD＝90°，∴CO＝CD．∵OD＝AO＝4，∴OC＝2．在Rt△AOC中，由勾股定理，得AC＝23．∵cos∠AOC=COAO=12，∴∠AOC＝60°．∵AO＝BO，OC⊥AB，∴∠AOB＝2∠AOC＝120°．AB＝2AC＝43．∴S扇形AOBD=120π×16360=163π．∵S△AOB=43×22=43．阴影部分的面积为：（163π―43）cm2．故答案为：（163π―43）cm2．总结提升：本题考查了轴对称的性质的运用，勾股定理的运用，三角函数值的运用，扇形的面积公式的运用，三角形的面积公式的运用，解答时运用轴对称的性质求解是关键．方法七重叠求余法例七（2022•鄂尔多斯二模）如图，直径AB为6的半圆，绕A点逆时针旋转60°，此时点B到了点B′，则图中阴影部分的面积是 ．思路引领：根据阴影部分的面积＝以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积，即可求解．解：阴影部分的面积＝以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积＝扇形ABB′的面积，则阴影部分的面积是：60π×62360=6π，故答案为：6π．总结提升：本题主要考查了扇形的面积的计算，正确理解阴影部分的面积＝以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积＝扇形ABB′的面积是解题的关键．针对训练1．（2022•市南区校级一模）如图所示，在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，BC＝2，将三角形绕着BC的中点O逆时针旋转60°，点A的对应点为E，则图中阴影部分的面积为 ．思路引领：如图，连接OE，OA．根据S阴＝S扇形EOA+S△EOF﹣S△BOF﹣S△AOB﹣S△PBE，求解即可．解：如图，连接OE，OA．由题意可知△BOF为等边三角形．∴OB＝OF＝BF＝1，∴S△BOF=3 4，在Rt△ABC中，∵BC＝2，∠CAB＝30°，∴AB＝2BC＝4，AC＝DE＝23，∴S△EOF=12•OF•DE=3，∵OF＝OD，∴S△EOF＝S△DEO=3，∵∠AOE＝60°，AO=AC2+OC2=(23)2+12=13，∴S扇形EOA=60⋅π⋅(13)2360=13π6，由题意，△BPE为直角三角形，BE＝EF﹣BF＝4﹣1＝3，∴BP=12BE=32，PE=32―(32)2=332，∴S△PBE=12×32×332=938，∴S阴＝S扇形EOA+S△EOF﹣S△BOF﹣S△AOB﹣S△PBE=13π6+3―34―3―938=13π6―1138．解法二：可以根据S阴＝S△APE+（S扇形AOE﹣S△AOE）计算．总结提升：本题考查扇形的面积，旋转变换，解直角三角形等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．第二部分专题提优训练一．选择题（共15小题）1．（2022•兰州）如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板，该展板的部分示意图如图2所示，它是以O为圆心，OA，OB长分别为半径，圆心角∠O＝120°形成的扇面，若OA＝3m，OB＝1.5m，则阴影部分的面积为（ ）A．4.25πm2B．3.25πm2C．3πm2D．2.25πm2思路引领：根据S阴＝S扇形DOA﹣S扇形BOC，计算即可．解：S阴＝S扇形DOA﹣S扇形BOC=120π×9360―120π×94360＝2.25πm2．故选：D．总结提升：本题考查的是扇形面积的计算，掌握扇形的面积公式S=nπR2360是解题的关键．2．（2022秋•西华县期末）如图，在半径为2，圆心角为90°的扇形内，以BC为直径作半圆，交弦AB于点D，则图中阴影部分的面积是（ ）A．π﹣1B．π﹣2C．12π﹣1D．12π+1思路引领：已知BC为直径，则∠CDB＝90°，在等腰直角三角形ABC中，CD垂直平分AB，CD＝DB，D为半圆的中点，阴影部分的面积可以看作是扇形ACB的面积与△ADC的面积之差．解：在Rt△ACB中，AB=22+22=22，∵BC是半圆的直径，∴∠CDB＝90°，在等腰Rt△ACB中，CD垂直平分AB，CD＝BD=2，∴D为半圆的中点，∴S阴影部分＝S扇形ACB﹣S△ADC=12π×22―12×（2）2＝π﹣1．故选：A．总结提升：本题主要考查扇形面积的计算，在解答此题时要注意不规则图形面积的求法．3．（2022•泰安）如图，四边形ABCD中，∠A＝60°，AB∥CD，DE⊥AD交AB于点E，以点E为圆心，DE为半径，且DE＝6的圆交CD于点F，则阴影部分的面积为（ ）A．6π﹣93B．12π﹣93C．6π―932D．12π―932思路引领：根据平行线的性质，扇形的面积公式，三角形面积公式解答即可．解：过点E作EG⊥DF交DF于点G，∵∠A＝60°，AB∥CD，DE⊥AD交AB于点E，∴∠GDE＝∠DEA＝30°，∵DE＝EF，∴∠EDF＝∠EFD＝30°，∴∠DEF＝120°，∵∠GDE＝30°，DE＝6，∴GE＝3，DG＝33，∴DF＝63，阴影部分的面积=120π×36360―12×63×3＝12π﹣93，故选：B．总结提升：本题主要考查了扇形面积和平行线的性质，熟练掌握扇形面积公式是解决本题的关键．4．（2022•达州）如图所示的曲边三角形可按下述方法作出：作等边△ABC，分别以点A，B，C为圆心，以AB长为半径作BC，AC，AB，三弧所围成的图形就是一个曲边三角形．如果一个曲边三角形的周长为2π，则此曲边三角形的面积为（ ）A．2π﹣23B．2π―3C．2πD．π―3思路引领：此三角形是由三段弧组成，如果周长为2π，则其中的一段弧长为2π3，所以根据弧长公式可得60πr 180=2π3，解得r＝2，即正三角形的边长为2．那么曲边三角形的面积就＝三角形的面积+三个弓形的面积．解：设等边三角形ABC的边长为r，∴60πr180=2π3，解得r＝2，即正三角形的边长为2，∴这个曲边三角形的面积＝2×3×12+（60π×4360―3）×3＝2π﹣23，故选：A．总结提升：本题考查了扇形面积的计算．此题的关键是明确曲边三角形的面积就＝三角形的面积+三个弓形的面积，然后再根据所给的曲边三角形的周长求出三角形的边长，从而求值．5．现在很多家庭都使用折叠型餐桌来节省空间，两边翻开后成圆形桌面（如图①），餐桌两边AB和CD 平行且相等（如图②），小华用皮尺量出BD＝1米，BC＝0.5米，则阴影部分的面积为（ ）A．（π12―38）平方米B．（π6―38）平方米C．（π12―34）平方米D．（π6―34）平方米思路引领：设圆心为O，连接CO，过点O作OE⊥CD于点E，进而得出CD，EO的长以及∠COD的度数，进而由S弓形CD面积＝S扇形COD﹣S△COD得出弓形CD的面积，进一步即可求得阴影部分的面积．解：设圆心为O，连接CO，过点O作OE⊥CD于点E，由题意可得出：∠BCD＝90°，∴BD是⊙O的直径，∵BD＝1米，BC＝0.5米，∴BC=12BD，CD=BD2―CD2=32米，∴∠BDC＝30°，∴OE=12OD=14米，∵OC＝OD，∴∠OCD＝∠BDC＝30°，∴∠COD＝120°，∴S弓形CD面积＝S扇形COD﹣S△COD=120π×(12)2360―12×14×32，＝（π12―316）平方米，∴阴影部分的面积为：2×（π12―316）＝（π6―38）平方米．∴故选：B．总结提升：此题主要考查了勾股定理以及扇形面积计算以及三角形面积求法等知识，熟练掌握特殊角的三角函数关系是解题关键．6．（2022•鞍山）如图，在矩形ABCD中，AB＝2，BC=3，以点B为圆心，BA长为半径画弧，交CD于点E，连接BE，则扇形BAE的面积为（ ）A．π3B．3π5C．2π3D．3π4思路引领：解直角三角形求出∠CBE＝30°，推出∠ABE＝60°，再利用扇形的面积公式求解．解：∵四边形ABCD是矩形，∴∠ABC＝∠C＝90°，∵BA＝BE＝2，BC=3，∴cos∠CBE=CBBE=32，∴∠CBE＝30°，∴∠ABE＝90°﹣30°＝60°，∴S扇形BAE=60⋅π⋅22360=2π3，故选：C．总结提升：本题考查扇形的面积，矩形的性质等知识，解题的关键是求出∠CBE的度数．7．（2022•赤峰）如图，AB是⊙O的直径，将弦AC绕点A顺时针旋转30°得到AD，此时点C的对应点D 落在AB上，延长CD，交⊙O于点E，若CE＝4，则图中阴影部分的面积为（ ）A．2πB．22C．2π﹣4D．2π﹣22思路引领：连接OE，OC，BC，推出△EOC是等腰直角三角形，根据扇形面积减三角形面积计算即可．解：连接OE，OC，BC，由旋转知AC＝AD，∠CAD＝30°，∴∠BOC＝60°，∠ACE＝（180°﹣30°）÷2＝75°，∴∠BCE＝90°﹣∠ACE＝15°，∴∠BOE＝2∠BCE＝30°，∴∠EOC＝90°，即△EOC为等腰直角三角形，∵CE＝4，∴OE＝OC＝22，∴S阴影＝S扇形OEC﹣S△OEC=90π×(22)2360―12×22×22=2π﹣4，故选：C．总结提升：本题主要考查旋转的性质及扇形面积的计算，熟练掌握扇形面积的计算是解题的关键．8．（2022•毕节市）如图，一件扇形艺术品完全打开后，AB，AC夹角为120°，AB的长为45cm，扇面BD 的长为30cm，则扇面的面积是（ ）A．375πcm2B．450πcm2C．600πcm2D．750πcm2思路引领：先求出AD的长，再根据扇形的面积公式求出扇形BAC和扇形DAE的面积即可．解：∵AB的长是45cm，扇面BD的长为30cm，∴AD＝AB﹣BD＝15cm，∵∠BAC＝120°，∴扇面的面积S＝S扇形BAC﹣S扇形DAE=120π×452360―120π×152360＝600π（cm2），故选：C．总结提升：本题考查了扇形的面积计算，能熟记扇形的面积公式是解此题的关键，注意：圆心角为n°，半径为r的扇形的面积S=nπr2 360．9．（2022•山西）如图，扇形纸片AOB的半径为3，沿AB折叠扇形纸片，点O恰好落在AB上的点C处，图中阴影部分的面积为（ ）A．3π﹣33B．3π―932C．2π﹣33D．6π―932思路引领：根据折叠的想找得到AC＝AO，BC＝BO，推出四边形AOBC是菱形，连接OC交AB于D，根据等边三角形的性质得到∠CAO＝∠AOC＝60°，求得∠AOB＝120°，根据菱形和扇形的面积公式即可得到结论．解：沿AB折叠扇形纸片，点O恰好落在AB上的点C处，∴AC＝AO，BC＝BO，∵AO＝BO，∴四边形AOBC是菱形，连接OC交AB于D，∵OC＝OA，∴△AOC是等边三角形，∴∠CAO＝∠AOC＝60°，∴∠AOB＝120°，∵AC＝3，∴OC＝3，AD=32AC=332，∴AB＝2AD＝33，∴图中阴影部分的面积＝S扇形AOB﹣S菱形AOBC=120π×32360―12×3×33=3π―932，故选：B．总结提升：本题考查了扇形面积的计算，菱形的判定和性质，等边三角形的判定和性质，正确地作出辅助线是解题的关键．10．（2022•连云港）如图，有一个半径为2的圆形时钟，其中每个相邻刻度间的弧长均相等，过9点和11点的位置作一条线段，则钟面中阴影部分的面积为（ ）A．23π―32B．23π―3C．43π﹣23D．43π―3思路引领：连接OA、OB，过点O作OC⊥AB，根据等边三角形的判定得出△AOB为等边三角形，再根据扇形面积公式求出S扇形AOB=23π，再根据三角形面积公式求出S△AOB=3，进而求出阴影部分的面积．解：连接OA、OB，过点O作OC⊥AB，由题意可知：∠AOB＝60°，∵OA＝OB，∴△AOB为等边三角形，∴AB＝AO＝BO＝2∴S扇形AOB=60π×22360=23π，∵OC⊥AB，∴∠OCA＝90°，AC＝1，∴OC=3，∴S△AOB=12×2×3=3，∴阴影部分的面积为：23π―3；故选：B．总结提升：本题考查有关扇形面积、弧长的计算，熟练应用面积公式，其中作出辅助线是解题关键．二．填空题11．（2020•巩义市二模）如图，点A、B、C在半径为8的⊙O上，过点B作BD∥AC，交OA延长线于点D．连接BC，且∠BCA＝∠OAC＝30°，则图中阴影部分的面积为　．思路引领：连接OB，交CA于E，根据圆周角定理得到∠BOA＝60°，根据平行线的性质得到∠D＝∠OAC ＝30°，即可得出∠OBD＝90°，解直角三角形求出BD，分别求出△BOD的面积和扇形AOB的面积，即可得出答案．解：连接OB，交CA于E，∵∠C＝30°，∠C=12∠BOA，∴∠BOA＝60°，∵BD∥AC，∴∠D＝∠OAC＝30°，∴∠OBD＝90°，∴BD=3OB＝83，∴S阴影＝S△BDO﹣S扇形AOB=12×8×83―60π×82360=323―32π3，故答案为323―32π3．总结提升：本题考查了平行线的性质，圆周角定理，扇形的面积，三角形的面积，解直角三角形等知识点的综合运用，题目比较好，难度适中．12．（2021•宛城区一模）如图所示，在扇形OAB中，∠AOB＝90°，OA＝2，长为2的线段CD的两个端点分别在线段OA、OB上滑动，E为CD的中点，点F在AB上，连接EF、BE．若AF的长是π3，则线段EF的最小值是 ，此时图中阴影部分的面积是 ．思路引领：如图，连接OF，OE，BF，取OF的中点T，连接BT．根据弧长求得∠AOF＝30°，jk证明△OBF是等边三角形，利用直角三角形斜边中线的性质求出OE，EF≥OF﹣OE＝1，推出当O，E，F共线时，EF的值最小，此时点E与点T重合，求出BT，然后根据S阴影＝S扇形BOF﹣S△BOT求得阴影的面积．解：如图，连接OF，OE，BF，取OF的中点T，连接BT．∵AF的长是π3，OA＝2，∴π3=nπ×2180，∴n＝30，∴∠AOF＝30°，∵∠AOB＝90°，∴∠BOF＝60°，∵CE＝DE，∴OE=12CD=12×2=1，∵OF＝2，∴EF≥OF﹣OE＝1，∴当O，E，F共线时，EF的值最小，此时点E与点T重合，∴此时EF＝1，∵OF＝OB，∠BOF＝60°，∴△BOF是等边三角形，∵OT＝TF，∴BT⊥OF，∴BE＝BT=32OB=3，∴此时S阴影＝S扇形BOF﹣S△BOT=60π×22360―12×3×1=23π―32．故答案为：1，23π―32．总结提升：本题考查了扇形的面积，等边三角形的判定，直角三角形斜边中线的性质等知识，明确当O，E，F共线时，EF的值最小是解题的关键．13．（2022•贵港）如图，在▱ABCD中，AD=23AB，∠BAD＝45°，以点A为圆心、AD为半径画弧交AB于点E，连接CE，若AB＝32，则图中阴影部分的面积是　．思路引领：过点D作DF⊥AB于点F，根据等腰直角三角形的性质求得DF，从而求得EB，最后由S阴影＝S▱ABCD−S扇形ADE−S△EBC结合扇形面积公式、平行四边形面积公式、三角形面积公式解题即可．解：过点D作DF⊥AB于点F，∵AD=23AB，∠BAD＝45°，AB＝32，∴AD=23×32=22，∴DF＝AD sin45°＝22×22=2，∵AE＝AD＝22，∴EB＝AB−AE=2，∴S阴影＝S▱ABCD−S扇形ADE−S△EBC＝32×2―45π×(22)2360―12×2×2＝52―π，故答案为：52―π．总结提升：本题考查等腰直角三角形、平行四边形的性质、扇形的面积公式等知识，是重要考点，准确添加辅助线是解题关键．14．（2020春•亭湖区校级期中）如图，AB是⊙O的直径，CD是弦，∠BCD＝30°，OA＝6，则阴影部分的面积是　．思路引领：根据扇形的面积公式计算即可．解：∵∠BOD＝2∠DCB，∠DCB＝30°，∴∠BOD＝60°，∴S扇形OBD=60⋅π⋅62360=6π，故答案为6π．总结提升：本题考查扇形的面积，圆周角定理等知识，解题的关键是计算扇形的面积公式，属于中考常考题型．15．（2022•黔西南州）如图，边长为4的正方形ABCD的对角线交于点O，以OC为半径的扇形的圆心角∠FOH＝90°．则图中阴影部分面积是 ．思路引领：证明△OBE≌△OCG（SAS），推出S△OBE＝S△OCG，推出S四边形OECG＝S△OBC＝4，再根据S 阴＝S扇形OFH﹣S四边形OECG，求解即可．解：如图，∵四边形ABCD是正方形，∴AC⊥BD，OA＝OC＝OB＝OD，∠OBE＝∠OCG＝45°，S△OBC=14S四边形ABCD＝4，∵∠BOC＝∠EOG＝90°，∴∠BOE＝∠COG，在△BOE和△COG中，∠BOE=∠COGOB=OC∠OBE=∠OCG，∴△OBE≌△OCG（SAS），∴S△OBE＝S△OCG，∴S四边形OECG＝S△OBC＝4，∵△OBC是等腰直角三角形，BC＝4，∴OB＝OC＝22，∴S阴＝S扇形OFH﹣S四边形OECG=90π⋅(22)2360―4＝2π﹣4，故答案为：2π﹣4．总结提升：本题考查扇形的面积，全等三角形的判定和性质，正方形的性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．16．（2020•康巴什一模）如图，边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1，边B1C1与CD交于点O，则图中阴影部分的面积为 ．思路引领：先根据正方形的边长，求得CB1＝OB1＝AC﹣AB1=2―1，进而得到S△OB1C=12（2―1）2，再根据S△AB1C1=12，以及扇形的面积公式即可得出图中阴影部分的面积．解：连接DC1，∵∠CAC1＝∠DCA＝∠COB1＝∠DOC1＝45°，∴∠AC1B1＝45°，∵∠ADC＝90°，∴A，D，C1在一条直线上，∵四边形ABCD是正方形，∴AC=2，∠OCB1＝45°，∴CB1＝OB1∵AB1＝1，∴CB1＝OB1＝AC﹣AB1=2―1，∴S△OB1C=12•OB1•CB1=12（2―1）2，∵S△AB1C1=12AB1•B1C1=12×1×1=12，∴图中阴影部分的面积=45⋅π⋅(2)2360―12（2―1）2―12=π4―2+2．故答案为π4―2+2．总结提升：本题考查了旋转的性质，正方形性质、勾股定理以及扇形面积的计算等知识点的综合应用，主要考查学生运用性质进行计算的能力．解题时注意：旋转前、后的图形全等．17．（2021秋•招远市期末）如图，在扇形OAB中，点C在AB上，∠AOB＝90°，∠ABC＝30°，AD⊥BC 于点D，连接AC，若OA＝4，则图中阴影部分的面积为　．思路引领：连接OC，作CM⊥OB于M，根据等腰直角三角形的性质得出∠ABO＝∠OAB＝45°，AB＝42，进而得出∠OCB＝OBC＝75°，即可得到∠BOC＝30°，解直角三角形求得AD、BD、CM，然后根据S阴影＝S△ABD+S△AOB﹣S扇形OAB+（S扇形OBC﹣S△BOC）计算即可求得．解：连接OC，作CM⊥OB于M，∵∠AOB＝90°，OA＝OB＝2，∴∠ABO＝∠OAB＝45°，AB=42，∵∠ABC＝30°，AD⊥BC于点D，∴AD=12AB=22，BD=32AB=26，∵∠ABO＝45°，∠ABC＝30°，∴∠OBC＝75°，∵OB＝OC，∴∠OCB＝∠OBC＝75°，∴∠BOC＝30°，∴∠AOC＝60°，CM=12OC=12×4=2，∴S阴影＝S△ABD+S△AOB﹣S扇形OAB+（S扇形OBC﹣S△BOC）＝S△ABD+S△AOB﹣S扇形OAC﹣S△BOC=12×22×26+12×4×4―12×4×2―60π×42360=4+43―8π3．故答案为：4+43―8π3．总结提升：此题考查了运用切割法求图形的面积．解决本题的关键是把所求的面积转化为容易算出的面积的和或差的形式．。

热点17 锐角三角函数【命题趋势】锐角三函数是中考数学中必考内容之一，所占比例8—15分，题目数量2-3题。

一般小题会有一个，一般为填空或计算，考查学生对几个特殊角的三角函数值的记忆情况。

大题一般也会有一题，主要是考查锐角三角函数的实际应用，往往会结合仰角和俯角，坡度等概念进行设计问题，当然在其他解答题中也可能会用到三角函数，比如在计算一些线段长度，会与解直角三角形，或者与圆、四边形结合而形成难度中等的解答题。

【满分技巧】一、整体把握知识结构二．重点知识1.Rt△ABC中(1)∠A的对边与斜边的比值是∠A的正弦，记作sinA＝∠A的对边斜边(2)∠A的邻边与斜边的比值是∠A的余弦，记作cosA＝∠A的邻边斜边(3)∠A的对边与邻边的比值是∠A的正切，记作tanA＝∠A的对边∠A的邻边(4)∠A的邻边与对边的比值是∠A的余切，记作cota＝∠A的邻边∠A的对边2.特殊值的三角函数：asin a cosa tana cota30° 12 32 33 345° 22 22 11 60° 3212333【限时检测】（建议用时：30分钟） 一、 选择题1. (2019 湖北省宜昌市)如图，在5×4的正方形网格中，每个小正方形的边长都是1，△ABC 的顶点都在这些小正方形的顶点上，则sin∠BAC 的值为（ ）A ．B ．C ．D ．【答案】D【解析】如图，过C 作CD ⊥AB 于D ，则∠ADC ＝90°， ∴AC ＝AD 2+CD 2＝5． ∴sin∠BAC ＝CD AC ＝45故选：D ．2. (2019 湖南省湘西市)如图，在△ABC 中，∠C ＝90°，AC ＝12，AB 的垂直平分线EF 交AC 于点D ，连接BD ，若cos∠BDC ＝，则BC 的长是（ ）A ．10B ．8C ．4D ．2【答案】D【解析】∵∠C ＝90°，cos∠BDC ＝57 ，设CD ＝5x ，BD ＝7x ， ∴BC ＝2 6 x ，∵AB 的垂直平分线EF 交AC 于点D ， ∴AD ＝BD ＝7x ， ∴AC ＝12x ， ∵AC ＝12， ∴x ＝1， ∴BC ＝2 6 ； 故选：D ．3. (2019 湖南省长沙市)如图，△ABC 中，AB ＝AC ＝10，tan A ＝2，BE ⊥AC 于点E ，D 是线段BE 上的一个动点，则CD +BD 的最小值是（ ）A ．2B ．4C ．5D ．10【答案】B【解析】如图，作DH ⊥AB 于H ，CM ⊥AB 于M ．∵BE ⊥AC ， ∴∠ABE ＝90°，∵tan A ＝BEAE =2，设AE ＝a ，BE ＝2a ，则有：100＝a 2+4a 2， ∴a 2＝20，∴a ＝2 5 或﹣2 5 （舍弃），∴BE ＝2a ＝4 5 ，∵AB ＝AC ，BE ⊥AC ，CM ⊥AC ，∴CM ＝BE ＝4 5 （等腰三角形两腰上的高相等））∵∠DBH＝∠ABE，∠BHD＝∠BEA，∴sin∠DBH＝＝＝，∴DH＝BD，∴CD+BD＝CD+DH，∴CD+DH≥CM，∴CD+BD≥4 5 ，∴CD+BD的最小值为4 5 ．故选：B．4. (2019 山东省泰安市)如图，一艘船由A港沿北偏东65°方向航行30km至B港，然后再沿北偏西40°方向航行至C港，C港在A港北偏东20°方向，则A，C两港之间的距离为（）km．A．30+30B．30+10C．10+30D．30【答案】B【解析】根据题意得，∠CAB＝65°﹣20°，∠ACB＝40°+20°＝60°，AB＝30，过B作BE⊥AC于E，∴∠AEB＝∠CEB＝90°，在Rt△ABE中，∵∠ABE＝45°，AB＝30，∴AE＝BE＝AB＝30km，在Rt△CBE中，∵∠ACB＝60°，∴CE＝BE＝10km，∴AC＝AE+CE＝30+10，∴A，C两港之间的距离为（30+10）km，故选：B．5. (2019 陕西省)如图，在△ABC中，∠B=30°，∠C=45°，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E。

专题17 四边形周长求最值问题1．（2021·四川遂宁·中考真题）如图，已知二次函数的图象与x 轴交于A 和B （－3，0）两点，与y 轴交于C （0，－3），对称轴为直线1x =-，直线y ＝－2x ＋m 经过点A ，且与y 轴交于点D ，与抛物线交于点E ，与对称轴交于点F ．（1）求抛物线的解析式和m 的值；（2）在y 轴上是否存在点P ，使得以D 、E 、P 为顶点的三角形与△AOD 相似，若存在，求出点P 的坐标；若不存在，试说明理由；（3）直线y ＝1上有M 、N 两点（M 在N 的左侧），且MN ＝2，若将线段MN 在直线y ＝1上平移，当它移动到某一位置时，四边形MEFN 的周长会达到最小，请求出周长的最小值（结果保留根号）．【答案】（1）()214y x =+-；m =2；（2）存在，()0,12P 或()0,14.5；（3） 【分析】（1）根据抛物线的对称性求出A （1，0），再利用待定系数法，即可求解；再把点A 坐标代入直线的解析式，即可求出m 的值；（2）先求出E （-5，12），过点E 作EP ⊥y 轴于点P ，从而得EDP ADO ∽，即可得到P 的坐标，过点E 作EP AE '⊥，交y 轴于点P '，可得P DE ADO '∽，再利用tan ∠ADO =tan ∠PE P '，即可求解；（3）作直线y =1，将点F 向左平移2个单位得到F '，作点E 关于y =1的对称点E '，连接E F ''与直线y =1交于点M ，过点F 作FN ∥E F ''，交直线y =1于点N ，在Rt EWF 中和 Rt E WF ''中分别求出EF ， E F ''，进而即可求解．【详解】（1）解：∵二次函数的图象与x 轴交于A 和B （－3，0）两点，对称轴为直线1x =-， ∴A （1，0），设二次函数解析式为：y =a (x -1)(x +3)，把C （0，－3）代入得：-3=a (0-1)(0+3)，解得：a =1， ∴二次函数解析式为：y = (x -1)(x +3)，即：()214y x =+-，∵直线y ＝－2x ＋m 经过点A ，∴0=-2×1+m ，解得：m =2；（2）由（1）得：直线AF 的解析式为：y =-2x +2，又∵直线y =-2x +2与y 轴交于点D ，与抛物线交于点E ，∴当x =0时，y =2，即D （0，2），联立()22214y x y x =-+⎧⎪⎨=+-⎪⎩，解得：11512x y =-⎧⎨=⎩，2210x y =⎧⎨=⎩， ∵点E 在第二象限，∴E （-5，12），过点E 作EP ⊥y 轴于点P ，∵∠ADO =∠EDP ，∠DOA =∠DPE =90°，∴EDP ADO ∽，∴P （0，12）；过点E 作EP AE '⊥，交y 轴于点P '，可得P DE ADO '∽，∵∠ED P '+∠PED =∠PE P '+∠PED =90°，∴∠ADO =∠ED P '=∠PE P '，即：tan ∠ADO =tan ∠PE P '， ∴OA PP OD EP '=，即：125PP '=，解得： 2.5PP '=， ∴P '（0，14.5），综上所述：点P 的坐标为（0，12）或（0，14.5）；（3）∵点E 、F 均为定点，∴线段EF 长为定值，∵MN=2，∴当EM +FN 为最小值时，四边形MEFN 的周长最小，作直线y =1，将点F 向左平移2个单位得到F '，作点E 关于y =1的对称点E '，连接E F ''与直线y =1交于点M ，过点F 作FN ∥E F ''，交直线y =1于点N ，由作图可知：EM E M F M FN ''==，，又∵E M F ''，，三点共线，∴EM +FN =E M F M E F ''''+=，此时，EM +FN 的值最小，∵点F 为直线y =-2x +2与直线x =-1的交点，∴F （-1，4），∴F '（-3，4），又∵E （-5，12），∴E '（-5，-10），延长F F '交线段E E '于点W ，∵F F '与直线y =1平行，∴FW ⊥E E '，∵在Rt EWF 中，由勾股定理得：EF =，在Rt E WF ''中，由勾股定理得：E F ''∴四边形MEFN 的周长最小值=ME +FN +EF +MN =2E F EF MN ''++=．【点睛】本题主要考查二次函数与平面几何的综合，掌握待定系数法，相似三角形的判定和性质，添加辅助线，利用轴对称图形的性质，构造线段和的最小值，是解题的关键．2．（2021·新疆沙依巴克·中考三模）如图，抛物线2y ax bx c =++经过点()0,3C ，与x 轴交于点()1,0A -和点B （点B 在点A 的右边），且OB OC =．（1）求抛物线的解析式和顶点坐标；（2）如图1，点D 、E 在直线1x =上的两个动点，且1DE =，点D 在点E 的上方，求四边形ACDE 的周长的最小值；（3）如图2，点P 为抛物线上一点，连接CP ，直线CP 把四边形CBPA 的面积分为3：5两部分，求点P 的坐标．【答案】（1）2y x 2x 3=-++，顶点坐标为（1，4）； （2）四边形ACDE的周长的最小值为1（3）点P 的坐标为（4，－5）或（8，－45）. 【分析】（1）根据待定系数法求得a 、b 、c 的值即可确定抛物线的解析式，再利用配方法得出顶点坐标．（2）把C 向下移1个单位得点C '，再作C '关于抛物线的对称轴的对称点C ''，连接AC ''，与对称轴交于点E ，再在对称轴上E 点上方取点D ，使得1DE =，连接CD ，此时四边形ACDE 的周长最小，根据勾股定理即可得出．（3）分:=35PCB PCA S S ：△△或:=53PCB PCA S S ：△△两种情况讨论即可． 【详解】解：（1）∵点()0,3C ，OB OC =，∴()3,0B ,把A 、B 、C 三点坐标代入2y ax bx c =++，得09303a b c a b c c -+=⎧⎪++=⎨⎪=⎩，解得123b b c =-⎧⎪=⎨⎪=⎩，∴抛物线的解析式为：2y x 2x 3=-++，∵()222314y x x x =-++=--+，∴顶点坐标为（1，4）；（2）把C 向下移1个单位得点C '，再作C '关于抛物线的对称轴的对称点C ''，连接AC ''，与对称轴交于点E ，再在对称轴上E 点上方取点D ，使得1DE =，连接CD ，此时四边形ACDE的周长最小，则"CD C E C E '==,∵()0,3C ,∴()0,2C ',∵对称轴是直线1x =，∴()2,2C '',∵()1,0A -,∴ACAC ''==11AE DE CD AC AE EC AE C E ''''+++=+++11AC ''==+∴四边形ACDE 的周长的最小值为1（3）如图，设直线CP 交x 轴于点E ，直线CP 把四边形CBPA 的面积分为3：5两部分，又∵()()11:::22PCB PCA C P C P S S EB y y AE y y BE AE =⨯-⨯-=△△， 则:3:5BE AE =或5:3，则 2.5AE =或1.5，即点E 的坐标为（1.5，0）或（0.5，0），将点E 的坐标代入直线CP 的表达式：3y kx =+，解得：6k =-或－2，故直线CP 的表达式为：23y x =-+或63y x =-+，联立方程组22323y x y x x =-+⎧⎨=-++⎩解得：4x =（不合题意值已舍去），解26323y x y x x =-+⎧⎨=-++⎩， 解得：x =8（不合题意值已舍去），故点P 的坐标为（4，－5）或（8，－45）.【点睛】本题考查二次函数综合题、涉及待定系数法求一次函数和二次函数解析式，二次函数图象与性质，勾股定理、轴对称、一次函数等知识，灵活掌握相关知识是解题的关键3．（2021·山东曹县·九年级期中）如图，抛物线24y ax bx =++的对称轴是直线3x =，与x 轴交于()2,0A -，B 两点，与y 轴交于点C ．（1）求抛物线的函数表达式；（2）若M 是抛物线上任意一点，过点M 作y 轴的平行线，交直线BC 于点N ，若3MN =，求点M 的坐标．（3）设点D ，E 是直线3x =上两动点，且1DE =，点D 在点E 上方，求四边形ACDE 周长的最小值．【答案】（1）213442y x x =-++；（2）点M 的坐标为(2,6)或(6,4)或()41-或()41+；（3）1【分析】（1）先求得点B 的坐标，再利用待定系数法即可求解；（2）先求得直线BC 的函数表达式，分点M 在直线BC 的上方和下方两种情况讨论，分别得到一元二次方程，解方程即可求解；（3）根据题意知当CD AE +最小时，四边形ACDE 的周长最小．过B 作BF ⊥x 轴于B ，并截取BF =DE =1，过F 作FD ∥BE 交直线x =3于D ，根据轴对称的性质得到CD + AE 的最小值为CF ，利用两点之间的距离公式即可求解．【详解】解：（1）∵点B 与点A 关于直线x =3对称，∴点B 的坐标为(8，0)，∴424064840a b a b -+=⎧⎨++=⎩ 解得14{32a b =-=， ∴抛物线的函数表达式为213442y x x =-++； （2）当x =0时，y =4,∴点C 的坐标为(0，4)，设直线BC 的函数表达式为y kx m =+，则8k m 0{m 4+==解得1{24k m =-=， 142y x ∴=-+ 设点M 的坐标为213m m m 442⎛⎫-++ ⎪⎝⎭，， 则点N 的坐标为1m m 42⎛⎫-+ ⎪⎝⎭， ①当点M 在直线BC 的上方时， 则2131m m 4m 43422⎛⎫-++--+= ⎪⎝⎭，21234m m ∴-+=，整理得28120m m -+=， 解得1m 2=，26m =,∴点M 的坐标为(2，6)或 (6，4)；②当点M 在直线BC 的下方时， 则2113m 4m m 43242⎛⎫-+--++= ⎪⎝⎭， 21234m m ∴-=，整理得28120m m --=，解得14m =-24m =+M ∴的坐标为()41-或()41+；所以点M 的坐标为(2，6)或 (6，4)或()41-或()41+； （3）∵()2,0A -，C (0，4)，∴AC ==又DE 1=，∴当CD AE +最小时，四边形ACDE 的周长最小．∵点B 与点A 关于直线x =3对称，∴AE =BE ，过B 作BF ⊥x 轴于B ，并截取BF =DE =1，连接CF ，点F 的坐标为(8，1)，过F 作FD ∥BE 交直线x =3于D ，∴四边形FDEB 是平行四边形，∴FD =EB =AE ，∴CD + AE = CD + FD ≥CF ，∴CD + AE 的最小值为CF ，∵C (0，4)，F (8，1)，∴CF∴四边形ACDE 的周长最小值为AC +DE +CF =1【点睛】本题是二次函数的综合题，主要考查了待定系数法，一次函数和二次函数的图象与性质，轴对称的性质，勾股定理，解答本题的关键是明确题意，找出所求问题需要的条件．4．（2021·四川岳池·中考三模）抛物线2y x x =x 轴交于点A ，B （点A 在点B 的左边），与y 轴交于点C ，点D 是该抛物线的顶点．（1）如图1，连接CD ，求线段CD 的长；（2）如图2，点P 是直线AC 上方抛物线上一点，PF x ⊥轴于点F ，PF 与线段AC 交于点E ；将线段OB 沿x 轴左右平移，线段OB 的对应线段是11O B ，当12PE EC +的值最大时，求四边形11PO B C 周长的最小值，并求出对应的点1O 的坐标．【答案】（1；（2）四边形11PO B C 1O 的坐标为⎛⎫ ⎪ ⎪⎝⎭ 【分析】（1）根据抛物线解析式即可求出点C 和点D 坐标，再利用两点的距离公式即可求出结果．（2）根据题意可求出()A -，)B ．从而求出直线AC 的解析式，即可设E x ⎛ ⎝，2P x x x ⎛+ ⎝．由此即可用x 表示出PF 和EF 的长．在Rt ACO 中，利用勾股定理可求出AC 30CAO ∠=︒，从而得出2AE EF =，即可用x 表示AE 的长．再利用()1122PE EC PE AC AE +=+-，即可用x 表示12PE EC +的长为：2x ++12PE EC +的值最大时，x =-(P -，由此可求出PC 的长，由题意可知11O B OB =即要使四边形11PO B C 周长的最小，即11PO B C +的值最小即可．将点P (1P ，连接11P B ，则111PO PB =，再作点1P 关于x 轴的对称点(2P ，则1121PB P B =，由所做图形易得112112PO B C P B B C P C +=+=，即求出2P C 的长即可求出四边形11PO B C 的周长最小值，最后利用1B 点为2P C 的中点，即可求出1B 坐标，从而得到1O 坐标．【详解】（1）当0x =时，代入抛物线解析式得：y =∴(0C ，将抛物线一般式改为顶点式为：22y x x =+∴D ⎛ ⎝⎭，∴CD =（2）在2y x x =中，令0y =，则20=，解得：1x =-2x∴()A -，)B ，∵(0C ，易得直线AC 的解析式为：y =设E x ⎛ ⎝，2P x ⎛ ⎝，∴2PF =-+EF x =在Rt ACO 中，AO =OC∴AC∴30CAO ∠=︒，∴23AE EF x ==+∴()21122PE EC x AC AE ⎡⎤⎛+=-+-⎢⎥ ⎢⎥⎝⎝⎣⎦，212⎡⎤=++⎢⎥⎢⎥⎝⎣⎦，263x =--+，2x =+，∴当12PE EC +的值最大时，x =-(P -，∴0C P PC x x =-=-=∵11O B OB =∴要使四边形11PO B C 周长的最小，即11PO B C +的值最小，如图，将点P 个单位长度得点(1P ，连接11P B ，则111PO PB =，再作点1P 关于x 轴的对称点(2P ，则1121PB P B =，∴11211PO B C P B B C +=+，∴连接2P C 与x 轴的交点即为使11PO B C +的值最小时的点1B ，∴2102p c x x B +⎛⎫ ⎪⎝⎭，，即10B ⎛⎫ ⎪ ⎪⎝⎭．将1B 个单位长度即得点1O ，∴112PO B C P C +=，∴在12Rt PP C 中，2P C =对应的点1O 的坐标为0⎛⎫- ⎪ ⎪⎝⎭，，即0⎛⎫ ⎪ ⎪⎝⎭．∴四边形11PO B C周长的最小值为1111211PO BC O B PC PC O C B P ++==+++ 【点睛】本题为二次函数综合题．考查抛物线图象与坐标轴的交点问题，抛物线的顶点式与最值问题，利用待定系数法求一次函数解析式，两点的距离公式以及轴对称变换等知识，为压轴题，困难题型．利用数形结合的思想是解答本题的关键．5．（2021·山东·济南外国语学校九年级月考）如图，抛物线y ＝ax 2＋bx ＋3经过A (1，0)、B (4，0)两点，与y 轴交于点C ．(1)求该抛物线的解析式；(2)如图，在抛物线的对称轴上是否存在点P ，使得四边形P AOC 的周长最小?若存在，求出四边形P AOC 周长的最小值；不存在，请说明理由．(3)在(2)的条件下，点Q 是线段OB 上一动点，当△BPQ 与△BAC 相似时，求点Q 的坐标．【答案】（1）2315344y x x =-+；（2）存在，9；（3）（238，0）或（78，0） 【分析】 （1）将A （1，0）、B （4，0）代入线y =ax 2+bx +3，求出a 、b 即可；（2）四边形P AOC 的周长最小值为：OC +OA +BC =1+3+5=9；（3）分两种情况讨论：①当△BPQ ∽△BCA ，②当△BQP ∽△BCA ．【详解】解：（1）把A (1，0)、B (4，0)代入y ＝ax 2＋bx ＋3得，3016430a b a b ++=⎧⎨++=⎩， 解得 34154a b ⎧⎪⎪⎨⎪-⎪⎩＝＝所以，抛物线的解析式为2315344y x x =-+； （2）∵A 、B 关于对称轴对称，如图，连接BC ，与对称轴的交点即为所求的点P ，此时P A +PC =BC ，∴四边形P AOC 的周长最小值为：OC +OA +BC ，∵A （1，0）、B （4，0）、C （0，3），∴OA =1，OC =3，BC =5，∴OC +OA +BC =1+3+5=9；∴在抛物线的对称轴上存在点P ，使得四边形P AOC 的周长最小，四边形P AOC 周长的最小值为9；（3）如图，设对称轴与x 轴交于点D ．∵A （1，0）、B （4，0）、C （0，3），∴OB =4，AB =3，BC =5，直线BC ：334y x =-+，由二次函数可得，对称轴直线x =52， ∴P （52，98），BP =158， ①当△BPQ ∽△BCA ，∴BQ BP BA BC=， ∴1538358BQ ==， ∴98BQ =，∴923488OQ OB BQ =-=-=， ∴123(,0)8Q ②当△BQP ∽△BCA ， ∴,BQ BP BC BA=， ∴1558538BQ ==， ∴BQ =258， ∴OQ =OB -BQ =4-258=78， ∴Q 2（78，0）， 综上，求得点Q 的坐标（238，0）或（78，0） 【点睛】 本题考查了二次函数，熟练运用二次函数的性质与相似三角形的性质是解题的关键． 6．（2021·云南·曲靖市九年级月考）如图1，在平面直角坐标系中，抛物线2y x bx c =-++经过点A 和点()10B ,，交y 轴于点()0,3C ．（1）求抛物线的解析式及顶点D 的坐标；（2）点P 是抛物线上A 、D 之间的一点，过点P 作PE x ⊥轴于点E ，PG y ⊥轴，交抛物线于点G ，过点G 作GF x ⊥轴于点F ，当矩形PEFG 的周长最大时，求点P 的坐标； （3）如图2，连接AD 、BD ，点M 在线段AB 上（不与A 、B 重合），作直线MN x ⊥轴交抛物线于点N ，是否存在点M ，使得AMN 与OBC 相似？若存在，求出点M 的坐标；若不存在，请说明理由．【答案】（1）223y x x =--+，()1,4-；（2）()2,3P -；（3）存在，()2,0-或2,03⎛⎫ ⎪⎝⎭【分析】（1）根据点B 、C 的坐标，利用待定系数法即可求出抛物线的解析式，再利用配方法将二次函数解析式变形为顶点式，由此即可得出顶点D 的坐标；（2）设点2(,23)P m m m --+，可得223PE m m =--+，2(1)22PG m m =--=--，矩形PEFG 的周长2()PE PG =+，即可求解；（3）设点(,0)M m ，则2(,23)N m m m --+，223MN m m =--+，根据相似三角形的性质,可得关于 m 的方程，可得 M 点的坐标，要分类讨论,以防遗漏．【详解】解：（1）∵抛物线2y x bx c =-++经过点A 和点()10B ,，交y 轴于点()0,3C ， 将B ，C 代入解析式得：013b c c =-++⎧⎨=⎩解得：b =－2，c =3∴抛物线的表达式为：223y x x =--+，∵223y x x =--+2(1)4x =-++∴点(1,4)D -；∴解析式为223y x x =--+，顶点坐标(1,4)D -（2）设点2(,23)P m m m --+，则223PE m m =--+，∵顶点坐标(1,4)D -，2(,23)P m m m --+∴2(1)22PG m m =--=--，矩形PEFG 的周长22()2(2322)PE PG m m m =+=--+--2282m m =--+，20-<，故当824m -=-=--时，矩形PEFG 周长最大， 此时，点P 的横坐标为2-；将-2，代入223y x x =--+得y =3∴坐标为()2,3P -；（3）设点(,0)M m ，则2(,23)N m m m --+，223MN m m =--+令y =0,得 2x 2x 30--+=解得：123,1x x =-=∴点A （-3,0），()10B , ∴AM =m +3 ,OB =1,OC =3∵90AMN COB ∠=∠=︒， ∴当AM MN BO OC=时AMN BOC ∆∆∽ 即223133m m m +--+=，解得:23m m =-=-或(舍去)∴(2,0)M -∵90AMN COB ∠=∠=︒， ∴当AM MN CO OB=时AMN COB ∆∆∽ 即223313m m m +--+=， 解得：233m m ==-或(舍去) ∴2,03M ⎛⎫ ⎪⎝⎭综上所述：存在点M ，即(2,0)M -或者2,03M ⎛⎫ ⎪⎝⎭，使得AMN 与OBC 相似． 【点睛】本题考查了二次函数综合题，涉及到待定系数求函数解析式、三角形相似和二次函数的最值；(1)的关键是顶点是函数解析式；解(2)的关键是利用已知条件把PE PG 、表示出来；(3)的关键是利用相似三角形的性质得出关于 m 的方程,要分类讨论，以防遗漏．7．如图，抛物线2y x bx c =-++的图象与x 轴交于A 、B 两点（点A 在点B 的左边），与y 轴交于点C ，点D 为抛物线的顶点．点A 坐标的为3,0，点C 的坐标为()0,3．（Ⅰ）求抛物线的解析式；（Ⅰ）点M 为线段AB 上一点（点M 不与点A 、B 重合），过点M 作i 轴的垂线，与直线AC 交于点E ，与抛物线交于点P ，过点P 作//PQ AB 交抛物线于点Q ，过点Q 作QN x ⊥轴于点N ．若点P 在点Q 左边，当矩形PMNQ 的周长最大时，求AEM △的面积；（Ⅰ）在（Ⅰ）的条件下，当矩形PMNQ 的周长最大时，连接DQ ，过抛物线上一点F 作y 轴的平行线，与直线AC 交于点G （点G 在点F 的上方）．若FG ，求点F 的坐标．【答案】（Ⅰ）223y x x =--+；（Ⅰ）12；（Ⅰ）()4,5F --或()1,0【分析】（Ⅰ）将点A ，点C 坐标代入解析式可求解；（Ⅰ）设M （x ，0），P （x ，-x 2-2x +3），利用对称性可求点Q （-2-x ，-x 2-2x +3），可求MP =-x 2-2x +3，PQ =-2-x -x =-2-2x ，则可用x 表示矩形PMNQ 的周长，由二次函数的性质可求当矩形PMNQ 的周长最大时，点P 的坐标，即可求点E ，点M 的坐标，由三角形面积公式可求解；（Ⅰ）先求出点D 坐标，即可求DQ FG =4，设F （m ，-m 2-2m +3），则G （m ，m +3），用含有m 的式子表示FG 的长度即可求解．【详解】解:（Ⅰ）依题意()()2330{3b c c --+⨯-+== 解得2{3b c =-= 所以223y x x =--+（Ⅰ）2223(1)4y x x x抛物线的对称轴是直线1x =-(,0)M x ，()2,23P x x x --+，其中31x -<<- ∵P 、Q 关于直线1x =-对称设Q 的横坐标为a则()11a x --=--∴2a x =--∴()22,23Q x x x ----+∴223MP x x =--+，222PQ x x x =---=--∴周长()222222232822(2)10d x x x x x x =----+=--+=-++ 当2x =-时，d 取最大值，此时，(2,0)M -∴2(3)1AM =---=设直线AC 的解析式为y kx b =+则303k b b -+=⎧⎨=⎩，解得13k b =⎧⎨=⎩∴设直线AC 的解析式为3y x 将2x =-代入3y x ，得1y = ∴(2,1)E -，∴1EM = ∴11111222AEM S AM ME ∆=⋅=⨯⨯= （Ⅰ）由（Ⅰ）知，当矩形PMNQ 的周长最大时，2x =-此时点()0,3Q ，与点C 重合， ∴3OQ =∵2223(1)4y x x x∴()1,4D -过D 作DK y ⊥轴于K ，则1DK =，4OK =∴431OK OK OQ =-=-=∴DKQ 是等腰直角三角形，DQ =∴4FG ==设()2,23F m m m --+，则(,3)G m m +()223233FG m m m m m =+---+=+∴234m m +=，解得14m =-，21m =当4m =-时，2235m m --+=-当1m =时，2230m m --+=．∴()4,5F --或()1,0【点睛】本题是二次函数综合题，考查了二次函数的性质，矩形的性质，等腰直角三角形的性质等，利用参数表示线段的长度是本题的关键．8．（2021·山东·济南市济阳区中考模拟预测）如图，抛物线y ＝2x ﹣2x ﹣3经过点A （﹣2，a ），与x 轴相交于B 、C 两点（B 点在C 点左侧）．（1）求a的值及B、C两点坐标；（2）点D在抛物线的对称轴上，且位于x轴的上方，将△BCD沿直线BD翻折得到△B C'D，若点C'恰好落在抛物线的对称轴上，求点C'和点D的坐标；（3）设P（m，-3)是该抛物线上一点，点Q为抛物线的顶点，在x轴、y轴分别找点M、N，使四边形MNQP的周长最小，请求出点M、N的坐标．【答案】（1）5；（-1,0），（3,0）（2）（1，；（1（3）（57，0）；（0，53-）【分析】（1）把A（-2，a）代入y＝x2﹣2x﹣3可得a的值，分别令y=0求出抛物线与x轴的交点坐标，从而可得B、C点坐标；（2）设对称轴于BC的交点为E，先求出点C，点E坐标，可求BC=4，BH=CH=2，由折叠的性质可得BC'的长，由勾股定理可求C'H，DH的长，即可求解；（4）作Q点关于y轴的对称点Q′（-1，-4），作点P（2，-3）关于x轴的对称点P′（2，3），连接Q′P′分别交x、y轴于点M、N，此时，四边形QPMN的周长最小，即可求解．【详解】解：（1）把A（-2，a)代入y＝x2﹣2x﹣3，得a=5；当y=0时，x2﹣2x﹣3=0 解得x1=3, x2=-1∵B点在C点左侧∴B(-1,0)，C(3,0)(2)如图，设抛物线的对称轴与x轴交于点H，则H点的坐标为（1，0），BH＝2，由翻折得C ′B ＝CB ＝4，在Rt △BHC ′中，由勾股定理，得C H '=∴点C ′的坐标为（1，，tan C H C BH BH ''∠=== ∴∠C ′BH ＝60°，由翻折得∠DBH ＝12∠C ′BH ＝30°，在Rt △BHD 中，DH ＝BH •tan ∠DBH ＝2•tan 30°∴点D 的坐标为（1． （3）如图2，∵Q 为抛物线的顶点，∴Q （1，﹣4），∴Q 关于y 轴的对称点Q '（﹣1，﹣4），∵P （m ,-3）在抛物线上，∴P （2，﹣3），∴点P 关于x 轴的对称点P '（2，3），连接Q ′、P ′分别交x 、y 轴于点M 、N ，此时，四边形OPMN 的周长最小，， 设直线Q ′P ′的解析式为y =kx +b ，则有234k b k b +=⎧⎨-+=-⎩ ，解得7353k b ⎧=⎪⎪⎨⎪=-⎪⎩， ∴直线P 'Q '的解析式为y ＝73x ﹣53， 当x =0时，y =﹣53；当y =0时，x =57; ∴M （57，0），N （0，﹣53）． 【点睛】本题是二次函数的综合题，考查了待定系数法求二次函数解析式，待定系数法求一次函数解析式，轴对称的性质等知识，其中（3），利用对称点性质求解是此类题目的一般解法，需要掌握．9．（重庆市九年级月考）如图1，抛物线y ＝﹣x 2﹣2x +3与x 轴从左到右交于A 、B 两点，与y 轴交于点C ，顶点为D（1）求直线AC 的解析式与点D 的坐标；（2）在直线AC 上方的抛物线上有一点E ，作EF ∥x 轴，与抛物线交于点F ，作EM ⊥x 轴于M ，作FN ⊥x 轴于N ，长度为PQ 在直线AC 上运动（点P 在点Q 右侧），当四边形EMNF 的周长取最大值求四边形DPQE 的周长的最小值及对应的点Q 的坐标；（3）如图2，平移抛物线，使抛物线的顶点D 在直线AD 上移动，点D 平移后的对应点为D ′，点A 平移后的对应点为A ′，△A ′D ′C 是否能为直角三角形？若能，请求出对应的线段D ′C 的长；若不能，请说明理由.【答案】（1）直线AC 的解析式为：3y x ，()1,4D -；（2）四边形DPQE 的周长的最小值是Q 的坐标为33,22Q ⎛⎫- ⎪⎝⎭；（3）'D C ==3. 【分析】(1)抛物线223y x x =--+与x 轴从左到右交于A 、B 两点，只要令y =0，即可求出A 、B 两点；与y 轴交于点C ，只要令x =0，即可求出点C ；由点A 、C 的坐标可得直线AC 的解析；D的坐标用顶点公式或者先求出对称轴代入解析式，即可求出；(2)作点E 关于直线AC 的对称点E'(0,1)，将点E'沿AC 方向平移E″(2,3)，连接E″D 交直线AC 于点P ，将点P 向下平移Q ，则点Q 为所求点即可求解，再根据个点坐标求出四边形的边长，进而计算周长；(3)分A 'D '是斜边、A'C 是斜边、CD'是斜边三种情况，分别求解即可．【详解】解：(1)∵抛物线223y x x =--+与x 轴从左到右交于A 、B 两点，∴令y =0，即223=0x x --+，解得：12= -3=1x x ，，则()()3,01,0A B -、，∵抛物线223y x x =--+与y 轴交于点C ，∴()0,3C ，由点A 、C 的坐标得，直线AC 的解析式为：3y x ；∵D 是抛物线223y x x =--+的顶点，抛物线的对称轴为：1x =-，∴()1,4D -；(2)设点2(,23)E m m m --+，∵抛物线的对称轴为：1x =-，//EF x 轴，∴22EF m =--，四边形EMNF 的周长222()2(2322)2(41)l EF EM m m m m m =+=--+--=--+， 当2m =-时，l 最大，此时点()2,3E -；∵()2,3E -，()1,4D -；∴ED =∵PQ =且P 、Q 在3y x 上∴P 、Q 两点横纵坐标差为2，作点()2,3E -关于直线AC 的对称点()'0,1E ，将点'E 沿AC 方向平移()2,3E "，由点DE "坐标得，直线DE "的解析式为：111 33y x =-+； 联立直线AC 、直线DE "的解析式并解得：12x =，故点17,22P ⎛⎫ ⎪⎝⎭，将点P 沿着直线CA 向左向下平移33,22Q ⎛⎫- ⎪⎝⎭； ∵()2,3E -，33,22Q ⎛⎫- ⎪⎝⎭，17,22P ⎛⎫ ⎪⎝⎭，()1,4D -；∴EQ =，PD =此时四边形DPQE的周长最小ED PQ EQ PD=+++=(3)由待定系数法求得直线AD的解析式为：26y x=+，则设抛物线向右平移m个单位，则向上平移2m个单位，∴'A()3,2m m-、'D()1,24m m-+，()0,3C，而点()0,3C，∴'DC=①当''A D是斜边时，如图2，分别过点'A、'D作y轴的垂线交于点N、M，则''D CM CA N∠=∠，则tan'tan'D CM CA N∠=∠，即321321m mm m--=-+，解得：0m=(舍去)或85；②当'A C是斜边时，如图3，过点'D作x轴的平行线交y轴于点N，交过点'A作y轴的平行线于点M，同理可得：tan'tan''ND C MA D∠=∠，则'''NC MDND MA=，即22141mm+=-，解得：1m=-；③当'CD是斜边时，同理可得：22343m m -=-，解得：1m =， 故85m =或−1或 1则'DC =3．【点睛】本题考查的是二次函数综合运用，涉及到一次函数的性质、点的对称性、解直角三角形等，其中第（3）问，要注意分类求解，避免遗漏．10．（2021·广东·广州市第五中学九年级期中）如图，过原点的抛物线2122y x x =-+与x 轴交于点A ，B 为抛物线的顶点，连接OB ，点P 是线段OA 上的一个动点，过点P 作PC OB ⊥，垂足为点C ．（1）将POC △绕着点P 按顺时针方向旋转90︒，得''PO C △，当点'C 落在抛物线上时，求点P 的坐标．（2）当PB OA ⊥时，将线段PC 绕平面某点旋转180︒得到线段EF ，若点E 、F 都落在抛物线上，求点E 和F 的坐标．（3）当（1）中的点'C 落在抛物线上时，将抛物线向左或向右平移()02n n <<个单位，点B 、'C 平移后对应的点分别记为M 、N ，是否存在n ，使得以O 、M 、N 、A 为顶点的四边形周长最短？若存在，请直接写出n 的值和抛物线平移的方向，若不存在，请说明理由．【答案】（1）（209，0）；（2）51528E ⎛⎫ ⎪⎝⎭，，7728F ⎛⎫ ⎪⎝⎭，；（3）存在27n =，抛物线向左平移 【分析】（1），过点B 作BQ ⊥x 轴于Q ，过点C '作C D '⊥O P '于D ，先证明△OQB 是等腰直角三角形，得到∠BOP =45°，从而可以证明△OCP 是等腰直角三角形，OC =CP ，∠OPC =45°，设P （m ，0），则3122C m m ⎛⎫' ⎪⎝⎭，，代入抛物线解析式求解即可； （2）过点C 作CD ⊥OA 于D ，求出C （1，1），将线段PC 绕平面某点旋转180°得到线段EF ，设这个点的坐标为（a ，b ），则22P E P E x x a y y b +⎧=⎪⎪⎨+⎪=⎪⎩，22C F C F x x a y y b +⎧=⎪⎪⎨+⎪=⎪⎩，从而得到()222E a b -，，()2121F a b --，，再根据E 、F 在抛物线上，求解即可；（3）将AC '沿C B '平移，使得C '与B 点重合，点A 落在A '处，，以过B 的直线y =2为对称轴，作A '的对称点A ''，连接OA ''，当点M 为OA ''与直线y =2的交点时，此时以O 、M 、N 、A为顶点的四边形周长最短，先求出8839A ⎛⎫' ⎪⎝⎭，，则82839A ⎛⎫'' ⎪⎝⎭，，再求出M 的坐标即可得到答案． 【详解】解：（1）如图所示，过点B 作BQ ⊥x 轴于Q ，过点C '作C D '⊥O P '于D ，∵点B 是抛物线()221122222y x x x =-+=--+的顶点， ∴B （2，2），∴OQ =BQ =2，∴△OQB 是等腰直角三角形，∴∠BOP =45°，又∵PC ⊥OB ，∴∠OCP =90°，∴△OCP 是等腰直角三角形，∴OC =CP ，∠OPC =45°，由旋转的性质可得==45O PC OPC ''∠∠，O C C P OC '''==，O P OP '=，OPO '∠=90 设P （m ，0），则O P OP m '==， ∴1122C D O P m ''==， ∴3122C m m ⎛⎫' ⎪⎝⎭， ∵C '在抛物线2122y x x =-+上， ∴21133222m m m ⎛⎫=-⨯+ ⎪⎝⎭即29200m m -=， 解得209m =或0m =（舍去）， ∴P （209，0）； （2）如图所示，过点C 作CD ⊥OA 于D ，∵B （2，2），PB ⊥OA ，∴OP =PB =2，△OBP 为等腰直角三角形，P （2，0），由（1）得PC =OC ，∵222OC PC OP +=，∴224PC =，∴PC OC ==又∵CD ⊥OA ，∴OD =CD =PD =1，∴C （1，1），将线段PC 绕平面某点旋转180°得到线段EF ，设这个点的坐标为（a ，b ），∴22P E P E x x a y y b +⎧=⎪⎪⎨+⎪=⎪⎩，22C F C F x x a y y b +⎧=⎪⎪⎨+⎪=⎪⎩， ∴222E E x a y b =-⎧⎨=⎩，2121F E x a y b =-⎧⎨=-⎩， ∴()222E a b -，，()2121F a b --，， 又∵E 、F 都在抛物线2122y x x =-+上， ∴()()()()2212222222121221212a ab a a b ⎧--+-=⎪⎪⎨⎪--+-=-⎪⎩， ∴222862526212a a b a a b ⎧-+-=⎪⎨-+-=-⎪⎩解得941516a b ⎧=⎪⎪⎨⎪=⎪⎩∴51528E ⎛⎫ ⎪⎝⎭，，7728F ⎛⎫ ⎪⎝⎭，； （3）存在27n =，抛物线向左平移，理由如下： 由（1）可知101039C ⎛⎫' ⎪⎝⎭，，如图将AC '沿C B '平移，使得C '与B 点重合，点A 落在A '处，，以过B 的直线y =2为对称轴，作A '的对称点A ''，连接OA ''，当点M 为OA ''与直线y =2的交点时，此时以O 、M 、N 、A 为顶点的四边形周长最短，∵A 是抛物线2122y x x =-+与x 轴的交点， ∴A （4，0）∵//BA AC ''，且BA AC ''=，101039C ⎛⎫' ⎪⎝⎭，，B （2，2）， ∴8839A ⎛⎫' ⎪⎝⎭，， ∴82839A ⎛⎫'' ⎪⎝⎭，， 设直线OA ''的解析式为y kx =， ∴28893k =， 解得76k =， ∴直线OA ''的解析式为76y x =， ∵M 在直线y =2上， ∴726x =， 解得127x =， ∴12,27M ⎛⎫ ⎪⎝⎭∴122277n =-=， ∴存在27n =，抛物线向左平移． 【点睛】本题主要考查了二次函数综合，旋转的性质，平移的性质，中心对称，等腰直角三角形的性质，一次函数，勾股定理等等，解题的关键在于能够熟练掌握相关知识进行求解．11．（重庆中考招生考试）如图，已知抛物线22y x =--x 轴交于A ，B 两点（A 点位于B 点左侧），与y 轴交于C 点，连接AC ．点Q 为抛物线的顶点，点G 为()0,3-．（1）点P 是第四象限内抛物线上的一点，过点P 作//PD x 轴交抛物线于点D ，作PF x ⊥轴于点F ，作DE x ⊥轴于点E ，点P 在点D 右边．点M 是直线BG 上一个动点，点N 是直线PD 上一个动点，当四边形PDEF 的周长最大时，求PM MN +的最小值； （2）如图2，将原抛物线绕其对称轴与x 轴的交点H 旋转180︒得新的抛物线1l ，点A ，Q 的对应点分别记为1A ，1Q ，把抛物线1l 沿直线1GA 平移，1A ，1Q 的对应点分别记为2A ，2Q 是否存在点2A ，使得22GA Q ∆是以2GA 为腰的等腰三角形？若存在，请直接写出2A 的坐标；若不存在，请说明理由．【答案】（1）PM MN +；（2）存在，2(3018A ----或23A -或2(3A --．【分析】(1) 设22P m m ⎛-- ⎝，则22PF m =++然后再确定抛物线的对称轴以及开口方向,即可确定最值；（2）由题意知，抛物线绕其对称轴与x 轴的交点H 旋转180︒得抛物线1l ，点A 的对应1A 与点B重合．设2,)A t ，2)Q t ，然后利用勾股定理得到()2222)(3)GA t =++；然后就22GQ GA =和222GA A Q =分别解答即可．【详解】解：（1）(A ，B ，(0,C -，Q -．设22P m m ⎛-- ⎝，则22PF m =++．抛物线22y x =--x =2(2PD m m ∴==-∴矩形PDEF 的周长()2PF PD =+224m ⎛=+ ⎝28m =++此函数的图象为抛物线，其对称轴为m =0m << 203a =-<，∴当m =PDEF 的周长最大，此时点P 的坐标为(-． 作点P 关于GB 的对称点1P ，30ABG ∠=︒，∴作1P N PC ⊥于N 交GB 于M ，此时PM MN +最小，PM MN +的最小值1P N =．延长BG 交PC 于H ，可求得9HC =-19PP HP ==PM MN +的最小值1PN ==（2）由题意知，抛物线绕其对称轴与x 轴的交点H 旋转180︒得抛物线1l ，点A 的对应1A 与点B 重合．设2,)A t ，2)Q t ，则()2222)3)GQ t =++， ()2222)(3)GA t =++，①当22GQ GA =时，()()2222GQ GA =即22)3)t ++22)(3)t =++．化简后解得18t =--②当222GA A Q =时，()()22222GA A Q =，即22)(3)60t ++=．化简后解得3t =-综上所述，2(3018A ----或23A -或2(3A --．【点睛】本题属于二次函数综合题，考查了矩形的性质、二次函数图像的性质、勾股定理等知识，掌握二次函数图像的性质和根据勾股定理列方程是解答本题的关键．。

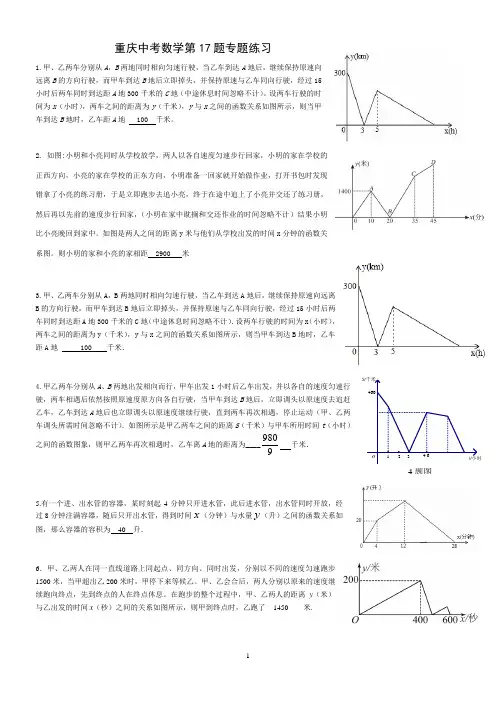
4.6321o t/小时S/千米4604题图 重庆中考数学第17题专题练习1.甲、乙两车分别从A ，B 两地同时相向匀速行驶，当乙车到达A 地后，继续保持原速向远离B 的方向行驶，而甲车到达B 地后立即掉头，并保持原速与乙车同向行驶，经过15小时后两车同时到达距A 地300千米的C 地（中途休息时间忽略不计）。

设两车行驶的时间为x （小时），两车之间的距离为y （千米），y 与x 之间的函数关系如图所示，则当甲车到达B 地时，乙车距A 地 100 千米。

2. 如图:小明和小亮同时从学校放学，两人以各自速度匀速步行回家，小明的家在学校的正西方向，小亮的家在学校的正东方向，小明准备一回家就开始做作业，打开书包时发现错拿了小亮的练习册，于是立即跑步去追小亮，终于在途中追上了小亮并交还了练习册，然后再以先前的速度步行回家，（小明在家中耽搁和交还作业的时间忽略不计）结果小明比小亮晚回到家中。

如图是两人之间的距离y 米与他们从学校出发的时间x 分钟的函数关系图。

则小明的家和小亮的家相距 2900 米3.甲、乙两车分别从A ，B 两地同时相向匀速行驶，当乙车到达A 地后，继续保持原速向远离B 的方向行驶，而甲车到达B 地后立即掉头，并保持原速与乙车同向行驶，经过15小时后两车同时到达距A 地300千米的C 地（中途休息时间忽略不计）．设两车行驶的时间为x （小时），两车之间的距离为y （千米），y 与x 之间的函数关系如图所示，则当甲车到达B 地时，乙车距A 地 100 千米．4.甲乙两车分别从A 、B 两地出发相向而行，甲车出发1小时后乙车出发，并以各自的速度匀速行驶，两车相遇后依然按照原速度原方向各自行驶，当甲车到达B 地后，立即调头以原速度去追赶乙车，乙车到达A 地后也立即调头以原速度继续行驶，直到两车再次相遇，停止运动（甲、乙两车调头所需时间忽略不计）．如图所示是甲乙两车之间的距离S （千米）与甲车所用时间t （小时）之间的函数图象，则甲乙两车再次相遇时，乙车离A 地的距离为____9809 千米．5.有一个进、出水管的容器，某时刻起4分钟只开进水管，此后进水管，出水管同时开放，经过8分钟注满容器，随后只开出水管，得到时间x （分钟）与水量y （升）之间的函数关系如图，那么容器的容积为 40 升．6．甲、乙两人在同一直线道路上同起点、同方向、同时出发，分别以不同的速度匀速跑步1500米，当甲超出乙200米时，甲停下来等候乙。

专题17 裁剪与拼接【典例分析】例1、将一个四边形截去一个角后，它不可能是()A. 六边形B. 五边形C. 四边形D. 三角形【答案】A【解析】【分析】本题考查了多边形，能够得出一个四边形截去一个角后得到的图形有三种情形，是解决本题的关键．根据一个四边形截去一个角后得到的多边形的边数即可得出结果．【解答】解：一个四边形截去一个角后得到的多边形可能是三角形，可能是四边形，也可能是五边形，但不可能是六边形．故选：A．例2、如图所示，三种不同类型地砖，若现在A类4块，B类4块，C类2块，要拼成一个正方形，则应多余出1块_________型地砖；这样地砖拼法表示了两数和的平方几何意义，这个两数和的平方是___________．【答案】C；(2m+n)2=4m2+4mn+n2【解析】【分析】本题考查了完全平方公式的几何意义，立意较新颖，注意面积的不同求解是解题的关键，对此类问题的要深入理解．分别计算出4块A的面积和4块B的面积、2块C的面积，再计算这三种类型的砖的总面积，用完全平方公式化简后，即可得出多了哪种类型的地砖．【解答】解：4块A的面积为：4×m×m=4m2；4块B的面积为：4×m×n=4mn；2块C的面积为2×n×n=2n2；那么这三种类型的砖的总面积应该是：4m2+4mn+2n2=4m2+4mn+n2+n2=(2m+n)2+n2，因此，多出了一块C型地砖，拼成的正方形，如图，拼成的正方形的面积为(2m+n)2=4m2+4mn+n2．故答案为C；(2m+n)2=4m2+4mn+n2．例3、如图，某数学兴趣小组用四块长方形纸板和一块小正方形纸板恰好拼成一个大正方形纸板，其中一块长方形纸板的长为8cm、宽为2cm，另一块长方形纸板的长为10cm、宽为4cm，求大正方形纸板的面积．【答案】解：如图，设小正方纸板的边长为xcm，所以2+x+4=10+8−x，解方程，得x=6，所以大正方形纸板边长=10+8−6=12(cm)，所以大正方形纸板的面积为122=144(cm2).【解析】本题主要考查了完全平方公式的几何背景，利用等量关系列出方程是解决问题的关键.设小正方形的边长为x，依据小正方形的边长的表达式，可得方程2+x+4=10+8−x，进而得出大正方形的边长及面积．【好题演练】一、选择题1.如图，将边长为a的正方形剪去两个小长方形得到S图案，再将这两个小长方形拼成一个新的长方形，求新的长方形的周长()A. 2a−3bB. 4a−8bC. 2a−4bD. 4a−16b2.如图1，分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC，EG剪开，拼成如图2所示的▱KLMN，若中间空白部分四边形OPQR恰好是正方形，且▱KLMN的面积为50，则正方形EFGH的面积为()A. 24B. 25C. 26D. 273.现有如图①的小长方形纸片若干块，已知小长方形的长为a，宽为b.用3个如图②的图形和8个如图①的小长方形，拼成如图③的大长方形，若大长方形的宽为30cm，则图③中阴影部分面积与整个图形的面积之比为()．A. 15B. 16C. 17D. 184.如图，由10根完全相同的小棒拼接而成，请你再添2根与前面完全相同的小棒，拼接后的图形恰好有3个菱形的方法共有()A. 3种B. 4种C. 5种D. 6种5.七巧板是我们祖先的一项创造，被誉为“东方魔板”.在一次数学活动课上，小明用边长为4cm的正方形纸片制作了如图所示的七巧板，并设计了下列四幅作品--“奔跑者”，其中阴影部分的面积为5cm2的是()A. B.C. D.6.如图，从边长为(a+3)的正方形纸片中剪去一个边长为3的正方形，剩余部分沿虚线又剪拼成一个如图所示的长方形(不重叠，无缝隙)，则拼成的长方形的另一边长是()A. a+3B. a+6C. 2a+3D. 2a+6二、填空题7.在某张三角形纸片上，取其一边的中点，沿着过这点的两条中位线分别剪去两个三角形，剩下的部分就是如图所示的四边形；经测量这个四边形的相邻两边长为10cm、6cm，一条对角线的长为8cm；则原三角形纸片的周长是______．8.如图，空白部分面积可表示为____________．9.如图所示，将一个长方形ABCD分割成4个小长方形，其中②与③的大小形状都相同，已知大长方形ABCD的边BC=5cm，则①与④两个小长方形的周长之和为________cm．10.如图是“俄罗斯方块”游戏中的一个图案，由四个完全相同的小正方形拼成，则∠ABC的度数为_____．11.在关于“折纸问题”的数学活动课中，小刚沿菱形纸片ABCD各边中点的连线裁剪得到四边形纸片EFGH，再将纸片EFGH按如图所示分别沿MN、PQ折叠，使点E，G 落在线段PN上点E′，G′处，当PN//EF时，若阴影部分的周长之和为16，△AEH，△CFG的面积之和为12，则菱形纸片ABCD的一条对角线BD的长为______．12.如图，将一段标有0～60均匀刻度的绳子铺平后折叠(绳子无弹性)，使绳子自身的一部分重叠，然后在重叠部分沿绳子垂直方向剪断，将绳子分为A、B、C三段，若这三段的长度由短到长的比为1：2：3，则折痕对应的刻度可能是________________．三、解答题13.我们经常利用图形描述问题和分析问题．借助直观的几何图形，把问题变得简明、形象，有助于探索解决问题的思路．(1)小明为了解释某一公式，构造了几何图形，如图1所示，将边长为a的大正方形剪去一个边长为b的小正方形，并沿图中的虚线剪开，拼接后得到图2，显然图1中的图形与图2中的图形面积相等，从而验证了公式．则小明验证的公式是______．(2)计算：(x+a)(x+b)=______；请画图说明这个等式．14.问题提出：某段楼梯共有10个台阶，如果某同学在上台阶时，可以一步1个台阶，也可以一步2个台阶．那么该同学从该段楼梯底部上到顶部共有多少种不同的走法？问题探究：为解决上述实际问题，我们先建立如下数学模型：如图①，用若干个边长都为1的正方形(记为1×1矩形)和若干个边长分别为1和2的矩形(记为1×2矩形)，要拼成一个如图②中边长分别为1和n的矩形(记为1×n矩形)，有多少种不同的拼法？(设A1×n表示不同拼法的个数)为解决上述数学模型问题，我们采取的策略和方法是：一般问题特殊化．探究一：先从最特殊的情形入手，即要拼成一个1×1矩形，有多少种不同拼法？显然，只有1种拼法，如图③，即A1×1=1种．探究二：要拼成一个1×2矩形，有多少种不同拼法？可以看出，有2种拼法，如图④，即A1×2=2种．探究三：要拼成一个1×3矩形，有多少种不同拼法？拼图方法可分为两类：一类是在图④这2种1×2矩形上方，各拼上一个1×1矩形，即这类拼法共有A1×2=2种；另一类是在图③这1种1×1矩形上方拼上一个1×2矩形，即这类拼法有A1×1=1种．如图⑤，即AA1×3=A1×2+A1×1=2+1=3(种)．探究四：仿照上述探究过程，要拼成一个1×4矩形，有多少种不同拼法？请画示意图说明并求出结果．探究五：要拼成一个1×5矩形，仿照上述探究过程，得出A1×5=______种不同拼法．(直接写出结果，不需画图)．问题解决：请你根据上述中的数学模型，解答“问题提出”中的实际问题．(写出解答过程，不需画图)．15.阅读下列材料，并解决问题：【实验操作】如图1，若干块如图所示的长方形和正方形硬纸片，拼成如图所示的大长方形，并用不同的方法计算它的面积，回答下列问题：①这个拼成的大长方形的面积可表示为多项式为_____________，也可以表示成因式积的形式为____________;②试借助拼图的方法，把二次三项式a2+3b2+4ab因式分解为________________【研究发现】如图2，两个边长分别为a，b，c的直角三角形和一个两条直角边都是c 的等腰直角三角形拼成如图。