Matlab 第三章作业

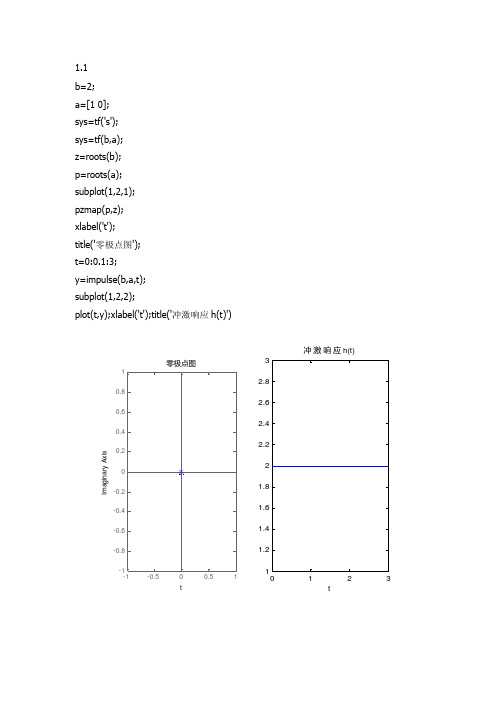
1.1 b=2; a=[1 0]; sys=tf('s'); sys=tf(b,a); z=roots(b); p=roots(a); subplot(1,2,1); pzmap(p,z); xlabel('t'); title('零极点图'); t=0:0.1:3; y=impulse(b,a,t); subplot(1,2,2);plot(t,y);xlabel('t');title('冲激响应h(t)')-1-0.500.51-1-0.8-0.6-0.4-0.200.20.40.60.81零极点图tI m a g i n a r y A x i s012311.21.41.61.822.22.42.62.83t冲激响应h(t)b=2;a=conv([1 7j],[1 -7j]); sys=tf('s'); sys=tf(b,a); z=roots(b); p=roots(a); subplot(1,2,1); pzmap(p,z); xlabel('t'); title('零极点图'); t=0:0.1:3; y=impulse(b,a,t); subplot(1,2,2);plot(t,y);xlabel('t');title('冲激响应h(t)')-1-0.500.51-8-6-4-22468零极点图tI m a g i n a r y A x i s0123-0.4-0.3-0.2-0.10.10.20.3t冲激响应h(t)b=2;a=conv([1 0.5+12j],[1 0.5-12j]); sys=tf('s'); sys=tf(b,a); z=roots(b); p=roots(a); subplot(2,2,1); pzmap(p,z); xlabel('t'); title('零极点图'); [h,w]=freqs(b,a); subplot(2,2,3);plot(w,abs(h));xlabel('w ');title('幅频特性 '); subplot(2,2,4);plot(w,angle(h));xlabel('w ');title('相频特性 '); t=0:0.1:3; y=impulse(b,a,t); subplot(2,2,2);plot(t,y);xlabel('t');title('冲激响应h(t)')-0.8-0.6-0.4-0.20-20-1001020零极点图tI m a g i n a r y A x i s5010000.050.10.150.2w幅频特性50100-4-3-2-10w相频特性0123-0.2-0.100.10.2t冲激响应h(t)b=[2,-2];a=conv([1 3+9j],[1 3-9j]); sys=tf('s'); sys=tf(b,a); z=roots(b); p=roots(a); subplot(2,2,1); pzmap(p,z); xlabel('t'); title('零极点图'); [h,w]=freqs(b,a); subplot(2,2,3);plot(w,abs(h));xlabel('w ');title('幅频特性 '); subplot(2,2,4);plot(w,angle(h));xlabel('w ');title('相频特性 '); t=0:0.1:3; y=impulse(b,a,t); subplot(2,2,2);plot(t,y);xlabel('t');title('冲激响应h(t)')5010000.10.20.30.4w幅频特性50100-2024w相频特性0123-112t冲激响应h(t)零极点图tI m a g i n a r y A x i s1.5 b=[2,-12];a=conv([1 -3+20j],[1 -3-20j]); sys=tf('s'); sys=tf(b,a); z=roots(b); p=roots(a); subplot(1,2,1); pzmap(p,z); xlabel('t'); title('零极点图'); t=0:0.1:3; y=impulse(b,a,t); subplot(1,2,2);plot(t,y);xlabel('t');title('冲激响应h(t)')零极点图tI m a g i n a r y A x i s0123-1.5-1-0.50.514t冲激响应h(t)02462.1高通滤波器 b= [0 0 1];a=conv([1 85+157j],[1 85-157j]); sys=tf('s'); sys=tf(b,a) p=roots(a); z=roots(b); figure(1)subplot(1,2,1); %零极点图 pzmap(p,z); xlabel('t');title('零极点图'); subplot(1,2,2); %对应的冲激响应h(t) plot(h); xlabel('t');title('冲激响应h(t)'); [H,w]=freqs(b,a); figure(2) %频谱图plot(w,abs(H));xlabel('w');title('频谱图');零极点图tI m a g i n a r y A x i s010203040-112345t冲激响应h(t)-100-500-200-150-100-5050100150200010020030040050060070080090010000.20.40.60.811.21.4w频谱图2.2低通滤波器 b=70* [0 0 1]; a=[1 8 70]; sys=tf('s'); sys=tf(b,a) p=roots(a); z=roots(b);pzmap(p,z); xlabel('t');title('零极点图'); subplot(1,2,2); %对应的冲激响应h(t) plot(h); xlabel('t');title('冲激响应h(t)'); [H,w]=freqs(b,a); figure(2) %频谱图plot(w,abs(H));xlabel('w');title('频谱图'); grid on-4-3-2-10零极点图tI m a g i n a r y A x i s10203040-112345t冲激响应h(t)01020304050607080901000.20.40.60.811.21.4w频谱图。

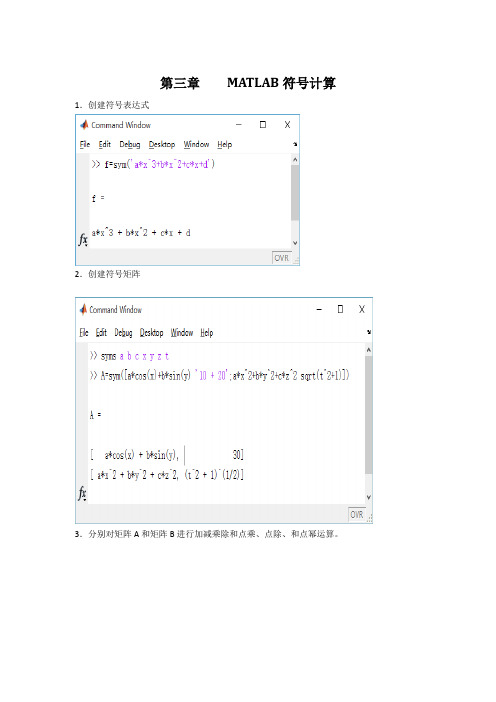
第三章MATLAB符号计算1．创建符号表达式
2．创建符号矩阵
3．分别对矩阵A和矩阵B进行加减乘除和点乘、点除、和点幂运算。

4．执行sym(pi/3)、sym(pi/3,’d’)和sym(‘pi/3’)语句，然后将exp(2)和sin(0.3*pi)代替pi/3分别执行前面3个语句，并观察结果。

5.确定下面个符号表达式的自由符号变量:
6.对式用simple 命令进行化简，并按排版形式显示。

7.已知表达式，，计算当x=1时f的值；计算f和g的复合函数，以及f,g的逆函数。

8.已知表达式，将其转化为多项式系数并将f中的X用5、a代替。

9.符号函数，分别对x、y、c、d进行微分，对y趋向于1求极限。

并计算对X的二次、三次微分，用findsym得出符号变量。

10.符号函数 ，分别对X 、y 进行定积分和不定积分，对y 的定积分区间为（0,1）。

第三章作业第一题：format longsyms xc1=int((x^4*(1-x)^4)/(1+x^2),0,1); %符号工具箱int计算c1=eval(c1); %指令eval一般应用于int后结果较复杂时，进一步求数值解。

f=@(x)(x.^4.*(1-x).^4)./(1+x.^2);c2=quad(f,0,1); %数值积分指令quad要求积分限为常数第二题：format longf=@(x)((2/sqrt(pi))*exp(-x.^2)); %定义误差函数for k=0.1:0.1:1.0c1=quad(f,0,k);c2=erf(k);c=abs(c1-c2);bar(k,c)hold onend第三题：vp=1578;f=@(v)((4/sqrt(pi))*((v.^2)/vp^3).*exp((-v.^2)/vp^2));c1=quad(f,0,vp)c2=quad(f,0,3.3*vp)c3=quad(f,3e4,3e8)结果：c1 =0.427593285448571c2 =0.999927444001040 在0~3.3间的分子数接近为全部c3 =3.520658577050803e-151 速度很大的分子数很少第四题：clear;R=1; y=-4:0.11:4; z=-4:0.11:4 ;the=-0.5*pi : pi/400 : 0.5*pi;[Y, Z,T]=meshgrid(y,z,the);r=sqrt(cos(T).^2+Z.^2+(Y-sin(T)).^2);dv = 1./r ;v=trapz(dv,3);[ey,ez]=gradient(-v,0.5);figure(1)subplot(2,2,1)contour(Y(:,:,1),Z(:,:,1),v,10)subplot(2,2,2)[SY,SZ]=meshgrid(-4:0.2:4,[0.1,-0.1]);streamline(Y(:,:,1),Z(:,:,1),ey,ez,SY,SZ); [SY,SZ]=meshgrid([-4:0.2:4],[-0.005,0.005]); streamline(Y(:,:,1),Z(:,:,1),ey,ez,SY,SZ);R=1; the= 0: pi/20 :2* pi;x= -0.2:0.11:3; y= -0.2:0.11:3; z= -0.2:0.11:3 ; [X,Y, Z,T]=ndgrid(y,x,z,the);r=sqrt((X-cos(T)).^2+(Y-sin(T)).^2+Z.^2);dv = 1./r ;v=trapz(dv,4);[ex,ey,ez]=gradient(-v,0.5);[XX,YY,ZZ]=meshgrid( -0.2:0.11:3);[SX,SY,SZ]=meshgrid(0:0.5:3, 0:0.5:3, [0.05]); subplot(2,2,3)Zmin=min(Z(:)); Zmax=max(Z(:));streamslice(XX,YY,ZZ,ex,ey,ez,[],[],0.01)subplot(2,2,4)x=cos(the);y=sin(the);z=zeros(1,length(the)); plot3(x,y,z,'LineWidth',3,'Color','r');hold onh1=streamline(XX,YY,ZZ,ex,ey,ez,SX,SY,SZ) ;h2=copyobj(h1,gca);rotate(h2,[1,0,0],180,[0 0 0]);h3=copyobj(allchild(gca),gca);rotate(h3,[0,1,0],180,[0 0 0]);view(-28,8)第五题：%亥姆霍兹线圈组成clear allM0=4*pi*1e-7; %初始化, 给定环半径、电流、图形I0=5.0; Rh=1;C0=M0 /(4* pi)* I0;Nx=21; Ny=21; % 设定观测点网格数x=linspace(-Rh,Rh,Nx); %设定观测点范围及数组y=linspace(-Rh,Rh,Ny);Nh=20; %电流环分段T0= linspace( 0, 2*pi, Nh+1); % 环的圆周角分段T1= T0( 1: Nh) ;yb= Rh* cos( T1);zb= Rh* sin(T1); % 设置环各段向量的起点坐标yb, zbT2= T0( 2: Nh+ 1) ;ye= Rh* cos( T2) ;ze= Rh* sin( T2) ; %设置环各段向量的终点坐标ye, zedlx=0; dly=ye- yb; dlz=ze- zb; % 计算环各段向量dl的三个长度分量xc=0; yc=( yb+ ye) /2; zc= ( zb+ ze) /2; %计算环各段向量中点的三个坐标分量for i=1:Ny %循环计算各网格点上的B( x, y)值for j=1:Nxrx=x(j) - xc; ry= y(i) - yc; rz= 0- zc; %观测点在z= 0平面上r3= sqrt( rx.^2+ ry.^2+ rz.^2).^3;dlXr_x=dly.*rz- dlz.*ry; %计算叉乘积dlX r的x 和y的分量dlXr_y=dlz.*rx- dlx.*rz;Bx(i,j)=sum(C0*dlXr_x./r3); %把环各段产生的磁场分量累加By(i,j)=sum(C0*dlXr_y./r3);endendBax= Bx(:,11:21) + Bx(:,1:11) ;Bay= By(:,11:21) + By(:,1:11) ;subplot(1,2,1);mesh(x(11:21),y,Bax); xlabel(x); ylabel(y) ; % 画出其B分布三维图subplot(1,2,2);plot(y,Bax), grid, xlabel(y); ylabel(Bx);。

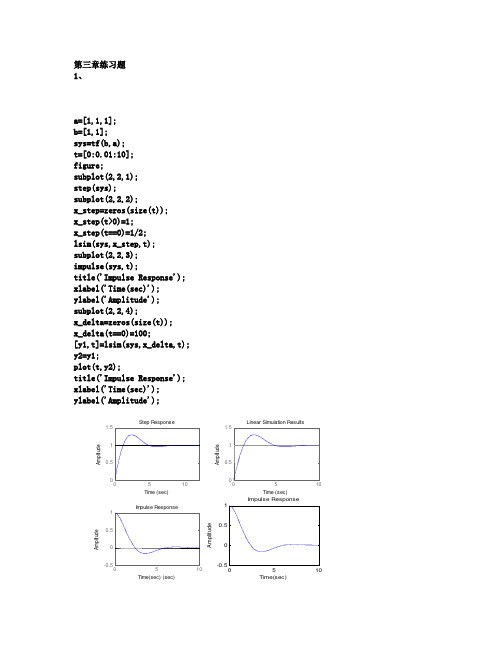
第三章练习题 1、a=[1,1,1]; b=[1,1]; sys=tf(b,a); t=[0:0.01:10]; figure;subplot(2,2,1); step(sys);subplot(2,2,2);x_step=zeros(size(t)); x_step(t>0)=1; x_step(t==0)=1/2; lsim(sys,x_step,t); subplot(2,2,3); impulse(sys,t);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude'); subplot(2,2,4);x_delta=zeros(size(t)); x_delta(t==0)=100;[y1,t]=lsim(sys,x_delta,t); y2=y1;plot(t,y2);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude');00.511.5Step ResponseTime (sec)A m p l i t u d eLinear Simulation ResultsTime (sec)A m p l i t u d e-0.500.51Impulse ResponseTime(sec) (sec)A m p l i t u d eImpulse ResponseTime(sec)A m p l i t u d e2、函数int1如下：function [F,tF]=int1(f,tf,a)T=tf(2)-tf(1);F=zeros(size(tf)); tF=zeros(size(tf));tF=tf;for n=1:length(tf)-1;F(n+1)=F(n)+T*f(n);end验证如下：t=[-1:0.01:4];e=zeros(size(t));e=(t>-1/2&t<1);[z,zz]=intl(e,t,-1);figure;plot(zz,z);第四章练习题1、T1=1;N1=10000; t1=linspace(0,T1-T1/N1,N1)';f1=1-2*t1;OMG=32*pi;K1=100;omg=linspace(-OMG/2,OMG/2-OMG/K1,K1)';X1=T1/N1*exp(-j*kron(omg,t1.'))*f1;fs1=OMG/2/pi/K1*exp(j*kron(t1,omg.'))*X1;T2=5;N2=10000;t2=linspace(0,T2-T2/N2,N2)';fs2=0*t2;f2=sawtooth(t2*2*pi,0);X2=T2/N2*exp(-j*kron(omg,t2.'))*f2;fs2=fs2+OMG/2/pi/K1*exp(j*kron(t2,omg.'))*X2;figure;subplot(2,2,1);plot(omg,abs(X1),'r');xlabel('Frequency'),ylabel('Amplitude')title('单个锯齿周期幅频特性曲线');subplot(2,2,2);plot(t1,fs1,'r');xlabel('Time'),ylabel('Amplitude')title('Function after recovered');subplot(2,2,3);plot(omg,abs(X2),'r');xlabel('Frequency'),ylabel('Amplitude')title('五个锯齿周期幅频特性曲线');subplot(2,2,4);plot(t2,fs2,'r');xlabel('Time'),ylabel('Function after recovered')title('Function after recovered');-100-5005000.20.40.60.8FrequencyA m p l i t u d e单个锯齿周期幅频特性曲线00.51-1-0.500.51TimeA m p l i t u d eFunction after recovered-100-5005000.511.52FrequencyA m p l i t u d e五个锯齿周期幅频特性曲线246-2-1012TimeF u n c t i o n a f t e r r e c o v e r e dFunction after recovered2、fsana 函数如下：function F=fsana(t,f,N); omg1=2*pi/(max(t)-min(t)); k=[-N:N]';F=1/length(t)*exp(-j*kron(k*omg1,t.'))*f; fssyn 函数如下：function f=fssyn(F,t)omg1=2*pi/(max(t)-min(t)); N=floor(length(F)/2); k=[-N:N];f=exp(j*kron(t,k*omg1))*F; 验证如下: clc clearclose allT1=1;N1=256; t=linspace(0,T1-T1/N1,N1)'; f=1-2*t;subplot(3,1,1); plot(t,f);title('验证原函数') N=25;F1=fsana(t,f,N); subplot(3,1,2); stem(abs(F1),'s');title('前N 项傅立叶级数系数幅度曲线') f2=fssyn(F1,t) ;subplot(3,1,3); plot(t,f2);xlabel('time[s]'),ylabel('Amplitude'); title('傅立叶逆变换后时域函数');00.10.20.30.40.50.60.70.80.91-101验证原函数00.20.4前N 项傅立叶级数系数幅度曲线00.10.20.30.40.50.60.70.80.91-202time[s]A m p l i t u d e傅立叶逆变换后时域函数第五章练习题1、(a) Residue计算a1=[1,5,6];b1=[4,5];[r1,p1,k1]=residue(b1,a1); t=[0:0.01:10];e1=zeros(size(t));for n=1:size(r1);e1=e1+r1(n)*exp(p1(n)*t); end;figure;subplot(1,2,1);plot(t,e1);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([4,5],[1,5,6]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h1=lsim(sys1,delta,t); subplot(1,2,2);plot(t,h1);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同（b）Residue计算t=[0,0.01,10];delta=zeros(size(t));delta(t==0)=100;e2=sin(t);figure;subplot(2,1,1);plot(t,e2);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([1,0,2],[1,0,1]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h2=lism(sys1,delta,t); subplot(2,1,2);plot(h,t2);axis([0,10,-1,1]);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同2、S=isstable(sys)函数：Function s=isstable(sys);X=ploe(sys);S=1;For n=1:Size(x)If x(n)>0S=0;break;End;End;稳定系统：Sys=tf(1,[1,2]);S=isstable(sys);S=1不稳定系统：Sys=tf(1,[1,-2]);S=isstable(sys);S=第七章练习题1、a=[1,0.5,-0.2,-0.1]; b=[1,-0.3];n=[0:10]';[hi,t]=impz(b,a,n); subplot(1,2,1);stem(n,hi);u=(n>=0);hn=filter(b,a,u); subplot(1,2,2);stem(n,hn);2、n1=[0:9]';n2=[10:19]';x1=(n1>=0);x2=-(n2>=10);a1=[1,-0.2,-0.1];a2=[1,-0.2,0.5];b=[1,0.01];[y1,wf1]=filter(b,a1,x1,[0,1]); [y2,wf2]=filter(b,a2,x2,wf1); stem(n1,y1);hold on;stem(n2,y2);。

1.编写一个Matlab程序，用一个N点的复数离散傅里叶变换计算两个长度为N的实数序列的N点离散傅里叶变换，并将结果同直接使用两个N点离散傅里叶变换得到的结果进行比较。

n=0:11; %设定n的范围x1=cos(pi/6.*n); %给定序列x1[n]x2=(4/5).^n; %给定序列x2[n]w1=x1+1i*x2; %由序列x1[n]和x2[n]组成复数序列w1[n]w2=x1-1i*x2; %序列w1[n]的共轭序列w2[n]figure,subplot(2,1,1),stem(n,x1); %指定位置1，绘制序列x1[n]xlabel('n'); %设定序列x1[n]的横轴标注和纵轴标注ylabel('x1[n]');subplot(2,1,2),stem(n,x2); %指定位置2，绘制序列x2[n]xlabel('n'); %设定序列x2[n]的横轴标注和纵轴标注ylabel('x2[n]');figure,subplot(4,1,1),stem(abs(w1)); %指定位置1，绘制序列w1[n]幅度谱xlabel('n'); %设定横轴标注，纵轴标注和标题ylabel('magnitude');title('W1的幅度谱');subplot(4,1,2),stem(angle(w1)); %指定位置2，绘制序列w1[n]相位谱xlabel('n'); %设定横轴标注，纵轴标注和标题ylabel('phase');title('W1的相位谱');subplot(4,1,3),stem(abs(w2)); %指定位置3，绘制序列w2[n]幅度谱xlabel('n'); %设定横轴标注，纵轴标注和标题ylabel('magnitude');title('W2的幅度谱');subplot(4,1,4),stem(angle(w2)); %指定位置4，绘制序列w2[n]相位谱xlabel('n'); %设定横轴标注，纵轴标注和标题ylabel('phase');title('W2的相位谱');X1=fft(x1); %求序列x1[n]的离散傅里叶变换X1(k)X2=fft(x2); %求序列x2[n]的离散傅里叶变换X2(k)W1=fft(w1); %求序列w1[n]的离散傅里叶变换W1(k)W2=fft(w2); %求序列w2[n]的离散傅里叶变换W2(k)Y1=(1/2)*(W1+W2); %由W1(k)和W2(k)来求X1(k)Y2=(1/(2*1i))*(W1-W2); %由W1(k)和W2(k)来求X2(k)figure,subplot(2,1,1),stem(abs(X1)); %指定位置1，绘制|X1(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|X1(k)|');subplot(2,1,2),stem(abs(Y1)); %指定位置2，绘制|Y1(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|Y1(k)|');figure,subplot(2,1,1),stem(abs(X2)); %指定位置1，绘制|X2(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|X2(k)|');subplot(2,1,2),stem(abs(Y2)); %指定位置2，绘制|Y2(k)|xlabel('k'); %设定横轴标注和纵轴标注 ylabel('|Y2(k)|');结果图：nx 1[n]024681012nx 2[n ]图1 序列x1[n]和x2[n]02468101212nm a g n i t u d eW1的幅度谱24np h a s eW1的相位谱02468101212nm a g n i t u d eW2的幅度谱024681012-4-20np h a s e图2 w1和w2的幅度谱和相位谱图246k|X 1(k )|246k|Y 1(k )|图3 两种计算X1(k)的方法比较024681012246k|X 2(k )|024681012246k|Y 2(k )|图4 两种计算X2(k)的方法比较2.编写一个Matlab 程序，用两个N 点的复数离散傅里叶变换计算一个长度为2N 的实数序列的2N 点离散傅里叶变换，并将结果同直接使用一个2N 点离散傅里叶变换得到的结果进行比较。

上机实验报告班级:机械工程及自动化02姓名:鄢文光学号:40902010221日期:2012年11月13日题目1-1:>> syms x;limit(cos(sqrt(x^(pi/x,x,0,'right'ans =exp(-1/2*pi题目1-2:>> syms x;limit((3*sin(x+(x^2*cos(1/x/((1+cos(x*log(1+x,x,0ans =3/2题目1-3:>> syms x;limit((sqrt(4*x^2+x-1+x+1/sqrt(x^2+sin(x,x,inf,'left'ans =3题目2-1:>> syms x;f=(tan(sqrt(x+sqrt(x+sqrt(2*x^2;diff(fans =tan((x+(x+2^(1/2*x^(1/2^(1/2^(1/2*(1+tan((x+(x+2^(1/2*x^(1/2^(1/2^(1/2^2/( x+(x +2^(1/2*x^(1/2^(1/2^(1/2*(1+1/2/(x+2^(1/2*x^(1/2^(1/2*(1+1/2*2^(1/2/x^(1/ 2题目2-2:>> syms x;f=(cos(x^2*((sin(1/x^3;diff(fans =-2*sin(x^2*x*sin(1/x^3-3*cos(x^2*sin(1/x^2*cos(1/x/x^2题目3-1:>> syms x;f=sqrt(sin(x-((sin(x^3;int(f,0,pians =4/3题目3-2:>> syms x;f=(1/x*sqrt((x+1/(x-1,int(ff =1/x*((1+x/(x-1^(1/2ans =((1+x/(x-1^(1/2*(x-1/((1+x*(x-1^(1/2*(-atan(1/(x^2-1^(1/2+log(x+(x^2-1^(1/2 题目4:>> dsolve('(x^2*Dy+x*y=y^2','y(1=1','x'ans =2*x/(1+x^2题目5:function ydot=fun1(t,yydot=[y(2;y(3;-4*y(1-3*y(2-11*y(3+3];%建立函数fun1.m>> y0=[1,1,1];[t,y]=ode45('fun1',[0:5:100],y0t =5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95100y =1.0000 1.0000 1.0000 0.8188 -1.4284 -1.4453 -0.6050 -0.09252.4517 0.5827 1.1672 -0.9268 0.6862 -0.8958 -1.1044 -0.3063 -0.1492 1.6221 0.4365 0.8076 -0.5001 0.5792 -0.5548 -0.8243 -0.1061 -0.1571 1.0644 0.3525 0.5537 -0.2522 0.4959 -0.3386 -0.6039 0.0270 -0.1424 0.6925 0.3058 0.3764 -0.1123 0.4330 -0.2030 -0.4357 0.1148 -0.1193 0.4466 0.2812 0.2538 -0.0372 0.3863 -0.1191 -0.31020.1723 -0.0951 0.28520.2692 0.1697 0.00060.3523 -0.0679 -0.21830.2095 -0.0734 0.1803 题目6:function xdot=fun2(t,xxdot=[x(2;x(3;-3*x(1-2*x(2-10*x(3+4];%建立函数fun2.m>> x0=[1,1,1];[t,x]=ode45('fun2',[0:5:100],x0 t = 5101520253035404550556065707580859095100x =1.0000 1.0000 1.00002.0548 -0.6565 -0.10700.6200 0.3125 0.16391.8778 -0.0948 -0.14980.9864 -0.0190 0.10911.5164 0.0627 -0.0667 1.2619 -0.0666 0.0333 1.3411 0.0528 -0.0115 1.3543 -0.0347 -0.00041.3051 0.0191 0.00531.3581 -0.0080 -0.0062882.波旁王朝是哪个国家的——法国883.太平天国由盛转衰的事件是——领导集团的内部斗争884.撒尿小孩铜像坐落于——布鲁塞尔885.中国第一个开发的海底油田位置在——渤海886.“究天人之际,通古今之变,成一家之言”是谁的名言——司马迁887.下列国家中森林覆盖率没有超过60%的是——中国1.3324 0.0011 0.00011.3344 -0.0005 -0.00021.3325 0.0002 0.00021.3339 0.0000 -0.00021.3330 -0.0001 0.0001题目7:>>(解析解 [x,y]=dsolve('Dx=y','Dy=-4x-3y+2','x(0=1','y(0=0' x = 1-5/2*t^2y =-5*t(数值解>> x0=[1,0];[t,x]=ode45('fun3',[0:5:100],x0t =510152025303540455055606570758085911.“布拉格之春”事件发生在——捷克斯洛伐克100913.印度最大的城市孟买人口超过—— 600万914.孙武字什么——子卿915.吴三桂在清朝初期在哪里宣布独立——云南916.直升机停在半空中时,它的旋翼是——仍在转动917.土耳其人最早制造硬币的材料是用——金银合金918.世界水城威尼斯有多少个岛屿——一百多个919.惟知跃进是谁的口号——李大钊920.世界上第一颗人造卫星是哪个国家发射的——苏联0.5000 -0.00000.5000 0.00000.5000 0.00000.5000 -0.00000.5000 -0.00000.5000 -0.00000.5000 0.00000.5000 0.00000.5000 -0.00000.5000 -0.00000.5000 0.00000.5000 0.00000.5000 0.00000.5000 0.0000题目8-1:>> syms t w;f1=sym('t*exp(-t^2'f1 =t*exp(-t^2>> F11=fourier(f1,wF11=-1/2*i*pi^(1/2*w*exp(-1/4*w^2>> F12=ifourier(f1F12 =1/4*i/pi^(1/2*x*exp(-1/4*x^2题目8-2:>> syms t w;f2=sym('(t^2*exp(-t^2'f2 =(t^2*exp(-t^2944.把地图着色,使得相邻的国家有不同的颜色,至少需要几种颜色——4种颜色F21 =1/2*pi^(1/2*exp(-1/4*w^2-1/4*pi^(1/2*w^2*exp(-1/4*w^2 >> F22=ifourier(f2F22 =-1/8/pi^(1/2*exp(-1/4*x^2*(-2+x^2题目9-1:>> syms t s;f1=sym('(sin(t*cos(3*t'f1 =(sin(t*cos(3*t>> F11=laplace(f1,sF11 =(s^2-8/(s^2+16/(s^2+4>> F12=ilaplace(f1F12 =4*ilaplace(sin(t*cos(t^3,t,x-3*ilaplace(sin(t*cos(t,t,x 题目9-2:>> syms t s;f2=sym('exp(-t^2'f2 =exp(-t^2 >> F21=laplace(f2,s F21 = 1/2*pi^(1/2*exp(1/4*s^2*erfc(1/2*s >> F22=ilaplace(f2 F22 = ilaplace(exp(-t^2,t,x。

1. p138 第6题在同一坐标轴中绘制下列两条曲线并标注两曲线交叉点。

>> t=0:0.01:pi;>> x1=t;>> y1=2*x1-0.5;>> x2=sin(3*t).*cos(t);>> y2=sin(3*t).*sin(t);>> plot(x1,y1,'r-',x2,y2,'g-')>> axis([-1,2,-1.5,1])>> hold on>> s=solve('y=2*x-0.5','x=sin(3*t)*cos(t)','y=sin(3*t)*sin(t)'); >> plot(double(s.x),double(s.y),'*');截图：p366 第4题绘制极坐标曲线，并分析对曲线形状的影响。

function [ output_args ] = Untitled2( input_args )%UNTITLED2 Summary of this function goes here% Detailed explanation goes heretheta=0:0.01:2*pi;a=input('请输入a的值：');b=input('请输入b的值：');n=input('请输入n的值：');rho=a*sin(b+n*theta);polar(theta,rho,'k');end下面以a=1，b=1，n=1的极坐标图形为基础来分析a、b、n的影响。

对a的值进行改变：对比发现a只影响半径值的整倍变化对b的值进行改变：对比发现b的值使这个圆转换了一定的角度对n的值进行改变：对比发现当n>=2时有如下规律1、当n为整数时，图形变为2n个花瓣状的图形2、当n为奇数时，图形变为n个花瓣状的图形分别让n为2、3、4、5同时改变b和n的值，对比发现图形变为2n个花瓣状，并且还旋转了一定角度1 绘制sin(x)曲线，通过句柄修改曲线的颜色，要求：a）生成曲线的同时，获取句柄，再修改颜色；>> x=0:pi/50:2*pi;>> y=sin(x);>> h=plot(x,y)h =174.0101>> set(h,'color','r');截图如下：b）先生成曲线，然后再获取句柄，再完成颜色修改。

3-1 编写程序，建立向量N=【1，2，3，4，5】，然后利用向量N产生下列向量：（1）2，4，6，8，10>> N=[1,2,3,4,5];>> 2*Nans =2 4 6 8 10（2）1/2，1，3/2，2，5/2>> 1/4*Nans =0.2500 0.5000 0.7500 1.0000 1.2500（3）1，1/2，1/3，1/4，1/5>> 1./Nans =1.0000 0.5000 0.3333 0.2500 0.2000（4）1，1/4，1/9，1/16，1/25>> 1./(N.*N)ans =1.0000 0.2500 0.1111 0.0625 0.04003-2 从键盘输入一个三位整数，将它反向输入。

如输入639，输出936.x=input('百位');y=input('十位');z=input('个位');a=x*100+y*10+zt=x;x=z;z=t;a=x*100+y*10+z>> f1百位3十位2个位1a =321a =1233-3输入一个百分制成绩，要求输出成绩等级A,B,C,D,E.其中90~100分为A，80~89分为B，70~79分为C，60~69分为D，60分以下的为E。

A='A';B='B';C='C';D='D';E='E';x=input('x=');if x>=90disp (A);elseif x>=80disp(B);elseif x>=70sisp(C);elseif x>=60disp(D);elseif x<60disp(E);end>> f1x=92A>> f1x=65D>> f1x=32E3-6输入20个数，求其中最大数和最小数。

第三章微积分问题的计算机求解一、实验内容：题目1．试求出如下极限。

①limx→∞(3x +9x )1/ x，②lim x→∞[(x+2)x+2(x+3)x+3 ]/(x+5)2x+5【分析】：该题为单变量函数的极限。

极限问题可以用limit()函数直接求出。

要注意该函数的调用格式为:L=limit(fun,x,x0)(求极限)，L=limit(fun,x,x0,’left’或’right’)(求极限)。

还需注意一开始要对函数的字符进行申明。

【解答】：（1）输入如下语句：>> syms x;f=(3^x+9^x)^(1/x);L=limit(f,x,inf)语句运行后显示如下：L =9（2）输入如下语句：>>syms x;f=(x+2)^(x+2)*(x+3)^(x+3)/(x+5)^(2*x+5);>> L=limit(f,x,inf)语句运行后显示如下：L =exp(-5)题目2.试求下面的双重极限。

①lim x→−1y→2 (x2y+xy3)/(x+y) 3，②limx→0 y→0 xy /√(xy+1)−1，③limx→0y→0 [1−cos(x2+y2)]/(x2+y2)e x2+y2。

【分析】：该题为多变量函数的极限问题。

他可以用嵌套使用limit()函数来解决。

在MATLAB上可以用L=limit(limit(f,x,x0),y,y0)或者L=limit(f,y,y0),x,x0)来解决。

其思想是所有的先关于X求导，再所有的关于y求导。

【解答】：(1)输入如下语句：>> syms x y>> f=(x^2*y+x*y^3)/(x+y)^3;>> L=limit(limit(f,x,-1),y,2)语句运行后显示如下：L =-6(2)输入如下语句：>> syms x yf=(x*y)/(sqrt(x*y+1)-1);L=limit(limit(f,x,0),y,0)按ENTER键，语句运行后显示如下：L =2(3)输入如下语句：>> syms x yf=(1-cos(x^2+y^2))/(sqrt(x^2+y^2)*exp(x^2+y^2));L=limit(limit(f,x,0),y,0)按ENTER键，语句运行后显示如下：L =题目3.求出下面函数的导数。