圆柱体积公式推导课件(动画演示好)

圆柱体体积的公式推导
一、几何方法推导圆柱体体积公式：
我们先来考虑一个圆柱体的侧面展开图。

将圆柱体展开，可得到一个
矩形和一个圆。

设圆柱体的底面半径为r，高度为h，那么圆柱体的侧面展开后，矩
形的宽度等于圆的周长，即2πr，矩形的高度等于圆柱体的高度h。

因此，矩形的面积为2πrh。

此外，圆柱体的底面的面积等于圆的面积，即πr^2
根据平行四边形的面积公式，可以得到矩形和圆柱体的侧面积之和等
于圆柱体的侧面展开图的面积：
侧面积+底面积=2πrh+πr^2
因此，圆柱体的体积等于侧面积乘以高度：
V = 2πrh + πr^2
=πr(2h+r)。

这就是圆柱体体积的公式。

二、积分方法推导圆柱体体积公式：
我们也可以通过积分来推导圆柱体体积的公式。

首先，我们先考虑一个具体的圆柱体，底面半径为r，高度为h。

将
圆柱体沿高度方向等分成n个小立方体。

每个小立方体的高度为Δh=h/n，底面积为πr^2
那么小立方体的体积可以近似表示为：
ΔV=πr^2Δh。

将n个小立方体的体积相加，可以得到圆柱体近似体积：
V≈ΣΔV
=Σπr^2Δh
=πr^2(h/n+h/n+...+h/n)
=πr^2(h/n)×n
=πr^2h。

当我们将n趋近无穷大时，圆柱体的近似体积趋近于真实体积。

因此，我们可以得到圆柱体的体积公式：
V=πr^2h。

这也是圆柱体体积的公式。

综上所述，圆柱体的体积可以通过几何方法和积分方法进行推导，得
到的结果都是πr^2h。

《圆柱的认识》PPT课件•圆柱基本概念与性质•圆柱表面积计算方法•圆柱体积计算公式及应用目录•典型例题解析与讨论•学生自主操作实践环节•课堂小结与课后作业布置圆柱基本概念与性质圆柱定义及特点圆柱定义圆柱特点底面侧面高030201底面、侧面和高等元素圆柱与长方体关系形状差异01面积与体积计算02应用场景03圆柱表面积计算方法侧面积计算公式推导公式推导圆柱侧面积定义设圆柱底面半径为面展开后矩形的长为底面周长2πr，宽为h。

因此，侧面积注意事项底面积计算方法回顾圆的面积公式圆柱底面积计算注意事项总表面积计算实例演示实例1解法实例2解法圆柱体积计算公式及应用体积计算公式推导过程圆柱体积公式为公式推导实际应用举例分析圆柱形水桶计算水桶能装多少水，需要用到圆柱体积公式。

已知水桶的底面半径和高，即可求出其容积。

圆柱形油罐计算油罐内油的容量，同样需要用到圆柱体积公式。

通过测量油罐的底面半径和高，可以计算出油的容量。

圆柱形零件在机械工程中，经常需要计算圆柱形零件的体积。

已知零件的底面半径和高，即可利用公式求出其体积。

与其他几何体积关系探讨与长方体体积关系与球体体积关系与圆锥体积关系典型例题解析与讨论求表面积或体积类问题01020304例题1解析例题2解析涉及比例关系类问题例题1解析例题2解析例题1解析例题2解析创新题型展示与思路拓展学生自主操作实践环节测量步骤首先使用卷尺或游标卡尺测量圆柱的高度；接着使用直尺或游标卡尺测量圆柱的底面直径。

准备工具卷尺、游标卡尺、直尺等测量工具。

数据记录将测量得到的高度和底面直径数据记录在表格中，以便后续计算使用。

利用工具测量圆柱尺寸计算给定条件下圆柱表面积和体积公式回顾回顾圆柱表面积和体积的计算公式，即表面积=2πrh+2πr²，体积=πr²h。

数据代入将测量得到的圆柱高度和底面直径数据代入公式中进行计算。

结果呈现将计算得到的圆柱表面积和体积结果呈现在表格中，以便后续分析使用。

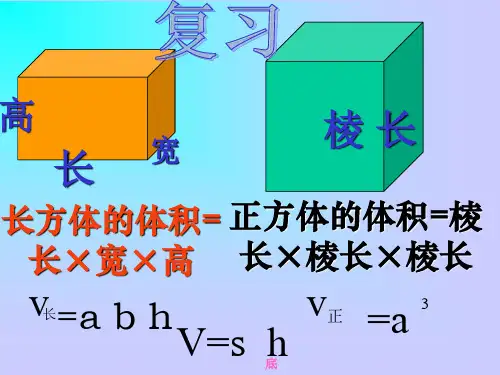
圆柱体体积公式推导圆柱体是指底面为圆形的立体，其体积是指圆柱体所占的空间大小。

圆柱体体积的公式是通过对圆柱体的相关特征进行推导得到的。

首先，我们来定义圆柱体的一些相关特征：-高度（h）：圆柱体的轴线上的两个平行圆底面之间的距离。

-底面半径（r）：圆柱体的底面圆的半径。

接下来，我们可以将圆柱体切割成一系列无限小的圆盘层。

我们可以将这些圆盘层看作是一系列平行的圆环。

每个圆环的面积可以通过圆的面积公式来计算，即πr²。

现在，让我们将一个圆环的面积乘以其高度来得到圆柱体的体积。

我们可以计算一个平行圆环的体积公式为V=πr²h，单位是立方单位。

但是，圆柱体包含了无穷多个这样的圆环。

要计算整个圆柱体的体积，我们就要对所有圆环的体积进行求和。

我们可以将圆柱体的体积公式表示为：V = ∫(πr²)dh其中，∫表示对变量h进行积分，积分范围是从底面到顶面的高度范围。

我们可以通过求解这个积分来得到圆柱体的体积公式。

首先，我们对圆柱体的高度进行积分，即：∫(πr²)dh = π∫r²dh要计算这个积分，我们需要确定积分的上下限。

根据圆柱体的定义，上限是圆柱体的顶面高度（h）,下限是圆柱体的底面高度（0）.因此积分范围是0到h。

接下来，我们将r表示为h的函数，即r=f(h)。

由于圆柱体的底面半径是常数，我们可以将r表示为h的函数r=g(h)。

这样我们就可以将上述积分转换为以h为变量的表达式：∫(πg(h)²)dh接下来，我们可以根据具体情况选择适当的方法来求解这个积分。

这里，我们假设g(h)是一个定义明确的函数，我们可以通过函数关系式来求解。

当然，这里我们还需考虑各种不同的边界条件和函数关系，比如可能存在圆柱体的半径是h的函数(r=f(h))，或者存在底面和顶面圆的半径不等的情况。

最后，根据具体函数形式，我们可以将上述积分进行求解，从而得到圆柱体的体积公式。

综上所述，我们推导了圆柱体体积的公式。

圆柱体积计算公式怎么推导圆柱体积公式推导过程把圆柱底面分成若干份相等的扇形(如分成16等份),沿着圆柱底面的扇形和圆柱的高把圆柱切开,可以得到大小相等的16块.把16块圆柱的底面拼成一个近似长方形,则圆柱体就接近长方体（如果分成的扇形越多,拼成的立体图形就越接近于长方体了）。

由于体积没有发生变化,所以可以通过求切拼后的长方体的体积来求圆柱的体积。

长方体的体积＝底面积×高长方体的底面积等于圆柱的底面积,长方体的高就是圆柱的高。

所以：圆柱的体积＝底面积×高,如果用V表示圆柱的体积,S表示圆柱的底面积,H表示圆柱的高,可以得到圆柱的体积公式；V＝SH圆柱体积相关公式圆柱体的体积=底面积×高=（V=πr²h）；圆的面积=圆周率×半径×半径。

圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆周率（π）是圆的周长与直径的比值，一般用希腊字母π表示，是一个在数学及物理学中普遍存在的数学常数。

π也等于圆形之面积与半径平方之比。

是精确计算圆周长、圆面积、球体积等几何形状的关键值。

在分析学里，π可以严格地定义为满足sinx= 0的最小正实数x。

圆柱体积的算法求圆柱体积先要求圆基的半径。

两个圆都会做，因为它们大小相同。

如果你已经知道半径，你可以继续前进。

如果你不知道半径，那么你可以用尺子测量圆的最宽部分，然后除以2。

这将比测量直径的一半更准确。

我们说，这个圆筒的半径是1英寸（2.5 厘米）。

把它写下来。

如果你知道这个圆的直径，就把它分成2个。

如果你知道周长，然后除以2π得到半径。

计算圆形基的面积。

要做到这一点，只是用公式求圆的面积，πR2 =。

只要把你找到的半径插进去就可以了。

这里是如何做到这一点：aπx 12 = =πx 1。

因为π约3.14到三的数字，你可以说，圆形底座的面积是3.14。

找到圆柱体的高度。

如果你已经知道高度了，继续前进。