下载文档原格式
平衡二叉树操作的演示1.需求分析本程序是利用平衡二叉树，实现动态查找表的基本功能：创建表，查找、插入、删除。
具体功能：（1）初始，平衡二叉树为空树，操作界面给出创建、查找、插入、删除、合并、分裂六种操作供选择。
每种操作均提示输入关键字。
每次插入或删除一个结点后，更新平衡二叉树的显示。
（2）平衡二叉树的显示采用凹入表现形式。
（3）合并两棵平衡二叉树。
（4）把一棵二叉树分裂为两棵平衡二叉树，使得在一棵树中的所有关键字都小于或等于x，另一棵树中的任一关键字都大于x。
如下图：2．概要设计平衡二叉树是在构造二叉排序树的过程中，每当插入一个新结点时，首先检查是否因插入新结点而破坏了二叉排序树的平衡性，若是则找出其中的最小不平衡子树，在保持二叉排序树特性的前提下，调整最小不平衡子树中各结点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。
具体步骤：（1）每当插入一个新结点，从该结点开始向上计算各结点的平衡因子，即计算该结点的祖先结点的平衡因子，若该结点的祖先结点的平衡因子的绝对值不超过1，则平衡二叉树没有失去平衡，继续插入结点；（2）若插入结点的某祖先结点的平衡因子的绝对值大于1，则找出其中最小不平衡子树的根结点；（3）判断新插入的结点与最小不平衡子树的根结点个关系，确定是那种类型的调整；（4）如果是LL型或RR型，只需应用扁担原理旋转一次，在旋转过程中，如果出现冲突，应用旋转优先原则调整冲突；如果是LR型或RL型，则需应用扁担原理旋转两次，第一次最小不平衡子树的根结点先不动，调整插入结点所在子树，第二次再调整最小不平衡子树，在旋转过程中，如果出现冲突，应用旋转优先原则调整冲突；（5）计算调整后的平衡二叉树中各结点的平衡因子，检验是否因为旋转而破坏其他结点的平衡因子，以及调整后平衡二叉树中是否存在平衡因子大于1的结点。
流程图3.详细设计二叉树类型定义：typedef int Status;typedef int ElemType;typedef struct BSTNode{ElemType data;int bf;struct BSTNode *lchild ,*rchild;} BSTNode,* BSTree;Status SearchBST(BSTree T,ElemType e)//查找void R_Rotate(BSTree &p)//右旋void L_Rotate(BSTree &p)//左旋void LeftBalance(BSTree &T)//插入平衡调整void RightBalance(BSTree &T)//插入平衡调整Status InsertAVL(BSTree &T,ElemType e,int &taller)//插入void DELeftBalance(BSTree &T)//删除平衡调整void DERightBalance(BSTree &T)//删除平衡调整Status Delete(BSTree &T,int &shorter)//删除操作Status DeleteAVL(BSTree &T,ElemType e,int &shorter)//删除操作void merge(BSTree &T1,BSTree &T2)//合并操作void splitBSTree(BSTree T,ElemType e,BSTree &T1,BSTree &T2)//分裂操作void PrintBSTree(BSTree &T,int lev)//凹入表显示附录源代码：#include<stdio.h>#include<stdlib.h>//#define TRUE 1//#define FALSE 0//#define OK 1//#define ERROR 0#define LH +1#define EH 0#define RH -1//二叉类型树的类型定义typedef int Status;typedef int ElemType;typedef struct BSTNode{ElemType data;int bf;//结点的平衡因子struct BSTNode *lchild ,*rchild;//左、右孩子指针} BSTNode,* BSTree;/*查找算法*/Status SearchBST(BSTree T,ElemType e){if(!T){return 0; //查找失败}else if(e == T->data ){return 1; //查找成功}else if (e < T->data){return SearchBST(T->lchild,e);}else{return SearchBST(T->rchild,e);}}//右旋void R_Rotate(BSTree &p){BSTree lc; //处理之前的左子树根结点lc = p->lchild; //lc指向的*p的左子树根结点p->lchild = lc->rchild; //lc的右子树挂接为*P的左子树lc->rchild = p;p = lc; //p指向新的根结点}//左旋void L_Rotate(BSTree &p){BSTree rc;rc = p->rchild; //rc指向的*p的右子树根结点p->rchild = rc->lchild; //rc的左子树挂接为*p的右子树rc->lchild = p;p = rc; //p指向新的根结点}//对以指针T所指结点为根结点的二叉树作左平衡旋转处理，//本算法结束时指针T指向新的根结点void LeftBalance(BSTree &T){BSTree lc,rd;lc=T->lchild;//lc指向*T的左子树根结点switch(lc->bf){ //检查*T的左子树的平衡度，并做相应的平衡处理case LH: //新结点插入在*T的左孩子的左子树，要做单右旋处理T->bf = lc->bf=EH;R_Rotate(T);break;case RH: //新结点插入在*T的左孩子的右子树上，做双旋处理rd=lc->rchild; //rd指向*T的左孩子的右子树根switch(rd->bf){ //修改*T及其左孩子的平衡因子case LH: T->bf=RH; lc->bf=EH;break;case EH: T->bf=lc->bf=EH;break;case RH: T->bf=EH; lc->bf=LH;break;}rd->bf=EH;L_Rotate(T->lchild); //对*T的左子树作左旋平衡处理R_Rotate(T); //对*T作右旋平衡处理}}//右平衡旋转处理void RightBalance(BSTree &T){BSTree rc,ld;rc=T->rchild;switch(rc->bf){case RH:T->bf= rc->bf=EH;L_Rotate(T);break;case LH:ld=rc->lchild;switch(ld->bf){case LH: T->bf=RH; rc->bf=EH;break;case EH: T->bf=rc->bf=EH;break;case RH: T->bf = EH; rc->bf=LH;break;}ld->bf=EH;R_Rotate(T->rchild);L_Rotate(T);}}//插入结点Status InsertAVL(BSTree &T,ElemType e,int &taller){//taller反应T长高与否if(!T){//插入新结点，树长高，置taller为trueT= (BSTree) malloc (sizeof(BSTNode));T->data = e;T->lchild = T->rchild = NULL;T->bf = EH;taller = 1;}else{if(e == T->data){taller = 0;return 0;}if(e < T->data){if(!InsertAVL(T->lchild,e,taller))//未插入return 0;if(taller)//已插入到*T的左子树中且左子树长高switch(T->bf){//检查*T的平衡度，作相应的平衡处理case LH:LeftBalance(T);taller = 0;break;case EH:T->bf = LH;taller = 1;break;case RH:T->bf = EH;taller = 0;break;}}else{if (!InsertAVL(T->rchild,e,taller)){return 0;}if(taller)//插入到*T的右子树且右子树增高switch(T->bf){//检查*T的平衡度case LH:T->bf = EH;taller = 0;break;case EH:T->bf = RH;taller = 1;break;case RH:RightBalance(T);taller = 0;break;}}}return 1;}void DELeftBalance(BSTree &T){//删除平衡调整BSTree lc,rd;lc=T->lchild;switch(lc->bf){case LH:T->bf = EH;//lc->bf= EH;R_Rotate(T);break;case EH:T->bf = EH;lc->bf= EH;R_Rotate(T);break;case RH:rd=lc->rchild;switch(rd->bf){case LH: T->bf=RH; lc->bf=EH;break;case EH: T->bf=lc->bf=EH;break;case RH: T->bf=EH; lc->bf=LH;break;}rd->bf=EH;L_Rotate(T->lchild);R_Rotate(T);}}void DERightBalance(BSTree &T) //删除平衡调整{BSTree rc,ld;rc=T->rchild;switch(rc->bf){case RH:T->bf= EH;//rc->bf= EH;L_Rotate(T);break;case EH:T->bf= EH;//rc->bf= EH;L_Rotate(T);break;case LH:ld=rc->lchild;switch(ld->bf){case LH: T->bf=RH; rc->bf=EH;break;case EH: T->bf=rc->bf=EH;break;case RH: T->bf = EH; rc->bf=LH;break;}ld->bf=EH;R_Rotate(T->rchild);L_Rotate(T);}}void SDelete(BSTree &T,BSTree &q,BSTree &s,int &shorter){if(s->rchild){SDelete(T,s,s->rchild,shorter);if(shorter)switch(s->bf){case EH:s->bf = LH;shorter = 0;break;case RH:s->bf = EH;shorter = 1;break;case LH:DELeftBalance(s);shorter = 0;break;}return;}T->data = s->data;if(q != T)q->rchild = s->lchild;elseq->lchild = s->lchild;shorter = 1;}//删除结点Status Delete(BSTree &T,int &shorter){ BSTree q;if(!T->rchild){q = T;T = T->lchild;free(q);shorter = 1;}else if(!T->lchild){q = T;T= T->rchild;free(q);shorter = 1;}else{SDelete(T,T,T->lchild,shorter);if(shorter)switch(T->bf){case EH:T->bf = RH;shorter = 0;break;case LH:T->bf = EH;shorter = 1;break;case RH:DERightBalance(T);shorter = 0;break;}}return 1;}Status DeleteAVL(BSTree &T,ElemType e,int &shorter){ int sign = 0;if (!T){return sign;}else{if(e == T->data){sign = Delete(T,shorter);return sign;}else if(e < T->data){sign = DeleteAVL(T->lchild,e,shorter);if(shorter)switch(T->bf){case EH:T->bf = RH;shorter = 0;break;case LH:T->bf = EH;shorter = 1;break;case RH:DERightBalance(T);shorter = 0;break;}return sign;}else{sign = DeleteAVL(T->rchild,e,shorter);if(shorter)switch(T->bf){case EH:T->bf = LH;shorter = 0;break;case RH:T->bf = EH;break;case LH:DELeftBalance(T);shorter = 0;break;}return sign;}}}//合并void merge(BSTree &T1,BSTree &T2){int taller = 0;if(!T2)return;merge(T1,T2->lchild);InsertAVL(T1,T2->data,taller);merge(T1,T2->rchild);}//分裂void split(BSTree T,ElemType e,BSTree &T1,BSTree &T2){ int taller = 0;if(!T)return;split(T->lchild,e,T1,T2);if(T->data > e)InsertAVL(T2,T->data,taller);elseInsertAVL(T1,T->data,taller);split(T->rchild,e,T1,T2);}//分裂void splitBSTree(BSTree T,ElemType e,BSTree &T1,BSTree &T2){ BSTree t1 = NULL,t2 = NULL;split(T,e,t1,t2);T1 = t1;T2 = t2;return;}//构建void CreatBSTree(BSTree &T){int num,i,e,taller = 0;printf("输入结点个数:");scanf("%d",&num);printf("请顺序输入结点值\n");for(i = 0 ;i < num;i++){printf("第%d个结点的值",i+1);scanf("%d",&e);InsertAVL(T,e,taller) ;}printf("构建成功，输入任意字符返回\n");getchar();getchar();}//凹入表形式显示方法void PrintBSTree(BSTree &T,int lev){int i;if(T->rchild)PrintBSTree(T->rchild,lev+1);for(i = 0;i < lev;i++)printf(" ");printf("%d\n",T->data);if(T->lchild)PrintBSTree(T->lchild,lev+1);void Start(BSTree &T1,BSTree &T2){int cho,taller,e,k;taller = 0;k = 0;while(1){system("cls");printf(" 平衡二叉树操作的演示 \n\n");printf("********************************\n");printf(" 平衡二叉树显示区 \n");printf("T1树\n");if(!T1 )printf("\n 当前为空树\n");else{PrintBSTree(T1,1);}printf("T2树\n");if(!T2 )printf("\n 当前为空树\n");elsePrintBSTree(T2,1);printf("\n********************************************************************* *********\n");printf("T1操作：1.创建 2.插入 3.查找 4.删除 10.分裂\n");printf("T2操作：5.创建 6.插入 7.查找 8.删除 11.分裂\n");printf(" 9.合并 T1,T2 0.退出\n");printf("*********************************************************************** *******\n");printf("输入你要进行的操作：");scanf("%d",&cho);switch(cho){case 1:CreatBSTree(T1);break;case 2:printf("请输入要插入关键字的值");scanf("%d",&e);InsertAVL(T1,e,taller) ;break;case 3:printf("请输入要查找关键字的值");scanf("%d",&e);if(SearchBST(T1,e))printf("查找成功！\n");elseprintf("查找失败！\n");printf("按任意键返回87"); getchar();getchar();break;case 4:printf("请输入要删除关键字的值"); scanf("%d",&e);if(DeleteAVL(T1,e,k))printf("删除成功！\n");elseprintf("删除失败！\n");printf("按任意键返回");getchar();getchar();break;case 5:CreatBSTree(T2);break;case 6:printf("请输入要插入关键字的值"); scanf("%d",&e);InsertAVL(T2,e,taller) ;break;case 7:printf("请输入要查找关键字的值"); scanf("%d",&e);if(SearchBST(T2,e))printf("查找成功！\n");elseprintf("查找失败！\n");printf("按任意键返回");getchar();getchar();break;case 8:printf("请输入要删除关键字的值"); scanf("%d",&e);if(DeleteAVL(T2,e,k))printf("删除成功！\n");elseprintf("删除失败！\n");printf("按任意键返回");getchar();getchar();break;case 9:merge(T1,T2);T2 = NULL;printf("合并成功，按任意键返回"); getchar();getchar();break;case 10:printf("请输入要中间值字的值"); scanf("%d",&e);splitBSTree(T1,e,T1,T2) ;printf("分裂成功，按任意键返回"); getchar();getchar();break;case 11:printf("请输入要中间值字的值"); scanf("%d",&e);splitBSTree(T2,e,T1,T2) ;printf("分裂成功，按任意键返回"); getchar();getchar();break;case 0:system("cls");exit(0);}}}main(){BSTree T1 = NULL;BSTree T2 = NULL;Start(T1,T2);}。
数据结构中平衡二叉树的定义平衡二叉树？哎呦，这个名字一听就让人有点晕，搞得我差点以为是个什么高深的数学公式，其实不然，它就是一种数据结构。
你想象一下，平衡二叉树就像一个超级讲究的家庭，每个人都必须保持“平衡”，不然就容易乱套。
这个家庭的成员，或者说是“节点”，总共有两个子节点，而且它们的“家务活”分配要特别均匀，不能有一个子节点忙得像打了鸡血，另一个却轻松得像度假。
说白了，平衡二叉树就是告诉你，“兄弟姐妹”们得公平分工，不能让某个“孩子”走得太远，另一个就被落下。
我们得弄清楚什么是“二叉树”。
嘿，其实二叉树就是每个节点最多只能有两个子节点的树形结构，简单点说，就是每个人最多只能有两个“孩子”，并且这两个“孩子”得排排坐，不能一个高一个矮，那样看起来就不和谐了。
可要是左边的“孩子”特别高，右边的又短得跟个小矮人一样，那也不行，得保持两边差不多高。
嘿，听起来像什么？就像家里有两个孩子，一个高得过头，一个低得不行，结果谁都不开心。
平衡二叉树特别讲究左右子树的“差距”。
差距得控制在一定范围内，通常说是不能超过1。
就是说，如果左边的子树高出了1层，右边的子树就不能高出2层。
否则呢，这个二叉树就不平衡了，像你站在一只跛脚的板凳上，随时可能摔倒。
再简单点说，平衡二叉树就像我们家常见的“八仙过海，各显神通”，每个节点都有各自的位置和作用，位置偏离太多就得重新调整调整，确保大家的体力和位置保持均衡。
有的朋友可能会问，既然这么讲究“平衡”，那它怎么判断自己是否平衡呢？嘿，这里就要用到一个神奇的“高度差”了。
我们通常用每个节点的左右子树的高度差来判断。
如果某个节点的左右子树的高度差超过了1，说明它就失去平衡了。
那么我们该怎么办呢？就像你掉进了泥潭，要不是用力蹬两下，要不就是找人来拉一把，二叉树也是一样，得“旋转”一下才能恢复平衡。
平衡二叉树一旦出现不平衡，就得做旋转操作。
别想歪了，旋转不是让树开个舞会，而是指用一种特别的方式重新安排节点的位置。
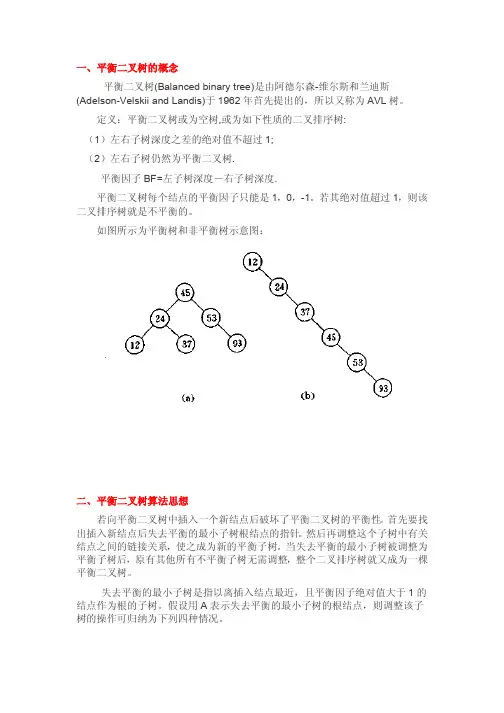
一、平衡二叉树的概念平衡二叉树(Balanced binary tree)是由阿德尔森-维尔斯和兰迪斯(Adelson-Velskii and Landis)于1962年首先提出的，所以又称为AVL树。
定义：平衡二叉树或为空树,或为如下性质的二叉排序树:（1）左右子树深度之差的绝对值不超过1;（2）左右子树仍然为平衡二叉树.平衡因子BF=左子树深度－右子树深度.平衡二叉树每个结点的平衡因子只能是1，0，-1。
若其绝对值超过1，则该二叉排序树就是不平衡的。
如图所示为平衡树和非平衡树示意图：二、平衡二叉树算法思想若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。
首先要找出插入新结点后失去平衡的最小子树根结点的指针。
然后再调整这个子树中有关结点之间的链接关系，使之成为新的平衡子树。
当失去平衡的最小子树被调整为平衡子树后，原有其他所有不平衡子树无需调整，整个二叉排序树就又成为一棵平衡二叉树。
失去平衡的最小子树是指以离插入结点最近，且平衡因子绝对值大于1的结点作为根的子树。
假设用A表示失去平衡的最小子树的根结点，则调整该子树的操作可归纳为下列四种情况。
1）LL型平衡旋转法由于在A的左孩子B的左子树上插入结点F，使A的平衡因子由1增至2而失去平衡。
故需进行一次顺时针旋转操作。
即将A的左孩子B向右上旋转代替A作为根结点，A向右下旋转成为B的右子树的根结点。
而原来B的右子树则变成A的左子树。
（2）RR型平衡旋转法由于在A的右孩子C 的右子树上插入结点F，使A的平衡因子由-1减至-2而失去平衡。
故需进行一次逆时针旋转操作。
即将A的右孩子C向左上旋转代替A作为根结点，A向左下旋转成为C的左子树的根结点。
而原来C的左子树则变成A的右子树。
（3）LR型平衡旋转法由于在A的左孩子B的右子数上插入结点F，使A的平衡因子由1增至2而失去平衡。
故需进行两次旋转操作（先逆时针，后顺时针）。
即先将A结点的左孩子B的右子树的根结点D向左上旋转提升到B结点的位置，然后再把该D结点向右上旋转提升到A结点的位置。
数据结构之⼆叉树（BinaryTree）⽬录导读 ⼆叉树是⼀种很常见的数据结构，但要注意的是，⼆叉树并不是树的特殊情况，⼆叉树与树是两种不⼀样的数据结构。
⽬录 ⼀、⼆叉树的定义 ⼆、⼆叉树为何不是特殊的树 三、⼆叉树的五种基本形态 四、⼆叉树相关术语 五、⼆叉树的主要性质（6个） 六、⼆叉树的存储结构（2种） 七、⼆叉树的遍历算法（4种） ⼋、⼆叉树的基本应⽤：⼆叉排序树、平衡⼆叉树、赫夫曼树及赫夫曼编码⼀、⼆叉树的定义 如果你知道树的定义（有限个结点组成的具有层次关系的集合），那么就很好理解⼆叉树了。
定义：⼆叉树是n(n≥0)个结点的有限集，⼆叉树是每个结点最多有两个⼦树的树结构，它由⼀个根结点及左⼦树和右⼦树组成。
（这⾥的左⼦树和右⼦树也是⼆叉树）。
值得注意的是，⼆叉树和“度⾄多为2的有序树”⼏乎⼀样，但，⼆叉树不是树的特殊情形。
具体分析如下⼆、⼆叉树为何不是特殊的树 1、⼆叉树与⽆序树不同 ⼆叉树的⼦树有左右之分，不能颠倒。
⽆序树的⼦树⽆左右之分。
2、⼆叉树与有序树也不同（关键） 当有序树有两个⼦树时，确实可以看做⼀颗⼆叉树，但当只有⼀个⼦树时，就没有了左右之分，如图所⽰：三、⼆叉树的五种基本状态四、⼆叉树相关术语是满⼆叉树；⽽国际定义为，不存在度为1的结点，即结点的度要么为2要么为0，这样的⼆叉树就称为满⼆叉树。
这两种概念完全不同，既然在国内，我们就默认第⼀种定义就好）。
完全⼆叉树：如果将⼀颗深度为K的⼆叉树按从上到下、从左到右的顺序进⾏编号，如果各结点的编号与深度为K的满⼆叉树相同位置的编号完全对应，那么这就是⼀颗完全⼆叉树。
如图所⽰：五、⼆叉树的主要性质 ⼆叉树的性质是基于它的结构⽽得来的，这些性质不必死记，使⽤到再查询或者⾃⼰根据⼆叉树结构进⾏推理即可。
性质1：⾮空⼆叉树的叶⼦结点数等于双分⽀结点数加1。
证明：设⼆叉树的叶⼦结点数为X，单分⽀结点数为Y，双分⽀结点数为Z。
数据结构：⼆叉树、平衡⼆叉树、红⿊树详解⼀、⼆叉树（binary tree）指每个节点最多含有两个⼦树的树结构。
时间复杂度为O(log N)，在退化成链表的情况下时间复杂度为O(N)。
特点：1.所有节点最多拥有两个⼦节点；2.节点的左⼦树只包含⼩于当前根节点的数，节点的右⼦树只包含⼤于当前根节点的数。
缺点：只会以我们第⼀次添加的节点为根节点，如果后⾯添加的节点值都⼤于或⼩于根节点的值，在这种情况下会退化成链表。
⼆、平衡⼆叉树（Balanced Binary Tree）⼜称为AVL树，具有⼆叉树的全部特性，解决⼆叉树退化成链表情况的问题，每个节点的左⼦树和右⼦树的⾼度之差不会超过1，AVL树是严格的平衡⼆叉树，追求完全平衡，⽐较严格。
缺点：由于要求每个节点的左⼦树和右⼦树⾼度之差不超过1，这个要求⾮常严格，追求完全平衡，这就导致了在频繁插⼊和删除的场景中，可能就会导致AVL树失去平衡，AVL树就需要频繁的通过左旋右旋使其重新达到平衡，这时就会时得其性能⼤打折扣。
三、红⿊树和AVL树相⽐，红⿊树放弃追求完全平衡，⽽是追求⼤致平衡，保证每次插⼊节点最多只需要三次旋转就能达到平衡，维持平衡的耗时较少，实现起来也更为简单，它的旋转次数较少，对于频繁插⼊和删除操作的场景，相⽐AVL树，红⿊树更具优势。
特征：1.红⿊树是也是平衡⼆叉树实现的⼀种⽅式2.节点只能是⿊⾊或者红⾊，root根节点⼀定是⿊⾊3.新增时默认新增的节点是红⾊，不允许两个红⾊节点相连4.红⾊节点的两个⼦节点⼀定是⿊⾊红⿊树变换规则三种规则：1.改变节点颜⾊2.左旋转3.右旋转变⾊的情况：当前节点的⽗亲节点是红⾊，并且它的祖⽗节点的另外⼀个⼦节点（叔叔节点）也是红⾊：以当前节点为指针进⾏操作1.将⽗亲节点变为⿊⾊2.将叔叔节点变为⿊⾊3.将祖⽗节点变为红⾊4.再把指针定义到祖⽗节点进⾏旋转操作左旋转：当⽗亲节点为红⾊情况，叔叔节点为⿊⾊情况，且当前节点是右⼦树，左旋转以⽗节点作为左旋。
