投影变形计算公式
- 格式:doc
- 大小:27.50 KB
- 文档页数:1

高斯投影长度变形公式
长度变形来源于以下两个方面
1、实地测量的边长长度换算到椭球面上产生的变形,即∆s1;
改正数误差方程式(此式较复杂这里省略)经最小二乘列出误差方程式,按级数展开后取其主项(其它项的影响甚微可忽略不计):
∆s1=−H m
R A
s(1)式中:R A—长度所在方向的椭球曲率半径;
H m—长度所在高程面对于椭球面的平均高程;
s—实地测量的水平距离。
2、椭球面上的长度投影至高斯平面
∆s2=+y m2
2R2
s0(2)式中:R—测区中点的平均曲率半径;
y m—距离的2端点横坐标平均值;
s0—为归算到椭球面上的长度。
在不影响推证严密性的前提下取, R A=R,s=s0,综合上两式可得,综合长度变形∆s为:
∆s=−H m
R
s+
y m2
2R2
s。
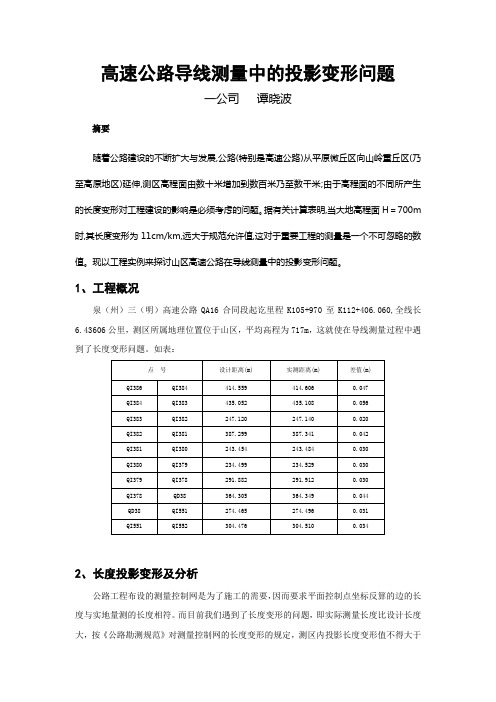
高速公路导线测量中的投影变形问题一公司谭晓波摘要随着公路建设的不断扩大与发展,公路(特别是高速公路)从平原微丘区向山岭重丘区(乃至高原地区)延伸,测区高程面由数十米增加到数百米乃至数千米;由于高程面的不同所产生的长度变形对工程建设的影响是必须考虑的问题。
据有关计算表明,当大地高程面H=700m 时,其长度变形为11cm/km,远大于规范允许值,这对于重要工程的测量是一个不可忽略的数值。
现以工程实例来探讨山区高速公路在导线测量中的投影变形问题。
1、工程概况泉(州)三(明)高速公路QA16合同段起讫里程K105+970至K112+406.060,全线长6.43606公里,测区所属地理位置位于山区,平均高程为717m,这就使在导线测量过程中遇到了长度变形问题。
如表:2、长度投影变形及分析公路工程布设的测量控制网是为了施工的需要,因而要求平面控制点坐标反算的边的长度与实地量测的长度相符。
而目前我们遇到了长度变形的问题,即实际测量长度比设计长度大,按《公路勘测规范》对测量控制网的长度变形的规定,测区内投影长度变形值不得大于2.5 cm/km ,即投影变形应达到1/40 000的精度。
这就要求要对实测长度进行改正,也就是要先将控制网边长归化到参考椭球面上,然后再将椭球面上的长度投影到高斯平面上,使其影响可以忽略不计。
2.1、投影变形数学模型长度变形来源于以下两个方面:2.1.1 实地测量的边长长度换算到椭球面上产生的变形,即1s ∆;改正数误差方程式(此式较复杂这里省略)经最小二乘列出误差方程式,按级数展开后取其主项(其它项的影响甚微可以忽略不计):s R H s Am-=∆1(1) 式中 A R -长度所在方向的椭球曲率半径;m H -长度所在高程面对于椭球面的平均高程; s -实地测量的水平距离。
2.1.2 椭球面上的长度投影至高斯平面02222s Ry s m+=∆ (2)式中 R -测区中点的平均曲率半径; m y -距离的2端点横坐标平均值; 0s -为归算到椭球面上的长度。

常用地图投影转换公式作者:青岛海洋地质研究所戴勤奋 投影计算公式往往表达方式不止一种,有时很难分辨谁对谁错,我只把“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影”(1:100万地形图规范中称作正轴等角圆锥投影,GB/T 14512-93)的正反转换公式列出,因为我基本能保证这些公式的正确性。
1.约定本文中所列的转换公式都基于椭球体a -- 椭球体长半轴b -- 椭球体短半轴f -- 扁率e -- 第一偏心率e’ -- 第二偏心率N -- 卯酉圈曲率半径R -- 子午圈曲率半径B -- 纬度,L -- 经度,单位弧度(RAD)-- 纵直角坐标,-- 横直角坐标,单位米(M)2.椭球体参数我国常用的3个椭球体参数如下(源自“全球定位系统测量规范 GB/T界面上的所谓“北京1954“西安1980”及“WGS 84”在实际计算中只涉及了相应的椭球体参数。
3.墨卡托(Mercator)投影3.1 墨卡托投影简介墨卡托(Mercator)投影,是一种"等角正切圆柱投影”,荷兰地图学家墨卡托(Gerhardus Mercator 1512-1594)在1569年拟定, 假设地球被围在一中空的圆柱里,其标准纬线与圆柱相切接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。
墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。
墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。
在地图上保持方向和角度的正确是墨卡托投影的优点,墨卡托投影地图常用作航海图和航空图,如果循着墨卡托投影图上两点间的直线航行,方向不变可以一直到达目的地,因此它对船舰在航行中定位、确定航向都具有有利条件,给航海者带来很大方便。


镜头透视形变公式
镜头透视形变是指相机或镜头在拍摄物体时,由于透视效应而导致物体呈现出变形的现象。
透视形变可以使用透视投影公式来描述,该公式通常表示为:
x' = (f * x) / z
y' = (f * y) / z
其中,(x, y, z)是物体在相机坐标系中的坐标,(x', y')是物体在
图像平面上的坐标,f是相机的焦距。
这个公式表示了物体的像素坐标与相机坐标之间的关系。
当物体距离相机较远时,z的值较大,根据公式可知,x'和y'的值
也较大,物体呈现出较小的形状。
而当物体距离相机较近时,
z的值较小,x'和y'的值也较小,物体呈现出较大的形状。
此外,还有其他的透视形变公式,比如针孔相机模型的公式为:
x' = f * (x / z)
y' = f * (y / z)
这个公式与前述的公式类似,只是计算方式不同。
需要注意的是,以上公式是基于理想情况下的透视形变描述,实际拍摄中可能还存在畸变等因素影响。

数量投影和投影的公式
数量投影和投影是两个常见的几何图形投影方法。
下面是它们的基本公式:
数量投影:
1. 数量投影公式
a =
b × rcosθ + s × sinθ,其中a、b为两点之间的距离,r 为圆弧半径,θ为两点之间的夹角。
例如,如果两点之间的距离为3米,圆弧半径为2米,夹角为90度,则通过数量投影可以得到:a = 3 × 0.618 × cos90° + 2 × 0.5 × sin90°,其中0.618和0.5为圆弧的半弦值。
2. 投影公式
sin2θ = 2sinθ.cosθ,其中2θ为两个点的夹角。
例如,如果两个点之间的夹角为45度,则可以用投影公式计
算:sin45° = 0.5,cos45° = 1,因此:2sin45°.cos45° = 0.25,
或者:sin2θ = 2sinθ.cosθ = 2(0.5) × 1 = 0.2,cos2θ = 2cos θ. - 1 = 1 - 2(0.5) = -0.375。
这些公式只是数量投影和投影的基本公式,实际应用中可能会有很多变形和修正。
投影计算公式往往表达方式不止一种,有时很难分辨谁对谁错,我只把“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影” (1:100万地形图规范中称作正轴等角圆锥投影,GB/T 14512-93)的正反转换公式列出,因为我基本能保证这些公式的正确性。
“海洋地质制图常用地图投影系列小程序已升级,原下载者请注意下载更新版本。
1.约定本文中所列的转换公式都基于椭球体a -- 椭球体长半轴b -- 椭球体短半轴f -- 扁率e -- 第一偏心率e’ -- 第二偏心率N -- 卯酉圈曲率半径R -- 子午圈曲率半径B -- 纬度,L -- 经度,单位弧度(RAD)-- 纵直角坐标, -- 横直角坐标,单位米(M)2.椭球体参数我国常用的3个椭球体参数如下(源自“全球定位系统测量规范 GB/T18314-2001”):需要说明的是,在“海洋地质制图常用地图投影系列小程序”中,程序界面上的所谓“北京1954“西安1980”及“WGS 84”在实际计算中只涉及了相应的椭球体参数。
3.墨卡托(Mercator)投影3.1 墨卡托投影简介墨卡托(Mercator)投影,是一种"等角正切圆柱投影”,荷兰地图学家墨卡托(Gerhardus Mercator 1512-1594)在1569年拟定, 假设地球被围在一中空的圆柱里,其标准纬线与圆柱相切接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。
墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。
墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。
在地图上保持方向和角度的正确是墨卡托投影的优点,墨卡托投影地图常用作航海图和航空图,如果循着墨卡托投影图上两点间的直线航行,方向不变可以一直到达目的地,因此它对船舰在航行中定位、确定航向都具有有利条件,给航海者带来很大方便。
各种投影转化的算法公式投影计算公式往往表达方式不止一种,有时很难分辨谁对谁错,我只把“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影” (1:100万地形图规范中称作正轴等角圆锥投影,GB/T 14512-93)的正反转换公式列出,因为我基本能保证这些公式的正确性。
1.约定本文中所列的转换公式都基于椭球体a -- 椭球体长半轴b -- 椭球体短半轴f -- 扁率e -- 第一偏心率e’ -- 第二偏心率N -- 卯酉圈曲率半径R -- 子午圈曲率半径B -- 纬度,L -- 经度,单位弧度(RAD)-- 纵直角坐标, -- 横直角坐标,单位米(M)2.椭球体参数我国常用的3个椭球体参数如下(源自“全球定位系统测量规范 GB/T18314-2001”):需要说明的是,在“海洋地质制图常用地图投影系列小程序”中,程序界面上的所谓“北京1954“西安1980”及“WGS 84”在实际计算中只涉及了相应的椭球体参数。
3.墨卡托(Mercator)投影3.1 墨卡托投影简介墨卡托(Mercator)投影,是一种"等角正切圆柱投影”,荷兰地图学家墨卡托(Gerhardus Mercator 1512-1594)在1569年拟定, 假设地球被围在一中空的圆柱里,其标准纬线与圆柱相切接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。
墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。
墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。
在地图上保持方向和角度的正确是墨卡托投影的优点,墨卡托投影地图常用作航海图和航空图,如果循着墨卡托投影图上两点间的直线航行,方向不变可以一直到达目的地,因此它对船舰在航行中定位、确定航向都具有有利条件,给航海者带来很大方便。