磁介质一章习题答案

第一章习题解答【习题1.1解】222222222222222222222222222222222222cos cos cos cos cos cos 1xx x y z yx y z z x y z x y z x y z x y z x y z x y z x y z 矢径r 与轴正向的夹角为，则同理，矢径r 与y 轴正向的夹角为，则矢径r 与z 轴正向的夹角为，则可得从而得证a a b b g g a b g =++=++=++++=++++++++++==++ 【习题1.2解】924331329(243)54(9)(243)236335x y z x y z x y z x y z x y z x y z x y z x y z A B e e e e e e e e e A B e e e e e e e e e A B e e e e e e A B +=--+-+=-+=----+=---∙=--∙-+=+-=⨯（）（）－（）(9)(243)19124331514x y z x y z x y z x y ze e e e e e e e e e e e =--⨯-+=---=--+【习题1.3解】已知,38,x y z x y z A e be ce B e e e =++=-++ （1）要使A B ⊥，则须散度 0A B =所以从 1380A B b c =-++=可得：381b c +=即只要满足3b+8c=1就可以使向量错误！未找到引用源。

和向量错误！未找到引用源。

垂直。

（2）要使A B ，则须旋度 0A B ⨯= 所以从1(83)(8)(3)0138xy zx y z e e e A B b c b c e c e b e ⨯==--+++=-可得 b=-3，c=-8 【习题1.4解】已知129x y z A e e e =++，x y B ae be =+，因为B A ⊥，所以应有0A B ∙= 即()()1291290xy z x y ee e ae be a b ++∙+=+= ⑴又因为 1B =; 所以221=； ⑵由⑴，⑵ 解得 34,55a b =±=【习题1.5解】由矢量积运算规则123233112()()()x y zx y z x x y y z ze e e A Ca a a a z a y e a x a z e a y a x e xyzB e B e B e B =?=-+-+-=++取一线元：x y z dl e dx e dy e dz =++则有xy z xyz e e e dlB B B dx dy dzB ?=则矢量线所满足的微分方程为 x y zd x d y d z B B B == 或写成233112()dx dy dzk a z a y a x a z a y a x==---＝常数 求解上面三个微分方程：可以直接求解方程，也可以采用下列方法k xa a y a a z a d z a a x a a y a d y a a z a a x a d =-=-=-323132132231211)()()( （1）k x a y a z zdzz a x a y ydy y a z a x xdx =-=-=-)()()(211332 （2）由（1）（2）式可得)()(31211y a a x a a k x a d -=)()(21322z a a x a a k y a d -= （3）)()(32313x a a y a a k z a d -= )(32xy a xz a k xdx -=)(13yz a xy a k ydy -= （4）)(21xz a yz a k zdz -=对（3）（4）分别求和0)()()(321=++z a d y a d x a d 0)(321=++z a y a x a d0=++zdz ydy xdx 0)(222=++z y x d所以矢量线方程为1321k z a y a x a =++ 2222k z y x =++【习题1.6解】已知矢量场222()()(2)x y z A axz x e by xy e z z cxz xyz e =++++-+- 若 A 是一个无源场 ，则应有 div A =0即： div A =0y x zA A A A x y z∂∂∂∇⋅=++=∂∂∂ 因为 2x A axz x =+ 2y A by xy =+ 22z A z z cxz xyz =-+- 所以有div A =az+2x+b+2xy+1-2z+cx-2xy =x(2+c)+z(a-2)+b+1=0 得 a=2, b= -1, c= - 2 【习题1.7解】设矢径 r的方向与柱面垂直，并且矢径 r到柱面的距离相等（r ＝a ） 所以，2sssr ds rds a ds a ah πΦ===⎰⎰⎰＝22a h π=【习题1.8解】已知23x y φ=,223y z A x yze xy e =+而 A A A A rot⨯∇+⨯∇=⨯∇=φφφφ)()(2222(6)3203xy zx y ze e e A xy x y e y e xyze x y z x yz xy ∂∂∂∇⨯==--+∂∂∂ 2223[(6)32]x y z A x y xy x y e y e xyze φ∴∇⨯=--+又y x z y x e x e xy ze y e x e 236+=∂∂+∂∂+∂∂=∇φφφφ 232233222630918603xy z x y z e e e A xyx x y e x y e x y ze x yz xy φ∇⨯==-+所以222()3[(6)32]x y z rot A A A x y xy x y e y e xyze φφφ=∇⨯+∇⨯=--+ +z y x e z y x e y x e y x 2332236189+-=]49)9[(3222z y x e xz e y e x x y x+--【习题1.9解】已知 222(2)(2)(22)x y zA y x z e x y z e x z y z e =++-+-+ 所以()()1144(22)0xyzyy x x z z x y z x yzx y z A A A A A A rot A A x y z y z z x x y A A A xz xz y y e e ee e e e e e ∂∂⎛⎫⎛⎫∂∂∂∂∂∂∂⎛⎫=∇⨯==-+-+- ⎪ ⎪ ⎪∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭-++-+-=由于场A 的旋度处处等于0，所以矢量场A 为无旋场。

电磁介质1．对各向同性非铁磁介质而言，下列说法不正确的是：（ ）(A) 顺磁质一定是分子固有磁矩不为零的媒质；(B) 顺磁性来在自分子的固有磁矩；(C) 抗磁性起因于电子的轨道运动在外磁场作用下的变化； 只有抗磁质才具有抗磁性。

2. 同轴电缆由两同心导体组成，内层是半径为R 1的导体圆柱，外层是半径分别为R 2、R 3的导体圆筒。

两导体内电流I 等量而反向，均匀分布在横截面上，导体的相对磁导率为1r μ，两导体间充满相对磁导率为2r μ的不导电的均匀磁介质。

则磁场强度H 在r ›R 3区域中的分布为：（ ）（A ）;)(2)(2223223R R r Ir R H --=π （B ）H=0； （C ）22R rIH π=； （D ）rI H π2=。

3.工程上把铁磁质分为软磁材料（软铁）和硬磁材料（硬铁）两大类，下列答案正确的是：（ ）（A ）软铁适合制造电磁铁，硬铁适合制造永磁铁；（B ）硬铁适合制造永磁铁，硬铁适合制造变压器；（C ）硬铁适合制造变压器，硬铁适合制造电机；（D ）硬铁适合制造电机，软铁适合制造电磁铁。

4.一无限长圆柱形直导线，外包一层相对磁导率为r μ的圆筒形磁介质，导线半径为R 1，磁介质的外半径为R 2，导线内有电流I 通过，在横截面上是均匀分布的。

则导线内（0<r <R 1）的磁场强度的分布为：（ ）（A ）2102R rI H π=； （B ）r I H π20=； （C ）rI H πμ200=； （D ）0=H 5.某种磁介质在外磁场0B 中被磁化后，其磁化强度M 总与外磁场方向相反，则该介质必是：（A ）顺磁质； （B ）铁磁质； （C ）抗磁质；（D ）以上三种介质都可以。

6.对介质中高斯定理：⎰⎰=∙Sq S d D 0 ，如有下列一些说法，其中正确的是：（A ）D 仅与自由电荷有关；（B ）若高斯面上处处D=0，则面内必不存在电荷；（C ）若高斯面内00=q ，则高斯面上处处0=D ；（D ）D 的通量仅与面内自由电荷的电量有关。

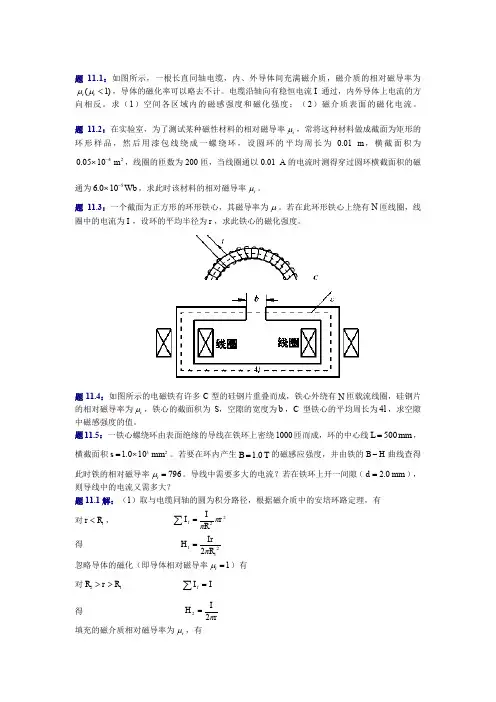
题11.1：如图所示，一根长直同轴电缆，内、外导体间充满磁介质，磁介质的相对磁导率为)1(r r <μμ，导体的磁化率可以略去不计。

电缆沿轴向有稳恒电流I 通过，内外导体上电流的方向相反。

求（1）空间各区域内的磁感强度和磁化强度；（2）磁介质表面的磁化电流。

题11.2：在实验室，为了测试某种磁性材料的相对磁导率r μ，常将这种材料做成截面为矩形的环形样品，然后用漆包线绕成一螺绕环，设圆环的平均周长为0.01 m ，横截面积为24m 1005.0-⨯，线圈的匝数为200匝，当线圈通以0.01 A 的电流时测得穿过圆环横截面积的磁通为Wb 100.65-⨯，求此时该材料的相对磁导率r μ。

题11.3：一个截面为正方形的环形铁心，其磁导率为μ。

若在此环形铁心上绕有N 匝线圈，线圈中的电流为I ，设环的平均半径为r ，求此铁心的磁化强度。

题11.4：如图所示的电磁铁有许多C 型的硅钢片重叠而成，铁心外绕有N 匝载流线圈，硅钢片的相对磁导率为r μ，铁心的截面积为S ，空隙的宽度为b ，C 型铁心的平均周长为l 4，求空隙中磁感强度的值。

题11.5：一铁心螺绕环由表面绝缘的导线在铁环上密绕1000匝而成，环的中心线mm 500=L ，横截面积23mm 100.1⨯=s 。

若要在环内产生T 0.1=B 的磁感应强度，并由铁的H B -曲线查得此时铁的相对磁导率796r =μ。

导线中需要多大的电流？若在铁环上开一间隙（mm 0.2=d ），则导线中的电流又需多大？题11.1解：（1）取与电缆同轴的圆为积分路径，根据磁介质中的安培环路定理，有 对1R r <， 22f r R I I ππ=∑ 得 2112R Ir H π= 忽略导体的磁化（即导体相对磁导率1r =μ）有对12R r R >> I I =∑f得 r IH π22=填充的磁介质相对磁导率为r μ，有rIMπμ2)1(r2-=；rIBπμμ2r2=对23RrR>>)()(2222223fRrRRIII---=∑ππ得)(2)(22232233RRrrRIH--=π同样忽略导体得磁化，有对3Rr>0f=-=∑III得04=H04=M04=B（2）由rMIπ2s⋅=。

磁介质习题1、螺线环中心周长l=10cm ，环上均匀密绕线圈N=200匝，线圈中通有电流I=100mA 。

（1）求螺线管内的磁感应强度B 0和磁场强度H 0 ；（2）若管内充满相对磁导率为μr=4200的磁性物质，则管内的B 和H 是多少？分析：螺线环内的磁感应强度具有同心圆的轴对称分布，对均匀密绕的细螺绕环可认为环内的磁感应强度均匀；环外的磁感应强度为零。

磁场强度H 的环流仅与传导电流有关，形式上与磁介质的磁化无关。

解：（1）管内为真空时，由安培环路定理，∑⎰=⋅ii L I d l H0 m A I lN nI H /2000=== 磁感应强度为T H B 40001051.2-⨯==μ（2）管内充满磁介质时，仍由安培环路定理可得m A I lN nI H /200=== 磁感应强度为T H H B r 06.10===μμμ2、一磁导率为μ1的无限长圆柱形直导线，半径为R 1，其中均匀地通有电流I ，在导线外包一层磁导率为μ2的圆柱形不导电的磁介质，其外半径为R 2。

试求磁场强度和磁感应强度的分布。

分析：系统具有轴对称性分布，因此，空间的磁场分布也应具有轴对称性。

利用安培环路定理可求出空间磁感应强度和磁场强度的分布。

解：以轴到场点的距离为半径，过场点作环面垂直于轴的环路，取环路的方向与电流方向成右手螺旋关系，应用安培环路定理。

当r<R 1时，环路包含的传导电流为2211r R I I ππ= 由安培环路定理1I d =⋅⎰l H ，得2112R Ir H π= 2111112R Ir H B πμμ== 当R 1<r<R 2时，环路包含的传导电流为I I =2， 由安培环路定理2I d =⋅⎰l H ，得 r IH π22= rI H B πμμ22222==当r>R 2时，环路包含的传导电流为I I =3， 由安培环路定理3I d =⋅⎰l H ，得 r IH π23= rI H B πμμ20303== 3、一根长直导线，其μ≈μ0 ，载有电流I ，已知电流均匀分布在导线的横截面上。

磁性材料的分类^《}第一章》第二章磁学基础知识答案：1、磁矩2、磁化强度3、·4、磁场强度 H5、磁感应强度 B磁感应感度，用B表示，又称为磁通密度，用来描述空间中的磁场的物理量。

其定义公式为（百度百科）磁感应强度（magnetic flux density），描述磁场强弱和方向的基本物理量。

是矢量，常用符号B表示。

磁感应强度也被称为磁通量密度或磁通密度。

在物理学中磁场的强弱使用磁感强度（也叫磁感应强度）来表示，磁感强度大表示磁感强；磁感强度小，表示磁感弱。

6、磁化曲线磁化曲线是表示物质中的磁场强度H与所感应的磁感应强度B或磁化强度M之间的关系7、磁滞回线—（）（6 磁滞回线 (hysteresis loop)：在磁场中，铁磁体的磁感应强度与磁场强度的关系可用曲线来表示，当磁化磁场作周期性变化时，铁磁体中的磁感应强度与磁场强度的关系是一条闭合线，这条闭合线叫做磁滞回线。

）8、磁化率磁化率，表征磁介质属性的物理量。

常用符号x表示，等于磁化强度M与磁场强度H之比。

对于各向同性磁介质，x是标量；对于各向异性磁介质，磁化率是一个二阶张量。

9、磁导率磁导率（permeability）：又称导磁系数，是衡量物质的导磁性能的一个物理量，可通过测取同一点的B、H值确定。

二'矫顽力----内禀矫顽力和磁感矫顽力的区别与联系矫顽力分为磁感矫顽力（Hcb）和内禀矫顽力（Hcj）。

磁体在反向充磁时，使磁感应强度B降为零所需反向磁场强度的值称之为磁感矫顽力。

但此时磁体的磁化强度并不为零，只是所加的反向磁场与磁体的磁化强度作用相互抵消。

（对外磁感应强度表现为零）此时若撤消外磁场，磁体仍具有一定的磁性能。

使磁体的磁化强度M降为零所需施加的反向磁场强度，我们称之为内禀矫顽力。

内禀矫顽力是衡量磁体抗退磁能力的一个物理量，是表示材料中的磁化强度M退到零的矫顽力。

在磁体使用中，磁体矫顽力越高，温度稳定性越好。

(2)退磁场是怎样产生的能克服吗对于实测的材料磁化特性曲线如何进行退磁校正产生：能否克服：因为退磁场只与材料的尺寸有关，短而粗的样品，退磁场就很大，因此可以将样品做成长而细的形状，退磁场就将会减小。

第 1 章 习 题1、 求函数()D Cz By Ax u +++=1的等值面方程。

解：根据等值面的定义：标量场中场值相同的空间点组成的曲面称为标量场的等值面，其方程为)( ),,(为常数c c z y x u =。

设常数E ，则，()E D Cz By Ax =+++1， 即：()1=+++D Cz By Ax E针对不同的常数E （不为0），对应不同的等值面。

2、 已知标量场xy u =，求场中与直线042=-+y x 相切的等值线方程。

解：根据等值线的定义可知：要求解标量场与直线相切的等值线方程，即是求解两个方程存在单解的条件，由直线方程可得：42+-=y x ，代入标量场C xy =，得到： 0422=+-C y y ，满足唯一解的条件：02416=⨯⨯-=∆C ，得到：2=C ，因此，满足条件的等值线方程为：2=xy3、 求矢量场z zy y y x xxy A ˆˆˆ222++=的矢量线方程。

解：由矢量线的微分方程：zy x A dz A dy A dx ==本题中，2xy A x =，y x A y 2=，2zy A z =， 则矢量线为：222zy dzy x dy xy dx ==，由此得到三个联立方程：x dy y dx =，z dz x dx =，zy dz x dy =2，解之，得到： 22y x =，z c x 1=，222x c y =，整理， y x ±=，z c x 1=，x c y 3±=它们代表一簇经过坐标原点的直线。

4、 求标量场z y z x u 2322+=在点M (2,0,-1)处沿z z y xy xx t ˆ3ˆˆ242+-=方向的方向导数。

解：由标量场方向导数的定义式：直角坐标系下，标量场u 在可微点M 处沿l 方向的方向导数为γβαcos cos cos zu y u x u l u ∂∂+∂∂+∂∂=∂∂α、β、γ分别是l 方向的方向角，即l 方向与z y xˆˆˆ、、的夹角。

磁性物理学习题与解答简答题1.简述洪德法则的内容。

答：针对未满壳层，洪德法则的内容依次为：〔1〕在泡利原理许可的条件下，总自旋量子数S取最大值。

〔2〕在满足〔1〕的条件下，总轨道角动量量子数L取最大值。

〔3〕总轨道量子数J有两种取法：在未满壳层中，电子数少于一半是;电子数大于一半时2.简述电子在原子核周围形成壳层结构，需遵循哪些原则法则？答：需遵循的原则法则依次为：〔1〕能量最低原则〔2〕泡利不相容原理〔3〕洪德法则3.简述自由电子对物质的磁性，可以有哪些贡献？答：可能的贡献有：〔1〕朗道抗磁〔2〕泡利顺磁4.简述晶体中的局域电子对物质的磁性，可能有哪些贡献？答：可能的贡献有：〔1〕抗磁〔2〕顺磁〔3〕通过交换作用导致铁磁、反铁磁等5.在磁性晶体中，为什么过渡元素的电子轨道角动量会被晶场“冻结〞，而稀土元素的电子轨道角动量不会被“冻结〞。

答：因为过渡元素的磁性来自未满壳层d轨道上的电子，d电子属于外层电子，在晶体中是裸露的，容易受到晶场的影响而被冻结；而稀土元素的磁性来自未满壳层f轨道上的电子，f电子属于内层电子，在晶体中不容易受到晶场的影响，所以不会冻结。

6.简述外斯分子场理论的成就与不足之处。

答：外斯分子场理论的成功之处主要有：唯象解释了自发磁化，成功得到第二类顺磁的居里—外斯定律和铁磁/顺磁相变的居里温度表达式等。

不足之处主要有：〔1〕低温下自发磁化与温度的关系与自旋波理论的结果差别很大，后者与实验符合较好;〔2〕在居里温度附近，自发磁化随温度变化的临界指数，分子场理论计算结果为1/2，而实验测量结果为1/3;〔3〕无法解释磁比热贡献在温度大于居里温度时的拖尾现象7.简述小口理论对分子场理论做了什么改进？答：小口理论认为在居里温度附近，虽然产生自发磁化的长程有序消失了，但体系仍然存在短程序，小口理论考虑了最近邻短程序，由此成功解释了磁比热贡献在温度大于居里温度时的拖尾现象。

8.简述海森堡直接交换作用的物体图像。

磁介质测试题及答案一、选择题1. 磁介质的磁性能主要取决于以下哪一项？A. 材料的化学成分B. 材料的微观结构C. 材料的制备工艺D. 外部磁场强度答案：B2. 以下哪种类型的磁介质具有最高的磁导率？A. 软磁材料B. 硬磁材料C. 铁磁材料D. 反铁磁材料答案：A3. 磁介质的磁滞回线反映了材料的哪些特性？A. 磁导率B. 磁饱和度C. 磁滞损失D. 所有上述选项答案：D二、填空题4. 磁介质的_______是指材料在没有外磁场作用时，内部磁畴的排列状态。

答案：初始磁化状态5. 磁介质的_______是指材料在外加磁场作用下，磁化强度达到最大值的能力。

答案：磁饱和度三、简答题6. 简述磁介质在存储设备中的应用及其重要性。

答案：磁介质在存储设备中主要用于数据的存储。

由于磁介质具有较高的磁导率和磁饱和度，它们能够存储大量的数据信息。

此外，磁介质的稳定性和可重复写入特性使其在硬盘驱动器、磁带和其他存储设备中得到广泛应用。

磁介质的性能直接影响存储设备的容量、速度和可靠性。

7. 描述磁介质的磁滞回线，并解释其物理意义。

答案：磁滞回线是描述磁介质在外加磁场作用下磁化强度与磁场强度之间关系的曲线。

当外加磁场逐渐增大时，磁介质的磁化强度随之增加，但存在一定的滞后现象。

当磁场减小到零时，磁介质的磁化强度不会立即回到零，而是存在一个剩余磁化强度。

这个剩余磁化强度与外加磁场的相互作用导致了磁滞损失，这是磁介质在反复磁化过程中能量损耗的来源。

磁滞回线的形状和位置反映了磁介质的磁性能，如磁导率、磁饱和度和磁滞损失等。

四、计算题8. 假设有一磁介质样品，其磁化强度M随外加磁场H的变化关系为M = 0.5H。

如果外加磁场从0增加到2000 A/m，计算磁介质样品的磁化强度变化范围。

答案：根据给定的关系M = 0.5H，当外加磁场H从0增加到2000 A/m时，磁化强度M的变化范围是从0增加到1000 A/m（即0.5 * 2000 A/m）。

磁介质一章习题答案习题10—1 将一有限长圆柱形的均匀抗磁质放在一无限长直螺线管内，其螺线管线圈的电流方向如图所示。

在a 、b 、c 三点的磁感应强度与未放入抗磁质前相比较其增减情况是：［ ］(A) a 点增加，b 点减小，c 点不变。

(B) a 点增加，b 点增加，c 点增加。

(C) a 点减小，b 点减小，c 点增加。

(D) a 点减小，b 点增加，c 点减小。

解：抗磁质放在一无限长直螺线管内，相当于把它放在均匀的外磁场中。

现 已知外场0B 方向向右。

对磁介质中的a 点来说，其本身磁化电流产生的附加磁场B '的方向与外场方向相反，叠加的结果使a 点的场减小；对介质外的b 点来说，外场0B 方向仍旧向右，这时的抗磁质相当于N 极在左、S 极在右的磁铁，其附加磁场B '的方向在b 点向左，因此，b 点的场也减小；对介质外侧的c 点来说，外场0B 方向仍旧向右，但是在该处B '的方向也向右，与外场同向，故c 点的场是增加的。

综上所述，应该选择答案(C)。

习题10—2 图示三种不同磁介质的磁化曲线，虚线表示真空中的B —H 关系。

则表示铁磁质的是曲线 ；表示抗磁质的是曲线 ；表示顺磁质的是曲线 。

解：真空中的B —H 关系为：H B 0μ=；对一般弱磁介质的B —H 关系为：H H B r μμμ0==，式中r μ为常数，若为顺磁质，则1>r μ因而0μμ>；若为抗磁质，则1<r μ因而0μμ<，所以若以真空中的B —H关系曲线为参考，则曲线Ⅱ表示的是顺磁质，曲线Ⅲ表示的是抗磁质。

对于铁磁质其B —H关系仍然为：H H B r μμμ0==，但是，由于其r μ不是常数，即)(H r r μμ=，因此其B —H 关系是非线性的，相应的B —H 关系曲线亦非直线，故而表示铁磁质的应是曲线Ⅰ。

习题10—3 关于稳恒磁场的磁场强度H 的下列几种说法中哪一个是正确的? (A) H 仅与传导电流有关。

电磁学练习题积累（含部分答案）⼀. 选择题（本⼤题15⼩题，每题2分）第⼀章、第⼆章1. 在静电场中，下列说法中哪⼀个是正确的？ [ ](A) 带正电荷的导体，其电位⼀定是正值(B) 等位⾯上各点的场强⼀定相等 (C) 场强为零处，电位也⼀定为零(D) 场强相等处，电位梯度⽮量⼀定相等2. 在真空中的静电场中，作⼀封闭的曲⾯，则下列结论中正确的是［］(A)通过封闭曲⾯的电通量仅是⾯内电荷提供的(B) 封闭曲⾯上各点的场强是⾯内电荷激发的(C) 应⽤⾼斯定理求得的场强仅是由⾯内电荷所激发的(D) 应⽤⾼斯定理求得的场强仅是由⾯外电荷所激发的3. 关于静电场下列说法中正确的是 [ ](A) 电场和试探电荷同时存在和消失 (B) 由E ＝F /q 知道，电场强度与试探电荷成反⽐(C) 电场强度的存在与试探电荷⽆关(D) 电场是试探电荷和场源电荷共同产⽣的4. 下列⼏个说法中正确的是： [ ](A) 电场中某点场强的⽅向，就是将点电荷放在该点所受电场⼒的⽅向(B) 在以点电荷为中⼼的球⾯上，由该点电荷所产⽣的场强处处相同(C) 场强⽅向可由E =F /q 定出，其中q 为试验电荷的电量，q 可正、可负，F 为试验电荷所受的电场⼒(D) 以上说法全不对。

5. ⼀平⾏板电容器中充满相对介电常数为ε的各向同性均匀电介质。

已知介质两表⾯上极化电荷⾯密度为 ±σ '，则极化电荷在电容器中产⽣的电场强度 [ ](B) 02εσ' (C) 0εεσ' (D) εσ' 6. 在平板电容器中充满各向同性的均匀电介质，当电容器充电后，介质中 D 、E 、P 三⽮量的⽅向将是 [ ](A) D 与E ⽅向⼀致，与P ⽅向相反(B) D 与E ⽅向相反，与P ⽅向⼀致(C) D 、E 、P 三者⽅向相同(D) E 与P ⽅向⼀致，与D ⽅向相反7. 在⼀不带电荷的导体球壳的球⼼处放⼀点电荷，并测量球壳内外的场强分布，如果将此点电荷从球⼼移到球壳内其它位置，重新测量球壳内外的场强分布，则将发现： [ ](A) 球壳内、外场强分布均⽆变化(B) 球壳内场强分布改变，球壳外的不变(C) 球壳外场强分布改变，球壳内的不变(D) 球壳内、外场强分布均改变8. ⼀电场强度为E 的均匀电场，E 的⽅向与x 轴正向平⾏，如图所⽰，则通过图中⼀半径为R 的半球⾯的电场强度通量为 [ ](A) 2R E π；(B) 212R E π； (C) 22R E π；(D ) 0。