2012-2013第1学期《数理经济学》课程期中试卷

-2012-2013学年-高等数学(2-1)期中考试试卷---答案2012—2013学年第一学期《高等数学(2-1)》期中试卷（工科）专业班级姓名学号开课系室基础数学系考试日期 2012年11月25日页号一二三四五六总分本页满分32 18 10 16 16 8本页得分阅卷人注意事项：1．请在试卷正面答题，反面及附页可作草稿纸；2．答题时请注意书写清楚，保持卷面清洁；3．本试卷共五道大题，满分100分；B ．(0)f 是()f x 的极小值；C ．(0,(0))f 是曲线()y f x =的拐点；D ．(0)f 是()f x 的极大值.3. 当x →∞时，若21ax bx c++与11x +为等价无穷小，则,,a b c 之值为（ B ）． A ．0,1,1a b c ===； B ．0,1a b ==,c 为任意常数；C ．0a =，,b c 为任意常数； D. ,,a b c 均为任意常数.4.设220()(),0x x f x x g x x ⎧>=≤⎩，其中()g x 是有界函数，则()f x 在 0x =处（ D ）. A ．极限不存在；B.极限存在但不连续；C.连续但不可导；D.可导. 5. 设()f x 在0x 可导且01()2f x '=，则0x ∆→时，0|x x dy =是x ∆的（ C ）.A ．等价无穷小；B.高阶无穷小；C.同阶但非等价无穷小；D 低阶无穷小.三、计算题（共4小题，每小题5分，共20分）1.求极限0x →解：（方法一）200sin 12lim lim 11cos 2x x x xx x→→==-；（方法二）001lim 11cos x x x →→==-； （方法三）洛比达法则001sin 11cos cos sin lim 1sin 2cos 21sin x x x x x x x x x x xx x →→→+-+-===+. 2. 设函数()y y x =由方程sin()(0,)xy y xe x x y ππ=>-<<确定，求其在1x =处的切线方程.解：两边取对数得：sin()(1)ln xy y x =-，两边对x 求导，有1cos()()ln y xy y xy y x x-''+=+， 又由于1x =时，sin 0y =，y ππ-<<，可得0y =，代入得(1)1y '=-，故在1x =处的切线方程为(1)y x =--，即10x y +-=.3. 设3arctan 6x t t y t t =+⎧⎪⎨=+⎪⎩，求221d y t dx =. 解：222363(1)111dy dy t dt t dx dx dt t +===+++； 22222()66(1)()1211d dy d y d dy t t t dt dx dx dx dx dx t dt t +====+++，故 2241d y t dx ==.本页满分10分本页得分4. 求极限21)(cos lim x x x →. 解：（方法一）2211cos 1cos 100lim(cos )lim(1cos 1)x x x x x x x x --→→=+- 20cos 11lim 2x x x e e →--==； （方法二）22222111sin 1222sin 2200lim(cos )lim (cos )lim(1sin )xx x x xx x x x x x e ---→→∞→==-=； （方法三）洛比达法则sin 2cos 220111ln(cos )lim 200lim(cos )lim x x x x x x x x x x e e e -→-→→===.四、应用题（共3小题，每小题8分，共24分）1. 已知()sin 2ln(1),0()1,0ax a b x x x x f x e x ++-⎧>⎪=⎨⎪-≤⎩在0x =处可导，试求出a 与b .解：由于()f x 在0x =处可导，必连续，故(0)(0)(0)0f f f -+===，又000()sin 2ln(1)()sin 2ln(1)(0)lim lim lim 2x x x a b x x a b x x f a b x x x++++→→→++-+-==+=+-，可得20a b +-=，即2a b +=；又由于()f x 在0x =处可导，则(0)(0)f f -+''=，又 01(0)lim ax x e f a x--→-'==， 本页满分16分 本页得分2200200()sin 2ln(1)sin ln(1)(0)lim 2lim 1cos 11lim lim [sin ]1(1)x x x x a b x x x x f x x x x x x x +++++→→→→++-+-'==--==--=--， 故1,3a b =-=.2. 有一底半径为R cm ，高为h cm 的圆锥容器，今以253cm /s 自顶部向容器内注水，试求当容器内水位等于锥高的一半时水面上升的速率.解：设t 时刻，水的体积，水面半径及水的深度分别为,,V r x ，由于2211()33V R h r h x ππ=--， 又从相似三角形可知：r h x R h -=，即h x r R h-=， 可得3222332211()1[()]333h x R V R h R h h x hh πππ-=-=--，两边对t 求导，得 222()dV R dx h x dt dt hπ=-， 由已知条件25dV dt =，2h x =，代入得2100dx dt R π=，即水面上升的速率为2100cm/s Rπ. 3. 试讨论方程)0(,ln >=a ax x 有几个实根.解：令()ln ,(0,)f x x ax x =-∈+∞，则 1()f x a x '=-，令()0f x '=，解得驻点1x a =，列表如下： x 10,a ⎛⎫ ⎪⎝⎭ 1a 1,a ⎛⎫+∞ ⎪⎝⎭ ()f x ' + 0 — 本页满分16分本页得分()f x 最大值1f a ⎛⎫ ⎪⎝⎭可得，()f x 的最大值为1(ln 1)f a a ⎛⎫=-+ ⎪⎝⎭，讨论如下： （1） 当1a e =时，10f a ⎛⎫= ⎪⎝⎭，方程ln x ax =有唯一的实根； （2） 当10a e <<时，10f a ⎛⎫> ⎪⎝⎭，又由于 00lim ()lim (ln )x x f x x ax ++→→=-=-∞； ln lim ()lim ()x x x f x x a x→+∞→+∞=-=-∞， 故方程ln x ax =有两实根，分别位于10,a ⎛⎫ ⎪⎝⎭与1,a ⎛⎫+∞ ⎪⎝⎭内； 当1a e >时，10f a ⎛⎫< ⎪⎝⎭，方程ln x ax =没有实根. 五、证明题（共2小题，每小题8分，共16分）1．设函数()f x 在[0,2]上连续，在(0,2)内可导，且(0)0f =，0)2(=f ，证明：存在(0,2)ξ∈，使得()()f f ξξ'=.证明：令()()x F x e f x -=，则()F x 在[0,2]上连续，在(0,2)内可导，且由于(0)0f =，0)2(=f ，易得(0)(2)0F F ==，根据罗尔定理，至少存在(0,2)ξ∈，使得()0F ξ'=，即()()0e f e f ξξξξ--'-+=，又0e ξ-≠，可得()()f f ξξ'=.本页满分8分本页2．证明：当0>x 时，x x x x <+<+)1ln(1. 证明：（方法一）设t t f ln )(=，则)(t f 在[1,1]x +上连续，在(1,1)x +内可导，由 Lagrange 中值定理，得ln(1)ln11x x ξ+-=，11x ξ<<+，故1111x ξ<<+，即1ln(1)11x x x +<<+，整理得，x x xx <+<+)1ln(1. （方法二）：对()ln(1)f t t =+在[0,]x 上应用Lagrange 中值定理.（方法三）：利用函数的单调性. 得分。

浙江科技学院考试试卷浙江科技学院2012 -2013学年第 I 学期考试试卷 A 卷考试科目 概率论与数理统计A 考试方式 闭卷 完成时限 2小时一、填空题。

将答案填在空格处（本大题共7小题，每小题3分， 总计21分）。

1、10把钥匙中有3把能打开门，今任取2把，则能把门打开的概率是 .2、若事件A , B 互不相容，且P (A ) =0.5，P (B ) =0.4，则()P AB = ，()P AB = .3、若连续型随机变量X 的分布函数为0, 0,(), 01,1, 1,x F x ax x x <⎧⎪=≤<⎨⎪≥⎩则a = ，{0.5 1.5}P X <<= .4、已知X 的概率密度为()X f x ,则22Y X =-的概率密度()Y f y = .5、右表给出了(X, Y ) 的分布， 则()E XY = ，X 与Y 的协方差(,)Cov X Y = .6、设123,,X X X 是取自总体X 的样本, X 为样本均值,若总体方差存在，则112d X X =-,2123121236d X X X =+-都是总体均值的 估计,最有效的是 . 专业班级 学号 姓名………………………………………………………………………装订线……………………………………………………………………………………浙江科技学院考试试卷7、设总体服从2(,)N μσ，1215(,,,)x x x 是取自该总体的一样本，计算得样本均值0.58x =，样本方差220.004s =，则2σ的置信度为0.95的置信区间为 .二、选择题。

将正确答案的代号填入题后括号中（本大题共7小题，每小题3分，共21分）。

1、从一批产品中，每次取出一个（取后不放回），抽取三次，用123(,,)i A i =表示“第i 次取到的是正品”，下列结论中不正确的是（ ）． (A)123123123123A A A A A A A A A A A A 表示“至少抽到2个正品”； (B)121323A A A A A A 表示“至少有1个是次品”；(C)123A A A 表示“至少有1个不是正品”；(D)123A A A 表示“至少有1个是正品”2、5(12)(1,2,)k k p a k ==⋅⋅⋅为某一离散型随机变量的概率分布，则常数a =（ ）． （A ）1/2； （B ）2； （C ）1/5； （D ）53、设2~(,)X N μσ，其概率密度2(3)()}4x f x +=-，则（ ）． ( A )3,2μσ==；( B )3,μσ==； ( C )3,2μσ=-=；( D )3,μσ=-=4、设两个随机变量X 与Y 相互独立且同分布，{1}{1}1/2P X P Y =-==-=， {1}{1}1/2P X P Y ====，则下列式子成立的是（ ）． （A ）X Y =；（B ）{}1P X Y ==；（C ）{}1/2P X Y ==；（D ）{}1/4P X Y ==。

《数理经济学》参考习题说明：以下习题主要在于帮助读者进一步理解和掌握相关的最优化方法。

而对相关数学最优化定理推导的深入理解将非常有助于对该原理的掌握，因此相关定理的证明可以作为习题，鉴于篇幅，在习题中不再重复。

另一方面，对经济学分析如何应用最优化数学方法，建议读者进一步阅读参考文献中的相关微观经济学和宏观经济学的高级教程。

另，以下习题中相关定理和例题的编号为教材中的编号。

第一部分 非线性规划与应用1. 如序中所提到的，目标函数和约束函数均为线性函数时称为线性规划问题，线性是非线性的一个特例，考虑以下的线性规划问题，min : T c x..:0s t Ax ≤ 0x ≥其中nx R ∈，c 为维向量，为n A m n ×矩阵。

导出该线性规划问题的Kuhn-Tucker 最优性条件。

2. 当非线性规划问题中的目标函数为二次函数，约束函数为线性函数时，称为二次规划问题。

导出以下二次规划问题的Kuhn-Tucker 最优性条件。

1min : 2T Ta c x x Hx ++..:s t Ax b =0x ≥其中为常数，为维向量，为a c n H n n ×对称矩阵，为A m n ×矩阵。

3. 考虑以下非线性规划问题：12max : x x −221..:0s t x x −+≤110x −≤ 20x −≤画图分析该问题的最优解，并讨论在最有解点是否满足Kuhn-Tucker 条件或Fritz John 条件。

14. 求解以下非线性规划问题：221122min : 23x x x x x −+− 212..:42s t x x −+≤1234x x +≤6)2 10x ≥，20x ≥5. 分析点*(4,3)是否为满足以下非线性规划问题的二阶条件的最优解：x =()(2212max : 34x x −+− 2212..:25s t x x +≤127x x +≥ 10x ≥，20x ≥6. 考虑下述含参数的非线性规划问题：11min : x u x −− 2212..:1s t x x u +≤−2用()x u 表示最优解，表示最优值函数，利用定理2.1.2和定理2.2.1的公式计算()u Φ()x u ∇，在和的值。

第二章 习题答案1．假设教材《数理经济学》的需求集为：{}6000|),(2==q p q p D ，其中，q 为需求量（万册），p 为价格（元）。

如果价格从20元提高为21元，则需求量将作如何变动？ 解：2220206000212160001513.61p q p q q q ======当时，，得；当时，，得 所以，价格从20元提高为21元，则需求量从15万册下降到13.61万册。

2．设某厂商的成本函数为323151500)(q q q q C +-+=，证明，其边际成本总是正的。

证明：因为边际成本函数，()()22C'156331120q q q q =-+=-+>所以，其边际成本总是正的。

3．设某厂商的成本函数为q q q q C +++=1201000)(，求边际成本函数。

解：边际成本函数为()C'20q =++4．设某一商品的需求函数为：18000)(2+==p p q q D，其中：q 为需求量，p 为价格。

若价格从9下降为8.50，问需求量将作如何变动？ 解：2280008000997.568.5109.22918.51p q p q ======++当时，；当时， 所以，价格从9下降为8.5时，需求量将从97.56上升为109.22.5．若某人的效用函数取下述形式：322121)3()2(),(++=x x x x u ，其中：u 为总效用函数，1x ，2x 为所消费商品的数量，要求计算：（1）每一商品的边际效用函数；（2）当消费的每种商品均为3个单位时，第一种商品的边际效用值。

解：（1）商品1的边际效用函数：()()3112223MU x x =++商品2的边际效用函数：()()22212323MU x x =++（2）123x x ==当时，()()31232332160MU =++= 6．假定某厂商的生产函数为：αα-=1),(L AK L K Q ，其中：0>A 及10<<α。

第二章习题答案1．假定教材《数理经济学》的需求集为： D ( p, q) | p2 q 6000 ，此中，q为需求量（万册）， p 为价钱（元）。

假如价钱从20 元提升为21 元，则需求量将作怎样改动？解：当 p2q 6000，得 q 15；当 p26000，得20时，20 21时，21 q因此，价钱从 20 元提升为21 元，则需求量从15 万册降落到13.61 万册。

2．设某厂商的成本函数为 C (q) 1500 15q 3q 2 q3，证明，其边沿成本老是正的。

证明：由于边沿成本函数，C' q 15 6q 3q2212 0 3 q 1因此，其边沿成本老是正的。

3．设某厂商的成本函数为C(q) 1000 20q q 1 q ，求边沿成本函数。

解：边沿成本函数为qC' q 20 1 q2 1 q4．设某一商品的需求函数为：q q D ( p) 8000 ，此中： q 为需求量， p 为价钱。

若价p 2 1格从 9 降落为，问需求量将作怎样改动？解：当 p 9时， q 8000 ；当 p 时， q 800092 1 2 1因此，价钱从 9 降落为 8.5 时，需求量将从97.56 上升为 109.22.5．若某人的功效函数取下述形式：u( x , x ) ( x 2) 2 ( x 3)3，此中： u 为总功效函数，1 2 1 2x1 ， x2 为所花费商品的数目，要求计算：（1）每一商品的边沿功效函数；（2）当花费的每种商品均为 3 个单位时，第一种商品的边沿功效值。

解：（ 1）商品1 的边沿功效函数：MU 1 2 x1 2 x23 3商品 2 的边沿功效函数：MU 2 3 x12x22 2 3（ 2）当 x1 x2 3时，2 3 2 332160MU 1 36．假定某厂商的生产函数为：Q( K , L) AK L1 ，此中： A 0 及 0 1。

证明：劳动的边沿产出是正的，且对于L 单一递减（固定K 时）。

-2012-2013学年-高等数学(2-1)期中考试试卷---答案2012—2013学年第一学期《高等数学(2-1)》期中试卷（工科）专业班级姓名学号开课系室基础数学系考试日期 2012年11月25日页号一二三四五六总分本页满分32 18 10 16 16 8本页得分阅卷人注意事项：1．请在试卷正面答题，反面及附页可作草稿纸；2．答题时请注意书写清楚，保持卷面清洁；3．本试卷共五道大题，满分100分；4．试卷本请勿撕开，否则作废； 5．本试卷正文共6页。

一、 填空题（共5小题，每小题4分，共20分）1．设函数1(1sin ),0(),xx x f x a x ⎧⎪-≠=⎨⎪=⎩ 在0x =处连续，则a =1e - .2．设()f x 在2x =处连续，且2()lim32x f x x →=-，则(2)f '= 3 . 3．设22ln arctana y x a x=+，则dy=22x adx x a-+ . 4. 函数ln(12)y x =+，则()(0)n y = 1(1)(1)!2n n n --- . 5. 曲线21x y e -=-的下凸区间是____[22_____________________.二、选择题（共5小题，每小题4分，共20分） 1．设函数11()tan ()()xxe e xf x x e e +=-，则0x =是()f x 的（ C ）．A ．连续点；B ．可去间断点；C. 跳跃间断点；D ．无穷间断点.2. 设()f x 有二阶连续导数且(0)0f '=，()lim 1||x f x x →''=，则下列说法正确的是（ B ）． A ．(0)f 不是()f x 的极值，(0,(0))f 不是曲线()y f x =的拐点；本页满分32分 本页得分B ．(0)f 是()f x 的极小值；C ．(0,(0))f 是曲线()y f x =的拐点；D ．(0)f 是()f x 的极大值. 3. 当x →∞时，若21ax bx c++与11x +为等价无穷小，则,,a b c 之值为（ B ）． A ．0,1,1a b c ===； B ．0,1a b ==,c 为任意常数； C ．0a =，,b c 为任意常数； D. ,,a b c 均为任意常数.4. 设220()(),x x f x xx g x x ⎧>⎪=⎨⎪≤⎩，其中()g x 是有界函数，则()f x 在0x =处（ D ）.A ．极限不存在；B.极限存在但不连续；C.连续但不可导；D.可导.5. 设()f x 在0x 可导且01()2f x '=，则0x ∆→时，0|x x dy =是x ∆的（ C ）.A ．等价无穷小；B.高阶无穷小；C.同阶但非等价无穷小；D 低阶无穷小.三、计算题（共4小题，每小题5分，共20分） 1. 求极限01sin 1x x x →+-解：（方法一）200sin 1sin 12lim lim 11cos 2x x x xx x x x→→+==-； （方法二）2001sin 1lim11cos 1sin 1x x x x x x x x →→+==-++； （方法三）洛比达法则本页满分18分 本页得分01sin 11cos cos sin lim 1sin 2cos 21sin x x x x x x x x xx xx x →→→+-+-===+. 2. 设函数()y y x =由方程sin()(0,)xy y xe x x y ππ=>-<<确定，求其在1x =处的切线方程.解：两边取对数得：sin()(1)ln xy y x =-，两边对x 求导，有1cos()()ln y xy y xy y x x-''+=+， 又由于1x =时，sin 0y =，y ππ-<<，可得0y =，代入得(1)1y '=-，故在1x =处的切线方程为(1)y x =--，即10x y +-=.3. 设3arctan 6x t t y t t=+⎧⎪⎨=+⎪⎩，求221d y t dx =. 解：222363(1)111dydy t dt t dx dx dt t +===+++；22222()66(1)()1211d dy d y d dy t t t dt dx dx dx dx dx t dt t +====+++，故 2241d yt dx ==.本页满分10分 本页得分4. 求极限21)(cos lim x x x →.解：（方法一）2211cos 1cos 10lim(cos )lim(1cos 1)x x x x x x x x --→→=+-20cos 11lim2x x xe e→--==；（方法二）22222111sin 1222sin 22lim(cos )lim (cos )lim(1sin )x x x x x x x x x x x e---→→∞→==-=；（方法三）洛比达法则sin 2cos 22111ln(cos )lim 2lim(cos )lim xx xx x x x x x x e e e-→-→→===.四、应用题（共3小题，每小题8分，共24分）1. 已知()sin 2ln(1),0()1,0ax a b x x x x f x e x ++-⎧>⎪=⎨⎪-≤⎩在0x =处可导，试求出a 与b .解：由于()f x 在0x =处可导，必连续，故(0)(0)(0)0f f f -+===，又00()sin 2ln(1)()sin 2ln(1)(0)lim lim lim 2x x x a b x x a b x x f a b x x x++++→→→++-+-==+=+-，可得20a b +-=，即2a b +=；又由于()f x 在0x =处可导，则(0)(0)f f -+''=，又 01(0)lim ax x e f a x--→-'==， 本页满分16分 本页得分2200200()sin 2ln(1)sin ln(1)(0)lim 2lim1cos 11lim lim [sin ]1(1)x x x x a b x x x x f x x x x x x x +++++→→→→++-+-'==--==--=--， 故1,3a b =-=.2. 有一底半径为R cm ，高为h cm 的圆锥容器，今以253cm /s 自顶部向容器内注水，试求当容器内水位等于锥高的一半时水面上升的速率. 解：设t 时刻，水的体积，水面半径及水的深度分别为,,V r x ，由于2211()33V R h r h x ππ=--，又从相似三角形可知：r h x R h -=，即h xr R h-=，可得3222332211()1[()]333h x R V R h R h h x hh πππ-=-=--，两边对t 求导，得 222()dV R dxh x dt dt hπ=-， 由已知条件25dV dt =，2hx =，代入得2100dx dt R π=，即水面上升的速率为2100cm/s Rπ. 3. 试讨论方程)0(,ln >=a ax x 有几个实根. 解：令()ln ,(0,)f x x ax x =-∈+∞，则1()f x a x '=-，令()0f x '=，解得驻点1x a=，列表如下：x10,a ⎛⎫⎪⎝⎭ 1a1,a ⎛⎫+∞ ⎪⎝⎭()f x '+—本页满分16分 本页得分()f x最大值1f a ⎛⎫ ⎪⎝⎭可得，()f x 的最大值为1(ln 1)f a a ⎛⎫=-+ ⎪⎝⎭，讨论如下：（1） 当1a e =时，10f a ⎛⎫= ⎪⎝⎭，方程ln x ax =有唯一的实根；（2） 当10a e<<时，10f a ⎛⎫> ⎪⎝⎭，又由于 00lim ()lim (ln )x x f x x ax ++→→=-=-∞；ln lim ()lim ()x x xf x x a x→+∞→+∞=-=-∞， 故方程ln x ax =有两实根，分别位于10,a ⎛⎫ ⎪⎝⎭与1,a ⎛⎫+∞ ⎪⎝⎭内；当1a e >时，10f a ⎛⎫< ⎪⎝⎭，方程ln x ax =没有实根.五、证明题（共2小题，每小题8分，共16分）1．设函数()f x 在[0,2]上连续，在(0,2)内可导，且(0)0f =，0)2(=f ，证明：存在(0,2)ξ∈，使得()()f f ξξ'=.证明：令()()x F x e f x -=，则()F x 在[0,2]上连续，在(0,2)内可导，且由于(0)0f =，0)2(=f ，易得(0)(2)0F F ==，根据罗尔定理，至少存在(0,2)ξ∈，使得()0F ξ'=，即()()0e f e f ξξξξ--'-+=，又0e ξ-≠，可得()()f f ξξ'=.本页满分8分 本页2．证明：当0>x 时，x x xx<+<+)1ln(1. 证明：（方法一）设t t f ln )(=，则)(t f 在[1,1]x +上连续，在(1,1)x +内可导，由 Lagrange 中值定理，得ln(1)ln11x x ξ+-=，11x ξ<<+，故1111x ξ<<+，即1ln(1)11x x x +<<+，整理得，x x xx<+<+)1ln(1. （方法二）：对()ln(1)f t t =+在[0,]x 上应用Lagrange 中值定理.（方法三）：利用函数的单调性.得分。

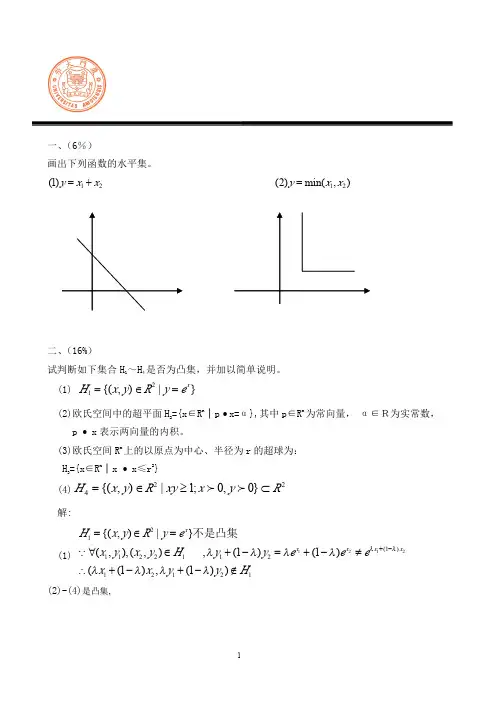
一、（6％）画出下列函数的水平集。

12 (1)y x x =+12 (2)min(,)y x x=二、（16%）试判断如下集合H 1～H 4是否为凸集，并加以简单说明。

(1)}|),{(21xe y R y x H =∈=(2)欧氏空间中的超平面H 2={x∈R n│p •x=α},其中p∈R n为常向量，α∈Ｒ为实常数，p •x 表示两向量的内积。

(3)欧氏空间R n上的以原点为中心、半径为r 的超球为：H 3={x∈R n │x •x≤r 2}(4)224}0,0;1|),{(R y x xy R y x H ⊂≥∈=≻≻解:(1)121221(1)112211212121{(,)|}(,),(,),(1)(1)((1),(1))x x x x x H x y R y e x y x y H y y e e e x x y y H λλλλλλλλλλ+−=∈=∀∈+−=+−≠∴+−+−∉∵不是凸集(2)-(4)是凸集,三、（10%）设某两个商品的需求量1q 和2q 分别是它们的价格1p 、2p 和收入I 的函数，形如:23/2121122126,4q p p I q p p I −−==。

目前的价格*1p =6，*2p =9，收入I *=2．当两种商品的价格均上升0.2，收入下降0.1时，1q 和2q 分别增加多少？1232212121211112222123133222221212121222121212::(,,)(0.2,0.2,0.1)*(6,9,2)6(*)4(*)1296448T Tx p p I x p p I F x p p I q q q pp I DF x q q q p p I p p I p p I p p p I p p I p p I −−−−−−−−∆=∆∆∆=−=⎛⎞⎜⎟=⎜⎟⎝⎠∂∂∂⎛⎞⎜⎟∂∂∂⎜⎟=⎜⎟∂∂∂⎜⎟∂∂∂⎝⎠⎛⎞−⎜⎟=⎜⎟−⎝⎠=解依题意1230.75 4.58/3 1.185232/3(*)(*)(*)0.230.75 4.50.9(*)0.28/3 1.185232/30.2370.1F x x F x DF x xq DF x x q −⎛⎞⎜⎟−⎝⎠+∆−≈∆⎛⎞∆−−⎛⎞⎛⎞⎛⎞⎜⎟≈∆≈≈⎜⎟⎜⎟⎜⎟⎜⎟∆−−⎝⎠⎝⎠⎝⎠⎜⎟−⎝⎠四、（12%）1/41/212121212121212/(,)(,)1(,)()(),x x f x x f x x f ff x x x x x x x y x =∂∂=+∂∂=保持不变的等产量线的斜率相等。

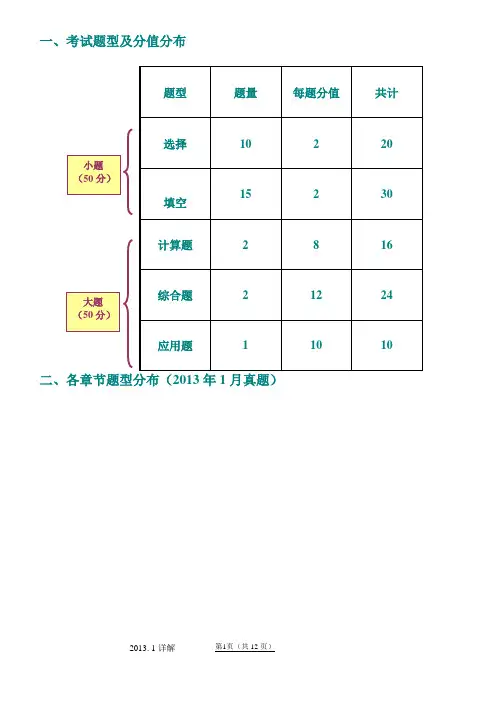
一、考试题型及分值分布题型 题量每题分值共计选择10 2 20填空 15 2 30计算题2 8 16综合题 2 12 24应用题 1 10 10二、各章节题型分布（2013年1月真题）小题 （50分）大题 （50分）题型章节小题部分大题部分分值(平均) 选择填空计算综合应用第一章2 3 1 18 第二章2 3 1 22 第三章1 2 1 14 第四章2 3 1 22第五章1 02第六章1 02 第七章1 2 6 第八章1 1 12第九章1 276分24分三、各章考点题型章次小题部分大题部分第一章随机事件与概率1.事件之间的关系与运算。

2.概率的基本性质3.古典概型4.条件概率、乘法公式5.全概率公式和贝叶斯公式6.事件的独立性1.事件的独立性2.全概率公式第二章随机变量及其概率分布1.随机变量及其分布函数2.离散型随机变量及其分布律3.连续型随机变量及其概率密度函数性质及计算4.两点分布、二项分布、泊松分布、均匀分布、指数分布及其计算5.正态分布及其计算6.简单随机变量函数的概率分布1.连续型随机变量概率密度函数性质及计算第三章多维随机变量及其概率分布1.二维离散型随机变量的分布律、性质、边缘分布律2.二维连续型随机变量的概率密度函数性质、边缘概率密度函数3.随机变量的独立性1.求边缘分布律以及边缘概率密度函数2.判断随机变量的独立性第四章随机变量的数字特征1.期望与方差的性质与计算2.随机变量函数的期望3.两点分布、二项分布、泊松分布、均匀分布、指数分布和正态分布的期望与方差4.协方差、相关系数的性质及求法1.期望与方差的性质与计算2.协方差、相关系数的求法四、常考题型（2013年1月真题为例）全国2013年1月自考概率论与数理统计(经管类)试题课程代码：04l83一、单项选择题(本大题共10小题，每小题2分，共20分)在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

《概率论与数理统计》课程试卷（ A ）参考答案及评分标准第1页共4页中国计量学院20 12 ~ 20 13 学年第二学期《概率论与数理统计》课程试卷（ A ）参考答案及评分标准开课二级学院：理学院学生班级：11信算1-3班,数学1，12金融工程1-3班，教师：孟艳姣吴跃生一、(本题24分, 每题3分) D B A A B A C B 二、(本题24分, 每题3分) 1. 0.6; 2. 1, 12,()0,Y y p y <<ì=íî其他3. 0.6 ; 4. X -1 0 2 P 0.3 0.4 0.3 5. 30; 6. 223e -7. 138. 19三、（6分）证明（1）() (3)A A A B B AB AB =W ==分（2）()()() (3)AAB A A B A A A B A B ===分四、（8分）解. (1) A={零件是合格品零件是合格品}，B i ={零件来自第i 台车床}，i=1,2 则1122()()(|)()(|) (2)P A P B P A B P B P A B =+分21(10.02)(10.05)330.97 (2)=-+-=分(2)222()(|)(|).....................(2)()P B P A B P B A P A =分10.0553.....................(2)10.979´==-分《概率论与数理统计概率论与数理统计 》课程试卷（ A ）参考答案及评分标准）参考答案及评分标准 第2页共4页五、（8分）分） 解：（1）X i +1的所有可能取值为0,1,2, 其分布律为其分布律为X i +1 0 1 2 P 1/4 1/2 1/4 故X i 分布律为分布律为X i -1 0 1 ………………………………………………(2(2分) P 1/4 1/2 1/4 于是(X 1,X 2)的联合分布律为的联合分布律为2X1X-1 0 1 i p × -1 0 140 14 0 140 1412 1 0 14 0 14j p ×1412141 ………………………………………………………………………………………… (3 (3分) (2) Cov ()21X X ，=E(X 1X 2)—E(X 1) E(X 2) =0 ………………………………………………………………..…………………… (3 (3分) 六、（12分）分）故k=6...........................................(3)分(23)00: (1) 1(,)x y p x y dxdy ke dxdy +¥+¥+¥+¥-+-¥-¥==òòòò解2300x y k e dx e dy+¥+¥--=òò230011--.236x ykk e e-+¥-+¥æöæö==ç÷ç÷èøèø《概率论与数理统计概率论与数理统计 》课程试卷（ A ）参考答案及评分标准）参考答案及评分标准 第3页共4页 (2) 12(23)00{(,):1,2}(3) (1,2)(,)6x y x y x y P X Y p x y dxdy dx edy-+<<<<==òòòò2132002611623(1)(1) (3)x y e e e e ----æöæö=--ç÷ç÷èøèø=--分七、（10分）分）解: (1)()101(1)............................................................(2)2E X x x dx q q q q +=+=+ò分 由矩法, 令12x q q+=+, 解之得q 的矩估计量为的矩估计量为121ˆ 2................................................(2)11x x xq-==---分 (2) 似然函数为似然函数为()1(1), 01..................................(2)0, nni i i x x L q q q =ì+<<ï=íïîÕ分其它 对数似然函数为对数似然函数为1ln ()ln(1)ln ni i L n x q q q==++å上式两边关于q 求导并令其为0,得似然方程得似然方程()1ln ln 0..................................(2)1ni i d L n x d q q q ==+=+å分 0(,)0,x p x y £=当时，时， ()(,)0X p x p x y dy+¥-¥==ò0x >当时，时， (23)()(,)6x y X p x p x y dy edy+¥+¥-+-¥==òò2320232 (3)xyxeedye+¥---==ò分0(,)0,y p x y £=当时，时， ()(,)0Y p y p x y dx +¥-¥==ò0y >当时，(23)()(,)6x y Y p y p x y dxe dx+¥+¥-+-¥==òò3230323 (3)yxyeedx e+¥---==ò分《概率论与数理统计概率论与数理统计 》课程试卷（ A ）参考答案及评分标准）参考答案及评分标准 第4页共4页解之得，解之得，1ˆ 1........................................................(1)ln nii n x q=-=-å分又()2ˆˆ22ln 0(1)d L nd qqq qq =-<+故ˆq 为q 的极大似然估计量. .................................................................(1)分八、（8分）分）解：这是关于正态总体均值的假设检验问题, 由于总体方差未知, 故用t 检 验. 要检验的原假设和备择假设分别为要检验的原假设和备择假设分别为01:50 vs :50,..........................(2)H H m m =¹分 拒绝域为1/2{||(1)}W t t n a -=³-. 由题知, 5, n =0.05,a =()0.975 4 2.7764,t = 故拒绝域为故拒绝域为{|| 2.7764}......................................(2)W t =³分 由已知条件计算得由已知条件计算得1(48.849.749.850.350.5)49.82.5x =++++=52211()0.437, 0.661.........................................(2)4i i s x x s ==-==å分于是可得检验统计量的值为于是可得检验统计量的值为5049.82500.6089...............................(1)/0.661/5x t s n --==»-分故t 值未落入拒绝域W 中 ，于是接受原假设H 0,可以认为每包化肥的平均可以认为每包化肥的平均质量为50kg 50kg………………………………………………………………………………………………………………………………………………………………………………………((1分)。

13—14学年第二学期 《数理金融学》期末考试试题（A ）注意事项：1.适用班级：11数学与应用数学本1.本2,2013数学（升本）2.本试卷共1页.满分100分.3.考试时间120分钟.4.考试方式：闭卷一、选择题（每小题3分，共15分）1．某证券组合由X 、Y 、Z 三种证券组成，它们的预期收益率分别为10%、16%、20% 它们在组合中的比例分别为30%、30%、40%，则该证券组合的预期收益率为______ A 15.3% B 15.8% C 14.7% D 15.0%2．无风险收益率和市场期望收益率分别是0.06和0.12.根据CAPM 模型，贝塔值为1.2的证券X 的期望收益率为A 0.06B 0.144C 0.12D 0.1323．无风险收益率为0.07，市场期望收益率为 0.15.证券X 的预期收益率为 0.12，贝塔值为1.3.那么你应该A 买入X ，因为它被高估了；B 卖空X ，因为它被高估了C 卖空X ，因为它被低估了；D 买入X ，因为它被低估了 4.一个看跌期权在下面哪种情况下不会被执行？ A 执行价格比股票价格高； B 执行价格比股票价格低C 执行价格与股票价格相等；D 看跌期权的价格高于看涨期权的价格5.假定IBM 公司的股价是每股95美元.一张IBM 公司4月份看涨期权的执行价格为100美元，期权价格为5美元.忽略委托佣金，看涨期权的持有者将获得一笔利润，如果股价 A 涨到104美元 B 跌到90美元 C 涨到107美元 D 跌到 96美元 二、填空题（每小题3分，共15分） 1.风险厌恶型投资者的效用函数为 2.设一投资者的效用函数为()axu x e-=-,则其绝对风险厌恶函数()A x =3.均值-方差投资组合选择模型是由 提出的.4.可以在到期日前任何一天行使的期权称之为5.考察下列两项投资选择：（1）风险资产组合40%的概率获得 15%的收益，60%的概率获得5%的收益；（2）银行存款收益率为6%;则风险投资的风险溢价是 三、分析题（每小题15分，共30分）1.设某人面临两种工作，需要从中选择出一种, 其收入R 1R 2都是不确定的.第一种工作是在私营公司里搞推销，薪金较高.如果干得好，每月可挣得2000元；干得一般，每月就只能挣得1000元.假定他挣得2000元和挣得1000元的概率各为1/2.第二种工作是在国营商店当售货员，每月工资1510元.但在国营商店营业状况极差的情况下，每月就只能得到510元的基本工资收入.不过，一般情况下国营商店营业状况不会极差，出现营业状况极差情况的可能性只有1％，因此第二种工作获得月收入1510元的可能性为99％.假设该人是风险厌恶者，这个人会选择哪一种工作呢？请说明理由.2.经济系统中有一只无风险资产与2只风险资产12,X X .无风险利率为r ，无风险收益为1R r =+，风险资产12,X X 在时间0的价格分别为121v v ==，在时期1有3个可能的状态，它们的收益矩阵为：Z=[3 1 2;2 2 4]T，试求正状态定价向量、等价概率分布，并讨论相应的套利机会. 四、计算题（共15分）某个股票现价为40美元.已知在1个月后，股票价格为42美元或38美元.无风险年利率为12%（连续复利）. 请用无套利原理说明，（1）执行价格为39美元的1个月后到期的欧式看涨期权的价值为多少？ （2）执行价格为39美元的1个月后到期的欧式看跌期权的价值为多少？（3）验证欧式看涨期权、看跌期权之间的平价关系.五、综合题（共25分）假设你的初始财富禀赋为单位资金1，将全部用于投资风险资产，证券市场上有n 种风险资产可供你选择，风险资产的收益率为随机向量12(,,,)T n X X X X =⋅⋅⋅,其期望收益率向量为12(,,,)T n μμμμ=⋅⋅⋅，假设你是风险厌恶者，期望收益率水平为r p ,目标是构建一投资组合w 实现风险最小化，现在请利用所学知识，完成如下任务：（1）建立一个投资组合优化数学模型；（2）求解最优组合w; （3）求解最小化风险σp 2的数学表达式；（4）假设市场上只有3种风险资产可以供你选择进行投资，其期望收益率向量为()(2,1,3)TE X m ==，协方差矩阵为∑=[1 0 0;0 20;0 0 4]，你的期望收益率为r p =2，请求解你此时的最优投资组合w 及面临的风险σp 2.装 订 线 内 不 要 答 题13—14学年第二学期《数理金融学》期末考试试题（B ）注意事项：1.适用班级：11数学与应用数学本1、本2,13数学升本1、2。

12级经济管理类“概率论与数理统计”期中考试试卷2013年11月16日系别 学号 姓名一．（6 （1）已知事件A ，B 满足条件P(A B )=P(B A ),且P(A )= p , 求P(B )．（2）设箱中有1件次品和9件合格品，在合格品中有6件一等品，3件二等品，从中任取3件，求其中至少有两件是一等品的概率．（3）设随机变量X 在区间[2，5]上服从均匀分布，现对X 进行三次独立观测，试求至少有两次观测值大于3的概率．（4）设随机变量X 服从柯西分布，即密度函数为 +∞<<∞-+=x x x p X , )1(1)(2π， 求Y=31X -的密度函数)(y p Y ．（5）设随机变量X服从参数为1的指数分布，设Y=2X+Xe3 , 求Y的数学期望．（6）设随机变量X和Y独立，且E(X)=E(Y)=1 , D(X)=2 , D(Y)=4 , 求E(X+Y)2．二．(12分)玻璃杯成箱出售，每箱20只，假设各箱含0，1，2只残次品的概率相应为0.8 , 0.1 和0.1 .一顾客欲购买一箱玻璃杯，在购买时，售货员随意取一箱，而顾客随机地察看4只，若无残次品，则买下该箱玻璃杯，否则退回．试求：（1）顾客买下该箱的概率；（2）在顾客买下的一箱中，确实没有残次品的概率．三．(12分)袋内有四张卡片，分别写有数字1，2，2，3，每次从中任取两张，记X ，Y 分别表示取到的两张卡片中的最小数字和最大数字，求（X ，Y ）的联合分布及X -Y 的概率分布．四．(10分)某人各月收入X 服从指数分布， 月平均收入EX=500元，如果月收入超过800元时要缴所得税，求一年中此人纳税月数的平均值．五．(14分)设随机向量（X ，Y ）在圆域 222r y x ≤+上服从均匀分布．（1）求X 和Y 的边际密度；（2）求相关系数 XY r ;（3）问X 和Y 是否相关？是否独立？（须说明理由）六．(8分)设一电路装有三个同种电器元件，其工作状态相互独立，且无故障工作时间都服从参数为λ>0 的指数分布，当三个元件都无故障时，电路正常工作，否则整个电路不能正常工作，试求电路正常工作时间T的分布函数，并说明是什么分布．七．(8分)设X1, X2, …, Xn为正的独立同分布的随机变量，求期望E(nXXXXX++++2121)．(n>2)。