超静定结构的位移计算

超静定结构的受力分析及特性一、超静定结构的特征及超静定次数超静定结构的静力特征是仅由静力平衡条件不能唯一地确定全部未知反力和内力。

结构的多余约束数或用静力平衡条件计算全部未知反力和内力时所缺少的方程数称为结构的超静定次数。

通常采用去除多余约束的方法来确定结构的超静定次数。

即去除结构的全部多余约束，使之成为无多余约束的几何不变体系，这时所去除的约束数就是结构的超静定次数。

去除约束的方法有以下几种：(一)切断一根两端铰接的直杆(或支座链杆)，相当于去除一个约束。

(二)切断一根两端刚接的杆件，相当于去除三个约束。

(三)切断——个单铰(或支座固定铰)，相当于去除二个约束;切断一个复铰(连接n根杆件的铰)，相当于去除2(n—1)个约束。

(四)将单刚结点改为单铰节点，相当于去除一个约束;将连接n个杆件的复刚节点改为复铰节点，相当于去除n—1个约束。

去除一个超静定结构多余约束的方法可能有几种，但不管采用哪种方法，所得超静定次数一定相同。

去除图4—1a所示超静定结构的多余约束的方法之一如图4—1b所示，去除六个多余约束后，就成为静定结构，故为超静定六次。

再用其他去除多余约束的方案确定其超静定次数，结果是相同的。

二、力法的基本原理(一)力法基本结构和基本体系去除超静定结构的多余约束，代以相应的未知力Xi (i=1、2、…、n)，Xi 称为多余未知力或基本未知力，其方向可以任意假定。

去除多余约束后的结构称为力法基本结构。

力法基本结构在各多余未知力、外荷载(有时还有温度变化、支座位移等)共同作用下的体系称为力法基本体系，它是用力法计算超静定结构的基础。

选取力法基本结构应注意下面两点：1.基本结构一般为静定结构，即无多余约束的几何不变体系。

有时当简单超静定结构的解为已知时，也可以将它作为复杂超静定结构的基本结构，以简化计算。

2.选取的基本结构应使力法典型方程中的系数和自由项的计算尽可能简便，并尽量使较多的副系数和自由项等于零。

第六章位移法超静定结构两类解法：力法：思路及步骤，适用于所有静定结构计算。

结合位移法例题中需要用到的例子。

有时太繁，例。

别的角度：内力和位移之间的关系随外因的确定而确定。

→位移法，E，超静定梁和刚架。

于是，开始有人讨论：有没有别的方法来求解或换一个角度来分析…，what？我们知道，当结构所受外因（外荷载、支座位移、温度变化等）一定⇒内力一定⇒变形一定⇒位移一定，也就是结构的内力和位移之间有确定的关系（这也可以从位移的公式反映出来）。

力法：内力⇒位移，以多余力为基本未知量…，能否反过来，也就是先求位移⇒内力，即以结构的某些位移为基本未知量，先想办法求出这些位移，再求出内力。

这就出现了位移法。

目前通用的位移法有两种：英国的、俄罗斯的，两者的实质是相同的。

以结构的某些结点位移作为基本未知量，由静力平衡条件先求出他们，再据以求出结构的内力和其它位移。

这种方法可以用于求解一些超静定梁和刚架，十分方便。

例：上面的例子，用位移法求解，只有结点转角一个未知量。

下面，我们通过一个简单的例子来说明位移法的解题思路和步骤：一个两跨连续梁，一次超静定，等截面EI=常数，右跨作用有均布荷载q，（当然可以用力法求解），在荷载q作用下，结构会发生变形，无N，无轴向变形，B点无竖向位移，只有转角ϕB。

且B点是一个刚结点传递M；变形时各杆端不能发生相对转动和移动，刚结点所连接的杆件之间角度受力以后不变。

也就是AB、BC杆在结点B处的转角是相同的。

原结构的受力和变形情况和b是等价的。

B当作固定端又产生转角ϕB。

a（原结构）AB：BC：b如果把转角ϕB 当作支座位移这一外因看，则原结构的计算就可以变成两个单跨超静定梁来计算。

显然，只要知道ϕB ，两个单跨静定梁的计算可以用力法求解出全部反力和内力，现在的未知量是ϕB （位移法的基本未知量）。

关键：如何求ϕB ？求出ϕB 后又如何求梁的内力？又如何把a ⇒b 来计算？ 我们采用了这样的方法：假定在刚结点B 附加一刚臂（▼），限制B 点转角，B ⇒固定端（无线位移，无转动）（略轴向变形）原结构就变成了AB 、BC 两个单跨超静定梁的组合体：AB ： ，BC ：但现在和原结构的变形不符，ϕB ，所以为保持和原结构等效，人为使B 结点发生与实际情况相同的转角ϕB （以Z 1表示，统一）。

第八节 超静定结构位移的计算根据单位荷载法计算位移，平面杆件结构在荷载作用下的位移计算公式可表示为：S N S N KP F F F F MM ds k ds ds EI GA EA∆=++∑∑∑⎰⎰⎰ （7-23） 式中，M 、S F 、N F 为虚拟状态中由单位荷载引起的内力，S N M F F 、、为实际荷载作用引起的内力，EI 、EA 、GA 分别为杆件截面抗弯刚度、抗拉压刚度和抗剪刚度，k 为剪应力分布不均匀修正系数。

式(7-23)不仅适用于静定结构的位移计算，同样适用于超静定结构。

对于静定结构，单位荷载作用下及实际荷载作用下的两组内力，均可以通过平衡条件较易确定。

下面讨论如何根据式(7-23)计算超静定结构的位移。

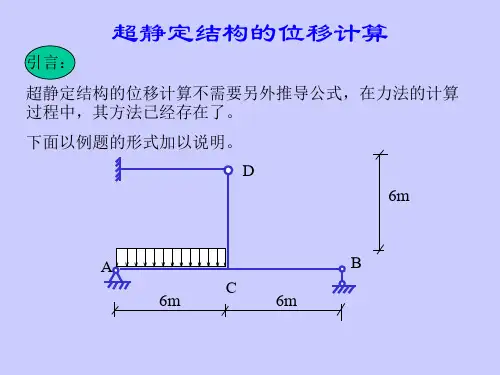
以图7-49(a)超静定梁为例，求在满跨均布荷载作用下梁中点C 的挠度CV ∆。

在7.2节中，已经通过力法计算得到其M 图如图7-49(b)所示。

用力法计算超静定结构，是根据基本结构在原荷载及多余未知力共同作用下（基本体系）其位移与原超静定结构相同这个条件来进行的。

基本体系与原结构的唯一区别是把多余未知力由原来的被动力换成主动力。

因此，只要多余未知力满足力法方程，则基本体系的受力与变形状态就与原结构完全相同，因而求原结构位移的问题就归结为求基本体系这个静定结构的位移问题。

比如，在力法计算中，可以选择将支座B 处支座链杆去掉后得到的悬臂梁作为原超静定梁的基本结构，图7-49(c)所示为相应的基本体系。

为求CV ∆,在基本结构的C 点施加竖向单位荷载1F =,并根据平衡条件作出弯矩图M (图7-49(d))。

利用M 图和M 图，根据图乘可得： 222410.50.52123()23831632882192CV MM l l ql ql l ql l ql ds EI EI EI ⎡⎤⎛⎫⨯∆==⨯⨯+⨯-⨯⨯⨯⨯=↓⎢⎥ ⎪⎝⎭⎣⎦∑⎰ 这就是利用基本体系求得的原结构跨中的竖向变形CV ∆。

位移法位移法也是计算超静定结构的基本方法。

位移法是以结构的结点位移（结点角位移和结点线位移）作为基本未知量，通过平衡条件建立位移法方程，求出位移后，即可利用位移和内力之间的关系，求出杆件和结构的内力。

在位移法求解超静定问题中，有七大步骤：第一步：分析结构体系（是否为几何不变体系，是否有结点位移），结构体系中的结点位移（结点角位移和结点线位移）就是结构的所求的基本未知量。

第二步：选取基本结构，即在原结构中的基本未知量（结点角位移和结点线位移）处加上约束（刚臂和链杆），均假设顺时针转动。

第三步：列位移法方程：01111=+P R Z r （一个结点位移未知量）当为n 次超静定时，0022112222212111212111=++++=++++=++++nP n nm n n P n n P n n R Z r Z r Z r R Z r Z r Z r R Z r Z r Z r第四步：画P M M 、1图，求nP nm R r 、（画P M M 、1图，通过查表得出，注意形常数及载常数的查法，记住是以顺时针转动为正。

）第五步：求解未知位移n Z 。

第六步：求杆端弯矩：P R Z M M +=11（一结点位移未知量）P n n i i R Z M Z M Z M Z M M ++++++= 2211（n 个结点位移未知量）此步骤的正负号规定容易与力法正负号规定混淆。

在位移法中，杆端弯矩以顺时针转动为正，逆时针转动为负。

第七步：求跨中弯矩（针对于集中力作用在跨中处以及均布荷载作用情况），作M图，Q图（注意：求跨中弯矩时的正负号规定，同力法一样）讨论：针对位移法中正负号规定判断需要注意的问题。

1、什么是杆端弯矩？例如：如图所示超静定梁假如截AB杆研究，就会暴露出三个内力（弯矩，剪力，轴力），现只研究弯矩，如图所示（夸张放大画出来）：图中所标的即为杆端弯矩，它的作用是相对于杆端而言的。

2、如何判断正负号及运用正负号画弯矩图？M为正的上图中杆端弯矩的方向是假设出来的，由图可知，杆ABM为负的（逆时针）。