电磁场理论复习题(含答案)

电磁场理论习题一1、求函数ϕ=xy+z-xyz 在点（1，1，2）处沿方向角πα=3，4πβ=，3πγ=的方向的方向导数.解：由于 M ϕ∂∂x =y －M yz = -1M y ϕ∂∂=2x y －(1,1,2)xz =0 Mzϕ∂∂=2z(1,1,2)xy -=31cos 2α=，cos 2β=，1cos 2γ=所以1cos cos cos =∂∂+∂∂+∂∂=∂∂γϕβϕαϕϕz y x lM2、 求函数ϕ＝xyz 在点（5, 1, 2）处沿着点（5, 1, 2）到点（9, 4, 19）的方向的方向导数。

解：指定方向l 的方向矢量为l ＝(9－5) e x +(4－1)e y +(19－2)e z ＝4e x +3e y +17e z其单位矢量zy x z y x e e e e e e l 314731433144cos cos cos ++=++=γβα5,10,2)2,1,5(==∂∂==∂∂==∂∂MMMMMxyzxzyyzxϕϕϕ所求方向导数314123cos cos cos =•∇=∂∂+∂∂+∂∂=∂∂ l z y x lMϕγϕβϕαϕϕ3、 已知ϕ=x 2+2y 2+3z 2+xy+3x-2y-6z ，求在点（0，0，0）和点（1，1，1）处的梯度。

解：由于ϕ∇=(2x+y+3) e x +(4y+x-2)e y +(6z-6)e z所以，(0,0,0)ϕ∇=3e x -2e y -6e z(1,1,1)ϕ∇=6e x +3e y4、运用散度定理计算下列积分：2232[()(2)]x y z sxz e x y z e xy y z e ds+-++⎰⎰I=S 是z=0 和 z=(a 2-x 2-y 2)1/2所围成的半球区域的外表面。

解：设：A=xz 2e x +(x 2y-z 3)e y +(2xy+y 2z)e z 则由散度定理Ω∇⎰⎰⎰⎰⎰sA ds=Adv可得2I r dvΩΩΩ=∇==⎰⎰⎰⎰⎰⎰⎰⎰⎰222Adv (z +x +y )dv2244220sin sin aar drd d d d r dr ππππθθϕϕθθ==⎰⎰⎰⎰⎰⎰525a π=5、试求▽·A 和▽×A:(1) A=xy 2z 3e x +x 3ze y +x 2y 2e z(2)22(,,)cos sin z A z e e ρρφρφρφ=+ (3 ) 211(,,)sin sin cos r A r r e e e r r θφθφθθθ=++解：（1）▽·A=y 2z 3+0+0= y 2z 3▽×A=23232(2)(23)x yx y x e xy xy z e ∂∂∂=---∂∂∂x y z23322e e e x y z xy z x z x y(2) ▽·A=()[()]z A A A z φρρρρρφ∂∂∂++∂∂∂1 =33[(cos )(sin )]ρφρφρρφ∂∂+∂∂1=3cos ρφ▽×A=ρφρφρρρφρ∂∂∂∂∂∂z ze e e 1z A A A =221cos 0ρφρρρφρφρφ∂∂∂∂∂∂z e e e z sin=cos 2sin sin ze e e ρφρφρφρφ-+(3) ▽·A=22(sin )()1[sin ]sin r A A r A r r r r φθθθθθφ∂∂∂++∂∂∂ =2322sin cos ()()1(sin )[sin ]sin r r r r r r r θθθθθθφ∂∂∂++∂∂∂ =222212[3sin 2sin cos ]3sin cos sin r r r θθθθθθ+=+▽×A=21sin rr r r rr θφθφθθθφθ∂∂∂∂∂∂e e rsin e A A rsin A =21sin 1sin sin cos rr r r r θφθθθφθθθθ∂∂∂∂∂∂e e rsin e rsin=33cos 2cos cos sin r e e e r r θφθθθθ+-习题二1、总量为q 的电荷均匀分布于球体中，分别求球内，外的电场强度。

电磁学复习题集及答案电磁学是物理学的重要分支之一，涉及电场、磁场以及它们之间的相互作用。

为了帮助大家复习电磁学知识，本文将提供一系列电磁学的复习题及答案。

希望通过这些题目的练习，能够加深对电磁学概念和原理的理解。

一、选择题1. 电场是指：A. 带电粒子所在空间B. 带电物体周围决定其它带电敏感物体运动状态的场C. 带电物体周围由于电介质作用而存在的场答案：B2. 磁感应强度的单位是：A. 特斯拉B. 高斯C. 法拉第答案：A3. 电路中最基本的电路元件是：A. 电源B. 电容器C. 电阻器答案：C4. 以下哪个物理量与电势差有关：A. 电场强度B. 电荷量C. 电容答案：A5. 以下哪个式子描述了法拉第电磁感应定律：A. U = IRB. F = maC. ε = -dφ/dt答案：C二、填空题1. 应用安培环路定理，计算通过一圈电流为2A的闭合回路的磁场的磁感应强度，如果这一圈回路的面积为0.5平方米，则磁感应强度大小为_________.答案：4特斯拉2. 自感系数也被称为________，单位是亨利。

答案：互感系数3. 电感为0.1亨的线圈通以频率为50Hz的交流电流，求其电感应电动势的峰值_________.答案：31.4伏三、解答题1. 一个长直导线中传过电流I，求与这根导线距离为r处点的磁感应强度B。

导线的长度为L。

解答：根据比奥-萨伐尔定律，磁感应强度B与电流I、距离r和导线长度L的关系为：B = (μ0 * I)/(2πr)其中，μ0 为真空中的磁导率，其数值为4π*10^(-7) 特斯拉·米/安培。

2. 有一个平行板电容器，两个平行金属板之间的空气介电常数为ε，两板间的距离为d，面积为A。

如果在这个电容器中加上电压U，求电场强度大小E以及电场能量密度u。

解答：电场强度E与电压U和板间距离d的关系为：E = U/d电场能量密度u与介质电容率ε、电场强度E的关系为：u = ε * E^2 / 2根据上述关系，将U和d代入公式可得到答案。

大学电磁场考试题及答案一、选择题（每题2分，共20分）1. 电磁场中，电场与磁场的相互作用遵循以下哪个定律？A. 高斯定律B. 法拉第电磁感应定律C. 安培环路定律D. 洛伦兹力定律答案：D2. 在真空中，电磁波的传播速度是多少？A. 100,000 km/sB. 300,000 km/sC. 1,000,000 km/sD. 3,000,000 km/s答案：B3. 一个点电荷产生的电场强度与距离的平方成什么关系？A. 正比B. 反比C. 对数关系D. 线性关系答案：B4. 以下哪种介质不能支持电磁波的传播？A. 真空B. 空气C. 玻璃D. 金属答案：D5. 麦克斯韦方程组中描述变化电场产生磁场的方程是？A. 高斯定律B. 高斯磁定律C. 法拉第电磁感应定律D. 安培环路定律答案：C6. 一个均匀带电球壳内部的电场强度是多少？A. 零B. 与球壳内的电荷分布有关C. 与球壳外的电荷分布有关D. 与球壳的总电荷量成正比答案：A7. 电磁波的频率和波长之间有什么关系？A. 频率与波长成正比B. 频率与波长成反比C. 频率与波长无关D. 频率越大，波长越小答案：B8. 根据洛伦兹力公式，一个带电粒子在磁场中运动时，其受到的力的方向与什么因素有关？A. 粒子的速度B. 磁场的方向C. 粒子的电荷D. 所有上述因素答案：D9. 电磁波的偏振现象说明电磁波是横波，这是因为？A. 电磁波的振动方向与传播方向垂直B. 电磁波的振动方向与传播方向平行C. 电磁波的传播不需要介质D. 电磁波在真空中传播速度最快答案：A10. 一个闭合电路中的感应电动势遵循以下哪个定律？A. 欧姆定律B. 基尔霍夫电压定律C. 法拉第电磁感应定律D. 安培环路定律答案：C二、填空题（每题2分，共20分）11. 电磁波的传播不需要______，因此它可以在真空中传播。

答案：介质12. 根据麦克斯韦方程组，电荷守恒定律可以表示为：∇⋅ E =______。

电磁场理论基础习题集（说明：加重的符号和上标有箭头的符号都表示矢量）一、填空题1.矢量场的散度定理为(1)，斯托克斯定理为(2)。

【知识点】：1.2 【难易度】：C 【参考分】：3【答案】：（1）()∫∫⋅=⋅∇SS d A d A v v v ττ （2）()S d A l d A SCvv v v ⋅×∇=⋅∫∫2.矢量场A v满足(1)时，可用一个标量场的梯度表示。

【知识点】：1.4 【难易度】：C 【参考分】：1.5【答案】：(1) 0=×∇A v 3.真空中静电场的基本方程的积分形式为(1)，(2)，微分形式为(3),(4)。

【知识点】：3.2 【难易度】：B【参考分】：6【答案】：(1) 0=⋅∫c l d E v v (2) ∑∫=⋅q S d D Sv v 0(3) 0=×∇E v (4)()r D vv ρ=⋅∇04.电位移矢量D v 、极化强度P v 和电场强度E v满足关系(1)。

【知识点】：3.6 【难易度】：B【参考分】：1.5【答案】：(1) P E P D D vv v v v +=+=00ε 5.有面电流s 的不同介质分界面上，恒定磁场的边界条件为(1),(2)。

【知识点】：3.8 【难易度】：B【参考分】：3【答案】：(1) ()021=−⋅B B n v v v (2) ()s J H H n v v vv =−×21 6.焦耳定律的微分形式为(1)。

【知识点】：3.8 【难易度】：B 【参考分】：1.5【答案】：(1) 2E E J p γ=⋅=v v 7.磁场能量密度=m w (1)，区域V中的总磁场能量为=m W (2)。

【知识点】：5.9 【难易度】：B 【参考分】：3【答案】：(1) 221H μ (2) ∫Vd H τμ2218.理想导体中，时变电磁场的=(1)，=(2) 。

【知识点】：6.1 【难易度】：A 【参考分】：3【答案】：(1)0 (2)0 9.理想介质中，电磁波的传播速度由(1)决定，速度=v (2)。

电磁场理论习题及答案电磁场理论是电磁学的基础，它描述了电荷和电流产生的电磁场在空间中的分布和演化规律。

在学习电磁场理论时，习题是巩固和深化理解的重要方式。

本文将介绍一些电磁场理论的习题及其答案，帮助读者更好地掌握这一理论。

一、电场和电势1. 问题：一个均匀带电球体，半径为R，总电荷为Q。

求球心处的电场强度。

答案：根据库仑定律，电场强度E与电荷Q和距离r的关系为E = kQ/r^2，其中k为库仑常数。

对于球体内部的点，距离球心的距离r小于半径R，所以电场强度为E = kQ/r^2。

对于球体外部的点，距离球心的距离r大于半径R，所以电场强度为E = kQ/R^3 * r。

2. 问题：一个无限长的均匀带电线，线密度为λ。

求距离线上一点距离为r处的电势。

答案：根据电势公式V = kλ/r，其中k为库仑常数。

所以距离线上一点距离为r处的电势为V = kλ/r。

二、磁场和磁感应强度1. 问题：一根无限长的直导线，电流为I。

求距离导线距离为r处的磁感应强度。

答案：根据安培环路定理，磁感应强度B与电流I和距离r的关系为B =μ0I/2πr，其中μ0为真空中的磁导率。

所以距离导线距离为r处的磁感应强度为B = μ0I/2πr。

2. 问题：一根长为L的直导线，电流为I。

求距离导线距离为r处的磁场强度。

答案：根据比奥萨伐尔定律，磁场强度H与电流I和距离r的关系为H = I/2πr。

所以距离导线距离为r处的磁场强度为H = I/2πr。

三、电磁场的相互作用1. 问题：一个半径为R的导体球，带电量为Q。

求导体球表面的电荷密度。

答案：导体球表面的电荷密度σ等于导体球上的电荷总量Q除以导体球表面的面积A。

导体球表面的面积A等于球的表面积4πR^2。

所以导体球表面的电荷密度为σ = Q/4πR^2。

2. 问题：一个平行板电容器，两个平行金属板之间的距离为d，电介质的介电常数为ε。

一块电介质板插入到电容器中间，使得电容器的电容增加了n倍。

习题5.1 设x0的半空间充满磁导率为的均匀介质，x0的半空间为真空，今有线电流沿z轴方向流动，求磁感应强度和磁化电流分布。

5.2 半径为a的无限长圆柱导体上有恒定电流J均匀分布于截面上，试解矢势A 的微分方程，设导体的磁导率为0，导体外的磁导率为。

5.3 设无限长圆柱体内电流分布，J azrJ0(r a)求矢量磁位A和磁感应B。

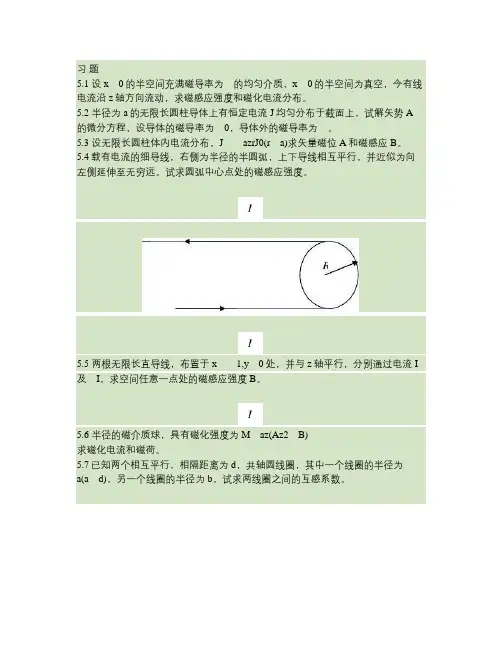
5.4载有电流的细导线，右侧为半径的半圆弧，上下导线相互平行，并近似为向左侧延伸至无穷远。

试求圆弧中心点处的磁感应强度。

5.5 两根无限长直导线，布置于x1,y0处，并与z轴平行，分别通过电流I 及I，求空间任意一点处的磁感应强度B。

5.6 半径的磁介质球，具有磁化强度为M az(Az2B)求磁化电流和磁荷。

5.7已知两个相互平行，相隔距离为d，共轴圆线圈，其中一个线圈的半径为a(a d)，另一个线圈的半径为b，试求两线圈之间的互感系数。

5.8 两平行无限长直线电流I1和I2，相距为d，求每根导线单位长度受到的安培力Fm。

5.9 一个薄铁圆盘，半径为a，厚度为b b a，如题5.9图所示。

在平行于z轴方向均匀磁化，磁化强度为M。

试求沿圆铁盘轴线上、铁盘内、外的磁感应强度和磁场强度。

5.10 均匀磁化的无限大导磁媒质的磁导率为，磁感应强度为B，若在该媒质内有两个空腔，，空腔1形状为一薄盘，空腔2像一长针，腔内都充有空气。

试求两空腔中心处磁场强度的比值。

5.11 两个无限大且平行的等磁位面D、N，相距h，mD10A，mN0。

其间充以两种不同的导磁媒质，其磁导率分别为10，220，分界面与等磁位面垂直，求媒质分界面单位面积受力的大小和方向。

题5.11图5.12 长直导线附近有一矩形回路，回路与导线不共面，如题5.12图 a所示。

证明：直导线与矩形回路间的互感为M0aln2R2b R2C22b2R2题5.12图a5.13 一环形螺线管的平均半径r015cm，其圆形截面的半径a2cm，铁芯的相对磁导率r1400，环上绕N1000匝线圈，通过电流I0.7A。

1. 两导体间的电容与_A__有关A. 导体间的位置B. 导体上的电量C. 导体间的电压D. 导体间的电场强度2. 下面关于静电场中的导体的描述不正确的是:____C__A. 导体处于非平衡状态。

B. 导体内部电场处处为零。

C. 电荷分布在导体内部。

D. 导体表面的电场垂直于导体表面3. 在不同介质的分界面上，电位是__B_。

A. 不连续的B. 连续的C. 不确定的D. 等于零4. 静电场的源是AA. 静止的电荷B. 电流C. 时变的电荷D. 磁荷5. 静电场的旋度等于__D_。

A. 电荷密度B. 电荷密度与介电常数之比C. 电位D. 零6. 在理想导体表面上电场强度的切向分量DA. 不连续的B. 连续的C. 不确定的D. 等于零7. 静电场中的电场储能密度为BA. B. C. D.8. 自由空间中静电场通过任一闭合曲面的总通量，等于BA. 整个空间的总电荷量与自由空间介电常数之比B. 该闭合曲面内所包围的总电荷量与自由空间介电常数之比。

C. 该闭合曲面内所包围的总电荷量与自由空间相对介电常数之比。

D. 该闭合曲面内所包围的总电荷量。

9. 虚位移法求解静电力的原理依据是GA. 高斯定律B. 库仑定律C. 能量守恒定律D. 静电场的边界条件10. 静电场中的介质产生极化现象，介质内电场与外加电场相比，有何变化？A. 变大B. 变小C. 不变D. 不确定11. 恒定电场中，电流密度的散度在源外区域中等于B____A. 电荷密度B. 零C. 电荷密度与介电常数之比D. 电位12. 恒定电场中的电流连续性方程反映了___A_A. 电荷守恒定律B. 欧姆定律C. 基尔霍夫电压定律D. 焦耳定律13. 恒定电场的源是___B_A. 静止的电荷B. 恒定电流C. 时变的电荷D. 时变电流14. 根据恒定电场与无源区静电场的比拟关系，导体系统的电导可直接由静电场中导体系统的DA. 电量B. 电位差C. 电感D. 电容15. 恒定电场中，流入或流出闭合面的总电流等于__C___A. 闭合面包围的总电荷量B. 闭合面包围的总电荷量与介电常数之比C. 零D. 总电荷量随时间的变化率16. 恒定电场是DA. 有旋度B. 时变场C. 非保守场D. 无旋场17. 在恒定电场中，分界面两边电流密度矢量的法向方向是BA. 不连续的B. 连续的C. 不确定的D. 等于零18. 导电媒质中的功率损耗反映了电路中的_D____A. 电荷守恒定律B. 欧姆定律C. 基尔霍夫电压定D. 焦耳定律19. 下面关于电流密度的描述正确的是AA. 电流密度的大小为单位时间垂直穿过单位面积的电荷量，方向为正电荷运动的方向。

电磁场与波复习题一、简答题：1、 静电场的基本方程（积分形式，微分形式）。

2、 恒定磁场的基本方程（积分形式，微分形式）。

3、 无外源区域中恒定电流场的基本方程（积分形式，微分形式）。

4、 麦克斯韦方程组的积分形式和微分形式。

5、 齐次波动方程。

6、 什么是传导电流？7、 什么是运流电流？8、 简述三类边值问题。

9、 简述镜像法的依据、实质和关键。

10、什么是唯一性定理？ 11、什么是色散？12、什么是电磁波的极化？13、写出时变电磁场中的能量定理方程，并简述其物理意义。

14、简述分离变量法求解静态场的定解问题的一般步骤。

15、判断下面电磁波的传播方向和极化方式？a 、 00cos()cos()x y E t z E t z ωβωβ=-+-E e e 答：线极化，+z 方向b 、 )sin()sin(00z t E e z t E e E y x βωβω-+-= 答：线极化，+z 方向c 、 )cos()sin(00z t E e z t E e E y x βωβω-+-= 答：左旋圆极化，+z 方向d 、 0()j zx y j E eβ-=-E e e答：右旋圆极化，+z 方向e 、 00sin()cos()44x y E t z E t z ππωβωβ=-++--E e e答：线极化，+z 方向 f 、 0()j xy z E e β-=+E e e答：线极化，+x 方向 g 、 0()jk zx y j E e-=-+E e e答：右旋圆极化，+z 方向 h 、 3cos()4sin()44y z t x t x ππωβωβ=--+-+E e e答：线极化，+x 方向二、证明推导题1. 证明0=∇⨯∇u2. 证明0)(=⨯∇⋅∇A0)()()()]()()([)()]()[()()(=∂∂-∂∂∂∂+∂∂-∂∂∂∂+∂∂-∂∂∂∂=∂∂-∂∂+∂∂-∂∂+∂∂-∂∂⋅∂∂+∂∂+∂∂=++⨯∂∂+∂∂+∂∂⋅∂∂+∂∂+∂∂=⨯∇⋅∇yA x A z x A z A y z A y A x y A x A e x A z A e z A y A e z e y e x e A e A e A e ze y e x e z e y e x e A x y z x y z x y z z x y y z x z y x z z y y x x z y x z y x3. 有人将一般时变场的场方程写成：∇⨯=H J t∂∇⨯=-∂B E 0=⋅∇B 0∇⋅=D你认为他写得对不对？如有错，请在错的式子旁边打叉，并写出正确的方程和名称。

电磁场理论期末复习题（附答案）一填空题1．静止电荷所产生的电场，称之为静电场；电荷Q在某点所受电场力为F，则该点电场强度的大小为QFE=。

2. 可以用电位的负梯度来表示电场强度；当电位的参考点选定之后，静电场中各点的电位值是唯一确定的。

3．__电荷_____的规则运动形成电流；将单位正电荷从电源负极移动到正极，非静电力__所做的功定义为电源的电动势4．由恒定电流或永磁体产生的磁场不随时间变化，称为恒定磁场。

5．磁感应强度B是无散场，它可以表示为另一个矢量场A的旋度，称A为矢量磁位，为了唯一地确定A，还必须指定A的散度为零，称为库仑规范。

6．静电场的边界条件，即边值问题通常分为三类：第一类为给定整个边界上的位函数值；第二类为给定边界上每一点位函数的法向导数值；第三类为给定一部分边界上每一点的位函数值，同时给定另一部分边界上每一点的位函数的法向导数值。

7．位移电流扩大了电流的概念，它由电场的变化产生，相对于位移电流我们称由电荷规则运动形成的电流为传导电流和运流电流。

8. 在电磁波传播中，衰减常数α的物理意义为表示电磁波每传播一个单位的距离，其振幅的衰减量，相位常数β的物理意义为表示电磁波每传播一个单位距离相位偏移量。

10.静电场是有势场，静电场中各点的电场与电位关系用公式表示是__Eφ=-∇_______。

13._____恒定电流________________产生的磁场，叫做恒定磁场。

14.库仑规范限制了矢量磁位A的多值性，但不能唯一确定A。

为了唯一确定A，还必须给定A的____散度为零________________________。

16.时变电磁场分析中，引入洛仑兹规范是为了解决动态位的____惟一性__________。

18.载流导体在磁场中会受到电磁力的作用，电磁力的方向由__左手_____定则确定。

二、选择题1.磁感应强度B与磁场强度H的一般关系为 ( B )A.H=μBB.B=μHC.H=μr BD.B=μ0H2 导体在静电平衡下，其内部电场强度( B )A.为常数B.为零C.不为零D.不确定3 真空中磁导率的数值为( C )A. ４π×10-5H/mB. ４π×10-6H/mC. ４π×10-7H/mD. ４π×10-8H/m4.磁通Φ的单位为( B )A.特斯拉B.韦伯C.库仑D.安匝5.矢量磁位的旋度是 ( A )A.磁感应强度B.磁通量C.电场强度D.磁场强度6.真空中介电常数ε0的值为 ( D )A.8.85×10-9F/mB.8.85×10-10F/mC.8.85×10-11F/mD.8.85×10-12F/m7.下面说法正确的是 ( A )A.凡是有磁场的区域都存在磁场能量B.仅在无源区域存在磁场能量C.仅在有源区域存在磁场能量D.在无源、有源区域均不存在磁场能量8 静电场中试验电荷受到的作用力大小与试验电荷的电量( C )A.成反比B.成平方关系C.成正比D.无关9.平板电容器的电容量与极板间的距离 ( B )A.成正比B.成反比C.成平方关系D.无关10.在磁场B中运动的电荷会受到洛仑兹力F的作用，F与B的空间位置关系 ( B )A.是任意的B.相互垂直C.同向平行D.反向平行2．高斯定理的积分形式描述了 B 的关系；A．闭合曲面内电场强度与闭合曲面内电荷之间的关系B. 闭合曲面的电场强度通量与闭合曲面内电荷之间的关系C．闭合曲面内电场强度与闭合曲面外电荷之间的关系D. 闭合曲面的电场强度通量与闭合曲面附近电荷之间的关系13．以下阐述中，你认为正确的一项为 D ；A. 可以用电位的函数的梯度表示电场强度B. 感应电场是保守场，其两点间线积分与路径无关C．静电场是无散场，其在无源区域的散度为零D．静电场是无旋场，其在任意闭合回路的环量为零14. 以下关于电感的阐述中，你认为错误的一项为 C ；A.电感与回路的几何结构有关B. 电感与介质的磁导率有关C．电感与回路的电流有关D．电感与回路所处的磁场强度无关17.若电介质中的极化强度矢量和电场强度成正比关系，则称这种电介质为 BC ；A.均匀的B.各向同性的C.线性的D.可极化的18. 均匀导电媒质是指其电导率无关于 B ；A.电流密度B.空间位置C.时间D.温度19.关于镜像法，以下不正确的是 B ；A.它是解静电边值问题的一种特殊方法B.用假想电荷代替原电荷C．假想电荷位于计算区域之外D．假想电荷与原电荷共同作用满足原边界条件20. 交变电磁场中，回路感应电动势与回路材料电导率的关系为 D ；A.电导率越大，感应电动势越大B.电导率越小，感应电动势越大C.电导率越大，感应电动势越小D.感应电动势大小与导电率无关22.相同尺寸和匝数的空心线圈的电感系数与铁心线圈的电感系数之比( C )A.大于1B.等于1C.小于1D.无确定关系24.真空中均匀平面波的波阻抗为 A ；A.377ΩB.237ΩC.277ΩD.337Ω25. 在磁场B 中运动的电荷会受到洛仑兹力F 的作用，F 与B 的空间位置关系 B ； A.是任意的 B.相互垂直 C.同向平行 D.反向平行三、简答题1.什么是接地电阻?其大小与哪些因素有关?答：接地设备呈现出的总电阻称之为接地电阻；其大小与土壤电导率和接地体尺寸（等效球半径）成反比2.写出微分形式的麦克斯韦的数学表达式。

第1~2章 矢量分析 宏观电磁现象的基本规律1. 设：直角坐标系中，标量场zx yz xy u ++=的梯度为A ρ，则M （1，1，1）处 A ρ= ，=⨯∇A ρ 0 。

2. 已知矢量场xz e xy e z y e A z y x ˆ4ˆ)(ˆ2+++=ρ，则在M （1，1，1）处=⋅∇A ρ 9 。

3. 亥姆霍兹定理指出，若唯一地确定一个矢量场（场量为A ρ），则必须同时给定该场矢量的 旋度 及 散度 。

4. 写出线性和各项同性介质中场量D ρ、E ρ、B ρ、H ρ、J ρ所满足的方程（结构方程）： 。

5. 电流连续性方程的微分和积分形式分别为 和 。

6. 设理想导体的表面A 的电场强度为E ρ、磁场强度为B ρ，则（a ）E ρ、B ρ皆与A 垂直。

（b ）E ρ与A 垂直，B ρ与A 平行。

（c ）E ρ与A 平行，B ρ与A 垂直。

（d ）E ρ 、B ρ皆与A 平行。

答案：B7. 两种不同的理想介质的交界面上，（A ）1212 , E E H H ==r r r r（B ）1212 , n n n n E E H H == (C) 1212 , t t t t E E H H == (D) 1212 , t t n n E E H H ==答案：C8. 设自由真空区域电场强度(V/m) )sin(ˆ0βz ωt E eE y -=ρ，其中0E 、ω、β为常数。

则ˆˆˆ222x y z e e e ++Aρ⋅∇A ρ⨯∇EJ H B E D ρρρρρρσ=μ=ε= , ,t q S d J S∂∂-=⋅⎰ρρtJ ∂ρ∂-=⋅∇ρ空间位移电流密度d J ρ（A/m 2）为：（a ） )cos(ˆ0βz ωt E ey - （b ） )cos(ˆ0βz ωt ωE e y -（c ） )cos(ˆ00βz ωt E ωey -ε （d ） )cos(ˆ0βz ωt βE e y -- 答案：C 9. 已知无限大空间的相对介电常数为4=εr ，电场强度(V/m) 2cos ˆ0dxeE x πρ=ρ，其中0ρ、d 为常数。

电磁场与电磁波复习资料填空题1．梯度的物理意义为，等值面、方向导数与梯度的关系是。

2．用方向余弦γβαcos ,cos ,cos 写出直角坐标系中单位矢量l e的表达式。

3．某二维标量函数x y u -=2，则其梯度u ∇=，梯度在正x 方向的投影为。

4．自由空间中一点电荷位于()4,1,3-S ，场点位于()3,2,2-P ，则点电荷的位置矢量为，场点的位置矢量为，点电荷到场点的距离矢量R为。

5．矢量场z e y e x eA z y x ˆˆˆ++=，其散度为，矢量场A在点()2,2,1处的大小为。

6．直角坐标系下方向导数lu∂∂的数学表达式 ，梯度的表达式为 ，任意标量的梯度的旋度恒为 ，任意矢量的旋度的散度恒为 。

7．矢量散度在直角坐标系的表达式为 ，在圆柱坐标系的表达式为 ，在球坐标系的表达式为 。

8．矢量微分运算符∇在直角坐标系、圆柱坐标系和球坐标系的表达式分别为 ， ， 。

9．高斯散度定理数学表达式为 ，斯托克斯定理数学表达式为 。

10．矢量通量的定义为 ，散度的定义为 ，环流的定义为 ，旋度的定义为 。

11．矢量的旋度在直角坐标系下的表达式为 。

12．矢量场F为无旋场的条件为，该矢量场是由 源所产生。

13．矢量场F为无散场的条件为，该矢量场是由源所产生。

14．电流连续性方程的微分形式为 。

15．在国际单位制中，电场强度的单位是 ，电位移的单位是 ，磁场强度的单位是 ，磁感应强度的单位是 ，介电常数的单位是 ，磁导率的单位是 ，电导率的单位是 。

16．在自由空间中，点电荷产生的电场强度与其电荷量成 比，与场点到源点的距离平方成 比。

17．从宏观效应来看，物质对电磁场的响应可分为 ， ， 三种现象。

18．线性且各向同性媒质的本构关系方程是： ， ， 。

19．麦克斯韦方程组的微分形式是： ， ， ， 。

20．麦克斯韦方程组的积分形式是： ， ， ， 。

21．求解时变电磁场或解释一切宏观电磁现象的理论依据是 。

《电磁场与电磁波》期末复习题及答案一，单项选择题１．电磁波的极化特性由＿＿B ＿＿＿决定。

A.磁场强度B.电场强度C.电场强度和磁场强度D. 矢量磁位2．下述关于介质中静电场的基本方程不正确的是＿＿D ＿＿＿A. ρ??=DB. 0??=EC. 0C d ?=? E lD.0S q d ε?=? E S 3. 一半径为a 的圆环（环面法向矢量z = n e ）通过电流I ，则圆环中心处的磁感应强度B 为＿＿D ＿＿＿A. 02r Ia μe B.02I a φμe C. 02z Ia μe D. 02z I a μπe4. 下列关于电力线的描述正确的是＿＿D ＿＿＿A.是表示电子在电场中运动的轨迹B. 只能表示E 的方向，不能表示E 的大小C. 曲线上各点E 的量值是恒定的D. 既能表示E 的方向，又能表示E 的大小5. 0??=B 说明＿＿A ＿＿＿A. 磁场是无旋场B. 磁场是无散场C. 空间不存在电流D. 以上都不是6. 下列关于交变电磁场描述正确的是＿＿C ＿＿＿A. 电场和磁场振幅相同，方向不同B. 电场和磁场振幅不同，方向相同C. 电场和磁场处处正交D. 电场和磁场振幅相同，方向也相同7．关于时变电磁场的叙述中，不正确的是：（D ）A. 电场是有旋场B. 电场和磁场相互激发C.电荷可以激发电场D. 磁场是有源场8. 以下关于在导电媒质中传播的电磁波的叙述中，正确的是＿＿B ＿＿＿A. 不再是平面波B. 电场和磁场不同相C.振幅不变D. 以ＴＥ波形式传播9. 两个载流线圈之间存在互感，对互感没有影响的是＿C ＿＿＿＿A. 线圈的尺寸B. 两个线圈的相对位置C. 线圈上的电流D. 空间介质10. 用镜像法求解静电场边值问题时，判断镜像电荷的选取是否正确的根据＿＿C ＿＿＿A. 镜像电荷是否对称B.电位?所满足的方程是否改变C. 边界条件是否保持不变D. 同时选择Ｂ和Ｃ11. 区域Ｖ全部全部用非导电媒质填充，当此区域中的电磁场能量减少时，一定是＿A ＿＿＿A. 能量流出了区域B.能量在区域中被损耗C.电磁场做了功D. 同时选择Ａ和Ｃ12. 磁感应强度为(32)x y z B axe y z e ze =+-+ , 试确定常数a 的值。

《电磁场理论》考试试卷（A 卷）（时间120分钟）1. 关于有限区域内的矢量场的亥姆霍兹定理，下列说法中正确的是 （A ）任意矢量场可以由其散度和旋度唯一地确定； （B ）任意矢量场可以由其散度和边界条件唯一地确定； （C ） 任意矢量场可以由其旋度和边界条件唯一地确定； （D ） 任意矢量场可以由其散度、旋度和边界条件唯一地确定。

2. 谐变电磁场所满足的麦克斯韦方程组中，能反映“变化的电场产生磁场”和“变化的磁场产生电场” 这一物理思想的两个方程是 （B5关于高斯定理的理解有下面几种说法， 其中正确的是、选择题（每小题2分，共20 分）(A)H 0, E —(B ) H J E, E(C H J,E 0(D )H 0, E -3.—圆极化电磁波从媒质参数为分量不产生反射，入射角应为 3 r 1的介质斜入射到空气中，要使电场的平行极化（B ）(A) 15°(B ) 30°(C ) 45(D) 604.在电磁场与电磁波的理论中分析中，常引入矢量位函数A ，并令B A ，其依据是（C ）(A)B 0 ;(C ) B 0;(B)B J ；(D) B J电磁学》试卷 第 2 页 共 7 页(A) 如果高斯面内无电荷，则高斯面上 E 处处为零； (B) 如果高斯面上 E 处处不为零，则该面内必有电荷； (C) 如果高斯面内有净电荷，则通过该面的电通量必不为零； (D) 如果高斯面上 E 处处为零，则该面内必无电荷。

6．若在某区域已知电位移矢量 ( A)2( B ) 2D xe x( C )ye y ，则该区域的电何体密度为 ( B )2( D )27. 两个载流线圈之间存在互感，对互感没有影响的是( C )(A )线圈的尺寸(B ) 两个线圈的相对位置(C )线圈上的电流 (D )线圈中的介质8 . 以下关于时变电磁场的叙述中，正确的是( B )(A )电场是无旋场 (B )电场和磁场相互激发(C)电场和磁场无关 (D )磁场是有源场9. 两个相互平行的导体平板构成一个电容器， 与电容无关的是10. 用镜像法求解静电场边值问题时， 判断镜像电荷设置是否正确的依据是 ( C )(A) 镜像电荷的位置是否与原电荷对称 (B) 镜像电荷是否与原电荷等值异号(C) 待求区域内的电位函数所满足的方程与边界条件是否保持不变 (D) 同时满足A 和B(A )导体板上的电荷(C )导体板的几何形状 (B) 平板间的介质(D) 两个导体板的相对位1 •电磁波在波导中传播的条件是波导管只能让频率 __________ 一特定值的电磁波通过，该特 定频率称为 _____________ 。

电磁原理基础理论知识单选题100道及答案解析1. 下列哪位科学家发现了电磁感应现象？（）A. 安培B. 法拉第C. 奥斯特D. 库仑答案：B解析：法拉第发现了电磁感应现象。

2. 通电导线周围存在磁场，其方向可用（）定则来判断。

A. 左手B. 右手C. 安培D. 楞次答案：C解析：通电导线周围磁场方向用安培定则判断。

3. 变化的磁场能够产生电场，这是（）的重要结论。

A. 法拉第电磁感应定律B. 麦克斯韦电磁场理论C. 楞次定律D. 安培定律答案：B解析：麦克斯韦电磁场理论指出变化的磁场能够产生电场。

4. 以下哪种材料的磁导率最高？（）A. 空气B. 铁C. 铜D. 铝答案：B解析：铁是磁性材料，磁导率较高。

5. 电磁感应现象中，产生的感应电动势的大小与（）成正比。

A. 磁通量的变化量B. 磁通量的变化率C. 磁场强度D. 导线长度答案：B解析：感应电动势的大小与磁通量的变化率成正比。

6. 真空中电磁波的传播速度是（）。

A. 3×10^5 m/sB. 3×10^6 m/sC. 3×10^7 m/sD. 3×10^8 m/s答案：D解析：真空中电磁波的传播速度约为3×10^8 m/s。

7. 以下哪种电磁波的频率最高？（）A. 无线电波B. 红外线C. 紫外线D. X 射线答案：D解析：X 射线的频率高于紫外线、红外线和无线电波。

8. 楞次定律是用来判断（）。

A. 感应电流的方向B. 磁场的方向C. 感应电动势的大小D. 磁通量的大小答案：A解析：楞次定律用于判断感应电流的方向。

9. 一个线圈的自感系数与（）无关。

A. 电流B. 线圈匝数C. 有无铁芯D. 线圈的几何形状答案：A解析：自感系数与电流无关。

10. 互感现象中，互感系数与（）有关。

A. 两个线圈的距离B. 两个线圈中的电流C. 两个线圈的电压D. 两个线圈的电阻答案：A解析：互感系数与两个线圈的距离等因素有关。

电磁场与电磁波期末考试复习资料11.圆柱坐标系中单位矢量 ， 。

2.对于矢量A ，若 ，则=+•y x a y x a x )(2 ，=⨯x z a y a x 2 。

3.给定两个矢量z y x a a a A 32-+=，z y a a B +-=4，则矢量A 的单位矢量为 ，矢量B A ⋅= 。

4.已知直角坐标系中点P 1(5,-2,1),P 2(3,1,2),则P1的位置矢量为 ,P1到P2的距离矢量为 。

5.已知球坐标系中单位矢量 。

6.在两半无限大导电平面组成的直角劈形中间放置一点电荷，此时点电荷的镜像电荷个数为 。

7.点电荷q 在自由空间任一点r 处电场强度为 。

8.静电场中导体内的电场为 ，电场强度与电位函数的关系为 。

9.高斯散度定理的积分式为 ，它广泛的用于将一个封闭面积分变成等价的体积分，或者将一个体积分变成等价的封闭面积分。

10.已知任意一个矢量场A ，则其旋度的散度为 。

11.真空中静电场的基本方程的微分形式为 、 、 。

12.分析恒定磁场时，在无界真空中，两个基本场变量为 ，它们之间的关系为 。

13.斯托克斯定理为 ，它表明矢量场A 的旋度沿曲面S 的方向分量的面积分等于该矢量沿围绕此面积曲线边界的线积分。

14.任意一个标量场u ，则其梯度的旋度为 。

15.对于某一矢量 ,它的散度定义式为 ，用哈密顿算子表示为 。

16.介质中静电场的基本方程的积分式为 ， ， 。

17.介质中恒定磁场的基本方程的微分形式为 、 、 。

18.介质中恒定磁场的基本方程的积分式为 ， ， 。

19.静电场中两种介质分界面的边界条件是 ， 。

20.在无限大的导体平面上方d 处放一点电荷q ，则其镜像电荷电量为 ，位置位于 ；如果一个点电荷置于两平行导体中间，则此点电荷有 镜像电荷。

21.矢量场223z a yz a y x a A z y x ++=在点P(1,1,0)的散度为 。

22.一个半径为a 的接地导体球，一点电荷q 位于距球心d 处，则其镜像电荷带电量为 ，位置位于 ；当点电荷q 向无限远处运动时，其镜像电荷向 运动。

电磁场与电磁波复习题一、填空题1、矢量的通量 物理含义是矢量穿过曲面的矢量线总数 ,散度的物理意义 矢量场中任意一点处通量对体积的变化率。

散度与通量的关系是矢量场中任意一点处通量对体积 的变化率。

div J ==散度在圆柱坐标系下的表达3、矢量函数的环量 定义矢量A 沿空间有向闭合曲线C 的线积分，旋度的定义 过点P 作一微小曲面S,它的边界曲线记为L,面的法线方与曲线绕向成右旋度的物理意义 点P 的旋度的大小是该点环量密度的最大值；点P 的旋度的方向是该点最大环量密度的方向。

4.矢量的旋度在直角坐标系 下的表达式5、梯度的物理意义 标量场的梯度是一个矢量，是空间坐标点的函数。

梯度的大小为该点标量函数 的最大变化率，即该点最 大方向导数；梯度的方向为该点最大方向导数的方向，即与等值线（面）相垂直的方向，它指向函数的增加方向等值面、方向导数与梯度的关系是梯度的大小为该点标量函数的最大变化率，即该点最大方向导数；梯度的方向为该点最大方向导数的方向 ，即与等值线（面）相垂直的方向，它指向函数的增加方向•；6、用方向余弦cos ,cos ,cos 写出直角坐标系中单位矢量e 的表达2、 散度在直角坐标系的表达式div AA x A z手螺旋法则。

当S 点P 时,存在极限环量密度。

二者的关系dCdSrot A e nS4dy些）+爲（坐-坐）+瓦（呂7、直角坐标系下方向导数彳的数学表达式是” = —cos + —^ cos + —^ cos l X y ZG 一e 一e y 一 egradx y z；_____________________________________ ?8 亥姆霍兹定理 的表述在有限区域内，矢量场由它的散度、 旋度及边界条件唯一地确定,说明的问题 是矢量场的散度应满足的关系及旋度应满足的关系决定了矢量场的基本性质。

9、麦克斯韦方程组的积分形式分别为10、麦克斯韦方程组的微分形式分别为r E / o r r E B/ t r B 0 2r r r c 2BJ / 0E/ t其物理意义分别为11 、时谐场是激励源按照单一频率随时间作正弦变化时所激发的也随时间按照正弦变化的场, ___ 一般采用时谐场来分析时变电磁场的一般规律，是因为 任何时变周期函 数都可以用正弦函数表示的傅里叶级数来表示；在线性条件下，可以使用叠加原理。

电磁学试题（含答案）⼀、单选题1、如果通过闭合⾯S 的电通量e Φ为零，则可以肯定A 、⾯S 没有电荷B 、⾯S 没有净电荷C 、⾯S 上每⼀点的场强都等于零D 、⾯S 上每⼀点的场强都不等于零2、下列说法中正确的是A 、沿电场线⽅向电势逐渐降低B 、沿电场线⽅向电势逐渐升⾼C 、沿电场线⽅向场强逐渐减⼩D 、沿电场线⽅向场强逐渐增⼤3、载流直导线和闭合线圈在同⼀平⾯，如图所⽰，当导线以速度v 向左匀速运动时，在线圈中A 、有顺时针⽅向的感应电流B 、有逆时针⽅向的感应电C 、没有感应电流D 、条件不⾜，⽆法判断 4、两个平⾏的⽆限⼤均匀带电平⾯，其⾯电荷密度分别为σ+和σ-，则P 点处的场强为 A 、02εσ B 、0εσ C 、02εσ D 、0 5、⼀束α粒⼦、质⼦、电⼦的混合粒⼦流以同样的速度垂直进⼊磁场，其运动轨迹如图所⽰，则其中质⼦的轨迹是A 、曲线1B 、曲线2C 、曲线3D 、⽆法判断 6、⼀个电偶极⼦以如图所⽰的⽅式放置在匀强电场E 中，则在电场⼒作⽤下，该电偶极⼦将A 、保持静⽌B 、顺时针转动C 、逆时针转动D 、条件不⾜，⽆法判断7、点电荷q 位于边长为a 的正⽅体的中⼼，则通过该正⽅体⼀个⾯的电通量为A 、0B 、0εqC 、04εqD 、06εq 8、长直导线通有电流A 3=I ，另有⼀个矩形线圈与其共⾯，如图所⽰，则在下列哪种情况下，线圈中会出现逆时针⽅向的感应电流？A 、线圈向左运动B 、线圈向右运动C 、线圈向上运动D 、线圈向下运动 9、关于真空中静电场的⾼斯定理0εi S q S d E ∑=?? ，下述说确的是：A. 该定理只对有某种对称性的静电场才成⽴；B. i q ∑是空间所有电荷的代数和；C. 积分式中的E ⼀定是电荷i q ∑激发的；σ-P 3ID.积分式中的E是由⾼斯⾯外所有电荷激发的。

10、下列各图为载流电路，其中虚线部分表⽰通向“⽆限远”，弧形部分为均匀导线，点O 磁感强度为零的图是A.B.C. D．11、两个带有同号电荷、形状完全相同的⾦属⼩球A和B，电量均为q，它们之间的距离远⼤于⼩球本⾝的直径。