2018年北京市东城区高考数学二模试卷(理科)

2018届北京市东城区高三第二学期综合练习(一)数学理北京市东城区2017-2018学年度第二学期高三综合练习（一）数学（理科） 2018. 4本试卷共4页，共150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

(1)若集合{}31A x x =-p p ,{}12B x x x =-f f 或，则A B =I (A) {}32x x -p p (B) {}31x x --p p(C) {}11x x -p p (D) {}11x x -p p(2）复数1iz i=-在复平面上对应的点位于 (A)第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限(3)已知,a b R ∈，且a b f ，则下列不等式一定成立的是 (A) 220ab -f (B) cos cos 0a b -f(C) 110a b-p (D) 0ab ee ---p(4)在平面直角坐标系xOy中，角θ以Ox 为始边，终边与单位圆交于点（35，45），则tan()θπ+的值为(A)43 (B)34(C)43-(D) 34-(5)设抛物线24y x=上一点P到y轴的距离是2，则P到该抛物线焦点的距离是(A)1 (B) 2 (C)3 (D)4(6)故宫博物院五一期间同时举办“戏曲文化展”、“明代御窖瓷器展”、“历代青绿山水画展”、“赵孟頫书画展”四个展览．某同学决定在五一当天的上、下午各参观其中的一个，且至少参观一个画展，则不同的参观方案共有(A)6种（B) 8种（C) 10种（D) 12种(7)设{}na是公差为d的等差数列，n S为其前n项和，则“d>0”是“{}nS为递增数列”的(A）充分而不必要条件（B)必要而不充分条件(C）充分必要条件（D）既不充分也不必要条件(8)某次数学测试共有4道题目，若某考生答对的题大于全部题的一半，则称他为“学习能手”，对于某个题目，如果答对该题的“学习能手”不到全部“学习能手”的一半，则称该题为“难题”．已知这次测试共有5个“学习能手”，则“难题”的个数最多为(A)4 (B) 3 (C)2 (D)1第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分。

北京市东城区达标名校2018年高考二月仿真备考数学试题一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．某装饰公司制作一种扇形板状装饰品，其圆心角为120°，并在扇形弧上正面等距安装7个发彩色光的小灯泡且在背面用导线相连(弧的两端各一个，导线接头忽略不计)，已知扇形的半径为30厘米，则连接导线最小大致需要的长度为（ ） A ．58厘米 B ．63厘米C ．69厘米D ．76厘米2．已知函数21()(1)()2x f x ax x e a R =--∈若对区间[]01，内的任意实数123x x x 、、，都有123()()()f x f x f x +≥，则实数a 的取值范围是( ）A ．[]12，B ．[]e,4C ．[]14， D ．[)[]12,4e ⋃， 3．等比数列{}n a 的各项均为正数，且384718a a a a +=，则3132310log log log a a a +++=( )A ．12B ．10C ．8D ．32log 5+4．设()'f x 函数()()0f x x >的导函数，且满足()()2'f x f x x>，若在ABC ∆中，34A π∠=，则（ ）A ．()()22sin sin sin sin f A B f B A <B ．()()22sinC sin sin sin f B f B C< C ．()()22cos sin sin cos f A B f B A >D ．()()22cosC sin sin cos f B f B C >5．记M 的最大值和最小值分别为max M 和min M ．若平面向量a 、b 、c ，满足()22a b a b c a b c ==⋅=⋅+-=，则（ ）A ．max3a c-=B ．max3a c+=C ．min3a c-= D ．min3a c+=6．设过点(),P x y 的直线分别与x 轴的正半轴和y 轴的正半轴交于,A B 两点，点Q 与点P 关于y 轴对称，O 为坐标原点，若2BP PA =，且1OQ AB ⋅=，则点P 的轨迹方程是（ ） A ．()223310,02x y x y +=>> B ．()223310,02x y x y -=>> C ．()223310,02x y x y -=>>D ．()223310,02x y x y +=>>7．若各项均为正数的等比数列{}n a 满足31232a a a =+，则公比q =（ ） A ．1B ．2C ．3D ．48．已知n S 是等差数列{}n a 的前n 项和，若312S a S +=，46a =，则5S =（ ）A ．5B ．10C ．15D ．209．已知集合A {}0,1,2=，B={}(2)0x x x -<,则A∩B= A．{}1B ．{}0,1C ．{}1,2D ．{}0,1,210．如图，在矩形OABC 中的曲线分别是sin y x =，cos y x =的一部分，,02A π⎛⎫⎪⎝⎭，()0,1C ，在矩形OABC 内随机取一点，若此点取自阴影部分的概率为1P ，取自非阴影部分的概率为2P ，则（ ）A ．12P P <B ．12P P >C ．12P P =D ．大小关系不能确定11．定义在R 上的函数()f x 满足(4)1f =，()f x '为()f x 的导函数，已知()y f x '=的图象如图所示，若两个正数,a b 满足(2)1f a b +<，11b a ++则的取值范围是（ ）A ．(11,53)B ．1(,)(5,)3-∞⋃+∞C ．(1,53)D ．(,3)-∞12．已知等差数列{}n a 的公差不为零，且11a ，31a ，41a 构成新的等差数列，n S 为{}n a 的前n 项和，若存在n 使得0n S =，则n =（ ） A ．10B ．11C ．12D ．13二、填空题：本题共4小题，每小题5分，共20分。

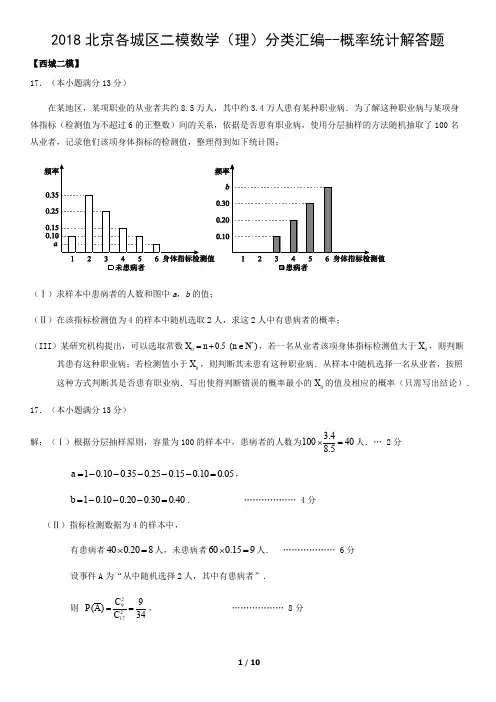
2018北京各城区二模数学（理）分类汇编--概率统计解答题【西城二模】17．（本小题满分13分）在某地区，某项职业的从业者共约8.5万人，其中约3.4万人患有某种职业病．为了解这种职业病与某项身体指标（检测值为不超过6的正整数）间的关系，依据是否患有职业病，使用分层抽样的方法随机抽取了100名从业者，记录他们该项身体指标的检测值，整理得到如下统计图：（Ⅰ）求样本中患病者的人数和图中a ，b 的值；（Ⅱ）在该指标检测值为4的样本中随机选取2人，求这2人中有患病者的概率；（III ）某研究机构提出，可以选取常数*00.5()X n n =+∈N ，若一名从业者该项身体指标检测值大于0X ，则判断其患有这种职业病；若检测值小于0X ，则判断其未患有这种职业病．从样本中随机选择一名从业者，按照这种方式判断其是否患有职业病．写出使得判断错误的概率最小的0X 的值及相应的概率（只需写出结论）． 17．（本小题满分13分）解：（Ⅰ）根据分层抽样原则，容量为100的样本中，患病者的人数为 3.4100408.5⨯=人．… 2分 10.100.350.250.150.100.05a =-----=，10.100.200.300.40b =---=． ……………… 4分（Ⅱ）指标检测数据为4的样本中，有患病者400.208⨯=人，未患病者600.159⨯=人． ……………… 6分 设事件A 为“从中随机选择2人，其中有患病者”．则 29217C 9(A)C 34P ==， ……………… 8分所以 25(A)1(A)34P P =-=． ……………… 9分 （Ⅲ）使得判断错误的概率最小的0 4.5X =． ………………11分 当0 4.5X =时，判断错误的概率为21100． ………………13分 【海淀二模】（16）（本小题13分）某中学为了解高二年级中华传统文化经典阅读的整体情况，从高二年级随机抽取10名学生进行了两轮测试，并把两轮测试成绩的平均分作为该名学生的考核成绩.记录的数据如下：（Ⅱ）从考核成绩大于90分的学生中再随机抽取两名同学，求这两名同学两轮测试成绩均大于等于90分的概率； （Ⅲ）记抽取的10名学生第一轮测试的平均数和方差分别为1x ，21s ，考核成绩的平均数和方差分别为2x ，22s ，试比较1x 与2x ， 21s 与22s 的大小.（只需写出结论） 16. （本小题共13分）解：（Ⅰ）这10名学生的考核成绩（单位：分）分别为：93，89.5，89，88，90，88.5，91.5，91，90.5，91．其中大于等于90分的有1号、5号、7号、8号、9号、10号，共6人.所以样本中学生考核成绩大于等于90分的频率为：60.610=， 从该校高二年级随机选取一名学生，估计这名学生考核成绩大于等于90分的概率为0.6.………………………………………….4分（Ⅱ）设事件A ：从上述考核成绩大于等于90分的学生中再随机抽取两名同学，这两名同学两轮测试成绩均大于等于90分.由（Ⅰ）知，上述考核成绩大于等于90分的学生共6人，其中两轮测试成绩均大于等于90分的学生有1号，8号，10号，共3人.所以，232631()155C P A C ===. ·················· 9分（Ⅲ）12x x =，2212s s >. ····················· 13分【东城二模】（16）（本小题13分）某银行的工作人员记录了3月1号到3月15日上午10:00在该银行取号后等待办理业务的人数， 如图所示：从这15天中，随机选取一天，随机变量X 表示当天上午10:00在该银行取号后等待办理业务的人数. （Ⅰ）请把X 的分布列补充完整；（Ⅱ）令m 为X 的数学期望，若()0.5,P n Xn m m -＃+>求正整数n 的最小值；（Ⅲ）由图判断，从哪天开始的连续五天上午10:00在该银行取号后等待办理业务的人数的均值最大？（结论不要求证明） （16） （共13分） 解：（I ）X 的分布列分别为………………………4分（Ⅱ）由（I ）可得X 的数学期望1211211()891011121314103155********E X =???????.所以10m =. 因为62(101101)0.5155P X-＃+==<, 5231213(102102)0.5,1515P X++++-＃+==>所以2n =. ………………………10分（Ⅲ）第10日或第11日. ………………………13分【朝阳二模】16.（本小题满分13分）某市旅游管理部门为提升该市26个旅游景点的服务质量,对该市26个旅游景点的交通、安全、环保、卫生、管理五项指标进行评分.每项评分最低分0分,最高分100分.每个景点总分为这五项得分之和,根据考核评分结果,绘制交通得分与安全得分散点图、交通得分与景点总分散点图如下:请根据图中所提供的信息，完成下列问题：（Ⅰ）若从交通得分排名前5名的景点中任取1个,求其安全得分大于90分的概率;（Ⅱ）若从景点总分排名前6名的景点中任取3个,记安全得分不大于90分的景点个数为ξ,求随机变量ξ的分布列和数学期望;（Ⅲ）记该市26个景点的交通平均得分为1x ,安全平均得分为2x ,写出1x 与2x 的大小关系.（只写出结果） 【解析】（Ⅰ）由图可知,交通得分前5名的景点中安全得分大于90分的景点有3个.故从交通得分前5名的景点中任取1个,其安全得分大于90分的概率为35（Ⅱ）由图可知,景点总分前6名的安全得分不大于90分的景点有2个.设从景点总分前6名的景点中任取3个,安全得分不大于90分的个数为ξ,则ξ的取值为0,1,2所以34361(0)5C P C ξ===2142363(1)5C C P C ξ===1242361(2)5C C P C ξ===故ξ的分布列为所以1310121555E ξ=⨯+⨯+⨯=（Ⅲ）12x x >【丰台二模】（16）（本小题共13分）某汽车生产厂家为了解某型号电动汽车的“实际平均续航里程数”，收集了使用该型号电动汽车1年以上的部分客户的相关数据，得到他们的电动汽车的“实际平均续航里程数”．从年龄在40岁以下的客户中抽取10位归为A 组，从年龄在40岁（含40岁）以上的客户中抽取10位归为B 组，将他们的电动汽车的“实际平均续航里程数”整理成下图，其中“+”表示A 组的客户，“⊙”表示B 组的客户．注：“实际平均续航里程数”是指电动汽车的行驶总里程与充电次数的比值．（Ⅰ）记A ，B 两组客户的电动汽车的“实际平均续航里程数”的平均值分别为m ，n ，根据图中数据，试比较m ，n 的大小（结论不要求证明）； （Ⅱ）从A ，B 两组客户中随机抽取2位，求其中至少有一位是A 组的客户的概率；（III ）如果客户的电动汽车的“实际平均续航里程数”不小于350，那么称该客户为“驾驶达人”．从A ，B 两组客户中，各随机抽取1位，记“驾驶达人”的人数为ξ，求随机变量ξ的分布列及其数学期望E ξ． （16）（本小题共13分）解：（Ⅰ）m n <． …………………3分 （Ⅱ）设“从抽取的20位客户中任意抽取2位，至少有一位是A 组的客户”为事件M ，则11210101022029()38C C C P M C +==． …………………6分年龄（岁）70605040302010所以从抽取的20位客户中任意抽取2位至少有一位是A 组的客户的概率是2938． （III ）依题意ξ的可能取值为0，1，2．则119811101018(0)25C C P C C ξ===； 1111189211101013(1)50C C C C P C C ξ+===； 11121110101(2)50C C P C C ξ===． …………………10分 所以随机变量ξ的分布列为：所以随机变量ξ的数学期望01225505010E ξ=⨯+⨯+⨯=． …………………12分 即103=ξE ． 【昌平二模】 16.（本小题13分）为评估大气污染防治效果，调查区域空气质量状况，某调研机构从A ，B 两地区一年的数据中随机抽取了相同20天的观测数据，得到A ，B 两地区的空气质量指数（AQI ）如下图所示：根据空气质量指数，将空气质量状况分为以下三个等级：（Ⅰ）试估计A 地区当年（365天）的空气质量状况“优良”的天数；（Ⅱ）假设两地区空气质量状况相互独立，记事件C ：“A 地区空气质量等级优于B 地区空气质量等级”. 根据所给数据，以事件发生的频率作为相应事件发生的概率，求事件C 的概率.（Ⅲ）若从空气质量角度选择生活地区居住，你建议选择A ，B 两地区哪个地区.（只需写出结论） 16．（共13分）解：（Ⅰ）从A 地区选出的20天中随机选出一天，这一天空气质量状况为“优良”的频率为510.7520-=，估计A 地区当年（365天）的空气质量状况“优良”的频率为0.75，A 地区当年（365天）的空气质量状况“优良”的天数约为3650.75274⨯≈天. -----------4分 （Ⅱ）记1A 表示事件：“A 地区空气质量等级为优良”；2A 表示事件：“A 地区空气质量等级为轻中度污染”； 1B 表示事件：“B 地区空气质量等级为轻中度污染”；2B 表示事件：“B 地区空气质量等级为重度污染”，则1A 与1B 独立，2A 与2B 独立，1B 与2B 互斥，111222C A B A B A B =.所以111222()()P C P A B A B A B =111222()()()P A B P A B P A B =++111222()()()()()()P A P B P A P B P A P B =++.由所给数据得1A ，2A ，1B ，2B 发生的频率分别为34，15，15，320.故13()4P A =，21()5P A =，11()5P B =，23()20P B =， 所以31313()()0.2925.4520520P C =⨯++⨯= --------------------10分（Ⅲ）从空气质量角度，建议选择A 地区居住 . --------------------13分【顺义二模】16．（本小题满分13分）2018年2月25日第23届冬季奥运会在韩国平昌闭幕，中国以1金6银2铜的成绩结束本次冬奥会的征程.某校体育爱好者协会在高三年级某班进行了“本届冬奥会中国队表现”的满意度调查（结果只有“满意”和“不满意”两种），按分层抽样从被调查的学生中随机抽取了11人，具体的调查结果如下表：（Ⅱ）在该班全体学生中随机抽取一名学生，由以上统计数据估计该生持满意态度的概率；（Ⅲ）若从该班调查对象中随机选取2人进行追踪调查，记选中的2人中对“本届冬奥会中国队表现”满意的人数为ξ，求随机变量ξ的分布列及其数学期望．16．（Ⅰ）不妨设女生人数为X ，男生人数为Y ，则可得X-Y=4 （1）又由分层抽样可知，65X Y=（2） 联立（1）（2）可解得X=24，Y=20（Ⅱ）设该生持满意态度为事件A ，则基本事件的总数有11种，事件A 中包含的基本事件有6种，所以()611P A =（Ⅲ）ξ的可能取值有0，1，2=0ξ对应的事件为从该班11名调查对象中抽取2人，2人中恰好有0人持满意态度基本事件的总数为211C =55，其中包含的基本事件数有2510C =种所以()10205511P ξ=== 同理：()116521*********C C P C ξ⋅====，()26211C 1532=C 5511P ξ=== 所以分布列为：所以期望26312E =0+1+2=11111111ξ⨯⨯⨯【房山二模】（16）（本小题13分）1995年联合国教科文组织宣布每年的4月23日为世界读书日，主旨宣言为“希望散居在全球各地的人们，都能享受阅读带来的乐趣，都能尊重和感谢为人类文明作出巨大贡献的文学、文化、科学思想的大师们，都能保护知识产权。

2018 年北京市高考理科数学二模测试题( 数学理)一、选择题：本大题共 12 小题，每题 5 分，满分 60 分。

在每题给出的四个选项中，只有一项为哪一项吻合题目要求的。

1. 已知会集 M ＝｛ x | x ＜ 3｝，N ＝｛ x |log 2x ＞ 1｝，则 M ∩ N ＝A.B.｛ x |0 ＜ x ＜3｝ C. ｛ x |1 ＜ x ＜ 3｝ D.｛ x |2 ＜ x ＜ 3｝2. 不等式11 的解集是x2A ． (, 2) B ． (2, ) C ． (0, 2) D ． ( ,0) (2,)3．设 P 为ABC 所在平面内一点，且5 AP 2 ABAC0 ，则 PAB 的面积与 ABC 的面积之比为A ．1B．2C ．1D．355454 从圆 x 22xy 22y 1 0 外一点P 3,2 向这个圆作两条切线，则两切线夹角的余弦值为A ．1B．3C．3D． 02525. 若曲线 yx 4 的一条切线 l 与直线 x4 y 20080 垂直，则直线 l 的方程为A ． 4x y 3 0B ． x 4y 3 0C. x4 y 2008 0 D ． x 4y 2008 06．已知正整数 a ， b 满足4a b 30 ，使得11 取最小值时，则实数对 ( a, b) 是 ( )a bA ． (5 ， 10)B ．(6 ，6)C ．(10 ， 5)D．(7 ， 2)7． cos20cos103 sin10 tan 702cos 40 =()sin 20A ．1B ．2C ．2D ． 32228．某队伍为了认识战士课外阅读状况，随机检查了 50 名战士，获得他们在某一天各自课外阅读所用时间的数据．结果用右边的条形图表示，依据条形图可得这 50名战士这天均匀每人的课外阅读时间为 ( )A ．B ．C ．D ．9．从数字 1， 2， 3，4， 5 中，随机抽取 3 个数字 ( 同意重复 ) 构成一个三位数，其各位数字之和等于9 的概率为 ( )A ．13B ． 16C ． 18D． 1912512512512510．计算2 4 x 2 dx 的结果是 ( )A ． 4B ． 2C ．D ．211．设斜率为2的直线 l 与椭圆x 2y 2 1，（ a b 0 ）交于不一样的两点，且这两个交点在x 轴上的2a2b 2 ( )射影恰好是椭圆的两个焦点，则该椭圆的离心率为A ．2 B．1C ．3 D ．122 3312．一个圆锥被过极点的平面截去了较小的一部分几何体，余下的几何体的三视图如图，则该圆锥的体积为 ( )A ．4B ． 2C ．8D． 10333二、填空题：本大题共4 小题．每题5 分，满分 20 分。

北京市东城区2018-2019学年度第二学期高三综合练习（二）数学 （理科）本试卷共4页，共150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将答题卡交回。

第一部分（选择题 共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合2{2,1,0,1,2},{20}A B x x x =--=--≤，则AB =R(A){2}- (B) {01}， (C) {2,1,2}-- (D) {1,0,1,2}- （2）执行如图所示的程序框图，输入2,5a b ==，那么输出的,a b 的值分别为（A ）7，3- （B ）3-，3- （C ）5，3- （D ）5， 2（3）已知向量a 与b 不共线，且AB m =+a b (1)m ≠，.AC n =+a b 若,,A B C 三点共线，则实数,m n 满足的条件为 (A)1m n +=(B) 1m n +=-(C) 1mn = (D)1mn =-（4）鲁班锁起源于中国古代建筑中首创的榫卯结构，相传由春 秋时代鲁国工匠鲁班所作. 右图是某个经典的六柱鲁班锁及其六个构件的图片，下图是其中一个构件的三视图（单位：mm ）， 则此构件的体积为（A ）334000mm （B ） 333000mm （C ） 332000mm （D ）330000mm （5）已知n S 是等差数列{}n a 的前n 项和，则“n n S na >对2n ≥恒成立”是“34a a >”的(A) 充分而不必要条件 (B) 必要而不充分条件 (C) 充分必要条件 (D)既不充分也不必要条件（6）教室的图书角摆放了一些阅读书目，其中有3本相同的论语、6本互不相同的近代文学名著，现从这9本书中选出3本，则不同的选法种数为(A) 84 (B) 42 (C) 41 (D)35（7）已知正方体1111ABCD A B C D -的棱长为2，P 是底面ABCD 上的动点，1PA PC ≥，则满足条件的点P 构成的图形的面积等于(A) 12 (B) 4π (C) 44π- (D) 72（8）在交通工程学中，常作如下定义：交通流量Q （辆/小时）：单位时间内通过某一道路横断面的车辆数； 车流速度V （千米/小时）：单位时间内车流平均行驶的距离； 车流密度K （辆/千米）：单位长度道路上某一瞬间所存在的车辆数. 一般的， V 和K 满足一个线性关系：00=(1)KV v k -（其中00,v k 是正数），则以下说法正确的是 (A) 随着车流密度的增大，车流速度在逐渐增大 (B) 随着车流密度的增大，交通流量在逐渐增大 (C) 随着车流速度的增大，交通流量先减小、后增大 (D) 随着车流速度的增大，交通流量先增大、后减小第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

东城区普通高中示范校高三综合练习(二)高三数学（理）2018.3一、选择题：本大题共8小题．每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合2{40}A x x =->，1{2}4x B x =<，则A B = （ ）A ．{}2x x > B. {}2x x <- C. {}22或x x x <-> D. 12x x ⎧⎫<⎨⎬⎩⎭2．已知复数2(1)(2)z a a i =-+-(a R ∈),则“1a =”是“z 为纯虚数”的（ ）A ．充分非必要条件 B. 必要非充分条件 C. 充要条件 D. 非充分非必要条件3．在极坐标系中，过点(3,)3π且垂直于极轴的直线方程（ ）A ．3sin 2=ρθ B. 3cos 2=ρθ C. 3sin 2=ρθ D.3cos 2=ρθ 4．如果执行右面的程序框图，那么输出的t =（ ）A.96B. 120C.144D. 3005．已知2,,z x y x y =+满足2y xx y x m ≥⎧⎪+≤⎨⎪≥⎩，且z 的最大值是最小值的4倍，则m 的值是（ ）A ．14B ．15C ．16D ．176．已知底面为正方形的四棱锥，其一条侧棱垂直于底面，那么该四棱锥的三视图可能是下列各图中的（ ） [ZA ． B. C. D.7．已知数列{}n a 满足*7(13)10,6(),6--+≤⎧=∈⎨>⎩N n n a n a n a n a n ，若{}n a 是递减数列，则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫13，1B.⎝ ⎛⎭⎪⎫13，12C. ⎝ ⎛⎭⎪⎫58，1 D. ⎝ ⎛⎭⎪⎫13，58 8．已知函数2342013()12342013x x x x f x x =+-+-++ 则下列结论正确的是（ ）A ．()f x 在(0,1)上恰有一个零点 B. ()f x 在(0,1)上恰有两个零点C. ()f x 在(1,0)-上恰有一个零点D. ()f x 在(1,0)-上恰有两个零点二.填空题（每题5分,共6小题）9．已知随机变量X 的分布列如下，则EX 的值等于10．若双曲线22221(0,0)x y a b a b-=>>与直线y =无交点，则离心率e 的取值范围是 .11.如图，是圆O 的切线，切点为A ，D 点在圆内，DB 与圆相交于C ，若3BC DC ==，2=OD ，6AB =，则圆O的半径为 .12．在ABC ∆中，D 为BC 中点，若120BAC ∠=︒，1AB AC ⋅=-，则AD的最小值是 .13．有6名同学参加两项课外活动，每位同学必须参加一项活动且不能同时参加两项，每项活动最多安排4人，则不同的安排方法有________种．（用数字作答）14．已知直线:1(R)l y ax a a =+-∈，若存在实数a 使得一条曲线与直线l 有两个不同的交点，且以这两个交点为端点的线段的长度恰好等于a ，则称此曲线为直线l 的“绝对曲线”．下面给出的三条曲线方程：①21y x =--；②22(1)(1)1x y -+-=；③2234x y +=．其中直线l 的“绝对曲线”有＿＿＿＿＿．（填写全部正确选项的序号）三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15.(本小题满分13分) 已知函数,2cos26sin 6sin )(2x x x x f ωπωπω-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+= 其中 R x ∈,0>ω.（1）求函数)(x f 的值域；（2）若函数)(x f 的图象与直线1-=y 的两个相邻交点间的距离为2π，求函数)(x f 的单调增区间.16．(本小题满分13分) 某地区举办了一次数学知识应用竞赛．有近万名学生参加，为了分析竞赛情况，在参赛学生中随机抽取了40名学生的成绩，并根据他们的成绩制作了频率分布直方图（如图所示）． (1) 试估计这40名学生成绩的众数；(2) 试估计这40名学生的成绩在(]84 72,之间的人数；(3) 从参加活动的学生中任取5人，求这5人中恰有2人的成绩在(]09 80, 之间的概率．17. (本小题满分13分) 在四棱锥ABCD P -中，底面ABCD 为矩形，ABCD PD 底面⊥，1=AB ，2=BC ，3=PD ，F G 、分别为CD AP 、的中点．（1）求证：PC AD ⊥； （2）求证：//FG 平面BCP ；（3）线段AD 上是否存在一点R ，使得平面⊥BPR 平面PCB ，若存在，求出AR的长；若不存在，请说明理由．18. (本小题满分13分) 设ax x x x f 22131)(23++-=（1）若)(x f 在),32(+∞上存在单调递增区间，求a 的取值范围； （2）当20<<a 时，)(x f 在]4,1[上的最小值为316-，求)(x f 在该区 间上的最大值.19．(本小题满分14分) 已知平面内一动点P到点)1,0(F的距离与点P到x轴的距离的差等于1．（1）求动点P的轨迹C的方程；（2）过点F作两条斜率存在且互相垂直的直线,l l，设1l与轨迹C相交于点12,A B，2l与轨迹C相交于点,D E，求 的最小值．20．(本小题满分14分) 已知数集{}),(,,,302121≥<<<≤=n a a a a a a A n n 具有性质P ：对)(,n j i j i ≤≤≤∀1 ，i j a a +与i j a a -两数中至少有一个属于A ． (1) 分别判断数集{}310,,与数集{}6420,,,是否具有性质P ，说明理由； (2) 求证：n n a na a a 221=+++ ；(3) 已知数集{}821a a a A ,,, =具有性质P ．证明：数列821a a a ,,, 是等差数列．东城区普通高中示范校高三综合练习(二)高三数学（理）参考答案2018.3一、选择题(本大题共8小题，每小题5分，共40分)二、填空题(本大题共6小题，每小题5分，共30分)三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15.已知函数2cos26sin 6sin )(2x x x x f ωπωπω-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+=其中 R x ∈,0>ω. （1）求函数)(x f 的值域；（2）若函数)(x f 的图象与直线1-=y 的两个相邻交点间的距离为2π，求函数)(x f 的单调增区间.解：（1）)cos 1(21cos 23sin 21cos 23sin )(x x x x x x f ωωωωω+-⋅-⋅+⋅+⋅= =1)6sin(21cos sin 3--=--πωωωx x x …………………………………5分所以函数)(x f 的值域为[]1,3- …………………………………………………7分（2）由2221πωπ=⋅得2=ω …………………………………………………9分所以1)62sin(2)(--=πx x f由πππππk x k 226222+≤-≤+-………………………………………11分得ππππk x k +≤≤+-36所以函数)(x f 的单调增区间为⎥⎦⎤⎢⎣⎡++-ππππk k 3,6)(Z k ∈. ………13分16．某地区举办了一次数学知识应用竞赛．有近万名学生参加，为了分析竞赛情况，在参赛学生中随机抽取了40名学生的成绩，并根据他们的成绩制作了频率分布直方图（如图所示）． (1) 试估计这40名学生成绩的众数；(2) 试估计这40名学生的成绩在(]8472,之间的人数；(3) 从参加活动的学生中任取5人，求这5人中恰有2人的成绩在(]0980,之间的概率．解：(1) 77.5；………………………………………3分(2) 所求为：直线72⨯，=x之间的直方图的面积40x与直线84=因此，6(=..⨯.+⨯ (7)+⨯)⨯0403.194400450355分答：这40名学生的成绩在(]8472,之间的有20人．（答19人也算对）……………8分(3) 设这5人中恰有2人的成绩在(]0980,之间为事件A，因为3.05)02.004.0(=⨯+ ……………………………………10分所以308701071033225.)(=⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛=C A P ……………………………………12分答：这5人中恰有2人的成绩在(]09 80,之间的概率为0．3087． ………13分17. 在四棱锥ABCD P -中，底面ABCD 为矩形，ABCD PD 底面⊥，1=AB ，2=BC ，3=PD ，FG 、分别为CD AP 、的中点．（1）求证：PC AD ⊥； （2）求证：//FG 平面BCP ；（3）线段AD 上是否存在一点R ，使得平面⊥BPR 平面PCB ， 若存在，求出AR 的长；若不存在，请说明理由．（1）证明： 底面ABCD 为矩形 CD AD ⊥∴ ABCD AD ABCD PD 平面底面⊂⊥ ,PD AD ⊥∴D PD CD = PDC AD 平面⊥∴ABCDPC 平面⊂PC AD ⊥∴ …………………………………4分（2）证明：取H BP 中点，连接CH GH , 中点分别为DC AP F G ,,GH ∴=//AB 21,FC =//AB 21 GH ∴=//FC GFCH 四边形∴是平行四边形，FG ∴//CH ，BCP CH 平面⊂，BCP FG 平面⊄FG∴//BCP 平面 ……………………………………8分(3) ABCD PD 平面⊥ ，以D 为坐标原点，以DP DC DA ,,所在的直线分别为x轴、y 轴、z 轴建立空间直角坐标系，假设在线段AD 上存在一点R ，使得平面⊥BPR 平面PCB ， 设),,(00m R ，)3,0,0(),0,1,2(),0,1,0(P B C )0,0,2(= )3,1,2(-= )0,1,2(m RB -= )3,0,(m RP -= 设平面BCP 的法向量为),,(1111z y x n =⎪⎩⎪⎨⎧=⋅=⋅011n n ， ⎩⎨⎧=-+=032021111z y x x ， 令 31=y ),,(1301=n设平面BPR 的法向量为),,(2222z y x n =⎪⎩⎪⎨⎧=⋅=⋅0022n n RB ⎩⎨⎧=+-=+-030)2(2222z m x y x m 令12=x ),,(3212m m n -= 021=⋅n n 0323=+-∴m m )( ，解得 23=m ∴线段AD 上存在点R ，且当21=AR 时，使得平面⊥BPR 平面PCB . ……………13分18.设ax x x x f 22131)(23++-=（1）若)(x f 在),32(+∞上存在单调递增区间，求a 的取值范围； （2）当20<<a 时，)(x f 在]4,1[上的最小值为316-，求)(x f 在该区间上的最大值.解答 （1）a x a x x x f 241)21(2)(22'++--=++-= ……………………………2分)(x f 在),(+∞32上存在单调递增区间∴存在),32(+∞的子区间),(n m ，使得),(n m x ∈时0>)('x f)('x f 在),(+∞32上单调递减032>∴)('f ，即0292)32('>+=a f 解得91->a∴当91->a 时，)(x f 在),(+∞32上存在单调递增区间 ………………………………6分（2）令0=)('x f 20<<a∴28111a x +-=；28112ax ++= ∴)(x f 在),(),,(+∞-∞21x x 上单调递减，在),(21x x 上单调递增20<<a 4121<<<∴x x∴)(x f 在),(21x 上单调递增，在),(42x 上单调递减 …………………………………8分 所以)(x f 的最大值为)(2x f0622714<+-=-a f f )()( ，31634084-=-=∴a f )( ………………………10分解得212==x a , 310)2()()(2==∴f x f x f 的最大值为 ……………………13分19．已知平面内一动点P 到点)1,0(F 的距离与点P 到x 轴的距离的差等于1． （I ）求动点P 的轨迹C 的方程；（II ）过点F 作两条斜率存在且互相垂直的直线12,l l ，设1l 与轨迹C 相交于点,A B ，2l 与轨迹C 相交于点,D E ，求AD EB ∙的最小值．解析：（1）设动点P 的坐标为(,)x y ，由题意得1)1(22=--+y y x ……………2分化简得y y x 222+=当0≥y 时y x 42=；当0<y 时0=x 所以动点P 的轨迹C 的方程为y x 42=和0=x （0<y ） ………………………5分（2）由题意知，直线1l 的斜率存在且不为0，设为k ，则1l 的方程为 1+=kx y ． 由 044x 4122=-⎩⎨⎧-=+=kx y x kx y 得 设1122(,),(,),A x y B x y 则4,42121-==+x x k x x ，1,2421221=+=+y y k y y (7)分因为12l l ⊥，所以2l 的斜率为1k-．设),(),,(4433y x E y x D ，则同理可得4,44343-=-=+x x k x x ，1,2443243=+=+y y ky y (8)分)1)(1()1)(1()()(2143+++++=+=⋅+⋅=⋅+⋅+⋅+⋅=+⋅+=∙y y y y FB FD FB AF EF FD EF AF1)(1)(21214343+++++++=y y y y y y y y …………………………………11分16248)1(484482222=⨯+≥++=++=k k k k ……………………………13分当且仅当221k k=即1k =±时，AD EB ∙ 取最小值16． …………………………14分20．已知数集{}),(,,,302121≥<<<≤=n a a a a a a A n n 具有性质P ：对)(,n j i j i ≤≤≤∀1 ，i j a a +与i j a a -两数中至少有一个属于A ．(1) 分别判断数集{}310,,与数集{}6420,,,是否具有性质P ，说明理由； (2) 求证：n n a na a a 221=+++ ；(3) 已知数集{}821a a a A ,,, =具有性质P ．证明：数列821a a a ,,, 是等差数列． 解： (1)由于13-和13+都不属于集合{}310,,，所以该集合不具有性质P ；由于02+、04+、06+、24+、26-、46-、00-、22-、44-、66-都属于集合{}6420,,,，所以该数集具有性质P ． …………………………………………4分(2){}n a a a A ,,, 21=具有性质P ，所以n n a a +与n n a a -中至少有一个属于A由n a a a <<<≤ 210，有n n n a a a >+，故A a a n n ∉+A a a n n ∈-=∴0，故01=a n a a a a <<<<= 3210n k n a a a >+∴，故),,,(n k A a a k n 32=∉+由A 具有性质P 知，),,,(n k A a a k n 32=∈-又121a a a a a a a a n n n n n n -<-<<-<-- ，1a a a n n =-∴，21a a a n n =--，…，12-=-n n a a a ，n n a a a =-1从而n n n n n n n a a a a a a a a a a a +++=-+-++-+-- 21121)()()()(故n n na a a a =+++)( 212n n a n a a a 221=+++∴ ……………………8分 (3)由(2)可知，),,,(n i a a a n i n i 211==+-+),,,(82189 ==+∴-i a a a i i …………………………① 由872a a a =+知，73a a +，74a a +，…，，77a a +均不属于A 由A 具有性质P ，37a a -，47a a -，…，，77-a a 均属于A 3837476777a a a a a a a a a a -<-<-<<-<-∴ 638a a a =-∴077=-∴a a ，267a a a =-，357a a a =-，…，537a a a =- 即),,,(72178 ==+-i a a a i i …………………………② 由①②可知),,,)((82117898 =--=-=--i a a a a a a i i i ),,,(821178 =-=-∴-i a a a a i i 故821a a a ,,, 构成等差数列． …………………………………13分。

北京市东城区2017-2018学年度第二学期高三综合练习（一）数学（理科） 2018. 4本试卷共4页，共150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

(1)若集合{}31A x x =-,{}12B x x x =-或，则A B =(A) {}32x x - (B) {}31x x --(C) {}11x x - (D) {}11x x -(2）复数1i z i=-在复平面上对应的点位于 (A)第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限(3)已知,a b R ∈，且a b ，则下列不等式一定成立的是(A) 220a b - (B) cos cos 0a b -(C) 110a b - (D) 0a be e ---(4)在平面直角坐标系xOy中，角θ以Ox 为始边，终边与单位圆交于点（35，45），则tan()θπ+的值为(A)43(B)34(C)43-(D) 34-(5)设抛物线24y x=上一点P到y轴的距离是2，则P到该抛物线焦点的距离是(A)1 (B) 2 (C)3 (D)4(6)故宫博物院五一期间同时举办“戏曲文化展”、“明代御窖瓷器展”、“历代青绿山水画展”、“赵孟頫书画展”四个展览．某同学决定在五一当天的上、下午各参观其中的一个，且至少参观一个画展，则不同的参观方案共有(A)6种（B) 8种（C) 10种（D) 12种(7)设{}na是公差为d的等差数列，n S为其前n项和，则“d>0”是“{}nS为递增数列”的(A）充分而不必要条件（B)必要而不充分条件(C）充分必要条件（D）既不充分也不必要条件(8)某次数学测试共有4道题目，若某考生答对的题大于全部题的一半，则称他为“学习能手”，对于某个题目，如果答对该题的“学习能手”不到全部“学习能手”的一半，则称该题为“难题”．已知这次测试共有5个“学习能手”，则“难题”的个数最多为(A)4 (B) 3 (C)2 (D)1第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分。

2018北京市东城区高三综合练习{二}数学（理）本试卷共 4 页，共 150 分。

考试时长 120 分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分{选择题共 40 分)一、选择题共 8小题，每小题5分，共 40 分。

在每小题列出的四个选项中，选出符合题目要求的-项。

(1)若集合 A= {xl-1<x<2} ，B= {xlx<-2 或 x>l} ，则 AUB=A.{xlx<一2 或 x>l}B.{xlx<-2 或 x> 一 1}C.{xl-2<x<2}D.{xI1<x<2}(2)复数(1 +i)(2一i)=A.3+iB.1+iC.3-ID.1-i（3）在（x+）5的展开式&x3中的系数10,则实数 a 等于A.-1B.C.1D.2（4）已知双曲线 C: -=1 的一条渐近线的倾斜角为60°，且与椭圆+y²=1有相等的焦距，则 C 的方程为（A）- y²（B）-=1（C）x²-=1（D）-=1(5)设 a ，b 是非零向量，则是"a//b"的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D. 既不充分也不必要条件(6)某公司为了解用户对其产品的满意度，从甲、乙两地区分别随机调查了 100 个用户，根据用户对产品的满意度评分，分别得到甲地区和乙地区用户满意度评分的频率分布直方图.若甲地区和乙地区用户满意度评分的中位数分别为叫m1，m2 ;标准差分别为 S1 ,S2则下面正确的是则下面正确的是(A)m1>m2，S1>S2(C)m1<m2，S1<S2(B)m1>m2，S1<S2(D)m1 <m2，S1 >S2(7) 己知函数 f(x) =log2 x ，g(x) =2x+α，若存在x1,x2∈，使得f(x1) = g(X2) ，则 a的取值范围是A.B.（-∞，-50+∞）C.(- 5，0)D.（-∞，-5）（0，+∞）(8)A，B，C，D 四名工人一天中生产零件的情况如图所示，每个点的横、纵坐标分别表示该工人一天中生产的Ⅰ型、Ⅱ型零件数，则下列说法错误的是A.四个工人中，D 的日生产零件总数最大B.A，B 日生产零件总数之和小于 C ，D 日生产零件总数之和C.A，B 日生产Ⅰ型零件总数之和小于Ⅱ型零件总数之和(D)A，B，C，D 日生产Ⅰ型零件总数之和小于Ⅱ型零件总数之和第二部分(非选择题共 110 分)二、填空题共 6小题，每小题 5 分，共 30 分。

北京市东城区2018-2018学年度第二学期综合练习（一）高三数学 （理科）学校_____________班级_______________姓名______________考号___________本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷（选择题 共40分）一、本大题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知全集{1,2,3,4}U =，集合{1,2}A =，那么集合U A ð为（A ）{3} （B ） {3,4} （C ）{1,2} （D ）{2,3} （2）已知ABCD 为平行四边形，若向量AB =a ，AC =b ，则向量BC 为（A ）-a b （B ）a +b （C ）-b a （D ）--a b（3）已知圆的方程为22(1)(2)4x y -+-=，那么该圆圆心到直线3,1x t y t =+⎧⎨=+⎩（t 为参数）的距离为（A ）2（B ）2（C ）2 （D ）2（4）某游戏规则如下：随机地往半径为1的圆内投掷飞标，若飞标到圆心的距离大于12，则成绩为及格；若飞标到圆心的距离小于14，则成绩为优秀；若飞标到圆心的距离大于14且小于12，则成绩为良好，那么在所有投掷到圆内的飞标中得到成绩为良好的概率为 （A ）316 （B ）14 （C ）34 （D ）116（5）已知数列{}n a 中，12a =，120n n a a +-=，2log n n b a =，那么数列{}n b 的前10项和等于（A ）130 （B ）120 （C ）55 （D ）50（6）已知1(,0)F c -，2(,0)F c 分别是双曲线1C ：22221x y a b-=(0,0)a b >>的两个焦点，双曲线1C 和圆2C ：222x y c +=的一个交点为P ，且12212PF F PF F ∠=∠，那么双曲线1C 的离心率为 （A（B（C ）2 （D1（7）已知定义在R 上的函数()f x 的对称轴为3x =-，且当3x ≥-时，()23x f x =-.若函数()f x 在区间(1,)k k -（k ∈Z ）上有零点，则k 的值为（A ）2或7- （B ）2或8- （C ）1或7- （D ）1或8-（8）已知向量OA ，AB ，O 是坐标原点，若AB k OA =，且AB 方向是沿OA 的方向绕着A 点按逆时针方向旋转θ角得到的，则称OA 经过一次(,)k θ变换得到AB .现有向量=(1,1)OA 经过一次11(,)k θ变换后得到1AA ，1AA 经过一次22(,)k θ变换后得到12A A ，…，如此下去，21n n A A --经过一次(,)n n k θ变换后得到1n n A A -.设1(,)n n A A x y -=，112n n θ-=，1cos nnk θ=，则y x -等于 （A ）1112sin[2()]211sin1sin sin 22n n --- （B ）1112sin[2()]211cos1cos cos 22n n ---（C ）1112cos[2()]211sin1sin sin 22n n --- （D ）1112cos[2()]211cos1cos cos 22n n ---第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分。