06_平面机构自由度计算

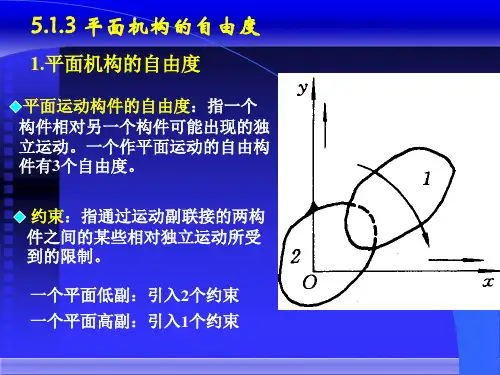
平面机构自由度名词解释引言在机械领域中，机构是由零件连接而成的一个特定结构，用于完成特定的运动或力学转换任务。

其中，平面机构是一种常见的机构类型，用于在平面内进行运动。

在设计和分析平面机构时，我们需要了解和考虑机构的自由度。

什么是自由度？自由度是指机构中能够独立变化的运动参数的数量。

简单来说，自由度是机构中可以自由变动的独立运动方式的个数。

在平面机构中，自由度可以进一步分为以下两个概念：1. 杆件的自由度杆件的自由度指的是杆件可以相对于其他杆件进行的独立旋转或平动的运动方式的数量。

根据杆件的运动方式，可以将杆件的自由度分为以下几种情况：•固定点：杆件不发生变化，没有自由度；•固定线：杆件沿着一条直线运动，有一个自由度；•固定面：杆件平行于一个平面，有两个自由度；•固定曲面：杆件沿着一个曲面运动，有三个自由度。

2. 机构的自由度机构的自由度是指机构整体进行运动时能够独立变化的运动参数的数量。

要计算机构的自由度，可以使用如下公式：自由度 = 3n - m其中，n为机构中的杆件数量，m为机构中的支撑约束数量。

支撑约束是指限制机构中某些杆件完全运动的约束条件，比如固定连接或者支座支撑。

平面机构的自由度计算平面机构是指所有的零件都位于同一平面内的机构。

在计算平面机构的自由度时，可以按照以下步骤进行：步骤1：确定杆件数量首先，我们需要确定平面机构中的杆件数量。

杆件是平面机构中传递力和实现运动的关键组成部分。

步骤2：确定支撑约束数量接下来，我们需要确定平面机构中的支撑约束数量。

支撑约束可以是固定连接或者支座支撑。

步骤3：计算自由度根据上述提到的公式，我们可以计算平面机构的自由度。

将杆件数量和支撑约束数量代入公式中，即可得到平面机构的自由度。

平面机构的应用自由度在平面机构的设计和分析中起着重要的作用。

了解平面机构的自由度可以帮助工程师理解机构的运动特性，从而更好地设计和优化机构。

平面机构广泛应用于各个领域，例如机械工程、汽车工程、航空航天工程等。

平面机构自由度计算例题及答案在机械设计和分析中，自由度是一个重要的概念，它用来描述机构的运动能力和约束程度。

特别是对于平面机构而言，自由度计算是机构设计和分析的基础。

本文将以一个例题为例，详细介绍平面机构自由度计算的方法，并给出答案。

例题描述：给定一个平面机构，该机构由三个连杆和两个旋转副组成，其中两个连杆用来传递运动，第三个连杆则作为链接杆。

假设该机构中的两个旋转副都分别由一对垂直的直线轴构成。

求该平面机构的自由度。

解题思路：为了计算平面机构的自由度，首先需要明确平面机构的自由度计算公式。

根据机构自由度的定义，平面机构的自由度等于其约束数目减去自由度减去已知条件数目。

对于本例中的平面机构，约束数目为2，已知条件数目为1，因此我们只需要计算平面机构的自由度即可。

解题步骤：1. 确定机构中的运动副：根据题目描述，该机构中的运动副是两个旋转副。

2. 统计机构中的连杆数目：根据题目描述，该机构中共有三个连杆。

3. 计算机构中的运动副数目：根据运动副的定义，旋转副的数目等于直线轴的数目减一。

因此，该机构中的旋转副数目为2。

4. 计算平面机构的自由度：根据平面机构的自由度计算公式，自由度等于连杆数目减去运动副数目。

因此，该机构的自由度为3-2=1。

5. 减去已知条件数目：根据已知条件的定义，已知条件是指在机构中已经确定的尺寸或位置关系。

根据题目描述，已知条件数目为1。

6. 最终计算结果：根据平面机构自由度的定义，平面机构的自由度等于约束数目减去自由度减去已知条件数目。

因此，该平面机构的自由度为2-1=1。

答案解析：根据计算结果，该平面机构的自由度为1。

这意味着该机构具有一个独立自由度，即只能在一个平面内进行单一的自由运动。

根据机构设计和分析的需要，可以对该机构进行进一步优化和改进，以满足特定的运动要求。

总结：通过上述例题的计算，我们了解了平面机构自由度的计算方法。

平面机构自由度的计算是机构设计和分析的基础，对于确定机构的运动能力和约束程度非常重要。

平面机构（运动链）自由度计算辅导运动链是指若干个构件通过运动副连接而成的系统。

运动链自由度计算主要解决的问题是：1、运动链的可动性；2、运动链运动的确定性，即运动链成为机构的条件。

一、平面机构（运动链）自由度：㈠、计算公式：F=3n-2P L-P H⑴式中：F—机构（运动链）自由度；n—机构（运动链）中的运动构件数；P L—机构（运动链）中低副数，包括移动副和转动副； P H—机构（运动链）中的高副数。

㈡、公式用途：运动链类型：⑴、固定运动链：组成运动链的构件之间没有相对运动。

如桥梁、钢结构支架等。

⑵、可动运动链：①、运动不确定的可动运动链：运动链可动，但运动链中构件的运动不能确定。

②、具有确定运动的运动链及机构。

运动链中构件的具有确定性。

1、判别运动链能否运动（运动链可动性分析）：⑴、当F﹥0 运动链能运动，即运动链是可动的。

⑵、当F≦0 运动链不动，即运动链为固定运动链。

例：判别下面运动链的可动性：图示：n=3，P L=4，P H=1 。

F=3n-2P L-P H =3×3-2×4-1=0运动链不可动。

图示：n=4，P L=5，P H=1 。

F=3n-2P L-P H =3×4-2×5-1=1﹥0运动链可动。

2、判别运动链是否成为机构：运动链的运动确定性分析。

⑴、当F≦0 运动链不可动，此种运动链不能成为机构；⑵、当F﹥0 运动链可动：①、若F﹥原动件数，运动链不能成为机构；②、若F=原动件数，运动链运动确定，运动链成为机构；③、若F﹤原动件数，运动链不能成为机构。

结论：运动链成为机构的条件:F﹥0,且F等于机构原动件数。

㈢、机构自由度计算时应注意的问题：1、复合铰链及其处理方法：⑴、概念：复合铰链:多个构件（含固定件）在同一处形成两个或两个以上转动副,该处成为复合铰链。

⑵、处理方法：P L=m-1,m为该处构件数（含固定件）。

⑶、常见形式：①、②、③、④、例：计算下面运动链自由度，说明要使运动链成为机构需要几个原动件。

平面机构自由度计算例题及答案在机械原理中，平面机构自由度的计算是一个重要的知识点。

通过计算机构的自由度，可以判断机构的运动可能性和确定性，为机构的设计和分析提供重要依据。

下面我们通过几个例题来详细讲解平面机构自由度的计算方法。

例题 1：如图所示的平面机构，由 4 个杆件组成，其中杆件 1 为机架，杆件2 和杆件 3 通过转动副连接，杆件 3 和杆件 4 通过移动副连接。

试计算该机构的自由度。

分析：首先，我们需要确定机构中的运动副类型和数量。

在这个机构中，有 2 个转动副（分别在杆件 2 和杆件 3 的连接处，以及杆件 1 和杆件 2 的连接处）和 1 个移动副（在杆件 3 和杆件 4 的连接处）。

接下来，我们根据自由度的计算公式 F ＝ 3n 2PL PH 进行计算。

其中，n 为活动构件的数目，PL 为低副的数目，PH 为高副的数目。

在这个机构中，活动构件的数目 n ＝ 3（杆件 2、3、4），低副的数目 PL ＝ 3（2 个转动副和 1 个移动副），高副的数目 PH ＝ 0。

将这些值代入公式，得到：F ＝ 3×3 2×3 0 ＝ 9 6 ＝ 3所以，该机构的自由度为 3。

例题 2：考虑一个平面机构，由 5 个杆件组成，杆件 1 固定不动，杆件 2 与杆件 1 通过转动副连接，杆件 2 与杆件 3 通过移动副连接，杆件 3 与杆件 4 通过转动副连接，杆件 4 与杆件 5 通过移动副连接。

计算该机构的自由度。

分析：首先明确运动副类型及数量。

此机构有 3 个转动副（分别在杆件 1 和杆件 2、杆件 3 和杆件 4 、杆件 4 和杆件 5 的连接处），2 个移动副（分别在杆件 2 和杆件 3、杆件 4 和杆件 5 的连接处）。

然后计算活动构件数目 n ＝ 4（杆件 2、3、4、5），低副数目 PL ＝ 5（3 个转动副和 2 个移动副），高副数目 PH ＝ 0。

将数值代入自由度计算公式：F ＝ 3×4 2×5 0 ＝ 12 10 ＝ 2所以该机构的自由度为 2。

平面机构自由度计算例题及答案在机械原理的学习中，平面机构自由度的计算是一个非常重要的知识点。

它能够帮助我们判断机构是否具有确定的运动，以及机构的运动是否受到合理的约束。

下面，我们通过几个具体的例题来深入理解平面机构自由度的计算方法。

例题 1如下图所示的平面机构，其中构件 1 为机架，构件 2 与构件 1 以转动副连接，构件 3 与构件 2 以移动副连接，构件 4 与构件 3 以转动副连接，构件 5 与构件 4 以转动副连接。

试计算该机构的自由度。

！平面机构示例 1(解题思路首先，我们需要确定活动构件的数量。

在这个机构中，活动构件有构件 2、3、4、5，共 4 个。

然后，计算低副的数量。

转动副有 4 个（构件 2 与构件 1 之间、构件 4 与构件 3 之间、构件 5 与构件 4 之间），移动副有 1 个（构件 3与构件 2 之间），所以低副总数为 5 个。

接下来，计算高副的数量。

在这个机构中没有高副。

最后，根据自由度的计算公式：F ＝ 3n 2PL PH （其中 F 为自由度，n 为活动构件数，PL 为低副数，PH 为高副数），代入数值计算。

n ＝ 4，PL ＝ 5，PH ＝ 0F ＝ 3×4 2×5 0＝ 12 10 0＝ 2答案该平面机构的自由度为 2。

例题 2如下图所示的平面机构，构件 1 为机架，构件 2 与构件 1 以转动副连接，构件 3 与构件 2 以转动副连接，构件 4 与构件 3 以转动副连接，同时构件 4 与构件 1 以移动副连接。

计算该机构的自由度。

！平面机构示例 2(解题思路活动构件有构件 2、3、4，共 3 个。

低副方面，转动副有 3 个（构件 2 与构件 1 之间、构件 3 与构件 2之间、构件 4 与构件 3 之间），移动副有 1 个（构件 4 与构件 1 之间），低副总数为 4 个。

高副数量为 0。

n ＝ 3，PL ＝ 4，PH ＝ 0F ＝ 3×3 2×4 0＝ 9 8 0＝ 1答案该平面机构的自由度为 1。

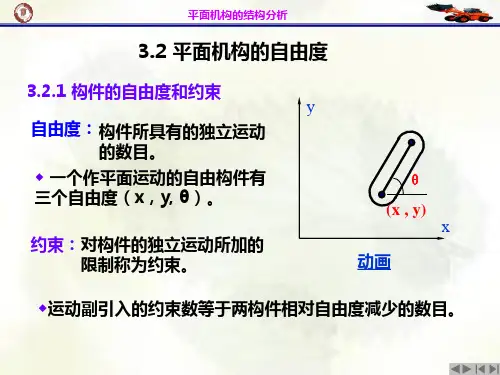
平面机构自由度的计算1、单个自由构件的自由度为 3如所示，作平面运动的刚体在空间的位置需要三个独立的参数（x ，y, θ）才能唯一确定。

2、构成运动副构件的自由度图2—19运动副自由度运动副 自由度数 约束数回转副 1（θ） + 2（x ，y ） =3 移动副 1（x ） + 2（y ，θ） =3 高 副 2（x,θ） + 1（y ） =3结论：构件自由度＝3－约束数3、平面机构的自由度1）机构的自由度：机构中活动构件相对于机架所具有的独立运动的数目。

2）.机构自由度计算公式 H P -=L 2P -3n F式中： n-------活动构件数目（不包含机架） L P -----低副数目（回转副、移动副） H P ------高副数目（点或线接触的）运动副低副(面接触)移动副高副(点或线接触)约束数为2约束数为1例题1： 计算曲柄滑块机构的自由度。

解：活动构件数n=3低副数 PL=4 高副数 PH=0H P -=L 2P -3n F 图 曲柄滑块机构=3×3 － 2×4 =1例题2：计算五杆铰链机构的自由度。

解：活动构件数n=4低副数 PL=5 高副数 PH=0H P -=L 2P -3n F 图 五杆铰链机构=3×4 － 2×4 =2例题3： 计算凸轮机构的自由度 解：活动构件数n=2低副数 PL=2 高副数 PH=1H P -=L 2P -3n F=3×2 －2×2－1=1 图 凸轮机构4．机构具有确定运动的条件原动件的数目＝机构的自由度数F （F ＞0或F≥1）。

若 原动件数＜自由度数，机构无确定运动； 原动件数＞自由度数，机构在薄弱处损坏。

(a)两个自由度(b)一个自由度(c)0个自由度图3-11 不同自由度机构的运动5．计算机构自由度时应注意的事项1）复合铰链：两个以上个构件在同一条轴线上形成的转动副。

由m个构件组成的复合铰链，共有(m-1)个转动副。

平面机构（运动链）自由度计算辅导运动链是指假设干个构件通过运动副连接而成的系统。

运动链自由度计算要紧解决的问题是：一、运动链的可动性；二、运动链运动的确信性，即运动链成为机构的条件。

一、平面机构（运动链）自由度：㈠、计算公式：F=3n-2P L-P H⑴式中：F—机构（运动链）自由度；n—机构（运动链）中的运动构件数；P L—机构（运动链）中低副数，包括移动副和转动副；P H—机构（运动链）中的高副数。

㈡、公式用途：运动链类型：⑴、固定运动链：组成运动链的构件之间没有相对运动。

如桥梁、钢结构支架等。

⑵、可动运动链：①、运动不确信的可动运动链：运动链可动，但运动链中构件的运动不能确信。

②、具有确信运动的运动链及机构。

运动链中构件的具有确信性。

一、判别运动链可否运动（运动链可动性分析）：⑴、当F﹥0 运动链能运动，即运动链是可动的。

⑵、当F≦0 运动链不动，即运动链为固定运动链。

例：判别下面运动链的可动性：图示：n=3，P L=4，P H=1 。

F=3n-2P L-P H =3×3-2×4-1=0运动链不可动。

图示：n=4，P L=5，P H=1 。

F=3n-2P L-P H =3×4-2×5-1=1﹥0运动链可动。

二、判别运动链是不是成为机构：运动链的运动确信性分析。

⑴、当F≦0 运动链不可动，此种运动链不能成为机构；⑵、当F﹥0 运动链可动：①、假设F﹥原动件数，运动链不能成为机构；②、假设F=原动件数，运动链运动确信，运动链成为机构；③、假设F﹤原动件数，运动链不能成为机构。

结论：运动链成为机构的条件:F﹥0,且F等于机构原动件数。

㈢、机构自由度计算时应注意的问题：一、复合铰链及其处置方式：⑴、概念：复合铰链:多个构件（含固定件）在同一处形成两个或两个以上转动副,该处成为复合铰链。

⑵、处置方式：P L=m-1,m为该处构件数（含固定件）。

⑶、常见形式：①、②、③、④、例：计算下面运动链自由度，说明要使运动链成为机构需要几个原动件。