八字翼墙体积公式
- 格式:docx
- 大小:71.02 KB
- 文档页数:3

【精品工程造价知识】八字墙翼墙(墙身)砼用量精确通用计算公式推导注:因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式
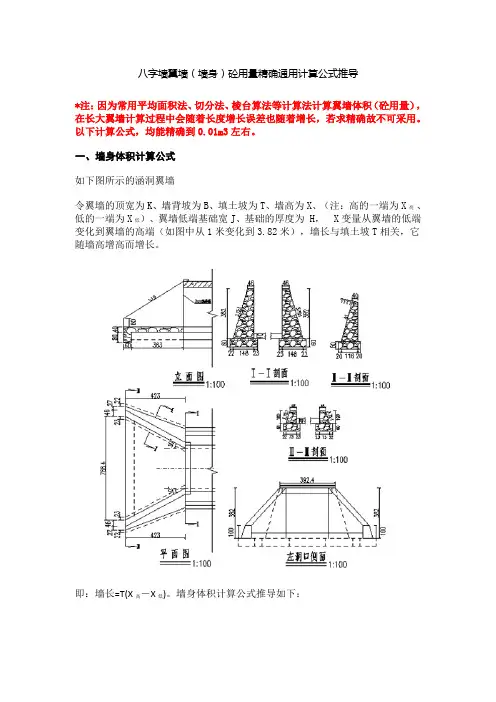
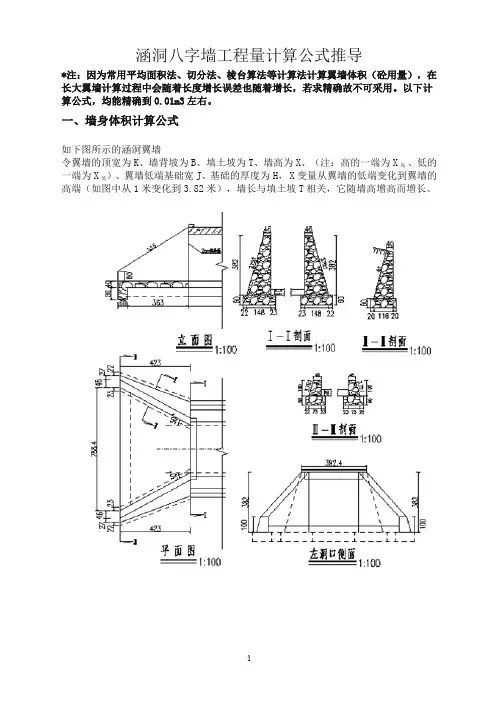
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X高、低的一端为X低)、翼墙低端基础宽J、基础的厚度为 H, X变量从翼墙的低端变化到翼墙的高端(如图中从1米变化到3.82米),墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X高-X低)。
墙身体积计算公式推导如下:
将(2)式脱出积分公式整理得
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X低=1、X高=3.82
三、基础体积计算公式
将 (4)式脱出积分公式整理得
四、基础体积计算例
上图中 T=1.5、J=1.18、H=0.6 、X=3.82-1=2.82
结语:借用拿破仑的一句名言:播下一个行动,你将收获一种习惯;播下一种习惯,你将收获一种性格;播下一种性格,你将收获一种命运。
事实表明,习惯左右了成败,习惯改变人的一生。
在现实生活中,大多数的人,对学习很难做到学而不厌,学习不是一朝一夕的事,需要坚持。
希望大家坚持到底,现在需要沉淀下来,相信将来会有更多更大的发展前景。

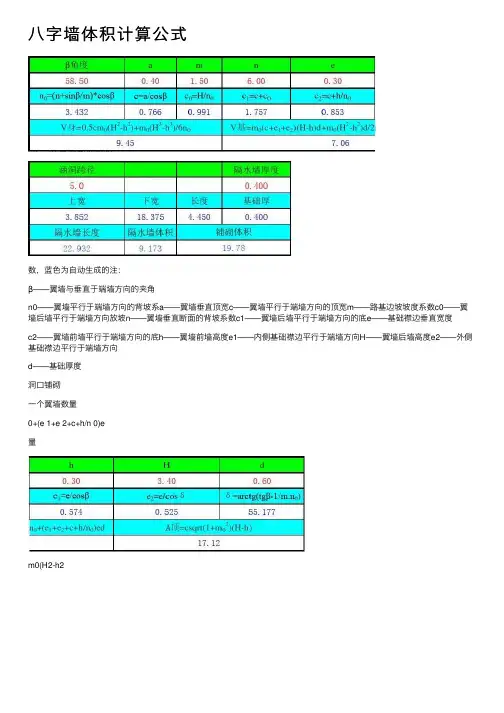
八字墙翼墙(墙身)砼用量精确通用计算公式推导
因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X高、低的一端为X低)、翼墙低端基础宽J、基础的厚度为 H,X 变量从翼墙的低端变化到翼墙的高端(如图中从1米变化到3.82米),
墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X高-X低)。
墙身体积计算公式推导如下:
将(2)式脱出积分公式整理得
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X低=1、X高=3.82
三、基础体积计算公式
将(4)式脱出积分公式整理得
四、基础体积计算例
上图中 T=1.5、J=1.18、H=0.6 、X=3.82-1=2.82。

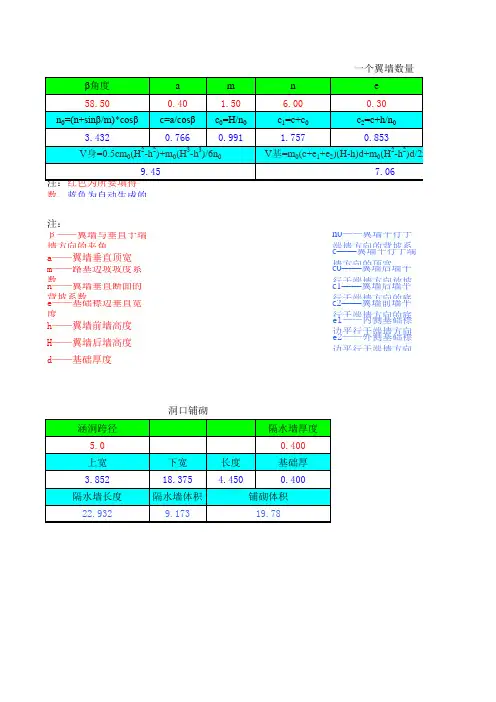
涵洞八字墙工程量计算
因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X高、低的一端为X低)、翼墙低端基础宽J、基础的厚度为H,X变量从翼墙的低端变化到翼墙的高端(如图中从1米变化到3.82米),墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X高-X低)。
墙身体积计算公式推导如下:将(2)式脱出积分公式整理得
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X低=1、X高=3.82
三、基础体积计算公式
将(4)式脱出积分公式整理得
四、基础体积计算例
上图中T=1.5、J=1.18、H=0.6、X=3.82-1=2.82。
八字墙翼墙(墙身)砼用量精确通用计算公式推导
*注:因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X
高
、
低的一端为X
低
)、翼墙低端基础宽J、基础的厚度为 H,X变量从翼墙的低端变化到翼墙的高端(如图中从1米变化到3.82米),墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X
高-X
低
)。
墙身体积计算公式推导如下:
将(2)式脱出积分公式整理得二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X
低=1、X
高
=3.82
三、基础体积计算公式
将(4)式脱出积分公式整理得
四、基础体积计算例
上图中 T=1.5、J=1.18、H=0.6 、X=3.82-1=2.82。

涵洞八字墙工程量计算公式推导
*注:因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大
翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到左右。
一、墙身体积计算公式
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X
高
、低的一端
为X
低
)、翼墙低端基础宽J、基础的厚度为H,X变量从翼墙的低端变化到翼墙的高端(如图中从1米变化到米),墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X
高-X
低
)。
墙身体积计算公式推导如下:
将(2)式脱出积分公式整理得二、墙身体积计算例
上图中K=、B=、T=、X
低=1、X
高
=
三、基础体积计算公式
将(4)式脱出积分公式整理得
其实八字墙基础是底面为梯形的一个棱柱体基础体积=梯形面积乘以高
四、基础体积计算例
上图中T=、J=、H=、X==。

八字墙翼墙(墙身)砼用量精确通用计算公式推
导
*注:因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X高、低的一端为X低)、翼墙低端基础宽J、基础的厚度为 H, X变量从翼墙的低端变化到翼墙的高端(如图中从1米变化
到3.82米),墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X高-X低)。
墙身体积计算公式推导如下:
将(2)式脱出积分公式整理得
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X低=1、X高=3.82
三、基础体积计算公式
将 (4)式脱出积分公式整理得
四、基础体积计算例
上图中 T=1.5、J=1.18、H=0.6 、X=3.82-1=2.82。
涵洞八字墙工程量计算公式推导*注:因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式如下图所示的涵洞翼墙、低的令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X高一端为X)、翼墙低端基础宽J、基础的厚度为H,X变量从翼墙的低端变化到翼墙的低高端(如图中从1米变化到3.82米),墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X 高-X 低)。
墙身体积计算公式推导如下:将(2)式脱出积分公式整理得二、墙身体积计算例上图中K=0.46、B=3.75、T=1.5、X 低=1、X 高=3.82339.875.36182.35.12182.346.05.113322=⨯-⨯+-⨯⨯=)()(、体积339.875.36182.35.1246.023.4182.3233=⨯-⨯+⨯⨯+=)()(、体积三、基础体积计算公式)()(基础体积低高40dx X x x BTH TJH ⎰+=-将 (4)式脱出积分公式整理得其实八字墙基础是底面为梯形的一个棱柱体 基础体积=梯形面积乘以高 四、基础体积计算例上图中 T=1.5、J=1.18、H=0.6 、X=3.82-1=2.82949.382.275.326.05.182.26.018.15.112=⨯⨯⨯+⨯⨯⨯=、基础体积947.36.0223.418.193.12=⨯⨯+=)(、基础体积欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习资料等等打造全网一站式需求。

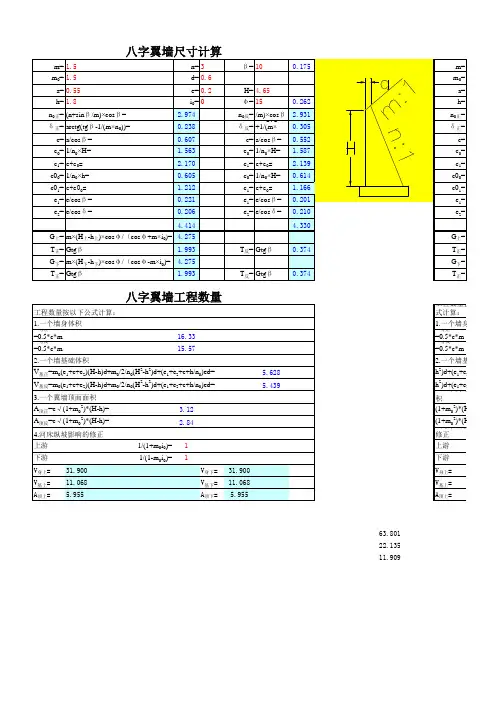
八字墙翼墙(墙身)砼用量精确通用计算公式推导
一、墙身体积计算公式
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X高、低的一端为X低)、翼墙低端基础宽J、基础的厚度为H, X变量从翼墙的低端变化到翼墙的高端(如图中从1米变化到3.82米),墙长与填土坡T 相关,它随墙高增高而增长。
即:墙长二T(X高—X低)。
墙身体积计算公式推导如下:
面积=—(1)注1:面积=〔上軒严咼体积可::(TKX+^X2)弘⑵.
将(2)式脱出积分公式整理得
体积=斗+呼
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X低=1、X高=3.82
体积
=1.5 X 0.46八3.8—1巧*讣八3竺7引
=8
.
339
二、基础体积计算公式
体积二严v(TJH+¥£血⑴ 将(4)式脱出积分公式整理得TH
体积=TJHX + —X2(5)
四、基础体积计算例
上图中T=1.5、J=1.18、H=0.6、X=3.82-仁2.82
亠心L 1*5 X 0.6 r
体积=lJx 1.13x0.6x2.82十一X 2.823 = 3.949
2 X 3.75
6 X 3.75。
涵洞八字墙工程量计算公式推导
*注:因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式
如下图所示的涵洞翼墙
、低令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X
高)、翼墙低端基础宽J、基础的厚度为 H, X变量从翼墙的低端变化到翼的一端为X
低
墙的高端(如图中从1米变化到3.82米),墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X高-X低)。
墙身体积计算公式推导如下:
将(2)式脱出积分公式整理得
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X 低=1、X 高=3.82
339.875
.36182.35.12182.346.05.113322=⨯-⨯+-⨯⨯=)()(、体积 339.875
.36182.35.1246.023.4182.3233=⨯-⨯+⨯⨯+=)()(、体积 三、基础体积计算公式
)()(基础体积低高40dx X x x B
TH TJH ⎰+=- 将 (4)式脱出积分公式整理得
其实八字墙基础是底面为梯形的一个棱柱体
基础体积=梯形面积乘以高
四、基础体积计算例
上图中 T=1.5、J=1.18、H=0.6 、X=3.82-1=2.82
949.382.275
.326.05.182.26.018.15.112=⨯⨯⨯+⨯⨯⨯=、基础体积 947.36.02
23.418.193.12=⨯⨯+=)(、基础体积。
八字墙翼墙(墙身)砼用量精确通用计算公式推
导
*注:因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X高、低的一端为X低)、翼墙低端基础宽J、基础的厚度为 H, X变量从翼墙的低端变化到翼墙的高端(如图中从1米变化
到3.82米),墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X高-X低)。
墙身体积计算公式推导如下:
将(2)式脱出积分公式整理得
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X低=1、X高=3.82
三、基础体积计算公式
将 (4)式脱出积分公式整理得
四、基础体积计算例
上图中 T=1.5、J=1.18、H=0.6 、X=3.82-1=2.82。