直线与平面平行的性质(课堂PPT)

思考6：设直线a，b为异面直线，经过
直线a可作几个平面与直线b平行？过a，
b外一点P可作几个平面与直线a，b都
平行？
a
b
p
b a a
p b
理论迁移
例1 在空间四边形ABCD中，E，F分别是 AB，AD的中点，求证：EF//平面BCD.
A E B
F D
C
例2 在长方体ABCD—A1B1C1D1中. （1）作出过直线AC且与直线BD1平行的
思考4：有一块木料如图，
E
P为面BCEF内一点，要求 过点P在平面BCEF内画一
F
P D
条直线和平面ABCD平行，
那么应如何画线？
A
C B
思考5：如图，设直线b在平面α内，直 线a在平面α外，猜想在什么条件下直线 a与平面α平行？
a
a//b
α
b
探究（二）：直线与平面平行的判断定理
思考1：如果直线a与平面α内的一条直 线b平行，则直线a与平面α一定平行吗？
D′
A′
P
C′
B′ D
C
A
B
例2 已知平面外的两条平行直线中的 一条平行于这个平面，求证另一条也 平行于这个平面.
如图，已知直线a，b
和平面α ，a∥b，
a
b
a∥α , a，b都在 平面α外 .
c α
求证：b∥α .
作业: P61练习，习题2.2A组：1，2. （做在书上） P62习题2.2A组：5，6. P63习题2.2B组：1，2.
由此可得什么推论？
推论 如果一个平 面内有两条相交直 线分别平行于另一
a
b
α
个平面内的两条直
线，那么这两个平 β

B
(2)在正方体ABCD-A1B1C1D1中,E,H分别为DD1,AB的中点,点F,G分别在棱BC, CC1上,且CF=CG=BC,则在F,G,H这三点中任取两点确定的直线中,与平面ACE平行的直线的条数为( )A.0 B.1 C.2 D.3
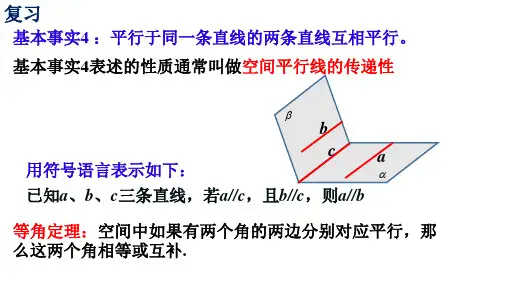
课堂考点探究
[解析]如图,取CE的中点I,CC1的中点K,连接AI,IG,EK,因为CI=IE,CG=GK,所以IG∥EK,且IG=EK,又AB∥EK, AB=EK,AH=AB,所以IG AH,所以四边形AHGI为平行四边形,则AI∥GH,又GH⊄平面ACE,AI⊂平面ACE,所以GH∥平面ACE.易知HF,GF均不与平面ACE平行,故选B.
6.下列说法中正确的是 .(填序号) ①若a,b是两条直线,且a∥b,则a平行于经过b的任何平面;②若直线a和平面α满足a∥α,则a与α内的任何直线平行;③平行于同一条直线的两个平面平行;④若直线a,b和平面α满足a∥b,a∥α,b⊄α,则b∥α.
课前基础巩固
[解析]对于①,a可以在经过b的平面内,故①错误;对于②,a与α内的直线平行或异面,故②错误;对于③,两平面也可以相交,故③错误;对于④,若a∥b,a∥α,b⊄α,则b∥α,故④正确.
D
(2)在正方体ABCD-A1B1C1D1中,E,H分别为DD1,AB的中点,点F,G分别在棱BC, CC1上,且CF=CG=BC,则在F,G,H这三点中任取两点确定的直线中,与平面ACE平行的直线的条数为( )A.0 B.1 C.2 D.3
课堂考点探究
[思路点拨]由题意作出图形,取CE的中点I,连接AI,证出AI∥GH,利用线面平行的判定定理可知GH∥平面ACE,又HF,GF均不与平面ACE平行,即可得解.
图7-39-1
4. [教材改编] 如图7-39-2,平面α∥平面β,△PAB所在的平面与α,β分别交于CD,AB,若PC=2,CA=3,CD=1,则AB= .

D C
O
A
B
技巧点拨：中点问题可考虑利用中位线的性质解决.
例3、如图，四棱锥P-ABCD中，底面ABCD是平行四边形，E、F 分别是AB，PC的中点， 求证：EF//平面PAD
技巧点拨：可通过构造平行四边形寻找平行线.
如果一条直线和一个平面平行，那么这条直线和这个平面内的 直线有怎样的位置关系？
•CD//AB →→ •CD//平面α
直线与平面平行的判定定理：
如果平面外一条直线与此平面内的一条直线平行，那么该直线与 此平面平行
例2、求证：空间四边形相邻两边中点的连线,平行于经过另两边的平面. 解题流程：画图→写出已知求证→作出辅助线→证明
已知:空间四边形ABCD中，E、F分别是AB，AD的中 点. 求证：EF∥平面BCD.
点，求证:四边形EFGH是平行四边形.
A
EH // GF
H E
D
B
G
F C
探究：若加上条件AC=BD,那么四边形EFGH为什么图形?
2.等角定理
A’
E’
D’
A
E
D
如果空间中两个角的两条边分别对应平行， 那么这两个角相等或互补.
推论：
如果两条相交直线和另两条相交直线分别平行， 那么这两组直线所成的锐角（或直角）相等.
a
α
平行或异面
三、直线与平面平行的性质定理
一条直线与一个平面平行，则过这条直线的任一平面与此 平面的交线与该直线平行.
βa
αb
线面平行
先找平面再线找线两平平行 面的交线
例4、有一块木料如图，已知棱BC平行于面A′C′ （1）要经过木料表面A′B′C′D′内的一点P和棱BC将木料
锯开，应怎样画线？ （2）所画的线和面AC有什么关系？

判定定理二：向量
03
共线法
向量共线法原理
定义
若两向量方向相同或相反，则称这两 向量共线。
性质
应用
在直线与平面平行判定中，通过判断 直线的方向向量与平面上两不共线向 量的关系，确定直线与平面的位置关 系。
共线的向量可以表示为同一基向量的 倍数。
向量运算规则
加法运算
向量加法满足平行四边形 法则或三角形法则。
$l parallel alpha$。
实例二
若直线$l$的方向向量$vec{a}$ 与平面$alpha$的法向量
$vec{n}$满足$vec{a} cdot vec{n} = 0$，则$l parallel
alpha$。
讨论
通过实例分析，我们可以发现向 量共线法在直线与平面平行判定 中的重要作用。同时，需要注意 判定条件的充分性和必要性，以
及特殊情况的处理。
判定定理三：距离
04
相等法
距离相等法原理
直线与平面平行时，直线上任意一点 到平面的距离都相等。
利用这一性质，可以通过比较直线上 不同点到平面的距离是否相等来判断 直线与平面是否平行。
点到直线距离公式
点$P(x_0, y_0, z_0)$到平面 $Ax + By + Cz + D = 0$的距 离公式为
直线与平面的距离为零
当直线上的任意一点到平面的距离都为零时，直线与平面平行。可 以通过计算点到平面的距离公式来判断。
复杂问题简化策略
转化为基本问题
将复杂问题转化为判断直线与平面是否平行的基本问题，以便运 用上述方法进行求解。
利用已知条件
充分利用题目中给出$d = frac{|Ax_0 + By_0 + Cz_0 + D|}{sqrt{A^2 + B^2 + C^2}}$

形,BD∩AC=G,∴G是BD的中点.又∵E是
BB1的中点,∴DB1∥GE.又DB1⊄平面
ACE,GE⊂平面ACE,∴B1D∥平面ACE.
变式 (1)如图,四棱锥P-ABCD的底面为平行四边形,M为棱PC的中点.
求证:(1)BC∥平面PAD;
(2)AP∥平面MBD.
证明:(1)因为四棱锥P-ABCD的底面为平行四边形,所以BC∥AD,又BC⊄平面
意可知四边形ABC1D1为平行四边形,则AD1∥BC1.又AD1∥EF,所以EF∥BC1.因
为EF⊄平面BCC1B1,BC1⊂平面BCC1B1,所以EF∥平面BCC1B1.显然正方体的其
余4个面都不与EF平行.故选B.
变式 (3)如图所示,四棱锥S - ABCD的底面是平行四边

形,M,N分别是SA,BD上的点,且 = .求证:MN∥平面

SBC.

证明:连接AN并延长,使之交BC于点P,连接SP.因为AD∥BC,所以 = .又



= ,所以 = ,所以MN∥SP.


因为MN⊄平面SBC,SP⊂平面SBC,所以MN∥平面SBC.
小结
1.利用直线与平面平行的判定定理证明线面平行的一般步骤
解析
思考►►►
如何判定一条直线与一个平面平行？
【解析】 如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面
平行．
解析
直线与平面平行的判定定理：
表示定理
直线与平面
平行的
判定定理
图形
文字
符号
如果平面外一条直线
a⊄α，
与此平面内的一条直
b⊂α，
线平行，那么该直线

第八章 立体几何初步
第三节 直线、平面平行的判定与性质
栏目一 知识·分步落实 栏目二 考点·分类突破 栏目三 微专题系列
栏目导引
课程标准
考向预测
1.以立体几何的定义、公理和定理为
出发，借助长方体，通过直观感知， 考情分析： 直线与平面以及平面与
了解空间中线面平行的有关性质与 平面平行的判定和性质仍会是高考
所以 A1G 綊 EB，所以四边形 A1EBG 是平行四边形，
所以 A1E∥GB. 因为 A1E⊄平面 BCHG，GB⊂平面 BCHG， 所以 A1E∥平面 BCHG. 又因为 A1E∩EF＝E，所以平面 EFA1∥平面 BCHG.
1．如图，平面 α∥平面 β，△PAB 所在的平面与 α，β分别交于 CD，AB，
平行命题的判断 (1)解决与平行相关命题的判断问题，以与平行相关的判定定理和性质定 理为依据，注意定理中相关条件的检验，必须进行严密的逻辑推理． (2)如果判断某个命题错误，则往往利用正方体或其他几何体作为模型构 造反例说明．
直线与平面平行的判定与性质 角度一 直线与平面平行的判定
如图所示，斜三棱柱 ABC-A1B1C1 中，点 D，D1 分别为 AC，A1C1 的中点．求证：
BC∥平面ADF
BC⊂平面BCPQ
⇒BC∥PQ.
平面BCPQ∩平面ADF＝PQ
PQ∥BC
PQ⊄平面ABCD PQ∥平面 ABCD.
BC⊂平面ABCD
应用线面平行的性质定理的关键是确定交线的位置，有时 需要经过已知直线作辅助平面来确定交线．该定理的作用是由线面平行转化 为线线平行．
1．(2020·深圳市统一测试)如图，在直四棱柱 ABCD-A1B1C1D1 中，底面 ABCD 是平行四边形，点 M，

若两向量的点积为零，则 它们垂直。
应用
通过计算直线方向向量与 平面法向量的点积，可以 判断直线与平面是否平行 。
判定定理三：法向量垂直
定义
若一直线与一平面平行， 则该直线的法向量与该平 面的法向量平行。
推论
若两向量平行，则它们的 分量成比例。
应用
通过比较直线法向量与平 面法向量的分量比例，可 以判断直线与平面是否平 行。
直线与平面平行的定义
阐述直线与平面平行的基本概念，为后续判定定理 的引入做铺垫。
判定定理的重要性
说明直线与平面平行判定定理在几何学中的地位和 作用，以及在实际应用中的价值。
教学目标
80%
知识与技能
掌握直线与平面平行的判定定理 及其证明方法，理解相关概念， 能够运用所学知识解决相关问题 。
100%
过程与方法
应用举例二：判断两平面是否平行
方法一
利用平行平面的性质，通过证明一个 平面内有两条相交直线分别与另一个 平面平行，从而判定两个平面平行。
方法二
利用向量法，通过计算两个平面的法 向量是否共线，从而判定两个平面是 否平行。
应用举例三：解决实际问题中的平行问题
1 2
实例一
在建筑设计中，利用直线与平面平行的性质，确 保建筑物的立面、地面等各部分保持平行，以达 到美观和稳定的效果。
定义
应用
若一直线与一平面平行，则该直线与 该平面内任意一条直线的斜率相等。
通过比较直线与平面内某一直线的斜 率，可以判断直线与平面是否平行。
推论
若两直线的斜率相等，则它们或者平 行或者重合。
判定定理二：方向向量平行
01
02
03
定义
若一直线与一平面平行， 则该直线的方向向量与该 平面的法向量垂直。

自测 自评
2．如果 a，b 是异面直线，且 a∥平面 α，那么 b 与 α 的位置关系是( )
A．b∥α B．b 与 α 相交
C．b⊂α D．不确定
解析：b 与 α 相交或 b⊂α 两种情况． 答案：D
自测 自评
3．如果一条直线和一个平面平行，夹在直线和平面间 的两线段相等，那么这两条线段所在直线的位置关系是
(2)证明线线平行常用的方法有： ①定义法：在同一个平面内没有公共点的两条直线 平行． ②平行公理：平行于同一条直线的两条直线平行． ③直线与平面平行的性质定理．
④反证法：假设两条直线不平行，然后推出矛盾， 进而证明两条直线应当是平行的．
跟踪 训练
2．已知：α∩β＝l，a∥α，a∥β，求证：a∥l.
跟踪 训练
3．如图，a∥α，A 是 α 另一侧的点，B，C，D∈a， 线段 AB，AC，AD 交 α 于 E，F，G 三点，若 BD＝4， CF＝4，AF＝2，求 EG.
跟踪 训练
解析：∵A∉a，∴A，a 可确定一个平面，设为 β. ∵B∈a，∴B∈β. 又 A∈β，∴AB⊂β.
同理 AC⊂β，AD⊂β. ∵点 A 与直线 a 在 α 的异侧， ∴β 与 α 相交． ∴平面 ABD 与平面 α 相交，设交线为 EG.
又∵l1∥l2，∴l2∥l3， ∴l1∥l3，l2∥l3. 点评：直线与平面平行的判定定理与直线与平面 平行的性质定理经常交替使用，也就是通过线线平行 推出线面平行，再通过线面平行推出新的线线平行， 复杂的题目还可继续推下去．
跟踪 训练
1．如图所示，过正方体 ABCDA1B1C1D1 的棱 BB1 作一平 面交平面 CDD1C1 于 EE1，求证：BB1∥EE1.
证明：因为EF∥平面BCD，BD＝面ABD∩面BCD，所 以EF∥BD，因为E为空间四边形ABCD的边AB的中点，所 以F是AD的中点．

4．底面是平行四边形的四棱柱中有________对面互相平 行．
[答案] 3
第二章 2.2 2.2.3
成才之路 ·高中新课程 ·学习指导 ·人教A版 ·数学 ·必修2
新知导学 直线与平面平行的性质定理
一条直线与一个平面平行，则过这条直线的任一 文字语言 平面与此平面的交线与该直线__平__行___
第二章 2.2 2.2.3
成才之路 ·高中新课程 ·学习指导 ·人教A版 ·数学 ·必修2
4．对于直线m、n和平面α，下面叙述正确的是( ) A．如果m⊂α，n⊄α，m、n是异面直线，那么n∥α B．如果m⊂α，n与α相交，那么m、n是异面直线 C．如果m⊂α，n∥α，m、n共面，那么m∥n D．如果m∥α，n∥α，m、n共面，那么m∥n [答案] C
成才之路 ·高中新课程 ·学习指导 ·人教A版 ·数学 ·必修2
3．已知平面α∩平面β＝a，平面β∩平面γ＝b，平面γ∩平面 α＝c，若a∥b，则c与a，b的位置关系是( )
A．c与a，b都是异面 B．c与a，b都相交 C．c至少与a，b中的一条相交 D．c与a，b都平行 [答案] D [解析] 由线面平行的判定及其性质定理易得c∥a，c∥b.
中与直线a平行的直线有( )
A．0条
B．1条
C．0或1条
D．无数条
[答案] C
第二章 2.2 2.2.3
成才之路 ·高中新课程 ·学习指导 ·人教A版 ·数学 ·必修2
3．如图所示，已知AB∥平面α，AC∥BD，且AC，BD与α 分别相交于点C，D.求证：AC＝BD.
[分析] 利用线面平行的性质定理证明AB∥CD，从而得四 边形ABCD是平行四边形．
成才之路 ·高中新课程 ·学习指导 ·人教A版 ·数学 ·必修2

线面平行 空间问题
例1、求证：空间四边形相邻两边中点的连线平行于经过另外两边 所在的平面
已知：如图，空间四边形ABCD中，E、F分别是AB，AD的中点.
求证：EF∥平面BCD.
A
证 明 ： 连 接BD. 因为AE EB, AF FD 所以EF // BD
E
F
D
B
C
因为EF 平面BCD，BD 平面BCD，
面有没有公共点．
但是，直线无限延长，平面无限延展，如何保证直线与 平面没有公共点呢
a
三、观察探究
1、门扇转动的一边与门框所在的平面之间的位置关系．
观察 在门扇的旋转过程中: 直线AB在门框所在的平面外 直线CD在门框所在的平面内 直线AB与CD始终是平行的
A1
A
B1
B
三、观察探究
2、 将一本书平放在桌面上，翻动书的封面，封面边缘AB所在直线 与桌面所在平面具有什么样的位置关系？
课堂练习
利用平行线分线段成比例定理
1、平面与ABC的两边AB, AC分别交于D, E，且 AD AE ,
DB EC
如图所示，则BC与平面的关系是( A )
A、 平 行
B、 相 交
C、异面 D、BC
C
B
E
D
α
A
2、 在 空 间 四 边 形ABCD中 ，E、F分 别 是AB和BC上 的 点 ，
复习
基本事实4 ：平行于同一条直线的两条直线互相平行。
基本事实4表述的性质通常叫做空间平行线的传递性
b
用符号语言表示如下：
c
a
已知a、b、c三条直线，若a//c，且b//c，则a//b
等角定理：空间中如果有两个角的两边分别对应平行，那 么这两个角相等或互补.

答案：平行 5．过三棱柱ABC－A1B1C1任意两条 棱的中点作直线，其中与平面ABB1A1平 行的直线共有__________条．
答案：6
课堂互动讲练
考点一 直线与平面平行的判定
判定直线与平面平行，主要有 三种方法：
(1)利用定义(常用反证法)． (2)利用判定定理：关键是找平 面内与已知直线平行的直线．可先 直观判断平面内是否已有，若没有， 则需作出该直线，常考虑三角形的 中位线、平行四边形的对边或过已 知直线作一平面找其交线．
规律方法总结
2．在解决线面、面面平行的判 定时，一般遵循从“低维”到“高维”的 转化，即从“线线平行”到“线面平行”， 再到“面面平行”；而在应用性质定理 时，其顺序恰好相反，但也要注意， 转化的方向总是由题目的具体条件而 定，决不可过于“模式化”．
规律方法总结
3．在应用有关定理、定义等解 决问题时，应当注意规范性训练，即 从定理、定义的每个条件开始，培养 一种规范、严密的逻辑推理习惯，切 不可只求目标，不顾过程，或言不达 意，出现推理“断层”的错误．
课堂互动讲练
∴PQ∥EK. 又 PQ⊄平面 BEC，EK⊂面 BEC， ∴PQ∥平面 BEC. 法三：如图所示，作 PH∥EB 交 AB 于 H，连结 HQ，则AHHB＝APEP， ∵AE＝BD，AP＝DQ， ∴PE＝BQ，
∴AH＝AP＝DQ， HB PE BQ
课堂互动讲练
∴HQ∥AD，即HQ∥BC. 又PH∩HQ＝H，BC∩EB＝B， ∴平面PHQ∥平面BCE， 而PQ⊂平面PHQ， ∴PQ∥平面BCE.
课堂互动讲练
【名师点评】 法一、法二均是 依据线面平行的判定定理在平面BCE 内寻找一条直线l，证得它与PQ平 行．
特别注意直线l的寻找往往是通过 过直线PQ的平面与平面BCE相交的交 线来确定．