计算指标权重的方法最终版.ppt

在企业人力资源管理中,有许多涉及到权重的设置，如素质评价、绩效考核等。

在一般的情况下，管理者都知道权重的重要性，但在设定权重时却往往会依凭自己积累起来的经验以及评价因素的定位来进行判断。

事实上，这种确定权重的方式存在很强的主观性，在实践中会导致一些不必要的偏差。

如何在设定权重时，既考量管理者多年来积累起来的经验判断，又科学客观地定位各评价因素，避免一些不必要的偏差，使评价结果更接近于实际情况呢？下面的几种方法，或许能给你带来一定的收获。

一、简单排序编码法这种方法通过管理者对各项考评因素的重视程度进行排序编码，然后确定权重的一种简单的方法，需要管理者从过去的历史数据及个人的经验对各项考评项目作出正确的排序。

比如在绩效考核过程中，某一职位有四个KPI的考评因素，分别为A，B，C，D，依企业的要求及目标设定者的经验，各项考评因素的重要性排序为B，D，C，A；然后再按照自然数顺序由大到小对其进行分配，分别为4，3，2，1。

然后将权数归一化，最后结果为A：1/(4+3+2+1)=0.1；B：4/(4+3+2+1)=0.4C：2/(4+3+2+1)=0.2；D：3/(4+3+2+1)=0.3。

这种简单排序编码法计算权数的方法简单，但也存在主观因素，存在一定的不合理性。

但至少它比管理者单纯地依据自身经验进行设定的方式要客观一些。

二、倍数环比法倍数环比法首先将各个考评因素随机排列，然后按照顺序对各项因素进行比较，得出各因素重要度之间的倍数关系，又称环比比率，再将环比比率进行统一转换为基准值，最后进行归一化处理，确定其最终权重。

这种方法需要对考评因素有客观的判断依据，需要有客观准确的历史数据作为支撑。

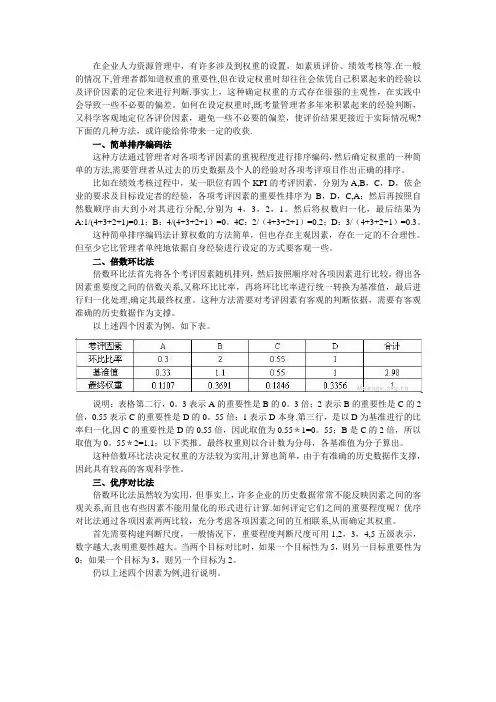
以上述四个因素为例，如下表。

说明:表格第二行，0.3表示A的重要性是B的0.3倍；2表示B的重要性是C的2倍，0.55表示C的重要性是D的0.55倍；1表示D本身。

第三行，是以D为基准进行的比率归一化，因C的重要性是D的0.55倍，因此取值为0.55*1=0.55；B是C的2倍，所以取值为0.55*2=1.1；以下类推。

在企业人力资源管理中，有许多涉及到权重的设置，如素质评价、绩效考核等.在一般的情况下,管理者都知道权重的重要性,但在设定权重时却往往会依凭自己积累起来的经验以及评价因素的定位来进行判断.事实上，这种确定权重的方式存在很强的主观性，在实践中会导致一些不必要的偏差。

如何在设定权重时,既考量管理者多年来积累起来的经验判断，又科学客观地定位各评价因素，避免一些不必要的偏差，使评价结果更接近于实际情况呢?下面的几种方法，或许能给你带来一定的收获.一、简单排序编码法这种方法通过管理者对各项考评因素的重视程度进行排序编码，然后确定权重的一种简单的方法,需要管理者从过去的历史数据及个人的经验对各项考评项目作出正确的排序。

比如在绩效考核过程中，某一职位有四个KPI的考评因素，分别为A,B，C，D，依企业的要求及目标设定者的经验，各项考评因素的重要性排序为B，D，C,A；然后再按照自然数顺序由大到小对其进行分配,分别为4，3，2，1。

然后将权数归一化，最后结果为A:1/(4+3+2+1)=0.1；B：4/(4+3+2+1）=0。

4C：2/（4+3+2+1）=0.2；D：3/（4+3+2+1）=0.3。

这种简单排序编码法计算权数的方法简单，但也存在主观因素，存在一定的不合理性。

但至少它比管理者单纯地依据自身经验进行设定的方式要客观一些。

二、倍数环比法倍数环比法首先将各个考评因素随机排列，然后按照顺序对各项因素进行比较，得出各因素重要度之间的倍数关系,又称环比比率，再将环比比率进行统一转换为基准值，最后进行归一化处理,确定其最终权重。

这种方法需要对考评因素有客观的判断依据，需要有客观准确的历史数据作为支撑。

以上述四个因素为例，如下表。

说明：表格第二行，0。

3表示A的重要性是B的0。

3倍；2表示B的重要性是C的2倍，0.55表示C的重要性是D的0。

55倍；1表示D本身.第三行，是以D为基准进行的比率归一化,因C的重要性是D的0.55倍，因此取值为0.55＊1=0。

指标权重的计算方法
在进行决策和评估时，需要对不同的指标进行权重的分配，以反映它们在决策或评估中的重要性。

指标权重的计算方法有很多种，下面介绍几种常用的方法。

1. 主观赋权法
主观赋权法是根据专家的经验和知识来确定指标权重的方法。

在这种方法中，专家会根据自己的判断和经验，对每个指标进行打分，然后根据打分的结果来确定权重。

2. 层次分析法
层次分析法是一种定量化的权重计算方法，它可以将复杂的决策问题分解成不同的层次结构，然后对每个层次结构进行比较和分析，最终得出权重。

在层次分析法中，需要确定决策目标、准则、方案和子方案，对每个层次进行两两比较，得出各层次的权重。

3. 熵权法
熵权法是一种基于信息熵理论的权重计算方法，它可以综合考虑指标之间的关联性和重要性，得出权重。

在熵权法中，需要计算各指标的
熵值和权重，然后通过归一化处理得到最终权重。

4. 灰色关联法
灰色关联法是一种将多个指标进行综合评价的方法，它可以考虑指标之间的相互依赖关系和权重，得出综合评价结果。

在灰色关联法中，需要将各指标进行标准化处理，然后计算各指标之间的关联度和权重，最终得出综合评价结果。

总之，不同的指标权重计算方法有各自的优缺点，需要根据实际情况选择适合的方法进行权重计算。

指标权重确定方法之优序图一、优序图法介绍优序图法最早是由美国穆蒂提出的，是基于主观判断的一种方法，需要具有大量的积累经验。

1. 优序图法原理简介优序图法是通过对多个指标或目标进行两两相对比较，最后给出重要性次序或者优先次序。

该方法应用较为简便，既能处理定性问题，又能处理定量问题。

优序图法由多个专家对系统指标或者工程方案，针对目的进行两两对比，最终确定系统指标重要程度或者工程方案优劣次序，以便对系统进行评价或者对工程方案决策进行优先排序。

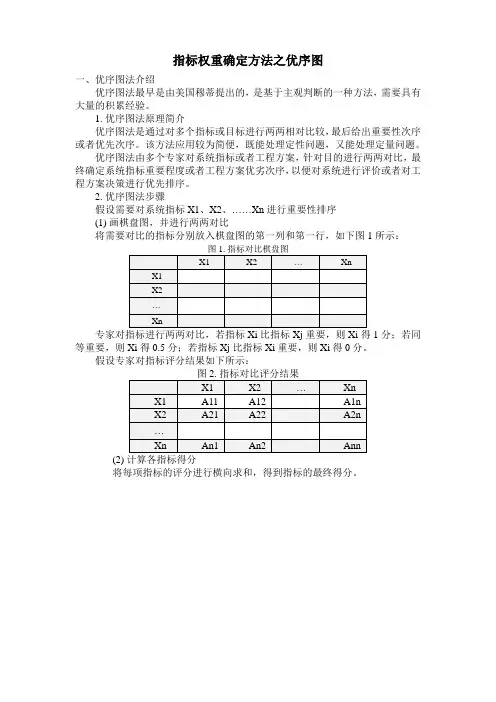
2. 优序图法步骤假设需要对系统指标X1、X2、……Xn进行重要性排序(1) 画棋盘图，并进行两两对比将需要对比的指标分别放入棋盘图的第一列和第一行，如下图1所示：图1. 指标对比棋盘图X1 X2 …XnX1X2…Xn专家对指标进行两两对比，若指标Xi比指标Xj重要，则Xi得1分；若同等重要，则Xi得0.5分；若指标Xj比指标Xi重要，则Xi得0分。

假设专家对指标评分结果如下所示：图2. 指标对比评分结果X1 X2 …XnX1 A11 A12 A1nX2 A21 A22 A2n…Xn An1 An2 Ann(2) 计算各指标得分将每项指标的评分进行横向求和，得到指标的最终得分。

(3) 根据得分进行排序，确定指标重要性下面来看一下优序图法在指标权重确定中的实际应用。

二、优序图法在指标权重确定中的应用1. 背景介绍某电脑生产厂商开发了一款新式电脑，目前需要该电脑与其竞争对手目前正在畅销的某型号电脑进行对比，判断是否具有竞争优势。

下面是调查得到的对比数据：表1 两款电脑指标满意度得分指标本公司产品满意度竞争对手产品满意度指标本公司产品满意度竞争对手产品满意度处理器类型 5 10 处理器10 6内存容量7 6 存储容量 5 9操作系统7 5 续航时间7 7数据接口10 9 屏幕分辨率10 10摄像头8 8 产品尺寸10 10 然而各指标对消费者选择电脑的影响程度不同，因此需要综合所有指标才能对两款电脑竞争强弱进行评价。

绩效考核指标权重的计算方法在企业人力资源管理中,有许多涉及到权重的设置，如素质评价、绩效考核等。

在一般的情况下，管理者都知道权重的重要性，但在设定权重时却往往会依凭自己积累起来的经验以及评价因素的定位来进行判断。

事实上，这种确定权重的方式存在很强的主观性，在实践中会导致一些不必要的偏差。

如何在设定权重时，既考量管理者多年来积累起来的经验判断，又科学客观地定位各评价因素，避免一些不必要的偏差，使评价结果更接近于实际情况呢,下面的几种方法，或许能给你带来一定的收获。

一、简单排序编码法这种方法通过管理者对各项考评因素的重视程度进行排序编码，然后确定权重的一种简单的方法，需要管理者从过去的历史数据及个人的经验对各项考评项目作出正确的排序。

比如在绩效考核过程中，某一职位有四个KPI的考评因素，分别为A，B，C，D，依企业的要求及目标设定者的经验，各项考评因素的重要性排序为B，D，C，A;然后再按照自然数顺序由大到小对其进行分配，分别为4，3，2，1。

然后将权数归一化，最后结果为A:1/(4+3+2+1)=0.1;B:4/(4+3+2+1)=0.4C:2/(4+3+2+1)=0.2;D:3/(4+3+2+1)=0.3。

这种简单排序编码法计算权数的方法简单，但也存在主观因素，存在一定的不合理性。

但至少它比管理者单纯地依据自身经验进行设定的方式要客观一些。

二、倍数环比法倍数环比法首先将各个考评因素随机排列，然后按照顺序对各项因素进行比较，得出各因素重要度之间的倍数关系，又称环比比率，再将环比比率进行统一转换为基准值，最后进行归一化处理，确定其最终权重。

这种方法需要对考评因素有客观的判断依据，需要有客观准确的历史数据作为支撑。

以上述四个因素为例，如下表。

说明:表格第二行，0.3表示A的重要性是B的0.3倍;2表示B的重要性是C的2倍，0.55表示C的重要性是D的0.55倍;1表示D本身。

第三行，是以D为基准进行的比率归一化，因C的重要性是D的0.55倍，因此取值为0.55*1=0.55;B 是C的2倍，所以取值为0.55*2=1.1;以下类推。

绩效考核指标权重的计算方法
绩效考核指标权重的计算方法可以根据不同的考核体系和组织的需求而有所不同，下
面提供一种常用的方法：
1. 确定考核指标：首先确定需要考核的指标，这些指标应该能够反映出员工工作的关
键表现和能力。

2. 制定指标权重：根据指标的重要性和对组织目标的贡献程度，制定每个指标的相对
权重。

一般来说，重要指标应该有较高的权重。

3. 评估指标的重要性：可以利用专家评估、问卷调查、经验法则等方式，对每个指标
的重要性进行评估和权重分配。

4. 相对评估法：通过比较各指标之间的相对重要性，并将其权重按比例分配。

5. 综合评估法：使用综合评估工具（如层次分析法）将各指标的重要性进行排序，再
将权重按比例分配。

6. 评估权重的效果：根据权重的分配结果，可以评估其对绩效评估的准确性和有效性。

如果评估结果和组织目标不符合，可以根据实际情况进行调整和优化。

需要注意的是，权重的分配应该是一个定期进行的过程，可以根据组织的战略目标和
员工的工作重点进行调整，以保持其有效性和公平性。

此外，在分配权重时，还要考
虑到员工的实际工作情况和能力水平，以确保评估结果具有更大的公信力和可操作性。

权重的确定方法在统计理论和实践中，权重是表明各个评价指标（或者评价项目）重要性的权数，表示各个评价指标在总体中所起的不同作用。

权重有不同的种类，各种类别的权重有着不同的数学特点和经济含义，一般有以下几种权重。

按照权重的表现形式的不同，可分为绝对数权重和相对数权重。

相对数权重也称比重权数，能更加直观地反映权重在评价中的作用。

按照权重的形成方式划分，可分为人工权重和自然权重。

自然权重是由于变换统计资料的表现形式和统计指标的合成方式而得到的权重，也称为客观权重。

人工权重是根据研究目的和评价指标的内涵状况，主观地分析、判断来确定的反映各个指标重要程度的权数，也称为主观权重。

按照权重形成的数量特点的不同划分，可分为定性赋权和定量赋权。

如果在统计综合评价时，采取定性赋权和定量赋权的方法相结合，获得的效果更好。

按照权重与待评价的各个指标之间相关程度划分，可分为独立权重和相关权重。

独立权重是指评价指标的权重与该指标数值的大小无关，在综合评价中较多地使用独立权重，以此权重建立的综合评价模型称为“定权综合”模型。

相关权重是指评价指标的权重与该指标的数值具有函数关系，例如，当某一评价的指标数值达到一定水平时，该指标的重要性相应的减弱；或者当某一评价指标的数值达到另一定水平时，该指标的重要性相应地增加。

相关权重适用于评价指标的重要性随着指标取值的不同而发生变化的条件下，基于相关权重建立的综合评价模型被称为“变权模型”。

比如评估环境质量多采用“变权综合”模型。

(一)统计平均法统计平均数法（Statistical average method）是根据所选择的各位专家对各项评价指标所赋予的相对重要性系数分别求其算术平均值，计算出的平均数作为各项指标的权重。

其基本步骤是：第一步，确定专家。

一般选择本行业或本领域中既有实际工作经验、又有扎实的理论基础、并公平公正道德高尚的专家；第二步，专家初评。

将待定权数的指标提交给各位专家，并请专家在不受外界干扰的前提下独立的给出各项指标的权数值；第三步，回收专家意见。

在企业人力资源管理中，有许多涉及到权重的设置，如素质评价、绩效考核等。

在一般的情况下，管理者都知道权重的重要性，但在设定权重时却往往会依凭自己积累起来的经验以及评价因素的定位来进行判断。

事实上,这种确定权重的方式存在很强的主观性，在实践中会导致一些不必要的偏差.如何在设定权重时，既考量管理者多年来积累起来的经验判断，又科学客观地定位各评价因素，避免一些不必要的偏差，使评价结果更接近于实际情况呢？下面的几种方法,或许能给你带来一定的收获。

一、简单排序编码法这种方法通过管理者对各项考评因素的重视程度进行排序编码，然后确定权重的一种简单的方法，需要管理者从过去的历史数据及个人的经验对各项考评项目作出正确的排序。

比如在绩效考核过程中，某一职位有四个KPI的考评因素，分别为A，B，C，D,依企业的要求及目标设定者的经验，各项考评因素的重要性排序为B，D，C,A；然后再按照自然数顺序由大到小对其进行分配，分别为4，3，2，1。

然后将权数归一化，最后结果为A:1/(4+3+2+1）=0。

1；B：4/（4+3+2+1）=0.4C：2/（4+3+2+1）=0.2；D:3/(4+3+2+1)=0.3。

这种简单排序编码法计算权数的方法简单，但也存在主观因素,存在一定的不合理性。

但至少它比管理者单纯地依据自身经验进行设定的方式要客观一些。

二、倍数环比法倍数环比法首先将各个考评因素随机排列,然后按照顺序对各项因素进行比较,得出各因素重要度之间的倍数关系,又称环比比率，再将环比比率进行统一转换为基准值，最后进行归一化处理,确定其最终权重.这种方法需要对考评因素有客观的判断依据,需要有客观准确的历史数据作为支撑。

以上述四个因素为例，如下表。

说明：表格第二行，0。

3表示A的重要性是B的0.3倍；2表示B的重要性是C的2倍，0。

55表示C的重要性是D的0.55倍；1表示D本身.第三行，是以D为基准进行的比率归一化,因C的重要性是D的0。