R 语言环境下用ARIMA模型做时间序列预测

时间序列分析R语言代码时间序列分析是统计学中的一个重要分支，主要用于研究随时间变化的数据。

它可以帮助我们了解数据的趋势、周期性和季节性等特征，从而为预测和决策提供依据。

R语言是一种功能强大的统计分析工具，提供了丰富的时间序列分析函数和包，以下是一个简单的时间序列分析R语言代码示例。

首先，我们需要加载需要用到的包，如`ggplot2`和`forecast`。

```Rlibrary(ggplot2)library(forecast)```接下来，我们可以导入时间序列数据，并将其转换为时间序列对象。

假设我们有一个名为`data.csv`的数据文件，其中包含每个月份的销售额数据。

```Rdata <- read.csv("data.csv")ts_data <- ts(data$Sales, start = c(2000, 1), frequency = 12) ```通过绘制时间序列图，我们可以直观地观察数据的趋势和季节性。

```Rggplot(data, aes(x = Month, y = Sales)) +geom_line( +xlab("Month") +ylab("Sales") +theme_minimal``````R```接下来，我们可以通过绘制分解后的趋势、季节性和随机成分图来进一步研究数据的特征。

```Rtheme_minimal```我们还可以使用自回归移动平均模型（ARIMA）对时间序列数据进行建模和预测。

首先，我们需要估计ARIMA模型的参数。

```Rarima_model <- auto.arima(ts_data)```通过`auto.arima(`函数，R会自动选择最佳的ARIMA模型。

然后，我们可以使用这个模型来进行预测。

假设我们希望对未来12个月的销售额进行预测。

```Rforecast_data <- forecast(arima_model, h = 12)```最后，我们可以绘制预测结果和置信区间的图表。

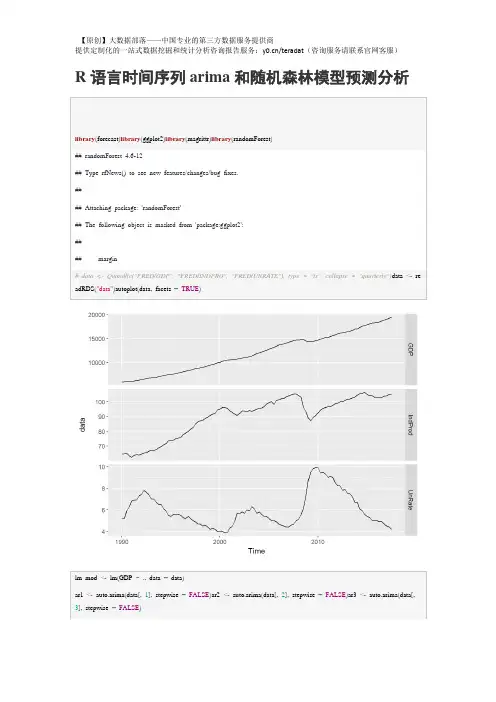
R语言时间序列有关各种函数总结R语言是一种强大的统计分析和数据可视化工具，提供了许多时间序列分析的函数和方法。

下面是一些重要的时间序列分析函数的总结：1. ts(函数：用于创建时间序列对象。

可以指定时间序列的起始时间、结束时间、时间间隔等。

例如，创建从1990年1月到1999年12月的月度时间序列对象可以使用以下代码：```Rts_data <- ts(data, start=c(1990, 1), end=c(1999, 12), frequency=12)``````R```3. stl(函数：基于季节性-趋势-随机性分解的局部回归方法，用于进行季节调整。

该函数可以根据时间序列的特性自动选择适当的分解模型。

以下是使用stl(函数进行季节调整的示例：```Rseasonally_adjusted <- stl(ts_data, s.window="periodic")```4. forecast(函数：用于时间序列的预测。

可以根据历史数据拟合不同的模型，例如ARIMA模型、指数平滑模型等，并生成未来一段时间的预测结果。

以下是使用forecast(函数生成未来12个月的预测结果的示例：```Rforecast_result <- forecast(ts_data, h=12)```5. autocorrelation(函数：用于计算时间序列的自相关系数。

自相关系数可以帮助我们了解时间序列的固定模式和周期性。

以下是计算时间序列的自相关系数的示例：```Racf_result <- autocorrelation(ts_data)```6. arima(函数：用于建立自回归移动平均模型（ARIMA）来拟合时间序列。

ARIMA模型是一种常用的时间序列预测模型，可以预测时间序列的未来值。

以下是使用arima(函数拟合ARIMA模型的示例：```Rarima_model <- arima(ts_data, order=c(p, d, q))```7. ets(函数：用于指数平滑时间序列模型的拟合和预测。

r语言arima函数用法一、介绍ARIMA（Autoregressive Integrated Moving Average）模型是一种常用的时间序列分析方法，它可以用来预测未来的数据趋势。

在R 语言中，arima函数是实现ARIMA模型的主要函数之一。

二、语法arima(x, order = c(p, d, q), seasonal = c(P, D, Q), ...)参数说明：x：时间序列数据order：一个长度为3的向量，分别表示AR、差分和MA的阶数seasonal：一个长度为4的向量，分别表示季节性AR、季节性差分和季节性MA的阶数以及周期...：其他可选参数三、使用方法1. 导入数据首先需要导入时间序列数据，可以使用read.csv等函数将csv文件导入为data.frame格式，再使用ts函数将其转换为时间序列格式。

2. 确定模型阶数确定ARIMA模型的阶数是非常重要的。

可以通过绘制自相关图ACF 和偏自相关图PACF来辅助判断。

如果ACF在滞后p处截尾，而PACF在滞后q处截尾，则可以考虑使用ARIMA(p,d,q)模型。

3. 拟合模型使用arima函数拟合ARIMA模型，并将结果保存在一个对象中。

例如：model <- arima(x, order = c(p, d, q), seasonal = c(P, D, Q))其中x是时间序列数据，p、d、q和P、D、Q分别表示ARIMA模型的阶数和周期。

4. 模型诊断拟合模型后，需要对其进行诊断。

可以使用checkresiduals函数检查残差是否符合正态分布和白噪声等假设。

如果残差不符合假设，则需要重新调整模型。

5. 预测未来值使用forecast函数可以预测未来的时间序列值。

例如：forecast(model, h = n)其中h表示预测的步数，n表示时间序列数据的长度。

四、示例以下是一个简单的ARIMA模型示例：1. 导入数据data <- read.csv("data.csv")ts_data <- ts(data$y, start = c(2010, 1), frequency = 12)2. 确定模型阶数acf(ts_data)pacf(ts_data)由自相关图和偏自相关图可以看出，ACF在1处截尾，而PACF在2处截尾，因此可以使用ARIMA(1,0,2)模型。

R语言arima模型时间序列分析报告(附代码数据)【原创】定制撰写数据分析可视化项目案例调研报告（附代码数据）有问题到淘宝找“大数据部落”就可以了R语言arima模型时间序列分析报告library(openxlsx)data=read.xlsx("hs300.xlsx")XXX收盘价(元)`date=data$日期date=as.Date(as.numeric(date),origin="1899-12-30")#1998-07-05#绘制时间序列图plot(date,timeseries)timeseriesdiff<-diff(timeseries,differences=1)plot(date[-1],timeseriesdiff)【原创】定制撰写数据分析可视化项目案例调研报告（附代码数据）有问题到淘宝找“大数据部落”就可以了#时间序列分析之ARIMA模型预测#我们可以通过键入下面的代码来得到时间序列（数据存于“timeseries”）的一阶差分，并画出差分序列的图:#时间序列分析之ARIMA模型预测#从一阶差分的图中可以看出，数据仍是不平稳的。

我们继续差分。

【原创】定制撰写数据分析可视化项目案例调研报告（附代码数据）有问题到淘宝找“大数据部落”就可以了#时间序列分析之ARIMA模型预测#二次差分（上面）后的时间序列在均值和方差上确实看起来像是平稳的，随着时间推移，时间序列的水平和方差大致保持不变。

因此，看起来我们需要对data进行两次差分以得到平稳序列。

#第二步，找到合适的ARIMA模型#如果你的时间序列是平稳的，或者你通过做n次差分转化为一个平稳时间序列，接下来就是要选择合适的ARIMA模型，这意味着需要寻找ARIMA(p,d,q)中合适的p值和q值。

为了得到这些，通常需要检查[平稳时间序列的（自）相关图和偏相关图。

#我们使用R中的“acf()”和“pacf”函数来分别（自）相关图和偏相关图。

基于ARIMA模型的时间序列预测分析时间序列预测分析是经济学和金融领域的重要应用之一，也是数据分析领域中非常基础的操作。

在实际的运用中，为了准确预测未来的数据趋势，我们必须有一种可靠的方法来对现有的时间序列数据进行建模和预测。

ARIMA模型，作为时间序列模型中的一个经典算法，可以解决这个问题。

ARIMA模型全称为自回归移动平均模型（Autoregressive Integrated Moving Average），是一种基于时间序列的统计分析方法，可以用于对非周期性、平稳时间序列样本的拟合与分析，以及预测其未来表现。

ARIMA模型的应用广泛，包括经济学、金融、气象、医学等领域，是时间序列预测中最常用的模型之一。

ARIMA模型的建立，需要对时间序列数据做许多处理和检验工作。

首先，我们需要检查所处理的时间序列数据是否符合ARIMA模型的假设：平稳性，即时间序列数据在不同时间段内的方差和均值都应该相等。

如果时间序列数据不符合平稳性假设，我们需要进行差分操作，将非平稳时间序列转化为平稳时间序列。

同时，根据检验结果，选择合适的阶数并确定ARIMA模型的系数。

阶数包括自回归阶数、差分阶数、移动平均阶数等，不同阶数的选择会影响ARIMA模型的预测效果。

ARIMA模型的预测目的是预测未来一段时间内的时间序列数据。

在进行模型预测时，我们需要确定预测的区间长度，根据之前的数据，计算需要预测的时间序列数据点所在的时间段内的均值和方差，并依照ARIMA模型的计算公式进行预测。

ARIMA模型在时间序列预测中的应用，已经非常成熟。

但是，ARIMA模型也有一些缺陷。

第一，ARIMA模型对于数据的通常要求非常苛刻，需要平稳且线性的时间序列数据；第二，ARIMA模型仅适用于描述非周期性时间序列数据，对于周期性和复杂时间序列数据，ARIMA模型效果欠佳。

因此，在实际预测中，我们需要针对数据的特点选择不同的方法和模型进行分析，以得到更加准确的预测结果。

⽤R做时间序列分析之ARIMA模型预测昨天刚刚把导⼊数据弄好，今天迫不及待试试怎么做预测，⽹上找的帖⼦跟着弄的。

第⼀步.对原始数据进⾏分析⼀.ARIMA预测时间序列指数平滑法对于预测来说是⾮常有帮助的，⽽且它对时间序列上⾯连续的值之间相关性没有要求。

但是，如果你想使⽤指数平滑法计算出预测区间，那么预测误差必须是不相关的，⽽且必须是服从零均值、⽅差不变的正态分布。

即使指数平滑法对时间序列连续数值之间相关性没有要求，在某种情况下，我们可以通过考虑数据之间的相关性来创建更好的预测模型。

⾃回归移动平均模型（ ARIMA）包含⼀个确定（explicit）的统计模型⽤于处理时间序列的不规则部分，它也允许不规则部分可以⾃相关。

⼆.确定数据的差分ARIMA 模型为平稳时间序列定义的。

因此，如果你从⼀个⾮平稳的时间序列开始，⾸先你就需要做时间序列差分直到你得到⼀个平稳时间序列。

如果你必须对时间序列做 d 阶差分才能得到⼀个平稳序列，那么你就使⽤ARIMA(p,d,q)模型，其中 d 是差分的阶数。

我们以每年⼥⼈裙⼦边缘的直径做成的时间序列数据为例。

从 1866 年到 1911 年在平均值上是不平稳的。

随着时间增加，数值变化很⼤。

下⾯是.dat数据：下⾯进⼊预测。

先导⼊数据：> skirts <- scan("/tsdldata/roberts/skirts.dat",skip=5) #导⼊在线数据，并跳过前5⾏Read 46 items #R控制台显⽰内容，表⽰共读取46⾏数据> skirts<- ts(skirts,start = c(1866)) #设定时间1866开始> plot.ts(skirts) #画出图我们可以通过键⼊下⾯的代码来得到时间序列（数据存于“skirtsts”）的⼀阶差分，并画出差分序列的图: > skirtsdiff<-diff(skirts,differences=1) #⼀阶差分> plot.ts(skirtsdiff) #画图从⼀阶差分的图中可以看出，数据仍是不平稳的。

r语言时间序列拟合在R语言中，我们可以使用`arima`函数来拟合时间序列。

将时间序列数据读取到一个向量或数据框中。

假设我们有一个名为`tsdata`的向量，表示一个时间序列。

然后，我们可以使用`arima`函数来拟合时间序列。

`arima`函数的基本语法如下：```Rfit <- arima(tsdata, order = c(p, d, q))```其中，`tsdata`是时间序列数据，`order`参数指定自回归阶数p、积分阶数d和移动平均阶数q。

根据实际情况，需要根据自己的数据选择合适的阶数。

一种常见的方法是使用自相关图ACF和偏自相关图PACF来确定阶数。

可以使用`acf`和`pacf`函数来绘制这两个图形。

接下来，我们可以使用拟合模型对未来的观测值进行预测。

使用`forecast`函数可以根据已有的观测值和拟合模型预测未来的观测值。

下面是一个完整的例子：```R# 读取时间序列数据tsdata <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)# 拟合时间序列fit <- arima(tsdata, order = c(1, 0, 0))# 绘制自相关图acf(tsdata)# 绘制偏自相关图pacf(tsdata)# 预测未来观测值forecast_values <- forecast(fit, h = 5) # h表示预测的步长# 输出预测结果print(forecast_values)```这将输出拟合模型的参数估计和预测的未来观测值。

一、概述ARIMA模型（自回归移动平均模型）是一种时间序列分析模型，用于预测和分析时间序列数据的趋势和季节性变动。

在ARIMA模型中，残差检验是非常重要的，用来验证模型的拟合效果和预测精度。

本文将使用R语言来进行ARIMA模型的残差检验，以期验证模型的有效性和稳健性。

二、ARIMA模型简介ARIMA模型是由自回归（AR）和移动平均（MA）两部分组成的，其中AR部分用来刻画时间序列数据的自相关性，MA部分用来刻画时间序列数据的移动平均性，而I部分则用来描述时间序列数据的差分性。

在R语言中，我们可以使用arima函数来构建ARIMA模型，其基本形式为：```model <- arima(data, order=c(p, d, q))```其中，data为时间序列数据，p为自回归项数量，d为差分阶数，q 为移动平均项数量。

三、残差检验方法残差检验是用来验证模型的拟合效果和预测精度的重要手段，通常包括自相关性检验、正态性检验和异方差性检验三个方面。

1. 自相关性检验自相关性检验用来验证模型的残差是否存在自相关性，常用的方法有Ljung-Box检验和Durbin-Watson检验。

在R语言中，我们可以使用acf函数和Box.test函数来进行自相关性检验。

2. 正态性检验正态性检验用来验证模型的残差是否符合正态分布，常用的方法有QQ图和Shapiro-Wilk检验。

在R语言中，我们可以使用qqnorm 函数和qqline函数来进行QQ图的绘制，使用shapiro.test函数来进行Shapiro-Wilk检验。

3. 异方差性检验异方差性检验用来验证模型的残差是否存在异方差性，常用的方法有Breusch-Pagan检验和White检验。

在R语言中，我们可以使用bptest函数和ncvTest函数来进行异方差性检验。

四、使用R语言进行ARIMA模型残差检验下面我们将使用R语言来演示如何进行ARIMA模型的残差检验。

r语言arima函数参数R语言中的arima函数是用于拟合自回归移动平均模型（ARIMA）的函数。

ARIMA模型是一种常用的时间序列分析方法，用于预测未来的观测值。

arima函数有多个参数，下面将逐个介绍这些参数的含义和用法。

## 参数1: xx是一个时间序列向量或者一个包含时间序列的矩阵。

它是我们要拟合ARIMA模型的数据。

## 参数2: orderorder是一个长度为3的向量，表示ARIMA模型中自回归(p)、差分(d)和移动平均(q)部分的阶数。

order=c(1,1,0)表示拟合一个一阶差分自回归移动平均模型。

## 参数3: seasonalseasonal是一个长度为4的向量，表示季节性部分的阶数。

seasonal=c(0,1,1,4)表示在每个季度进行一次一阶差分操作，并且使用一个一阶差分移动平均过程。

## 参数4: include.meaninclude.mean是一个逻辑值，表示是否在ARIMA模型中包含均值项。

默认情况下，include.mean为TRUE，即包含均值项。

## 参数5: methodmethod是用于估计ARIMA模型参数的方法。

常见的方法有“CSS-ML”（条件最大似然估计）和“CSS”（条件和平方误差）。

默认情况下，method为“CSS-ML”。

## 参数6: optim.controloptim.control是一个控制优化算法的参数。

可以通过optim.control 函数设置参数的值，例如控制迭代次数、收敛容限等。

## 参数7: kappakappa是一个正则化参数，用于减小模型中的过拟合。

默认情况下，kappa为0。

## 参数8: xregxreg是一个可选的外部回归变量矩阵。

如果提供了xreg，则ARIMA模型中会包含这些外部回归变量。

## 参数9: testtest是一个逻辑值，表示是否进行残差诊断检验。

默认情况下，test为FALSE，即不进行残差诊断检验。