编译原理 龙书 第二版 第4章

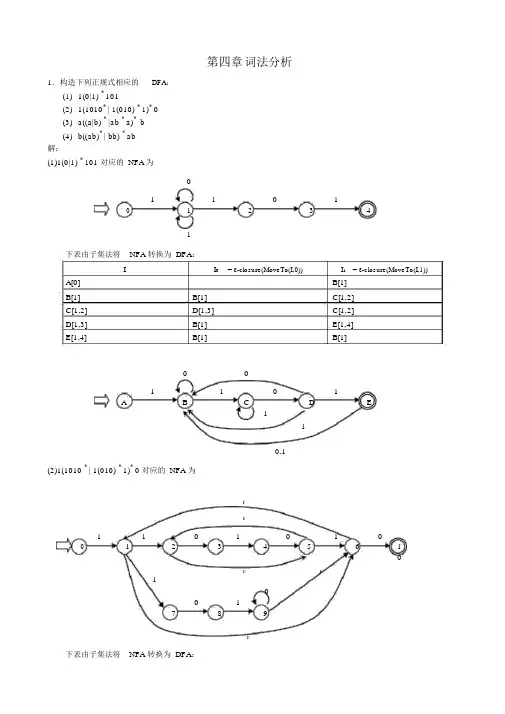
第四章词法分析1．构造下列正规式相应的DFA：(1)1(0|1) * 101(2)1(1010* | 1(010) * 1)* 0(3)a((a|b) * |ab * a)* b(4)b((ab)* | bb) * ab解：(1)1(0|1) * 101 对应的 NFA为1101012341下表由子集法将NFA 转换为 DFA：I I0=ε-closure(MoveTo(I,0))I1=ε-closure(MoveTo(I,1))A[0]B[1]B[1]B[1]C[1,2]C[1,2]D[1,3]C[1,2]D[1,3]B[1]E[1,4]E[1,4]B[1]B[1]001101A B C D E110,1(2)1(1010 * | 1(010) * 1)* 0 对应的 NFA 为εε1101010 01234561εε101978ε下表由子集法将NFA 转换为 DFA：I I=ε-closure(MoveTo(I,0))I1= ε-closure(MoveTo(I,1))A[0]B[1,6]B[1,6]C[10]D[2,5,7]C[10]D[2,5,7]E[3,8]B[1,6]E[3,8]F[1,4,6,9] F[1,4,6,9]G[1,2,5,6,9,10]D[2,5,7]G[1,2,5,6,9,10]H[1,3,6,9,10]I[1,2,5,6,7] H[1,3,6,9,10]J[1,6,9,10]K[2,4,5,7] I[1,2,5,6,7]L[3,8,10]I[1,2,5,6,7] J[1,6,9,10]J[1,6,9,10]D[2,5,7]K[2,4,5,7]M[2,3,5,8]B[1,6]L[3,8,10]F[1,4,6,9] M[2,3,5,8]N[3]F[1,4,6,9] N[3]O[4]O[4]P[2,5]P[2,5]N[3]B[1,6]1L111111010B I KA D E F M00110 00C11G H J101NP O(3)a((a|b) * |ab * a)* b(略 )(4)b((ab) * | bb) * ab(略 )2．已知 NFA=（ {x,y,z},{0,1},M,{x},{z} ）其中：M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ ,M(z,1)={y},构造相应的 DFA。

Fa | (E)
描述IF语句的二义文法
<stmt>→ if <expr> then <stmt>
| if <expr> then <stmt> else <stmt>
| other
(4.7)
根据if语句中else与then配对情况将其分为配对 的语句和不配对的语句两类。
上述if语句的文法没有对这两个不同的概念加 以区分，只是简单地将它们都定义为<stmt>， 从而导致该文法是二义性的。
if e1 then if e2 then s1 else s2的语法树
二义性（ambiquity)的定义
对于文法G，如果L(G)中存在一个具有两 棵或两棵以上分析树的句子，则称G是二 义性的。也可以等价地说：如果L(G)中
存在一个具有两个或两个以上最左(或最
右)推导的句子，则G是二义性文法。 如果一个文法G是二义性的，假设
2021/4/25
计算机学院 辛明影
E E→a a
E
E→a a
一棵树！
9
关于语法树的几点结论
短语：一棵子树的 所有叶子自左至右 排列起来形成一个 相对于子树根的短 语。教材p50
短语：
a, a,a,
a+a, a+a*a
2021/4/25
E E* E E +E
a
aa
10
关于语法树的几点结论
直接短语：仅有父子两 代的一棵子树，它的 所有叶子自左至右排列 起来所形成的符号串。
对于一般情况而言，若某一文法G的产生 式具有如下形式：
A→A α1| A α2 |…| A αm| β1| β2|…| βn

为一个句子(合式程序)。
单词符号
语法分
源程序 词法分
语法分 析树 编译程序
析器 取下一单词 析器
后续部分
... 符号表
• 语法分析的方法： • 自下而上分析法(Bottom-up)
• 基本思想：从输入串开始，逐步进行“归约”，
直到文法的开始符号。即从树末端开始，构造语法 树。所谓归约，是指根据文法的产生式规则，把产 生式的右部替换成左部符号。
FIRST( i)∩FOLLOW(A)= i=1,2,...,n
如果一个文法G满足以上条件，则称该文法G为L L(1)文法。
• 对于一个满足上述条件的文法，可以对其输入串进行有效的无回溯的自上而下分析。假 设要用非终结符A进行匹配，面临的输入符号为a，A的所有产生式为 A→ 1 | 2 | … | n 1. 若aFIRST( i)，则指派 i执行匹配任务；
Q→Sab | ab | b • 现在的Q不含直接左递归，把它代入到S的有关候选后，S变成
S→Sabc | abc | bc | c
• 例 考虑文法G(S)
S→Qc|c Q→Rb|b R→Sa|a
• S变成
S→Sabc | abc | bc | c
• 消除S的直接左递归后： S→abcS | bcS | cS S→abcS | Q→Sab |ab | b R→Sa|a
P P
含有左递归的文法将使自上而下的分 析陷入无限循环。
4.3 LL(1)分析法
• 构造不带回溯的自上而下分析算法 • 要消除文法的左递归性 • 克服回溯
4.3.1 左递归的消除
• 直接消除见诸于产生式中的左递归：假定关于非终结符P的规则为 P→P |
其中不以P开头。 我们可以把P的规则等价地改写为如下的非直接左递归形式：

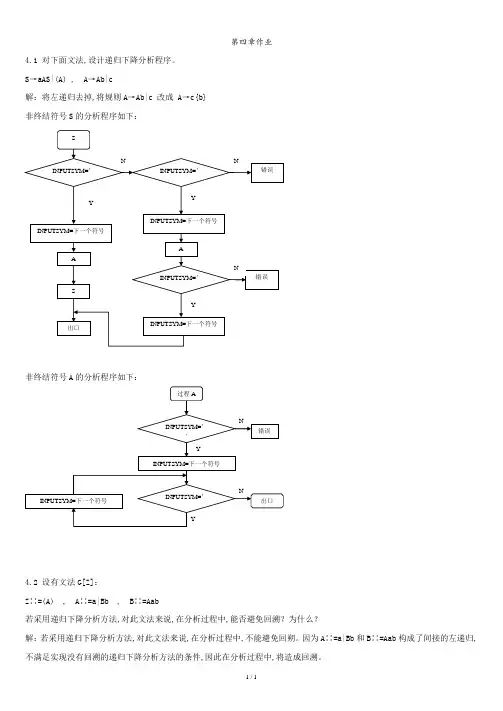
第四章作业4.1 对下面文法,设计递归下降分析程序。

S→aAS|(A) , A→Ab|c解：将左递归去掉,将规则A→Ab|c 改成 A→c{b}非终结符号S的分析程序如下：非终结符号A的分析程序如下：4.2 设有文法G[Z]：Z∷=(A) , A∷=a|Bb , B∷=Aab若采用递归下降分析方法,对此文法来说,在分析过程中,能否避免回溯？为什么？解：若采用递归下降分析方法,对此文法来说,在分析过程中,不能避免回朔。

因为A∷=a|Bb和B∷=Aab构成了间接的左递归,不满足实现没有回溯的递归下降分析方法的条件,因此在分析过程中,将造成回溯。

4.3 若有文法如下,设计递归下降分析程序。

<语句>→<语句><赋值语句>|ε<赋值语句>→ID=<表达式><表达式>→<项>|<表达式>＋<项>|<表达式>－<项><项>→<因子>|<项>*<因子>|<项>/<因子><因子>→ID|NUM|(<表达式>)解：首先,去掉左递归（1）<语句>→<语句><赋值语句>|ε改为： <语句>→{<赋值语句>}（3）<表达式>→<项> | <表达式> + <项> | <表达式> - <项> 改为：<表达式>→<项>{（+ | -）<项>}（4）<项>→<因子> | <项> * <因子> | <项> / <因子>改为：<项>→<因子>{（* | /）<因子>}则文法变为：<语句>→{<赋值语句>}<赋值语句>→ID=<表达式><表达式>→<项>{（+ | -）<项>}<项>→<因子>{（* | /）<因子>}<因子>→ID|NUM|(<表达式>)非终结符号 <语句>→{<赋值语句>} 的分析程序如下：非终结符号 <赋值语句>→ID=<表达式> 的分析程序如下：非终结符号<表达式>→<项>{（+ | -）<项>} 的分析程序如下：非终结符号 <项>→<因子>{（* | /）<因子>} 的分析程序如下：非终结符号 <因子>→ID|NUM|(<表达式>) 的分析程序如下：4.4 有文法G[A]：A::=aABe|ε,B::=Bb|b（1）求每个非终结符号的FOLLOW集。

S-> S’ S’->(S)SS’| First( (S)SS’) = { （ } Follow(S)=Follow(S’)= { (, ),$ }
预测分析表
非终结符 S （ S->S’ ） S->S’ $ S->S’
S’
S’->(S)SS’
S’->
S’->
S’->
冲突
仔细分析后，发现该文法 S->S(S)S| 是二义性文法。 二义性文法不可能是LL(1)文法。 例如：( ) ( )
S->aS’ S’->aS’AS’|Ɛ A->+|*
First(S) = First(aS’)={a} First(S’)= First(aS’AS’) ∪ First(Ɛ)= {a} ∪{Ɛ}= {a, Ɛ} First(A) = { +,*}
Follow(S) ={$} 因为 S->aS’，所以把Follow(S)加入到Follow(S’)中。 因为 S’->aS’AS’的第一个S’ ，所以把First(AS’)={+,*}加入到Follow(S’)中。 因为 S’->aS’AS’的第二个S’ ，所以Follow(S)加入到Follow(S’)中。 所以，Follow(S’)= {$, +,*} 对 S’->aS’AS’的A ，当A后面的S’推导出非空时，把First(S’)-{Ɛ}={a}加入到Follow(A)中。 对 S’->aS’AS’的A ，当A后面的S’推导出空时，把Follow(S’)={$,+,*}加入到Follow(A)中。 所以，Follow(A)= {a, +,*,$} 对于S’->aS’AS’|Ɛ，因为First(aS’AS’) ∩Follow(S’)={a} ∩{$,+,*}=空集,所以没有冲突。 对于A->+|*，因为First(+) ∩First(*)={+} ∩{*}=空集,所以没有冲突。 所以该文法是LL(1)文法。

type array[simple] of type {注:A=type,a=array,
type→array[simple ] of type}
array[num dotdot num] of type
{注:A=simple, a=num
simple→num dotdot num }
array[num dotdot num] of simple
aSbAa (SbA) aSbbaa (ba) aabbaa (a)
S
a
A
S
S
b
A
a
aபைடு நூலகம்
ba
精品文档
7
4.2预测分析器 4 .2 .1 预测分析 预测分析的原理 4 .2 .2 递归预测分析器的构造 用一组递归过程实现预测分析，产生式的状 态转换图可作为编写递归过程的兰图。 4 .2 .3 非递归预测分析器的构造—LL(1) 对于每一步分析，分析表项M[A,a]=‘A ’ 表示：面对非终结符号精A品和文档向前看符号a应选 8
A 1 2 ... n
i,j(1 i,j n i<>j),从 i推导出来的第一个 终结符号集合（称为FIRST( i) ）和从 j推 导出来的第一个终结符号集合（称为FIRST( j) ）不相交，即， FIRST( i) FIRST( j)=
精品文档
12
定义4.1 令G[S]=(VT,VN,S,P),则
FIRST( )= a a*… a VT
例4.2 文法G[S]，其产生式如下:
S→aA|d A→bAS|ε （4.2)
若 w=abd，则构造最左推导的过程如下:
S aA {注：A=S，a=a，S→aA}
abAS {注：A=A，a=b，A→ bAS}

b∶=10; end (q); procedure s; var c,d; procedure r;
var e,f;
begin (r)
call q;
end (r); begin (s)
call r; end (s);
begin (p) call s;
end (p);
begin (main)
第６题 计算机执行用高级语言编写的程序有哪些途径?它们之间的主要区别是什么?
答案：计算机执行用高级语言编写的程序主要途径有两种，即解释与编译。 像 Basic 之类的语言，属于解释型的高级语言。它们的特点是计算机并不事先对高级语
言进行全盘翻译，将其变为机器代码，而是每读入一条高级语句，就用解释器将其翻译为一 条机器代码，予以执行，然后再读入下一条高级语句，翻译为机器代码，再执行，如此反 复。
CAL L A 调用过程，完成填写静态链、动态链、返回地址，给出被调用过程的基地址值，送入基址 寄存器 B 中，目标程序的入口地址 A 的值送指令地址寄存器 P 中，使指令从 A 开始执 行。 第 6题
给出对 PL/0 语言作如下功能扩充时的语法图和 EBNF 的语常前端包括词法分析、语法分析、语义分析和中间代码生成这些阶 段，某些优化工作也可在前端做，也包括与前端每个阶段相关的出错处理工作和符 号表管理等工作。 （5） 后端：指那些依赖于目标机而一般不依赖源语言，只与中间代码有关的那些阶段， 即目标代码生成，以及相关出错处理和符号表操作。 （6） 遍：是对源程序或其等价的中间语言程序从头到尾扫视并完成规定任务的过程。
(2) 扩充 repeat 语句的语法图为：
EBNF 的语法描述为： 〈 重复语句〉::= repeat〈语句〉{；〈语句第 3 章 文法和语言

Lw.《编译原理》课后习题答案第一章第1章引论第1题解释下列术语：（1）编译程序（2）源程序（3）目标程序（4）编译程序的前端（5）后端（6）遍答案：（1）编译程序：如果源语言为高级语言，目标语言为某台计算机上的汇编语言或机器语言，则此翻译程序称为编译程序。

（2）源程序：源语言编写的程序称为源程序。

（3）目标程序：目标语言书写的程序称为目标程序。

（4）编译程序的前端：它由这样一些阶段组成：这些阶段的工作主要依赖于源语言而与目标机无关。

通常前端包括词法分析、语法分析、语义分析和中间代码生成这些阶段，某些优化工作也可在前端做，也包括与前端每个阶段相关的出错处理工作和符号表管理等工作。

（5）后端：指那些依赖于目标机而一般不依赖源语言，只与中间代码有关的那些阶段，即目标代码生成，以及相关出错处理和符号表操作。

（6）遍：是对源程序或其等价的中间语言程序从头到尾扫视并完成规定任务的过程。

第2题一个典型的编译程序通常由哪些部分组成？各部分的主要功能是什么？并画出编译程序的总体结构图。

答案：一个典型的编译程序通常包含8个组成部分，它们是词法分析程序、语法分析程序、语义分析程序、中间代码生成程序、中间代码优化程序、目标代码生成程序、表格管理程序和错误处理程序。

其各部分的主要功能简述如下。

词法分析程序：输人源程序，拼单词、检查单词和分析单词，输出单词的机内表达形式。

语法分析程序：检查源程序中存在的形式语法错误，输出错误处理信息。

语义分析程序：进行语义检查和分析语义信息，并把分析的结果保存到各类语义信息表中。

中间代码生成程序：按照语义规则，将语法分析程序分析出的语法单位转换成一定形式的中间语言代码，如三元式或四元式。

中间代码优化程序：为了产生高质量的目标代码，对中间代码进行等价变换处理。

盛威网（）专业的计算机学习网站1《编译原理》课后习题答案第一章目标代码生成程序：将优化后的中间代码程序转换成目标代码程序。

表格管理程序：负责建立、填写和查找等一系列表格工作。

也称基地址。 SL： 静态链，指向定义该过程的直接外过程（或主程序）运行时最新数据段的基地址，
用以引用非局部（包围它的过程）变量时，寻找该变量的地址。 DL： 动态链，指向调用该过程前正在运行过程的数据段基地址，用以过程执行结束释放
数据空间时，恢复调用该过程前运行栈的状态。 RA： 返回地址，记录调用该过程时目标程序的断点，即调用过程指令的下一条指令的地
编译程序大致有哪几种开发技术？
答案：
（1）自编译：用某一高级语言书写其本身的编译程序。 （2）交叉编译：A 机器上的编译程序能产生 B 机器上的目标代码。 （3）自展：首先确定一个非常简单的核心语言 L0，用机器语言或汇编语言书写出它的编
译程序 T0，再把语言 L0 扩充到 L1，此时 L0⊂ L1 ,并用 L0 编写 L1 的编译程序 T1，再把语 言 L1 扩充为 L2，有 L1 ⊂ L2 ,并用 L1 编写 L2 的编译程序 T2，……，如此逐步扩展下 去， 好似滚雪球一样，直到我们所要求的编译程序。 （4）移植：将 A 机器上的某高级语言的编译程序搬到 B 机器上运行。
(main).
答案： 程序执行到赋值语句 b∶=10 时运行栈的布局示意图为：
1
《编译原理》课后习题答案第二章
第 3题 写出题 2 中当程序编译到 r 的过程体时的名字表 table 的内 容。
name
kind
level/val
adr
size
答案：
题 2 中当程序编译到 r 的过程体时的名字表 table 的内容为：
盛威网（）专业的计算机学习网站
2
《编译原理》课后习题答案第一章
合实现方案，即先把源程序翻译成较容易解释执行的某种中间代码程序，然后集中解释执行 中间代码程序，最后得到运行结果。

3)
First( A' ) Follow ( A' ) {d , } {), b}
4.4(2)
见课后答案 规则见课本P66
问题？
Select( E gAf ) Select( E c) First( gAf ) Frist(c) {g} {c}
4.2
对下面的文法G： E→TE’ E’→+TE’|ε T→FT’ T’→*FT’|ε F→(E)|id (1)计算这个文法的每个非终结符的FIRST和FOLLOW。 (2)证明这个文法是LL(1)的。 (3)构造它的预测分析表。 (4)构造它的递归下降分析程序。
第四章习题
4.1 4.2 4.3 4.4
4.1
1、考虑下面文法G[A]： A→BCc|gDB B→bCDE|ε C→DaB|ca D→dD|ε E→gAf|c （1）FIRST集和FOLLOW集 （2）是否是LL（1）文法。
4.1(1) First集
First( A) First( BCc) First( gDB) First( B) \ { } First(C ) {g} {b} First( D) \ { } {a} First(ca) {g} {b} {d } {a} {c} {g} {a, b, c, d , g}
E’→ε T→FT ’ T’→ε F→idFra bibliotekE’→ε
T’→ε
4.2(4)
规则见课本P66 见课后答案 E→TE’ T→FT’ F→(E)|id E’→+TE’|ε T’→*FT’|ε
4.3
文法G[S]: S→A A→B|AiB B→C|B+C C→)A*|( 1)改写为LL(1)文法 2)求改写后的文法的每个非终结符的First集和Follow集 3)构造相应的预测分析表

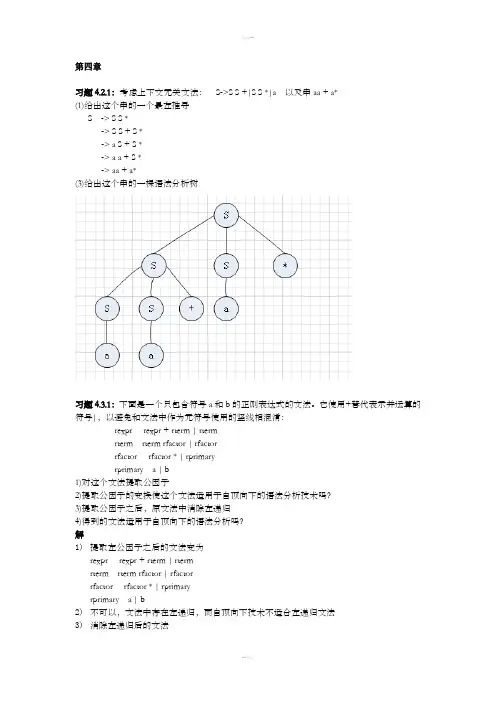
第四章习题4.2.1：考虑上下文无关文法：S->S S +|S S *|a 以及串aa + a*(1)给出这个串的一个最左推导S -> S S *-> S S + S *-> a S + S *-> a a + S *-> aa + a*(3)给出这个串的一棵语法分析树习题4.3.1：下面是一个只包含符号a和b的正则表达式的文法。

它使用+替代表示并运算的符号|，以避免和文法中作为元符号使用的竖线相混淆：rexpr rexpr + rterm | rtermrterm rterm rfactor | rfactorrfactor rfactor * | rprimaryrprimary a | b1)对这个文法提取公因子2)提取公因子的变换使这个文法适用于自顶向下的语法分析技术吗？3)提取公因子之后，原文法中消除左递归4)得到的文法适用于自顶向下的语法分析吗？解1)提取左公因子之后的文法变为rexpr rexpr + rterm | rtermrterm rterm rfactor | rfactorrfactor rfactor * | rprimaryrprimary a | b2)不可以，文法中存在左递归，而自顶向下技术不适合左递归文法3)消除左递归后的文法rexpr -> rterm rexpr’rexpr’-> + rterm rexpr’|εrterm-> rfactor rterm’rterm’-> rfactor rterm’|εrfactor-> rprimay rfactor’rfactor’-> *rfactor’|εrprimary-> a | b4)该文法无左递归，适合于自顶向下的语法分析习题4.4.1：为下面的每一个文法设计一个预测分析器，并给出预测分析表。

可能要先对文法进行提取左公因子或消除左递归(3)S->S(S)S|ε(5)S->(L)|a L->L,S|S解(3)①消除该文法的左递归后得到文法S->S’S’->(S)SS’|εFIRST(S)={(,ε} FOLLOW(S)={),$}FIRST(S’)={(,ε} FOLLOW(S’)={),$}③(5)①消除该文法的左递归得到文法S->(L)|aL->SL’L’->,SL’|ε用类Pascal语言的一个预测分析器：PROCEDURE SBEGINif (lookahead==’(')THEN BEGINmatch ('(');L;match (')');END;ELSE IF (lookahead=='a')THEN match('a')ELSE errorEND;PROCEDURE L;BEGINS;WHILE (lookahead =='，');BEGINmatch ('，');S;END;END;②计算FIRST与FOLLOW集合FIRST(S)={(,a} FOLLOW(S)={ ),, ,$}FIRST(L)={(,a} FOLLOW(L)={ ) }FIRST(L’)={,,ε} FOLLOW(L’)={ ) }③非终结符号输入符号(),a$ S S->(L)S->aL L->SL’L->SL’L’L’->εL’->,SL’习题4.4.4 计算练习4.2.2的文法的FIRST和FOLLOW集合3)S S(S)S|ε5)S(L)|a,L L,S|S解：3)FIRST(S)={ ε,( } FOLLOW(S)={ (,),$ }5)FIRST(S)={ (,a } FOLLOW(S)={ ),,,$ }FIRST(L)={ (,a } FOLLOW(L)={ ),, }习题4.6.2 为练习4.2.1中的增广文法构造SLR 项集，计算这些项集的GOTO 函数，给出这个文法的语法分析表。

第四章部分习题解答Aho：《编译原理技术与工具》书中习题（Aho）4.1 考虑文法S → ( L ) | aL → L, S | Sa)列出终结符、非终结符和开始符号解：终结符：(、)、a、，非终结符：S、L开始符号：Sb)给出下列句子的语法树i)(a, a)ii)(a, (a, a))iii)(a, ((a, a), (a, a)))c)构造b)中句子的最左推导i)S(L)(L, S) (S, S) (a, S) (a, a)ii)S(L)(L, S) (S, S) (a, S) (a, (L)) (a, (L, S)) (a, (S, S)) (a, (a, S) (a, (a, a))iii)S(L)(L, S) (S, S) (a, S) (a, (L)) (a, (L, S)) (a, (S, S)) (a, ((L), S)) (a, ((L, S), S)) (a, ((S, S), S)) (a, ((a, S), S))(a, ((a, a), S)) (a, ((a, a), (L))) (a, ((a, a), (L, S))) (a, ((a, a), (S, S))) (a, ((a, a), (a, S))) (a, ((a, a), (a, a)))d)构造b)中句子的最右推导i)S(L)(L, S) (L, a) (S, a) (a, a)ii)S(L)(L, S) (L, (L)) (L, (L, S)) (L, (L, a)) (L, (S, a)) (L, (a, a)) (S, (a, a)) (a, (a, a))iii)S(L)(L, S) (L, (L)) (L, (L, S)) (L, (L, (L))) (L, (L, (L, S))) (L, (L, (L, a))) (L, (L, (S, a))) (L, (L, (a, a))) (L, (S,(a, a))) (L, ((L), (a, a))) (L, ((L, S), (a, a))) (L, ((L, a), (a,a))) (L, ((S, a), (a, a))) (L, ((a, a), (S, S))) (S, ((a, a), (a,a))) (a, ((a, a), (a, a)))e)该文法产生的语言是什么解：设该文法产生语言（符号串集合）L，则L = { (A1, A2, …, A n) | n是任意正整数，A i=a，或A i∈L，i是1～n之间的整数}（Aho）4.2考虑文法S→aSbS | bSaS |a)为句子构造两个不同的最左推导，以证明它是二义性的S aSbS abS abaSbS ababS ababS aSbS abSaSbS abaSbS ababS ababb)构造abab对应的最右推导S aSbS aSbaSbS aSbaSb aSbab ababS aSbS aSb abSaSb abSab ababc)构造abab对应语法树d)该文法产生什么样的语言？解：生成的语言：a、b个数相等的a、b串的集合（Aho）4.3 考虑文法bexpr→bexpr or bterm | btermbterm→bterm and bfactor | bfactorbfactor→not bfactor | ( bexpr ) | true | falsea)试为句子not ( true or false)构造分析树解：b)试证明该文法产生所有布尔表达式证明：一、首先证明文法产生的所有符号串都是布尔表达式变换命题形式——以bexpr、bterm、bfactor开始的推导得到的所有符号串都是布尔表达式最短的推导过程得到true、false，显然成立假定对步数小于n的推导命题都成立考虑步数等于n 的推导，其开始推导步骤必为以下情况之一bexpr bexpr or btermbexpr btermbterm bterm and bfactorbexpr bfactorbfactor not bfactorbfactor ( bexpr )而后继推导的步数显然<n，因此由归纳假设，第二步句型中的NT推导出的串均为布尔表达式，这些布尔表达式经过or、and、not运算或加括号，得到的仍是布尔表达式因此命题一得证。

第4章习题解答：1，2，3，4 解答略！5. 解答：(1)× (2)√ (3)× (4)√ (5)√ (6)√(7)×(8)×6. 解答：(1)A：④ B：③ C：③ D：④ E：②(2)A：④ B：④ C：③ D：③ E：②7.解答：(1) 消除给定文法中的左递归，并提取公因子：bexpr→bterm {or bterm }bterm→bfactor {and bfactor}bfactor→not bfactor | (bexpr) | true |false(2) 用类C语言写出其递归分析程序:void bexpr();{bterm();WHILE(lookahead =='or') { match ('or');bterm();}}void bterm();{bfactor();WHILE(lookahead =='and'){ match ('and');bfactor();}} void bfactor();{if (llokahead=='not') then {match ('not');bfactor();}else if(lookahead=='(') then {match (‘(');bexpr();match(')');}else if(lookahead =='true')then match ('true) else if (lookahead=='false')then match ('false');else error;}8. 解答：消除所给文法的左递归，得G'：S →(L)|aL → SL'L'→ ,SL' |实现预测分析器的不含递归调用的一种有效方法是使用一张分析表和一个栈进行联合控制，下面构造预测分析表：根据文法G'有：First(S) = { ( , a ) Follow(S) = { ) , , , #}First(L) = { ( , a ) Follow(L) = { ) }First(L') = { ,} Follow(L') = { ) }按以上结果，构造预测分析表M如下：文法G'是LL(1)的，因为它的LL(1)分析表不含多重定义入口。

第四章语义分析和中间代码生成4.1 完成下列选择题：(1) 四元式之间的联系是通过实现的。

a. 指示器b. 临时变量c. 符号表d. 程序变量(2) 间接三元式表示法的优点为。

a. 采用间接码表，便于优化处理b. 节省存储空间，不便于表的修改c. 便于优化处理，节省存储空间d. 节省存储空间，不便于优化处理(3) 表达式(┐A∨B)∧(C∨D)的逆波兰表示为。

a. ┐AB∨∧CD∨b. A┐B∨CD∨∧c. AB∨┐CD∨∧d. A┐B∨∧CD∨(4) 有一语法制导翻译如下所示：S→bAb {print″1″}A→(B {print″2″}A→a {print″3″}B→Aa) {print″4″}若输入序列为b(((aa)a)a)b，且采用自下而上的分析方法，则输出序列为。

a. 32224441 b. 34242421c. 12424243d. 34442212【解答】(1) b (2) a (3) b (4) b4.2 何谓“语法制导翻译”？试给出用语法制导翻译生成中间代码的要点，并用一简例予以说明。

【解答】语法制导翻译(SDTS)直观上说就是为每个产生式配上一个翻译子程序(称语义动作或语义子程序)，并且在语法分析的同时执行这些子程序。

也即在语法分析过程中，当一个产生式获得匹配(对于自上而下分析)或用于归约(对于自下而上分析)时，此产生式相应的语义子程序进入工作，完成既定的翻译任务。

用语法制导翻译(SDTS)生成中间代码的要点如下：(1) 按语法成分的实际处理顺序生成，即按语义要求生成中间代码。

(2) 注意地址返填问题。

(3) 不要遗漏必要的处理，如无条件跳转等。

例如下面的程序段：if (i>0) a=i+e-b*d; else a=0;在生成中间代码时，条件“i>0”为假的转移地址无法确定，而要等到处理“else”时方可确定，这时就存在一个地址返填问题。

此外，按语义要求，当处理完(i>0)后的语句(即“i>0”为真时执行的语句)时，则应转出当前的if语句，也即此时应加入一条无条件跳转指令，并且这个转移地址也需要待处理完else之后的语句后方可获得，就是说同样存在着地址返填问题。

2、主旨：对任何输入串，试图用一切可能的 办法，从开始符号出发，自上而下 地为输入串建立一棵语法树。
4
§4.2自上而下面临的问题
二、举例： 自上而下方法的分析过程本质上
是一种试探过程，是反复使用不同产生 式谋求匹配输入串的过程。
5
§4.பைடு நூலகம்自上而下面临的问题
例：文法 SxAy A**|*
输入串α :x*y
（１）把文法Ｇ的所有ＶＮ按任一种顺序排列成 P1,P2,…,Pn;按此顺序执行； （２）FOR i = 1 To n Do
Begin For j :=1 To i-1 Do 把形如PiPjγ的规则改写成 Piδ1γ|δ2γ|…|δkγ 其中Pjδ1|δ2|…|δk是关 于Pj的所有规则； 消除关于Pi规则的直接左递归性
Ｆ Ｔ’ + T
iℇ
Ｅ’ ℇ
F（E） ｜i
F
Ｔ’
输入串：ｉ＋ｉ； 如右图所示
ｉ
ℇ
19
§4.３LL(1)分析法
２、由上分析是不是就意味着：当非终结符 Ａ面临输入符号ａ，且ａ不属于Ａ的任意候 选首符集，但Ａ的某个候选首符集包含ℇ时， 就一定可以使Ａ自动匹配？
分析：只有当ａ是在文法的某个句型中允许跟在Ａ 后的终结符时，才可能允许Ａ自动匹配，否则，ａ 在这里的出现是一种语法错误。
14
§4.３LL(1)分析法
２、当不得回溯时，对文法有什么要求？
∀ 非终结符Ａ的各个候选的首符集的交集均为空。
分析：Ａα
first(α)={a|α⇒* a…,a∈ VT} 若α⇒* ℇ ,则规定ℇ∈ first(α)
即:first(α)是α的所有可能推导的开头终结符或可能
的ℇ。
此时，当要求A匹配输入串时，A根据它所面临的第

expression expression + term expression expression – term expression term term term * factor term term / factor term factor factor ( expression ) factor id
码生成 支持语言的演化和迭代
3
语法分析器的作用
• 基本作用
– 从词法分析器获得词法单元的序列，确认该序列是否 可以由语言的文法生成
– 对于语法错误的程序，报告错误信息 – 对于语法正确的程序，生成语法分析树 (简称语法树)
• 通常并不真的生产这棵语法分析树
4
语法分析器的分类
• 通用语法分析器
– 可以对任意文法进行语法分析 – 效率很低，不适合用于编表示形式
– 根结点的标号时文法的开始符号 – 每个叶子结点的标号是非终结符号、终结符号或ε – 每个内部结点的标号是非终结符号 – 每个内部结点表示某个产生式的一次应用
• 内部结点的标号为产生式头，结点的子结点从左到右是产生 式的体
• 树的叶子组成的序列是根的文法符号的一个句型 • 一棵语法分析树可对应多个推导序列，但每颗分
18
词法分析和语法分析的比较
阶段
输入
输出
描述体系
词法分析 源程序符号串 词法单元序列 正则表达式
语法分析 词法单元序列 语法树 上下文无关文法
19
上下文无关文法和正则表达式 (1)
• 上下文无关文法比正则表达式的能力更强
– 所有的正则语言都可以使用文法描述 – 但是一些用文法描述的语言不能用正则表达式描述
| other open_stmt if expr then stmt

第四章部分习题解答Aho：《编译原理技术与工具》书中习题（Aho）4.1 考虑文法S →( L ) | aL →L, S | Sa)列出终结符、非终结符和开始符号解：终结符：(、)、a、，非终结符：S、L开始符号：Sb)给出下列句子的语法树i)(a, a)ii)(a, (a, a))iii)(a, ((a, a), (a, a)))c)构造b)中句子的最左推导i)S⇒(L)⇒(L, S) ⇒(S, S) ⇒(a, S) ⇒(a, a)ii)S⇒(L)⇒(L, S) ⇒(S, S) ⇒(a, S) ⇒(a, (L)) ⇒(a, (L, S)) ⇒(a, (S, S)) ⇒(a, (a, S) ⇒(a, (a, a))iii)S⇒(L)⇒(L, S) ⇒(S, S) ⇒(a, S) ⇒(a, (L)) ⇒(a, (L, S)) ⇒(a, (S, S)) ⇒(a, ((L), S)) ⇒(a, ((L, S), S)) ⇒(a, ((S, S), S)) ⇒(a, ((a, S), S)) ⇒(a, ((a, a), S)) ⇒(a, ((a, a), (L)))⇒(a, ((a, a), (L, S))) ⇒(a, ((a, a), (S, S))) ⇒(a, ((a, a), (a, S))) ⇒(a, ((a, a), (a, a))) d)构造b)中句子的最右推导i)S⇒(L)⇒(L, S) ⇒(L, a) ⇒(S, a) ⇒(a, a)ii)S⇒(L)⇒(L, S) ⇒ (L, (L)) ⇒(L, (L, S)) ⇒(L, (L, a)) ⇒(L, (S, a)) ⇒(L, (a, a)) ⇒(S, (a, a)) ⇒(a, (a, a))iii)S⇒(L)⇒(L, S) ⇒(L, (L)) ⇒(L, (L, S)) ⇒(L, (L, (L))) ⇒(L, (L, (L, S))) ⇒(L, (L, (L,a))) ⇒(L, (L, (S, a))) ⇒(L, (L, (a, a))) ⇒(L, (S, (a, a))) ⇒(L, ((L), (a, a))) ⇒(L, ((L,S), (a, a))) ⇒(L, ((L, a), (a, a))) ⇒(L, ((S, a), (a, a))) ⇒(L, ((a, a), (S, S))) ⇒(S, ((a,a), (a, a))) ⇒(a, ((a, a), (a, a)))e)该文法产生的语言是什么解：设该文法产生语言（符号串集合）L，则L = { (A1, A2, …, A n) | n是任意正整数，A i=a，或A i∈L，i是1～n之间的整数}（Aho）4.2考虑文法S→aSbS | bSaS | εa)为句子构造两个不同的最左推导，以证明它是二义性的S⇒aSbS⇒abS⇒abaSbS⇒ababS⇒ababS⇒aSbS⇒abSaSbS⇒abaSbS⇒ababS⇒ababb)构造abab对应的最右推导S⇒aSbS⇒aSbaSbS⇒aSbaSb⇒aSbab⇒ababS⇒aSbS⇒aSb⇒abSaSb⇒abSab⇒ababc)构造abab对应语法树d)该文法产生什么样的语言？解：生成的语言：a、b个数相等的a、b串的集合（Aho）4.3 考虑文法bexpr→bexpr or bterm | btermbterm→bterm and bfactor | bfactorbfactor→not bfactor | ( bexpr ) | true | falsea)试为句子not ( true or false)构造分析树解：b)试证明该文法产生所有布尔表达式证明：一、首先证明文法产生的所有符号串都是布尔表达式变换命题形式——以bexpr、bterm、bfactor开始的推导得到的所有符号串都是布尔表达式最短的推导过程得到true、false，显然成立假定对步数小于n的推导命题都成立考虑步数等于n 的推导，其开始推导步骤必为以下情况之一bexpr⇒bexpr or btermbexpr⇒btermbterm⇒bterm and bfactorbexpr⇒bfactorbfactor⇒not bfactorbfactor⇒ ( bexpr )而后继推导的步数显然<n，因此由归纳假设，第二步句型中的NT推导出的串均为布尔表达式，这些布尔表达式经过or、and、not运算或加括号，得到的仍是布尔表达式因此命题一得证。